Calculation Methodologies of Complex Permeability for Various Magnetic Materials

Abstract

In order to design power converters and wireless power systems using high-frequency magnetic materials, the magnetic characteristics for the inductors and transformers should be specified in detail w.r.t. the operating frequency. For investigating the complex permeability of the magnetic materials by simply test prototypes, the inductor model-based calculation methodologies for the complex permeability are suggested to find the core loss characteristics in this paper. Based on the measured results of the test voltage V_e, current I_e, and phase difference θ_e, which can be obtained simply by an oscilloscope and a function generator, the real and imaginary permeability can be calculated w.r.t. operating frequency by the suggested calculation methodologies. Such information for the real and imaginary permeability is important to determine the size of the magnetic components and to analyze the core loss. To identify the superiority of the high-frequency magnetic materials, three prototypes for a ferrite core, amorphous core, and nanocrystalline core have been built and verified by experiment. As a result, the ferrite core is superior to the other cores for core loss, and the nanocrystalline core is recommended for compact transformer applications. The proposed calculation for the complex (i.e., real and imaginary) permeability, which has not been revealed in the datasheets, provides a way to easily determine the parameters useful for industrial electronics engineers.

1. Introduction

The magnetic materials are essential for the magnetic energy storage of various applications such as power converters and wireless power transfer systems. As low operating frequency applications (50 Hz/60 Hz), silicon steel sheet materials are widely used for the utility transformers or pole transformers in various industries [1]. On the other hands, most electric devices are designed based on the high-frequency magnetic materials, operating at several tens of kHz high operating frequency, for compact size of the magnetic components [2,3]. In general, high-frequency ferrite cores are highly preferred due to high-frequency characteristics, low core loss, and easy manufacturing [3]. Recently, amorphous cores, which are formed by multi layers of laminated cores, are also the alternative solutions for 60 Hz–100 kHz of operating frequency applications [4]. Such amorphous cores have a high saturated magnetic field B_sat (≈1.5 T) and can reduce the eddy loss due to ultra-thin-laminated Fe-based plates [1,4]. In order to miniaturize the magnetic materials, Nanocrystalline alloy, which is usually composed of Fe, Si, B with the other chemical combinations, can be utilized over 1 kHz–100 kHz of operating frequency applications [5]. Such magnetic materials mentioned above have their own merits and demerits for various applications. Thus, by referring to inherent magnetic characteristics of the magnetic materials, the most appropriate magnetic materials should be selected, according to the operating frequency of its applications.

In order to design the magnetic components applied to industrial applications, the major characteristics of the magnetic materials, e.g., saturated magnetic flux density, initial permeability, Curie temperature, power loss [mW/cm³], etc., should be analyzed. As one of the important factors, the permeability is the baseline design parameter to determine the size of the magnetic components and analyze the core loss [1,2,3,4,5,6,7]. Although the major characteristics of the selected magnetic cores were already described in datasheets, the complex permeability characteristics w.r.t. the operating frequency need to be further investigated, if the permeability is not revealed in detail. Especially, imaginary permeability, which implies the core loss, is not usually described in datasheets; hence, investigating the imaginary permeability becomes important for estimating the core loss and managing the heat dissipation of the magnetic core. As the typical methods to investigate the complex permeability, high resolution based LCR meters for kHz ranges [7], microwave generators for MHz-GHz [8], vector network analyzers (VNA) for GHz ranges [9,10,11], and millimeter-wave spectrometers for GHz ranges [12] could be utilized to derive the complex permeability as well as inductance and resistance. Although several special measurement methods to investigate the complex permeability have been presented for various purposes, e.g., ultra-wideband permeability measurements [8], transmission bridge method [9], and using rod samples inside a rectangular waveguide [10], they are limited to be used for millimeter-wave frequency ranges. Because such measurement devices cannot provide appropriate AC test current levels [7,8,9,10,11,12,13], the measurement results of the complex permeability may not be accurate for the specified frequency ranges; hence, they are not suitable for the general magnetic components applied in power applications due to extremely low AC test currents in magnetic components. Furthermore, the previous literatures mentioned above require complicated experimental environments, which make the power engineers difficult to investigate the major characteristics of the magnetic materials. For this reason, an appropriate AC power supply based complex permeability measurement is required so that appropriate AC test current is applied to the magnetic components [14].

In this paper, a simple but useful calculation methodology to find the complex permeability is proposed. The complex permeability is composed of real permeability for the size of the magnetic core and imaginary permeability for the core loss. By virtue of the proposed calculation methodology of complex permeability, the real permeability μr′ and imaginary permeability μ_r″ can be specified w.r.t. the operating frequency. To evaluate a comparative analysis of different magnetic materials, a ferrite core, an amorphous core, and a nanocrystalline core have been selected and verified by experiments. By virtue of the proposed calculation methodology for the complex permeability, the major characteristics of the magnetic materials for the design of the magnetic components can be found for a wide operating frequency range.

2. Proposed Calculation Methodology of the Complex Permeability

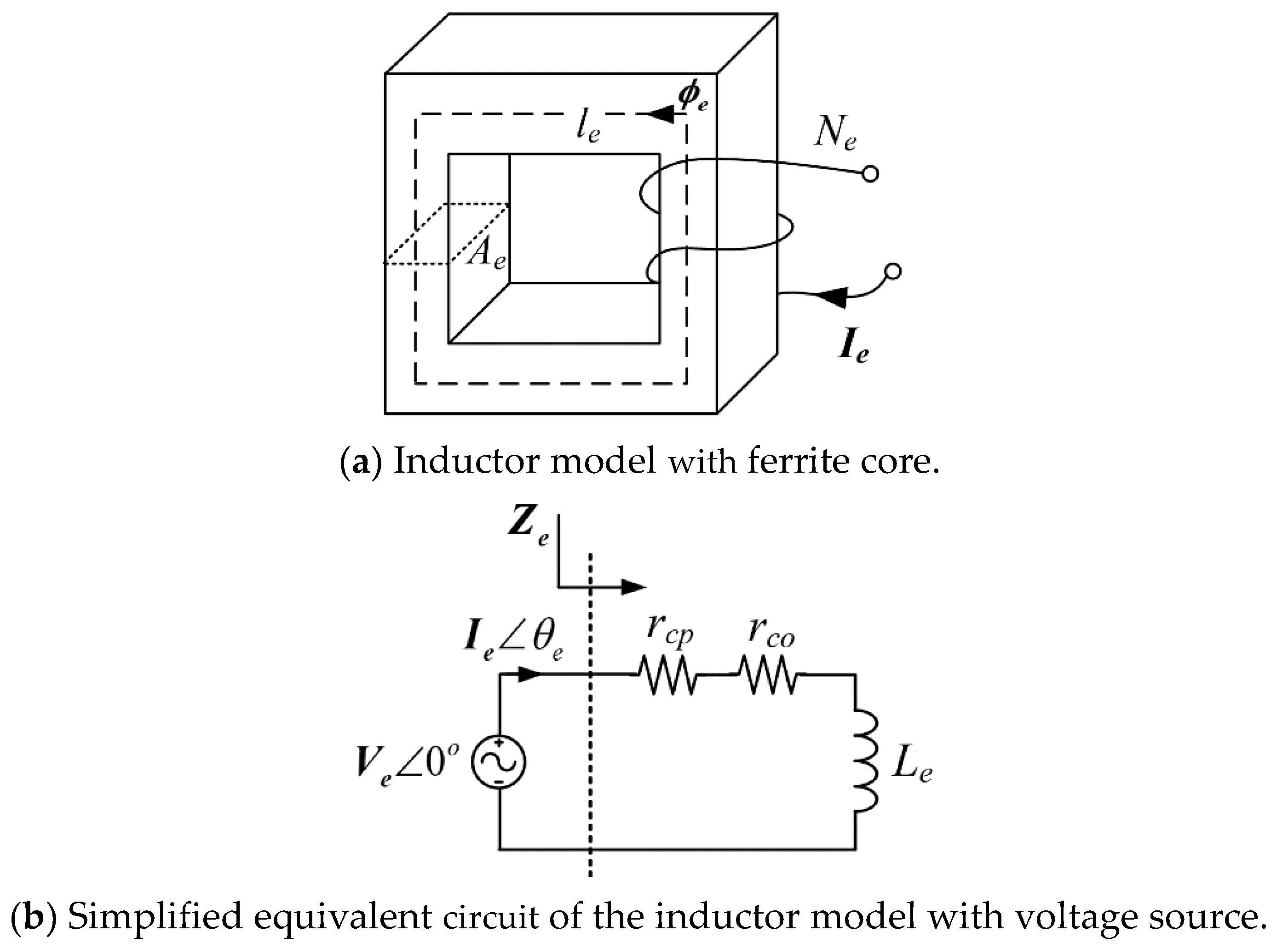
According to the datasheet of the PM11 ferrite core used in this paper, the real permeability is well described w.r.t different f_s. However, the imaginary permeability, which is related to the core loss resistance, is not described below f_s = 250 kHz from the PM11 datasheet [15]. For this reason, in order to exactly find the value of imaginary permeability of PM11 for f_s < 250 kHz, a simple inductor model with a ferrite core has been built, as shown in Figure 1a. A simplified equivalent circuit of Figure 1a is shown in Figure 1b, where the voltage source is connected to the inductor model in series to evaluate the characteristics of the inductor model. For simplicity of analysis, all the magnetic field is assumed to be in the magnetic core in this paper. In Figure 1b, the complex impedance of the inductor model Z_e can be defined as follows:

$${\mathit{Z}}_{\mathit{e}}\left({\omega }_s\right)=r_{cp}\left({\omega }_s\right)+j{\omega }_s{\mathit{L}}_{\mathit{e}}=r_{cp}\left({\omega }_s\right)+r_{co}\left({\omega }_s\right)+j{\omega }_s{L}_e$$

(1a)

$$\because j{\omega }_s{\mathit{L}}_{\mathit{e}}\equiv r_{co}\left({\omega }_s\right)+j{\omega }_s{L}_e\hspace{0.17em}\hspace{0.17em}\to \hspace{0.17em}\hspace{0.17em}{\mathit{L}}_{\mathit{e}}=\left(L_e-j\frac{r_{co}\left({\omega }_s\right)}{{\omega }_s}\right)$$

(1b)

where f_s is the operating frequency, and ω_s is the angular switching frequency. Bold characters mean a complex value. Z_e and L_e are the complex values for the impedance and inductance, and r_cp is the copper loss-term resistance including the skin effect and eddy effect determined by frequency. From (1b), the complex inductance L_e includes core loss resistance r_co because r_co depends on the magnetic characteristics [6].

To calculate the inductance in terms of the physical dimensions of the inductor model in Figure 1a, the complex inductance L_e can be expressed by the complex permeability as follows:

$${\mathit{L}}_{\mathit{e}}{\mathit{I}}_{\mathit{e}}=N_e{\mathit{\varphi }}_{\mathit{e}}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\to \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\mathit{L}}_{\mathit{e}}=\frac{N_e^2{A}_e{\mu }_o{\mathit{\mu }}_r}{l_e}$$

(2a)

$$\because {\mathit{\varphi }}_{\mathit{e}}={\mathit{{\rm B}}}_{\mathit{e}}{A}_e,$$

(2b)

where A_e and l_e are effective magnetic area and effective magnetic path length, respectively.

From (1) and (2), the real and imaginary permeability can be found as follows:

$${\mathit{\mu }}_{\mathit{r}}=\frac{l_e}{N_e^2{A}_e{\mu }_o}{\mathit{L}}_{\mathit{e}}=\frac{l_e}{N_e^2{A}_e{\mu }_o}\left(L_e-j\frac{r_{co}}{{\omega }_s}\right)\equiv {\mu }_r^{\prime }-j{\mu }_r^{″}$$

(3a)

$${\mu }_r^{\prime }\equiv \frac{l_e}{N_e^2{A}_e{\mu }_o}{L}_e\hspace{0.17em}\hspace{0.17em}\hspace{0.17em},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\mu }_r^{″}\equiv \frac{l_e}{N_e^2{A}_e{\mu }_o{\omega }_s}{r}_{co}$$

(3b)

From (3), the real permeability ${\mu }_r^{\prime }$ is proportional to the inductance L_e and the imaginary permeability ${\mu }_r^{″}$ is proportional to the core loss resistance r_co.

A function generator to provide a high-frequency voltage source V_e is used, as shown in Figure 1b. Depending on the electrical and magnetic characteristics of the inductor model, test current I_e and phase difference between the voltage and current θ_e are different as follows:

$${\mathit{{\rm I}}}_{\mathit{e}}\equiv I_e\angle {\theta }_e=\frac{V_e\angle 0^{°}}{r_{co}+r_{cp}+j{\omega }_s{L}_e}$$

(4a)

$$\therefore \left|{\mathit{{\rm I}}}_{\mathit{e}}\right|\equiv I_e=\frac{V_e}{\sqrt{{\left(r_{co}+r_{cp}\right)}^2+{\left({\omega }_s{L}_e\right)}^2}}\hspace{0.17em}\hspace{0.17em},\hspace{0.17em}\hspace{0.17em}{\theta }_e={\tan }^{-1}\left(\frac{{\omega }_s{L}_e}{r_{co}+r_{cp}}\right),$$

(4b)

where such I_e and θ_e can be measured by an oscilloscope, and r_cp can be found by measuring only the copper wire resistance without the ferrite core.

Based on the measured results of V_e, I_e and θ_e, the values of L_e and r_cp can be obtained as follows:

$$L_e=\frac{V_e\tan {\theta }_e}{{\omega }_s{I}_e\sqrt{1+{\tan }^2{\theta }_e}}$$

(5a)

$$r_{co}=\frac{V_e}{I_e\sqrt{1+{\tan }^2{\theta }_e}}-r_{cp}$$

(5b)

Based on the calculated results in (5), the real and imaginary permeability can be calculated from (3). Contrary to the conventional complicated methods [8,9,10,11,12], the suggested (1)–(5) are so simple and intuitive; thus, the real and imaginary permeability can be easily and immediately found by simple test prototypes in Figure 1.

3. Experimental Verification

In order to identify the real and imaginary permeability of the magnetic cores and to evaluate the comparative analysis for different magnetic cores, test prototypes for the inductor have been built, as shown in Figure 2. Physical parameters of A_e, l_e, and N_e in Figure 1 were arbitrarily selected based on a piece of magnetic core, commercially available in markets: A_e is magnetic flux area, l_e is the length of effective magnetic path, and N_e is the number of winding turns. The physical parameters are summarized in

Table 1. Physical dimensions for experimental verification.

Classification	Ae (mm2)	le (mm)	Ne (Turns)
Ferrite core (PM11)	576	600	10
Amorphous core (AMOGREENTECH)	600	480	10
Nanocrystalline core (VITROPERM)	250	280	10

. A PM11 magnetic material from TODAISU has been selected for Mn-Zn-type ferrite core [15]. The AMLB-8320 amorphous core from AMOGREENTECH, which is formed by layers of laminated 40-µm-thin amorphous-metal-film, has been selected for the amorphous core, as shown in Figure 2b. A VITROPERM 500F core from VACUUMSCHMELZE has been selected for the Nanocrystalline core, as shown in Figure 2c [16]. Considering the applicable operating frequency of kHz ~ several MHz for three major magnetic materials, e.g., ferrite core, Amorphous core, and Nanocrystalline core in this paper, 1 kHz to 1 MHz frequency range has been specified.

Based on the measurement results of V_e, I_e, and θ_e in (4) by a function generator (KEYSIGHT 33522A) and an oscilloscope (Lecroy 104Xi-A oscilloscope), the inductance and resistance in (5) w.r.t. operating frequency can be calculated, as shown in Figure 3 and Figure 4, where LCR measurement results have been obtained by a KEYSIGHT network analyzer E5071C. In case of LCR measurement used in this paper, uncertainty below a 10 MHz frequency range is highly less than 0.1(dB) [17,18]. A little discrepancy between calculation and LCR measurement, i.e., lower than 8%, comes from leakage magnetic flux, which is leaking out to the air, not circulating through the test prototypes of the magnetic materials in Figure 2. Because the proposed idea to calculate the inductance and resistance in (1)–(5) is assumed to be ideal inductor having no leakage magnetic flux, this inherent leakage magnetic component is not reflected to the calculated results of Figure 3 and Figure 4. Unfortunately, this leakage component cannot be analytically modeled due to the unpredictable radiation of the magnetic field and the non-linear property of the ferrite core [3]. This leakage magnetic flux could be minimized if a manufactured piece of the magnetic core in Figure 2 is small enough so that the generated magnetic flux from the test currents is all passing through the magnetic cores, not leaking to the air. Because the manufactured pieces of the magnetic cores in Figure 2 are the commercialized products in markets, and the size of magnetic pieces are already fixed, this small discrepancy is inevitable in this case. Nevertheless, the confirmation of the tendency for the permeability w.r.t. operating frequency is highly similar, and the relative comparison w.r.t. operating frequency can be obtained by the proposed idea. The real permeability of the ferrite core increases w.r.t. frequency, whereas that of the amorphous core and nanocrystalline core decreases. The imaginary permeability always increases for three core cases due to the increment of the core loss, which is usually proportional to the operating frequency.

From the results of Figure 3 and Figure 4, the real and imaginary permeability can be found, as shown in Figure 5. In case of the PM11 ferrite core, the calculated results of the real and imaginary permeability w.r.t. frequency are shown in Figure 5a. The values of real and imaginary permeability for f_s > 250 kHz, which were already described in the datasheet [15], are matched well with the calculation and measurement results. According to the datasheet [15], unfortunately, the information for the imaginary permeability has not been revealed for the f_s < 250 kHz range. From the matching tendency between datasheet and calculation results, it can be said that the values of real and imaginary permeability for f_s < 250 kHz is reliable. Although the magnetic characteristic of the amorphous core is not revealed, the real and imaginary permeability can be found by the proposed methodology, as shown in Figure 5b. In case of the nanocrystalline core, the calculation results are also in good agreement with the datasheet that has described only the tendency of the permeability w.r.t. the operating frequency [16]; hence, the numerical values for the permeability can be specified. The test current level I_e and the calculated magnetic flux density inside the ferrite core B_e w.r.t. the operating frequency is shown in Figure 6. The magnetic field inside the magnetic cores B_e can be calculated from (2), and the cases of amorphous core and nanocrystalline core are omitted due to the same tendency of Figure 6. It is noteworthy that the test currents and magnetic flux density can be increased until B_e < B_sat ≈ 0.3 T by the other AC power supply devices, so that the exact complex permeability can be obtained under rated operating condition, although the function generator, which can provide a convenient frequency modulation function, has been used in this paper.

All the calculated results w.r.t. the different operating frequency are summarized in

Table 2. Experimental results for different core materials.

Classification	fs = 10 kHz			fs = 100 kHz			fs = 500 kHz
	μ′	μ″	tan δμ	μ′	μ″	tan δμ	μ′	μ″	tan δμ
Ferrite core (PM11)	2148	2.1	0.001	2186	6.5	0.0029	2301	61.5	0.0267
Amorphous core (AMOGREENTECH)	601	5.8	0.009	602	83.3	0.1383	464	217.7	0.4692
Nanocrystalline core (VITROPERM)	75,281	25,743	0.3419	28,743	22,018	0.7660	11,064	9063	0.8191

. Magnetic loss tangent tan δ_μ is defined as μ″/μ′, which represents the magnetic core loss and can be usefully utilized for a finite-element-method (FEM) simulation analysis [3]. Magnetic loss tangent δ_μ in Table 2 is essential to specify the core loss resistance modeling from the 3D FEM simulation analysis [2,3]. Based on the core loss resistance obtained by magnetic loss tangent δ_μ, the static core loss resistance can be obtained to analyze the core loss of the magnetic components for power converters and wireless power transfer systems. According to the results of tan δ_μ in Table 2, the ferrite core is superior to the amorphous core and nanocrystalline core for coil loss term. The complex permeability of the amorphous core is relatively lower than the others. The nanocrystalline core has very high real permeability, i.e., the core can be highly minimized. However, the imaginary permeability is also very high, i.e., the nanocrystalline core is of inferior core efficiency, although the magnetic component can be minimized by the nanocrystalline core. From the measured results in Table 2, the core loss of amorphous core may be almost 2.7 times larger than that of ferrite core at f_s = 10 kHz under the same physical and operating conditions. If the operating frequency increases, the loss gap significantly increases. Therefore, in terms of the low core loss and high-frequency characteristics, the ferrite core is recommended. On the other hand, the nanocrystalline core is recommended for compact magnetic core. According to the magnetic results obtained by the proposed calculation methodology, the optimal magnetic core can be appropriately selected at the specified operating frequency condition.

4. Conclusions

In this paper, a simple but useful calculation methodology to specify the complex permeability has been derived and verified by the simple test prototypes. The proposed methodologies have been proved to be accurate to derive real and imaginary permeability by comparing the calculation results and the datasheet. As a strong merit of the proposed methodology, only one function generator is used to specify the characteristics of the magnetic materials. To evaluate the superiority of the magnetic materials, three different magnetic cores have been introduced and verified by experiments. As a result, a ferrite core is preferred for low core loss applications, whereas nanocrystalline core is recommended for compact size of magnetic components. By virtue of the proposed calculation methodology, it is expected that the magnetic cores can be usefully designed for various industrial applications, e.g., energy conversion system using magnetic cores, power converters and wireless power transfer systems.