Towards Precision Fertilization: Multi-Strategy Grey Wolf Optimizer Based Model Evaluation and Yield Estimation

Abstract

Precision fertilization is a major constraint in consistently balancing the contradiction between land resources, ecological environment, and population increase. Even more, it is a popular technology used to maintain sustainable development. Nitrogen (N), phosphorus (P), and potassium (K) are the main sources of nutrient income on farmland. The traditional fertilizer effect function cannot meet the conditional agrochemical theory’s conditional extremes because the soil is influenced by various factors and statistical errors in harvest and yield. 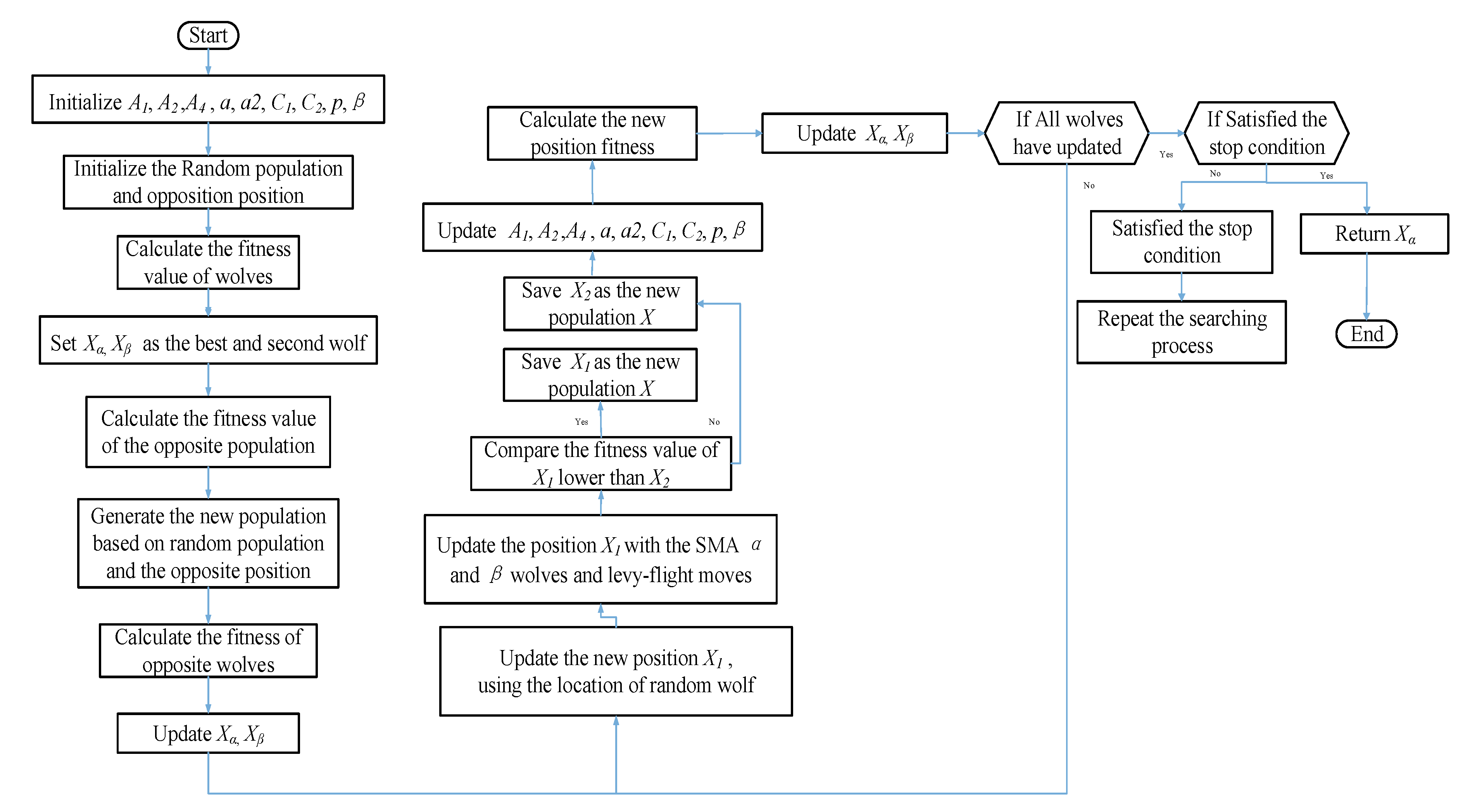In order to find more accurate scientific ratios, it has been proposed a multi-strategy-based grey wolf optimization algorithm (SLEGWO) to solve the fertilizer effect function in this paper, using the “3414” experimental field design scheme, taking the experimental field in Nongan County, Jilin Province as the experimental site to obtain experimental data, and using the residuals of the ternary fertilizer effect function of Nitrogen, phosphorus, and potassium as the target function. The experimental results showed that the SLEGWO algorithm could improve the fitting degree of the fertilizer effect equation and then reasonably predict the accurate fertilizer application ratio and improve the yield. It is a more accurate precision fertilization modeling method. It provides a new means to solve the problem of precision fertilizer and soil testing and fertilization.

1. Introduction

The ecosystem formed by “crop-soil-fertilizer” seems to continue indefinitely, but in each cycle, there is more or less natural loss, which needs to be replenished and controlled by human factors to continue the cycle [1,2,3,4,5,6]. Since its introduction in the 1980s, precision fertilization has been a significant constraint on balancing the contradiction between land resources, ecology, and population growth and a key technology for maintaining sustainable development [7,8,9,10,11]. Precision fertilization is based on soil testing, and field application trials and a comprehensive grasp of crop fertilization patterns, soil supply properties, and fertilizer effects are the primary means to ensure scientific fertilizer with yield increase, improve product quality, and food security while reducing environmental pollution and soil friendliness [12,13,14]. The growth of output depends on inputs, and crops need “food” to satisfy their growth. Plants need chemical elements, water, and carbon dioxide to synthesize organic matter under photosynthesis in sunlight, and fertilizers are essential “food” for crops [9,10,11,12,13,14,15]. The roots of crop growth are in the soil, and 60–70% of plant nutrients are absorbed from the soil [16,17,18,19,20,21,22]. There are many types of fertilizers, including massive elements (nitrogen, phosphorus, potassium), trace elements (calcium, magnesium, sulfur, manganese, boron, iron, copper, molybdenum), and organic fertilizers [23,24,25,26]. Nitrogen (N) is a constituent element of proteins, nucleic acids (DNA and RNA), and chlorophyll in chloroplasts and other compounds in plants, which plays a significant role in plant growth and development [27,28]. Phosphorus (P) is a constituent element of many compounds in plants, such as nucleic acids (DNA and RNA), proteins, and enzymes, which promote plant growth and enhances the cold and drought resistance of crops [29]. Potassium (K) can promote photosynthesis so that cellular osmotic pressure can use water uptake and enhance the plant’s ability to tolerate various adverse conditions [30,31,32]. When soil nutrient supply is insufficient, it is supplemented by fertilizer application to balance fertilizer supply and crop fertility requirements to reduce crop diseases and yield reduction of different degrees. According to the data, the role of fertilizer in increasing crop yield accounts for 30% to 65% [33]. At the same time, the basic principles of fertilization in nutrient cycling and plant nutrition follow the dominant principle, i.e., there is a synergistic change in the content of individual nutrients, which means that if the nutrients in the soil are sufficient or the blending ratio is imbalanced, if fertilizers are used blindly, it will not only cause waste of fertilizers but also cause toxic effects on crops, resulting in food safety problems and even yield reduction.

Since the relationship between crop nutrient requirements and output is highly complex [34], the algebraic form of the fertilizer effect equation and the values of various parameters will depend on many factors such as crop, fertilizer, soil type, and cultivation techniques [35]. Fertilizer effect equation is also named nutrient equation; the main objective is to determine a suitable fertilizer effect equation based on the information from the available field plot fertility trials to reflect exactly the quantitative relationship between fertilizer application and output and to seek the amount of fertilizer applied to achieve high yield, quality, and efficiency from this effect equation [36,37]. The fertilizer effect equation is based on field experiments, and its specific method is to inverse design the yields obtained from different treatments, apply the fertilizer effect equation to fit the crop fertilization model, estimate the parameters of the equation, and test it with the regression equation and regression coefficients to determine the final fertilizer effect model. At the same time, a comprehensive evaluation of the established model was carried out to determine the maximum yield and the best economic ratios from the obtained fertilizer effect equation and to determine the proper formula fertilizer application according to the regional economic development objectives and the soil testing results [38].

Precision fertilization achieves a balanced fertilizer application on each operating unit, depending on the soil and crop. Moreover, its main steps include scientific soil testing and the determination of fertilizer recipes. It significantly improves the fertilizer utilization rate and economic efficiency of fertilizer application and reduces the negative impact on the environment. Precision fertilization is one of the vital elements of precision agriculture. It can reduce the cost of agricultural production, effectively avoid wasting resources and reduce environmental pollution caused by fertilizer and pest control without minimizing production reduction. It also provides rational use of the material nutrients of crops and ensures the production and quality of agricultural products. In practice, soil testing and fertilization is a critical way to achieve precise fertilization.

As early as the 1840s, the founder of agricultural chemistry, Justus von Liebig, created the famous “law of minimum nutrients”, and scholars from various countries began to study the complex and close relationship between crop yield and fertilizer application, which entered the era of metric fertilization [39]. In the mid-20th century, the fertilizer effect function approach was widely promoted in India [40]. Domestic and foreign researchers have also conducted a large number of model studies and applications. Zhang et al. [41] proposed Monte Carlo modeling, which improved the fertilizer effect function model list’s accuracy at the expense of time in exchange. Colwell et al. [42] proposed a regression coefficient averaging method. Chen et al. [43] proposed the dynamic clustering method. There are more than 10 types of fertilizer effect functions available, mainly includes: linear equations [44], polynomial binomial [45], trigonometric polynomial [46], Mee’s equation [47], Spearman’s equation [48], linear and platform function [49], quadratic and platform function [50], inverse linear polynomial [51], quadratic polynomials [52], 0.5 polynomials [53], logarithmic conversion [54], and reduced yield inverse polynomials [55], etc. The Mee’s and Spearman equations cannot reflect the diminishing returns after overfertilization, and the applicability is only applicable to areas with low fertility. At the same time, polynomials and inverse polynomials can show the law of diminishing returns for overfertilization, which can further expand the applicability, but still cannot overcome the problems of model setting bias and multicollinearity. Chen et al. [43] compared nitrogen and phosphorus polynomial fertilizer effect models of 0.5, 0.75, 1.5, and 2 times and obtained that the applicability of different models differed and concluded that in irrigated land, the quadratic polynomial could better respond to the fertilization efficiency of wheat. In Cerrato and Blackmer’s study [56] of the linear and quadratic platform, polynomial nitrogen fertilizer efficiency functions were compared, and the test results showed that the quadratic model performed best in winter wheat, summer maize, and vegetable crops with generalizability.

In 2006, the Ministry of Agriculture (MOA) proposed the “3414” test scheme in the national soil testing and fertilizer application work, which has the advantages of regression to optimal design, fewer steps, and high efficiency, and can establish one-, two-, and three-dimensional fertilizer effect functions and the code is intuitively comparable and more suitable for field application. According to the Technical Specification for Soil Testing and Fertilizer Application Project of the Ministry of Agriculture, the “3414” design scheme for nitrogen, phosphorus, and potassium has been considered the best fertilizer effect test scheme since it was proposed nearly 15 years ago, after nationwide promotion and demonstration trials of the project. Fertilizer effect function theoretically puts forward the law of the influence of various factors on plant growth, which connotes: “Various factors constrain plant growth, and the range of variation of various factors is extensive, and the ability of plants to adapt is limited, only when each factor is at a specific value, it is considered to be the most suitable for plant growth, and this optimal value is, on the whole, the most suitable for plant growth [57]. It can be said that there is only one hypersurface in n-dimensional space composed between crop yield and each nutrient influencing factor. Its characteristics correspond to a class of constrained optimization problems that are the main problems solved by modern computational optimization methods. The swarm intelligence optimization algorithm has an absolute advantage in solving optimization problems with strong local exploitation capability and fast convergence.

Optimization methods have been classified using valid metrics on their originality, source of inspiration, number of objectives, and evolutionary basis [58,59,60,61,62,63,64,65,66,67]. Due to their stochastic nature and flexibility, they have been utilized to deal with feature space without gradient info [68,69,70,71]. Most of these methods work based on switching the exploration and exploitation phases using stochastic operations [62,72]. Most researchers try to boost the efficacy based on balancing the initial cores of these methods [59,73,74,75,76,77,78,79,80,81,82]. The recent efficient variants of swarm intelligence optimization algorithms are simulated annealing algorithm (SA) [83,84], fruit fly optimization algorithm (FOA) [85,86], sine cosine algorithm (SCA) [71,87,88,89], moth-flame optimization (MFO) [90,91], particle swarm optimization (PSO) [92], whale optimizer (WOA) [93], different evolution (DE) [94], bat-inspired algorithm (BA) [95], grey wolf optimization (GWO) [96,97,98,99,100,101], grasshopper optimization algorithm (GOA) [102], Harris hawks optimization (HHO) (https://aliasgharheidari.com/HHO.html, accessed on 28 August 2021) [81,103,104], genetic algorithm (GA) [105], chaotic BA (CBA) [106], multi-verse optimizer (MVO) [107], cuckoo search via Lévy flights (CS) [108], firefly algorithm (FA) [109], salp swarm algorithm (SSA) [110,111], gravitational search algorithm (GSA) [112], ant colony optimization (ACO) [72,113,114], krill herd algorithm (KHA) [115], artificial bee colony (ABC) [116]. Meanwhile, there are many corresponding improvement algorithms [70,117], such as enhanced comprehensive learning particle swarm optimization (GLOPSO) [118], chaotic moth-flame optimization (CMFO) [91], hybridizing grey wolf optimization (HGWO) [119], balanced whale optimization algorithm (BWOA) [120], double adaptive random spare reinforced whale optimization algorithm (RDWOA) [121], chaotic mutative moth-flame-inspired optimizer (CLSGMFO) [122], orthogonal learning sine cosine algorithm (OLSCA) [88], multi-strategy enhanced sine cosine algorithm (MSCA) [123], enhanced whale optimizer with associative learning (BMWOA) [124], enhanced moth flame optimization (SMFO) [125], ant colony optimizer with random spare strategy and chaotic intensification strategy (RCACO) [126], etc.

These methods are widely used to solve the field of agricultural engineering optimization. Wang et al. [127] used a multi-objective chaotic particle swarm algorithm for water-saving crop planning to develop sustainable agriculture and soil resources. Saranya et al. [128] provided a crop plan optimization method using social spider optimization algorithms. Wu et al. [129] proposed an improved chaotic genetic algorithm for optimal reservoir scheduling. Amir Abbas et al. [130] proposed optimal route planning for farming operations based on an ant colony algorithm. Chagwiza et al. [88] proposed a mixed integer programming poultry feed ration optimization problem using the bat algorithm. Qazi et al. [131] proposed to solve the agricultural product scheduling problem using an improved particle swarm algorithm.

In this paper, we propose a multi-strategy improved grey wolf optimization (GWO) algorithm (SLEGWO) using combined with SMA foraging (SMA), levy flight (LF), opposition-based learning (OBL), and greedy strategy (GS) to enhance the GWO algorithm. Unlike GWO, the command wolves are reduced, and only α and β wolves command the other wolves for foraging. Firstly, the initial α wolves are using OBL to accelerate the convergence to quality solutions. Secondly, the wolves are flown by LF and SMA mechanism to avoid getting into local optimum, enhancing the search balance. Finally, GS is used to fast convergence to the optimal solution. The proposed algorithm outperforms other competitors on 30 Classical functions and the CEC2014 test set. The SLEGWO proposed solving the nutrient equation coefficients and the highest yield (maximize fertilizer effect) in this paper. The established model is evaluated and compared with other swarm intelligence optimization algorithms using the decision coefficient R2. Experiments show that using the SLEGWO is a new feasible method that can improve the accuracy of soil measurement, better match the fertilizer application model, and ultimately provide a new computational tool for scientific fertilizer application decisions.

The rest of the paper is organized as follows. Chapter 2 introduces the improved multi-strategy grey wolf algorithm (SLEGWO). Chapter 3 compares the experiment of SLEGWO on Classical functions and CEC2014. Chapter 4 presents the precision fertilization dataset and the process and implementation of the 3414-fertilizer effect function model combined with SLEGWO, experimental results, and model evaluation. Chapter 5 presents a summary and future work.

2. Materials and Methods

2.1. GWO

Grey Wolf Optimizer (GWO) is a swarm intelligence optimization algorithm proposed in 2014 [132], and its performance has been the subject of analysis in many works, from clustering to global optimization [61,67,96,133,134,135]. The algorithm was inspired by the prey hunting activity of grey wolves, which has strong convergence performance, few parameters, and easy implementation. It has been widely concerned by scholars in recent years, and it has been successfully applied to the fields of workshop schedule, parameter optimization, image classification, etc. The GWO can be regarded as an improvement of the firefly algorithm (FA). The firefly flies toward the individual due to itself, while the grey wolf has more demanding conditions and advances toward the top three of the group. The FA controls the search range by the step size, while the GWO directly defines the search range parameter A and makes A linearly decreasing.

The structure of the GWO is simple, but it is not easy to improve. Several improvements only change the ratio of global search capability and local search capability, and the combined capability does not change much.

In GWO, the initial population should be divided into a number of categories, including alpha (α), beta (β), delta (δ), and omega (ω). The best wolves are considered α, β, and δ to help other wolves (ω) explore more favorable solution spaces.

In GWO, the wolves can identify the location of prey and encircle the process. Mathematically modeling this behavior, the equation is as follows.

$$\overrightarrow{D}=\left|\left(\overrightarrow{C}·\overrightarrow{X}\mathrm{p}\left(\mathrm{t}\right)-\overrightarrow{X}\left(\mathrm{t}\right)\right)\right|,$$

(1)

$$\overrightarrow{X}\left(t+1\right)={\overrightarrow{X}}_p\left(t\right)-\overrightarrow{A}·\overrightarrow{D},$$

(2)

where $\overrightarrow{A}$ and $\overrightarrow{C}$ are random coefficients; t is the number of iterations; $\overrightarrow{X}\left(t\right)$ is the current position vector of the grey wolf; and ${\overrightarrow{X}}_p\left(t\right)$ is the position vector of the prey.

The calculation of $\overrightarrow{A}$ and $\overrightarrow{C}$ is shown below:

$$\overrightarrow{A}=2\overrightarrow{a}·{\overrightarrow{r}}_1-\overrightarrow{a},$$

(3)

$$\overrightarrow{C}=2{\overrightarrow{r}}_2,$$

(4)

where $\overrightarrow{a}$ is decreasing from 2 to 0 as the local optimum is continuously searched and as the number of iterations increases; ${\overrightarrow{r}}_1$ and ${\overrightarrow{r}}_2$ are random numbers between [0, 1].

A wolf usually leads the hunting process. In a wolf pack, $\mathsf{\alpha }$ has the highest rank in the pack. $\mathsf{\beta }$ ranks lower than $\mathsf{\alpha }$ but higher than $\mathsf{\delta }$. in the algorithm, $\mathsf{\beta }$ and $\mathsf{\delta }$ help $\mathsf{\alpha }$ to determine the position of the pack and direct the $\mathsf{\omega }$ wolves to hunt. So, the behavior is described by the following equation:

$${\overrightarrow{D}}_{\alpha }=\left|{\overrightarrow{C}}_1·{\overrightarrow{X}}_{\alpha }-\overrightarrow{X}\right|,$$

(5)

$${\overrightarrow{D}}_{\beta }=\left|{\overrightarrow{C}}_2·{\overrightarrow{X}}_{\beta }-\overrightarrow{X}\right|,$$

(6)

$${\overrightarrow{D}}_{\delta }=\left|{\overrightarrow{C}}_3·{\overrightarrow{X}}_{\delta }-\overrightarrow{X}\right|,$$

(7)

$${\overrightarrow{X}}_1={\overrightarrow{X}}_{\alpha }-{\overrightarrow{A}}_1·\left({\overrightarrow{D}}_{\alpha }\right),$$

(8)

$${\overrightarrow{X}}_2={\overrightarrow{X}}_{\beta }-{\overrightarrow{A}}_2·\left({\overrightarrow{D}}_{\beta }\right),$$

(9)

$${\overrightarrow{X}}_3={\overrightarrow{X}}_{\delta }-{\overrightarrow{A}}_3·\left({\overrightarrow{D}}_{\delta }\right),$$

(10)

$$\overrightarrow{X}\left(t+1\right)=\frac{{\overrightarrow{X}}_1+{\overrightarrow{X}}_2+{\overrightarrow{X}}_3}{3},$$

(11)

where ${\overrightarrow{A}}_1$, ${\overrightarrow{A}}_2$, and ${\overrightarrow{A}}_3$ are random coefficient vectors, and the GWO algorithm uses the random vectors $A$ and $C$ to coordinate the command to complete the hunt.

It can be seen that $A$ and $C$ are the keys to determine the exploration and detection capability. The most effective way to avoid local optimum is by using the enhancement of $A$ and $C$. Although GWO has achieved wide application, it still suffers from stagnation in local optimum and slow convergence when solving high-dimensional tasks.

2.2. Opposition-Based Learning

Opposition-based learning (OBL) was proposed by Tizhoosh [136] in 2005, initially using opposites and later using approximate opposites and inverse approximate opposites. It is an improved mechanism widely used in evolutionary computation, which is designed so that an outcome opposite to the estimate is treated as the best possible outcome. When the GWO is initialized, a stochastic strategy is used. Then, in the process of random allocation of prey and food, suppose there are two opposing wolves; one of them is assumed to be the initial $\mathsf{\alpha }$ wolf. The contrast learning is used, then the opposite one is selected as the $\mathsf{\alpha }$ wolf, and the two wolves are compared, and the better one has been searched as the initial $\mathsf{\alpha }$ wolf, which increases the accuracy of the selection of the $\mathsf{\alpha }$ wolf and thus improves the convergence speed. Then there are:

$${\overrightarrow{X}}_{OBL}=LB+UB-{\overrightarrow{X}}_{\alpha }+r_3\left({\overrightarrow{X}}_{\alpha }-\overrightarrow{X}\right),$$

(12)

where ${\overrightarrow{X}}_{OBL}$ is the position of the opposite wolf in the search space, LB is the lower bound, UB is the upper bound, and ${\overrightarrow{X}}_{\alpha }$ is the position of the $\mathsf{\alpha }$ wolf. $r_3$ is a random vector within (0,1), and $\overrightarrow{X}$ is the position vector of the initial random population.

2.3. Slime Mould Foraging

The slime mould algorithm (SMA), proposed by Li et al. (https://aliasgharheidari.com/SMA.html, accessed on 28 August 2021) [137] in 2020, is inspired by the diffusion and foraging behavior of slime mould, and mainly simulates the behavior and morphological changes of slime mould during the foraging process without modeling their approach, wrapping, and searching for food. SLEGWO mainly draws on SMA’s foraging process. Firstly, it approaches the food according to the odor in the air; the higher the concentration of food, the stronger the bio-oscillator wave, the faster the cytoplasmic flow, and the thicker the mucilage venous tubules. A functional expression simulated this behavior with the following position update equation:

$$\overrightarrow{X\left(t+1\right)}=\{\begin{array}{c}\overrightarrow{X_b\left(t\right)}+\overrightarrow{vb}·\left(\overrightarrow{W}·\overrightarrow{X_A\left(t\right)}-\overrightarrow{X_B\left(t\right)}\right),r<p\\ \overrightarrow{vc}·\overrightarrow{X\left(t\right)},r\ge p\end{array},$$

(13)

where $\overrightarrow{vb}$ ranges from [−a, a], $\overrightarrow{vc}$ decreases linearly from 1 to 0. $t$ denotes the current number of iterations, $\overrightarrow{X_b\left(t\right)}$ denotes the position of the currently found individual with the highest fitness value, $\overrightarrow{X\left(t\right)}$ denotes the position of the slime, $\overrightarrow{W}$ denotes the weight of the slime, and $\overrightarrow{X_A\left(t\right)}$ and $\overrightarrow{X_B\left(t\right)}$ denote the two randomly selected individuals from the slime.

where the equation for $p$ is given as follows:

$$p=\tanh \left|S\left(i\right)-DF\right|,$$

(14)

where $i\in 1,2,\dots ,n$, $S\left(i\right)$ denotes the fitness value of $\overrightarrow{X\left(t\right)}$ and $DF$ is the currently obtained best fitness value.

The equation for $\overrightarrow{vb}$ is given as follows:

$$\overrightarrow{vb}=\left[-a,a\right]$$

(15)

$$a=\mathrm{arctanh}\left(-\left(\frac{t}{\max \_t}\right)+1\right)$$

(16)

The equation for $\overrightarrow{W}$ is given by:

$$\overrightarrow{W\left(SmellIndex\left(i\right)\right)}=\{\begin{array}{c}1+r·\log \left(\frac{bF-S\left(i\right)}{bF-wF}+1\right),condition\\ 1-r·\log \left(\frac{bF-S\left(i\right)}{bF-wF}+1\right),others\end{array},$$

(17)

$$SmellIndex=sort\left(S\right),$$

(18)

where $condition$ denotes the top half of $S\left(i\right)$ in the population, $r$ denotes the random number in [0, 1], $bF$ is the best fitness value obtained in the current iteration, $wF$ denotes the worst fitness value obtained in the current iteration, and $SmellIndex$ denotes the sorted sequence of fitness values (in the minimum value problem in ascending order).

$\overrightarrow{X_A}$ and $\overrightarrow{X_B}$ denote two randomly selected best positions from the SMA, which are used instead of the best positions of $\mathsf{\alpha }$ and $\mathsf{\beta }$ wolf in SLEGWO. There are only $\mathsf{\alpha }$ and $\mathsf{\beta }$ wolves and no delta wolves in SLEGWO. The adaptive weights $\overrightarrow{W}$ using SMA provide dynamic perturbations that fall into local optima in the search for the best position of $\overrightarrow{X}$, which can mitigate search stagnation and premature convergence:

$${\overrightarrow{D}}_{SMA}=\left|2r_4{\overrightarrow{X}}_{SMA}-\overrightarrow{X}\right|,$$

(19)

$${\overrightarrow{X}}_{SMA}\left(t\right)={\overrightarrow{X}}_{SMA}-{\overrightarrow{A}}_4·{\overrightarrow{D}}_{SMA},$$

(20)

where ${\overrightarrow{A}}_4$ is calculated as follows.

$${\overrightarrow{A}}_4=2a{r}_5{\overrightarrow{X}}_{SMA}-\overrightarrow{X},$$

(21)

where ${\overrightarrow{A}}_4$ is calculated in a similar way to ${\overrightarrow{A}}_1$ and ${\overrightarrow{A}}_2$ in GWO.

2.4. Levy Flight

Levy flight (LF), which is named after the French mathematician Paul Levy [138], refers to a random walk with a heavy-tailed probability distribution of step lengths.

$$L\left(z\right)~{\left|z\right|}^{-1-\beta },0<\beta \le 2,$$

(22)

where $z$ denotes the variable and $\beta$ shows an important Levy index to adjust the stability, and the $\beta$ equation is updated with the following equation.

$$\beta =2r\left(1-\frac{t}{T}\right)=r{\mathrm{a}}_2,$$

(23)

where $r$ is a random value within (0, 1), and LF is used to update the distance of $\mathsf{\alpha }$ and $\mathsf{\beta }$ wolves’ position. Then we have the following equation:

$${\overrightarrow{D}}_{\alpha }=\left|{\overrightarrow{C}}_1·{\overrightarrow{X}}_{\alpha }-\overrightarrow{X}\right|,$$

(24)

$${\overrightarrow{D}}_{\beta }=\left|{\overrightarrow{C}}_2·{\overrightarrow{X}}_{\beta }-\overrightarrow{X}\right|,$$

(25)

$${\overrightarrow{X}}_1={\overrightarrow{X}}_{\alpha }-{\overrightarrow{A}}_1·\left({\overrightarrow{D}}_{\alpha }\right),$$

(26)

$${\overrightarrow{X}}_2={\overrightarrow{X}}_{\beta }-{\overrightarrow{A}}_2·\left({\overrightarrow{D}}_{\beta }\right).$$

(27)

New update positions of $\mathsf{\alpha }$ and $\mathsf{\beta }$ wolves were obtained according to LF. SLEGWO’s LF-based stochastic decreasing operator $\beta$ was combined with the wolf’s equation of motion to increase the chance of exploration and exploitation.

$${\overrightarrow{X}}_{levy}\left(t\right)=\frac{1}{2}\left({\overrightarrow{X}}_1+{\overrightarrow{X}}_1\right)+rand\left(1,dim\right)⨂Levy\left(dim,\beta \right),$$

(28)

where ${\overrightarrow{X}}_{levy}\left(t\right)$ is the position vector of the temporary wolf pack with the LF decision.

2.5. GS (Greedy Strategy)

According to the greedy strategy, the better positions ${\overrightarrow{X}}_{levy}\left(t\right)$ and ${\overrightarrow{X}}_{SMA}\left(t\right)$ among the resulting better positions based on SMA and LF can be selected as the best position vector of individuals in the next generation population according to the evaluation function.

$$\{\begin{array}{l}{\overrightarrow{X}}_{SMA}\left(t\right),f\left({\overrightarrow{X}}_{SMA}\left(t\right)\right)<{\overrightarrow{X}}_{levy}\left(t\right)\\ {\overrightarrow{X}}_{levy}\left(t\right),f\left({\overrightarrow{X}}_{levy}\left(t\right)\right)<{\overrightarrow{X}}_{SMA}\left(t\right)\end{array}.$$

(29)

This strategy helps SLEGWO to preserve the optimal solution and eliminate the suboptimal solutions.

2.6. Multi-Strategy Grey Wolf Optimizer (SLEGWO)

The proposed SLEGWO is based on an improvement of the GWO algorithm, reduced from three types of leader wolves to two types of leader wolves for command hunting. A random coefficient ${\overrightarrow{A}}_4$ and a random coefficient $p$ in the SMA strategy similar to GWO is used for adjusting the execution strategy of SLEGWO. The integration of OBL can be used to accelerate the selection of the $\mathsf{\alpha }$ wolf’s high-quality solution in the initial stage, use the foraging mechanism of SMA and LF to keep SLEGWO balanced in exploration and detection performance, increase the possibility of jumping out of the local optimal solution while improving both exploration and detection. Finally, the GS is used to improve the quality of the optimal solution while accelerating the convergence speed. Figure 1 below shows the SLEGWO flowchart.

3. Experiments and Results for Benchmark Function

This chapter focuses on the comparison experiments between the proposed algorithm and other algorithms. In this paper, 23 single-mode and multi-mode classical benchmark functions and seven combined benchmark functions of CEC2014 are used to conduct unified experiments, expressed in Appendix A

Table A3. Benchmark function.

ID.	Function Equation	Range	fmin
23 classical functions
F1	$f_1\left(x\right)={\displaystyle \sum }_{i=1}^n{x}_i^2$	[−100,100]	0
F2	$f_2\left(x\right)={\displaystyle \sum }_{i=1}^n\left|x_i\right|+{\displaystyle \prod _{i=1}^n}\left|x_i\right|$	[−10,10]	0
F3	$f_3\left(x\right)={\displaystyle \sum }_{i=1}^n{\left({\displaystyle \sum }_{j-1}^i{x}_j\right)}^2$	[−100,100]	0
F4	$f_4\left(x\right)=ma{x}_i\{\left|x_i\right|,1\le i\le n$}	[−100,100]	0
F5	$f_5\left(x\right)={\displaystyle \sum }_{i=1}^{n-1}[100{\left(x_{i+1}-x_i^2\right)}^2+{\left(x_i-1\right)}^2]$	[−30,30]	0
F6	$f_6\left(x\right)={\displaystyle \sum }_{i=1}^n{\left(\left[x_i+0.5\right]\right)}^2$	[−100,100]	0
F7	$f_7\left(x\right)={\displaystyle \sum }_{i=1}^{n}i{x}_i^4+random\left[0,1\right)$	[−1.28,1.28]	0
F8	$f_8\left(x\right)={\displaystyle \sum }_{i=1}^n-x_i\sin \left(\sqrt{\left|x_i\right|}\right)$	[−500,500]	−418.9829 × n
F9	$f_9\left(x\right)={\displaystyle \sum }_{i=1}^n\left[x_i^2-10\cos \left(2\pi x_i\right)+10\right]$	[−5.12,5.12]	0
F10	$f_{10}\left(x\right)=-20\exp \left\{-0.2\sqrt{\frac{1}{n}{\displaystyle \sum }_{i=1}^n{x}_i}\right\}$ $-\exp \left\{\frac{1}{n}{\displaystyle \sum }_{i=1}^n\cos \left(2\pi x_i\right)\right\}+20+e$	[−32,32]	0
F11	$f_{11}\left(x\right)=\frac{1}{4000}{\displaystyle \sum }_{i=1}^n{x}_i^2-{\displaystyle \prod }_{i=1}^n\cos \left(\frac{x_i}{\sqrt{i}}\right)+1$	[−600,600]	0
F12	$f_{12}\left(x\right)=\frac{\pi }{n}\left\{10\sin \left(a{y}_1\right)+{\displaystyle \sum }_{i=1}^{n-1}{(y_i-1)}^2\left[1+10{\sin }^2\left(\pi y_{i+1}\right)\right]+{(y_n-1)}^2+{\displaystyle \sum }_{i=1}^n\mu \left(x_i,10,100,4\right)\right\}$  $y_i=1+\frac{x_i+1}{4}$  $\mu \left(x_i,a,k,m\right)=\{\begin{array}{cc}k{\left(x_i-a\right)}^m\hfill & \hfill x_i>a\\ 0\hfill & \hfill -a<x_i<a\\ k{\left(-x_i-a\right)}^m\hfill & \hfill x_i<-a\end{array}$	[−50,50]	0
F13	$f_{13}\left(x\right)=0.1\{{\sin }^2\left(3\pi x_i\right)+{\displaystyle \sum }_{i=1}^n{\left(x_i-1\right)}^2\left[1+{\sin }^2\left(3\pi x_i+1\right)\right]+{(x_n-1)}^2\left[1+{\sin }^2\left(2\pi x_n\right)\right]+{\displaystyle \sum }_{i=1}^n\mu \left(x_i,5,100,4\right)$	[−50,50]	0
F14	$f_{14}\left(x\right)={\left(\frac{1}{500}+{\displaystyle \sum }_{j=1}^{25}\frac{1}{j+{{\displaystyle \sum }}_{i=1}^2{\left(x_i-a_{ij}\right)}^6}\right)}^{-1}$	[−65,65]	1
F15	$f_{15}\left(x\right)={\displaystyle \sum }_{i=1}^{11}{\left[a_i-\frac{x_1\left(b_i^2+b_i{x}_2\right)}{b_i^2+b_i{x}_3+x_4}\right]}^2$	[−5,5]	0.00030
F16	$f_{16}\left(x\right)=4x_1^2-2.1x_i^4+\frac{1}{3}{x}_1^6+x_1{x}_2-4x_2^2+4x_2^4$	[−5,5]	−1.0316
F17	$f_{17}\left(x\right)={\left(x_2-\frac{5.1}{4{\pi }^2}{x}_1^2+\frac{5}{\pi }{x}_1-6\right)}^2+10\left(1-\frac{1}{8\pi }\right)\cos x_1+10$	[−5,5]	0.398
F18	$f_{18}\left(x\right)=\left[1+{\left(x_1+x_2+1\right)}^2\left(19-14x_1+3x_1^2-14x_2+6x_1{x}_2+3x_2^2\right)\right]\times \left[30+{\left(2x_1-3x_2\right)}^2\times \left(18-32x_1+12x_1^2+48x_2-36x_1{x}_2+27x_2^2\right)\right]$	[−2,2]	3
F19	$f_{19}\left(x\right)=-{\displaystyle \sum }_{i=1}^4{c}_i\exp \left(-{\displaystyle \sum }_{j=1}^3{a}_{ij}{\left(x_{j-}{p}_{ij}\right)}^2\right)$	[1,3]	−3.86
F20	$f_{20}\left(x\right)=-{\displaystyle \sum }_{i=1}^4{c}_i\exp \left(-{\displaystyle \sum }_{j=1}^6{a}_{ij}{\left(x_{j-}{p}_{ij}\right)}^2\right)$	[0,1]	−3.32
F21	$f_{21}\left(x\right)=-{\displaystyle \sum }_{i=1}^5{\left[\left(X-a_i\right){\left(X-a_i\right)}^T+c_i\right]}^{-1}$	[0,10]	−10.1532
F22	$f_{22}\left(x\right)=-{\displaystyle \sum }_{i=1}^7{\left[\left(X-a_i\right){\left(X-a_i\right)}^T+c_i\right]}^{-1}$	[0,10]	−10.4028
F23	$f_{23}\left(x\right)=-{\displaystyle \sum }_{i=1}^{10}{\left[\left(X-a_i\right){\left(X-a_i\right)}^T+c_i\right]}^{-1}$	[0,10]	−10.5363
CEC’14 Test Functions
F24	Composition Function 1 (N = 5)	$\left[-100,100\right]$	2300
F25	Composition Function 2 (N = 3)	$\left[-100,100\right]$	2400
F26	Composition Function 3 (N = 3)	$\left[-100,100\right]$	2500
F27	Composition Function 4 (N = 5)	$\left[-100,100\right]$	2600
F28	Composition Function 5 (N = 5)	$\left[-100,100\right]$	2700
F29	Composition Function 6 (N = 5)	$\left[-100,100\right]$	2800
F30	Composition Function 7 (N = 3)	$\left[-100,100\right]$	2900
F31	Composition Function 8 (N = 3)	$\left[-100,100\right]$	3000

, presenting the benchmark function. There are six classical algorithms: GWO [132], MVO [107], WOA [93], SCA [139], SSA [110], MFO [140], and five improved grey wolf optimization algorithms: IGWO [100], HGWO [119], MEGWO [141], CAGWO [96], and RWGWO [142] that are compared to ensure the fairness of the experiments [143]. All experiments were coded on Matlab2018b. All experiments were performed using the same computer with a 3.40 GHz Intel® Core i7 processor and 16GB RAM. The population size was set to 30, and the maximum number of evaluations was set to 300,000. To make the experiments less affected by random conditions, the Wilcoxon signed-rank test [144] and the Freidman test [145] were also used to check the experimental results.

3.1. Benchmark Function Validation

The convergence curves of SLEGWO and other compared algorithms on unimodal, multimodal, and combinatorial functions with the number of evaluations set to 300,000 times are shown in Figure 2. From the results of the convergence curves, it was evident that the convergence is faster, and the convergence accuracy is better than other algorithms on F8, F21, F27, F28, F29, and F30. It is better than other algorithms because the position-based learning strategy is carried out in the initial stage, which converges toward more high-quality solutions in the search space at the beginning of the population iteration. It is better to avoid falling into the local optimum, so it can be seen that the strategy used in this paper can effectively help converge to the optimal value quickly. Using the foraging mechanism of SMA and LF to keep SLEGWO improving both exploration and detection. Meanwhile, GS is helping to improve the quality of the optimal solution while accelerating the convergence speed. In general, SLEGWO can quickly approach the global optimal solution in the initial solution stage and converge extremely fast compared to other algorithms.

3.2. Comparison with Competitive Algorithms

In this part, SLEGWO is compared with 10 competitors on F1–F30 in

Table 1. The comparison of SLEGWO and other competitors in F1–F30.

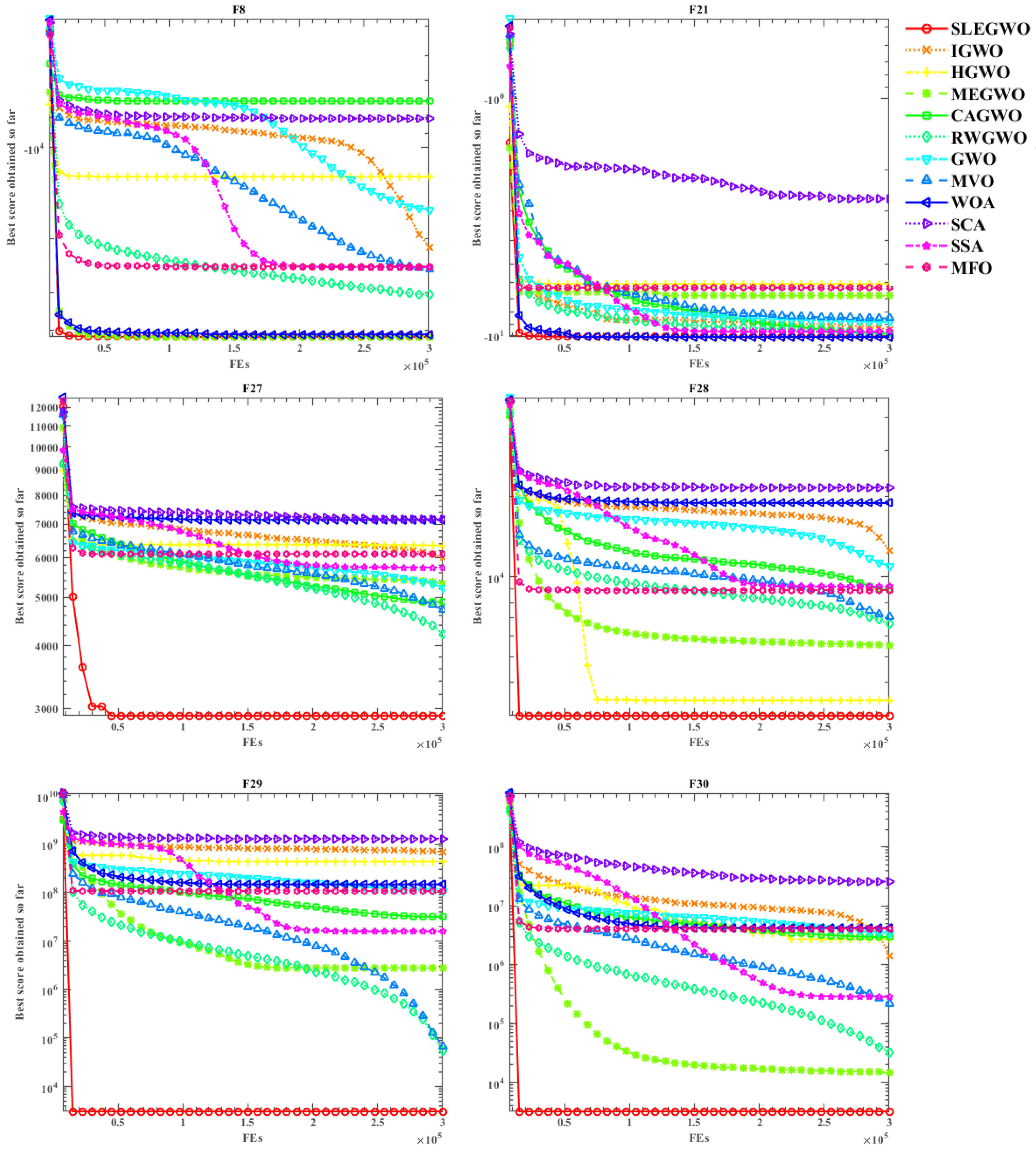
Fun	Item	SLEGWO	IGWO	HGWO	MEGWO	CAGWO	RWGWO	GWO	MVO	WOA	SCA	SSA	MFO
F1	AVG	−1331.51	2.7 × 10−227	2.1 × 10−109	1.7 × 10−224	0	0	0	0.377589	0	67.30338	7.34 × 10−8	23,158.27
	STD	2360.505	0	1.1 × 10−108	0	0	0	0	0.069891	0	129.9382	6.24 × 10−9	14,153.6
F2	AVG	7.34 × 10−8	1.8 × 10−155	8.99 × 10−57	6 × 10−169	0	5.5 × 10−199	1.4 × 10−195	155.4305	0	1.56 × 10−10	6.758953	171.437
	STD	6.24 × 10−9	6.8 × 10−155	3.26 × 10−56	0	0	0	0	159.9712	0	8.28 × 10−10	3.344396	58.2167
F3	AVG	0	1.97 × 10−10	3.95 × 10−60	7.752124	0	0.004055	1.64 × 10−39	2654.797	113,898.4	91623	1693.51	121,429.3
	STD	0	8.66 × 10−10	1.2 × 10−59	8.899336	0	0.016243	9 × 10−39	490.6424	65,149.74	25,312.9	693.5275	70,381.1
F4	AVG	1.64 × 10−39	26.53917	1.18 × 10−41	0.001197	0	1.14 × 10−12	1.42 × 10−46	11.58725	69.67589	68.89166	23.12652	93.5248
	STD	9 × 10−39	10.05357	1.36 × 10−41	0.004828	0	4.66 × 10−12	7.76 × 10−46	3.949519	30.25219	5.572644	2.548403	1.72357
F5	AVG	0	93.94355	97.61669	74.7726	97.35178	95.96096	96.90633	302.6562	94.80001	4,343,512	133.4677	30,236,771
	STD	0	0.156227	0.530452	34.0226	0.694438	0.895951	1.008211	423.8337	0.297515	6,348,072	71.87389	39,297,288
F6	AVG	97.61669	0.058413	14.83148	0	5.654709	2.478095	8.969564	0.400519	0.003117	245.7205	7.14 × 10−08	21,686.28
	STD	0.530452	0.020347	0.987473	0	1.463226	0.660457	1.080796	0.059468	0.000823	711.4785	8.23 × 10−09	13,877.34
F7	AVG	0.00071	0.000509	3.77 × 10−6	0.000245	2.32 × 10−5	0.000734	0.000158	0.05959	0.000203	2.733715	0.1504	132.9684
	STD	0.000299	0.000297	3.36 × 10−6	0.000188	1.85 × 10−5	0.000178	6.27 × 10−5	0.01153	0.000252	3.958237	0.031311	78.8043
F8	AVG	7.14 × 10−8	−21,283.8	−12457.6	−41,898.3	−7037.65	−30,495.8	−16,019.5	−25,055.5	−41,100.5	−8050.41	−24,731.5	−24,574.7
	STD	8.23 × 10−9	1543.243	1104.052	7.4 × 10−12	678.0691	805.3699	2207.976	1544.938	1334.409	301.3053	1685.193	2796.393
F9	AVG	0.000203	0	0	3.79 × 10−14	0	0.573707	0	545.265	0	92.62241	204.2647	639.1003
	STD	0.000252	0	0	6.89 × 10−14	0	1.809054	0	73.43741	0	72.46977	34.67572	79.74732
F10	AVG	−16,019.5	19.96771	8.88 × 10−16	9.65 × 10−15	8.88 × 10−16	9.65 × 10−15	1.51 × 10−14	4.182003	3.02 × 10−15	18.62133	3.689958	19.91576
	STD	2207.976	0.005099	0	3.58 × 10−15	0	3.06 × 10−15	1.62 × 10−15	6.099735	2 × 10−15	5.368344	1.345793	0.054933
F11	AVG	0	0	0	0	0	0.001574	0	0.443156	0	1.973343	0.005334	132.7391
	STD	0	0	0	0	0	0.004495	0	0.054693	0	2.377727	0.008451	107.7275
F12	AVG	8.88 × 10−16	0.010058	0.422108	4.71 × 10−33	0.090109	0.032334	0.209642	3.720577	4.46 × 10−5	5,621,433	10.17	68,877,889
	STD	0	0.004419	0.019583	1.39 × 10−48	0.034777	0.004912	0.053209	0.981665	8.97 × 10−6	7,403,512	2.683234	1.34 × 108
F13	AVG	−1.8 × 1020	8.335435	8.021308	1.35 × 10−32	5.733004	3.050118	5.68814	0.59167	0.016182	12,643,164	131.1453	1.78 × 108
	STD	7.23 × 1020	0.234103	0.453929	5.57 × 10−48	2.340503	0.511731	0.386743	1.367509	0.029934	23,872,069	32.14261	2.51 × 108
F14	AVG	0.005334	0.998004	2.099489	1.776171	1.098259	0.998004	3.083372	0.998004	0.998004	0.998004	0.998004	2.015553
	STD	0.008451	3.82 × 10−15	1.077885	2.961409	0.399314	1.68 × 10−13	3.929513	2.28 × 10−13	1.43 × 10−14	5.01 × 10−7	1.89 × 10−16	2.201543
F15	AVG	4.46 × 10−5	0.000369	0.000639	0.000338	0.000397	0.000491	0.005717	0.007869	0.000433	0.000493	0.000718	0.001625
	STD	8.97 × 10−6	0.000232	0.001003	0.000167	6.18 × 10−5	0.000373	0.008986	0.009677	0.000285	0.00035	0.000412	0.003828
F16	AVG	5.68814	−1.03163	−1.03163	−1.03163	−1.03163	−1.03163	−1.03163	−1.03163	−1.03163	−1.03163	−1.03163	−1.03163
	STD	0.386743	3.14 × 10−13	1.95 × 10−6	5.42 × 10−16	3.55 × 10−9	1.78 × 10−11	3.69 × 10−11	2.79 × 10−9	1.42 × 10−14	2.22 × 10−6	5.71 × 10−16	6.78 × 10−16
F17	AVG	1.098259	0.397887	0.39789	0.397887	0.397887	0.397887	0.397887	0.397887	0.397887	0.397951	0.397887	0.397887
	STD	0.399314	3.19 × 10−11	1.68 × 10−5	0	5.19 × 10−8	1.14 × 10−9	7.56 × 10−10	9.03 × 10−10	2.2 × 10−10	5.63 × 10−5	0	0
F18	AVG	0.000639	3	3	3	3	3	3	3	3	3	3	3
	STD	0.001003	3.33 × 10−14	4.83 × 10−10	7.24 × 10−14	2.56 × 10−7	6.81 × 10−8	1.24 × 10−7	1.55 × 10−8	6.08 × 10−8	1.67 × 10−7	1.52 × 10−14	1.76 × 10−15
F19	AVG	−2633.88	−3.86278	−3.85717	−3.86278	−3.86273	−3.86278	−3.86252	−3.86278	−3.86249	−3.85609	−3.86278	−3.86278
	STD	2563.64	2.27 × 10−9	0.002676	2.68 × 10−15	0.000129	1.69 × 10−7	0.001439	1.34 × 10−8	0.001435	0.002877	1.58 × 10−15	2.71 × 10−15
F20	AVG	−1.03163	−3.24669	−3.24217	−3.322	−3.30438	−3.25443	−3.25542	−3.24669	−3.22803	−2.86684	−3.21895	−3.2151
	STD	5.71 × 10−16	0.058279	0.078321	1.33 × 10−15	0.041476	0.060094	0.080108	0.058277	0.135411	0.488199	0.041107	0.0595
F21	AVG	0.397887	−9.47954	−6.06721	−6.80354	−9.82978	−9.8147	−8.78442	−8.4645	−10.1532	−2.6484	−9.64796	−6.30772
	STD	2.2 × 10−10	1.746857	1.351953	3.107006	1.230198	1.287595	2.309654	2.429039	5.8 × 10−7	2.331862	1.54164	3.330133
F22	AVG	3	−9.87278	−6.69993	−8.91454	−10.4025	−10.05	−10.2258	−9.34811	−10.4029	−4.45958	−10.2271	−8.1097
	STD	1.24 × 10−7	1.617665	1.753764	2.543845	0.000625	1.343317	0.970431	2.145711	6.37 × 10−7	2.903878	0.962918	3.3411
F23	AVG	−3.86273	−9.81849	−7.99209	−8.51432	−10.536	−10.5364	−10.5364	−9.27927	−10.5364	−6.15382	−10.0003	−7.32147
	STD	0.000129	1.861635	2.182385	2.972819	0.000355	1.01 × 10−6	9.19 × 10−7	2.317731	1.06 × 10−6	1.932419	1.635722	3.562409
F24	AVG	−3.24217	2600.009	2600	2763.339	2600	2600.036	2600.005	2807.984	2600.269	3019.457	2845.148	3248.063
	STD	0.078321	0.005171	0	2.7789	8.85 × 10−5	0.007925	0.002116	8.478631	0.367461	85.82027	13.46129	177.5211
F25	AVG	−10.1532	2700	2700	2756.081	2700	2753.5	2700	2743.85	2700	2871.156	2799.376	2810.309
	STD	9.8 × 10−6	8.86 × 10−13	0	12.3697	0	13.33252	1.41 × 10−12	4.905463	3.16 × 10−13	96.24425	15.91985	48.23941
F26	AVG	−9.64796	2718.352	2800	2783.706	2800	2812.046	2800	2800.153	2800	2886.275	2740.976	2887.716
	STD	1.54164	95.04286	0	37.86236	0	58.59796	1.34 × 10−12	18.78098	4.14 × 10−13	241.4137	50.13788	143.6934
F27	AVG	−10.4029	6011.265	6335.837	5323.321	4891.355	4228.536	5224.738	4720.318	7146.985	7161.302	5736.293	6105.338
	STD	6.37 × 10−7	156.9779	94.23755	138.0383	208.3492	339.0886	208.0741	192.8484	233.3886	130.8646	215.1167	156.7122
F28	AVG	−10.5364	12,575.68	3429.832	5495.977	8930.888	6662.108	10,987.61	7056.54	18,971.95	21,679.37	9192.939	8904.229
	STD	9.19 × 10−7	1323.278	2354.285	101.0421	1093.201	751.9647	1203.031	1010.415	3389.128	1042.555	1143.594	1121.484
F29	AVG	2600	6.89 × 108	4.32 × 108	2,779,972	31,623,999	55,133.71	1.07 × 108	68,226.85	1.47 × 108	1.29 × 109	15,809,171	1.08 × 108
	STD	8.85 × 10−5	2.9 × 108	2.73 × 108	15,188,473	17,205,306	15,912.48	66,312,410	24,482.82	54,849,254	1.47 × 108	86,214,993	15,590,444
F30	AVG	2700	1,410,898	2,722,919	14,405.74	2,974,286	32,396.81	3,481,516	216,133.7	4,213,191	26,017,432	284,733.1	4,135,673
	STD	0	682,601.7	7,178,390	1356.606	886,199.6	6952.204	1,360,222	76,851.09	2,496,624	6,695,086	92,690.85	2,538,938

, which contains the AVG and STD of the experimental results of SLEGWO and other algorithms. The 10 competitive optimizers are GWO, MVO, WOA, SCA, SSA, MFO, IGWO, HGWO, MEGWO, CAGWO, and RWGWO. Including AVG, STD,

Table 2. Comparison results of SLEGWO with 10 other competitors on classical function.

Function	Rank	Mean	+/−/=
SLEGWO	1	2.3883	-
IGWO	5	6.3138	23/4/3
HGWO	9	6.7872	23/3/4
MEGWO	2	4.175	22/5/3
CAGWO	6	6.3994	23/3/4
RWGWO	3	5.8144	26/4/0
GWO	7	6.575	25/4/1
MVO	10	7.7883	24/3/3
WOA	4	5.8527	21/6/3
SCA	12	10.8522	27/2/1
SSA	8	6.6794	25/5/0
MFO	11	8.3738	27/2/1

shows the Mean, Rank, and result of the Wilcoxon sign rank test of experimental results and the results of the Freidman test.

According to the results shown in Table 1, SLEGWO works best. SLEGWO is the smallest on the average of 30 classical functions, which means that SLEGWO outperforms other improved algorithms in most benchmark functions. In addition, Table 2 shows the comparative results of the data analysis in Table 1 using the Wilcoxon signed-rank test and the Freidman test. The Mean indicates the result obtained from the analysis using the Freidman test, and the smaller the value of the Mean, the better the algorithm’s performance. Meanwhile, where “+” represents that SLEGWO performs better than others, “-” represents that SLEGWO performs worse than others, and “=” represents that the performance of SLEGWO and others is equal. It can be seen that SLWGWO has the best performance among the 30 benchmark functions. The second ranking is MEGWO; the RWGWO, IGWO, CAGWO, and HGWO have relatively insignificant advantages. It can be concluded that SLEGWO still performs better than the improved algorithms proposed in recent years on most of the benchmark function

4. SLEGWO Precision Fertilization Model

For the various mineral nutrients required by plants, Nitrogen (N), phosphorus(P), and potassium (K) play an important role in improving crop yields. The soil is both the place for terrestrial plants to take root and a supplier of mineral nutrients, and it bears the heavy burden of providing various nutrients. Therefore, crops N, P, and K are all needed in high amounts in the soil and are usually available in agricultural soils in sufficient quantities for crop uptake. These three nutrients are needed in relatively high amounts and are the most deficient elements in the soil. Therefore, these three nutrients are often supplemented by the artificial fertilizer application for crop uptake and utilization, called the three elements of fertilizer. This chapter describes the process of implementing the SLEGEO-based three-element NPK precision fertilization method, the experimental environment, and the dataset.

4.1. SLEGWO and NPK Precision Fertilization Method

The flowchart of SLEGWO for a precise fertilizer model of NPK quadratic equation according to the maize test field in Nong’an country, Jilin Province, China, is shown in Figure 3. Using 3414 experimental schedules to obtain different yields of NPK at different levels, SLEGWO processed the data to obtain the ternary quadratic nonlinear equation. The polynomial coefficients of the equation are negative according to the constraints of the rule of diminishing returns of N, P, and K, and the quadratic term coefficients respond to the fact that an increase in N, P, and K at a certain level can increase the yield, but as the amount of N, P and K input exceeds the demand, it is instead a reduction in yield. The primary term coefficient responds to the parameter constraint of multiple conditions such as yield increase effect, and the equation coefficients of the fertilizer effect function are obtained by fitting using the swarm intelligence optimization method. Then, the maximum value, that is, the maximum yield of the crop, is obtained from the function model of the obtained equation coefficients. Finally, the results of the derived model are evaluated using the coefficient of determination R².

4.2. Experimental Environment

The following experiments are conducted under the Windows 10 operating system using MATLAB R2018b, using hardware platform configuration Intel® Core i7 processor 3.40 GHz and 16GB RAM. To ensure the fairness of the experiments, all experiments are conducted under the conditions of equal parameter settings, the population number N is 30, the dimension of the objective function is 3, the maximum number of evaluations Max_iteration is set as 50,000 and followed by 30 parallel runs.

4.3. Experimental Dataset

This paper used a maize test field in Nong’an County, Jilin Province [146] as the experimental site. The “3414” method was used as a fertilizer effect field experiment, where “3414” refers to 3 factors, 4 levels, and 14 different treatments of N, P, and K. Level 0 is no fertilizer application; level 2 is the optimal fertilizer application. Level 1 1 = level 2 $\times$0.5, level 3 = level 2 $\times$ 1.5 (over-fertilization). The area of each plot was 30 m², no replication, and randomized. The experiments were based on the regional soil nutrient abundance index and the fertilizer nutrient application index to determine the relative optimum fertilizer application. Level 2 for $N,P_2{O}_5,K_{2}O$ at 180 kg/hm², 75 kg/hm², and 90 kg/hm² respectively. For fitting using the ternary quadratic fertilizer effect model [34], the equations used were:

$${\widehat{y}}_1=b_0+b_1{x}_1+b_2{x}_2+b_3{x}_3+b_4{x}_1^2+b_5{x}_2^2+b_6{x}_3^2+b_7{x}_1{x}_2+b_8{x}_1{x}_3+b_9{x}_2{x}_3,$$

(30)

where ${\widehat{y}}_1$ is the predicted value of the fertilizer effect function model; $b_0$ is the yield without fertilizer application, and $b_1,b_2,b_3,\dots ,b_9$ are the effect coefficients.

Table 3. Dataset obtained from the test field ($\mathrm{Kg}/{\mathrm{hm}}^2$).

Label	Proportion	N(x1)	P2O5(x2)	K2O(x3)	Yield(y)
1	N0P0K0	0	0	0	5805
2	N0P2K2	0	75	75	7290
3	N1P2K2	90	75	75	8385
4	N2P0K2	180	0	75	6930
5	N2P1K2	180	37.5	75	8115
6	N2P2K2	180	75	75	9000
7	N2P3K2	180	112.5	75	8580
8	N2P2K0	180	75	0	7350
9	N2P2K1	180	75	37.5	8475
10	N2P2K3	180	75	112.5	8460
11	N3P2K2	270	75	75	8445
12	N1P1K2	90	37.5	75	7545
13	N1P2K1	90	75	37.5	7845
14	N2P1K1	180	37.5	37.5	7575

below shows the fertilizer use and yield at each plot of the experiment, where x₁, x₂, x₃ are the fertilizer application amounts of N, P, and K, and y is the actual yield.

Based on the experimental data in Table 3, the experiments were conducted using the “3414” field experiment design and data.

4.4. Solution of Equation Coefficients

The fertilizer effect model, an $\mathrm{n}$-dimensional space composed between crop yield $\mathrm{y}$ and the individual total nutrient influences $x$. According to the NPK fertilizer effect function Equation (31):

Set $X_1=x_1,X_2=x_2,\dots \dots X_9=x_2{x}_3$. Then, the ternary quadratic polynomial regression equation is change into a nine-element linear regression equation.

$$\widehat{y}=b_0+b_1{X}_1+b_2{X}_2+b_3{X}_3+b_4{X}_4+b_5{X}_5+b_6{X}_6+b_7{X}_7+b_8{X}_8+b_9{X}_9$$

(31)

The residual function in the least square method is used as the objective function.

$$\begin{gathered} \mathrm{Q}={{\displaystyle \sum }}_{i=1}^N(y_i-{\widehat{y}}_i){}^2=, \\ {{\displaystyle \sum }}_{i=1}^N(y_i-b_0+b_1{X}_{i1}+b_2{X}_{i2}+b_3{X}_{i3}+b_4{X}_{i4}+b_5{X}_{i5}+b_6{X}_{i6}+b_7{X}_{i7}+b_8{X}_{i8}+b_9{X}_{i9}){}^2, \end{gathered}$$

(32)

where N is 14 and $y_i$ is the true yield in the dataset.

The residual function’s minimum value is obtained to obtain better results using a shorter time. In the experiments of this section, the algorithm containing SLEGWO with the original GWO is applied to find the fertilizer effect function. The upper and lower bounds for the values of each coefficient are set as shown in

Table 4. The upper and lower limits of each coefficient.

Coefficient	b0	b1	b2	b3	b4	b5	b6	b7	b8	b9
Lower limit	4000	1	1	1	−50	−50	−50	0.01	0.01	0.01
Upper limit	7000	10	50	50	0	0	0	50	50	50

.

Table 5. Coefficients of fertilizer effect function obtained by different methods.

Method	SLEGWO	GWO
b0	5754.329	5751.6511
b1	7.0731	6.9660
b2	28.3594	29.4164
b3	12.8472	16.0958
b4	−0.0259	−0.0346
b5	−0.1853	−0.2085
b6	−0.154	−0.1927
b7	0.1131	0.0312
b8	0.0469	0.0642
b9	0.0841	0.0614

shows the values of each coefficient in the fertilizer effect function using SLEGWO, which has the better competitive performance in finding the minimum of the residual function. Appendix A

Table A1. Results of the coefficients of the fertilizer equation by SLEGWO.

b0	b1	b2	b3	b4	b5	b6	b7	b8	b9	Q
5754.329	7.073107	28.35942	12.84725	0.011312	0.04699	0.084148	−0.02597	−0.18531	−0.15405	378,509.5
5700	6.622148	28.80353	12.33958	0.011401	0.013812	0.011282	−0.01882	−0.16126	−0.06424	691,006.4
5700	5.479195	28.01243	15.16322	0.011465	0.010854	0.01622	−0.01345	−0.15021	−0.09395	694,599.6
5762.077	6.904515	28.05115	10.47243	0.043093	0.010225	0.058764	−0.02449	−0.21705	−0.06216	610,291.9
5700	6.104488	28	15.02233	0.018366	0.011503	0.021621	−0.01745	−0.16983	−0.09064	624,800.3
5702.778	6.399281	28.16619	12.26713	0.030507	0.015354	0.010606	−0.0217	−0.17566	−0.06105	621,190.5
5701.892	7.79628	28	10.353	0.041675	0.013482	0.010371	−0.0292	−0.18804	−0.03855	672,781.8
5722.567	5.734792	28.15601	14.46746	0.01993	0.026555	0.027083	−0.01951	−0.16689	−0.10974	518,099.3
5700	5.491433	28	10	0.013663	0.01024	0.010007	−0.01364	−0.15612	−0.01992	869,026.9
5706.218	6.129533	28.06963	10	0.014334	0.011943	0.010116	−0.01638	−0.1582	−0.02933	789,519.8
5702.219	5.646291	28.3347	12.32205	0.010636	0.018197	0.011328	−0.01505	−0.15043	−0.06833	684,916.4
5705.509	6.583881	28	10.07989	0.027872	0.014446	0.013401	−0.02179	−0.1748	−0.03309	710,139.9
5706.647	9.097236	28	11.64792	0.017451	0.029039	0.084579	−0.03131	−0.1998	−0.12073	417,860.8
5700	6.230138	28.20619	16.21636	0.01431	0.017633	0.012196	−0.0188	−0.15939	−0.11188	601,844.3
5700	6.056048	28.09793	15.94561	0.01156	0.026461	0.011424	−0.01904	−0.15303	−0.1178	559,427.1
5700	5.962434	28.48493	12.06434	0.014213	0.014852	0.019599	−0.01578	−0.15955	−0.07186	668,617.9
5700	6.039274	28.24675	13.39305	0.018857	0.025993	0.031801	−0.01911	−0.1691	−0.10307	527,288.7
5700	7.682415	28.18741	15.40904	0.011728	0.014294	0.012234	−0.02345	−0.15898	−0.10619	648,384.1
5708.004	7.300888	28.02038	12.34074	0.018653	0.017688	0.054421	−0.02195	−0.18414	−0.09667	525,116.4
5700	5.160513	28.02297	17.15531	0.021925	0.011809	0.028064	−0.01411	−0.17268	−0.11936	607,321.7
5745.965	5.06117	28.71811	13.78617	0.018855	0.040242	0.010975	−0.01961	−0.15702	−0.1131	501,225.8
5700	6.710944	28.35967	10.03877	0.01648	0.01436	0.010426	−0.02064	−0.16293	−0.03089	754,172.2
5710.19	5.57907	29.88454	10.89311	0.014254	0.023855	0.019157	−0.01607	−0.17357	−0.06818	645,510.9
5700.825	6.813902	28.2746	13.72604	0.011531	0.015544	0.049297	−0.01864	−0.1753	−0.10555	565,872.4
5700	6.327866	28	10.05013	0.012763	0.010402	0.012482	−0.01699	−0.15877	−0.02423	821,978.9
5700	5.86649	28	17.78831	0.031923	0.011352	0.016264	−0.01981	−0.1828	−0.11598	555,851.4
5700	5.574536	28	17.92274	0.012501	0.015183	0.012418	−0.01497	−0.15486	−0.12827	645,713.3
5700	5.270098	28.57715	10	0.01283	0.010091	0.011834	−0.01221	−0.16169	−0.02151	879,075.7
5700	5.828422	28	10.0153	0.015201	0.010711	0.016403	−0.01491	−0.16125	−0.02815	807,022.9
5711.885	5.173948	28.43892	10	0.024884	0.011094	0.010503	−0.0152	−0.17553	−0.01453	873,579

shows the results of the coefficients of the fertilizer equation by SLEGWO by random run 30 times.

4.5. Model Evaluation and Yield Estimation

4.5.1. Model Evaluation

The coefficient of determination $R^2$ s used to evaluate the model. The $R^2$ can be used to test how well the model fits the sample data and takes values between 0 and 1. The closer the value of the $R^2$ is to 1, the better the model fits. The models with higher coefficients of determination are usually used in real-world problems. The formula for the coefficient of determination $R^2$ is shown below.

$$\begin{array}{c}{R}^2=1-\frac{{{\displaystyle \sum }}_i{\left({\widehat{y}}_i-y_i\right)}^2}{{{\displaystyle \sum }}_i{\left(y_i-\overline{y}\right)}^2},\end{array}$$

(33)

where ${\widehat{y}}_i$ s the predicted value of the fertilizer effect function model; $\overline{y}$ is the average of the actual yield; and $y_i$ is the actual yield.

Table 6. The coefficients of determination of fertilizer effect function models.

Method	SLEGWO	GWO
R2	0.9646	0.9645

shows the values of the $R^2$ for the two kinds of fertilizer effect function models—SLEGWO and GWO.

Table 6 above shows that the fertilizer effect function obtained with SLEGWO is better than GWO.

4.5.2. Yield Estimation

The SLEGWO was used to obtain the maximum fertilizer effect function models yield of the crop. The objective function is the fertilizer effect residual function with dimension 3, corresponding to the fertilizer effect function model of nitrogen, phosphorus, and potassium fertilizer application, respectively. The upper and lower bounds for each dimension are $d_1\in \left[0,300\right],d_2\in \left[0,120\right],\mathrm{and}{d}_3\in \left[0,120\right]$, and the maximum number of iterations of the algorithm is 50,000 with a population size of 30.

Table 7. Nitrogen, phosphorus, potassium fertilizer, and the corresponding maximum yield of different models.

(Kg/hm2)	SLEGWO	GWO	ABC	BA	SSA	PSO	WOA
Nitrogen	251.1772	233.762	233.9363	233.9625	233.9363	233.937	233.9363
Phosphorus	107.2981	103.893	103.2966	103.2954	103.2966	103.2992	103.2966
Potassium	107.748	97.959	97.71588	97.71619	97.71588	97.718	97.71587
Maximum yield	8947.845	8886.522	8877.856	8877.856	8877.856	8877.856	8877.856

lists the maximum crop yields and the corresponding NPK fertilizer applications according to SLEGWO and the other six algorithm models. Appendix A

Table A2. Nitrogen, phosphorus, potassium, and yield prediction by SLEGWO.

N	P	K	Y *
266.2026	108.4913	112.874	8948.987
261.4381	109.8989	109.8989	8949.758
254.7399	110.5993	110.5992	8949.103
265.0755	109.474	109.474	8948.769
258.5937	111.184	111.1842	8949.649
259.9413	108.8042	108.525	8949.043
256.7255	107.7489	107.748	8948.295
258.9043	109.2919	109.2919	8949.622
257.1843	109.6504	109.6164	8949.652
262.3832	109.6065	109.6096	8949.502
260.405	107.2981	109.1784	8948.779
265.1687	107.8935	112.7555	8948.779
258.2416	110.0589	110.0589	8949.828
265.092	107.9177	110.0326	8948.638
262.595	110.314	110.2932	8949.73
263.7118	108.1379	112.1662	8949.365
257.9559	109.4389	109.4389	8949.663
257.3209	110.5453	110.5434	8949.69
254.3663	110.1731	107.8439	8947.991
259.3602	110.6875	111.2366	8949.964
258.8103	110.2831	110.2883	8949.879
263.7813	109.837	109.837	8949.352
259.555	108.0039	108.0016	8948.47
260.736	110.7611	110.7606	8949.894
260.8581	109.1714	109.0368	8949.347
261.2375	111.0092	111.0274	8949.847
261.1015	107.9926	108.0165	8948.245
251.8526	107.7699	108.3058	8947.845
261.6727	109.2414	109.1431	8949.313
251.1772	109.3376	108.6273	8947.898

* Y is the predicted yield.

expresses the result of nitrogen, phosphorus, potassium, and yield prediction by SLEGWO 30 times randomly.

The above experiments demonstrate the superiority of SLEGWO over other comparative swarm intelligence optimization algorithms in solving the fertilizer effect function model. Swarm intelligence optimization has the advantage of internal constructs encapsulability and better portability than traditional methods and also has some advantages in the maximum yield obtained. It can be seen that GWO works better compared to other algorithms, so it is good to choose GWO as the improved base algorithm for the improved algorithm. Other optimization algorithms have no apparent advantages.

5. Discussions

The performance of the proposed GWO-based method is not limited to yield estimation, and it can also be tested based on other real-world applications, such as energy storage planning and scheduling [147], service ecosystem [148,149], image editing [150,151,152], epidemic prevention and control [153,154], social recommendation and QoS-aware service composition [155,156,157], active surveillance [158], large scale network analysis [159], spatial analysis [160], crop evapotranspiration prediction [161], control engineering [162,163], pedestrian dead reckoning [164] and evaluation of human lower limb motions [165]. The SLEGWO proposed is based on the improved GWO multi-strategy optimization method and it is applied to solve the fertilizer effect function, which is a new idea based on the traditional precision fertilizer application operation technology. It performs well in equation coefficient solving fitting and maximum yield solving. Exploring the method of combining swarm intelligence optimization algorithm with fertilizer effect function can help provide a new solution for precision agriculture. Since there are many uncertainties in the agricultural production process and the final criteria cannot be fully determined by a particular method, the swarm intelligent optimization method can be used to present multiple possibilities of validation results under multiple random conditions, which is more in line with the real needs than traditional validation methods such as regression.

6. Conclusions

In this paper, a multi-strategy grey wolf optimization algorithm (SLEGWO) is proposed. Using an opposition-based learning strategy increases the number of early high-quality solutions, and the slime foraging and Levy flight strategies effectively avoid falling into local optima and increase the algorithm’s ability to balance exploration and detection. The greedy selection strategy speeds up the final convergence to the optimal solution quickly. The SLEGWO algorithm outperforms other competing algorithms on both the classical function set and the CEC2014 function. Meanwhile, the SLEGWO algorithm applied to optimize the model for solving the fertilizer effect function in the maize NPK “3414” program obtained higher accuracy and more yield with good stability, which is an effective method to optimize the model for accurate prediction fertilizer application. It improves the scientific and scalability of the soil test and fertilizer application relationship model. However, since the constraints of the engineering problem are determined by the actual requirements and scenarios, the required constraints will increase when the algorithm is applied in practice. Therefore, the experimental results as well as the actual constraints may lead to deviations in the results but will not affect the application of the method.

In future research work, the SLEGWO algorithm will explore a library of pre-defined fertilization models with multiple model fits to address the scientific fertilization management needs of different regions and different needs. The SLEGWO algorithm will also be effectively used in more areas of agricultural engineering optimization problems, such as supply chain optimization problems, to improve the thematic research on agricultural engineering optimization problems and improve the yield and efficiency of agricultural products to create a cleaner agricultural practice.