A Novel Fundamental Frequency Switching Operation for Conventional VSI to Enable Single-Stage High-Gain Boost Inversion with ANN Tuned QWS Controller
Abstract
:1. Introduction
- Low PIV across switches;
- Low total blocking voltage (TBV) of converter, signifying minimal semiconductor loss;
- Filter-free low THD output waveform;
- Fundamental-frequency switching eliminates switching losses;
- Supports resistive, inductive as well as non-linear loads;
- Low passive component requirement.
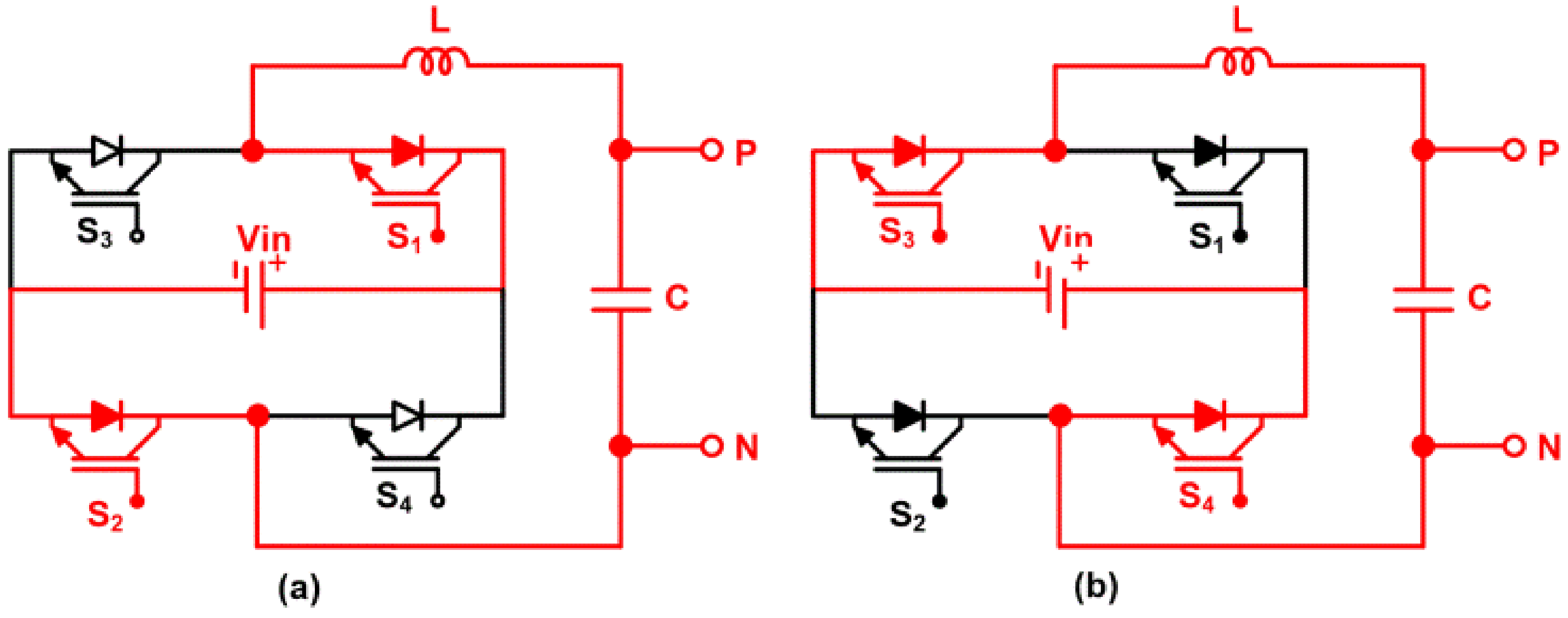
2. Circuit Operation
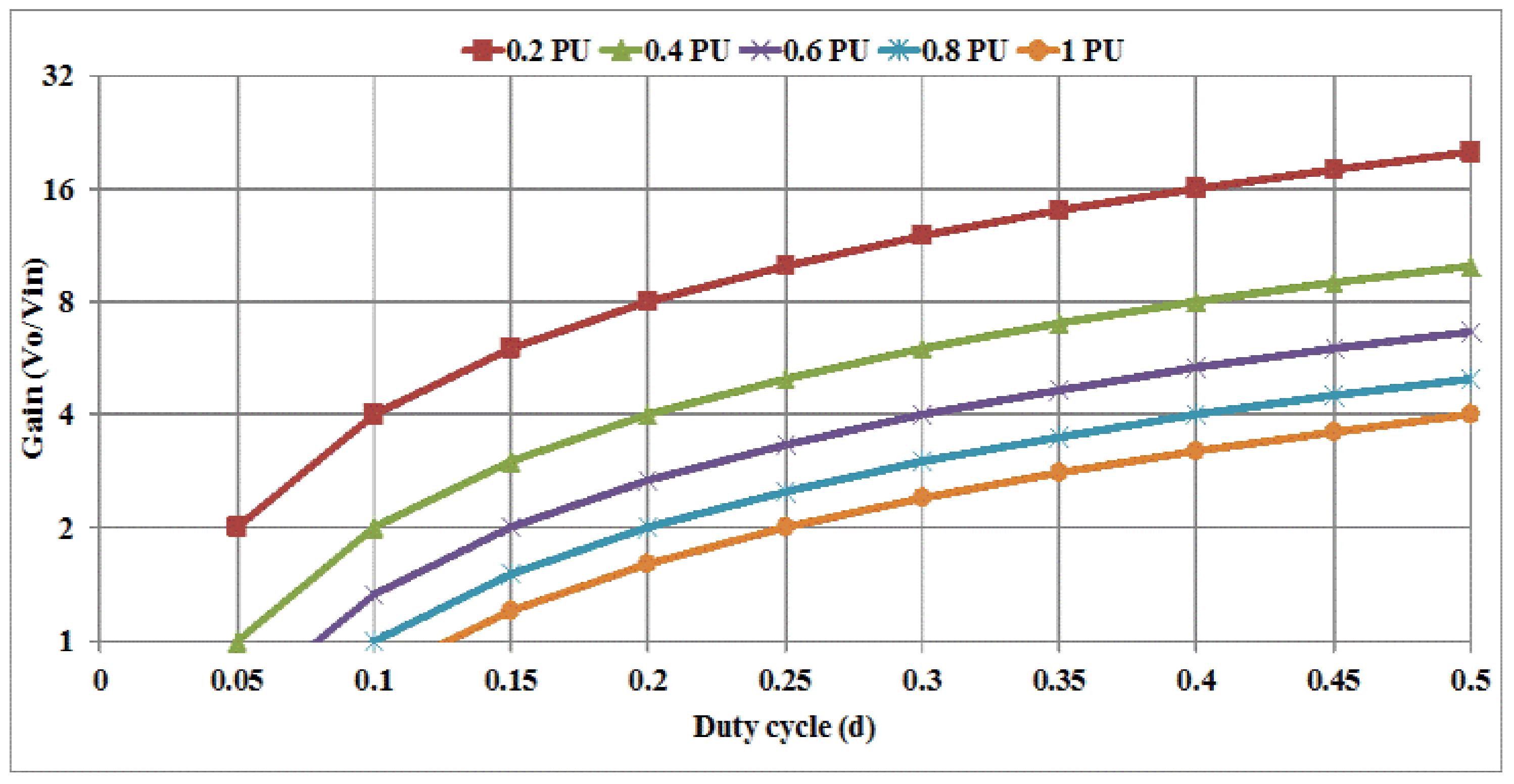
2.1. Steady-State and Dynamic Operation
2.2. Loss and Efficiency Calculation
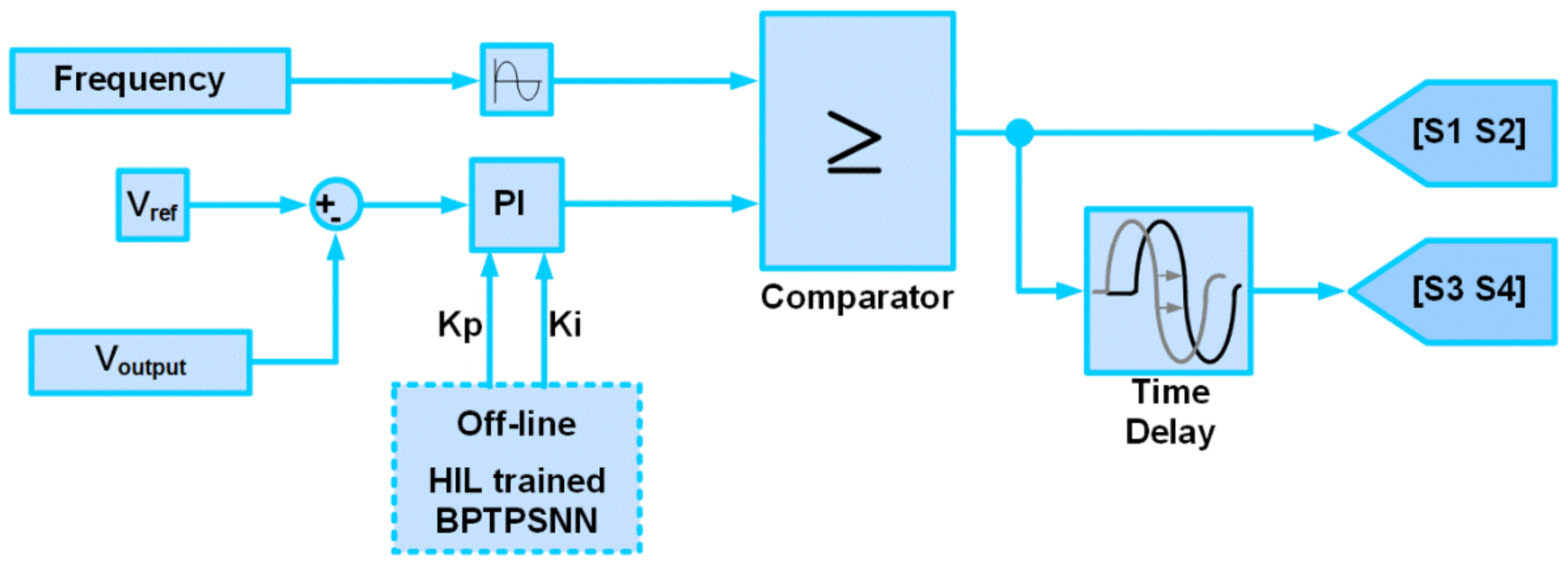
3. Variable Voltage Variable Frequency Controller
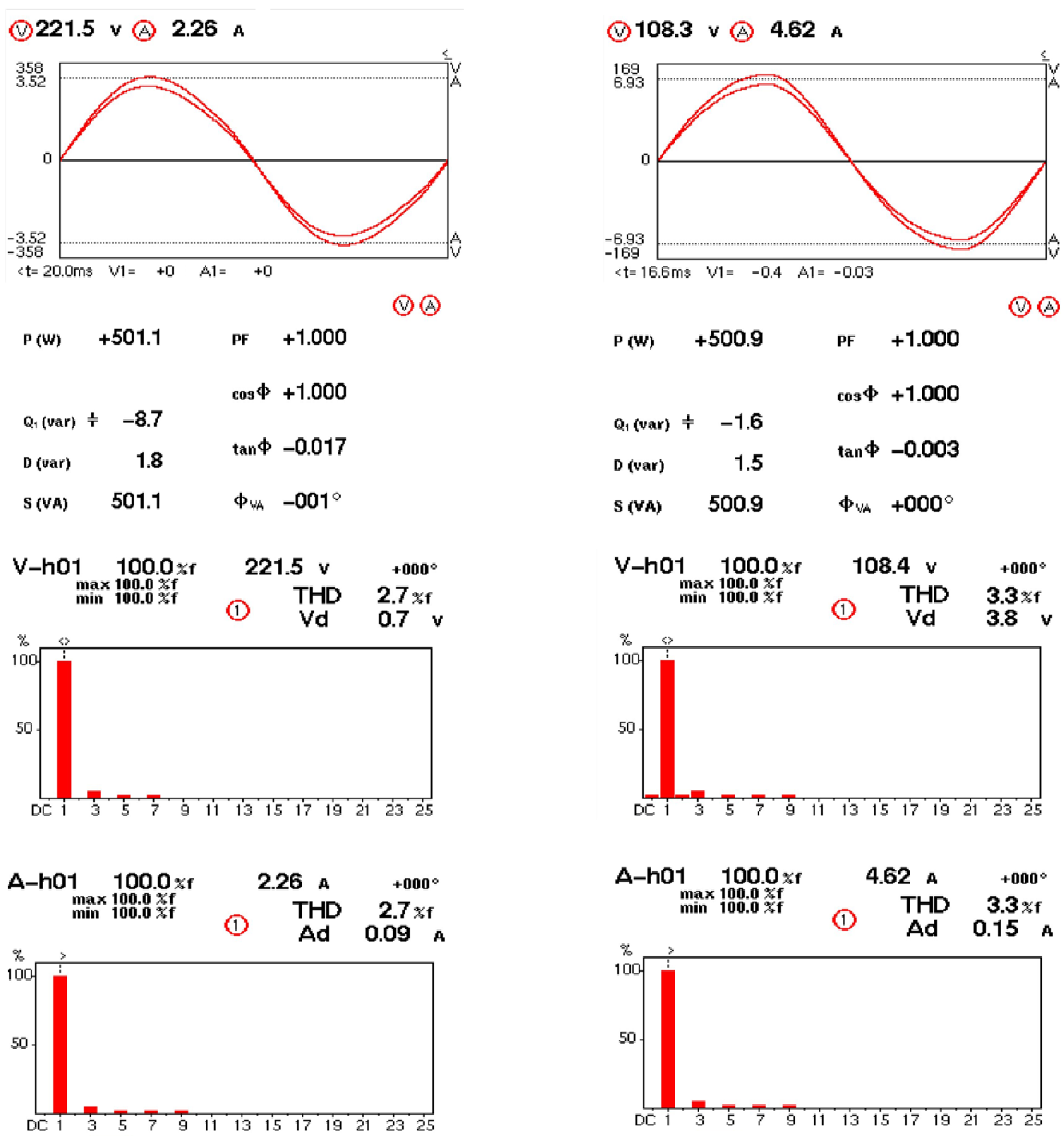
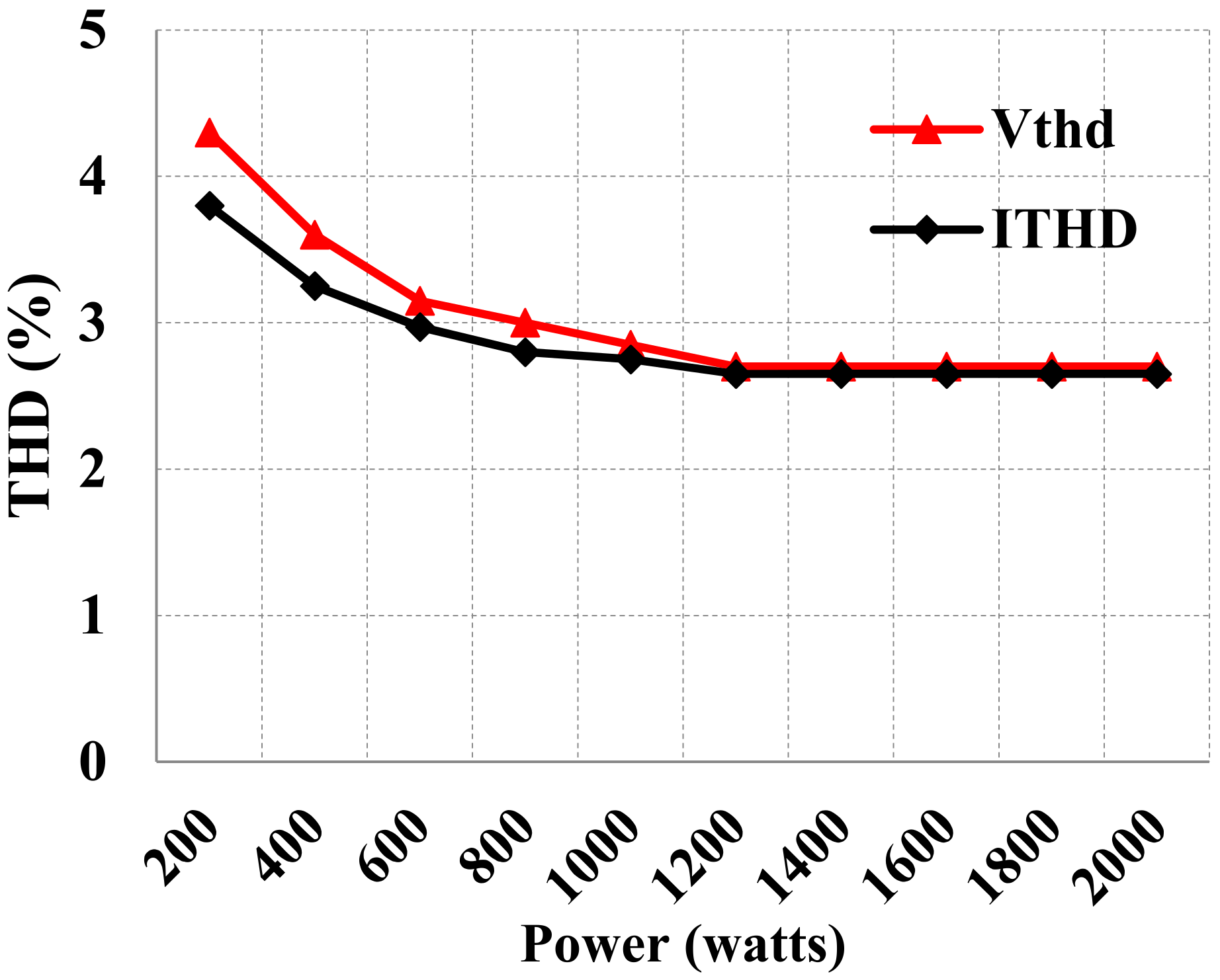
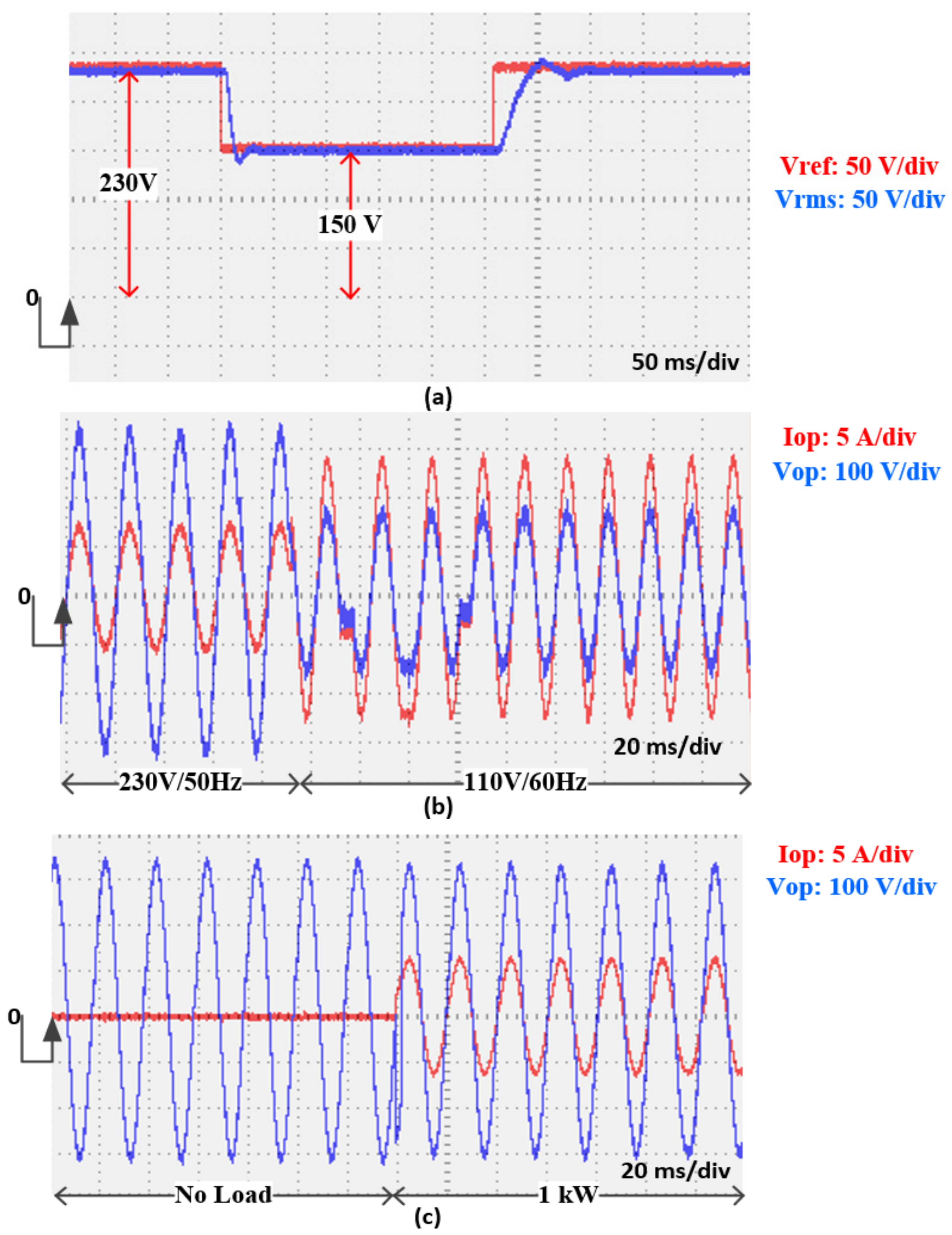
4. Experimental Validation
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- International Renewable Energy Agency. Global Renewables Outlook: Energy Transformation 2050; International Renewable Energy Agency: Abu Dhabi, United Arab Emirates, 2020; ISBN 978-92-9260-238-3. [Google Scholar]
- Javed, K.; Ashfaq, H.; Singh, R.; Hussain, S.M.S.; Ustun, T.S. Design and Performance Analysis of a Stand-alone PV System with Hybrid Energy Storage for Rural India. Electronics 2019, 8, 952. [Google Scholar] [CrossRef] [Green Version]
- Ustun, T.S.; Aoto, Y. Analysis of Smart Inverter’s Impact on the Distribution Network Operation. IEEE Access 2019, 7, 9790–9804. [Google Scholar] [CrossRef]
- Islam, R.; Mahfuz-Ur-Rahman, A.M.; Muttaqi, K.M.; Sutanto, D. State-of-the-Art of the Medium-Voltage Power Converter Technologies for Grid Integration of Solar Photovoltaic Power Plants. IEEE Trans. Energy Convers. 2019, 34, 372–384. [Google Scholar] [CrossRef]
- Jiahui, J.; Yanhui, Q.; Daolian, C. A distributed maximum power point tracking flyback type PV grid-connected inverter. In Proceedings of the IECON 2017—43rd Annual Conference of the IEEE Industrial Electronics Society, Beijing, China, 29 October–1 November 2017; pp. 7713–7717. [Google Scholar]
- Samir, A.; Taha, M.; Sayed, M.M.; Ibrahim, A. Efficient PV-grid system integration with PV-voltage-source converter reactive power support. J. Eng. 2018, 2018, 130–137. [Google Scholar] [CrossRef]
- Rajeev, M.; Agarwal, V. Single Phase Current Source Inverter with Multiloop Control for Transformerless Grid–PV Interface. IEEE Trans. Ind. Appl. 2018, 54, 2416–2424. [Google Scholar] [CrossRef]
- Dash, P.P.; Kazerani, M. Dynamic Modeling and Performance Analysis of a Grid-Connected Current-Source Inverter-Based Photovoltaic System. IEEE Trans. Sustain. Energy 2011, 2, 443–450. [Google Scholar] [CrossRef]
- Peng, F.Z. Z-source inverter. IEEE Trans. Ind. Appl. 2003, 39, 504–510. [Google Scholar] [CrossRef]
- Ellabban, O.; Abu-Rub, H. Z-Source Inverter: Topology Improvements Review. IEEE Ind. Electron. Mag. 2016, 10, 6–24. [Google Scholar] [CrossRef]
- Wang, T.; Nian, H.; Zhu, Z.Q. Using inverter-based renewable generators to improve the grid power quality—A review. Chin. J. Electr. Eng. 2018, 4, 16–25. [Google Scholar] [CrossRef]
- Tang, Y.; Xie, S.; Zhang, C.; Xu, Z. Improved Z-Source Inverter with Reduced Z-Source Capacitor Voltage Stress and Soft-Start Capability. IEEE Trans. Power Electron. 2009, 24, 409–415. [Google Scholar] [CrossRef]
- Loh, P.C.; Li, D.; Blaabjerg, F. Γ-Z-Source Inverters. IEEE Trans. Power Electron. 2013, 28, 4880–4884. [Google Scholar] [CrossRef]
- Cao, D.; Jiang, S.; Yu, X.; Peng, F.Z. Low-Cost Semi-Z-source Inverter for Single-Phase Photovoltaic Systems. IEEE Trans. Power Electron. 2011, 26, 3514–3523. [Google Scholar] [CrossRef]
- Ahmad, A.; Singh, R.K.; Beig, B.A. Switched-Capacitor Based Modified Extended High Gain Switched Boost Z-Source Inverters. IEEE Access 2019, 7, 179918–179928. [Google Scholar] [CrossRef]
- Tripathi, P.R.; Thakura, P.; Keshri, R.K.; Ghosh, S.; Guerrero, J.M. 25 Years of Single-Stage Buck-Boost Inverters: Development and Challenges. IEEE Ind. Electron. Mag. 2021. [Google Scholar] [CrossRef]
- Khenar, M.; Taghvaie, A.; Adabi, J.; Rezanejad, M. Multi-level inverter with combined T-type and cross-connected modules. IET Power Electron. 2018, 11, 1407–1415. [Google Scholar] [CrossRef]
- Das, M.K.; Jana, K.C.; Sinha, A. Performance evaluation of an asymmetrical reduced switched multi-level inverter for a grid-connected PV system. IET Renew. Power Gener. 2018, 12, 252–263. [Google Scholar] [CrossRef]
- Kumar, N.V.; Chinnaiyan, V.K.; Murukesapillay, P.; Karthikeyan, S.P. Multilevel inverter topology using single source and double source module with reduced power electronic components. J. Eng. 2017, 2017, 139–148. [Google Scholar] [CrossRef]
- Samsami, H.; Taheri, A.; Samanbakhsh, R. New bidirectional multilevel inverter topology with staircase cascading for symmetric and asymmetric structures. IET Power Electron. 2017, 10, 1315–1323. [Google Scholar] [CrossRef]
- Kim, I.; Chan, R.; Kwak, S. Model predictive control method for CHB multi-level inverter with reduced calculation complexity and fast dynamics. IET Electr. Power Appl. 2017, 11, 784–792. [Google Scholar] [CrossRef]
- Salehahari, S.; Babaei, E.; Hosseini, S.H.; Ajami, A. Transformer-based multilevel inverters: Analysis, design and implementation. IET Power Electron. 2019, 12, 1–10. [Google Scholar] [CrossRef]
- Caceres, R.; Barbi, I. A boost DC-AC converter: Operation, analysis, control and experimentation. In Proceedings of the IECON’95—21st Annual Conference on IEEE Industrial Electronics, Orlando, FL, USA, 6–10 November 2002; Volume 1, pp. 546–551. [Google Scholar]
- Caceres, R.; Barbi, I. A boost DC-AC converter: Analysis, design, and experimentation. IEEE Trans. Power Electron. 1999, 14, 134–141. [Google Scholar] [CrossRef]
- Gloire, N.; Lei, D.; Xiaozhong, L.; Furong, X. Single phase grid-connected PV inverter applying a boost coupled inductor. In Proceedings of the 2014 IEEE Conference and Expo Transportation Electrification Asia-Pacific (ITEC Asia-Pacific), Beijing, China, 31 August–3 September 2014; pp. 1–5. [Google Scholar]
- Zhang, L.; Ruan, X.; Ren, X. Second-Harmonic Current Reduction for Two-Stage Inverter with Boost-Derived Front-End Converter: Control Schemes and Design Considerations. IEEE Trans. Power Electron. 2018, 33, 6361–6378. [Google Scholar] [CrossRef]
- Zhang, L.; Ruan, X. Control Schemes for Reducing Second Harmonic Current in Two-Stage Single-Phase Converter: An Overview From DC-Bus Port-Impedance Characteristics. IEEE Trans. Power Electron. 2019, 34, 10341–10358. [Google Scholar] [CrossRef]
- Tran, T.-T.; Nguyen, M.-K.; Choi, J.-H.; Lim, Y.-C. A Single-Phase Common-Ground-Type Boost Inverter for Photovoltaic Applications. In Proceedings of the 2019 21st European Conference on Power Electronics and Applications (EPE ’19 ECCE Europe), Genova, Italy, 3–5 September 2019; pp. 10341–10358. [Google Scholar]
- Wu, X.; Zaman, H.; Zheng, X.; Khan, S.; Ali, H. Carrier-Based Double Integral Sliding-Mode Controller of Class-D Amplifier. IEEE Access 2018, 7, 1275–1283. [Google Scholar] [CrossRef]
- Jiang, X. Fundamentals of Audio Class D Amplifier Design: A Review of Schemes and Architectures. IEEE Solid-State Circuits Mag. 2017, 9, 14–25. [Google Scholar] [CrossRef]
- Chien, S.-H.; Chen, Y.-W.; Kuo, T.-H. A Low Quiescent Current, Low THD+N Class-D Audio Amplifier with Area-Efficient PWM-Residual-Aliasing Reduction. IEEE J. Solid-State Circuits 2018, 53, 3377–3385. [Google Scholar] [CrossRef]
- Xu, D.; Zhong, S.; Xu, J. Bipolar Phase Shift Modulation Single-Stage Audio Amplifier Employing a Full Bridge Active Clamp for High Efficiency Low Distortion. IEEE Trans. Ind. Electron. 2021, 68, 1118–1129. [Google Scholar] [CrossRef]
- Jain, P. Resonant Power Conversion: Insights from a Lifetime of Experience. IEEE J. Emerg. Sel. Top. Power Electron. 2020. [Google Scholar] [CrossRef]
- Kjaer, S.B.; Pedersen, J.K.; Blaabjerg, F. A Review of Single-Phase Grid-Connected Inverters for Photovoltaic Modules. IEEE Trans. Ind. Appl. 2005, 41, 1292–1306. [Google Scholar] [CrossRef]
- Abeywardana, D.B.W.; Hredzak, B.; Agelidis, V.G. An Input Current Feedback Method to Mitigate the DC-Side Low-Frequency Ripple Current in a Single-Phase Boost Inverter. IEEE Trans. Power Electron. 2016, 31, 4594–4603. [Google Scholar] [CrossRef]
- Jang, M.; Agelidis, V.G. A Minimum Power-Processing-Stage Fuel-Cell Energy System Based on a Boost-Inverter with a Bidirectional Backup Battery Storage. IEEE Trans. Power Electron. 2010, 26, 1568–1577. [Google Scholar] [CrossRef]
- Yilmaz, A.S.; Özer, Z. Pitch angle control in wind turbines above the rated wind speed by multi-layer perceptron and radial basis function neural networks. Expert Syst. Appl. 2009, 36, 9767–9775. [Google Scholar] [CrossRef]
- Tiwari, R.; Krishnamurthy, K.; Neelakandan, R.B.; Padmanaban, S.; Wheeler, P.W. Neural Network Based Maximum Power Point Tracking Control with Quadratic Boost Converter for PMSG—Wind Energy Conversion System. Electronics 2018, 7, 20. [Google Scholar] [CrossRef] [Green Version]
- Şahin, S.; Güzeliş, C. Online Learning ARMA Controllers with Guaranteed Closed-Loop Stability. IEEE Trans. Neural Netw. Learn. Syst. 2015, 27, 2314–2326. [Google Scholar] [CrossRef]
- IEEE Recommended Practice and Requirements for Harmonic Control in Electric Power Systems; IEEE Std. 519-2014; IEEE: New York, NY, USA, 2014; pp. 1–29. [CrossRef]
- Sandeep, N.; Ali, J.S.M.; Yaragatti, U.R.; Vijayakumar, K. Switched-Capacitor-Based Quadruple-Boost Nine-Level Inverter. IEEE Trans. Power Electron. 2019, 34, 7147–7150. [Google Scholar] [CrossRef]











| Component | Voltage Stress | Current Stress |
|---|---|---|
| Switch | dVin | dIo/2α |
| Inductor | - | dIo/2α |
| Capacitor | Vo | Io − dIo/√2α |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tripathi, P.R.; Laxmi, V.; Keshri, R.K.; Appasani, B.; Ustun, T.S. A Novel Fundamental Frequency Switching Operation for Conventional VSI to Enable Single-Stage High-Gain Boost Inversion with ANN Tuned QWS Controller. Electronics 2021, 10, 2499. https://doi.org/10.3390/electronics10202499
Tripathi PR, Laxmi V, Keshri RK, Appasani B, Ustun TS. A Novel Fundamental Frequency Switching Operation for Conventional VSI to Enable Single-Stage High-Gain Boost Inversion with ANN Tuned QWS Controller. Electronics. 2021; 10(20):2499. https://doi.org/10.3390/electronics10202499
Chicago/Turabian StyleTripathi, Prabhat R., V. Laxmi, Ritesh K. Keshri, Bhargav Appasani, and Taha Selim Ustun. 2021. "A Novel Fundamental Frequency Switching Operation for Conventional VSI to Enable Single-Stage High-Gain Boost Inversion with ANN Tuned QWS Controller" Electronics 10, no. 20: 2499. https://doi.org/10.3390/electronics10202499
APA StyleTripathi, P. R., Laxmi, V., Keshri, R. K., Appasani, B., & Ustun, T. S. (2021). A Novel Fundamental Frequency Switching Operation for Conventional VSI to Enable Single-Stage High-Gain Boost Inversion with ANN Tuned QWS Controller. Electronics, 10(20), 2499. https://doi.org/10.3390/electronics10202499








