A Multi-Cache System for On-Chip Memory Optimization in FPGA-Based CNN Accelerators
Abstract
:1. Introduction
- design of a cache system that aims at reducing on-chip memory usage by properly re-using input feature maps data and by optimizing on-chip memory footprint for convolutional filters.
- in hardware implementation and validation of the proposed architectural improvements on a Xilinx ZCU106 Evaluation Board for a case study CNN.
- characterization of the main system metrics carried on with physical measurements in order to present a benchmark between the developed system and an alternative hardware accelerator for the same CNN reported in the literature [13].
- detailed analysis on power consumption performed by reporting the current trends of the main system rails during the inference via the Maxim Digital PowerTool Dongle [33].
- analysis of the enhanced device portability of the design together with the achievable benefits in terms of power consumption and component costs
- broader evaluation about the applicability of the presented methods to other CNN models and comparison in terms of memory usage with alternative accelerators presented in the literature.
2. Background
- fully on-chip: both the input image and the hidden layers feature maps are stored in the FPGA on-chip memories. Such an approach allows for reducing the overheads of off-chip data transfers at the cost of a higher memory occupation. Whenever the CNN memory footprint exceeds the FPGA memory budget, this technique is not viable. The fully on-chip paradigm is the one adopted in [34,35].
- input image off-chip: a possible strategy to reduce memory usage is to store the input image in an external memory. This solution offers good trade-offs in terms of memory occupation and performance, but it still requires the hidden layers feature maps of the whole CNN to match the FPGA memory availability. Examples of this approach can be found in [36,37].
3. Methods
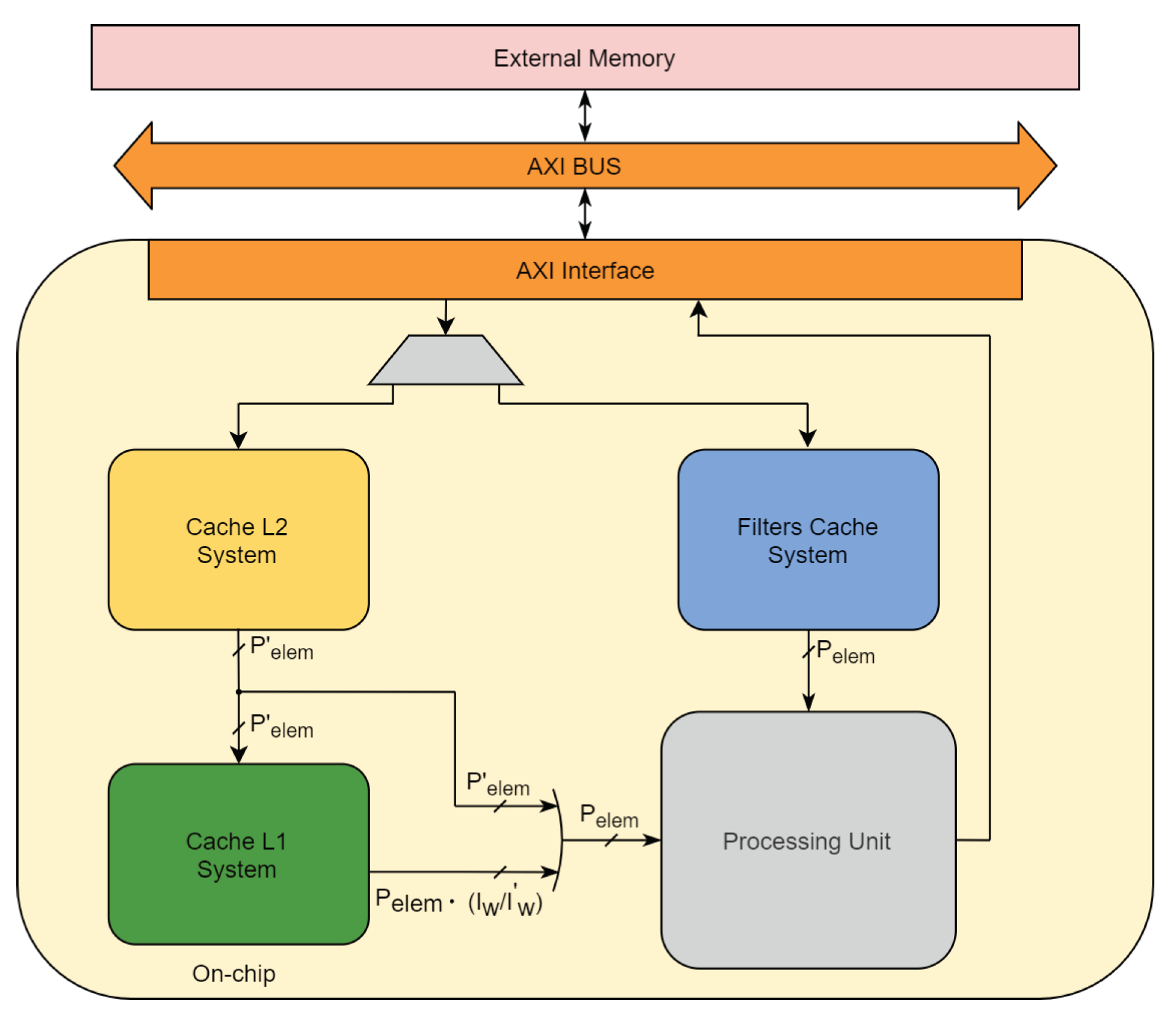
3.1. Cache L1 System
3.2. Filters Cache System
4. Results
- Xilinx Zynq Ultrascale+ ZU3EG;
- Xilinx Zynq 7000 Z7030;
- Xilinx Kyntex Ultrascale KU025;
- Xilinx Artix 7 XC7A200T;
- Intel Arria 10 GX 270.
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| AXI | Advanced eXtendible Interface |
| BRAM | Block RAM |
| CNN | Convolutional Neural Network |
| CPU | Central Processing Unit |
| DDR | Double Data Rate |
| DSP | Digital Signal Processing |
| FPGA | Field Programmable Gate Array |
| GPU | Graphics Processing Unit |
| LUT | Look Up Table |
| MAC | Multiplay and Accumulate |
| RAM | Random Access Memory |
| URAM | Ultra RAM |
| VHDL | VHSIC Hardware Description Language |
| VHSIC | Very High Speed Integrated Circuits |
| VPU | Visual Processing Unit |
| XPE | Xilinx Power Estimator |
References
- Chauhan, R.; Ghanshala, K.K.; Joshi, R.C. Convolutional Neural Network (CNN) for Image Detection and Recognition. In Proceedings of the 2018 First International Conference on Secure Cyber Computing and Communication (ICSCCC), Jalandhar, India, 15–17 December 2018; pp. 278–282. [Google Scholar] [CrossRef]
- Traore, B.B.; Kamsu-Foguem, B.; Tangara, F. Deep convolution neural network for image recognition. Ecol. Inform. 2018, 48, 257–268. [Google Scholar] [CrossRef] [Green Version]
- Hershey, S.; Chaudhuri, S.; Ellis, D.P.W.; Gemmeke, J.F.; Jansen, A.; Moore, R.C.; Plakal, M.; Platt, D.; Saurous, R.A.; Seybold, B.; et al. CNN architectures for large-scale audio classification. In Proceedings of the 2017 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), New Orleans, LA, USA, 5–9 March 2017; pp. 131–135. [Google Scholar] [CrossRef] [Green Version]
- Avanzato, R.; Beritelli, F.; Di Franco, F.; Puglisi, V.F. A Convolutional Neural Networks Approach to Audio Classification for Rainfall Estimation. In Proceedings of the 2019 10th IEEE International Conference on Intelligent Data Acquisition and Advanced Computing Systems: Technology and Applications (IDAACS), Metz, France, 18–21 September 2019; Volume 1, pp. 285–289. [Google Scholar] [CrossRef]
- Nishani, E.; Çiço, B. Computer vision approaches based on deep learning and neural networks: Deep neural networks for video analysis of human pose estimation. In Proceedings of the 2017 6th Mediterranean Conference on Embedded Computing (MECO), Bar, Montenegro, 11–15 June 2017; pp. 1–4. [Google Scholar] [CrossRef]
- Karpathy, A.; Toderici, G.; Shetty, S.; Leung, T.; Sukthankar, R.; Fei-Fei, L. Large-scale Video Classification with Convolutional Neural Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Columbus, OH, USA, 23–28 June 2014. [Google Scholar]
- Szegedy, C.; Ioffe, S.; Vanhoucke, V.; Alemi, A. Inception-v4, Inception-ResNet and the Impact of Residual Connections on Learning. In Proceedings of the Thirty-First AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–9 February 2017; Volume 31. [Google Scholar]
- Khan, R.U.; Zhang, X.; Kumar, R.; Aboagye, E.O. Evaluating the Performance of ResNet Model Based on Image Recognition. In Proceedings of the 2018 International Conference on Computing and Artificial Intelligence, Chengdu, China, 12–14 March 2018; Association for Computing Machinery: New York, NY, USA, 2018; pp. 86–90. [Google Scholar] [CrossRef]
- Véstias, M. A Survey of Convolutional Neural Networks on Edge with Reconfigurable Computing. Algorithms 2019, 12, 154. [Google Scholar] [CrossRef] [Green Version]
- Oh, S.; Kim, M.; Kim, D.; Jeong, M.; Lee, M. Investigation on performance and energy efficiency of CNN-based object detection on embedded device. In Proceedings of the 2017 4th International Conference on Computer Applications and Information Processing Technology (CAIPT), Kuta Bali, Indonesia, 8–10 August 2017; pp. 1–4. [Google Scholar] [CrossRef]
- Strigl, D.; Kofler, K.; Podlipnig, S. Performance and Scalability of GPU-Based Convolutional Neural Networks. In Proceedings of the 2010 18th Euromicro Conference on Parallel, Distributed and Network-Based Processing, Pisa, Italy, 17–19 February 2010; pp. 317–324. [Google Scholar] [CrossRef]
- Shi, W.; Dustdar, S. The Promise of Edge Computing. Computer 2016, 49, 78–81. [Google Scholar] [CrossRef]
- Rapuano, E.; Meoni, G.; Pacini, T.; Dinelli, G.; Furano, G.; Giuffrida, G.; Fanucci, L. An FPGA-Based Hardware Accelerator for CNNs Inference on Board Satellites: Benchmarking with Myriad 2-Based Solution for the CloudScout Case Study. Remote Sens. 2021, 13, 1518. [Google Scholar] [CrossRef]
- Liu, S.; Liu, L.; Tang, J.; Yu, B.; Wang, Y.; Shi, W. Edge Computing for Autonomous Driving: Opportunities and Challenges. Proc. IEEE 2019, 107, 1697–1716. [Google Scholar] [CrossRef]
- Greco, L.; Percannella, G.; Ritrovato, P.; Tortorella, F.; Vento, M. Trends in IoT based solutions for health care: Moving AI to the edge. Pattern Recognit. Lett. 2020, 135, 346–353. [Google Scholar] [CrossRef] [PubMed]
- Dinelli, G.; Meoni, G.; Rapuano, E.; Fanucci, L. Advantages and Limitations of Fully on-Chip CNN FPGA-Based Hardware Accelerator. In Proceedings of the 2020 IEEE International Symposium on Circuits and Systems (ISCAS), Seville, Spain, 12–14 October 2020; pp. 1–5. [Google Scholar] [CrossRef]
- Lee, Y.; Tsung, P.; Wu, M. Techology trend of edge AI. In Proceedings of the 2018 International Symposium on VLSI Design, Automation and Test (VLSI-DAT), Hsinchu, Taiwan, 16–19 April 2018; pp. 1–2. [Google Scholar] [CrossRef]
- Intel® Movidius™ Myriad™ X Vision Processing Unit Specifications. Available online: https://www.intel.it/content/www/it/it/products/docs/processors/movidius-vpu/myriad-x-product-brief.html (accessed on 2 April 2021).
- NVIDIA Jatson AGX Xavier. Available online: https://www.nvidia.com/it-it/autonomous-machines/embedded-systems/jetson-agx-xavier/ (accessed on 5 April 2021).
- Google Coral Specifications. Available online: https://coral.ai/docs/accelerator/datasheet/ (accessed on 5 April 2021).
- Gyrfalcon Lightspeeur 5801 Specifications. Available online: https://www.gyrfalcontech.ai/solutions/lightspeeur-5801/ (accessed on 5 April 2021).
- Zhang, C.; Li, P.; Sun, G.; Guan, Y.; Xiao, B.; Cong, J. Optimizing FPGA-based Accelerator Design for Deep Convolutional Neural Networks. In Proceedings of the 2015 ACM/SIGDA International Symposium on Field-Programmable Gate Arrays, Monterey, CA, USA, 22–24 February 2015; pp. 161–170. [Google Scholar] [CrossRef]
- Qiu, J.; Wang, J.; Yao, S.; Guo, K.; Li, B.; Zhou, E.; Yu, J.; Tang, T.; Xu, N.; Song, S.; et al. Going Deeper with Embedded FPGA Platform for Convolutional Neural Network. In Proceedings of the 2016 ACM/SIGDA International Symposium on Field-Programmable Gate Arrays, Monterey, CA, USA, 21–23 February 2016. [Google Scholar]
- Mittal, S. A survey of FPGA-based accelerators for convolutional neural networks. Remote Neural Comput. Appl. 2018, 32, 1109–1139. [Google Scholar] [CrossRef]
- Kyntex XQRKU060 Specifications. Available online: https://www.xilinx.com/support/documentation/data_sheets/ds882-xqr-kintex-ultrascale.pdf (accessed on 20 May 2021).
- Microsemi Polarfire Specifications. Available online: https://www.microsemi.com/product-directory/rad-tolerant-fpgas/5559-rt-polarfire-fpgas#documents (accessed on 20 May 2021).
- NanoXplore NG-Large NX1H140TSP Specifications. Available online: https://www.nanoxplore.com/uploads/NanoXplore_NG-LARGE_Datasheet_v1.0.pdf (accessed on 2 June 2021).
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar] [CrossRef] [Green Version]
- Howard, A.; Zhu, M.; Chen, B.; Kalenichenko, D.; Wang, W.; Weyand, T.; Andreetto, M.; Adam, H. MobileNets: Efficient Convolutional Neural Networks for Mobile Vision Applications. arXiv 2017, arXiv:1704.04861. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. In Proceedings of the International Conference on Learning Representations, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Esposito, M.; Conticello, S.S.; Pastena, M.; Domínguez, B.C. In-orbit demonstration of artificial intelligence applied to hyperspectral and thermal sensing from space. In CubeSats and SmallSats for Remote Sensing III; Pagano, T.S., Norton, C.D., Babu, S.R., Eds.; International Society for Optics and Photonics: Bellingham, WA, USA, 2019; Volume 11131, pp. 88–96. [Google Scholar] [CrossRef]
- Giuffrida, G.; Diana, L.; de Gioia, F.; Benelli, G.; Meoni, G.; Donati, M.; Fanucci, L. CloudScout: A Deep Neural Network for On-Board Cloud Detection on Hyperspectral Images. Remote Sens. 2020, 12, 2205. [Google Scholar] [CrossRef]
- Maxim Integrated MAXPOWERTOOL002. Available online: https://www.maximintegrated.com/en/products/power/switching-regulators/MAXPOWERTOOL002.html (accessed on 7 June 2021).
- Dinelli, G.; Meoni, G.; Rapuano, E.; Benelli, G.; Fanucci, L. An FPGA-Based Hardware Accelerator for CNNs Using On-Chip Memories Only: Design and Benchmarking with Intel Movidius Neural Compute Stick. Int. J. Reconfigurable Comput. 2019, 2019. [Google Scholar] [CrossRef] [Green Version]
- Li, H.; Fan, X.; Jiao, L.; Cao, W.; Zhou, X.; Wang, L. A high performance FPGA-based accelerator for large-scale convolutional neural networks. In Proceedings of the 2016 26th International Conference on Field Programmable Logic and Applications (FPL), Lausanne, Switzerland, 29 August–2 September 2016; pp. 1–9. [Google Scholar]
- Shen, Y.; Ferdman, M.; Milder, P. Maximizing CNN accelerator efficiency through resource partitioning. In Proceedings of the 2017 ACM/IEEE 44th Annual International Symposium on Computer Architecture (ISCA), Toronto, ON, Canada, 24–28 June 2017; pp. 535–547. [Google Scholar]
- Nguyen, D.T.; Nguyen, T.N.; Kim, H.; Lee, H. A High-Throughput and Power-Efficient FPGA Implementation of YOLO CNN for Object Detection. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2019, 27, 1861–1873. [Google Scholar] [CrossRef]
- Guo, K.; Sui, L.; Qiu, J.; Yao, S.; Han, S.; Wang, Y.; Yang, H. Angel-Eye: A Complete Design Flow for Mapping CNN onto Customized Hardware. In Proceedings of the 2016 IEEE Computer Society Annual Symposium on VLSI (ISVLSI), Pittsburgh, PA, USA, 11–13 July 2016; pp. 24–29. [Google Scholar] [CrossRef]
- Zhao, R.; Niu, X.; Wu, Y.; Luk, W.; Liu, Q. Optimizing CNN-Based Object Detection Algorithms on Embedded FPGA Platforms. In Applied Reconfigurable Computing; Wong, S., Beck, A.C., Bertels, K., Carro, L., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 255–267. [Google Scholar]
- Alwani, M.; Chen, H.; Ferdman, M.; Milder, P. Fused-layer CNN accelerators. In Proceedings of the 2016 49th Annual IEEE/ACM International Symposium on Microarchitecture (MICRO), Taipei, Taiwan, 15–19 October 2016; pp. 1–12. [Google Scholar] [CrossRef]
- Shen, Y.; Ferdman, M.; Milder, P. Escher: A CNN Accelerator with Flexible Buffering to Minimize Off-Chip Transfer. In Proceedings of the 2017 IEEE 25th Annual International Symposium on Field-Programmable Custom Computing Machines (FCCM), Napa, CA, USA, 30 April–2 May 2017; pp. 93–100. [Google Scholar] [CrossRef]
- Zhang, N.; Shi, H.; Chen, L.; Lin, T.; Shao, X. A Novel CNN Architecture on FPGA-based SoC for Remote Sensing Image Classification. In Proceedings of the 2019 IEEE International Conference on Signal, Information and Data Processing (ICSIDP), Chongqing, China, 11–13 December 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Liu, B.; Zou, D.; Feng, L.; Feng, S.; Fu, P.; Li, J. An FPGA-Based CNN Accelerator Integrating Depthwise Separable Convolution. Electronics 2019, 8, 281. [Google Scholar] [CrossRef] [Green Version]
- Chen, T.; Du, Z.; Sun, N.; Wang, J.; Wu, C.; Chen, Y.; Temam, O. DianNao: A Small-Footprint High-Throughput Accelerator for Ubiquitous Machine-Learning. ACM SIGARCH Comput. Archit. News 2014, 49, 269–284. [Google Scholar] [CrossRef]
- Dinelli, G.; Meoni, G.; Rapuano, E.; Pacini, T.; Fanucci, L. MEM-OPT: A Scheduling and Data Re-Use System to Optimize On-Chip Memory Usage for CNNs On-Board FPGAs. IEEE J. Emerg. Sel. Top. Circuits Syst. 2020, 10, 335–347. [Google Scholar] [CrossRef]
- Stoutchinin, A.; Conti, F.; Benini, L. Optimally Scheduling CNN Convolutions for Efficient Memory Access. arXiv 2019, arXiv:1902.01492. [Google Scholar]
- Niu, Y.; Kannan, R.; Srivastava, A.; Prasanna, V. Reuse Kernels or Activations? In A Flexible Dataflow for Low-Latency Spectral CNN Acceleration. In Proceedings of the 2020 ACM/SIGDA International Symposium on Field-Programmable Gate Arrays, Seaside, CA, USA, 23–25 February 2020; Association for Computing Machinery: New York, NY, USA, 2020; pp. 266–276. [Google Scholar] [CrossRef] [Green Version]
- Blott, M.; Preußer, T.; Fraser, N.; Gambardella, G.; O’Brien, K.; Umuroglu, Y.; Leeser, M.; Vissers, K. FINN- R: An End-to-End Deep-Learning Framework for Fast Exploration of Quantized Neural Networks. ACM Trans. Reconfigurable Technol. Syst. 2018, 11, 1–23. [Google Scholar] [CrossRef]
- AMBA Advanced Extensible Interface 4 Specifications. Available online: https://www.arm.com/products/silicon-ip-system/embedded-system-design/amba-specifications (accessed on 2 June 2021).
- Huang, C.; Ni, S.; Chen, G. A layer-based structured design of CNN on FPGA. In Proceedings of the 2017 IEEE 12th International Conference on ASIC (ASICON), Guiyang, China, 25–28 October 2017; pp. 1037–1040. [Google Scholar] [CrossRef]
- Yonekawa, H.; Nakahara, H. On-Chip Memory Based Binarized Convolutional Deep Neural Network Applying Batch Normalization Free Technique on an FPGA. In Proceedings of the 2017 IEEE International Parallel and Distributed Processing Symposium Workshops (IPDPSW), Lake Buena Vista, FL, USA, 29 May–2 June 2017; pp. 98–105. [Google Scholar] [CrossRef]
- Park, J.; Sung, W. FPGA based implementation of deep neural networks using on-chip memory only. In Proceedings of the 2016 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Shanghai, China, 20–25 March 2016; pp. 1011–1015. [Google Scholar] [CrossRef] [Green Version]
- Accurate Design Power Measurement Made Easier. Available online: https://developer.xilinx.com/en/articles/accurate-design-power-measurement.html (accessed on 20 May 2021).
- ZCU106 Evaluation Board User Guide. Available online: https://www.xilinx.com/support/documentation/boards_and_kits/zcu106/ug1244-zcu106-eval-bd.pdf (accessed on 22 May 2021).
- Micron MT40A256M16GE-075E Specifications. Available online: https://media-www.micron.com/-/media/client/global/documents/products/data-sheet/dram/ddr4/4gb_ddr4_dram.pdf?rev=a4122900efb84963a0d9207033a5a286 (accessed on 25 May 2021).
- Zynq UltraScale+ MPSoC Data Sheet: DC and AC Switching Characteristics. Available online: https://www.xilinx.com/support/documentation/data_sheets/ds925-zynq-ultrascale-plus.pdf (accessed on 22 May 2021).
- Piyasena, D.; Wickramasinghe, R.; Paul, D.; Lam, S.K.; Wu, M. Reducing Dynamic Power in Streaming CNN Hardware Accelerators by Exploiting Computational Redundancies. In Proceedings of the 2019 29th International Conference on Field Programmable Logic and Applications (FPL), Barcelona, Spain, 8–12 September 2019; pp. 354–359. [Google Scholar] [CrossRef]
- Irmak, H.; Alachiotis, N.; Ziener, D. An Energy-Efficient FPGA-based Convolutional Neural Network Implementation. In Proceedings of the 2021 29th Signal Processing and Communications Applications Conference (SIU), Istanbul, Turkey, 9–11 June 2021; pp. 1–4. [Google Scholar] [CrossRef]
- Ma, Y.; Suda, N.; Cao, Y.; Seo, J.S.; Vrudhula, S. Scalable and modularized RTL compilation of Convolutional Neural Networks onto FPGA. In Proceedings of the 2016 26th International Conference on Field Programmable Logic and Applications (FPL), Lausanne, Switzerland, 29 August–2 September 2016; pp. 1–8. [Google Scholar] [CrossRef]
- Li, J.; Un, K.F.; Yu, W.H.; Mak, P.I.; Martins, R.P. An FPGA-Based Energy-Efficient Reconfigurable Convolutional Neural Network Accelerator for Object Recognition Applications. IEEE Trans. Circuits Syst. II Express Briefs 2021, 68, 3143–3147. [Google Scholar] [CrossRef]
- Li, G.; Liu, Z.; Li, F.; Cheng, J. Block Convolution: Towards Memory-Efficient Inference of Large-Scale CNNs on FPGA. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 2021. [Google Scholar] [CrossRef]








| Sw | bin | (Chinq) | (Pq) | (Chinq) | (Pq) |
|---|---|---|---|---|---|
| 1 | 16 | 256 | 2 | 3 | 2 |
| Ich | Ih | Iw | I’w | Pelem | P’elem |
| 1 | 3 | 3 | 1 | 9 | 3 |
| Resources | Available | Base Accelerator [13] | Memory Optimized Accelerator |
|---|---|---|---|
| LUTs | 230,400 | 53,188 (23.09%) | 59,195 (25.69%) |
| Flip-Flops | 460,800 | 17,454 (3.79%) | 20,771 (4.51%) |
| LUTRAM | 101,760 | 755 (0.74%) | 1128 (1.11%) |
| BlockRAM | 312 | 68 (21.79%) | 39 (12.5%) |
| UltraRAM | 96 | 54 (56.25%) | 18 (18.75%) |
| DSP | 1728 | 1163 (67.3%) | 1158 (67.0%) |
| Frequency (MHz) | , | ||
| Metrics | Base Accelerator | Memory Optimized Accelerator | Intel Movidius Myriad 2 VPU |
|---|---|---|---|
| Pc (W) | 4.39 | 4.51 | 1.8 |
| Tinf (ms) | 141.7 | 144.8 | 346 |
| Einf (J) | 0.62 | 0.65 | 0.63 |
| Acc (%) | 92 | 92 | 92.3 |
| Base Accelerator | Memory Optimized Accelerator | ||
|---|---|---|---|
| Rail | Voltage (V) | Current (A) | |
| PSINTFP | 0.85 | 1.29 | 1.35 |
| PSINTLP | 0.85 | 0.35 | 0.35 |
| VCCINT | 0.85 | 1.65 | 2.00 |
| VCCBRAM | 0.9 | 0.01 | 0.01 |
| VCCAUX | 1.8 | 0.14 | 0.15 |
| VCC1V2 | 1.2 | 0.01 | 0.10 |
| VCC3V3 | 3.3 | 0.02 | 0.01 |
| VADJ_FMC | 1.8 | 0.08 | 0.07 |
| DDR4_DIMM_VDDQ | 1.2 | 0.61 | 0.62 |
| Resources | ZU3EG | Z7030 | XC7A200T | KU025 | A10 GX 270 |
|---|---|---|---|---|---|
| LUTs | 52,346 (74.19%) | 53,097 (67.55%) | 53,004 (39.38%) | 52,339 (35.99%) | 16,688 (16%) |
| Flip-Flops | 13,705 (9.71%) | 13,927 (8.86%) | 13,865 (5.15%) | 13,710 (4.71%) | 11,600 (2.85%) |
| LUTRAM | 368 (1.28%) | 432 (1.62%) | 432 (0.94%) | 368 (0.54%) | 511 (1.01%) |
| RAM Blocks | 215 (99.54%) | 215 (81.13%) | 215 (58.90%) | 215 (59.72%) | 350 (47%) |
| UltraRAM | - | - | - | - | - |
| DSP | 294 (81.67%) | 294 (73.50%) | 294 (39.73%) | 294 (25.52%) | 763 (92.0%) |
| Frequency (MHz) | , | ||||
| LeNet-5 | NiN | VGG-16 | ||||
|---|---|---|---|---|---|---|
| # Conv. Filters | 33,412 | 969,822 | 14,714,688 | |||
| bin | 16 | 16 | 16 | 16 | 8 | 8 |
| bfilter | 16 | 16 | 8 | 8 | 4 | 4 |
| Conv. Filters Footprint (Mbit) | 0.51 | 0.51 | 7.4 | 7.4 | 56.1 | 56.1 |
| Ich | 1 | 2 | 1 | 1 | 1 | 2 |
| Ih | 5 | 5 | 3 | 5 | 3 | 3 |
| Iw | 5 | 5 | 3 | 5 | 3 | 3 |
| Pelem | 25 | 50 | 9 | 25 | 9 | 18 |
| I’w | 1 | 1 | 1 | 1 | 1 | 1 |
| P’elem | 5 | 10 | 3 | 5 | 3 | 6 |
| w/o Cache system (Mbit) | 0.565 | 1.09 | 12.57 | 21.7 | 62.6 | 67.9 |
| w/ Cache system (Mbit) | 0.107 | 0.25 | 5.24 | 6.39 | 9.6 | 12.9 |
| Literature (Mbit) | 0.98 [57], 1.02 [58] | 52.0 [59] | 16.42 [60], 9.3 [61] | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pacini, T.; Rapuano, E.; Dinelli, G.; Fanucci, L. A Multi-Cache System for On-Chip Memory Optimization in FPGA-Based CNN Accelerators. Electronics 2021, 10, 2514. https://doi.org/10.3390/electronics10202514
Pacini T, Rapuano E, Dinelli G, Fanucci L. A Multi-Cache System for On-Chip Memory Optimization in FPGA-Based CNN Accelerators. Electronics. 2021; 10(20):2514. https://doi.org/10.3390/electronics10202514
Chicago/Turabian StylePacini, Tommaso, Emilio Rapuano, Gianmarco Dinelli, and Luca Fanucci. 2021. "A Multi-Cache System for On-Chip Memory Optimization in FPGA-Based CNN Accelerators" Electronics 10, no. 20: 2514. https://doi.org/10.3390/electronics10202514
APA StylePacini, T., Rapuano, E., Dinelli, G., & Fanucci, L. (2021). A Multi-Cache System for On-Chip Memory Optimization in FPGA-Based CNN Accelerators. Electronics, 10(20), 2514. https://doi.org/10.3390/electronics10202514






