A 6.89-MHz 143-nW MEMS Oscillator Based on a 118-dBΩ Tunable Gain and Duty-Cycle CMOS TIA
Abstract
:1. Introduction
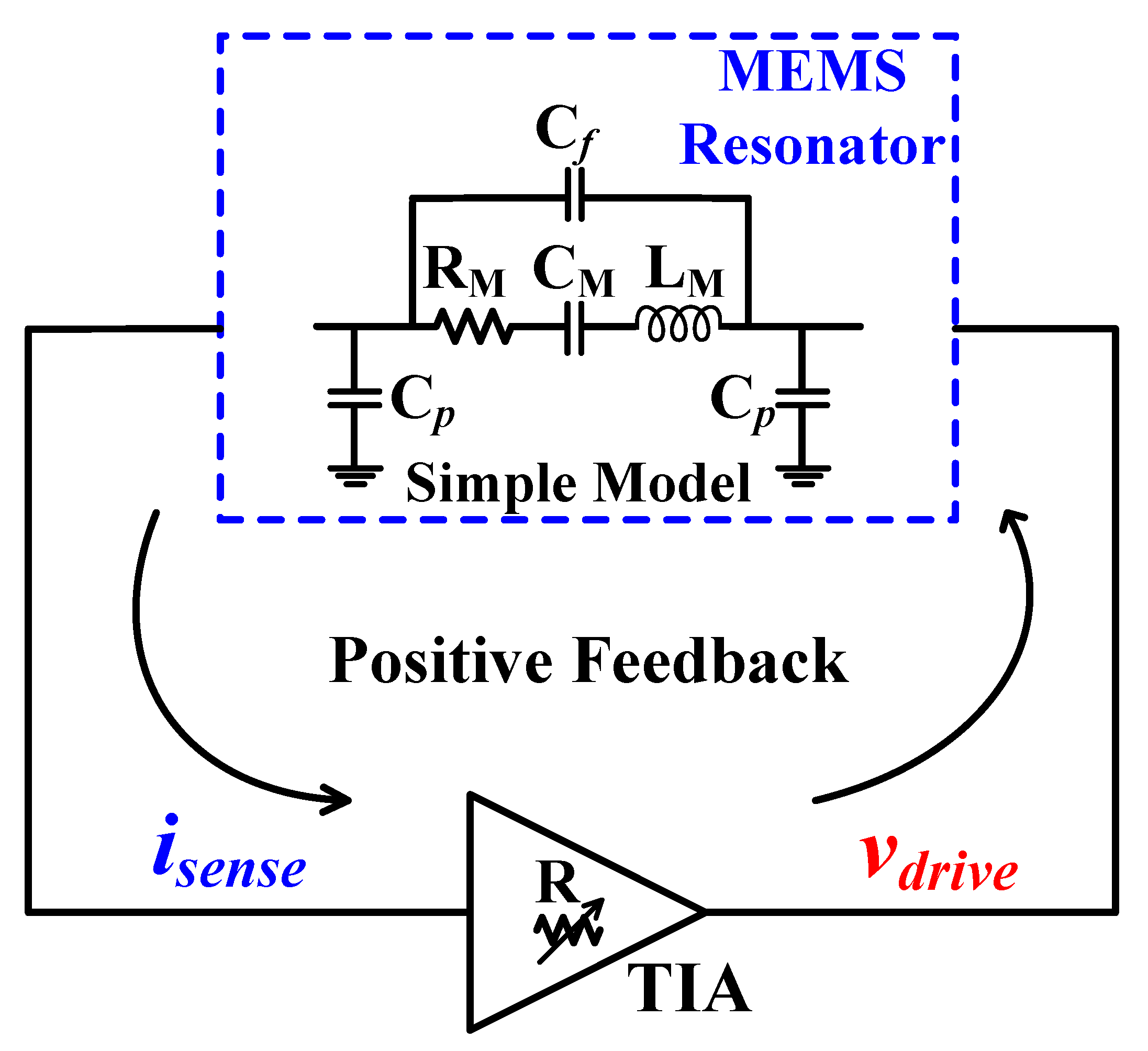
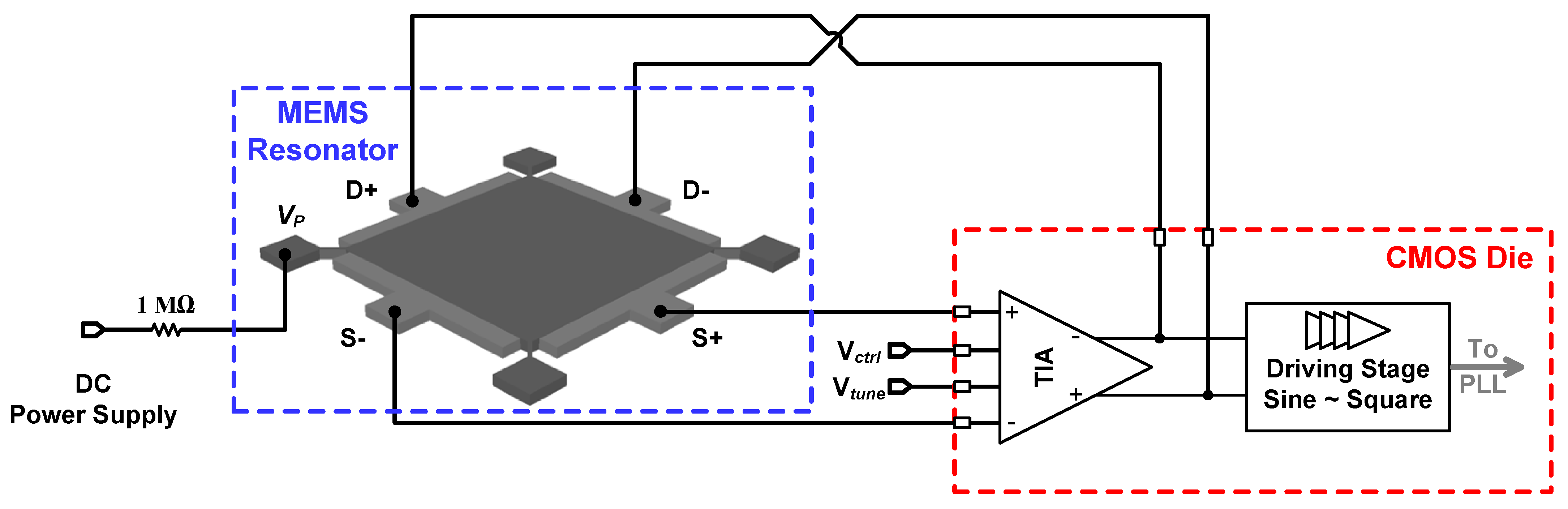
2. MEMS-Based Oscillator
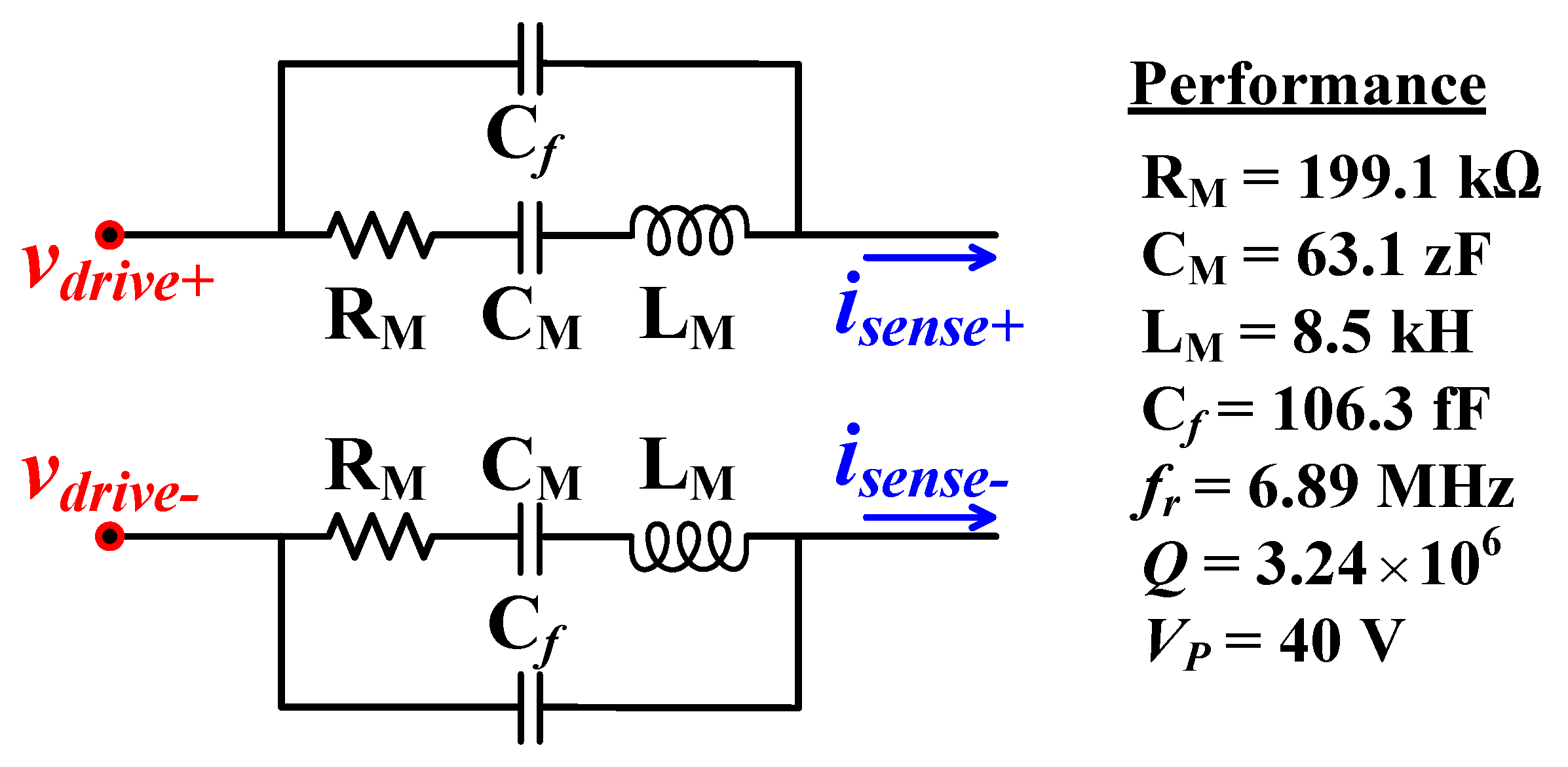
2.1. Bulk Lamé-Mode Square Resonator
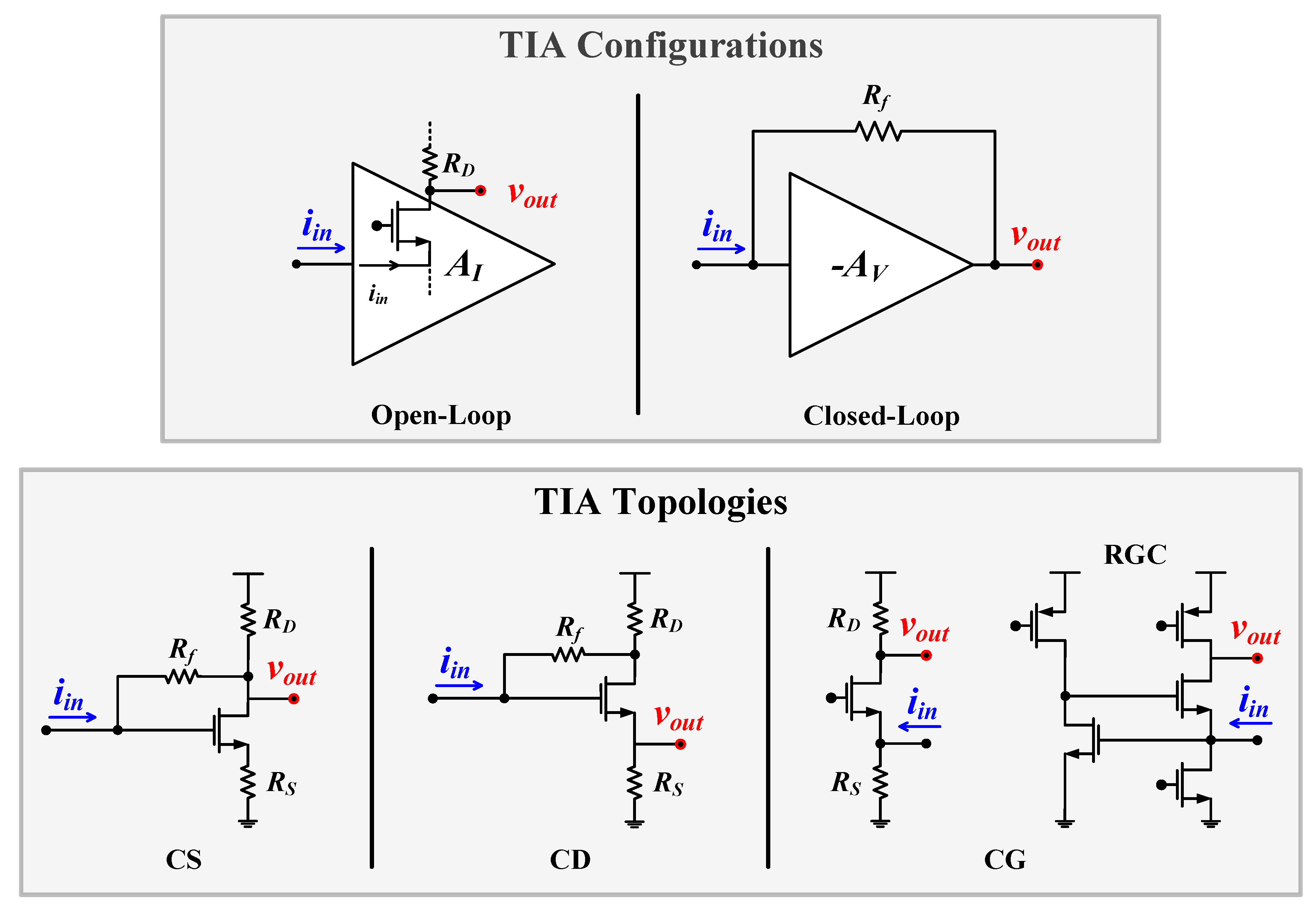
2.2. Sustaining Amplifier Configurations and Topologies
2.3. Proposed Methodology and TIA Circuit
2.4. Noise Analysis
3. System Performance and Robustness
3.1. Specifications and Performance
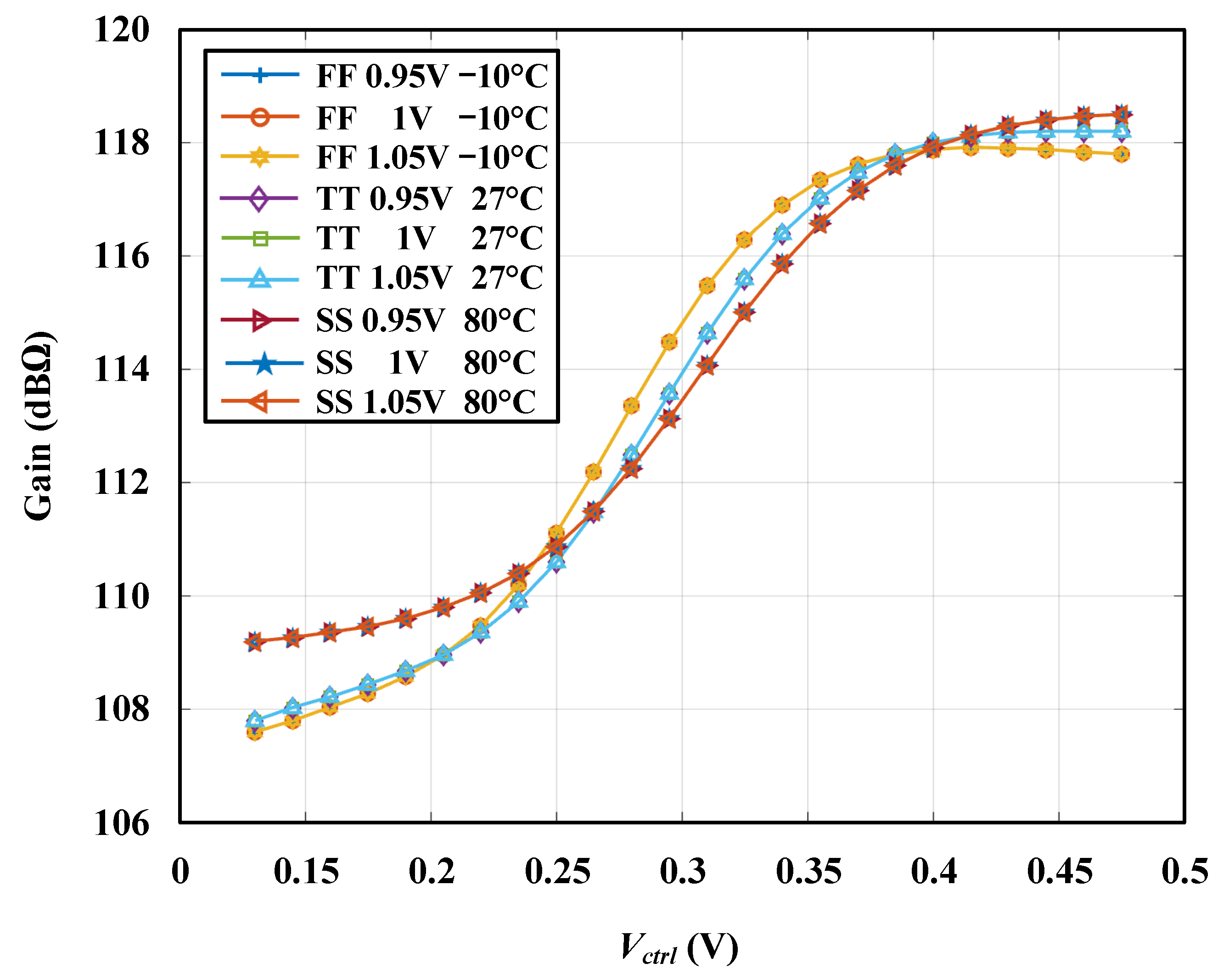
3.2. Robustness
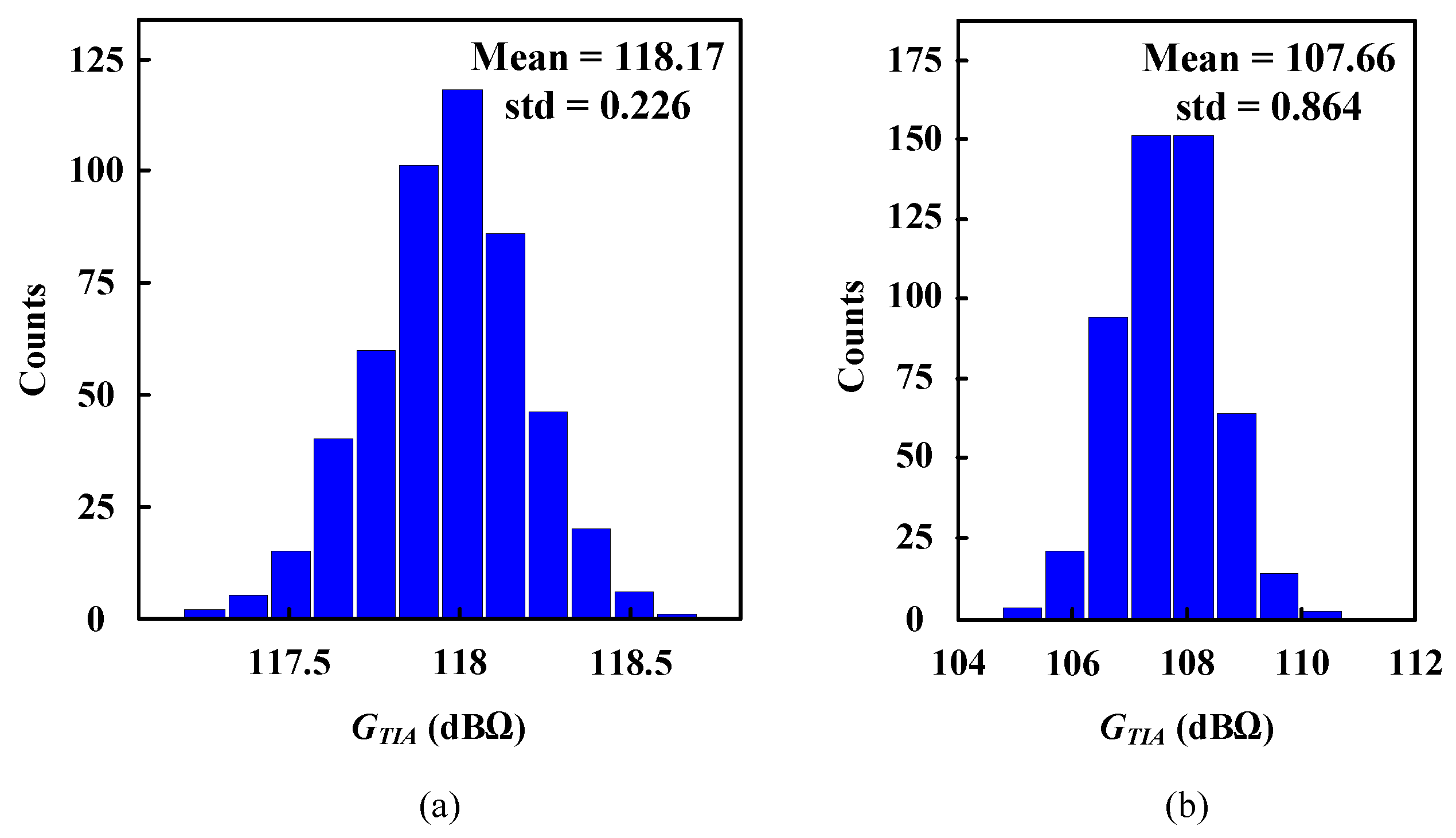
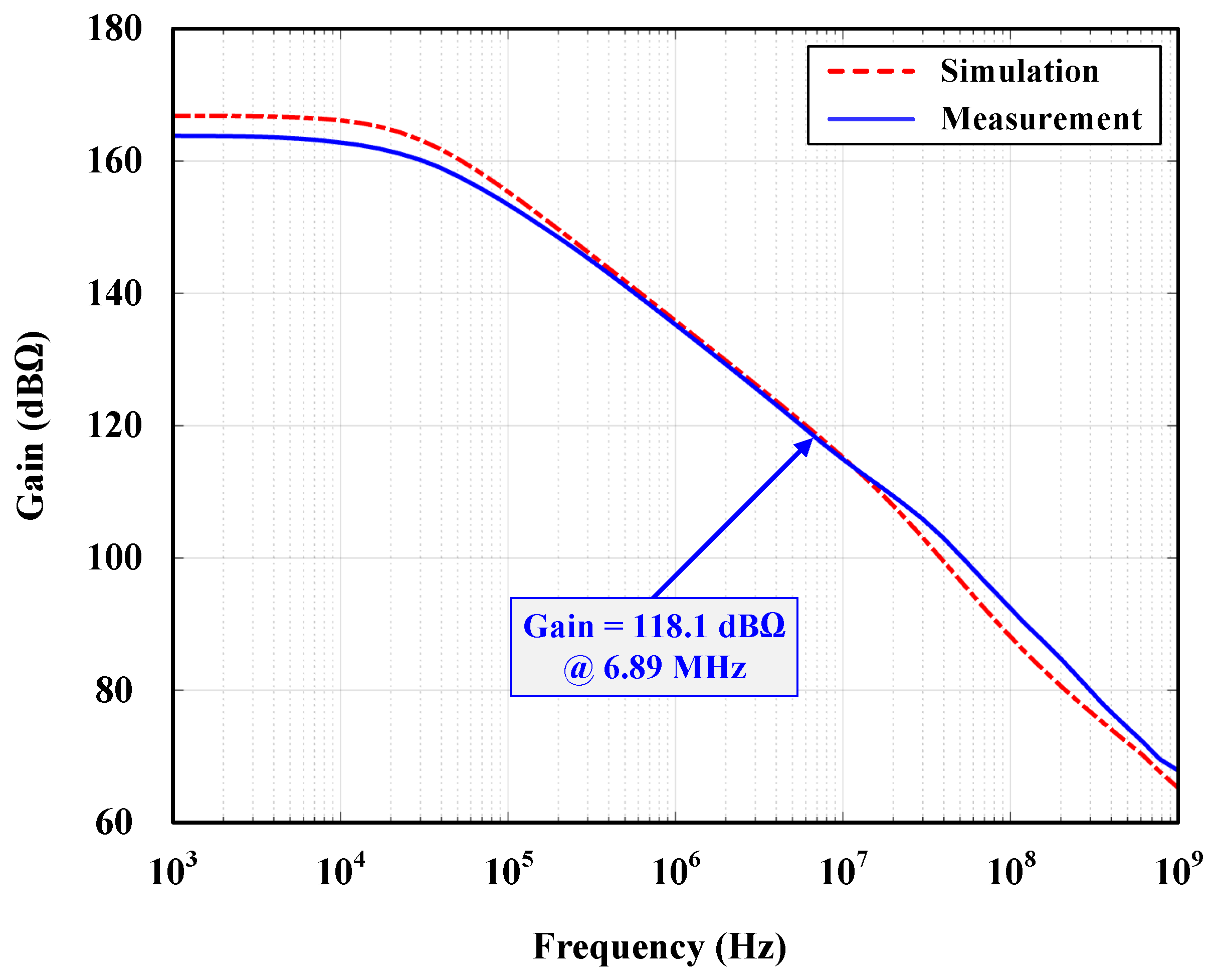
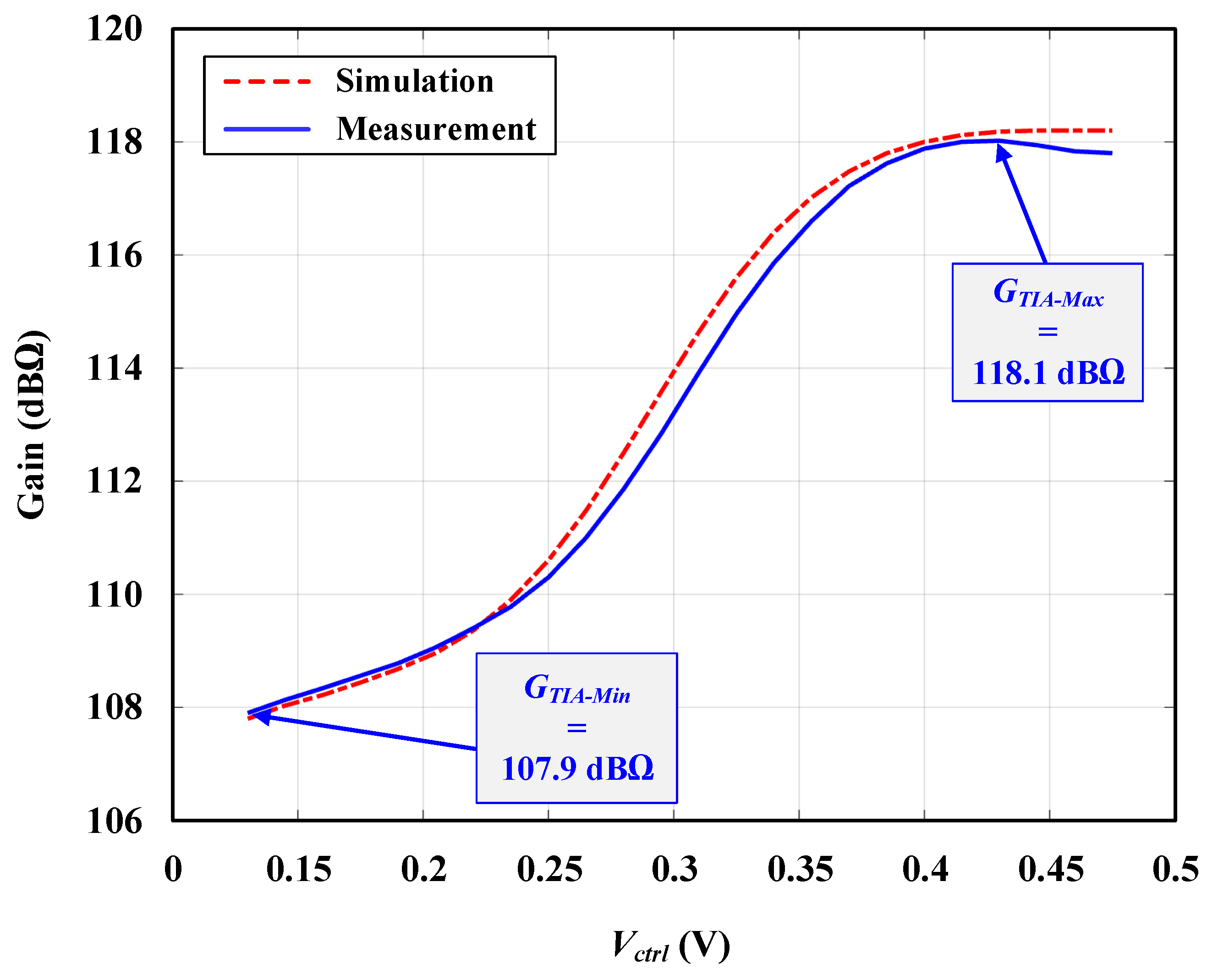
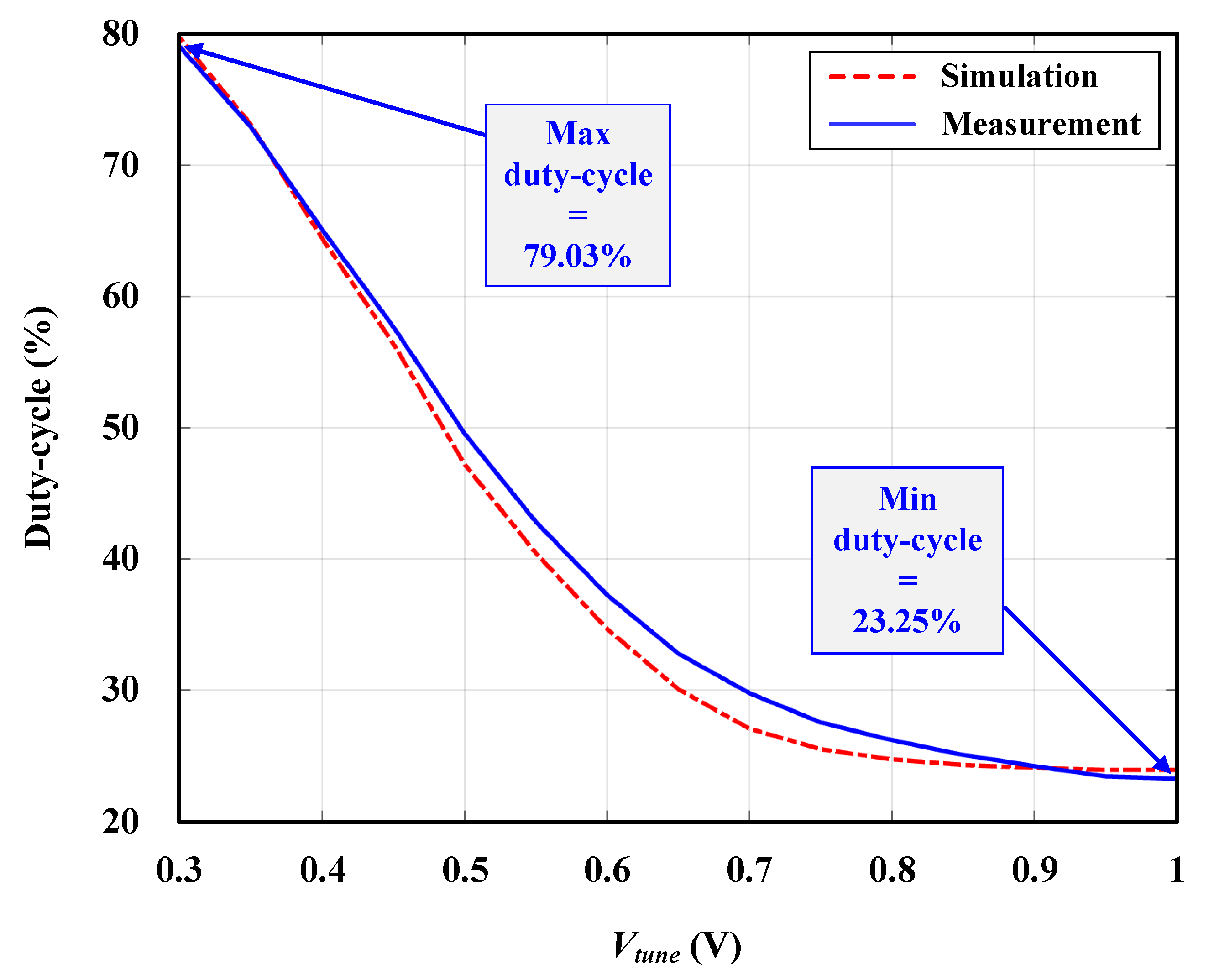
4. Experimental Results
4.1. Open-Loop Validation
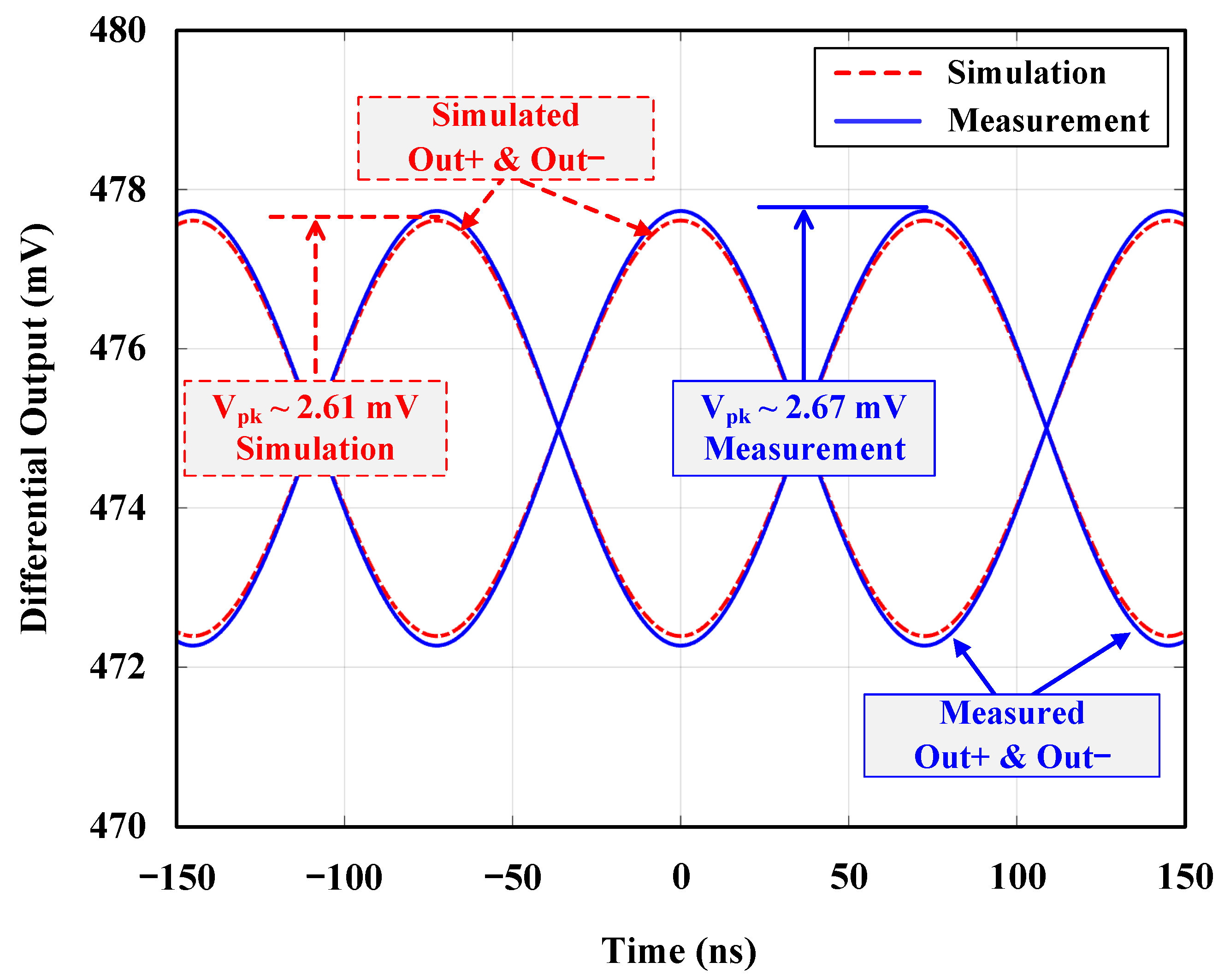
4.2. Closed-Loop Validation
4.3. Figure of Merit
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Nguyen, C.T.C. MEMS Technology for Timing and Frequency Control. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2007, 54, 251–270. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bouchami, A.; Elsayed, M.Y.; Nabki, F. A 1.4-mW 14-MHz MEMS Oscillator Based on a Differential Adjustable-Bandwidth Transimpedance Amplifier and Piezoelectric Disk Resonator. IEEE Trans. Circuits Syst. I Regul. Pap. 2018, 65, 3414–3423. [Google Scholar] [CrossRef]
- Nabki, F.; Allidina, K.; Ahmad, F.; Cicek, P.; El-Gamal, M.N. A Highly Integrated 1.8 GHz Frequency Synthesizer Based on a MEMS Resonator. IEEE J. Solid-State Circuits 2009, 44, 2154–2168. [Google Scholar] [CrossRef]
- Li, M.; Li, C.; Hou, L.; Liu, Y.; Li, S. A 1.57mW 99dBΩ CMOS transimpedance amplifier for VHF micromechanical reference oscillators. In Proceedings of the 2012 IEEE International Symposium on Circuits and Systems (ISCAS), Seoul, Korea, 20–23 May2012; pp. 209–212. [CrossRef]
- Nabki, F.; El-Gamal, M.N. A high gain-bandwidth product transimpedance amplifier for MEMS-based oscillators. In Proceedings of the ESSCIRC 2008—34th European Solid-State Circuits Conference, Edinburgh, UK, 15–19 September 2008; pp. 454–457. [Google Scholar] [CrossRef]
- Alsolami, A.; Zaman, A.; Rivera, I.F.; Baghelani, M.; Wang, J. Improvement of Deep Reactive Ion Etching Process For Motional Resistance Reduction of Capacitively Transduced Vibrating Resonators. IEEE Sens. Lett. 2018, 2, 1–4. [Google Scholar] [CrossRef]
- Rocheleau, T.O.; Naing, T.L.; Nguyen, C.T.C. Long-Term Stability of a Hermetically Packaged MEMS Disk Oscillator. In Proceedings of the 2013 Joint European Frequency and Time Forum International Frequency Control Symposium (EFTF/IFC), Prague, Czech Republic, 21–25 July 2013; pp. 209–212. [Google Scholar] [CrossRef]
- Pourkamali, S.; Hashimura, A.; Abdolvand, R.; Ho, G.; Erbil, A.; Ayazi, F. High-Q Single Crystal Silicon HARPSS Capacitive Beam Resonators With Self-Aligned Sub-100-nm Transduction Gaps. Microelectromech. Syst. J. 2003, 12, 487–496. [Google Scholar] [CrossRef] [Green Version]
- Clark, J.; Hsu, W.T.; Abdelmoneum, M.; Nguyen, C.C. High-QUHF Micromechanical Radial-ContourMode Disk Resonators. J. Microelectromech. Syst. 2005, 14, 1298–1310. [Google Scholar] [CrossRef]
- Lin, Y.W.; Lee, S.; Li, S.S.; Xie, Y.; Ren, Z.; Nguyen, C.C. Series-Resonant VHF Micromechanical Resonator Reference Oscillators. IEEE J. Solid-State Circuits 2004, 39, 2477–2491. [Google Scholar] [CrossRef]
- Nguyen, C.T.C. Integrated Micromechanical Radio Front-Ends. In Proceedings of the 2008 International Symposium on VLSI Technology, Systems and Applications (VLSI-TSA), Hsinchu, Taiwan, 21–23 April 2008; pp. 3–4. [Google Scholar] [CrossRef]
- Xiao, S.; Silva, J.; Moon, U.K.; Temes, G. A Tunable Duty-Cycle-Controlled Switched-R-MOSFET-C CMOS Filter for Low-Voltage and High-Linearity Applications. In Proceedings of the 2004 IEEE International Symposium on Circuits and Systems (IEEE Cat. No.04CH37512), Vancouver, BC, Canada, 23–26 May 2004; Volume 1, p. I-433. [Google Scholar] [CrossRef]
- Cheng, K.h.; Su, C.w.; Chang, K.f.; Hung, C.l.; Yang, W.b. A High Linearity and Fast-Locked PulseWidth Control Loop with Digitally Programmable Output Duty Cycle for Wide Range Operation. In Proceedings of the 2006 32nd European Solid-State Circuits Conference, Montreaux, Switzerland, 19–21 September 2006; pp. 178–181. [Google Scholar] [CrossRef]
- Xereas, G. Wafer-Level Vacuum Encapsulated Resonators with Low Motional Resistance; McGill University: Montréal, QC, Canada, 2016. [Google Scholar]
- Razavi, B. Design of Integrated Circuits for Optical Communications; Wiley: Hoboken, NJ, USA, 2012. [Google Scholar]
- Lavasani, H.M.; Pan, W.; Harrington, B.; Abdolvand, R.; Ayazi, F. A 76 dBΩ 1.7 GHz 0.18 μm CMOS tunable transimpedance amplifier using broadband current pre-amplifier for high frequency lateral micromechanical oscillators. In Proceedings of the 2010 IEEE International Solid-State Circuits Conference - (ISSCC), San Francisco, CA, USA, 7–11 February 2010; pp. 318–319. [Google Scholar] [CrossRef]
- Seth, S.; Wang, S.; Kenny, T.; Murmann, B. A -131-dBc/Hz, 20-MHz MEMS oscillator with a 6.9-mW, 69-kΩ, gain-tunable CMOS TIA. In Proceedings of the 2012 ESSCIRC (ESSCIRC), Bordeaux, France, 17–21 September 2012; pp. 249–252. [Google Scholar] [CrossRef]
- Baek, K.; Gim, J.; Kim, H.; Na, K.; Kim, N.; Kim, Y. Analogue circuit design methodology using self-cascode structures. Electron. Lett. 2013, 49, 591–592. [Google Scholar] [CrossRef]
- Galup-Montoro, C.; Schneider, M.; Loss, I. Series-parallel association of FET’s for high gain and high frequency applications. IEEE J. Solid-State Circuits 1994, 29, 1094–1101. [Google Scholar] [CrossRef]
- Fujimori, I.; Sugimoto, T. A 1.5 V, 4.1 mW dual-channel audio delta-sigma D/A converter. IEEE J. Solid-State Circuits 1998, 33, 1863–1870. [Google Scholar] [CrossRef]
- Gerosa, A. Enhancing output voltage swing in low-voltage micro-power OTA using self-cascode. Electron. Lett. 2003, 39, 638–639. [Google Scholar] [CrossRef]
- Hajimiri, A.; Lee, T.H. A general theory of phase noise in electrical oscillators. IEEE J. Solid-State Circuits 1998, 33, 179–194. [Google Scholar] [CrossRef] [Green Version]
- Johansson, H. A Simple Precharged CMOS Phase Frequency Detector. IEEE J. Solid-State Circuits 1998, 33, 295–299. [Google Scholar] [CrossRef]
- Lee, T.; Hajimiri, A. Oscillator phase noise: A tutorial. IEEE J. Solid-State Circuits 2000, 35, 326–336. [Google Scholar] [CrossRef] [Green Version]
- Effect of Parasitic Capacitance in OpAmp Circuits, 2000.Rev.A. Available online: https://www.ti.com/lit/an/sloa013a/sloa013a.pdf (accessed on 3 June 2021).
- AN-1205 Electrical Performance of Packages, 2004.Rev.A. Available online: https://www.ti.com/lit/an/snoa405a/snoa405a.pdf (accessed on 3 June 2021).
- Agilent InfiniiVision 2000 X-Series Oscilloscopes, 3rd ed. 2011. Available online: http://literature.cdn.keysight.com/litweb/pdf/75015-97012.pdf (accessed on 3 June 2021).
- Quad Flat No-Lead (QFN) Package Comparison Tables. Available online: https://www.ti.com/pdfs/logic/qfncompare.pdf (accessed on 3 June 2021).
- Mekky, R.H.; Cicek, P.; El-Gamal, M.N. Ultra low-power low-noise transimpedance amplifier for MEMS-based reference oscillators. In Proceedings of the 2013 IEEE 20th International Conference on Electronics, Circuits, and Systems (ICECS), Abu Dhabi, United Arab Emirates, 8–11 December 2013; pp. 345–348. [Google Scholar] [CrossRef]
- Riverola, M.; Sobreviela, G.; Torres, F.; Uranga, A.; Barniol, N. Single-Resonator Dual-Frequency BEOL-Embedded CMOS-MEMS Oscillator With Low-Power and Ultra-Compact TIA Core. IEEE Electron Device Lett. 2017, 38, 273–276. [Google Scholar] [CrossRef]
- Wu, G.; Xu, J.; Zhang, X.; Wang, N.; Yan, D.; Lim, J.L.K.; Zhu, Y.; Li, W.; Gu, Y. Wafer-Level Vacuum-Packaged High-Performance AlN-on-SOI Piezoelectric Resonator for Sub-100-MHz Oscillator Applications. IEEE Trans. Ind. Electron. 2018, 65, 3576–3584. [Google Scholar] [CrossRef]
- Bouchami, A.; Elsayed, M.Y.; Nabki, F. A Sub-mW 18-MHz MEMS Oscillator Based on a 98-dBΩ Adjustable Bandwidth Transimpedance Amplifier and a Lamé-Mode Resonator. Sensors 2019, 19, 2680. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Naing, T.L.; Rocheleau, T.O.; Alon, E.; Nguyen, C.T.C. Low-Power MEMS-Based Pierce Oscillator Using a 61-MHz Capacitive-Gap Disk Resonator. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2020, 67, 1377–1391. [Google Scholar] [CrossRef] [PubMed]
- Li, M.H.; Chen, C.Y.; Liu, C.Y.; Li, S.S. A Sub-150-μW BEOL-Embedded CMOS-MEMS Oscillator With a 138-dBΩ Ultra-Low-Noise TIA. IEEE Electron Device Lett. 2016, 37, 648–651. [Google Scholar] [CrossRef]
- Perelló-Roig, R.; Verd, J.; Bota, S.; Segura, J. A Tunable-Gain Transimpedance Amplifier for CMOS-MEMS Resonators Characterization. Micromachines 2021, 12, 82. [Google Scholar] [CrossRef] [PubMed]





| Parasitic/Load Type | Symbol | Value |
|---|---|---|
| Oscilloscope | COsc ROsc | 11 pF 1 MΩ |
| SMA Connector | CSMA1 CSMA2 | 104.15 pF 62.6 pF |
| Package Lead | CPkg | 0.25 pF |
| PCB Trace | CTr | 1 pF |
| Ref. No. | [2] | [17] | [29] | [30] | [31] * | [32] | [33] | [34] | [35] | This Work |
|---|---|---|---|---|---|---|---|---|---|---|
| Trans Mech ″ | Piezo + | Cap ! | Cap | Cap | Piezo | Cap | Cap | Cap | Cap | Cap |
| Process | 65 nm | 0.35 μm | 0.13 μm | 0.35 μm | 0.18 μm | 65 nm | 0.35 μm | 0.35 μm | 0.35 μm | 65 nm |
| (MHz) | 14.42 | 20 | 20 | 0.551 | 75.01 ** | 17.93 | 61 | 1.23 | 1.12 | 6.89 |
| ⊗ (V) | - | - | 5 | 18 | - | 100 | 7.45 | 7 | 25 | 40 |
| Q | 4.9 × 103 | 1.6 × 105 | 104 | 2 × 103 | 9.5 × 103 | 8.9 × 105 | 80 × 103 | 1.9 × 103 | 2.1 × 103 | 3.24 × 106 |
| (kΩ) | 0.9 | 65 | 31 | 930 | 0.0326 | 35 | 13.8 | 16 × 103 | 2 × 103 • | 199.1 |
| (dBΩ) | 69 | - | 112.5 | 157 | - | 98 | - | 138 | 121 | 118.1 |
| 1.4 mW | 6.9 mW | 360 μW | 8.5 μW | 7.8 mW | 900 μW | 78 μW | 150 μW | 930 μW | 143 nW | |
| PN|1 kHz (dBc/Hz) | −116 | − | −125.6 | −103.8 | −108 | −120 | −130 | −106 | - | −128.1 |
| PN1 MHz (dBc/Hz) | −130 | −131 $ | −131.9 | −121 $ | −133.15 | −127 | −152 $ | −111 $ | - | −133.7 |
| FoM1 MHz (Hz2Ω2) | 4.98 × 1015 | 1.4 × 1019 | 6.8 × 1019 | 1.6 × 1020 | 6.56 × 1013 | 3.8 × 1019 | 5.96 × 1022 | 1.44 × 1021 | - | 1.3 × 1024 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kira, A.; Elsayed, M.Y.; Allidina, K.; Chodavarapu, V.P.; El-Gamal, M.N. A 6.89-MHz 143-nW MEMS Oscillator Based on a 118-dBΩ Tunable Gain and Duty-Cycle CMOS TIA. Electronics 2021, 10, 2646. https://doi.org/10.3390/electronics10212646
Kira A, Elsayed MY, Allidina K, Chodavarapu VP, El-Gamal MN. A 6.89-MHz 143-nW MEMS Oscillator Based on a 118-dBΩ Tunable Gain and Duty-Cycle CMOS TIA. Electronics. 2021; 10(21):2646. https://doi.org/10.3390/electronics10212646
Chicago/Turabian StyleKira, Ahmed, Mohannad Y. Elsayed, Karim Allidina, Vamsy P. Chodavarapu, and Mourad N. El-Gamal. 2021. "A 6.89-MHz 143-nW MEMS Oscillator Based on a 118-dBΩ Tunable Gain and Duty-Cycle CMOS TIA" Electronics 10, no. 21: 2646. https://doi.org/10.3390/electronics10212646
APA StyleKira, A., Elsayed, M. Y., Allidina, K., Chodavarapu, V. P., & El-Gamal, M. N. (2021). A 6.89-MHz 143-nW MEMS Oscillator Based on a 118-dBΩ Tunable Gain and Duty-Cycle CMOS TIA. Electronics, 10(21), 2646. https://doi.org/10.3390/electronics10212646







