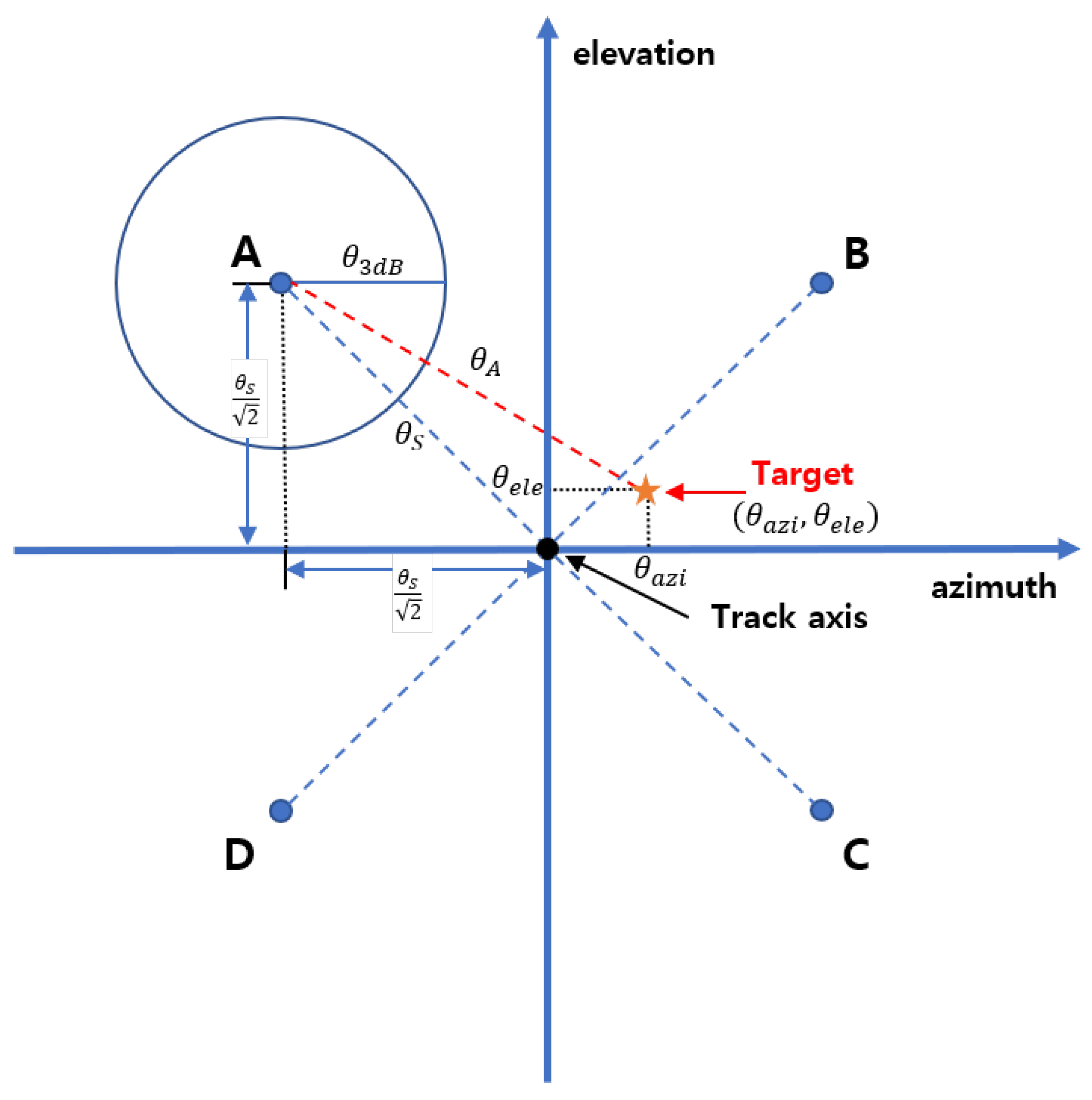
1. Introduction
A radar measures the distance, direction, and speed information of a target using electromagnetic waves and can perform search and tracking functions. The search mode explores a given volume space in the absence of information about the target and detects the target. When a target is detected, the tracking mode is activated. In this case, the target is tracked while measuring states such as distance, angle, and speed. Amplitude-comparison monopulse radar (ACM) is classified as tracking radar, and it is possible to accurately measure the tracking error of a target with only one pulse (monopulse). The monopulse radar-receiving antenna consists of four receiving beam patterns with the same squint angle. The received signals are incident on the four receiving beam patterns, and the signals incident on the receiving antenna are inputted through the sum channel and the difference channels. The azimuth and elevation tracking error are calculated through the signal amplitude ratio of these channels [
1,
2,
3].
In [
4,
5,
6], many methods were proposed to improve the angular performance of the monopulse radar. In [
4], the angle of the target was estimated using multiple antennas in the amplitude comparison monopulse radar. Although the amplitudes of the signal received by each antenna vary according to the angle of the target, it is assumed that the arrival time of the signals are the same. The generalized likelihood ratio test is used to express the detection and parameter-estimation method for the radar receiver. In [
5], an adaptive array for estimated angle was used. The maximum likelihood theory was applied to sum and difference monopulse beams that suppress external noise sources. In addition, their method was shown to perform well in the presence of side lobe and main beam interference. In [
6], the author dealt with the DOA resolution problem of two targets in the four-channel monopulse radar and proposed a new solution to solve them.
The proposed methods of the above-mentioned papers mainly dealt with improving the angle estimation performance of monopulse radar. In this regard, we analyze and compare the angle estimation performance of the methods proposed in the above papers in detail with various noises. Therefore, methods to efficiently and accurately calculate the estimated angle MSE under the influence of various noises are studied.
In general, the return signal and noise are received by the receiving antenna [
7]. Noise is caused by several environmental variables (interference and propagation effects). In the ACM, this noise has a great influence on the ability to estimate the angular position of the target. Therefore, it is necessary to calculate the target angle estimation accuracy by explicitly analyzing the angle estimation error caused by additive noise to the actual incident angle of the ACM.
Previously, studies on the performance analysis of monopulse radar have been conducted in a similar manner. In [
8,
9,
10,
11], the authors dealt with the performance analysis of the angle estimation of monopulse radar. In [
8], the author considered the performance of the monopulse receiver in relation to the cause of the internal error. Four main types of monopulse receivers were analyzed, and an analysis was performed based on a mathematical model. However, external errors were excluded. In [
9], the estimated angle performance of a monopulse radar with receiving inconsistency was analyzed. In the estimated angle performance, it was shown that not only the algorithm but also the amplitude-phase mismatch affects the estimated angle performance. However, performance analysis considering various measurement noises was not conducted. In [
10], the author dealt with the angle estimation problem of ACM radar when thermal noise is present internally. Similarly, performance analysis on the influence of external measurements was not performed. In [
11], the authors presented the ACM algorithm and the covariance prediction equation. The proposed covariance equation was simple, but it predicted the RMS error very accurately.
Most of the papers considered only the influence of internal noise and did not consider the measurement noise caused by external variables. In this regard, we previously conducted a performance analysis of the ACM radar considering external noise. In a previous study [
12], the MSE of the ACM Direction-of-Arrival (DOA) estimated angle was expanded as an analytic expression using the first-order Taylor approximation and the second-order Taylor approximation and compared with the Monte-Carlo method. In order to improve the analytic MSE of the second-order Taylor approximation in [
12], we propose an analytic MSE of the third-order Taylor approximation.
In this paper, we focus on improving the accuracy of the analytic expression of the estimated angle MSE of the ACM algorithm using the first-order Taylor approximation and the second-order Taylor approximation proposed in the previous study [
12]. Therefore, we improve the MSE calculation accuracy of the estimated angle considering noise through the third-order Taylor approximation of the analytic expression. In order to analyze the accuracy of angle estimation under various noise effects, studies are conducted in the case of several standard deviations. The MSE of the ACM angle estimation algorithm is derived through Monte-Carlo simulation, and the MSE is analytically derived using the third-order Taylor approximation. In addition, we confirm that the computational complexity of the analytic MSE is lower than that of the MSE based on Monte-Carlo method.
In
Section 2.1, the angle estimation principle of ACM radar is described. In
Section 2.2, angle estimation equations of the ACM radar considering additive noise are derived. In
Section 2.3, the simulation MSE and analytic MSE are defined. In
Section 3, the performances of analytic MSEs and simulation MSEs are analyzed. In addition, the errors of the analytic MSEs of the second-order Taylor approximation are improved by using the analytic MSEs of the third-order Taylor approximation. In the Appendix, the analytic MSEs of the third-order Taylor approximation are derived.
4. Discussion
The estimation of various parameters of radar targets is affected by various noises. The types of noise include cosmic noise and thermal noise. There are also amplitude irregularities due to interference from external sources and propagation effects. The most significant of these is the thermal noise that occurs inside the receiver [
7].
In this work, performance analysis is conducted for several noises without being limited to a specific noise. Therefore, the experiment is conducted using various standard deviations of the noise variables, and in most cases, the MSE of the estimated angle is calculated. When the standard deviation of the noise variable is known, the MSE can be calculated accurately and efficiently by using the analytic MSE based on the third-order Taylor approximation.
However, there are limits to this work. First, the proposed method only considers the case where the beam pattern is a specific Gaussian pattern. Therefore, this cannot be applied to a case with a beam pattern other than Gaussian. Next, we considered only the specific case where the noises in the incident signal are not correlated with each other. This makes the noise used in the MSE calculation limited. Finally, the MSE of the proposed method with the third-order Taylor expansion is slightly different from that of the original monopulse algorithm without approximation.
5. Conclusions
In this study, in order to judge the reliability of the ACM’s angle estimation ability in an environment where various noises are given, we focus on accurately calculating the MSE. Therefore, we propose an analytical MSE based on the third-order Taylor approximation with improved accuracy in terms of the MSE. The analytic MSE method based on the third-order Taylor approximation can efficiently and accurately calculate the MSE of an angle estimate quantitatively once the variance of additive noise is given.
The MSEs associated with the third-order Taylor expansion are much smaller than those with the second-order Taylor expansion. In addition, the computational complexity of the analytically-derived MSE is much smaller than that of the Monte-Carlo simulation-based MSE.
In the Monte-Carlo simulation based approach, for the MSEs to be reliable, the number of realizations should be large enough, which results in the increase in the computational complexity. From
Figure 2, for the simulation-based MSE to be reliable, the number of realizations should be greater than 10,000. When comparing the analytical MSE through the third-order Taylor approximation and the MSE through the Monte-Carlo method, it can be seen that the computational amount of the analytical MSE method is less than that of the Monte-Carlo method. In
Table 6, the operation time of the analytically-derived MSE is 0.76% of that of the simulation-based MSE from 10,000 realizations, and the operation time of the analytically-derived MSE is 0.07% of that of the simulation-based MSE from 100,000 realizations. This means that the operation speed is 1355 times faster. Therefore, the proposed analytic approach is much better than the Monte-Calro simulation-based approach in terms of the computational complexity.
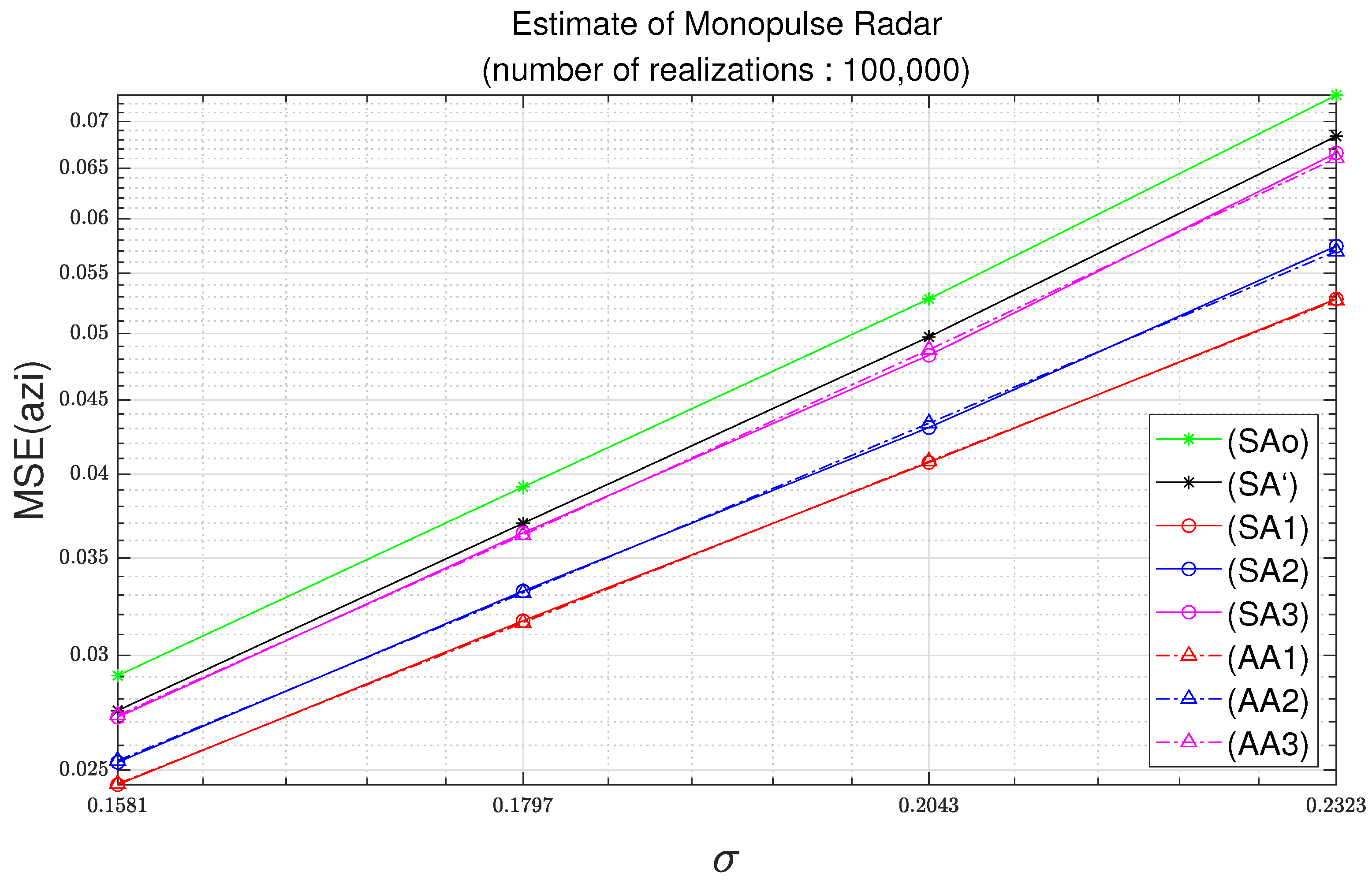
In addition, by adopting the third-order Taylor expansion, the estimation accuracy is improved in comparison with the approaches based on the first-order Taylor expansion and the second-order Taylor expansion. In Tests 1 and 2, analytic MSEs based on the third-order Taylor approximation almost overlap with the simulation MSE results of estimation equations to which gain approximations are applied. In particular, in Test 2, it can be seen that analytic MSEs based on third-order Taylor approximation respond better to various noise environments than analytic MSEs based on the first and second-order Taylor approximations proposed in a previous study. In
Table 5, it can be seen that the error of the analytic MSE based on the third-order Taylor approximation is reduced by approximately 89.5% compared to the error of the analytic MSE based on the second-order Taylor approximation. However, the computational complexity of the third-order Taylor expansion is slightly greater than that of the second-order Taylor expansion.
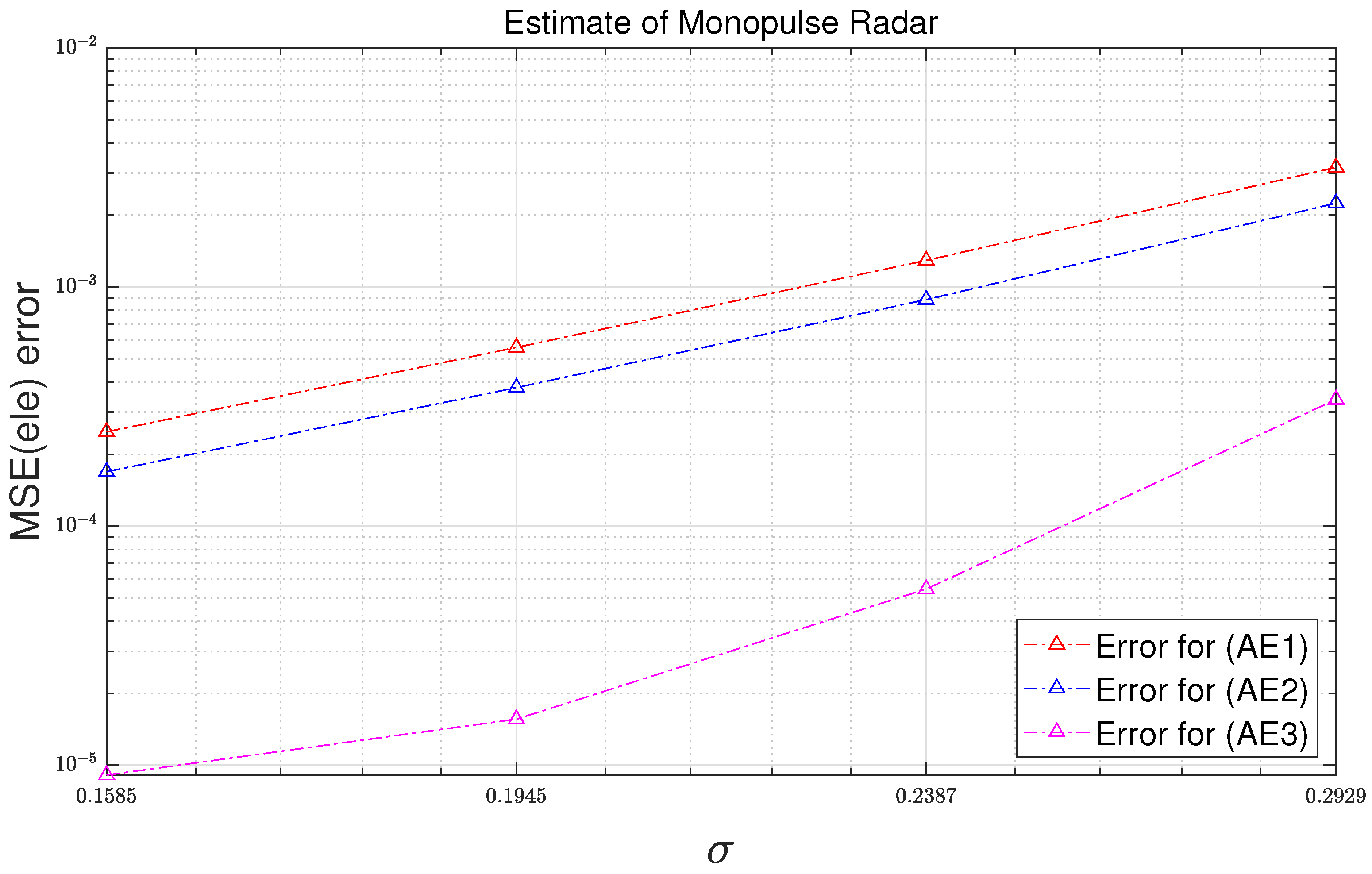
As mentioned in the Discussion, in
Figure 3 and
Figure 5, there is always a certain difference between the result of (SAo) and the result of (SA3). The same observations are also found in
Figure 4 and
Figure 6, which illustrates the elevation MSEs. Obtaining analytic expressions for the results with legend (SAo) and the results with legend (SEo) will be a future research topic. In addition, analyzing the estimated angle MSE of the ACM radar considering the correlated noise will also be a future research topic.