Theoretical and Experimental Substractions of Device Temperature Determination Utilizing I-V Characterization Applied on AlGaN/GaN HEMT
Abstract
:1. Introduction
2. Theory
2.1. Electrical Model
2.2. Average Temperature Definition
2.3. Ambient Temperature Variation
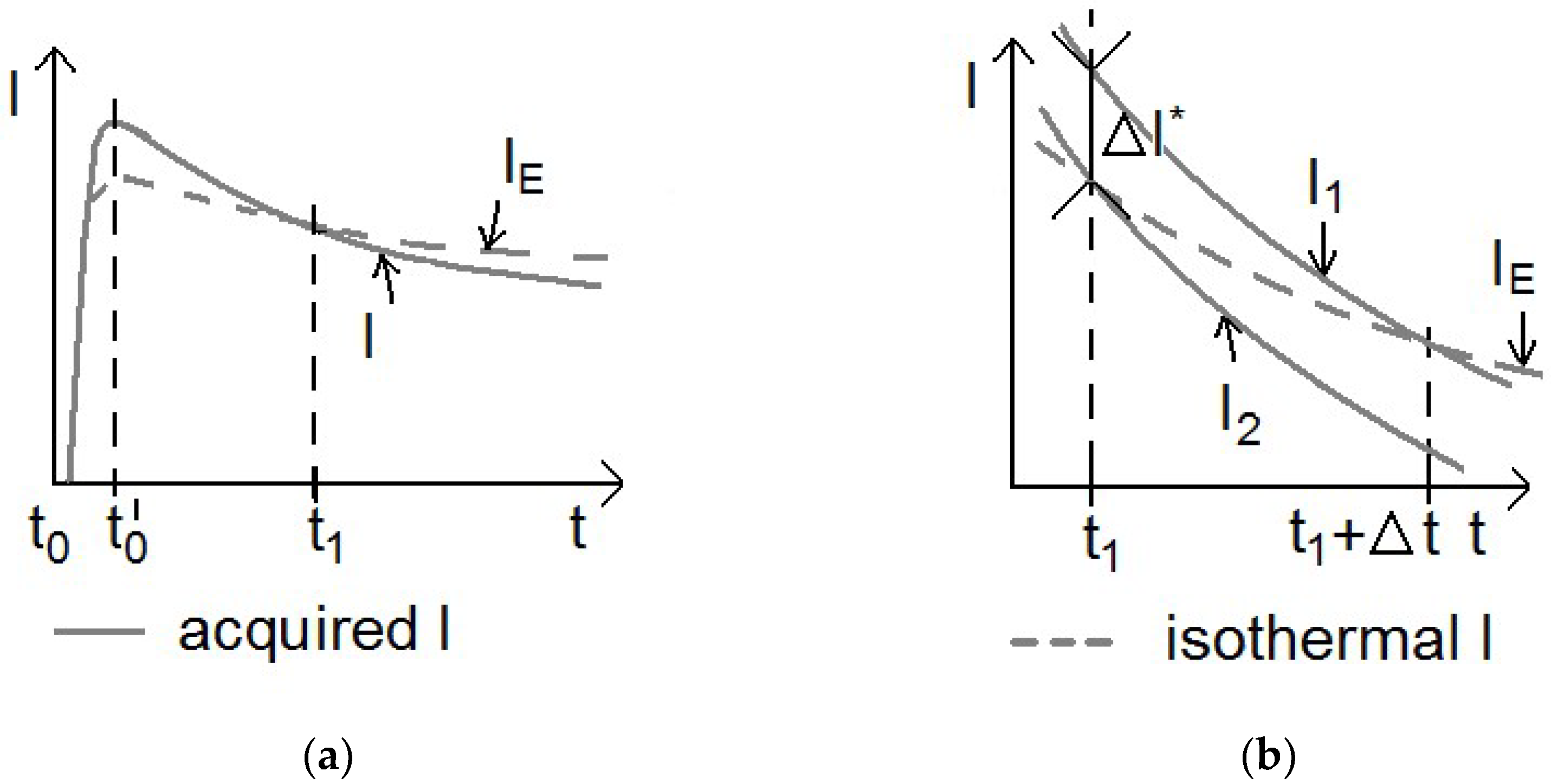
2.4. Trapping Effects Approximation in FET
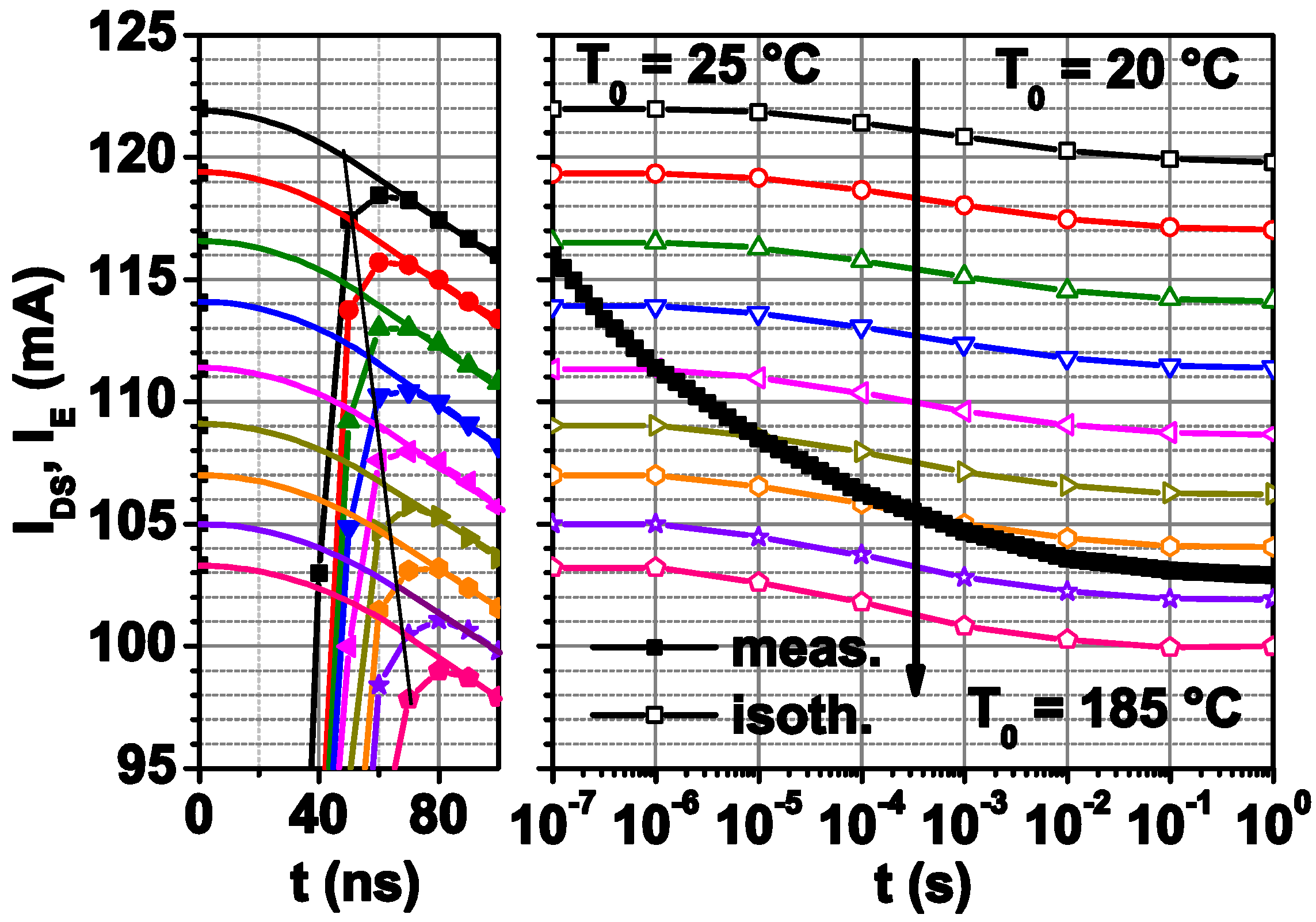
2.5. Short Time Response Current Utilization
3. Experimental
3.1. Structure Design and Experimental Setup
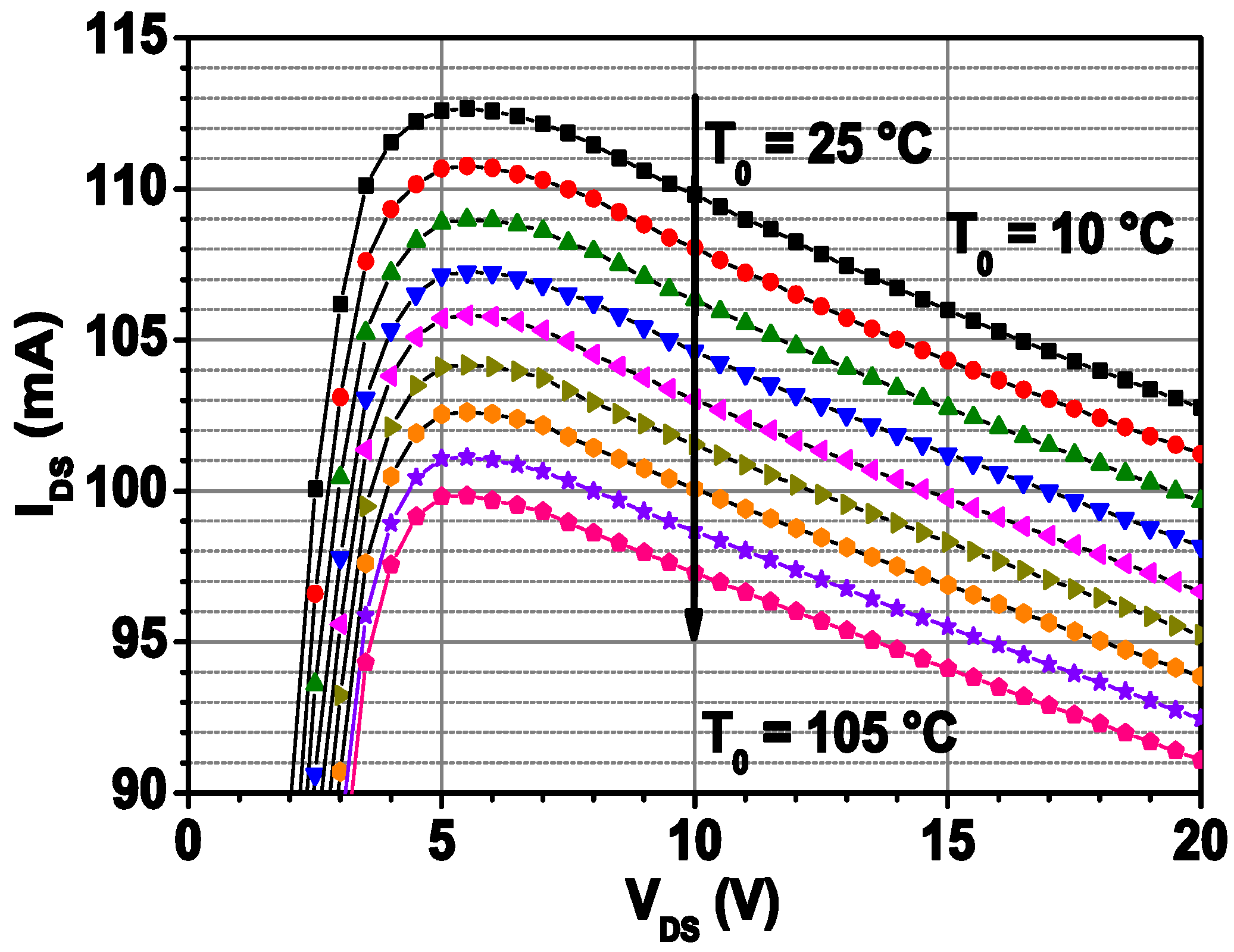
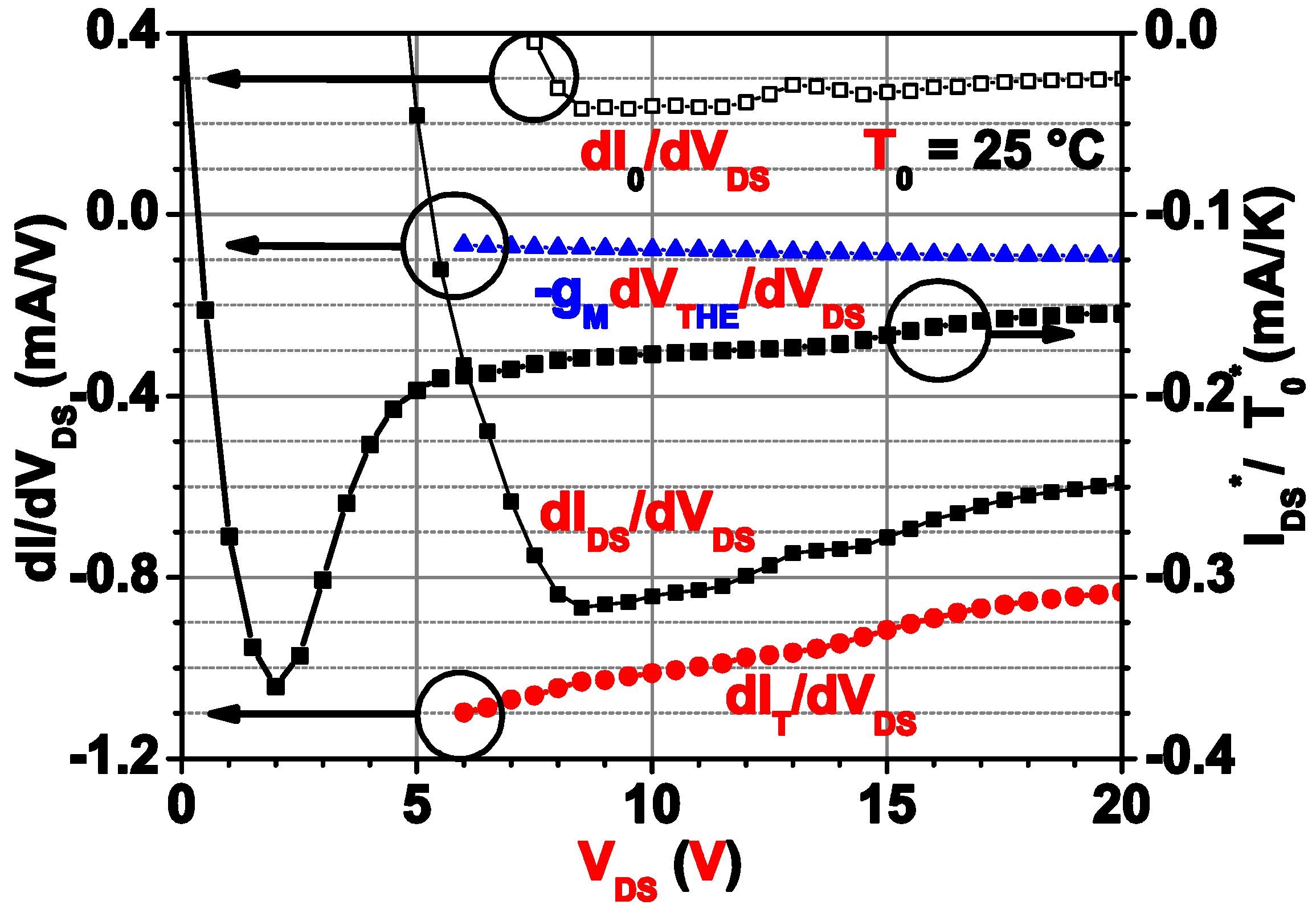
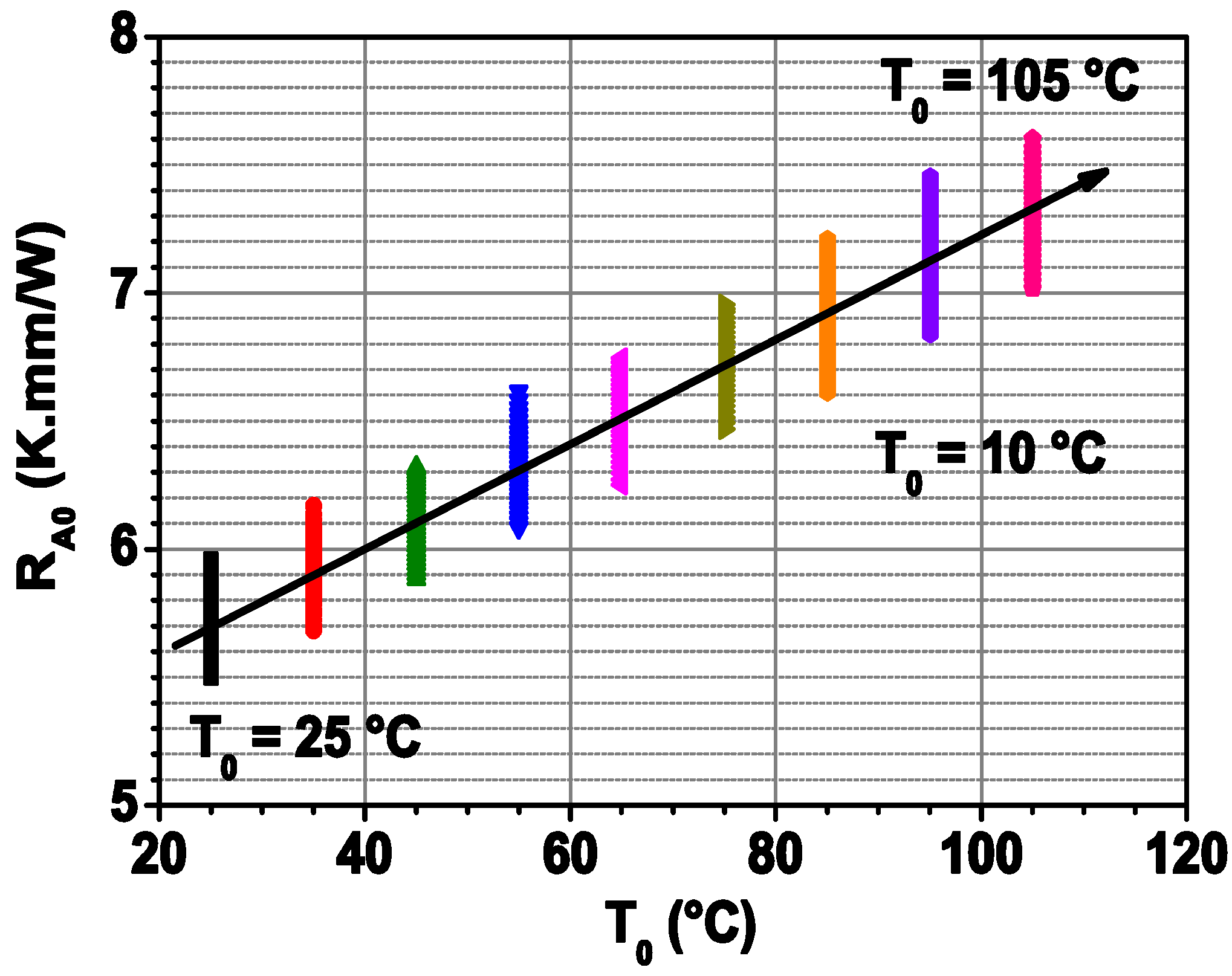
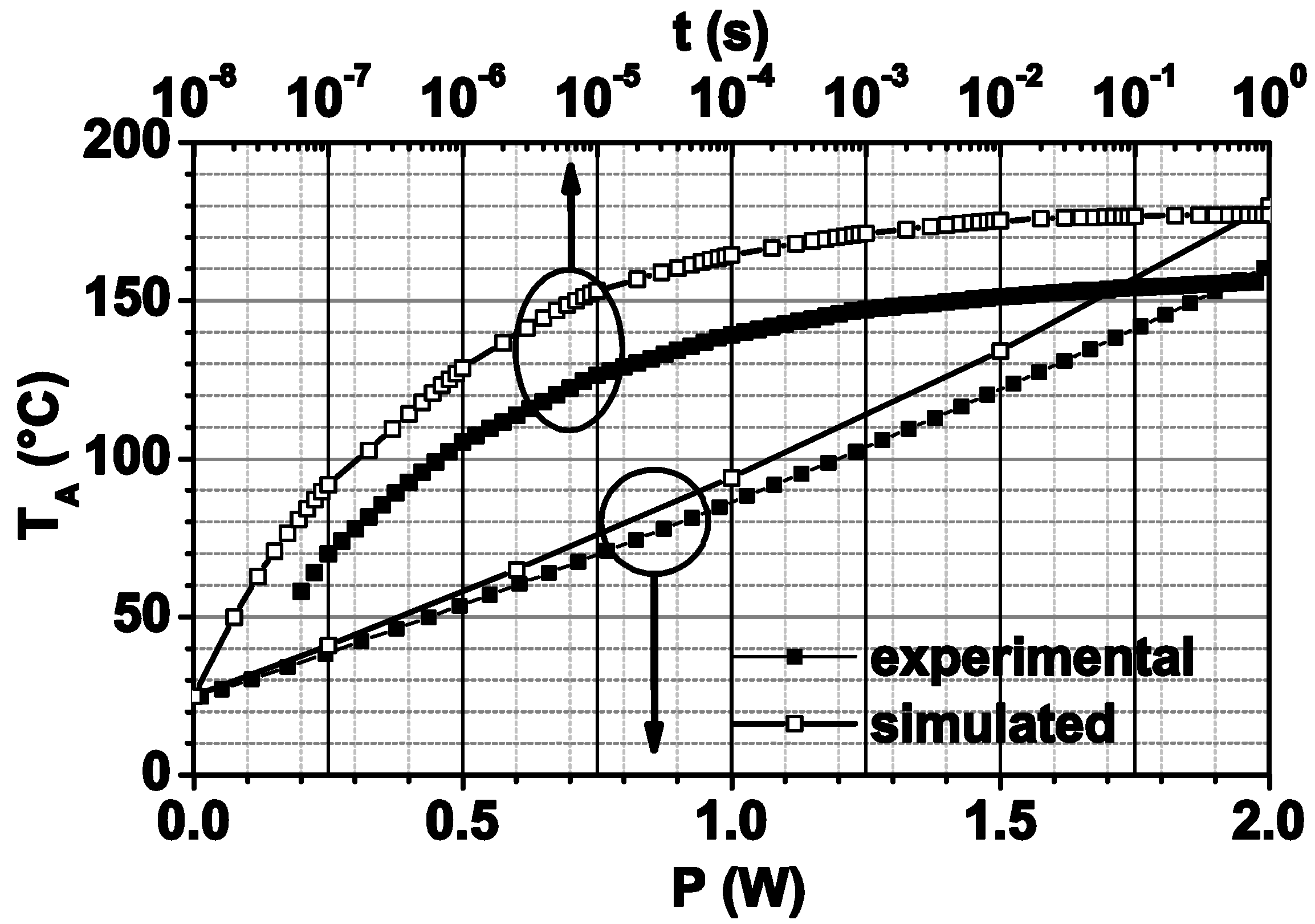
3.2. Average Channel Temperature Determination
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ambacher, O.; Smart, J.; Shealy, J.R.; Weimann, N.G.; Chu, K.; Murphy, M.; Schaff, W.J.; Eastman, L.F. Two-dimensional electron gases induced by spontaneous and piezoelectric polarization charges in N- and Ga-face AlGaN/GaN heterostructures. J. Appl. Phys. 1999, 85, 3222. [Google Scholar] [CrossRef] [Green Version]
- Chattopadhyay, M.K.; Tokekar, S. Thermal model for dc characteristics of AlGaN/GaN HEMTs including self-heating effect and non-linear polarization. Microelectron. J. 2008, 39, 1181. [Google Scholar] [CrossRef]
- Doré, J.-B.; Belot, D.; Mercier, E.; Bicaïs, S.; Gougeon, G.; Corre, Y.; Miscopein, B.; Ktenas, D.; Strinati, E.C. Technology Roadmap for Beyond 5G Wireless Connectivity in D-band. In Proceedings of the 2nd 6G Wireless Summit (6G SUMMIT), Levi, Finland, 17–20 March 2020. [Google Scholar] [CrossRef]
- Chowdhury, S. Gallium nitride based power switches for next generation of power conversion. Phys. Stat. Sol. A 2015, 212, 1066. [Google Scholar] [CrossRef]
- Berthet, F.; Guhel, Y.; Gualous, H.; Boudart, B.; Trolet, J.L.; Piccione, M.; Gaquière, C. Characterization of the self-heating of AlGaN/GaN HEMTs during an electrical stress by using Raman spectroscopy. Microel. Rel. 2011, 51, 1796–1800. [Google Scholar] [CrossRef]
- Kuball, M.; Rajasingam, S.; Sarua, A. Measurement of temperature distribution in multifingerAlGaN/GaN heterostructure field-effect transistors using micro-Raman spectroscopy. Appl. Phys. Lett. 2003, 82, 124. [Google Scholar] [CrossRef]
- Kim, J.; Freitas, J.A.; Mittereder, J.; Fitch, R.; Kang, B.S.; Pearton, S.J.; Ren, F. Effective temperature measurements of AlGaN/GaN-based HEMT under various load lines using micro-Raman technique. Solid-State Electr. 2006, 50, 408–411. [Google Scholar] [CrossRef]
- Kuzmik, J.; Javorka, P.; Alam, A.; Marso, M.; Heuken, M.; Kordos, P. Determination of channel temperature in AlGaN/GaN HEMTs grown on sapphire and silicon substrates using DC characterization method. IEEE Trans. Electr. Dev. 2002, 49, 1496–1498. [Google Scholar] [CrossRef]
- Menozzi, R.; Membreno, G.A.U.; Nener, B.D.; Parish, G.; Sozzi, G.; Faraone, L.; Mishra, U.K. Temperature-dependent characterization of AlGaN/GaN HEMTs: Thermal and source/drain resistances. IEEE Trans. Dev. Mat. Rel. 2008, 8, 255. [Google Scholar] [CrossRef]
- Tarter, T.S. A Novel Circuit for the Evaluation of Thermal Impedance Characteristics of MOS Integrated Circuits. In Proceedings of the IEEE Semiconductor Thermal and Temperature Measurement (SEMI-THERM) Symp., San Diego, CA, USA, 7–9 February 1989; pp. 131–135. [Google Scholar] [CrossRef]
- Raj, B.; Bindra, S. Thermal Analysis of AlGaN/GaN HEMT: Measurement and Analytical Modeling Techniques. Int. J. Comp. Appl. 2013, 75, 4–13. [Google Scholar] [CrossRef]
- Synopsys. Sentaurus Device User Guide; v. L-2017.09; TCAD Sentaurus: San Jose, CA, USA, 2017. [Google Scholar]
- Heo, D.; Chen, E.; Gebara, E.; Yoo, S.; Laskar, J.; Anderson, T. Temperature Dependent MOSFET RF Large Signal Model Incorporating Self Heating Effects. In Proceedings of the IEEE MTT-S Int. Microwave Symp. Dig., Anaheim, CA, USA, 13–19 June 1999; Volume 1, pp. 415–418, ISBN 0-7803-5136-3. [Google Scholar]
- Florovic, M.; Kovac, J., Jr.; Kovac, J.; Chvala, A.; Weis, M.; Jacquet, J.C.; Delage, S.L. Models for the self-heating evaluation of GaN-based HEMT. Semicond. Sci. Technol. 2021, 36, 025019. [Google Scholar] [CrossRef]
- Chenming, C.H. MOS Transistor and MOSFETs in ICs—Scaling, Leakage and Other Topics. In Modern Semiconductor Devices for Integrated Circuits, 1st ed.; Prentice Hall: Midland Park, NJ, USA, 2010; Chapters 6 and 7; pp. 200–214, 266–269. ISBN 9780136085256. [Google Scholar]
- Florovic, M.; Szobolovszky, R.; Kovac, J., Jr.; Kovac, J.; Chvala, A.; Weis, M.; Jacquet, J.C.; Delage, S.L. Thermal analysis of AlGaN/GaN HEMT: Measurement and analytical modeling techniques. Semicond. Sci. Technol. 2019, 34, 065021. [Google Scholar] [CrossRef]
- Alim, A.A.; Rezazadeh, A.A.; Gaquiere, C. Temperature dependence of the threshold voltage of AlGaN/GaN/SiC high electron mobility transistors. Semicond. Sci. Technol. 2016, 31, 125016. [Google Scholar] [CrossRef]
- Florovic, M.; Szobolovszky, R.; Kovac, J.; Kovac, J., Jr.; Chvala, A.; Jacquet, J.C.; Delage, S.L. AlGaN/GaN HEMT channel temperature determination utilizing external heater. IEEE Semicond. Sci. Technol. 2020, 35, 025006. [Google Scholar] [CrossRef]
- Chvala, A.; Szobolovszky, R.; Kovac, J.; Florovic, M.; Marek, J.; Cernaj, L.; Donoval, D.; Dua, C.; Delage, S.L.; Jacquet, J.C. Advanced characterization techniques and analysis of thermal properties of AlGaN/GaN multifinger power HEMTs on SiC substrate supported by three-dimensional simulation. J. Electron. Packag. 2019, 141, 031007. [Google Scholar] [CrossRef] [Green Version]
- Chvala, A.; Marek, J.; Pribytny, P.; Satka, A.; Stoffels, S.; Posthuma, N.; Decoutere, S.; Donoval, D. Analysis of multifinger power HEMTs supported by effective 3-D deviceelectrothermal simulation. Microelectron. Reliab. 2017, 78, 148–155. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Florovič, M.; Kováč, J., Jr.; Chvála, A.; Kováč, J.; Jacquet, J.-C.; Delage, S.L. Theoretical and Experimental Substractions of Device Temperature Determination Utilizing I-V Characterization Applied on AlGaN/GaN HEMT. Electronics 2021, 10, 2738. https://doi.org/10.3390/electronics10222738
Florovič M, Kováč J Jr., Chvála A, Kováč J, Jacquet J-C, Delage SL. Theoretical and Experimental Substractions of Device Temperature Determination Utilizing I-V Characterization Applied on AlGaN/GaN HEMT. Electronics. 2021; 10(22):2738. https://doi.org/10.3390/electronics10222738
Chicago/Turabian StyleFlorovič, Martin, Jaroslav Kováč, Jr., Aleš Chvála, Jaroslav Kováč, Jean-Claude Jacquet, and Sylvain Laurent Delage. 2021. "Theoretical and Experimental Substractions of Device Temperature Determination Utilizing I-V Characterization Applied on AlGaN/GaN HEMT" Electronics 10, no. 22: 2738. https://doi.org/10.3390/electronics10222738
APA StyleFlorovič, M., Kováč, J., Jr., Chvála, A., Kováč, J., Jacquet, J.-C., & Delage, S. L. (2021). Theoretical and Experimental Substractions of Device Temperature Determination Utilizing I-V Characterization Applied on AlGaN/GaN HEMT. Electronics, 10(22), 2738. https://doi.org/10.3390/electronics10222738






