Modulation Technique for Modified Active Quasi-Z-Source Inverter with Common-Mode Voltage Reduction
Abstract
:1. Introduction
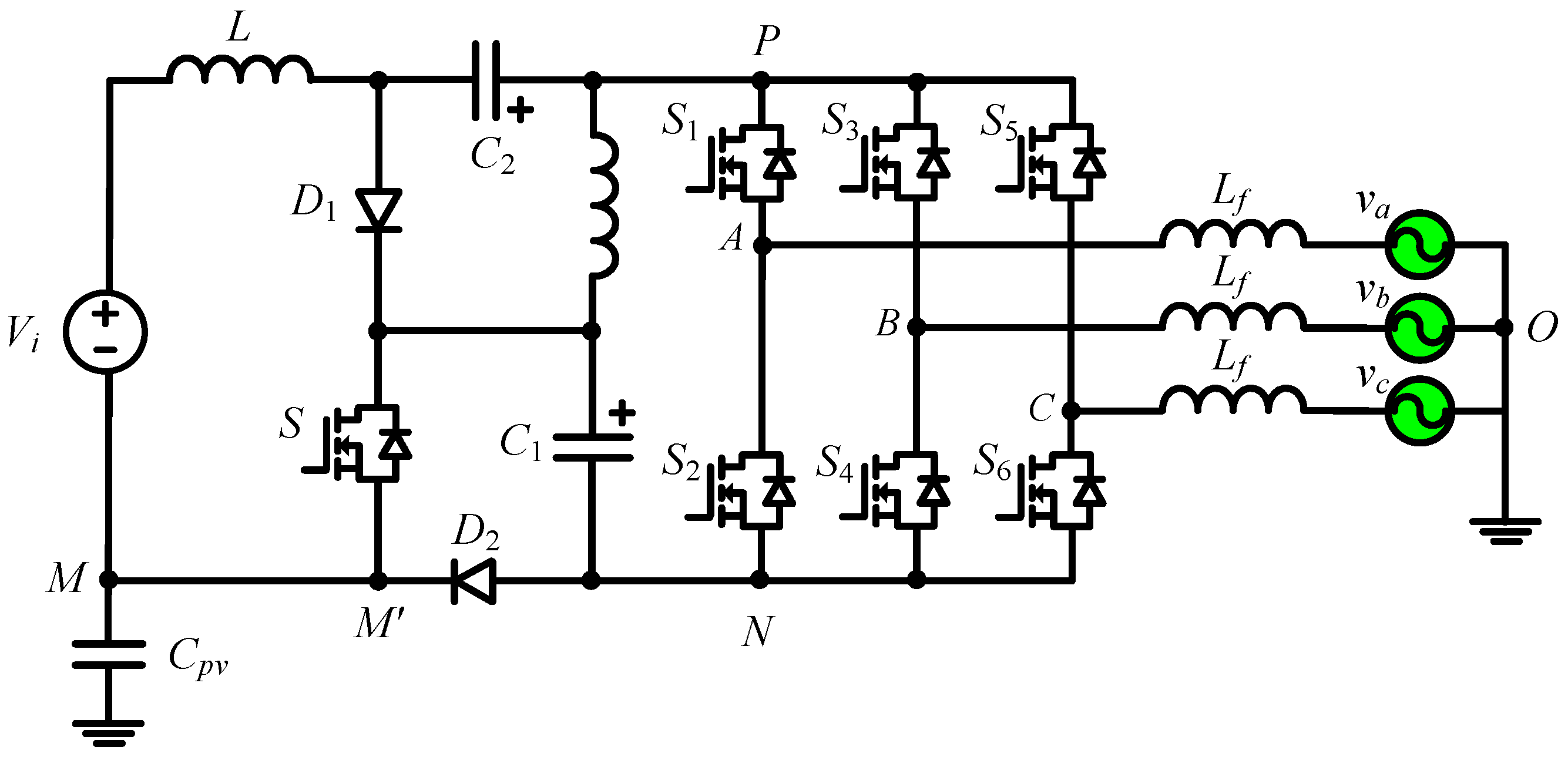
2. AqZSI Using Conventional SVM Method
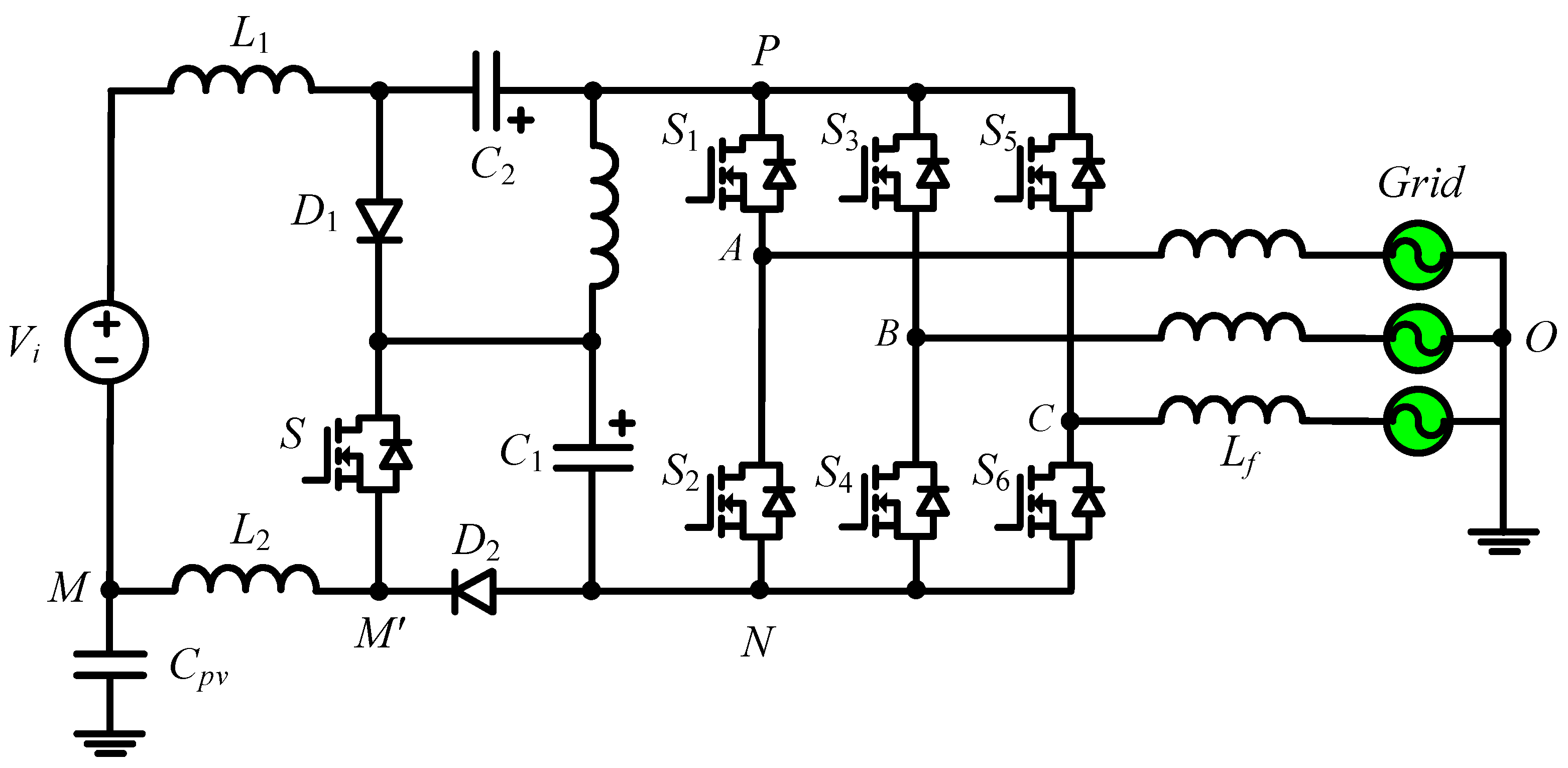
3. Modified Active Quasi-Z-Source Topology with Proposed CMV-SVM Method
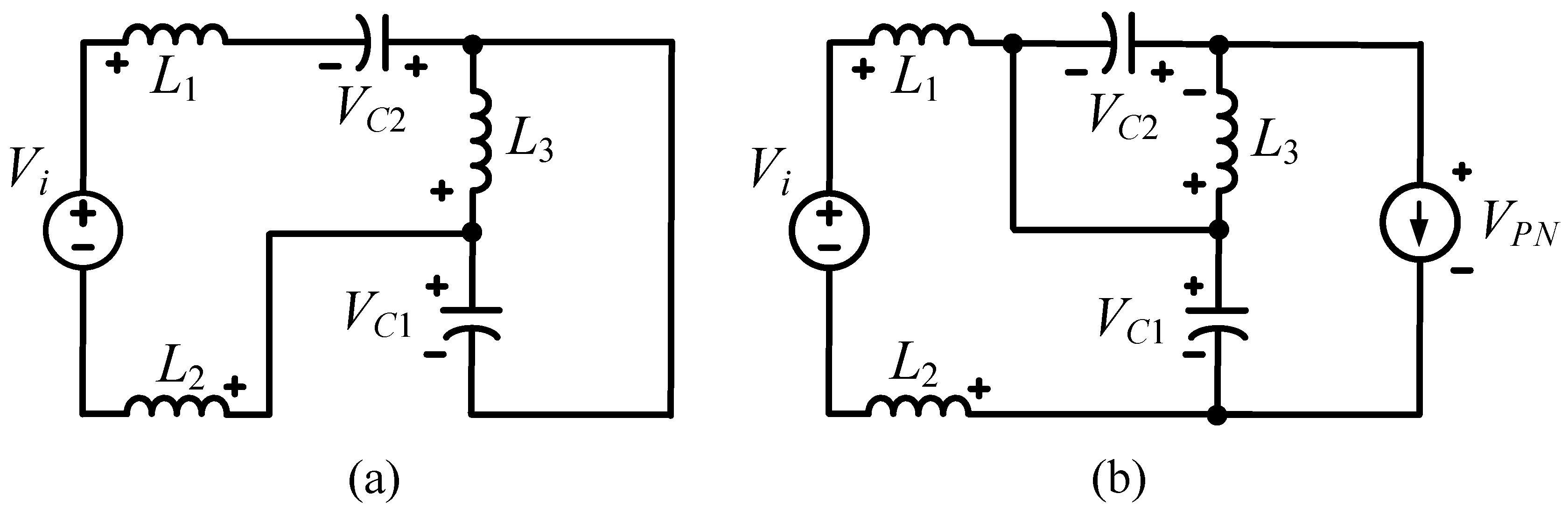
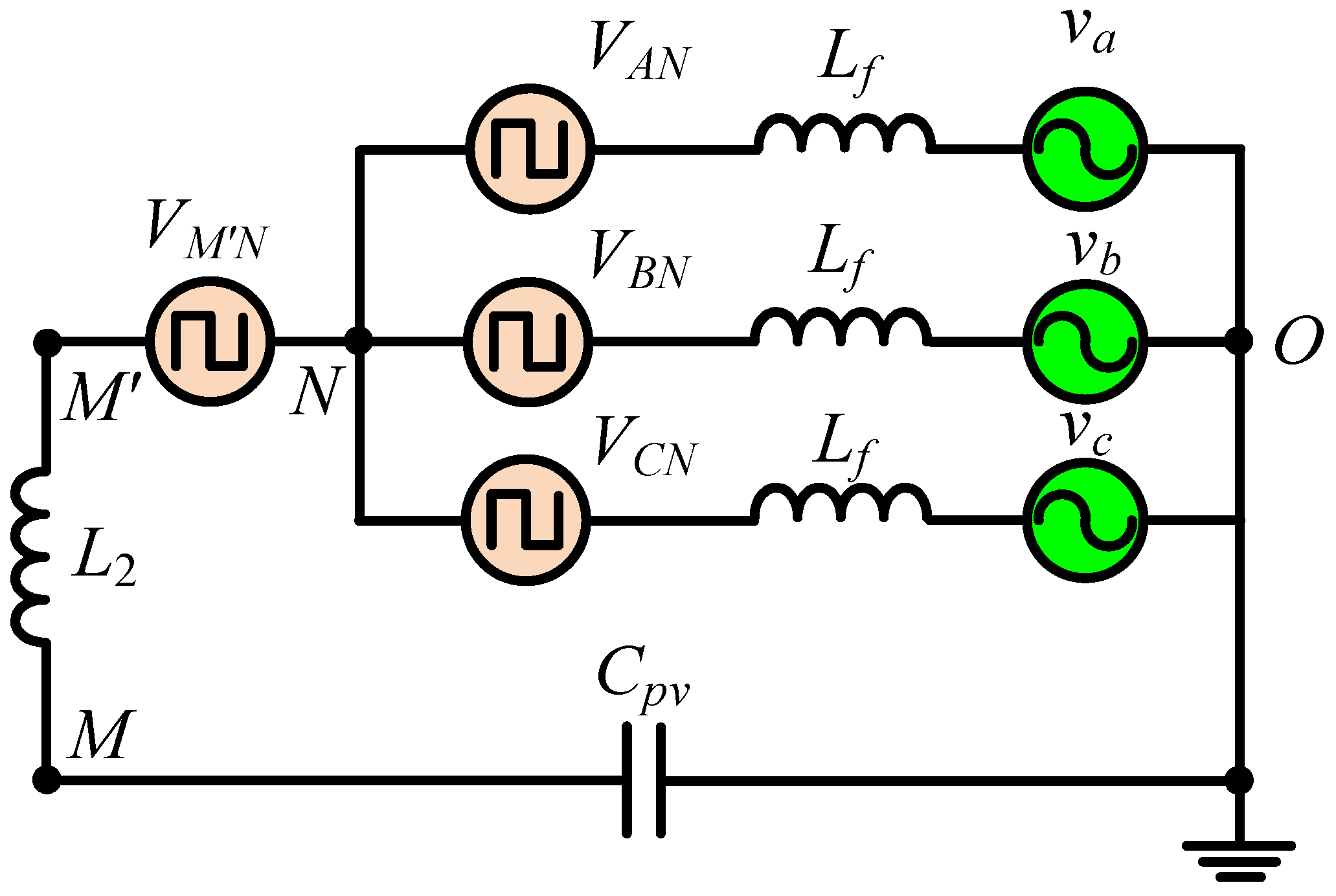
3.1. Operating Principle of MAqZS Topology
3.2. CMV of MAqZSI
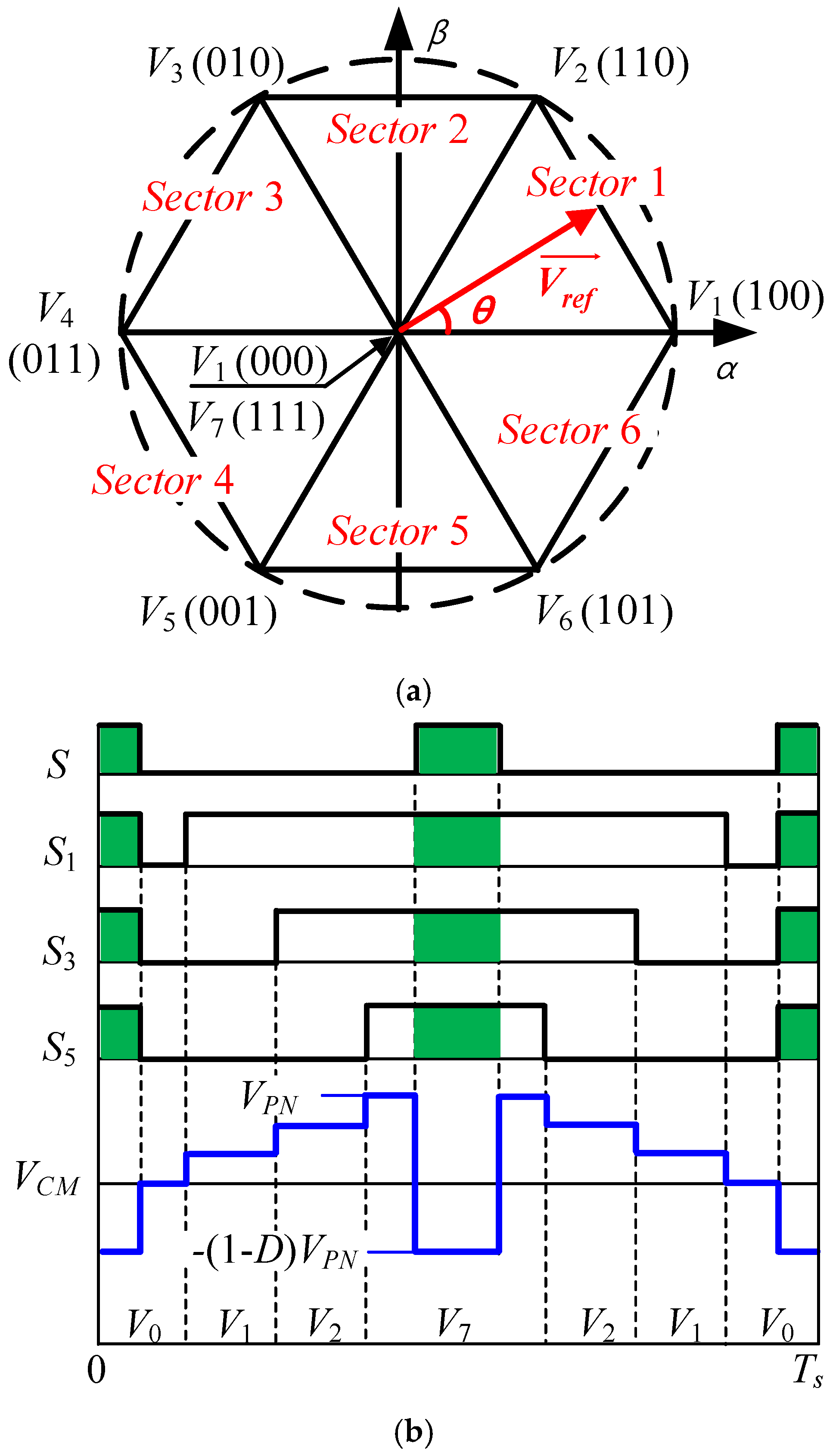
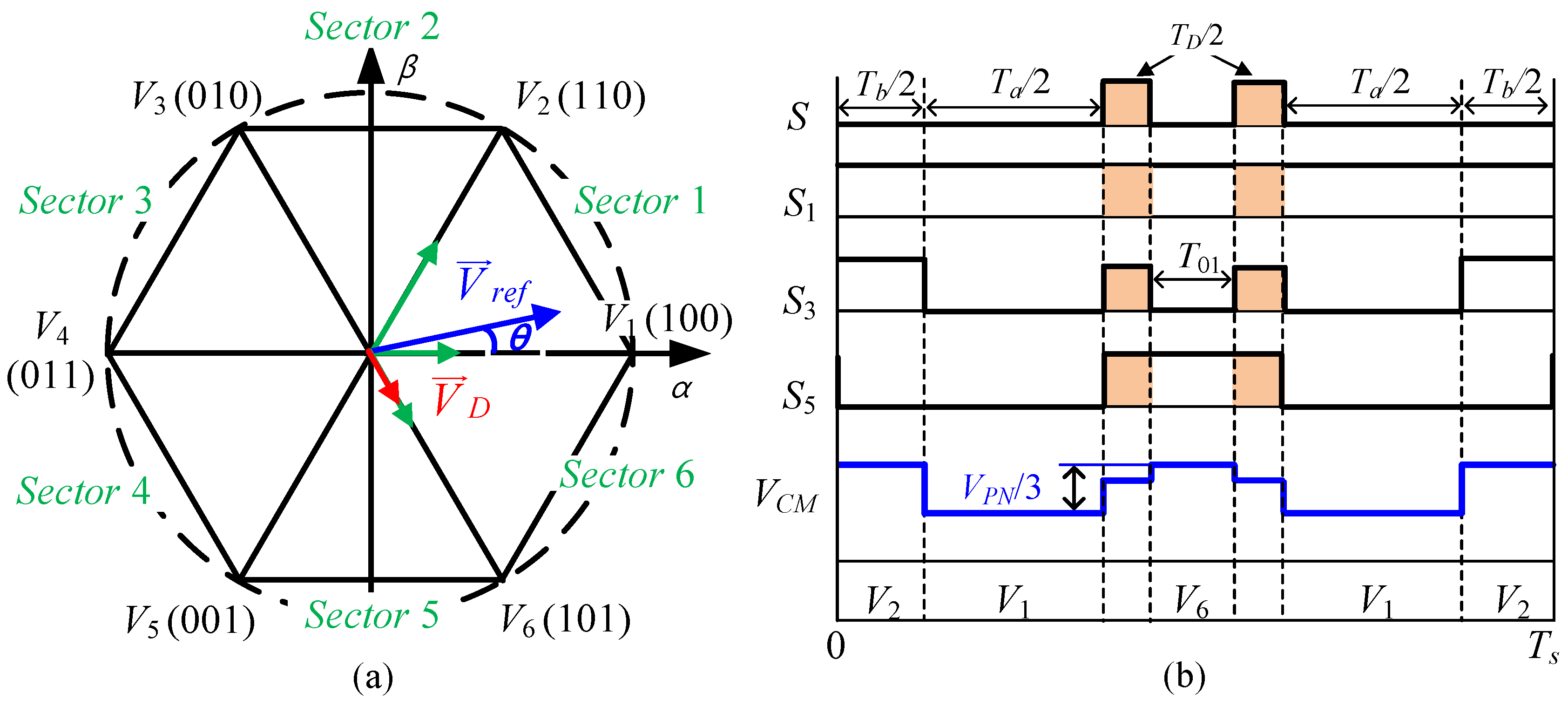
3.3. Implementation of the Proposed CMR-SVM Method
4. Passive Component Selection
4.1. Inductance Selection
4.2. Capacitance Selection
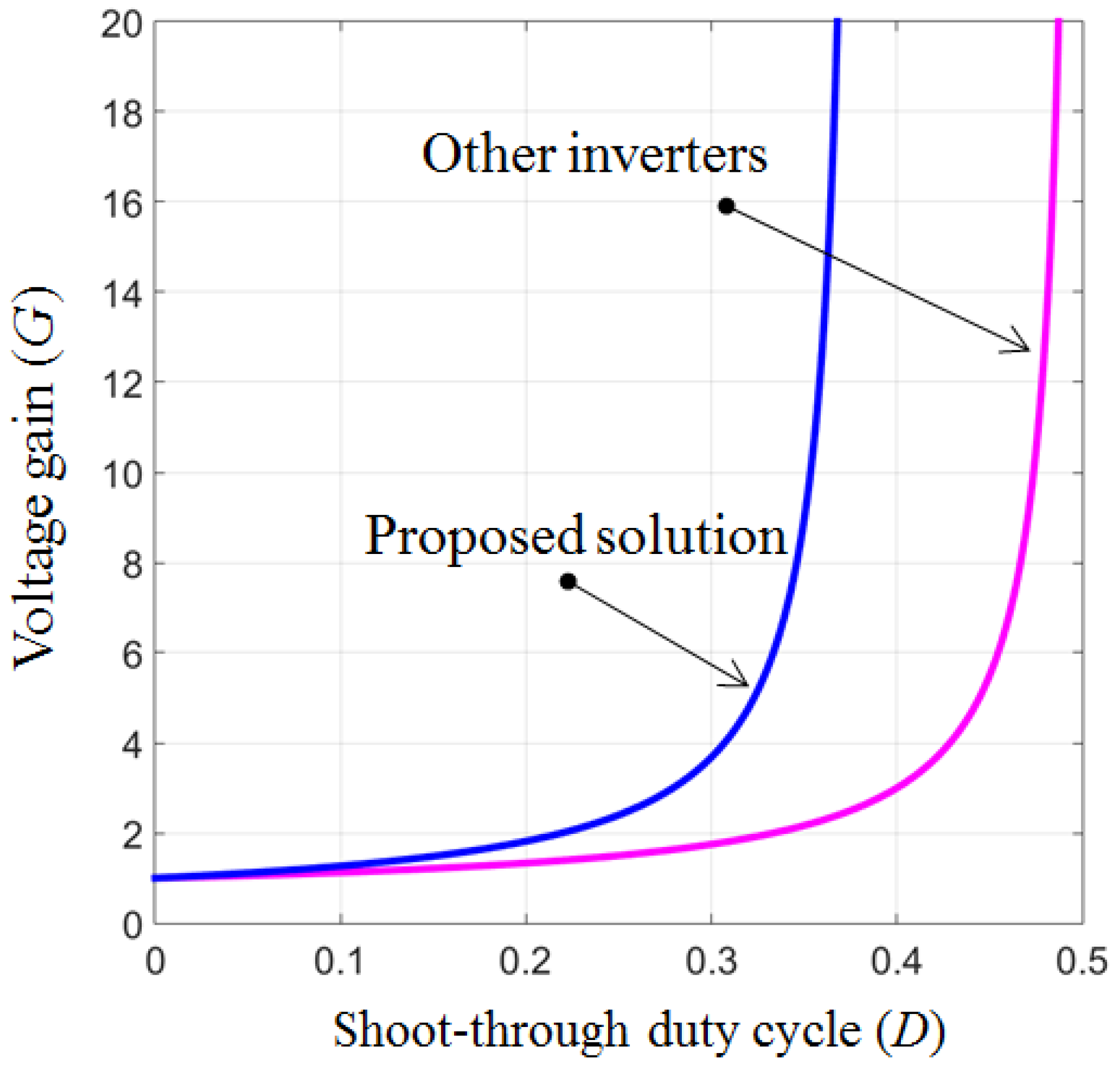
4.3. Comparison with Other Two-Level Three-Phase Z-Source Inverters
5. Results
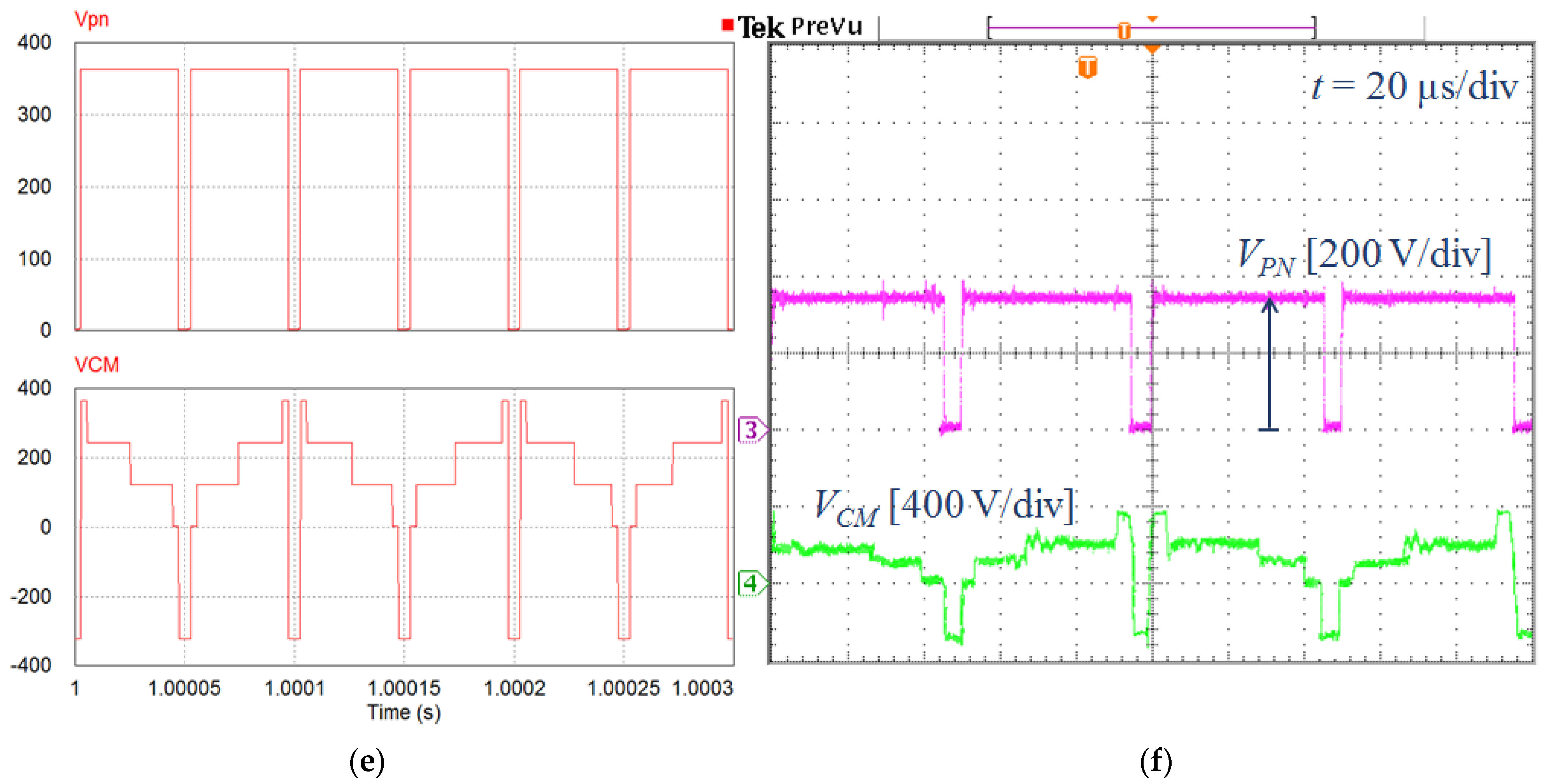
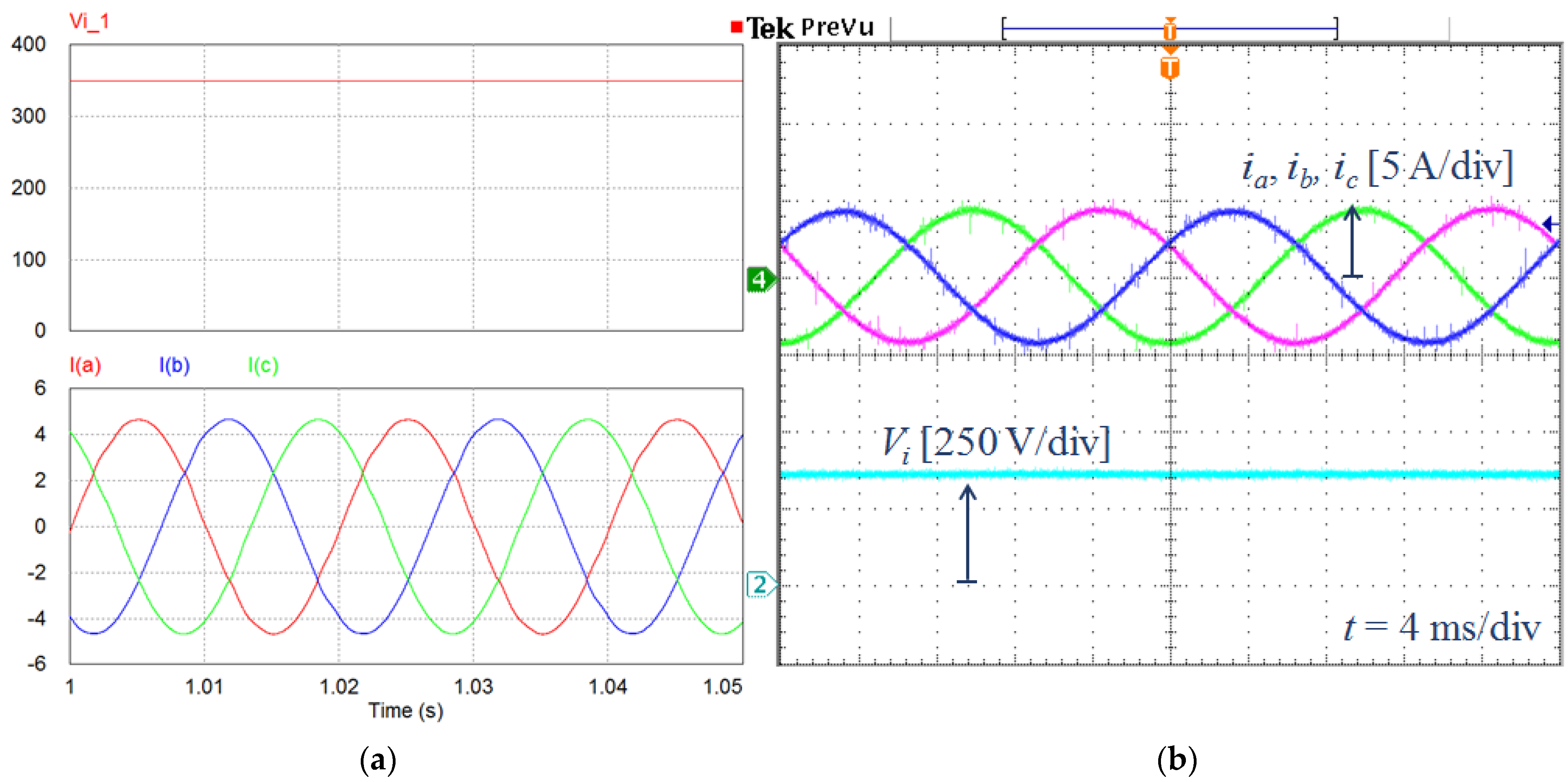
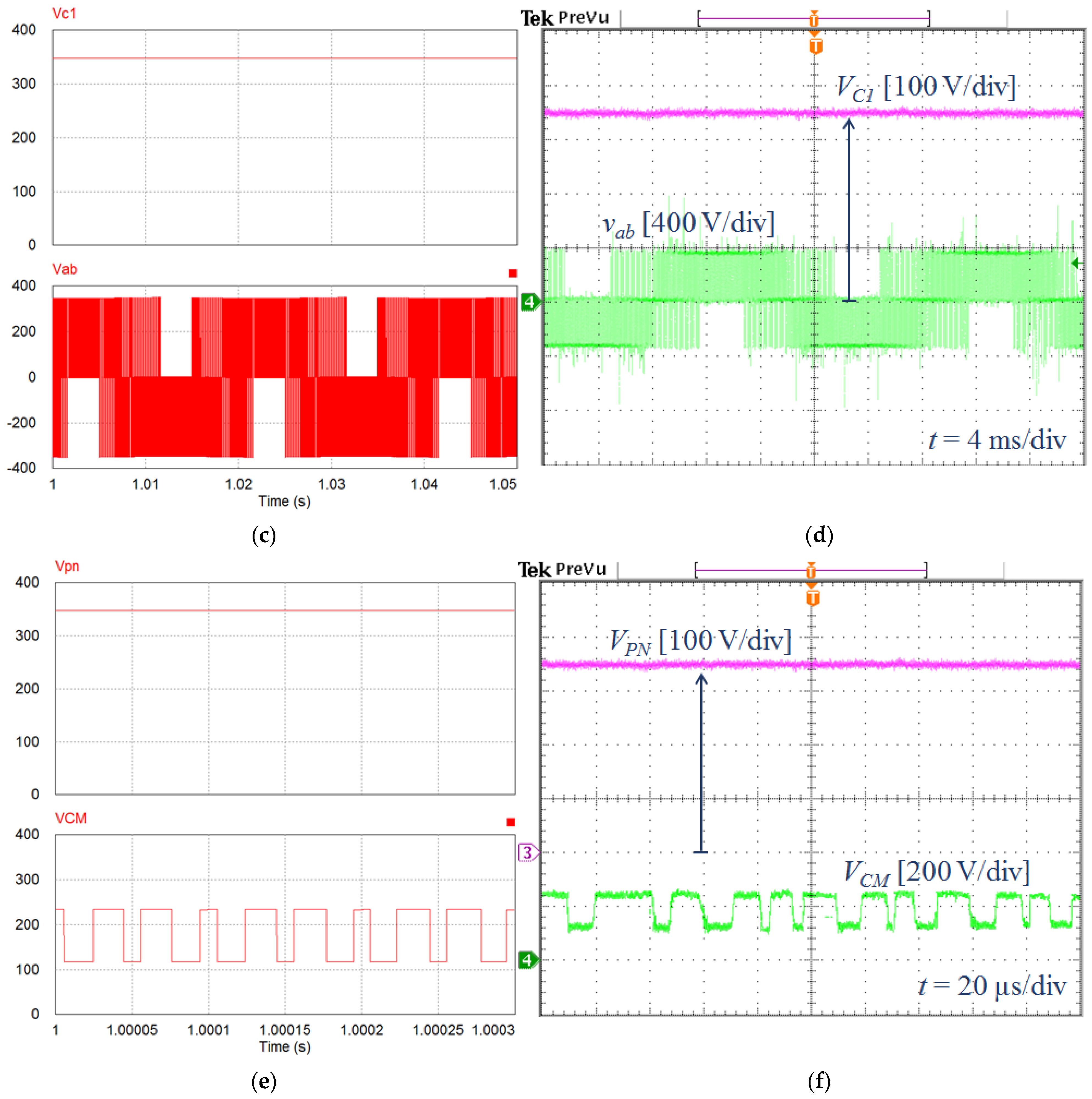
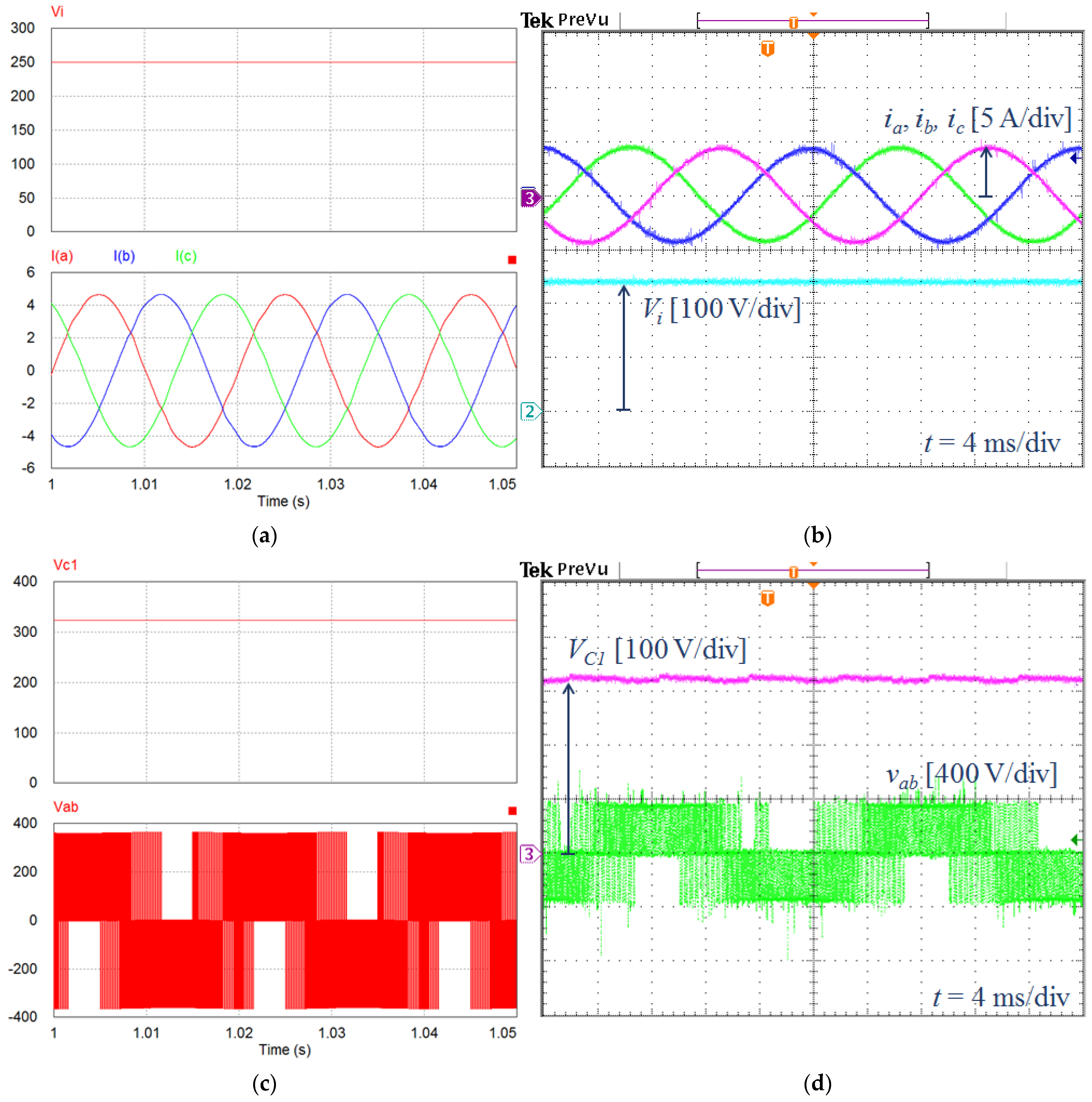
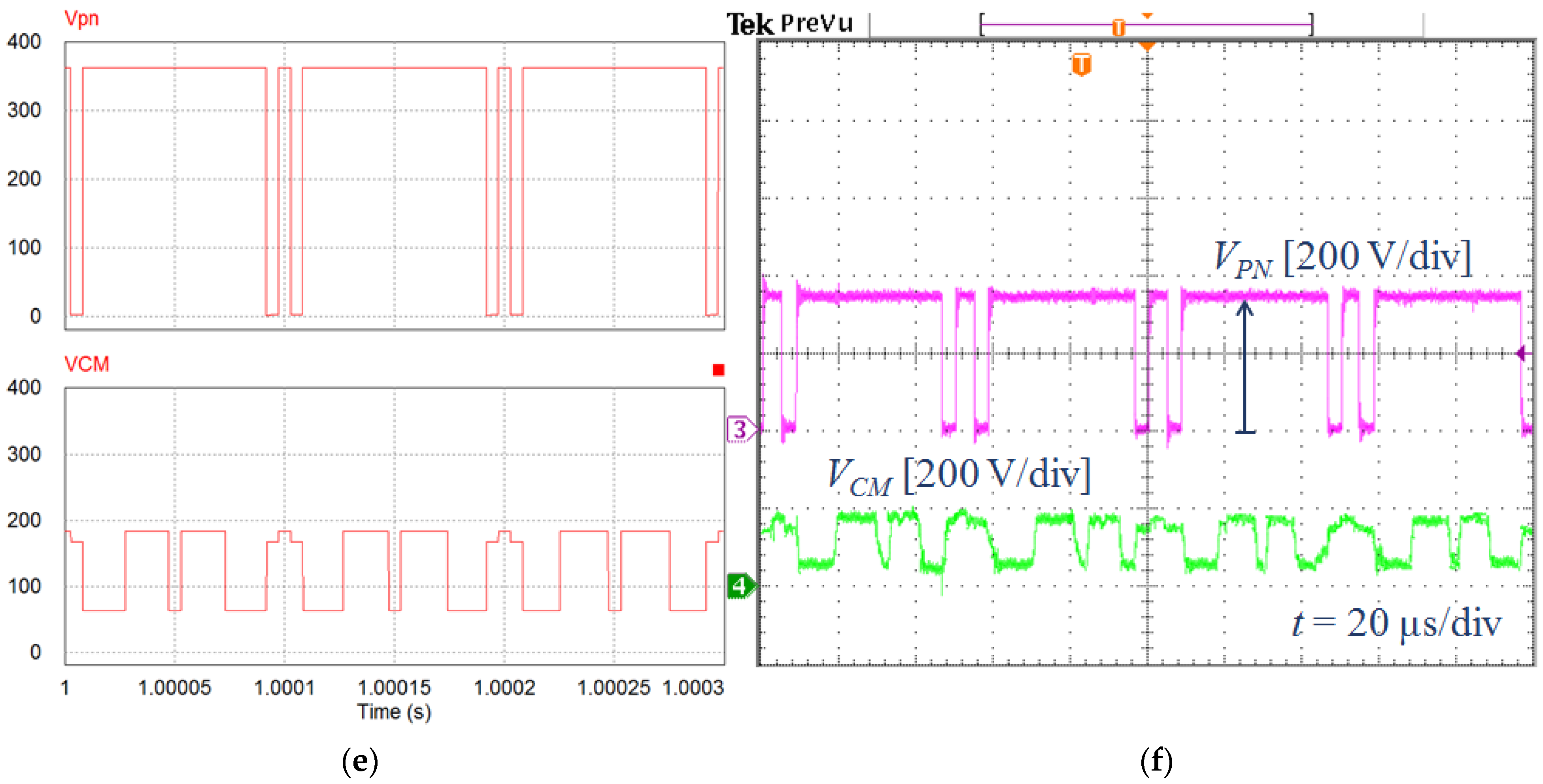
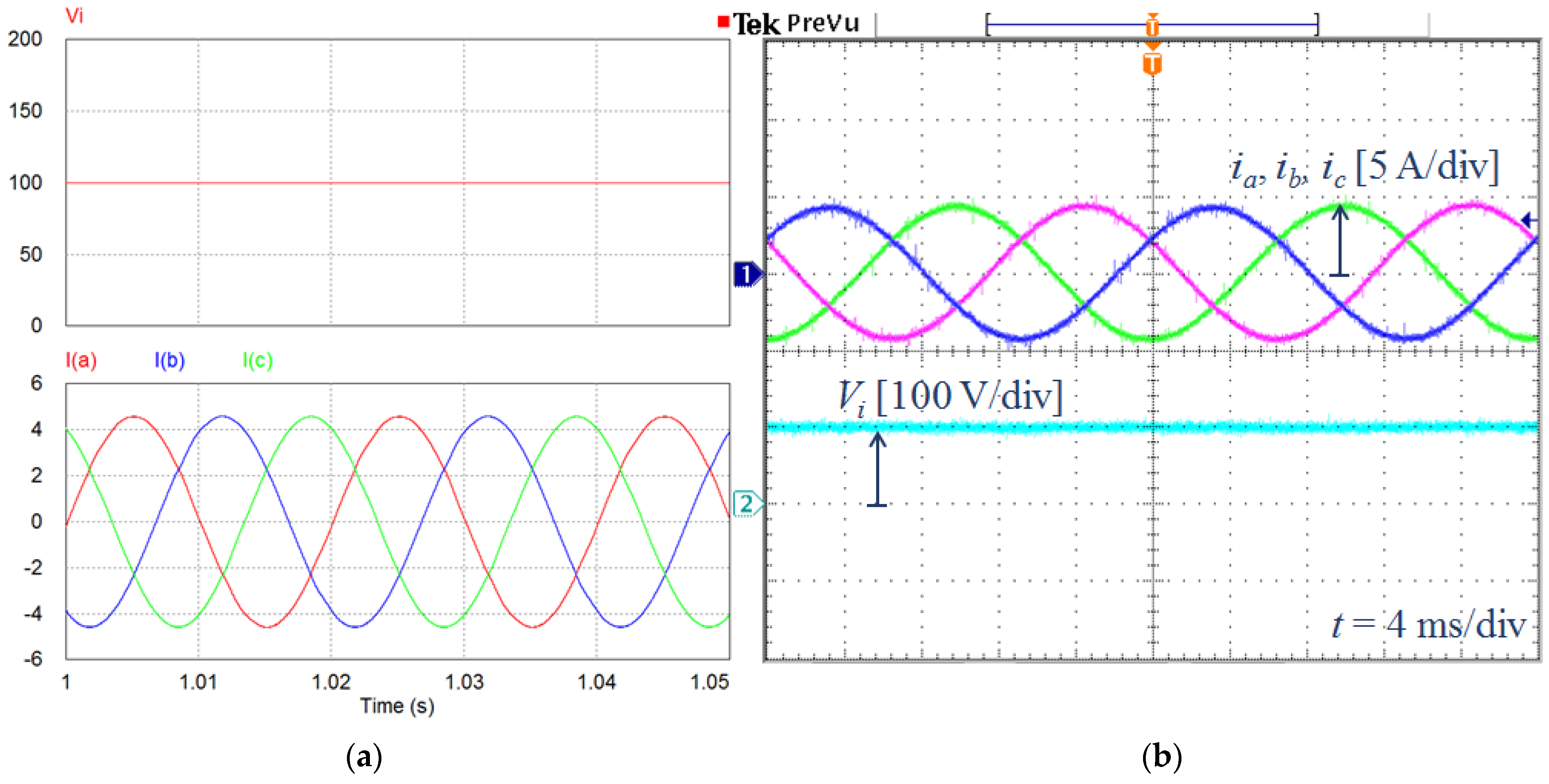
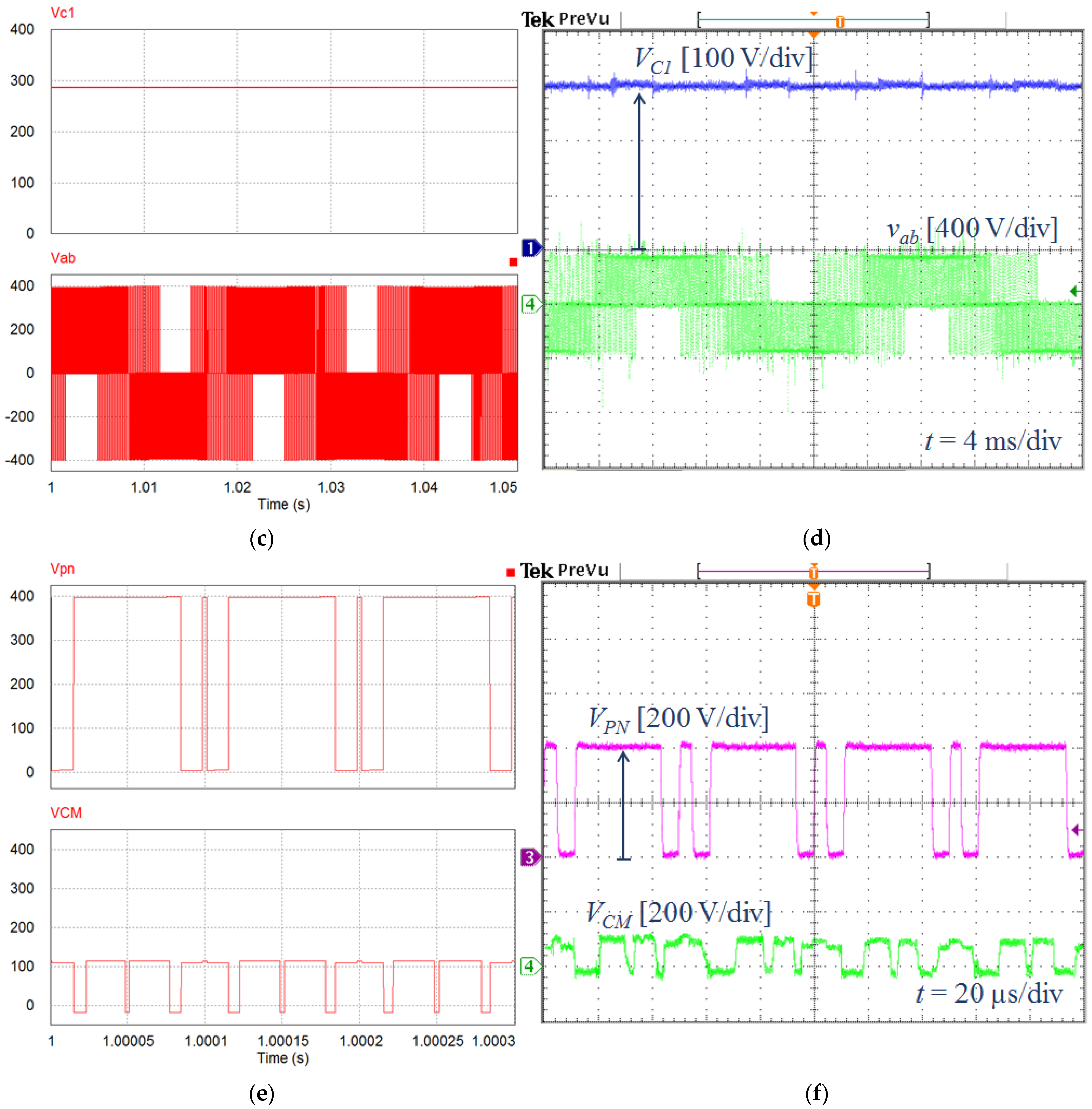
5.1. Simulation Results
5.2. Experimental Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, L.; Sun, K.; Feng, L.-L.; Wu, H.-F.; Xing, Y. A family of neutral point clamped full-bridge topologies for transformerless photovoltaic grid-tied inverters. IEEE Trans. Power Electron. 2013, 28, 730–739. [Google Scholar] [CrossRef]
- Kouro, S.; Leon, J.-I.; Vinnikov, D.; Franquelo, L.G. Grid-connected photovoltaic systems: An overview of recent research and emerging PV converter technology. IEEE Ind. Electron. Mag. 2015, 9, 47–61. [Google Scholar] [CrossRef]
- Meneses, D.; Blaabjerg, F.; Garcıa, O.; Cobos, J.A. Review and comparison of step-up transformerless topologies for photovoltaic ac-module application. IEEE Trans. Power Electron. 2013, 28, 2649–2663. [Google Scholar] [CrossRef] [Green Version]
- Lopez, O.; Freijedo, F.-D.; Yepes, A.-G.; Fernandez, P.-C.; Malvar, J.; Teodorescu, R.; Doval, J. –G. Eliminating ground current in a transformerless photovoltaic application. IEEE Trans. Energy Convers. 2010, 25, 140–147. [Google Scholar] [CrossRef]
- Guo, X.; Zhang, X.; Guan, H.; Kerekes, T.; Blaabjerg, F. Three-phase ZVR topology and modulation strategy for transformerless PV system. IEEE Trans. Power Electron. 2019, 34, 1017–1021. [Google Scholar] [CrossRef] [Green Version]
- Guo, X.; He, R.; Jian, J.; Lu, Z.; Sun, X.; Guerrero, J.-M. Leakage current elimination of four-leg inverter for transformerless three-phase PV systems. IEEE Trans. Power Electron. 2016, 31, 1841–1846. [Google Scholar] [CrossRef] [Green Version]
- Gupta, A.-K.; Agrawal, H.; Agarwal, V. A Novel three-phase transformerless H-8 topology with reduced leakage current for grid-tied solar PV applications. IEEE Trans. Ind. Appl. 2019, 55, 1765–1774. [Google Scholar] [CrossRef]
- Anand, S.; Gundlapalli, S.K.; Fernandes, B.-G. Transformer-less grid feeding current source inverter for solar photovoltaic system. IEEE Trans. Ind. Electron. 2014, 61, 5334–5344. [Google Scholar] [CrossRef]
- Tran, T.T.; Nguyen, M.K.; Duong, T.D.; Choi, J.H.; Lim, Y.C.; Zare, F. A Switched-Capacitor-Voltage-Doubler Based Boost Inverter for Common-Mode Voltage Reduction. IEEE Access 2019, 7, 98618–98629. [Google Scholar] [CrossRef]
- Hou, C.; Shih, C.; Cheng, P.; Hava, A.-M. Common-mode voltage reduction pulse-width modulation techniques for three-phase grid-connected converters. IEEE Trans. Power Electron. 2013, 28, 1971–1979. [Google Scholar] [CrossRef]
- Chen, H.; Zhao, H. Review on pulse-width modulation strategies for common-mode voltage reduction in three-phase voltage-source inverters. IET Power Electron. 2016, 9, 2611–2620. [Google Scholar] [CrossRef]
- Janabi, A.; Wang, B. Hybrid SVPWM scheme to minimize the common-mode voltage frequency and amplitude in voltage source inverter drives. IEEE Trans. Power Electron. 2019, 34, 1595–1610. [Google Scholar] [CrossRef]
- Liu, Y.; Ge, B.; Abu, R.-H.; Sun, D. Comprehensive modeling of single-phase quasi-Z-source photovoltaic inverter to investigate low frequency voltage and current ripple. IEEE Trans. Ind. Electron. 2015, 62, 4194–4202. [Google Scholar] [CrossRef]
- Rahman, M.-M.; Iqbal, A.; Ben-Brahim, L.; Abu-Rub, H.; Khan, I. Novel Level-Shifted PWM Technique for Cascaded Multilevel Quasi-Impedance Source Inverter. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 5918–5928. [Google Scholar] [CrossRef]
- Barath, J.N.; Soundarrajan, A.; Stepenko, S.; Husev, O.; Vinnikov, D.; Nguyen, M.-K. Topological Review of Quasi-Switched Boost Inverters. Electronics 2021, 10, 1485. [Google Scholar] [CrossRef]
- Nguyen, M.-K.; Duong, T.-D.; Lim, Y.-C.; Choi, J.-H.; Vilathgamuwa, D.-M.; Walker, G.-R. DC-Link quasi-switched boost inverter with improved PWM strategy and its comparative evaluation. IEEE Access 2020, 8, 53857–53867. [Google Scholar] [CrossRef]
- Nguyen, M.-K.; Choi, Y.-O. Maximum boost control method for single-phase quasi-switched-boost and quasi-Z-source inverters. Energies 2017, 10, 553. [Google Scholar] [CrossRef]
- Nguyen, M.-K.; Duong, T.-D.; Lim, Y.-C.; Choi, J.-H. High Voltage Gain Quasi-Switched Boost Inverters with Low Input Current Ripple. IEEE Trans. Ind. Inform. 2018, 15, 4857–4866. [Google Scholar] [CrossRef]
- Duong, T.-D.; Nguyen, M.-K.; Lim, Y.-C.; Choi, J.-H.; Vilathgamuwa, D.-M. SiC-Based Active Quasi-Z-Source Inverter with Improved PWM Control Strategy. IET Power Electron. 2019, 12, 3810–3821. [Google Scholar] [CrossRef]
- Qin, C.; Zhang, C.; Chen, A.; Xing, X.; Zhang, G. A space vector modulation scheme of the quasi-Z-source three-level T-type inverter for common-mode voltage reduction. IEEE Trans. Ind. Electron. 2018, 65, 8340–8350. [Google Scholar] [CrossRef]
- Li, X.; Xing, X.; Zhang, C.; Chen, A.; Qin, C.; Zhang, G. Simultaneous common-mode resonance circulating current and leakage current suppression for transformerless three-level T-type PV inverter system. IEEE Trans. Ind. Electron. 2019, 66, 4457–4467. [Google Scholar] [CrossRef]
- Nicolas, M.; Carlos, R.-C.; Ana, M.-L.; Oleksandr, H. A simple space vector modulation method with DC-link voltage balancing and reduced common-mode voltage strategy for a three-level T-type quasi-Z source inverter. IEEE Access 2021, 9, 82747–82760. [Google Scholar]
- Guo, X.; Yang, Y.; He, R.; Wang, B.; Blaabjerg, F. Leakage current reduction of three-phase Z-source three-level four-leg inverter for transformerless PV system. IEEE Trans. Power Electron. 2019, 34, 6299–6308. [Google Scholar] [CrossRef]
- Guo, X.; Yang, Y.; He, R.; Wang, B.; Blaabjergm, F. Transformerless Z-source four-leg PV inverter with leakage current reduction. IEEE Trans. Power Electron. 2019, 34, 4343–4352. [Google Scholar] [CrossRef]
- Noroozi, N.; Yaghoubi, M.; Zolghadri, M.R. A modulation method for leakage current reduction in a three-phase grid-tie quasi-Z-source inverter. IEEE Trans. Power Electron. 2019, 34, 5439–5450. [Google Scholar] [CrossRef]
- Bradaschia, F.; Cavalcanti, M.-C.; Ferraz, P.-E.-P.; Neves, F.-A.-S. Modulation for three-phase transformerless Z-source inverter to reduce leakage currents in photovoltaic systems. IEEE Trans. Ind. Electron. 2011, 58, 5385–5395. [Google Scholar] [CrossRef]
- Erginer, V.; Sarul, M.H. A novel reduced leakage current modulation technique for Z-source inverter used in photovoltaic systems. IET Power Electron. 2014, 7, 496–502. [Google Scholar] [CrossRef]
- Noroozi, N.; Zolghadri, M.-R. Three-phase quasi-Z-source inverter with constant common-mode voltage for photovoltaic application. IEEE Trans. Ind. Electron. 2018, 65, 4790–4798. [Google Scholar] [CrossRef]
- Duong, T.-D.; Nguyen, M.-K.; Tran, T.-T.; Lim, Y.-C.; Choi, J.-H.; Wang, C. Modulation Techniques for a Modified Three-Phase Quasi-Switched Boost Inverter with Common-Mode Voltage Reduction. IEEE Access 2020, 8, 160670–160683. [Google Scholar] [CrossRef]
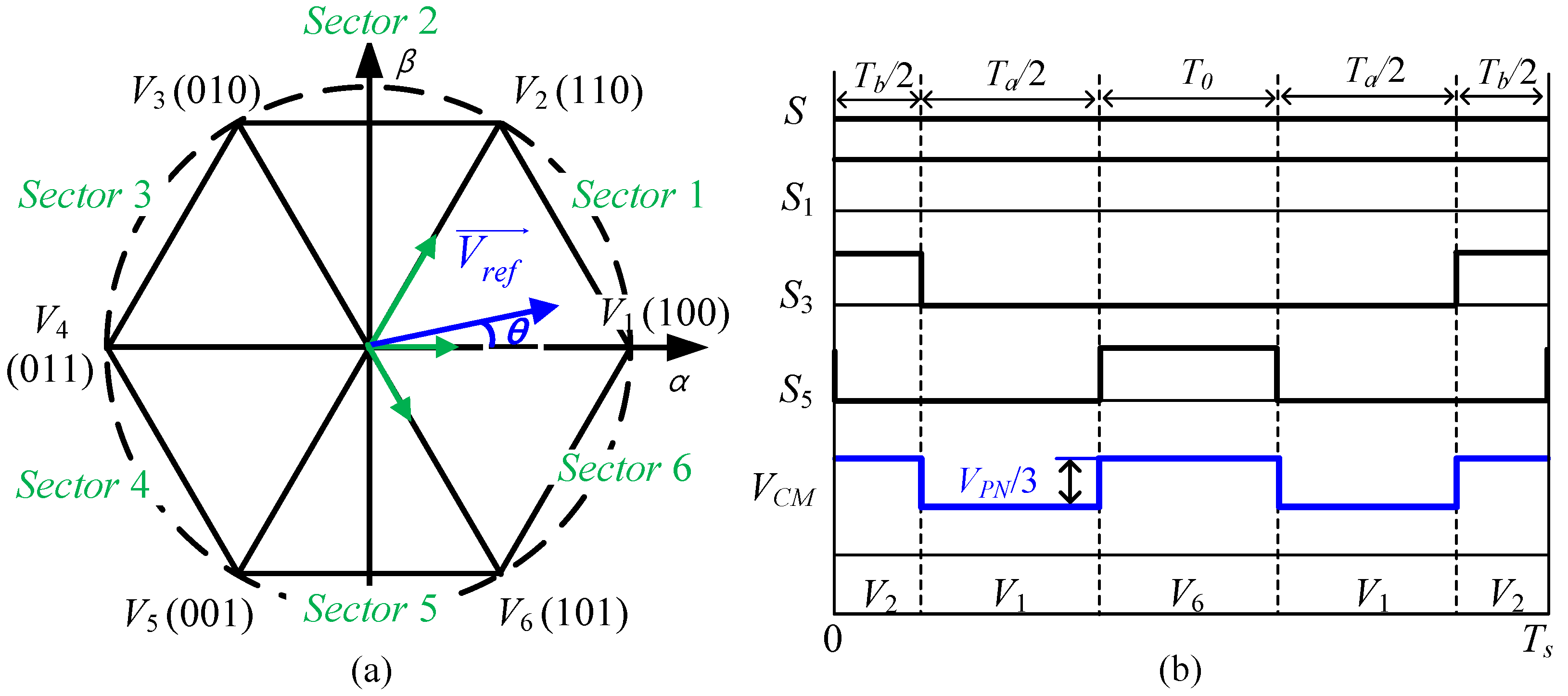

| Vector | Common-Mode Voltage |
|---|---|
| (Odd vectors) | VPN/3 |
| (Even vectors) | 2VPN/3 |
| (zero vector) | 0 |
| (zero vector) | VPN |
| (ST vector) | −(1 − D)VPN |
| Vector | Common-Mode Voltage |
|---|---|
| (Odd vectors) | |
| (Even vectors) | |
| (ST vector) |
| Switch | Diode | Inductor | Capacitor | Total | Voltage Gain | Modulation Index | VCMV | |
|---|---|---|---|---|---|---|---|---|
| ZSI [26] | 6 | 2 | 2 | 2 | 12 | 0 to 0.57 | Constant | |
| Modified ZSI [27] | 6 | 1 | 2 | 2 | 11 | 0.66 to 1 | VPN/3 | |
| qZSI [28] | 6 | 1 | 2 | 2 | 11 | 0 to 0.57 | Constant | |
| Modified qSBI [29] | 8 | 1 | 2 | 1 | 12 | 0 to 1 | VPN/3 | |
| Proposed inverter | 7 | 2 | 3 | 2 | 14 | 0.66 to 1 | VPN/3 |
| Parameters | Values | |
|---|---|---|
| DC input voltage | 100 V–350 V | |
| Output RMS voltage | 110 V | |
| Output power | 1 kW | |
| Switching frequency | 10 kHz | |
| Inductors | L1 | 1 mH |
| L2 | 4 mH | |
| L3 | 2 mH | |
| Capacitors | C1 | 680 µF/450 V |
| C2 | 680 µF/100 V | |
| Switching frequency | 60 kHz | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nguyen, M.-K.; Choi, Y.-O. Modulation Technique for Modified Active Quasi-Z-Source Inverter with Common-Mode Voltage Reduction. Electronics 2021, 10, 2968. https://doi.org/10.3390/electronics10232968
Nguyen M-K, Choi Y-O. Modulation Technique for Modified Active Quasi-Z-Source Inverter with Common-Mode Voltage Reduction. Electronics. 2021; 10(23):2968. https://doi.org/10.3390/electronics10232968
Chicago/Turabian StyleNguyen, Minh-Khai, and Youn-Ok Choi. 2021. "Modulation Technique for Modified Active Quasi-Z-Source Inverter with Common-Mode Voltage Reduction" Electronics 10, no. 23: 2968. https://doi.org/10.3390/electronics10232968
APA StyleNguyen, M.-K., & Choi, Y.-O. (2021). Modulation Technique for Modified Active Quasi-Z-Source Inverter with Common-Mode Voltage Reduction. Electronics, 10(23), 2968. https://doi.org/10.3390/electronics10232968







