Mutual Inductance Calculation of Circular Coils Sandwiched between 3-Layer Magnetic Mediums for Wireless Power Transfer Systems
Abstract
:1. Introduction
2. Modeling of Mutual Inductance for Circular Coils Sandwiched between 3-Layer Magnetic Mediums
2.1. Model of Mutual Inductance
2.2. Magnetic Vector Potential Analysis
2.3. Mutual Inductance Calculation
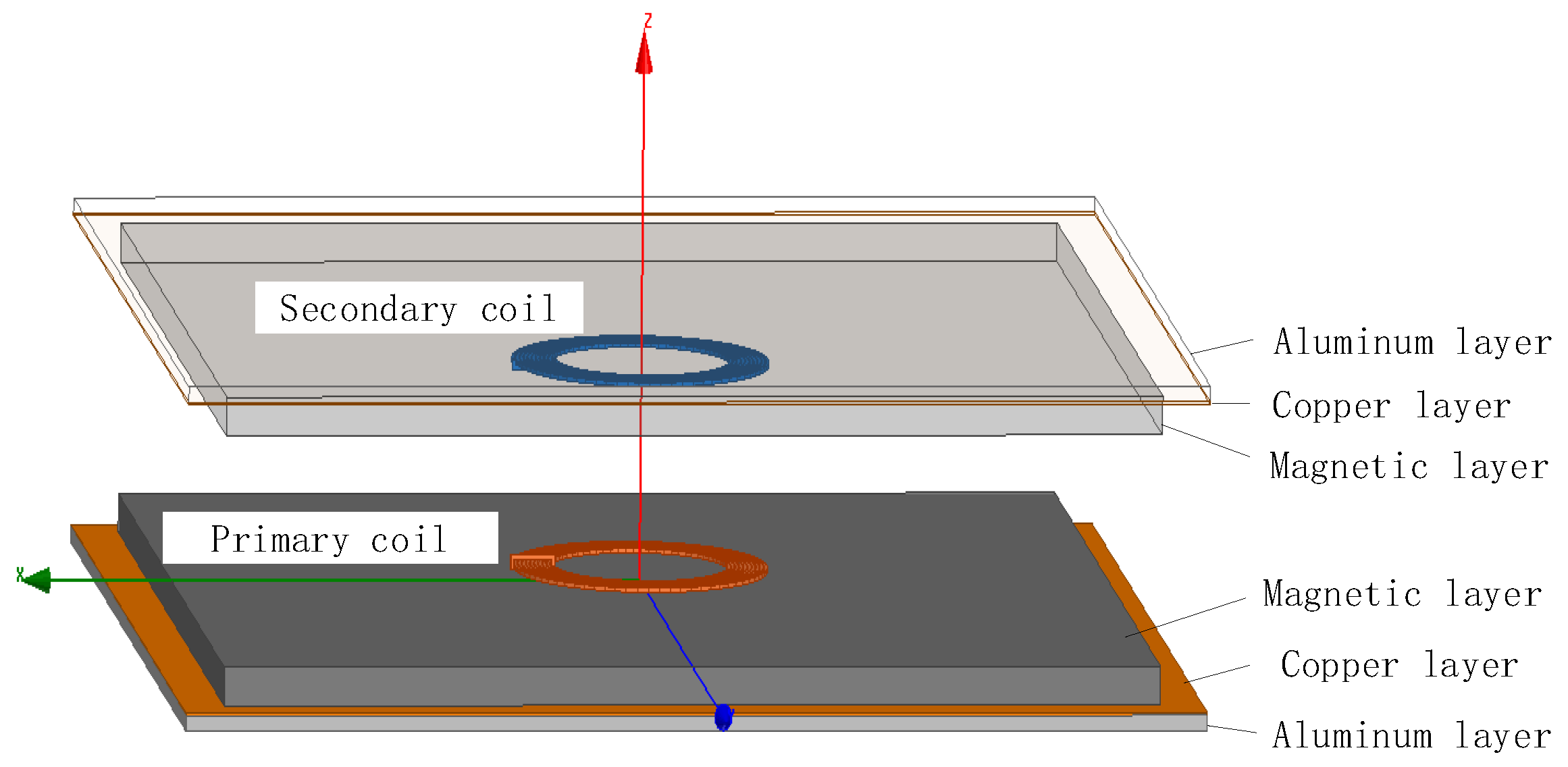
3. Simulation and Experimental Verification
3.1. Simulation Model
3.2. Experimental Verification
3.3. Analysis of Experimental Results
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Lee, J.; Lee, K. Effects of Number of Relays on Achievable Efficiency of Magnetic Resonant Wireless Power Transfer. IEEE Trans. Power Electron. 2020, 35, 6697–6700. [Google Scholar] [CrossRef]
- Lin, W.; Ziolkowski, R.W. A Circularly Polarized Wireless Power Transfer System for Internet-of-Things (IoT) Applications. In Proceedings of the 2020 4th Australian Microwave Symposium (AMS) IEEE, Sydney, Australia, 13–14 February 2020. [Google Scholar]
- Yao, Y. Energy Efficiency Characterization in Heterogeneous IoT System With UAV Swarms Based on Wireless Power Transfer. IEEE Access 2020, 8, 967–979. [Google Scholar] [CrossRef]
- Luo, Y. A new method for mutual inductance calculation of parallel axis circular coil. Trans. China Electrotech. Soc. 2016, 31, 31–37. [Google Scholar]
- Babic, S.I.; Akyel, C. New analytic-numerical solutions for the mutual inductance of two coaxial circular coils with rectangular cross section in air. IEEE Trans. Magn. 2006, 42, 1661–1669. [Google Scholar] [CrossRef]
- Grover, F.W. The calculation of the mutual inductance of circular filaments in any desired positions. Proc. IRE 1944, 32, 620–629. [Google Scholar] [CrossRef]
- Xiong, H.; Liu, L. Improved calculation method of mutual inductance coefficient at any relative position. IEEE Trans. Magn. 2018, 24, 7–11. [Google Scholar]
- Conway, J.T. Inductance calculations for non-coaxial coils using Bessel functions. Sens. World 2007, 43, 1023–1034. [Google Scholar]
- Poletkin, K.V.; Korvink, J.G. Efficient calculation of the mutual inductance of arbitrarily oriented circular filaments via a generalisation of the Kalantarov-Zeitlin method. J. Magn. Magn. Mater. 2019, 48, 10–20. [Google Scholar] [CrossRef] [Green Version]
- Babic, S.; Sirois, F. Mutual inductance calculation between circular filaments arbitrarily positioned in space alternative to grover’s formula. IEEE Trans. Magn. 2010, 46, 3591–3600. [Google Scholar] [CrossRef]
- Luo, Y.; Chen, B.C. Mutual Inductance Calculations of Inclined Axial Air-Core Circular Coils with Rectangular Cross-Sections. Trans. China Electrotech. Soc. 2012, 20, 132–136. [Google Scholar]
- Xie, Y.; Pan, W.L. Mutual inductance calculation method of arbitrary space positioned coils. Electr. Mach. Control 2016, 20, 63–67. [Google Scholar]
- Li, Z.Q.; Zhang, M. Mutual inductance calculation of circular coils arbitrary positioned with magnetic tiles for wireless power transfer system. IET Power Electron. 2020, 13, 3522–3527. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, P.C. Magnetic Shielding Design and Analysis for Wireless Charging Coupler of Electric Vehicles Based on Finite Element Method. Trans. China Electrotech. Soc. 2016, 31, 71–79. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, P.C. Analytical solutions to eddy-current probe-coil problems. J. Appl. Phys. 1968, 39, 2829–2838. [Google Scholar]
- Claycomb, J.R.; Tralshawala, N. Theoretical investigation of eddy-current induction for nondestructive evaluation by superconducting quantum interference devices. IEEE Trans. Magn. 2000, 36, 292–298. [Google Scholar] [CrossRef]
- Hurley, W.G.; Duffy, M.C. Calculation of self and mutual impedances in planar magnetic structures. IEEE Trans. Magn. 1995, 31, 2416–2422. [Google Scholar] [CrossRef]
- Hurley, W.G.; Duffy, M.C. Calculation of self- and mutual impedances in planar sandwich inductors. IEEE Trans. Magn. 1997, 33, 2282–2290. [Google Scholar] [CrossRef]
- Hurley, W.G.; Duffy, M.C. Impedance formulas for planar magnetic structures with spiral windings. IEEE Trans. Ind. Electron. 1999, 46, 271–278. [Google Scholar] [CrossRef]
- Roshen, W.A. Effect of finite thickness of magnetic substrate on planar inductors. IEEE Trans. Magn. 1990, 26, 270–275. [Google Scholar] [CrossRef]
- Carretero, C.; Acero, J. Modeling mutual impedances of loaded non-coaxial inductors for induction heating applications. IEEE Trans. Magn. 2008, 44, 4115–4118. [Google Scholar] [CrossRef]
- Su, Y.P.; Liu, X. Mutual inductance calculation of movable planar coils on parallel surfaces. IEEE Trans. Power Electron. 2009, 24, 1115–1123. [Google Scholar] [CrossRef]
- Acero, J.; Alonso, R. Modeling of planar spiral inductors between two multilayer media for induction heating applications. IEEE Trans. Magn. 2006, 42, 3719–3729. [Google Scholar] [CrossRef]
- Acero, J.; Carretero, C. Analysis of the mutual inductance of planar-lumped inductive power transfer systems. IEEE Trans. Ind. Electron. 2013, 60, 410–420. [Google Scholar] [CrossRef]



| Parameter | Value |
|---|---|
| Initial radius of primary coil | 51 mm |
| Initial radius of secondary coil | 51 mm |
| Turns of primary coil | 1∼10 |
| Turns of secondary coil | 1∼10 |
| Diameter of the field excitation conductor | 2.4 mm |
| Height of primary coil | 2 mm |
| Height of secondary coil | 5 mm |
| Side length of the magnetic medium | 550 mm |
| Thickness of magnetic medium | 15 mm |
| Relative permeability of magnetic medium | 1000 |
| Conductivity of magnetic medium | 0.01 (S/m) |
| Side length of copper | 600 mm |
| Thickness of copper | 1 mm |
| Conductivity of magnetic copper | (S/m) |
| Side length of aluminum | 600 mm |
| Thickness of aluminum | 6 mm |
| Relative permeability of aluminum | 1 |
| Conductivity of magnetic aluminum | (S/m) |
| (H) | (H) | |||
|---|---|---|---|---|
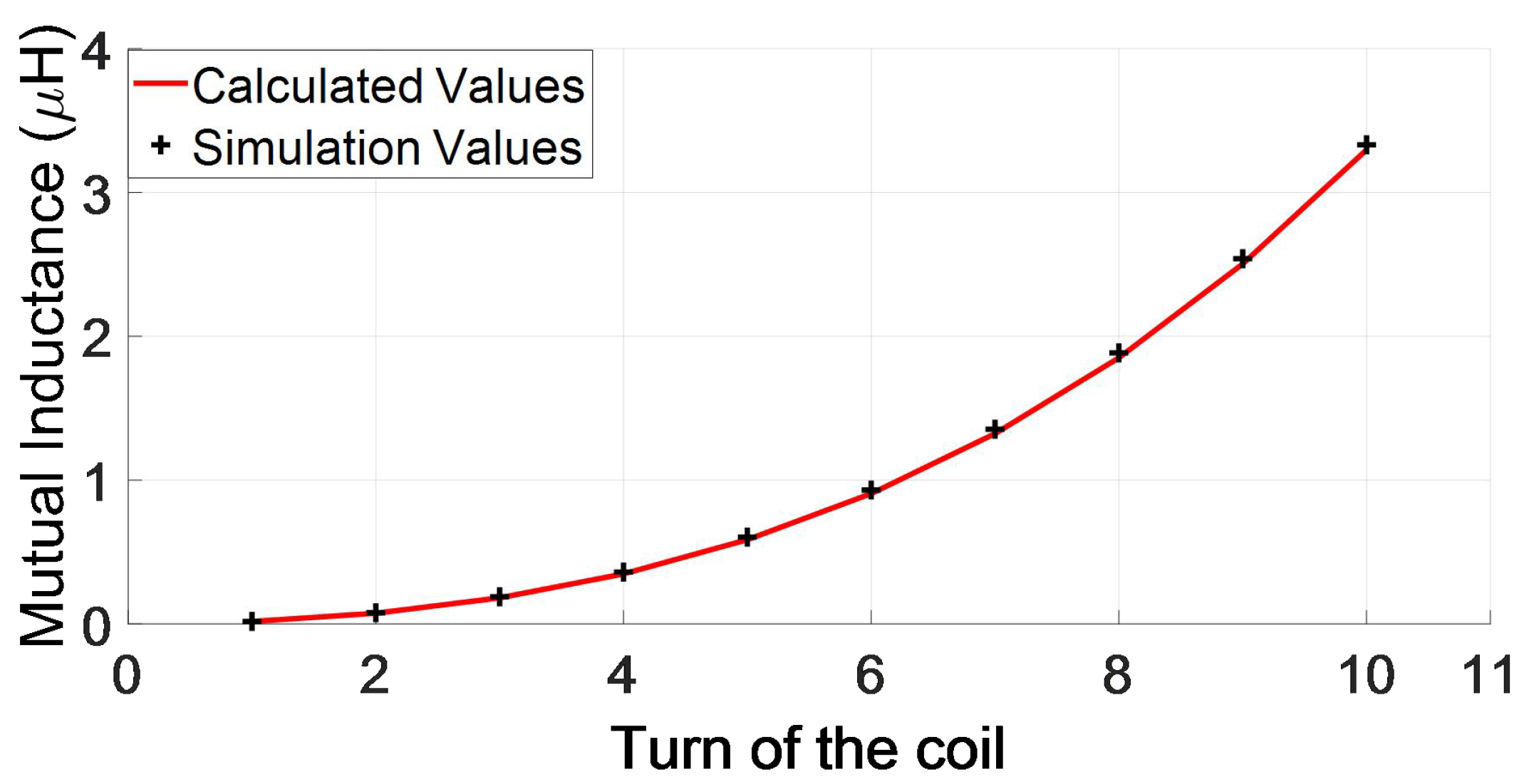
| 1 | 1 | 0.0172 | 0.0174 | 1.15% |
| 2 | 2 | 0.0746 | 0.0779 | 4.24% |
| 3 | 3 | 0.1816 | 0.1887 | 3.76% |
| 4 | 4 | 0.3482 | 0.3605 | 3.41% |
| 5 | 5 | 0.5859 | 0.6039 | 2.98% |
| 6 | 6 | 0.9066 | 0.9312 | 2.64% |
| 7 | 7 | 1.3236 | 1.3536 | 2.22% |
| 8 | 8 | 1.8509 | 1.8850 | 1.81% |
| 9 | 9 | 2.5035 | 2.5400 | 1.44% |
| 10 | 10 | 3.2973 | 3.3319 | 1.04% |
| Parameter | Value |
|---|---|
| Initial radius of primary coil | 51 mm |
| Initial radius of secondary coil | 51 mm |
| Turns of primary coil | 10 |
| Turns of secondary coil | 10 |
| Variable quantity of the radius | 85 kHz |
| Diameter of the field excitation conductor | 2.4 mm |
| Height of primary coil | 2 mm |
| Height of secondary coil | 5 mm |
| Side length of the magnetic medium | 550 mm |
| Thickness of magnetic medium | 15 mm |
| Conductivity of magnetic medium | 0.01 (S/m) |
| Side length of copper | 600 mm |
| Thickness of copper | 1 mm |
| Relative permeability of copper | 1 |
| Conductivity of magnetic copper | (S/m) |
| Side length of aluminum | 600 mm |
| Thickness of aluminum | 6 mm |
| Relative permeability of aluminum | 1 |
| D (mm) | (H) | (H) | (H) | ||
|---|---|---|---|---|---|
| 100 | 4.5976 | 4.8269 | 4.7670 | 4.75% | 3.55% |
| 110 | 3.8803 | 3.9954 | 3.9605 | 2.88% | 2.02% |
| 120 | 3.2973 | 3.3319 | 3.3236 | 1.04% | 0.79% |
| 130 | 2.8201 | 2.8029 | 2.7915 | 0.61% | 1.02% |
| 140 | 2.4269 | 2.3722 | 2.3463 | 2.31% | 3.44% |
| 150 | 2.1006 | 2.0223 | 2.0214 | 3.87% | 3.92% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, M.; Li, Z.; Zhang, M.; Wan, J. Mutual Inductance Calculation of Circular Coils Sandwiched between 3-Layer Magnetic Mediums for Wireless Power Transfer Systems. Electronics 2021, 10, 3043. https://doi.org/10.3390/electronics10233043
Yang M, Li Z, Zhang M, Wan J. Mutual Inductance Calculation of Circular Coils Sandwiched between 3-Layer Magnetic Mediums for Wireless Power Transfer Systems. Electronics. 2021; 10(23):3043. https://doi.org/10.3390/electronics10233043
Chicago/Turabian StyleYang, Minsheng, Zhongqi Li, Min Zhang, and Jingying Wan. 2021. "Mutual Inductance Calculation of Circular Coils Sandwiched between 3-Layer Magnetic Mediums for Wireless Power Transfer Systems" Electronics 10, no. 23: 3043. https://doi.org/10.3390/electronics10233043
APA StyleYang, M., Li, Z., Zhang, M., & Wan, J. (2021). Mutual Inductance Calculation of Circular Coils Sandwiched between 3-Layer Magnetic Mediums for Wireless Power Transfer Systems. Electronics, 10(23), 3043. https://doi.org/10.3390/electronics10233043





