Identification of Buffer and Surface Traps in Fe-Doped AlGaN/GaN HEMTs Using Y21 Frequency Dispersion Properties
Abstract
:1. Introduction
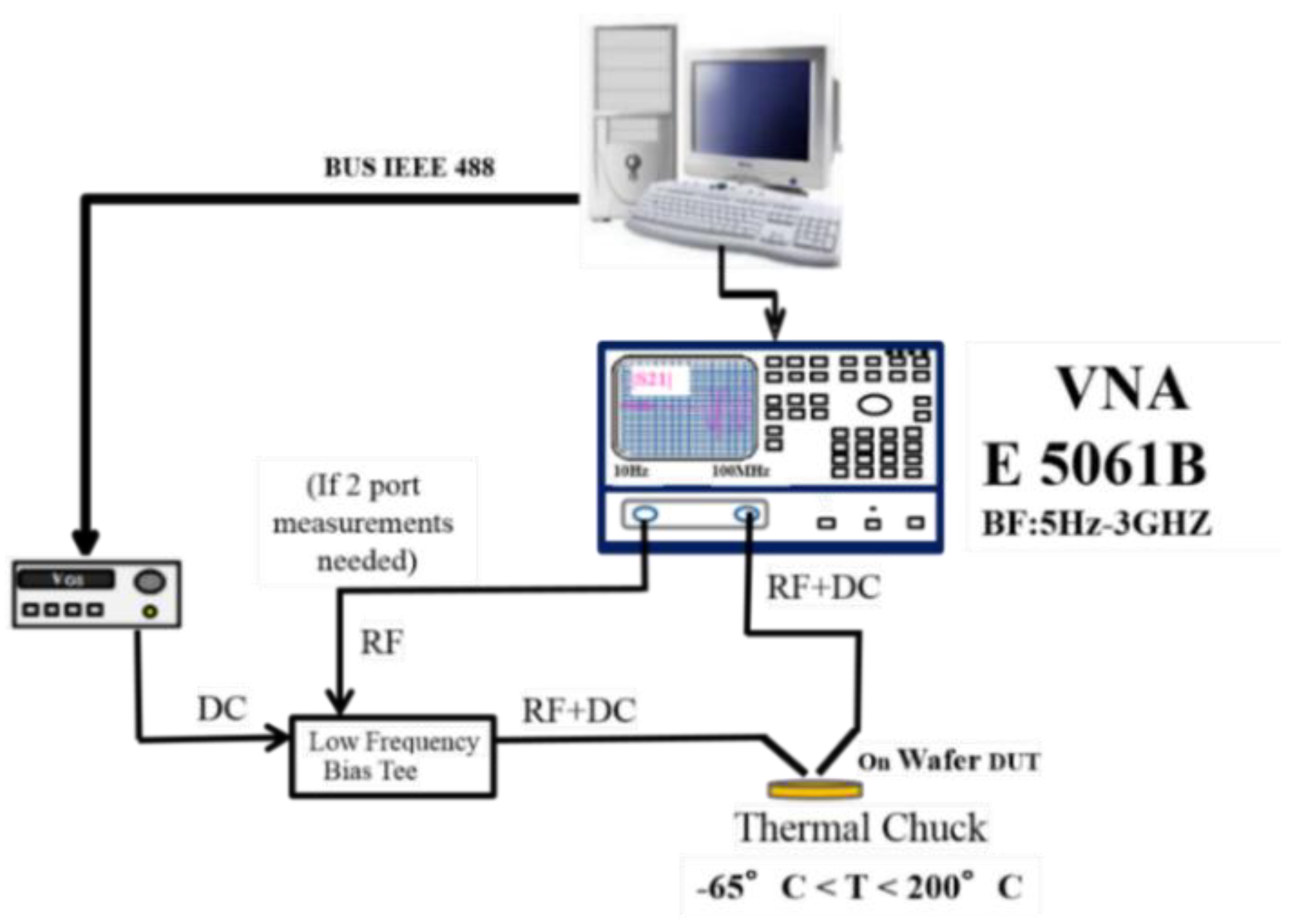
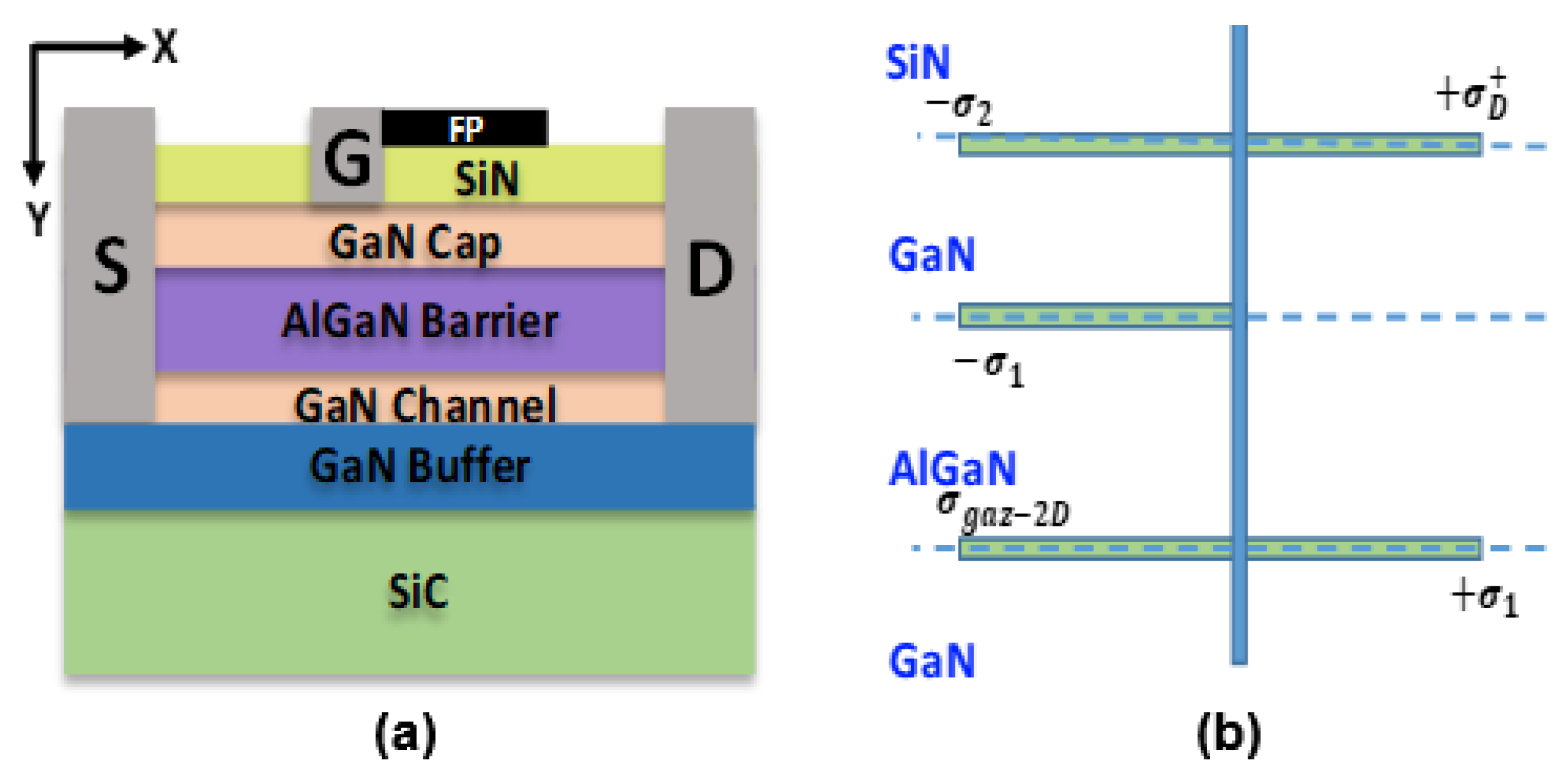
2. Experiment
2.1. DCT Characterization
2.2. Y-parameter Characterization
3. Simulation Details
4. Results and Discussion
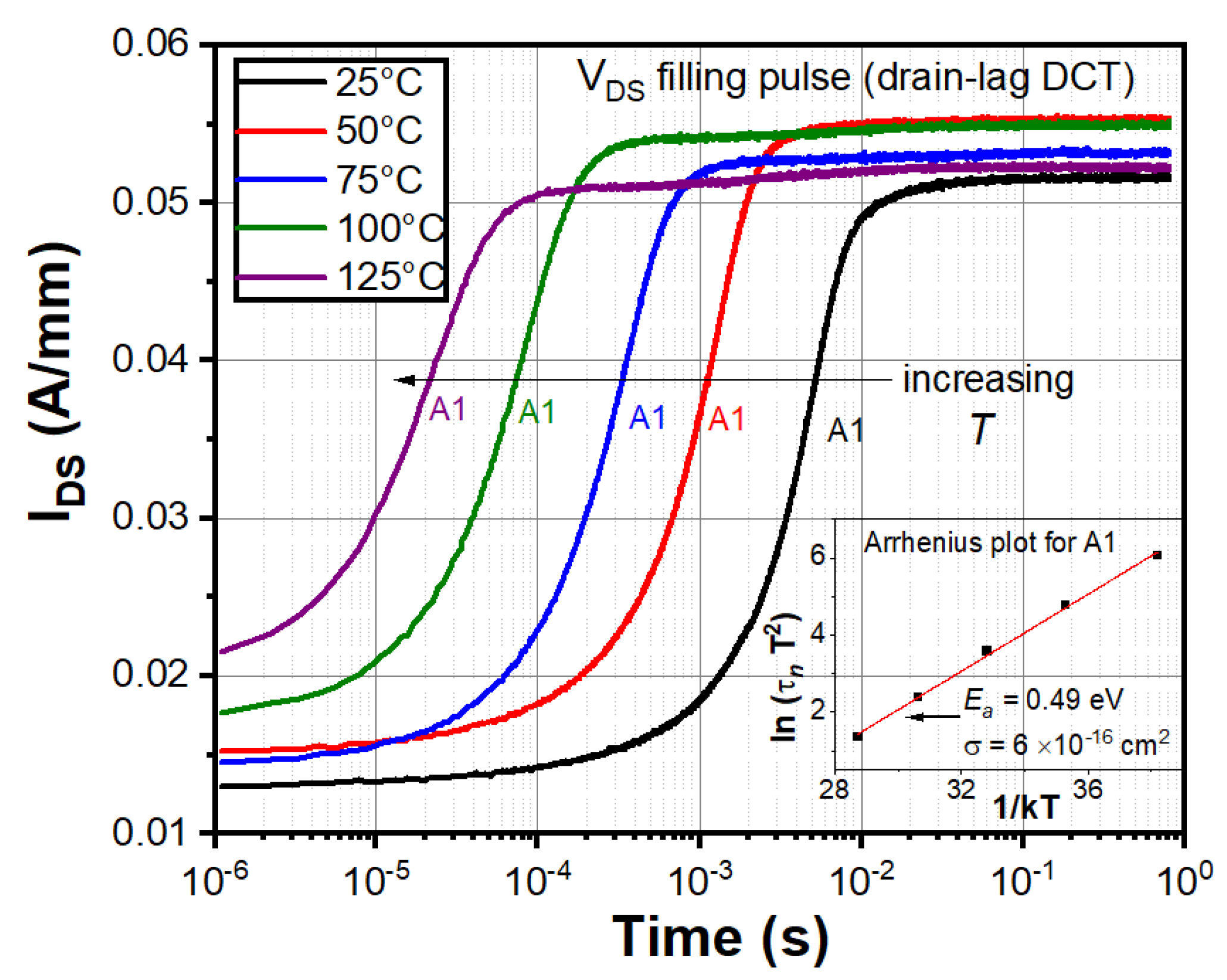
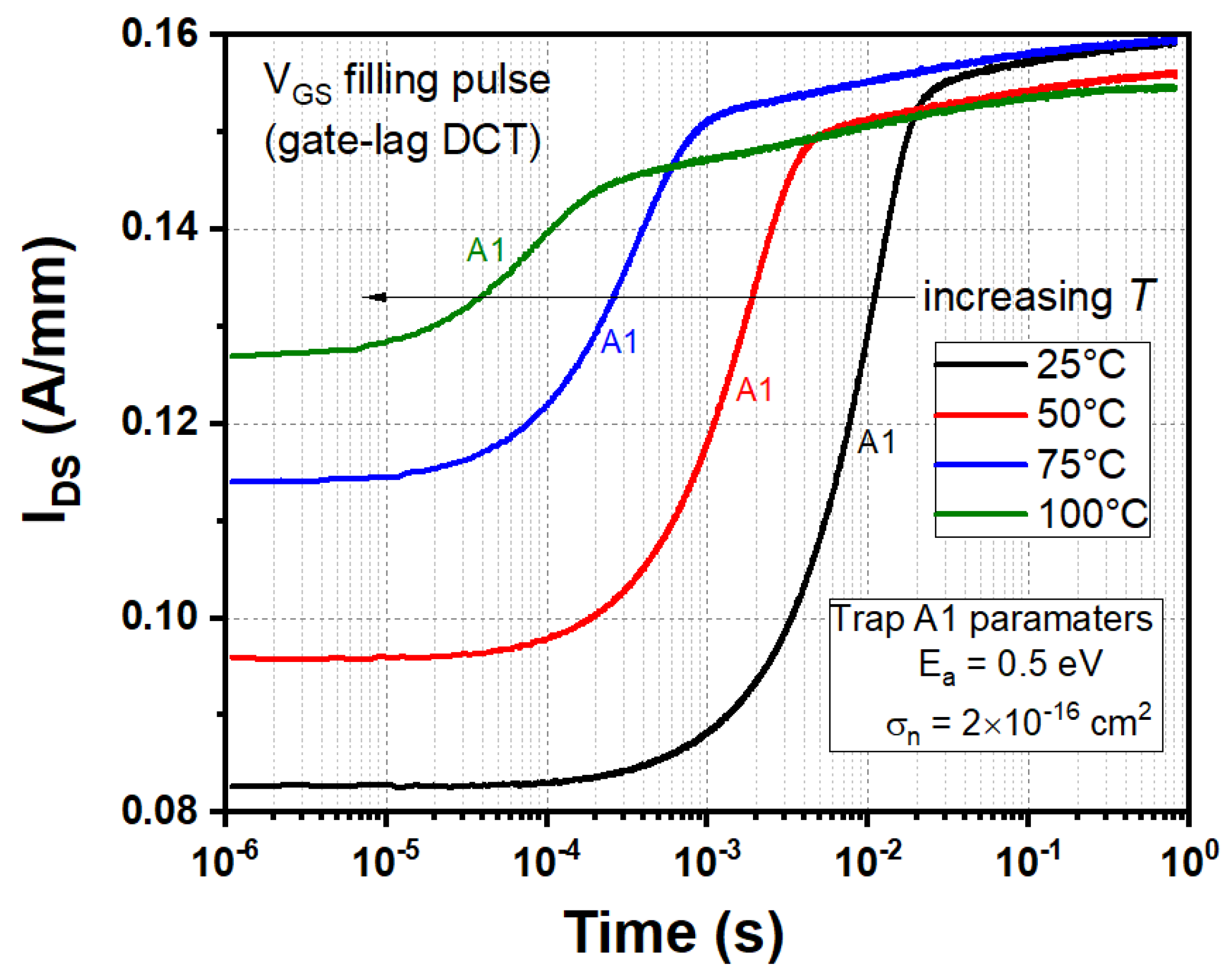
4.1. Measured DCT Spectroscopy
4.2. Calibration of TCAD Physical Model
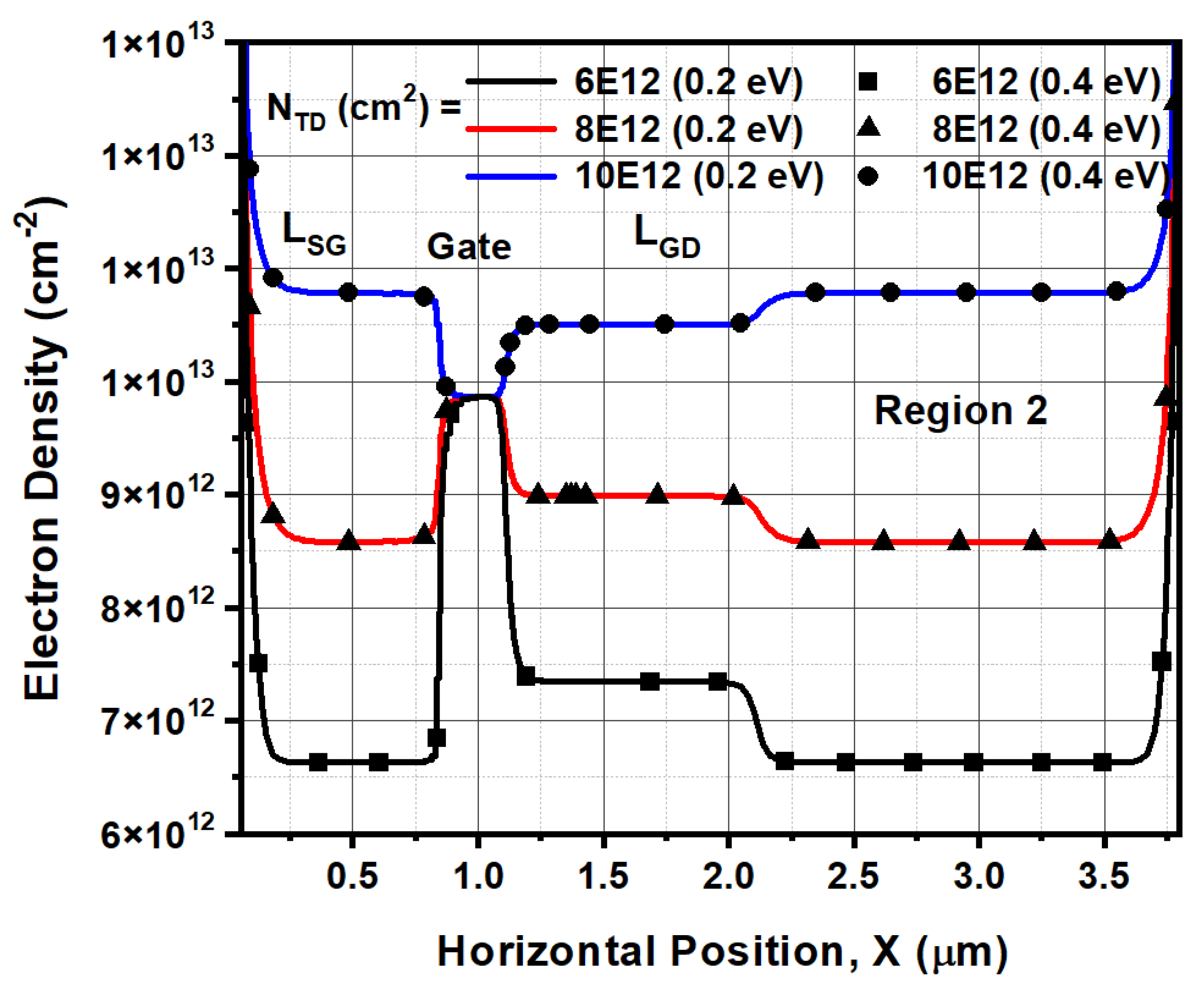
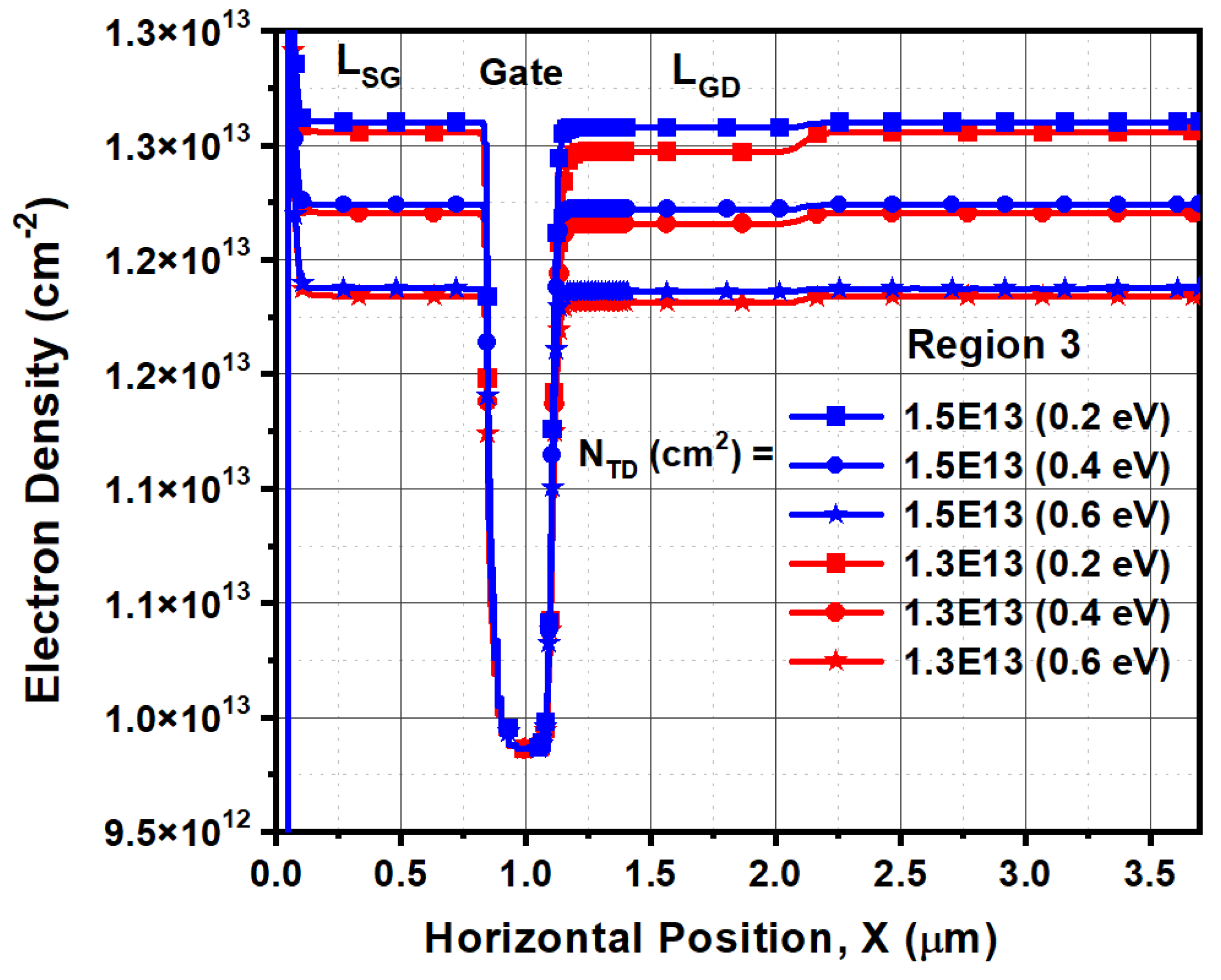
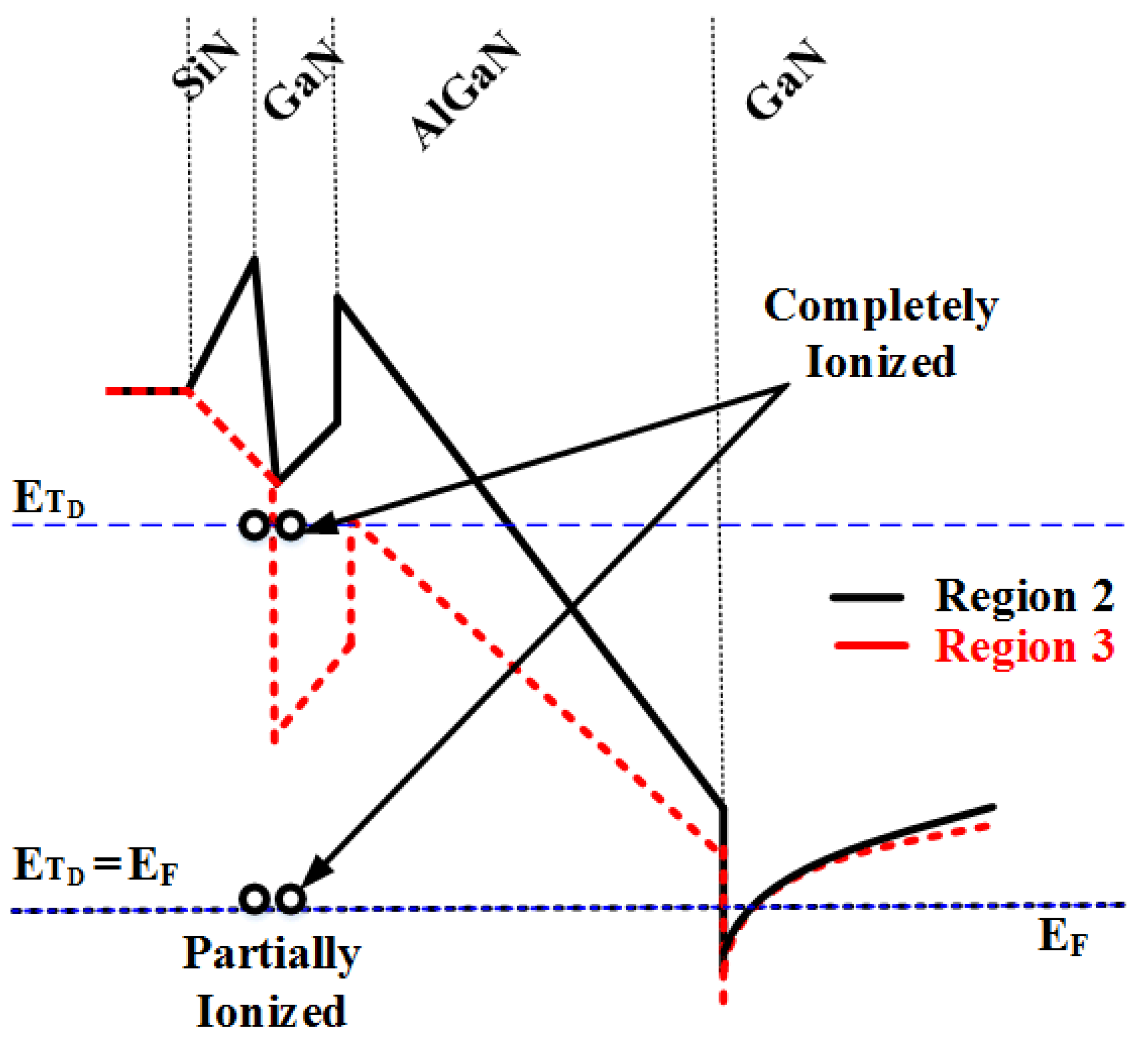
4.2.1. Influence of ETD and NTD on 2DEG
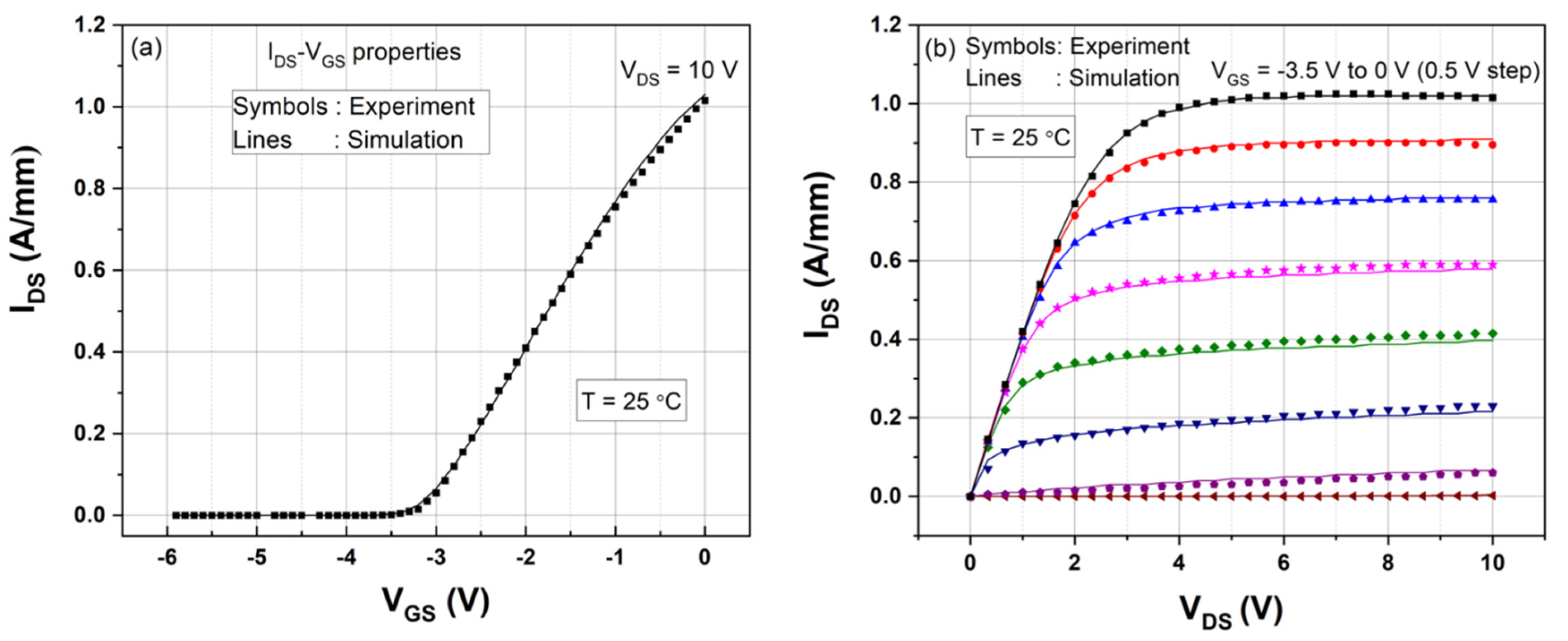
4.2.2. Validation of DC Characteristics
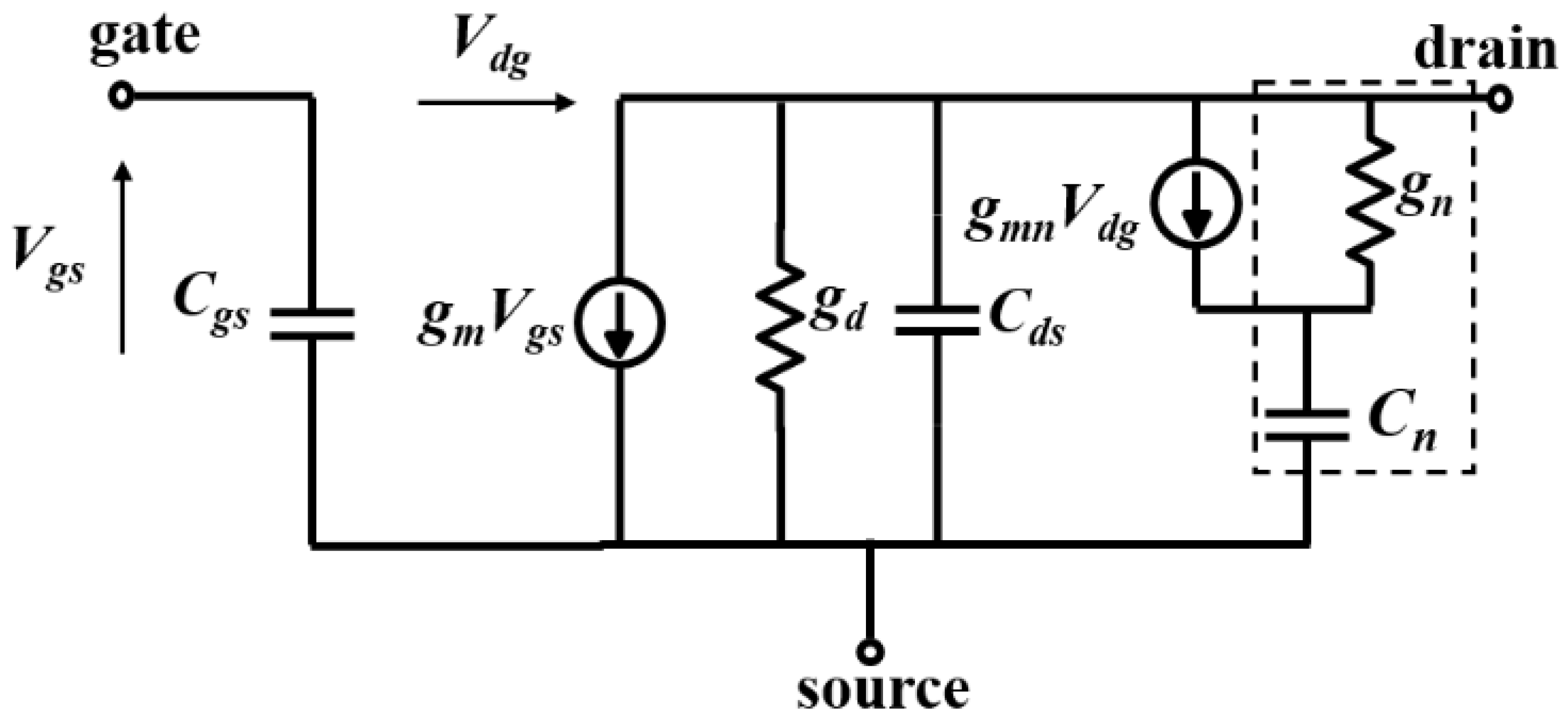
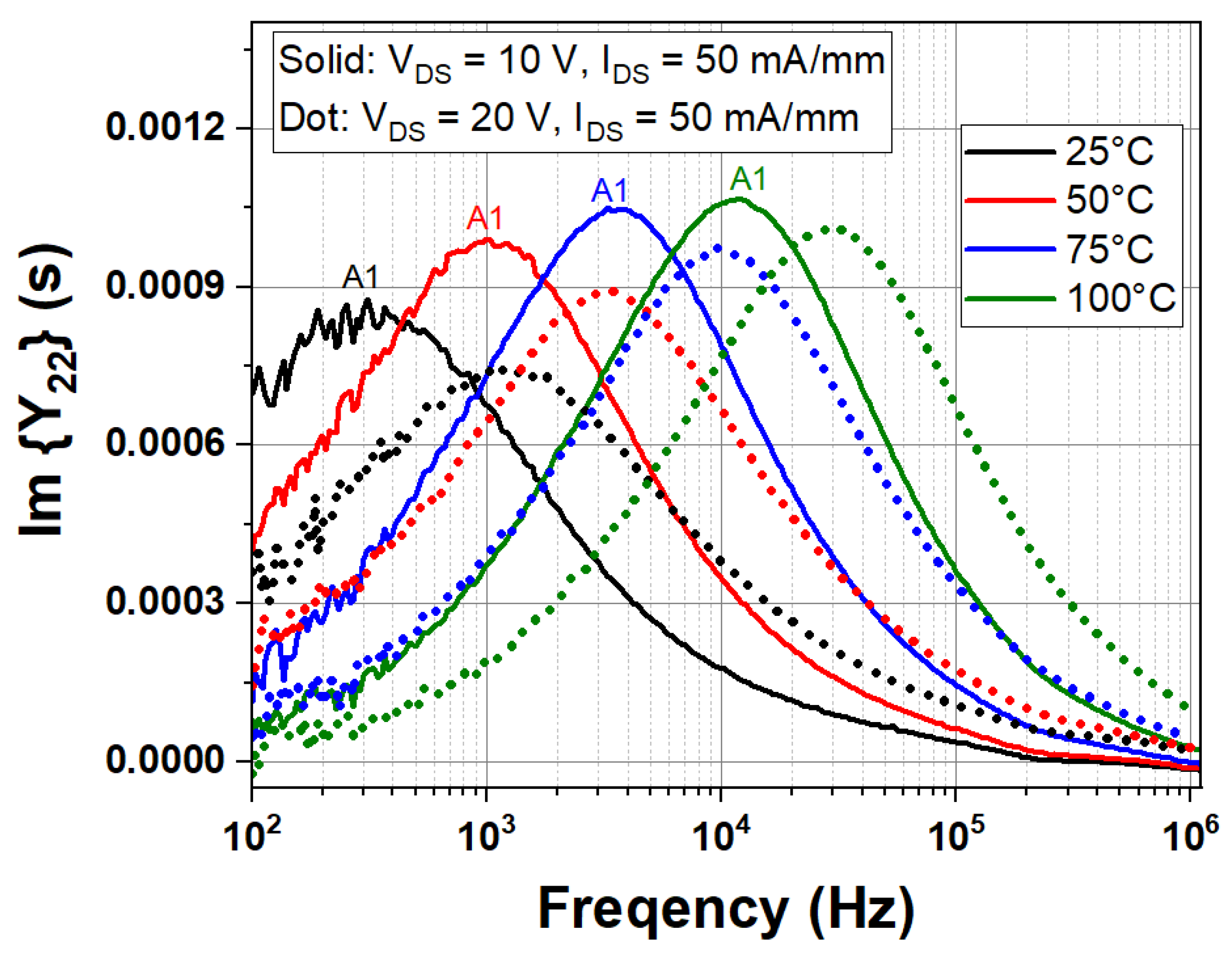
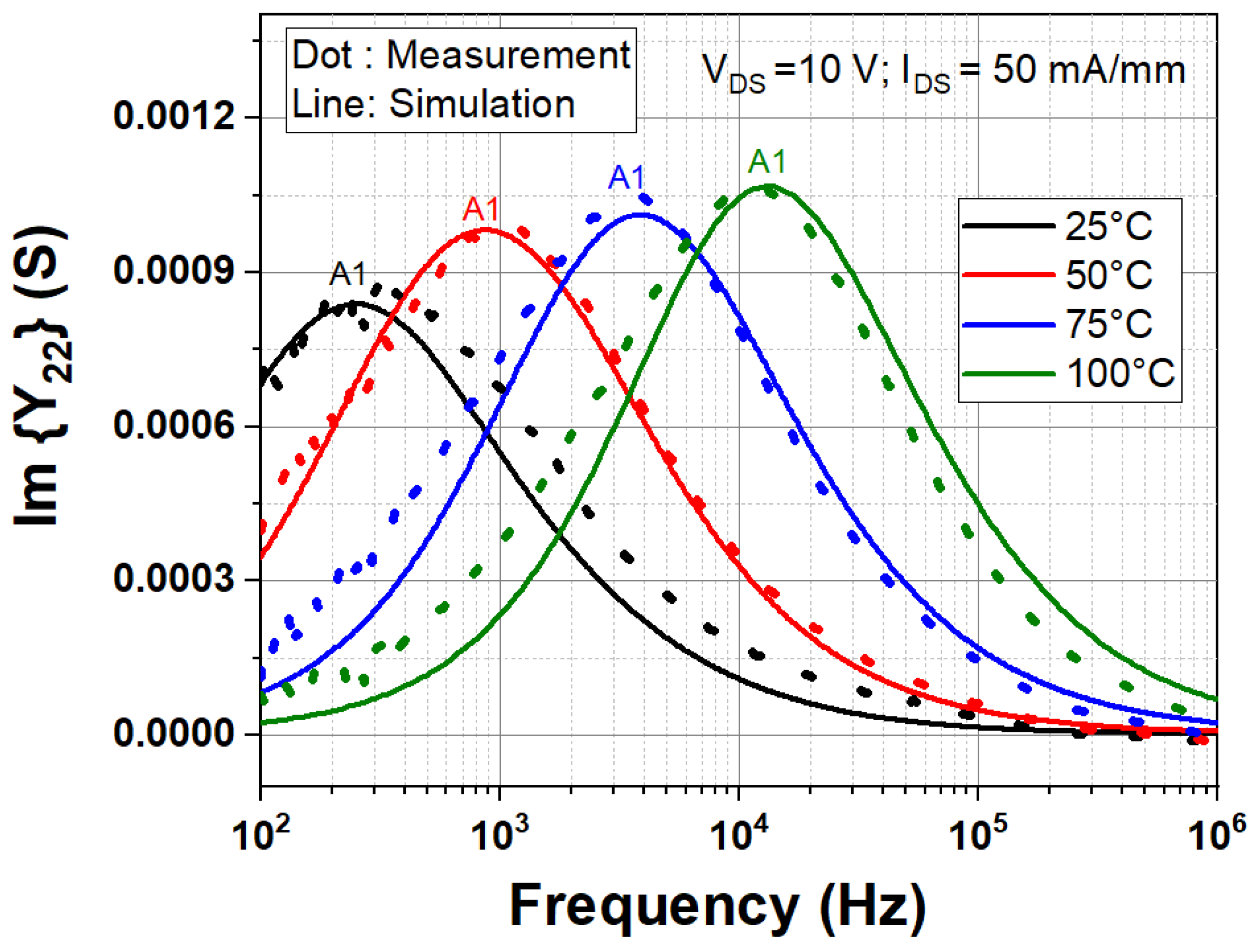
4.3. Measured and Simulated Y22 Parameters
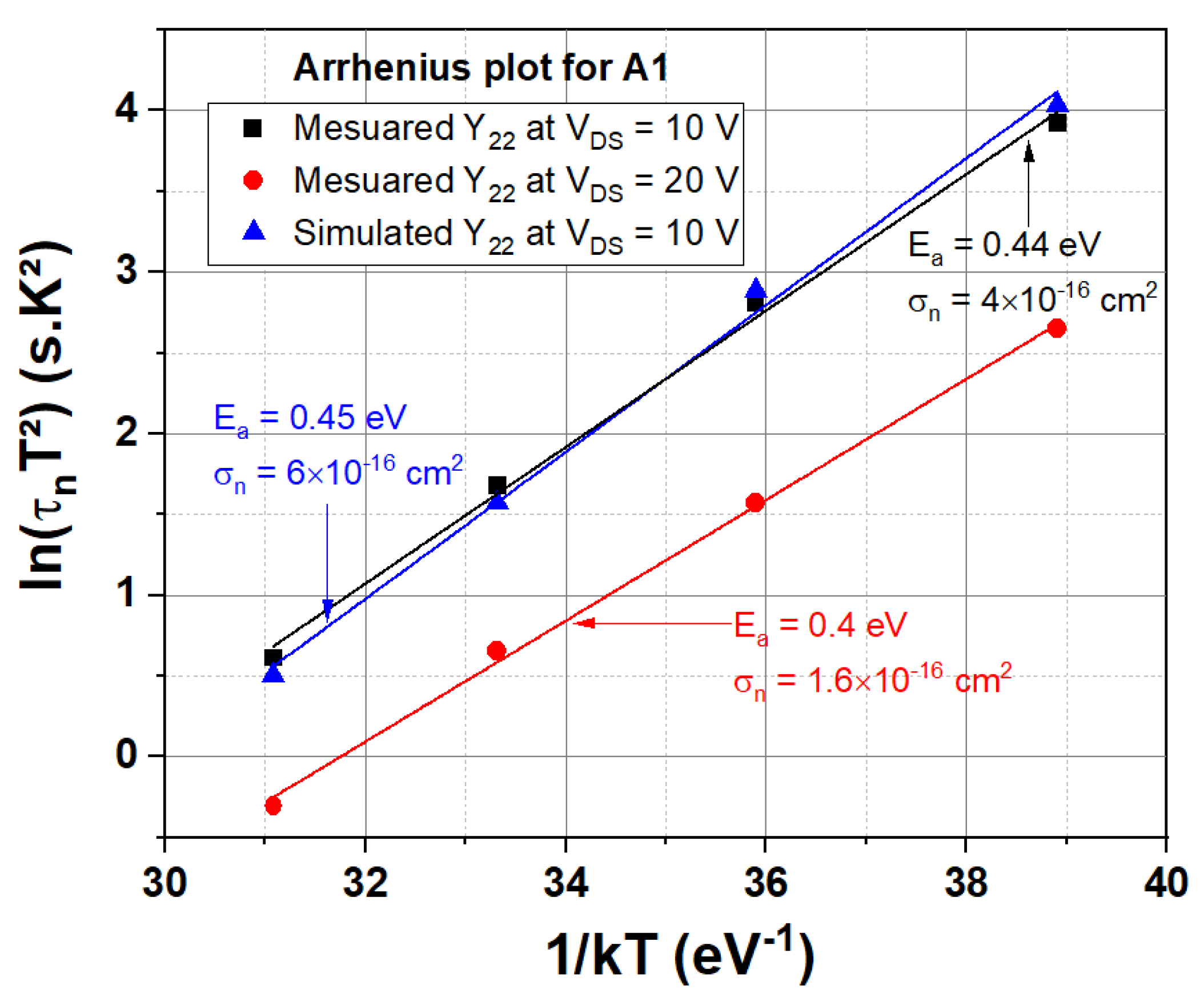
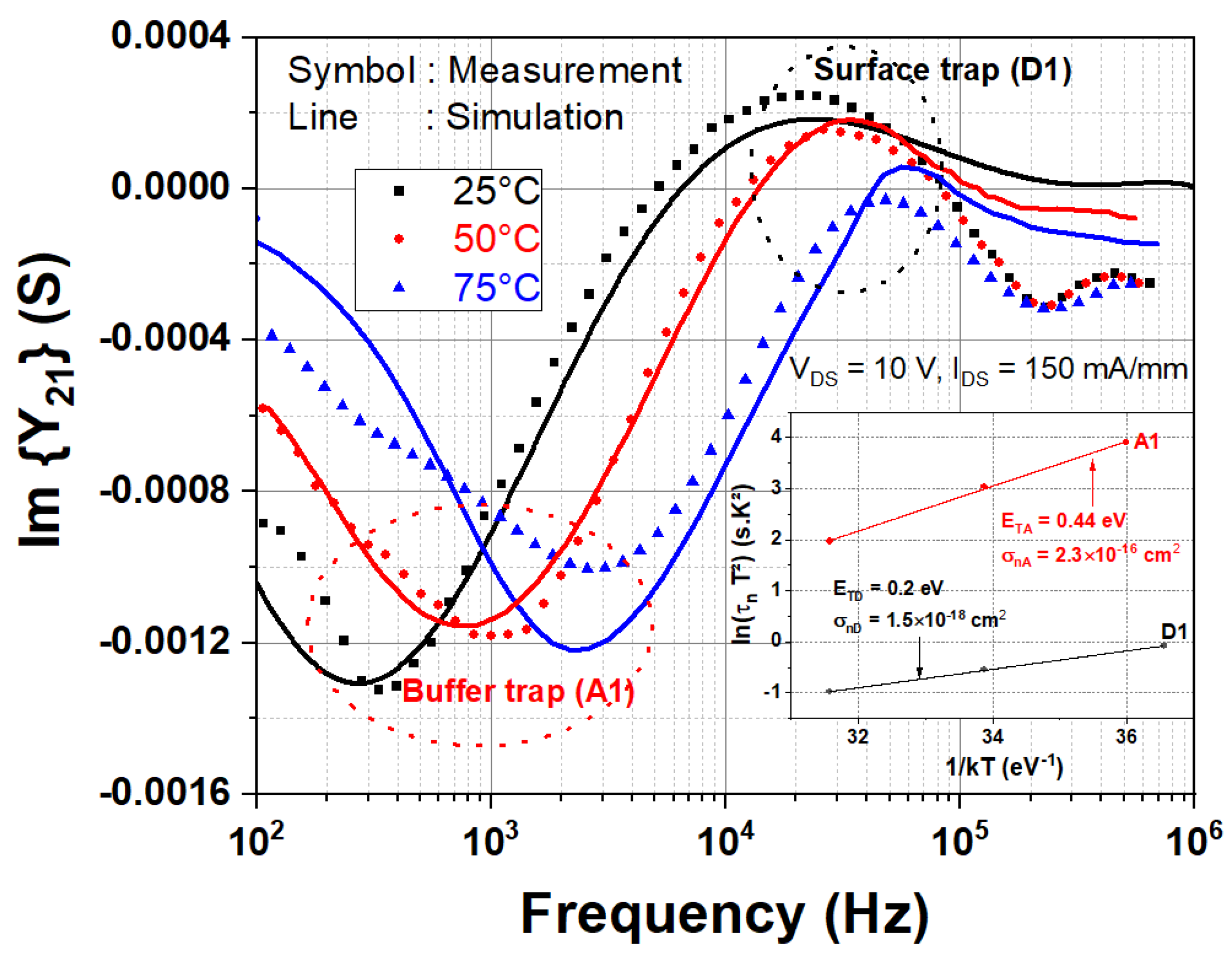
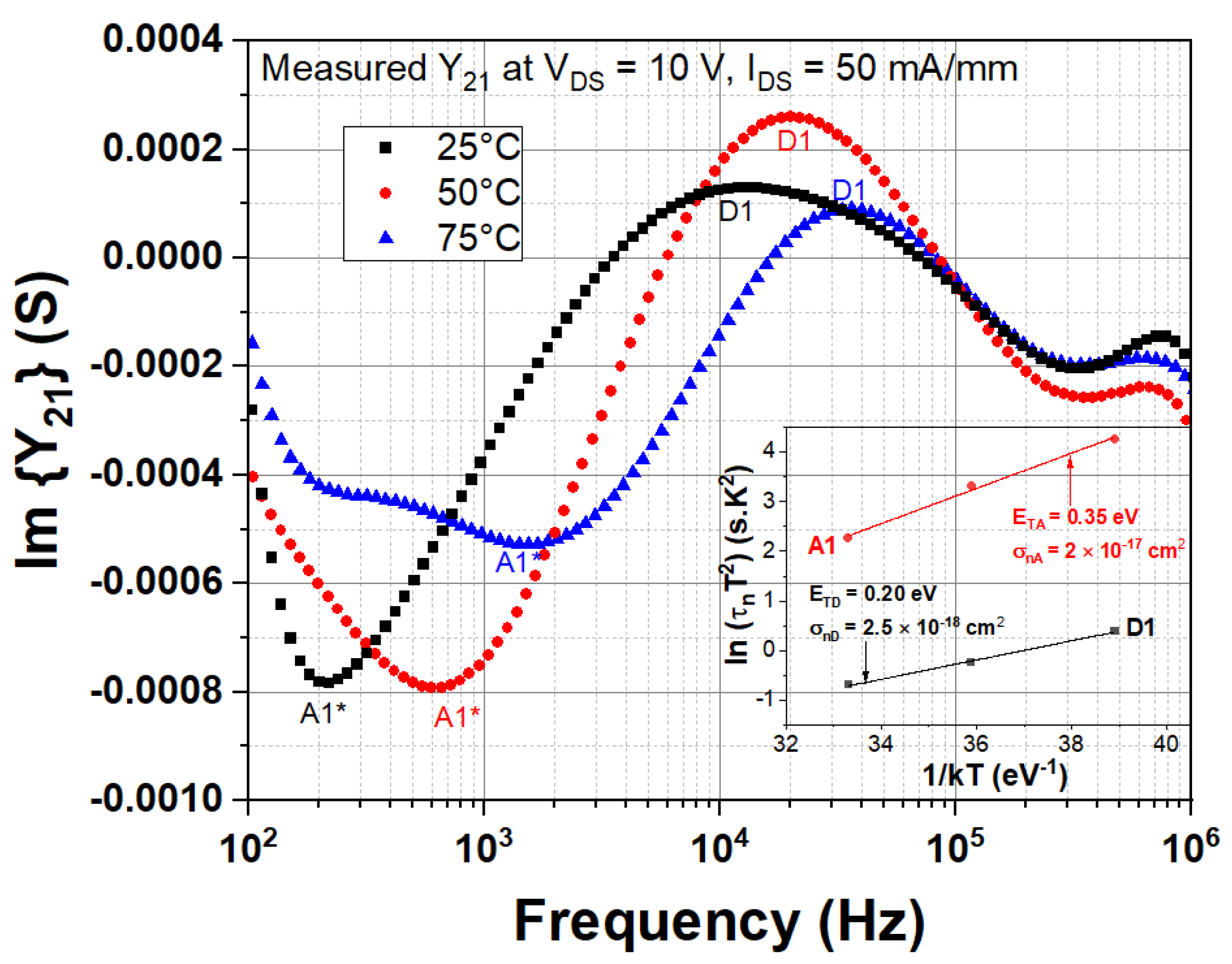
4.4. Measured and Simulated Y21 Parameters
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mishra, U.K.; Shen, L.; Kazior, T.E.; Wu, Y.F. GaN-based RF power devices and amplifiers. Proc. IEEE 2008, 96, 287–305. [Google Scholar] [CrossRef]
- Meneghesso, G.; Verzellesi, G.; Pierobon, R.; Rampazzo, F.; Chini, A.; Mishra, U.K.; Canali, C.; Zanoni, E. Surface-related drain current dispersion effects in AlGaN-GaN HEMTs. IEEE Trans. Electron Devices 2004, 51, 1554–1561. [Google Scholar] [CrossRef]
- Tirado, J.M.; Sanchez-Rojas, J.L.; Izpura, J.I. Trapping effects in the transient response of AlGaN/GaN HEMT devices. IEEE Trans. Electron Devices 2007, 54, 410–417. [Google Scholar] [CrossRef]
- Faqir, M.; Verzellesi, G.; Chini, A.; Fantini, F.; Danesin, F.; Meneghesso, G.; Zanoni, E.; Dua, C. Mechanisms of RF current collapse in AlGaN-GaN high electron mobility transistors. IEEE Trans. Device Mater. Reliab. 2008, 8, 240–247. [Google Scholar] [CrossRef]
- Uren, M.J.; Moreke, J.; Kuball, M. Buffer design to minimize current collapse in GaN/AlGaN HFETs. IEEE Trans. Electron Devices 2012, 59, 3327–3333. [Google Scholar] [CrossRef] [Green Version]
- Zhou, X.; Feng, Z.; Wang, L.; Wang, Y.; Lv, Y.; Dun, S.; Cai, S. Impact of bulk traps in GaN buffer on the gate-lag transient characteristics of AlGaN/GaN HEMTs. Solid-State Electron. 2014, 100, 15–19. [Google Scholar] [CrossRef]
- Raja, P.V.; Nallatamby, J.C.; DasGupta, N.; DasGupta, A. Trapping effects on AlGaN/GaN HEMT characteristics. Solid-State Electron. 2021, 176, 107929. [Google Scholar] [CrossRef]
- Joh, J.; Alamo, J.A.D. A current-transient methodology for trap analysis for GaN high electron mobility transistors. IEEE Trans. Electron Devices 2010, 58, 132–140. [Google Scholar] [CrossRef] [Green Version]
- Bisi, D.; Meneghini, M.; De Santi, C.; Chini, A.; Dammann, M.; Brueckner, P.; Mikulla, M.; Meneghesso, G.; Zanoni, E. Deep-level characterization in GaN HEMTs-Part I: Advantages and limitations of drain current transient measurements. IEEE Trans. Electron Devices 2013, 60, 3166–3175. [Google Scholar] [CrossRef]
- Chini, A.; Soci, F.; Meneghini, M.; Meneghesso, G.; Zanoni, E. Deep levels characterization in GaN HEMTs-Part II: Experimental and numerical evaluation of self-heating effects on the extraction of traps activation energy. IEEE Trans. Electron Devices 2013, 60, 3176–3182. [Google Scholar] [CrossRef]
- Meneghesso, G.; Meneghini, M.; Bisi, D.; Rossetto, I.; Cester, A.; Mishra, U.K.; Zanoni, E. Trapping phenomena in AlGaN/GaN HEMTs: A study based on pulsed and transient measurements. Semicond. Sci. Technol. 2013, 28, 074021. [Google Scholar] [CrossRef]
- Meneghini, M.; Rossetto, I.; Bisi, D.; Stocco, A.; Chini, A.; Pantellini, A.; Lanzieri, C.; Nanni, A.; Meneghesso, G.; Zanoni, E. Buffer traps in Fe-doped AlGaN/GaN HEMTs: Investigation of the physical properties based on pulsed and transient measurements. IEEE Trans. Electron Devices 2014, 61, 4070–4077. [Google Scholar] [CrossRef]
- Axelsson, O.; Gustafsson, S.; Hjelmgren, H.; Rorsman, N.; Blanck, H.; Splettstoesser, J.; Thorpe, J.; Roedle, T.; Thorsell, M. Application relevant evaluation of trapping effects in AlGaN/GaN HEMTs with Fe-doped buffer. IEEE Trans. Electron Devices 2015, 63, 326–332. [Google Scholar] [CrossRef]
- Bergsten, J.; Thorsell, M.; Adolph, D.; Chen, J.T.; Kordina, O.; Sveinbjörnsson, E.Ö.; Rorsman, N. Electron trapping in extended defects in microwave AlGaN/GaN HEMTs with carbon-doped buffers. IEEE Trans. Electron Devices 2018, 65, 2446–2453. [Google Scholar] [CrossRef]
- Bouslama, M.; Gillet, V.; Chang, C.; Nallatamby, J.C.; Sommet, R.; Prigent, M.; Quéré, R.; Lambert, B. Dynamic performance and characterization of traps using different measurements techniques for the new AlGaN/GaN HEMT of 0.15 µm ultrashort gate length. IEEE Trans. Microw. Theory. Tech. 2019, 67, 2475–2482. [Google Scholar] [CrossRef]
- Raja, P.V.; Bouslama, M.; Sarkar, S.; Pandurang, K.R.; Nallatamby, J.C.; DasGupta, N.; Dasgupta, A. Deep-level traps in AlGaN/GaN-and AlInN/GaN-based HEMTs with different buffer doping technologies. IEEE Trans. Electron Devices 2020, 67, 2304–2310. [Google Scholar] [CrossRef]
- Angelotti, A.M.; Gibiino, G.P.; Florian, C.; Santarelli, A. Trapping dynamics in GaN HEMTs for millimeter-wave applications: Measurement-based characterization and technology comparison. Electronics 2021, 10, 137. [Google Scholar] [CrossRef]
- Santi, C.D.; Buffolo, M.; Meneghesso, G.; Zanoni, E.; Meneghini, M. Dynamic performance characterization techniques in gallium nitride-based electronic devices. Crystals 2021, 11, 1037. [Google Scholar] [CrossRef]
- Umana-Membreno, G.A.; Dell, J.M.; Nener, B.D.; Faraone, L.; Parish, G.; Wu, Y.F.; Mishra, U.K. Low-temperature shallow-trap related output-admittance frequency dispersion in AlGaN/GaN MODFETs. In Proceedings of the IEEE Conference on Optoelectronic and Microelectronic Materials and Devices. Proceedings (Cat. No. 98EX140), Perth, Australia, 14–16 December 1998; pp. 252–255. [Google Scholar] [CrossRef]
- Nsele, S.D.; Escotte, L.; Tartarin, J.G.; Piotrowicz, S.; Delage, S.L. Broadband frequency dispersion small-signal modeling of the output conductance and transconductance in AlInN/GaN HEMTs. IEEE Trans. Electron Devices 2013, 60, 1372–1378. [Google Scholar] [CrossRef] [Green Version]
- Yamaguchi, Y.; Oishi, T.; Otsuka, H.; Nanjo, T.; Koyama, H.; Kamo, Y.; Yamanaka, K. Modeling of frequency dispersion at low frequency for GaN HEMT. In Proceedings of the IEEE Asia-Pacific Microwave Conference, Sendai, Japan, 4–7 November 2014; pp. 798–800. [Google Scholar]
- Potier, C.; Jacquet, J.C.; Dua, C.; Martin, A.; Campovecchio, M.; Oualli, M.; Jardel, O.; Piotrowicz, S.; Laurent, S.; Aubry, R.; et al. Highlighting trapping phenomena in microwave GaN HEMTs by low-frequency S-parameters. Int. J. Microw. Wirel. Technol. 2015, 7, 287–296. [Google Scholar] [CrossRef]
- Gustafsson, S.; Chen, J.T.; Bergsten, J.; Forsberg, U.; Thorsell, M.; Janzén, E.; Rorsman, N. Dispersive effects in microwave AlGaN/AlN/GaN HEMTs with carbon-doped buffer. IEEE Trans. Electron Devices 2015, 62, 2162–2169. [Google Scholar] [CrossRef]
- Benvegnù, A.; Bisi, D.; Laurent, S.; Meneghini, M.; Meneghesso, G.; Barataud, D.; Zanoni, E.; Quere, R. Drain current transient and low-frequency dispersion characterizations in AlGaN/GaN HEMTs. Int. J. Microw. Wirel. Technol. 2016, 8, 663–672. [Google Scholar] [CrossRef]
- Subramani, N.K.; Couvidat, J.; Hajjar, A.A.; Nallatamby, J.C.; Sommet, R.; Quéré, R. Identification of GaN buffer traps in microwave power AlGaN/GaN HEMTs through low frequency S-parameters measurements and TCAD-based physical device simulations. IEEE J. Electron Devices Soc. 2017, 5, 175–181. [Google Scholar] [CrossRef]
- Subramani, N.K.; Couvidat, J.; Hajjar, A.A.; Nallatamby, J.C.; Floriot, D.; Prigent, M.; Quéré, R. Low-frequency noise characterization in GaN HEMTs: Investigation of deep levels and their physical properties. IEEE Electron Device Lett. 2017, 38, 1109–1112. [Google Scholar] [CrossRef]
- Oishi, T.; Otsuka, T.; Tabuchi, M.; Yamaguchi, Y.; Shinjo, S.; Yamanaka, K. Bias dependence model of peak frequency of GaN trap in GaN HEMTs using low-frequency Y₂₂ parameters. IEEE Trans. Electron Devices 2021, 68, 5565–5571. [Google Scholar] [CrossRef]
- Green, B.M.; Chu, K.K.; Chumbes, E.M.; Smart, J.A.; Shealy, J.R.; Eastman, L.F. The effect of surface passivation on the microwave characteristics of undoped AlGaN/GaN HEMTs. IEEE Electron Device Lett. 2000, 21, 268–270. [Google Scholar] [CrossRef]
- Subramani, N.K.; Couvidat, J.; Hajjar, A.A.; Nallatamby, J.C.; Quéré, R. Low-frequency drain noise characterization and TCAD physical simulations of GaN HEMTs: Identification and analysis of physical location of traps. IEEE Electron Device Lett. 2017, 39, 107–110. [Google Scholar] [CrossRef] [Green Version]
- Subramani, N.K.; Sahoo, A.K.; Nallatamby, J.C.; Sommet, R.; Rolland, N.; Medjdoub, F.; Quéré, R. Characterization of parasitic resistances of AlN/GaN/AlGaN HEMTs through TCAD-based device simulations and on-wafer measurements. IEEE Trans. Microw. Theory. Tech. 2016, 64, 1351–1358. [Google Scholar] [CrossRef]
- Sentaurus TCAD User Guide; Version N-2017.09; Synopsys Inc.: San Jose, CA, USA, 2017.
- Ambacher, O.; Foutz, B.; Smart, J.; Shealy, J.R.; Weimann, N.G.; Chu, K.; Murphy, M.; Sierakowski, A.J.; Schaff, W.J.; Eastman, L.F. Two dimensional electron gases induced by spontaneous and piezoelectric polarization in undoped and doped AlGaN/GaN heterostructures. J. Appl. Phys. 2000, 87, 334–344. [Google Scholar] [CrossRef]
- Longobardi, G.; Udrea, F.; Sque, S.; Hurkx, G.A.; Croon, J.; Napoli, E.; Šonský, J. Impact of donor traps on the 2DEG and electrical behavior of AlGaN/GaN MISFETs. IEEE Electron Device Lett. 2013, 35, 27–29. [Google Scholar] [CrossRef]
- Mukherjee, J.; Malik, A.; Vinayak, S.; Rawal, D.S.; Dhaka, R.S. Deep trap characterization and the kink effect in AlGaN/GaN HEMTs. IETE Tech. Rev. 2020, 1–8. [Google Scholar] [CrossRef]
- Smorchkova, I.P.; Elsass, C.R.; Ibbetson, J.P.; Vetury, R.; Heying, B.; Fini, P.; Haus, E.; DenBaars, S.P.; Speck, J.S.; Mishra, U.K. Polarization-induced charge and electron mobility in AlGaN/GaN heterostructures grown by plasma-assisted molecular-beam epitaxy. J. Appl. Phys. 1999, 86, 4520–4526. [Google Scholar] [CrossRef]
- Ibbetson, J.P.; Fini, P.T.; Ness, K.D.; DenBaars, S.P.; Speck, J.S.; Mishra, U.K. Polarization effects, surface states, and the source of electrons in AlGaN/GaN heterostructure field effect transistors. Appl. Phys. Lett. 2000, 77, 250–252. [Google Scholar] [CrossRef]
- Ťapajna, M.; Jurkovič, M.; Válik, L.; Haščík, Š.; Gregušová, D.; Brunner, F.; Cho, E.M.; Hashizume, T.; Kuzmík, J. Impact of GaN cap on charges in Al2O3/(GaN/)AlGaN/GaN metal-oxide-semiconductor heterostructures analyzed by means of capacitance measurements and simulations. J. Appl. Phys. 2014, 116, 104501. [Google Scholar] [CrossRef]
- Matys, M.; Adamowicz, B.; Domanowska, A.; Michalewicz, A.; Stoklas, R.; Akazawa, M.; Yatabe, Z.; Hashizume, T. On the origin of interface states at oxide/III-nitride heterojunction interfaces. J. Appl. Phys. 2016, 120, 225305. [Google Scholar] [CrossRef] [Green Version]
- Mitrofanov, O.; Manfra, M. Poole-Frenkel electron emission from the traps in AlGaN/GaN transistors. J. Appl. Phys. 2004, 95, 6414–6419. [Google Scholar] [CrossRef] [Green Version]
- Rossetto, I.; Bisi, D.; Santi, C.; Stocco, A.; Meneghesso, G.; Zanoni, E.; Meneghini, M. Performance-limiting traps in GaN based HEMTs: From native defects to common impurities. In Power GaN Devices Materials, Applications and Reliability, 1st ed.; Springer: Basel, Switzerland, 2017; pp. 197–236. [Google Scholar]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Raja, P.V.; Subramani, N.K.; Gaillard, F.; Bouslama, M.; Sommet, R.; Nallatamby, J.-C. Identification of Buffer and Surface Traps in Fe-Doped AlGaN/GaN HEMTs Using Y21 Frequency Dispersion Properties. Electronics 2021, 10, 3096. https://doi.org/10.3390/electronics10243096
Raja PV, Subramani NK, Gaillard F, Bouslama M, Sommet R, Nallatamby J-C. Identification of Buffer and Surface Traps in Fe-Doped AlGaN/GaN HEMTs Using Y21 Frequency Dispersion Properties. Electronics. 2021; 10(24):3096. https://doi.org/10.3390/electronics10243096
Chicago/Turabian StyleRaja, P. Vigneshwara, Nandha Kumar Subramani, Florent Gaillard, Mohamed Bouslama, Raphaël Sommet, and Jean-Christophe Nallatamby. 2021. "Identification of Buffer and Surface Traps in Fe-Doped AlGaN/GaN HEMTs Using Y21 Frequency Dispersion Properties" Electronics 10, no. 24: 3096. https://doi.org/10.3390/electronics10243096
APA StyleRaja, P. V., Subramani, N. K., Gaillard, F., Bouslama, M., Sommet, R., & Nallatamby, J.-C. (2021). Identification of Buffer and Surface Traps in Fe-Doped AlGaN/GaN HEMTs Using Y21 Frequency Dispersion Properties. Electronics, 10(24), 3096. https://doi.org/10.3390/electronics10243096





