Investigations on Quench Recovery Characteristics of High-Temperature Superconducting Coated Conductors for Superconducting Fault Current Limiters
Abstract
:1. Introduction
2. Experimental Details
2.1. Sample
2.2. Experimental System
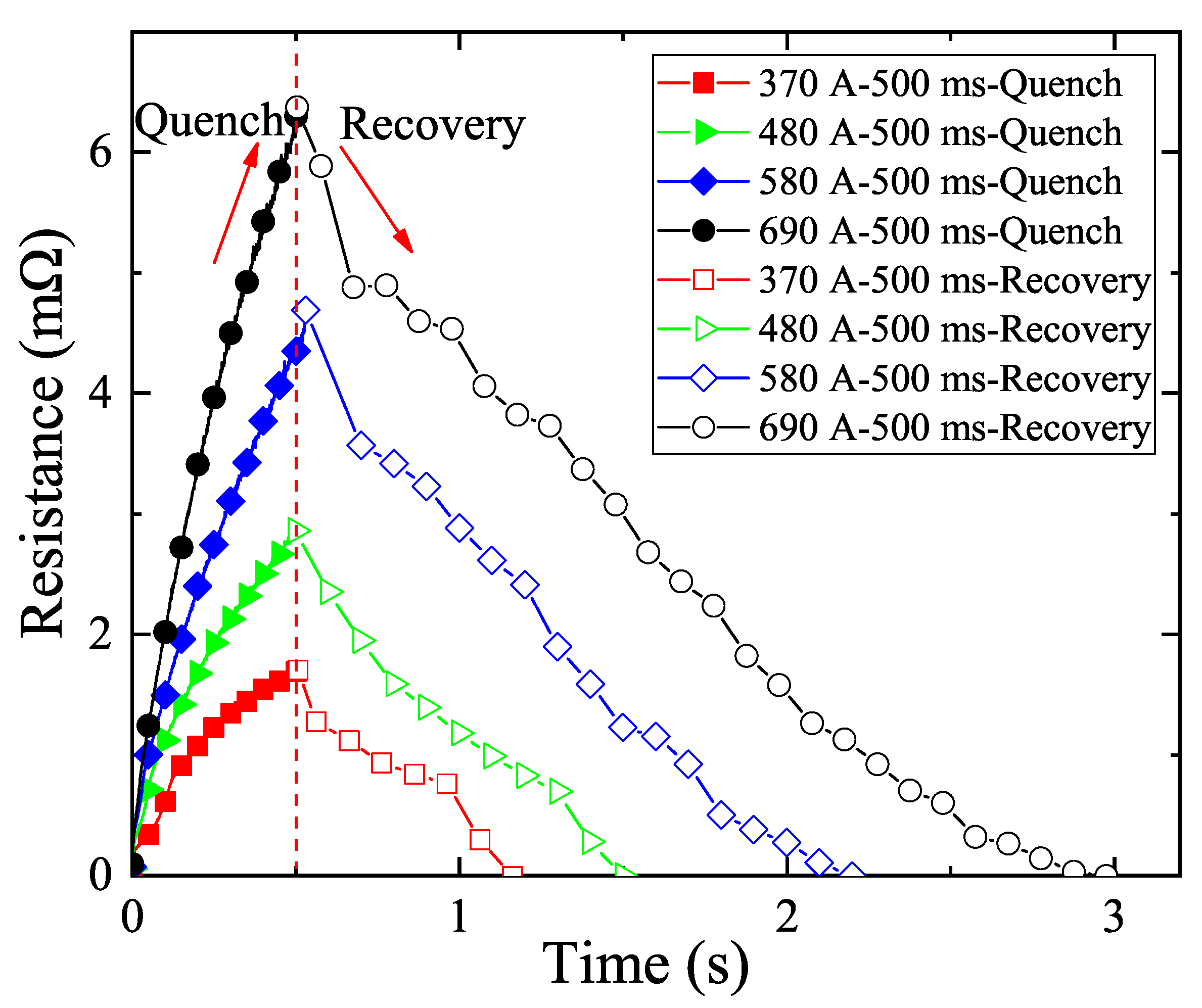
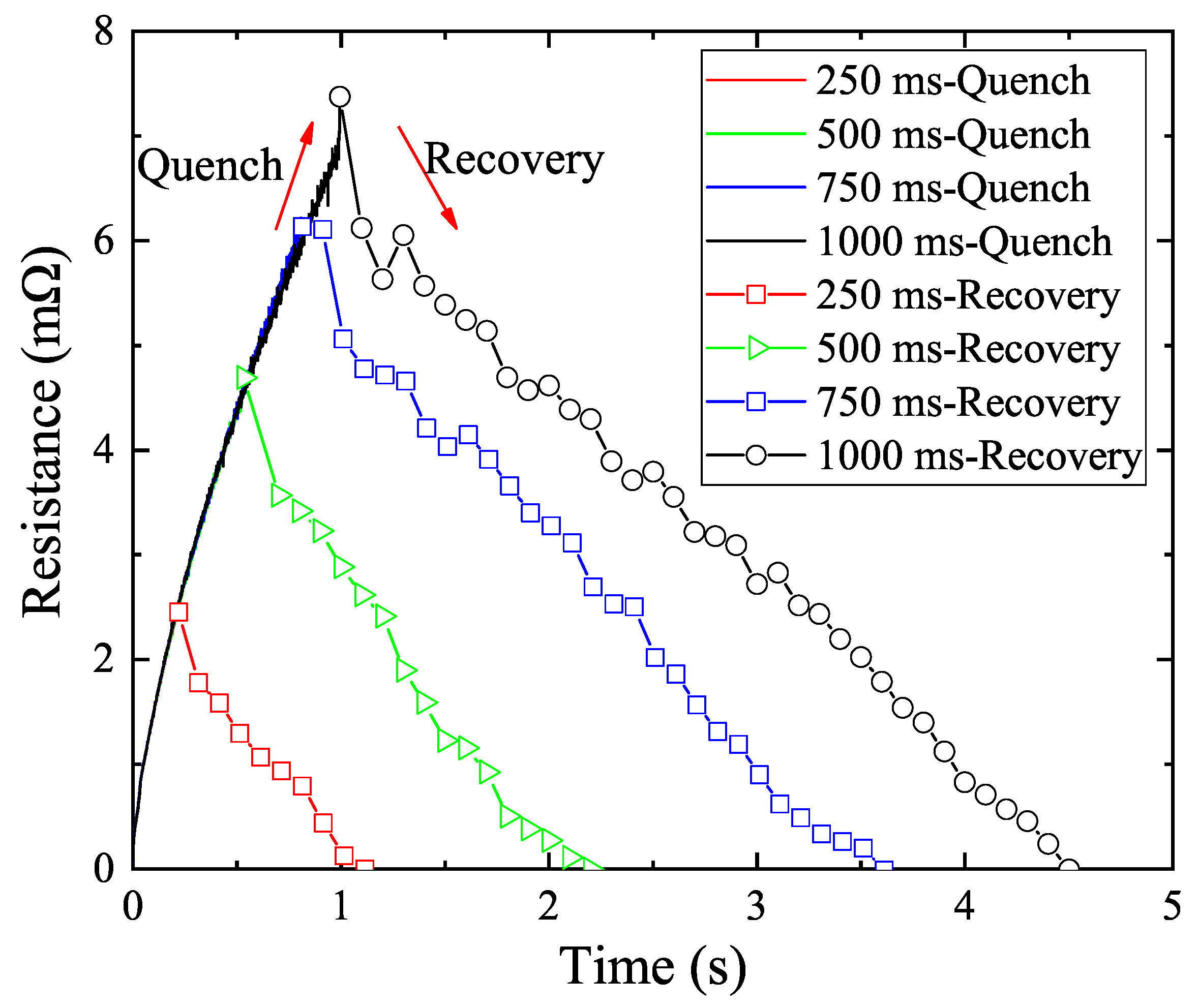
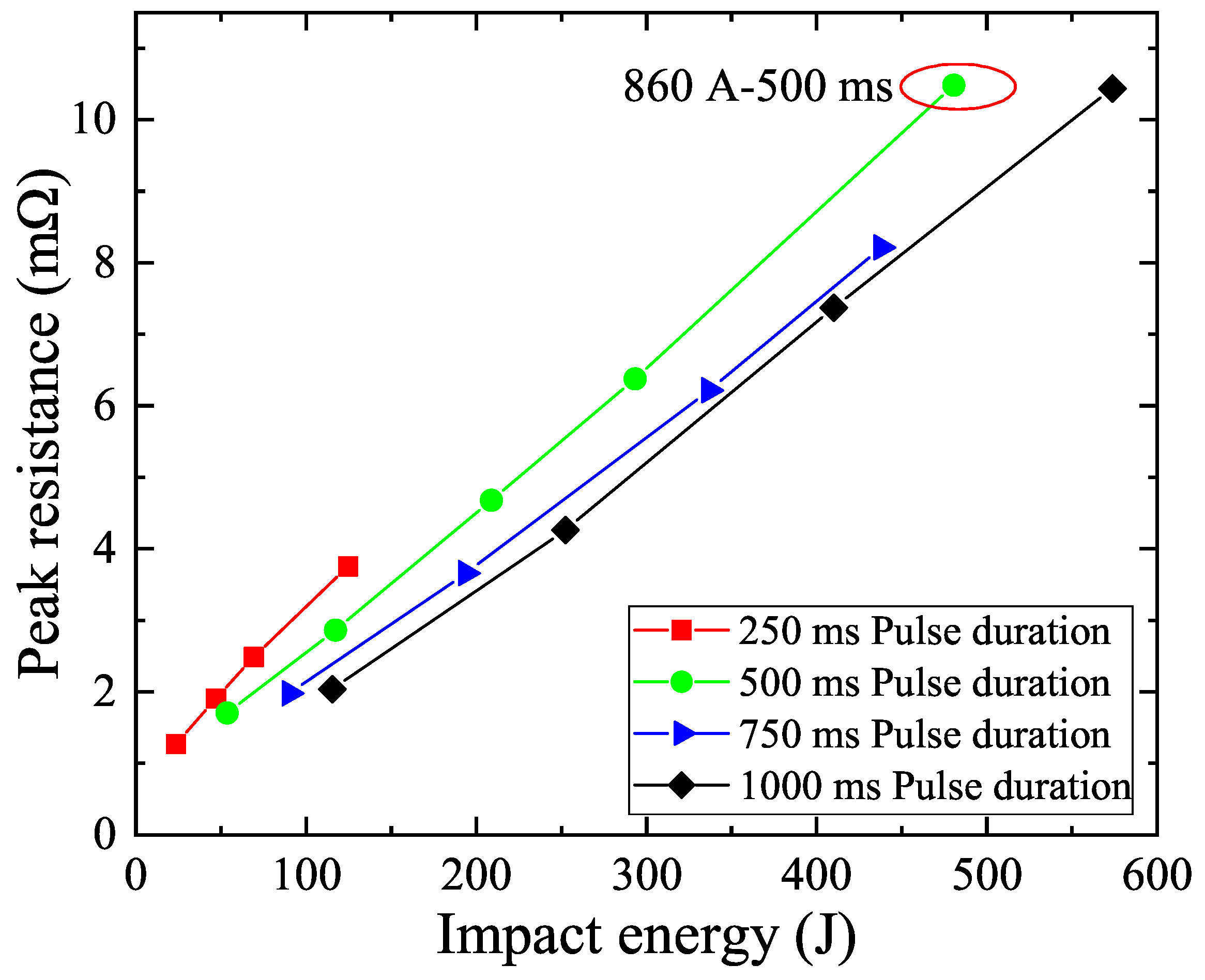
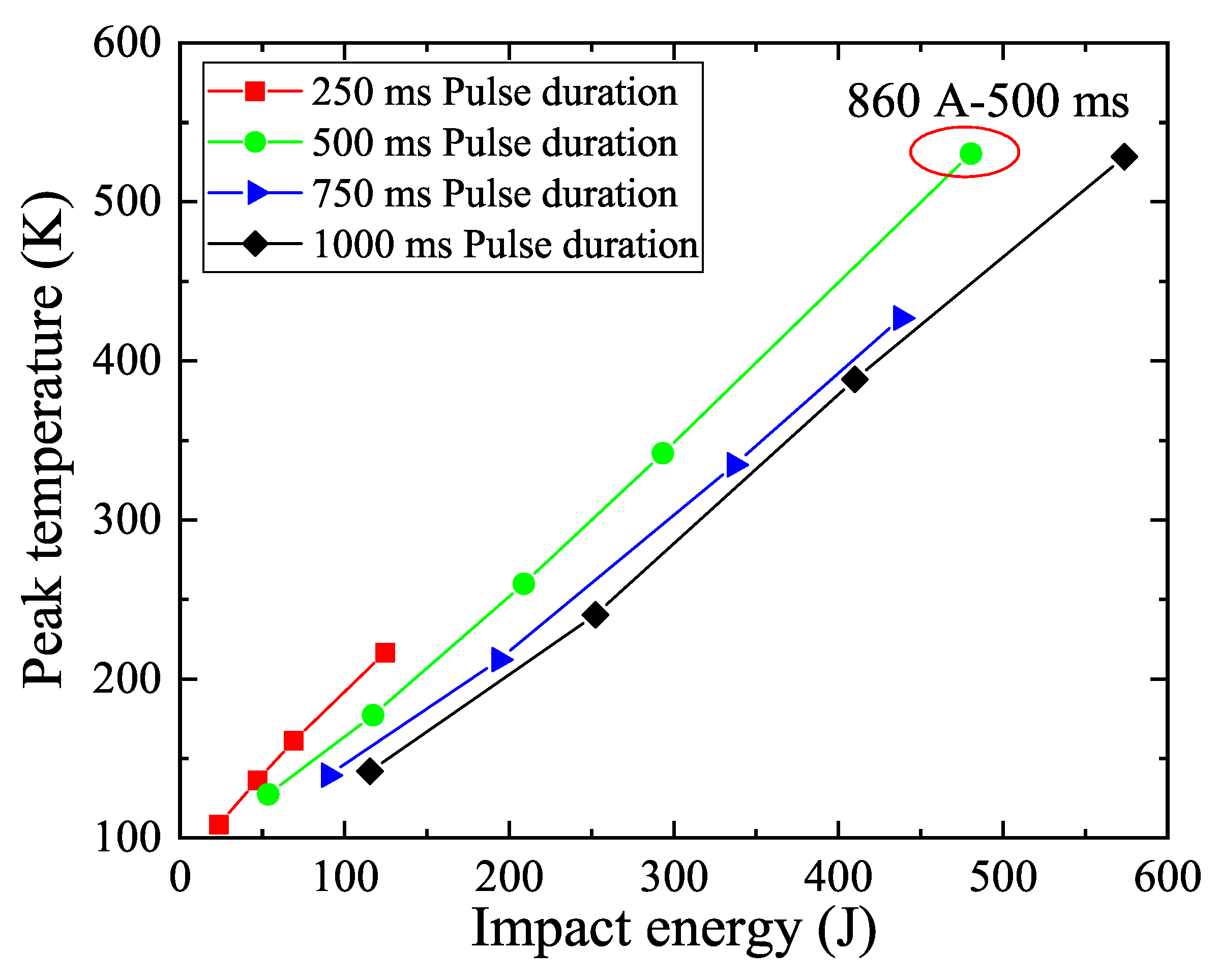
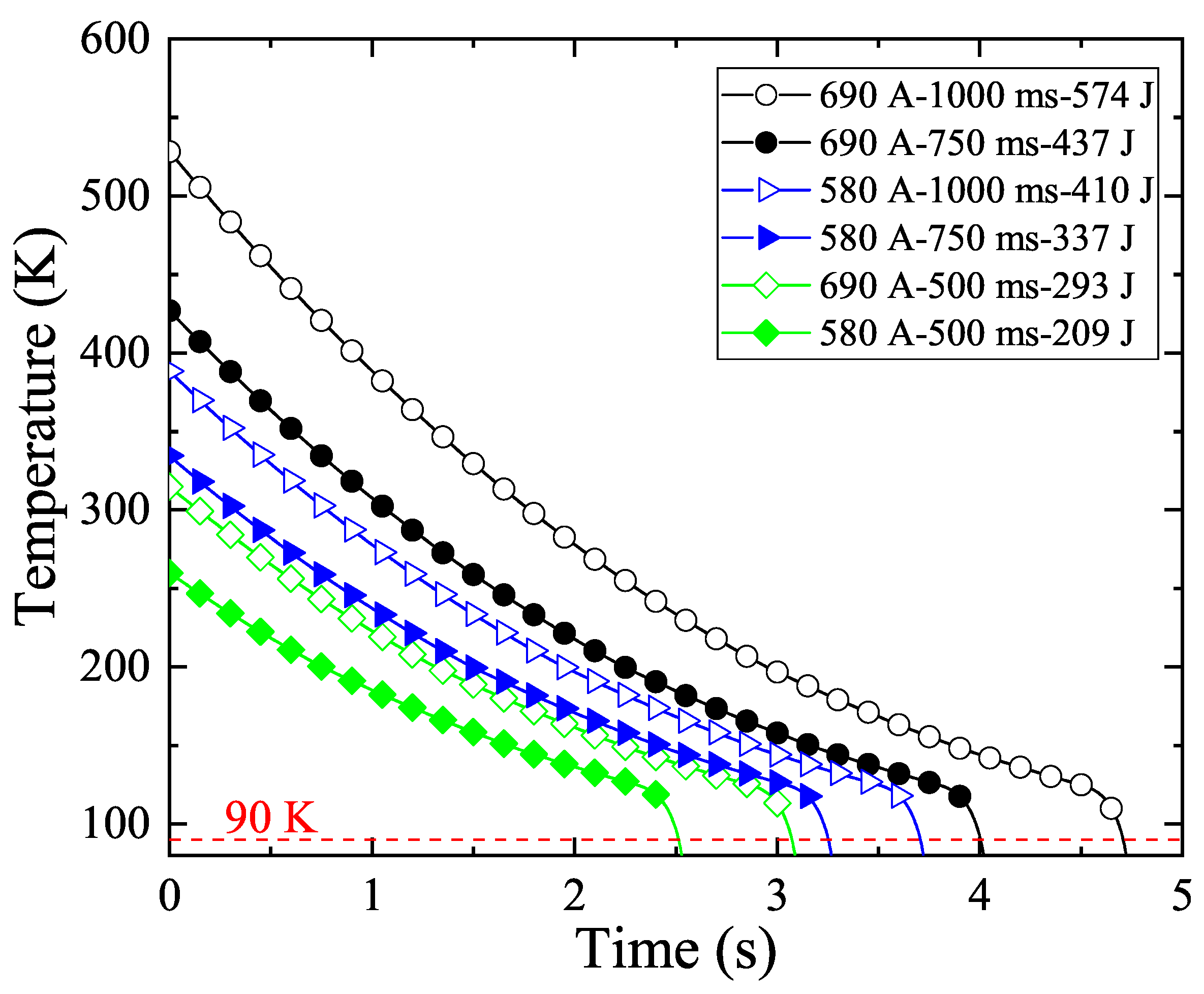
3. Results
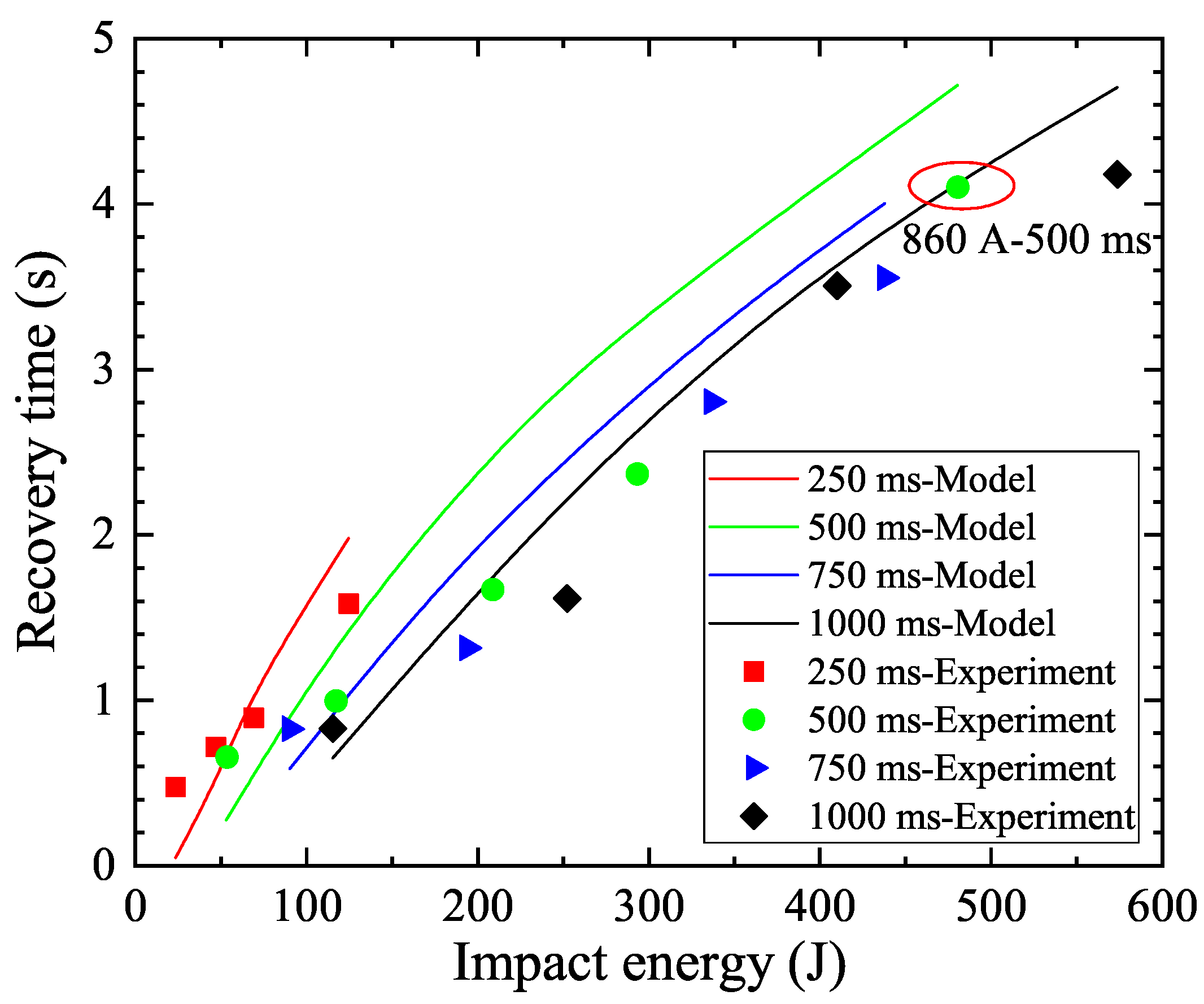
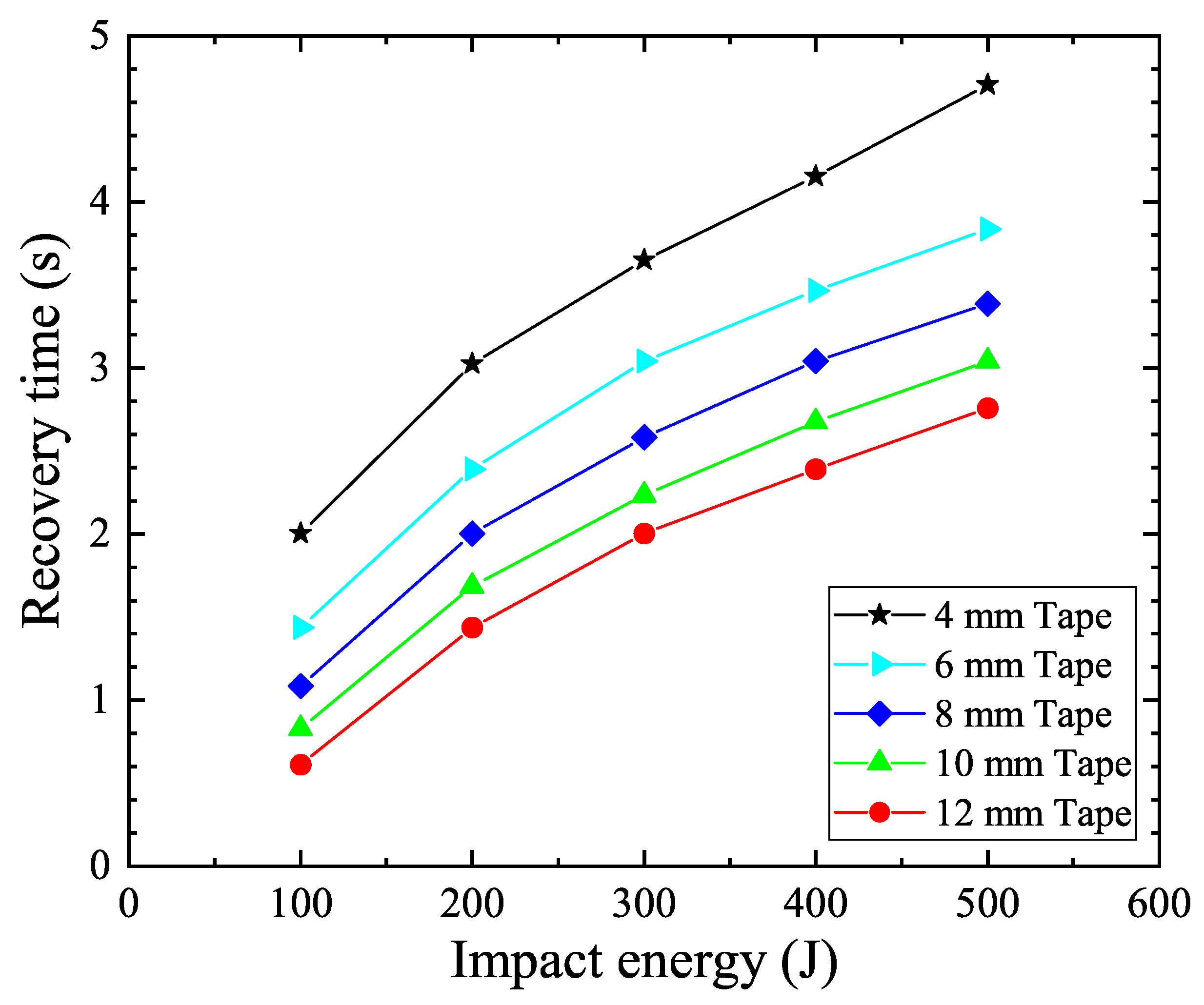
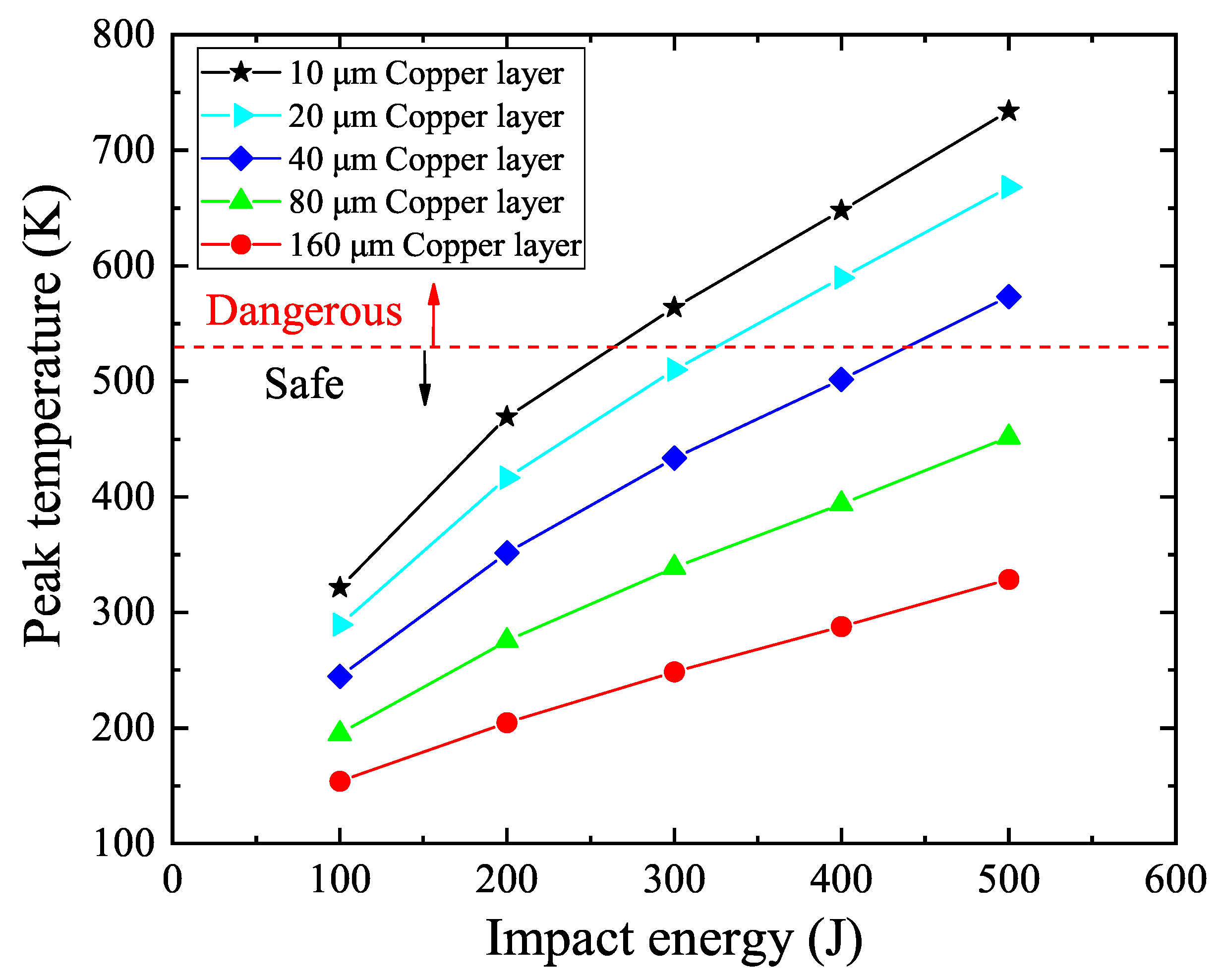
4. Numerical Model
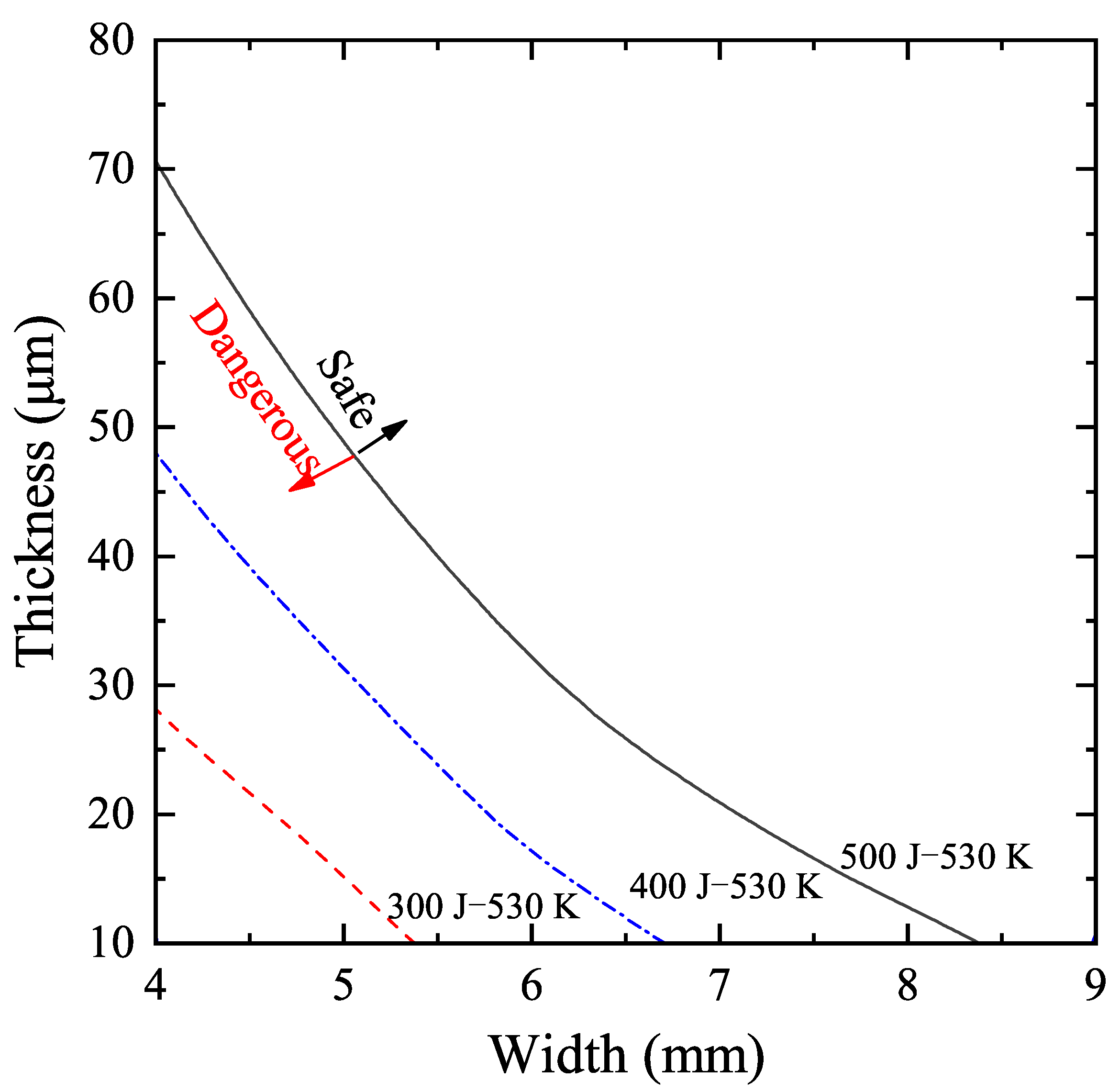
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bayindir, R.; Colak, I.; Fulli, G.; Demirtas, K. Smart grid technologies and applications. Renew. Sustain. Energy Rev. 2016, 66, 499–516. [Google Scholar] [CrossRef]
- Hossain, M.; Madlool, N.; Rahim, N.; Selvaraj, J.; Pandey, A.; Khan, A.F. Role of smart grid in renewable energy: An overview. Renew. Sustain. Energy Rev. 2016, 60, 1168–1184. [Google Scholar] [CrossRef]
- Kakran, S.; Chanana, S. Smart operations of smart grids integrated with distributed generation: A review. Renew. Sustain. Energy Rev. 2018, 81, 524–535. [Google Scholar] [CrossRef]
- Pueschel, T. DC-powered office buildings and data centres: The first 380 VDC micro grid in a commercial building in germany. In Proceedings of the 2018 International Power Electronics Conference (IPEC-Niigata 2018-ECCE Asia), Niigata, Japan, 20–24 May 2018; pp. 190–195. [Google Scholar]
- Yoldaş, Y.; Önen, A.; Muyeen, S.; Vasilakos, A.V.; Alan, İ. Enhancing smart grid with microgrids: Challenges and opportunities. Renew. Sustain. Energy Rev. 2017, 72, 205–214. [Google Scholar] [CrossRef]
- Loder, D.C.; Bollman, A.; Armstrong, M.J. Turbo-electric distributed aircraft propulsion: Microgrid architecture and evaluation for ECO-150. In Proceedings of the 2018 IEEE Transportation Electrification Conference and Expo (ITEC), Long Beach, CA, USA, 13–15 June 2018; pp. 550–557. [Google Scholar]
- Jin, Z.; Sulligoi, G.; Cuzner, R.; Meng, L.; Vasquez, J.C.; Guerrero, J.M. Next-generation shipboard dc power system: Introduction smart grid and dc microgrid technologies into maritime electrical netowrks. IEEE Electrif. Mag. 2016, 4, 45–57. [Google Scholar] [CrossRef] [Green Version]
- Garcia, W.R.L.; Tixador, P.; Raison, B.; Bertinato, A.; Luscan, B.; Creusot, C. Technical and economic analysis of the R-type SFCL for HVDC grids protection. IEEE Trans. Appl. Supercond. 2017, 27, 2739642. [Google Scholar]
- Zhang, Y.; Dougal, R.A. State of the art of fault current limiters and their applications in smart grid. In Proceedings of the 2012 IEEE Power and Energy Society General Meeting, San Diego, CA, USA, 22–26 July 2012. [Google Scholar]
- Angioni, A.; Shang, J.; Ponci, F.; Monti, A. Real-time monitoring of distribution system based on state estimation. IEEE Trans. Instrum. Meas. 2016, 65, 2234–2243. [Google Scholar] [CrossRef]
- McGuckin, P.; Burt, G. Overview and assessment of superconducting technologies for power grid applications. In Proceedings of the 2018 53rd International Universities Power Engineering Conference (UPEC), Glasgow, Scotland, 4–7 September 2018. [Google Scholar]
- Kim, H.; Lee, J.Y.; Kim, H.R.; Yang, S.E.; Yu, S.D.; Kim, W.S.; Hyun, O.B.; Ko, J.; Yeom, H. An effect of HTS wire configuration on quench recovery time in a resistive SFCL. IEEE Trans. Appl. Supercond. 2013, 23, 5604104. [Google Scholar]
- Nam, K.; Kang, H.; Lee, C.; Ko, T.K.; Seok, B.Y. Visualization study on boiling of nitrogen during quench for fault current limiter applications. IEEE Trans. Appl. Supercond. 2006, 16, 727–730. [Google Scholar] [CrossRef]
- Sun, J.; Du, J.; Li, Y.; Mo, S.; Cai, Y.; Yuan, W.; Ma, T. Design and Performance Test of a 20-kV DC Superconducting Fault Current Limiter. IEEE Trans. Appl. Supercond. 2020, 30, 2963410. [Google Scholar] [CrossRef]
- Lee, H.Y.; Asif, M.; Park, K.H.; Lee, B.W. Feasible Application Study of Several Types of Superconducting Fault Current Limiters in HVDC Grids. IEEE Trans. Appl. Supercond. 2018, 28, 5601205. [Google Scholar] [CrossRef]
- Li, B.; Wang, C.; Wei, Z.; Xin, Y.; Li, B.; He, J. Technical requirements of the DC superconducting fault current limiter. IEEE Trans. Appl. Supercond. 2018, 28, 5602805. [Google Scholar] [CrossRef]
- Jiang, Z.; Wang, Y.; Dai, S.; Ma, T.; Yuan, X.; Liu, M.; Chen, H.; Wang, M.; Peng, C. Application and design of resistive SFCL in ±160 kV MMC-HVdc system. IEEE Trans. Appl. Supercond. 2019, 29, 5603505. [Google Scholar] [CrossRef]
- Hayakawa, N.; Maeno, Y.; Kojima, H. Fault current limitation coordination in electric power grid with superconducting fault current limiters. IEEE Trans. Appl. Supercond. 2018, 28, 5602304. [Google Scholar] [CrossRef]
- Hong, Z.; Sheng, J.; Yao, L.; Gu, J.; Jin, Z. The structure, performance and recovery time of a 10 kV resistive type superconducting fault current limiter. IEEE Trans. Appl. Supercond. 2012, 23, 5601304. [Google Scholar] [CrossRef]
- Qiu, Q.; Xiao, L.; Zhang, J.; Zhang, Z.; Song, N.; Jing, L.; Zha, W.; Du, X.; Teng, Y.; Zhou, Z.; et al. Design and Test of 40-kV/2-kA DC Superconducting Fault Current Limiter. IEEE Trans. Appl. Supercond. 2020, 30, 2988068. [Google Scholar] [CrossRef]
- Dai, S.; Ma, T.; Xue, C.; Zhao, L.; Huang, Y.; Hu, L.; Wang, B.; Zhang, T.; Xu, X.; Cai, L.; et al. Development and test of a 220 kV/1.5 kA resistive type superconducting fault current limiter. Phys. C Supercond. Its Appl. 2019, 565, 1253501. [Google Scholar] [CrossRef]
- Kempski, A.; Rusiński, J.; Hajdasz, S. Analysis of recovery time of HTS tapes with electrical insulation layers for superconducting fault current limiters under load conditions. IEEE Trans. Appl. Supercond. 2019, 29, 5603910. [Google Scholar] [CrossRef]
- Zha, W.; Qiu, Q.; Cao, S.; Wang, H. Quench and Recovery Characteristics of Solenoid and Pancake SFCLs Under DC Impact Current. IEEE Trans. Appl. Supercond. 2019, 30, 5600106. [Google Scholar] [CrossRef]
- Lim, S.H.; Lim, S.T. Current Limiting and Recovery Characteristics of a Trigger-Type SFCL Using Double Quench. IEEE Trans. Appl. Supercond. 2018, 28, 5601305. [Google Scholar] [CrossRef]
- Baldan, C.A.; Shigue, C.Y.; Guedes, L.C.; Bernardes, A.A.; Ruppert, E. Recovery tests of an hybrid current limiter composed of a SFCL in parallel to an air-core power reactor. J. Supercond. Nov. Magn. 2015, 28, 691–695. [Google Scholar] [CrossRef]
- Lai, L.; Gu, C.; Yue, Y.; Chen, S.; Song, M.; Hu, N.N.; Qu, T.; Zou, S. Characterization of I c Degradation in Bent YBCO Tapes. IEEE Trans. Appl. Supercond. 2019, 29, 9001505. [Google Scholar] [CrossRef]
- Maeda, C.; Yanai, S.; Shirai, Y.; Shiotsu, M.; Honda, G.; Isojima, S. Recovery Characteristics of GdBCO Tape in a Pressurized Liquid Nitrogen for a Resistive SFCL. IEEE Trans. Appl. Supercond. 2019, 29, 5602505. [Google Scholar] [CrossRef]
- Jiang, Z.; Wang, Y.; Dai, S.; Ma, T.; Peng, C.; Liu, M.; Chen, H. Influence of Insulation on Quench and Recovery of YBCO Tape Under DC Impact. IEEE Trans. Appl. Supercond. 2018, 29, 7700305. [Google Scholar] [CrossRef]
- Xiang, B.; Junaid, M.; Gao, L.; Liu, Z.; Geng, Y.; Wang, J.; Yanabu, S. Influencing Factors on Quench and Recovery of YBCO Tapes for DC Superconducting Fault Current Limiter. IEEE Trans. Appl. Supercond. 2018, 29, 5600806. [Google Scholar] [CrossRef]
- Du, H.I. Evaluation on Resistance Tendency and Recovery Characteristics of 2G Wire With Insulation Layer. IEEE Trans. Appl. Supercond. 2013, 23, 6602004. [Google Scholar]
- Xiang, B.; Junaid, M.; Gao, L.; Liu, Z.; Geng, Y.; Wang, J.; Yanabu, S. Effects of Short Circuit Currents on Quench and Recovery Properties of YBCO Tapes for DC SFCL. IEEE Trans. Appl. Supercond. 2018, 29, 5600706. [Google Scholar] [CrossRef]
- Wang, Y.; Chan, W.K.; Schwartz, J. Self-protection mechanisms in no-insulation (RE) Ba2Cu3O x high temperature superconductor pancake coils. Supercond. Sci. Technol. 2016, 29, 045007. [Google Scholar] [CrossRef]
- Wang, Y.; Weng, F.; Li, J.; Šouc, J.; Gömöry, F.; Zou, S.; Zhang, M.; Yuan, W. No-Insulation High-Temperature Superconductor Winding Technique for Electrical Aircraft Propulsion. IEEE Trans. Transp. Electrif. 2020, 6, 1613–1624. [Google Scholar] [CrossRef]
- Usak, P.; Mozola, P. How to Speed Up Y–Ba–Cu–O Tape Recovery. IEEE Trans. Appl. Supercond. 2013, 23, 4701011. [Google Scholar] [CrossRef]
- Zou, S.; Zermeño, V.; Baskys, A.; Patel, A.; Grilli, F.; Glowacki, B. Simulation and experiments of stacks of high temperature superconducting coated conductors magnetized by pulsed field magnetization with multi-pulse technique. Supercond. Sci. Technol. 2016, 30, 014010. [Google Scholar] [CrossRef] [Green Version]
- Ekin, J.W.; Zimmerman, G.O. Experimental Techniques for Low-Temperature Measurements: Cryostat Design, Material Properties, and Superconductor Critical-Current Testing. Phys. Today 2007, 60. [Google Scholar] [CrossRef] [Green Version]
- Ye, L.; Juengst, K.-P. Modeling and simulation of high temperature resistive superconducting fault current limiters. IEEE Trans. Appl. Supercond. 2004, 14, 839–842. [Google Scholar] [CrossRef]
- de Sousa, W.T.B.; Näckel, O.; Noe, M. Transient simulations of an air-coil SFCL. IEEE Trans. Appl. Supercond. 2014, 24, 5601807. [Google Scholar] [CrossRef]
- Matula, R.A. Electrical resistivity of copper, gold, palladium, and silver. J. Phys. Chem. Ref. Data 1979, 8, 1147–1298. [Google Scholar] [CrossRef] [Green Version]
- Ariyama, T.; Takagi, T.; Nakayama, D.; Sasaki, E.; Takao, T.; Tsukamoto, O.; Matsuoka, T. Quench protection of YBCO coils: Co-winding detection method and limits to hot-spot temperature. IEEE Trans. Appl. Supercond. 2016, 26, 4702205. [Google Scholar] [CrossRef]
- Ariyama, T.; Takagi, T.; Takao, T.; Tsukamoto, O.; Matsuo, R.; Matsuda, N. Study on hot-spot temperature limits for YBCO epoxy-impregnated coil to be safe from damages caused by quenches. IEEE Trans. Appl. Supercond. 2016, 27, 4600504. [Google Scholar] [CrossRef]
- Ishiyama, A.; Arai, M.; Momotari, H.; Wang, X.; Ueda, H.; Saito, T.; Aoki, Y.; Yagi, M.; Machi, T.; Fujiwara, N. Degradation of YBCO coated conductors due to an over-current pulse. IEEE Trans. Appl. Supercond. 2010, 21, 3025–3028. [Google Scholar] [CrossRef]
- Kim, H.R.; Park, C.R.; Yim, S.W.; Yu, S.D.; Hyun, O.B. Recovery characteristics of coated conductors. IEEE Trans. Appl. Supercond. 2010, 20, 2194–2198. [Google Scholar]
- Hellmann, S.; Noe, M. Influence of different surface treatments on the heat flux from solids to liquid nitrogen. IEEE Trans. Appl. Supercond. 2013, 24, 0501605. [Google Scholar] [CrossRef]
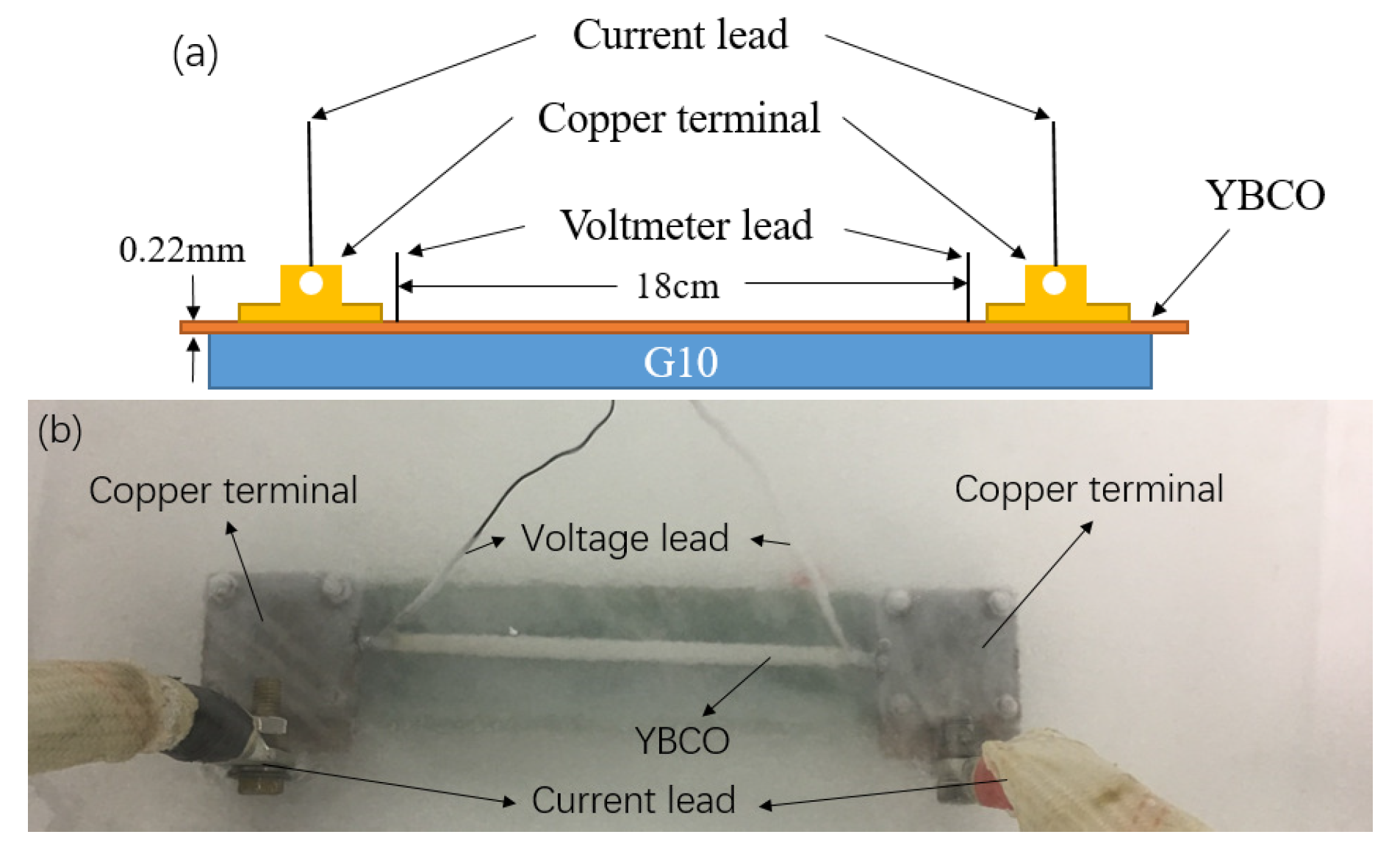
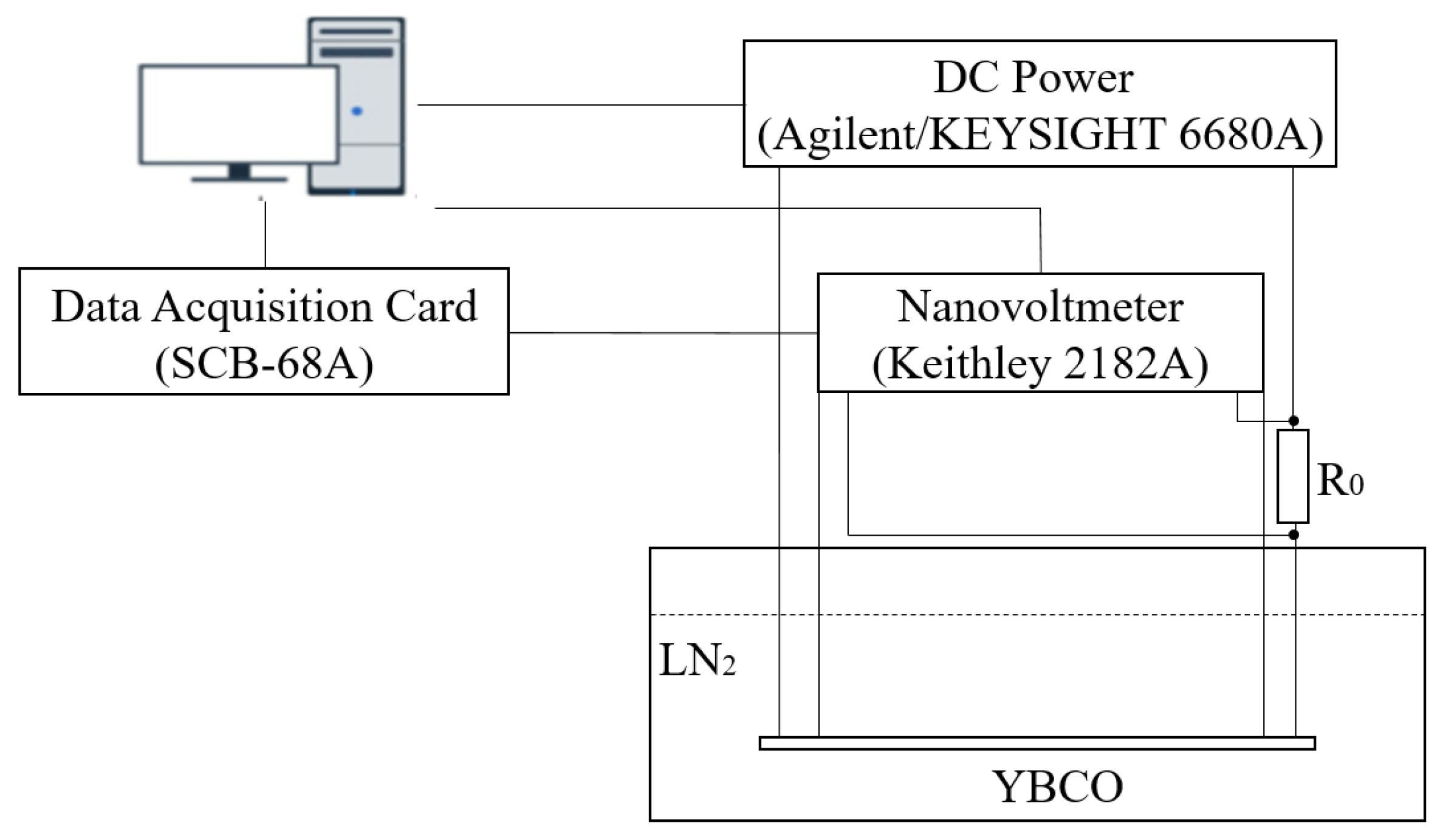



| Properties | Parameters |
|---|---|
| Manufacturer | Shanghai Superconductor |
| Brand type | ST-4.8-L |
| Width/Thickness | 4.8 mm/0.22 mm |
| Critical current (at 77 K, self-field) | 168 A |
| Stablizers | Cu, 75 μm (both sides) |
| Substrate | Hastelloy, 50 μm |
| Pulse Duration (ms) | Impact Current (A) | Impact Energy (J) | Recovery Time (s) |
|---|---|---|---|
| 250 | 370 | 23.47 | 0.476 |
| 480 | 53.60 | 0.657 | |
| 580 | 90.34 | 0.825 | |
| 690 | 115.49 | 0.829 | |
| 500 | 370 | 47.08 | 0.720 |
| 480 | 117.26 | 0.996 | |
| 580 | 193.79 | 1.315 | |
| 690 | 252.29 | 1.616 | |
| 750 | 370 | 69.09 | 0.895 |
| 480 | 208.78 | 1.669 | |
| 580 | 336.69 | 2.803 | |
| 690 | 410.06 | 3.505 | |
| 1000 | 370 | 124.78 | 1.586 |
| 480 | 293.23 | 2.368 | |
| 580 | 437.94 | 3.555 | |
| 690 | 573.32 | 4.179 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, W.; Song, P.; Jiang, H.; Zhu, J.; Zou, S.; Qu, T. Investigations on Quench Recovery Characteristics of High-Temperature Superconducting Coated Conductors for Superconducting Fault Current Limiters. Electronics 2021, 10, 259. https://doi.org/10.3390/electronics10030259
Chen W, Song P, Jiang H, Zhu J, Zou S, Qu T. Investigations on Quench Recovery Characteristics of High-Temperature Superconducting Coated Conductors for Superconducting Fault Current Limiters. Electronics. 2021; 10(3):259. https://doi.org/10.3390/electronics10030259
Chicago/Turabian StyleChen, Wei, Peng Song, Hao Jiang, Jiahui Zhu, Shengnan Zou, and Timing Qu. 2021. "Investigations on Quench Recovery Characteristics of High-Temperature Superconducting Coated Conductors for Superconducting Fault Current Limiters" Electronics 10, no. 3: 259. https://doi.org/10.3390/electronics10030259
APA StyleChen, W., Song, P., Jiang, H., Zhu, J., Zou, S., & Qu, T. (2021). Investigations on Quench Recovery Characteristics of High-Temperature Superconducting Coated Conductors for Superconducting Fault Current Limiters. Electronics, 10(3), 259. https://doi.org/10.3390/electronics10030259







