Abstract
Reputation expresses the beliefs or opinions about someone or something that are held by an individual or by a community. Reputation Management Systems (RMSs) handle representation, computation, and storage of reputation in some quantitative form, suitable for grounding trust relations among parties. Quantifying reputation is important in situations, like online service provision, which involve interaction between parties who do not know (and potentially distrust) each other. The basic idea is to let parties rate each other. When a party is considered for interaction, its ratings can be aggregated in order to derive a score for deciding whether to trust it or not. While much valuable research work has been done on reputation-based trust schemes, the problem of establishing collective trust in the reputation management system itself has never been fully solved. Recently, several researchers have put forward the idea of using Distributed Ledger Technology (DLT) as the foundation for implementing trustworthy RMSs. The purpose of this paper is to identify some critical problems that arise when DLTs are used in order to manage evidence about previous interaction and compute reputations. The paper proposes some practical solutions and describes methods to deploy them on top of standard DLT of the Ethereum family.
1. Introduction
The introduction of digital technologies in all spheres of life has profoundly changed the nature and modality of interactions, increasing the number of one-time transactions between parties that are represented by software agents, possibly acting autonomously according to an interaction protocol. In this regard, the impact of technology on the problem of trust has become particularly relevant. Indeed, trusting some “faceless” computer node that executes mathematical computations, instead of some “known” human counterpart is a new mental paradigm that many users are still not used to. Getting to trust a digital entity of course requires some assumptions regarding the context where the trust relation is established. First of all, both sides of the trust relations are represented via user agents that are assumed to be trusted (this assumption may be hard to enforce in some practical situations; nevertheless, making it allows for focusing the discussion). Secondly, trustworthy procedures (e.g., error-free authentication protocols) are in place to confirm the authenticity of the interaction participants. Thirdly, provisions have been made for ensuring integrity (and, if needed, confidentiality) of the information transfer between the interaction participants. Once we are satisfied that these three assumptions about the interaction context hold, we still have a problem of providing a criterion for the interlocutors in order to decide whether (and possibly how much) to trust each other.
Reputation is a classic solution to this problem: the trust relation is established or refused based on available evidence of the parties’ past behavior. In the last twenty years, considerable research has been made toward Reputation Management Systems (RMSs), which is capable of collecting such evidence and computing some reputation score, to be taken into account to decide whether a certain party should be trusted [,]. Reputation management systems are also called collaborative sanctioning systems to reflect their collaborative nature, and are related to collaborative filtering systems. While many interesting schemes have been proposed, difficulties that are related to behavioral evidence collection and storage have never been fully solved. Indeed, behavioral evidence itself needs to be trustworthy, and avoiding injection and spreading of fake evidence proved to be difficult in the context of the original Internet. This field, as well as many others, has been revitalized with the advent of Blockchain. Blockchain is a Distributed Ledger (DL) whose spectacular success as an infrastructure for crypto-currency transactions has triggered hopes in its suitability as an infrastructure for creating, storing, and managing trustworthy records of behavior, offering reliability, confidentiality, transparency, and immutability. A natural side effect of the immutability of behavioral records is that it provides an incentive for good behavior. Today, besides the original Blockchain that was used for supporting the Bitcoin crypto-currency, many different Distributed Ledger Technology (DLT) schemes are available. However, DLTs being a relatively new technology, there is a need for investigating its capability to support behavioral evidence collection []. DLT is not a modular technology that can just fit in any scenario. Accordingly, one of the most important and commonly disregarded problems is determining whether (and through which features) DLT would be a feasible solution to satisfy RMSs requirements []. While there is a lot of research on incorporating DLT into reputation systems in their different domains [,,,], there is limited discussion regarding the technical difficulties and challenges of implementing a functional system in general. In this paper, we discuss some recurrent problems that arise when implementing RMSs via DLT, and then provide the essential techniques to avoid such pitfalls. The contribution of this paper is threefold:
- Survey current research difficulties in DLT-based RMSs and its enabling technologies. Highlighting some of the common pitfalls in designing and implementing a reputation system that is based on DLT.
- Provide insight into the challenges that are faced with recommendations and solutions to avoid the respective pitfalls. We discuss in detail the nature of the difficulties of merging a DLT with a reputation system.
- Analyze the effect of utilizing a fraction of service feedbacks to provide an accurate reputation with minimal feedbacks. We produce simulations that show that truncating the available feedbacks to a certain level will still maintain the reputation level. This is possible by taking the temporal behavior change into account.
The paper is organized, as follows: Section 2 discusses the On-chain and Off-chain interactions of a blockchain-based RMS. Section 3 presents the nature of external interactions in smart contracts, while Section 4 deals with the related issue of deterministic results. Section 5 and Section 6 are concerned with time management issues, and reputation updates alternatives, respectively. Section 7 presents approaches for reducing the system overhead. Finally, Section 8 gives the concluding remarks.
2. On-Chain and Off-Chain Tradeoffs
A key step when designing a system architecture based on DLT is to define the exact functionality of the DLT in the system, deciding what is processed and stored by it. A common misconception is that DLT can take care of all the storage and computation requirements. This is far from the truth []. As with any system, non-functional requirements need to be taken into account and optimized when designing the architecture. Depending on the architecture of the system utilizing the DLT, some data will be “on-chain”, residing on the ledger, while other will be “off-chain”, i.e., managed without the involvement of the DL []. Figure 1 shows a general view of a DLT, showing three main components where storage and computation systems can be included or excluded to serve the goal of the application relying on the DLT. For the sake of clarity, we distinguish three conceptual functions of the DLT: the Consensus Computation logic, the Data Management logic, and the Integrity and Reliability logic, which are classically ensured via chain-hashing.
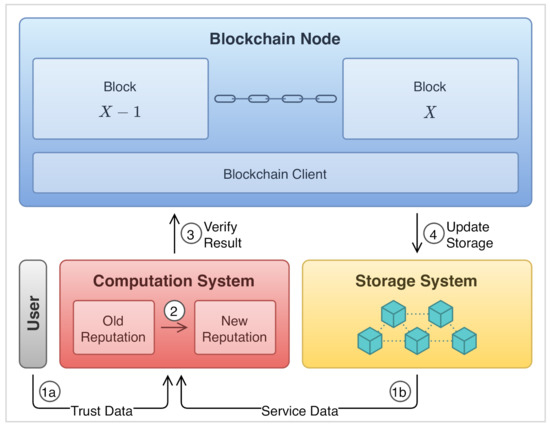
Figure 1.
On-chain and Off-chain computation and storage model.
2.1. Consensus Computation
The blockchain nodes execute the specified protocol in order to ensure that transactions to be carried out on the DL have certain desired properties. The most popular consensus algorithm is Proof-of-Work (PoW), which is secure by requiring a solution to relatively difficult puzzle, but in return it consumes a lot of computational power []. However, as the platform evolves other consensus algorithms are proving to be very hard to pass on with their evolving security and efficiency. However, commercial DLT’s, in general, have yet to prove the ability to achieve high throughput and scalability []. As more users participate, the network grows larger in size, with more data for the network to process and, consequentially, the transaction queue grows larger, which, in turn, limits the ability of new transactions to be processed. The blocks are generated within a certain time and then propagated to the network, a new block cannot be propagated until every node already downloaded and appended the latest block to the blockchain. There is an expected block size that affects the block generation time, in addition to the mining time. In Bitcoin, the block time is known to be around 10 minutes, while the block size is approximately 1 MB []. A simple change of these variables cannot solve the issue, as increasing the block size would increase the time of download for nodes, which also increases the block time and, since we cannot start with a new block until the first is mined, the network has to wait for all nodes to receive and download the block. Thus, the block time has to be greater than the propagation time, so even adjusting the time itself would be infeasible. A tradeoff between off-chain and on-chain transactions should be achieved in order to overcome such limitations, and based on the requirements of time and space.
2.2. Data Management
If everything is on-chain, then we are sure of the integrity of the data and transparency of viewing it, but, on the other hand, all of these data will be stored on the DL and then processed by it. In this way, the DL will have a lot of traffic to deal with, which hinders its performance []. The generated traffic means there are more transactions to save, and more validation/authentication operations to execute, which requires monitoring of storage and computation. In terms of storage, a DL is not an ideal storage system due to its decentralized nature, in a typical case it would keep growing and scaling in size, but the participants have to save all of the DL to actively participate, which is a leisure that not everybody may be able to afford. In worse cases, the DL itself could be bloated, where there is redundancy, unnecessary transactions, and irrelevant data being saved that are taking up resources of participants. Thus, it is crucial to filter and control data being stored on the DL, and this is something that is commonly disregarded. To put things into perspective, the bitcoin network currently has a size of approximately 290 GB [], which is a substantial storage space that might prevent some nodes from joining the network due to their limited resources.
2.3. Integrity and Reliability
Integrity and reliability are other concerns that affect the design choices of the system. Integrity is inherently maintained through the hash-chain mechanism of the blockchain. Each block of transactions has a hash that is used in generating the hash of the header in the next block. Changing a single bit in one of the transactions in a block will invalidate the current block and every block that follows it [].
Reliability is also a result of this concept, where users trust and rely on the data, due to its immutability. Furthermore, the redundancy of the network through the distribution of data through the nodes means that there is no single point of failure, increasing availability, and reliability.
While integrity and reliability are inherent features of the blockchain, they are not provided by off-chain environments. In order to establish such security measurements off-chain, mechanisms of integrity-checks, authentication schemes, and obscurity methods are needed.
While the blockchain efficiently offers such a model, it is still the case that some transactions are more appropriate to be executed as off-chain transactions. However, a different approach for enforcing trust is needed when data leave the DL system and venture off-chain.
2.4. The Case of Reputation Systems
While blockchain offers a lot of advantageous features, such features may not be needed by all of the transactions, in which case they can instead be executed off-chain. Off-chain transactions do not expend network costs (blockchain costs), and the transactions are not impacted by the blockchain transaction queue or consensus delays.
In reputation systems, trust data will be the main form of data being exchanged. In such systems, there would be a mechanism to keep track of participants’ reputation and credibility. There are also mechanisms for authentication and authorization. Some of the transactions that are involved in these mechanisms do not necessarily have to be processed by the blockchain. The storage of important metadata that should be visible to everyone, such as the reputation has to be on the blockchain, but the service data can be stored somewhere else. Assuming that the solutions utilize smart contracts, the contracts would have to process the service data and its metadata. These data will have to be stored in the smart contract storage, which is on the blockchain, which is not ideal. Assuming that the data are large and, for a huge number of transactions, the blockchain size would get out of hand. Accordingly, in this case, it would make sense to store such data off-chain, but have it governed by the smart contracts to still ensure the decentralization of governance. This can apply to other information that needs to be stored, such as the users of the system, the services, and their associated metadata.
Another aspect of concern is computation, deciding on whether the reputation should be computed on-chain while using smart contracts or delegated to some other entity. Where, in the latter case, trust has to be established with the entity handling such computation, so as to not jeopardize the maintained trust of the system. If the computation of reputation is done on the smart-contracts themselves, then the chain resources could be occupied with frequent computation, which, in turn, also creates traffic on the network. Doing so off-chain, the transparency and immutability features of the blockchain are untapped, losing the main benefits of the technology. Thus, it is a requirement to determine when is the right time to compute, how often, and where. Introducing off-chain storage systems to aid the blockchain is also not straightforward, and concerns of access, security, and performance need to be taken into account [].
Off-chain transactions have to be monitored and managed with mechanisms that maintain authenticity, integrity, and anonymity. This would require the authentication of data from the point it is out of the blockchain to the point it comes back to it. Additionally, at some point the status of an off-chain transaction needs to be logged on the blockchain to consistently maintain the built network trust. This could be done while using unique tokens, hash comparison, message signatures, along with Zero-Knowledge proofs, such as ZK-SNARKs (Zero-Knowledge Succinct Non-Interactive Argument of Knowledge) or bulletproofs [,]. Such methods can also be added on top of the blockchain, an example of private transactions implementation that leverages ZK-SNARKs is Nightfall, a project by Ernst & Young to create a hybrid public-private blockchain []. Smart contracts offer a lot of features and flexibility to execute decentralized logic, which complements the governance and supervision of off-chain actions, feasibly, with the right mechanisms. However, smart contracts also still have their limitations, such as the extent of their external interaction, which will be discussed in the next section.
3. External Interaction Issues
The initial blockchain presented in 2009 has changed slightly after a decade in what it has to offer, and smart contracts have been one of those remarkable changes. Smart contracts can enforce contractual agreement logic digitally without any third party involvement [], or, as stated by Nick Szabo in 1994, it is “a computerized transaction protocol that executes the terms of a contract” []. Smart contracts can be seen as a gateway of interaction with the blockchain, where certain logic is offered through functions to users; this comes in the form of code and data in the smart contract. Thus, a transaction takes place on the blockchain with the stated rules in the smart contract, the result always has to be the same, regardless of who executes the logic when given the same input, yielding deterministic results that have the consensus of the network participants.
Smart contracts pave the way for accomplishing more than just transaction recording. Using smart contracts, it is possible to implement the logic for specific cases that could involve storing information, performing calculations, sharing states, editing states, and providing access conditions. However, smart contracts have their limitations, as mentioned in the previous section. They are unable to query or start an interaction with the outside world. Smart contracts are limited to the data within their network that mainly come from the users. This acts as a crucial bottleneck, as some systems would need outside information, especially when its architecture relies on off-chain transactions.
3.1. Enabling External Interaction
This limitation has been recognized and solutions were proposed for it. Smart contracts can communicate through “oracles”, which are third-party services that provide the needed external information to the smart contract, they can be seen as the connection link between on-chain and off-chain counterparts. Relying on oracles, it is possible to have them fetch, query, and compute data.
Oracles can be used in different settings in order to provide the most efficient method of external interaction, design patterns of oracles are mentioned by Abdeljalil Beniiche as: (1) request-response, (2) publish-subscribe, and (3) immediate-read []. The most relevant of the three models would be the request-response approach, which is in line with a client requesting the reputation of a service provider. The publish–subscribe might be effective in certain cases, where the network is compact and needs to always be up to date. However, in a model that uses smart contracts for this task, polling would incur significant charges. While other alternatives will require significant user interaction rather than oracle interaction, unlike polling. The third possible model, immediate-read, is applicable in models with instantaneous data requirements, which would require the oracle to have the data ready beforehand or have direct access to. Such oracles are usually deployed by an entity in order to handle requests on its behalf for specific data, but would not be fit to handle a diverse or large amount of requests.
Oracles would serve as a solution for the off-chain trust data that need to be processed and somehow recorded on the blockchain, oracles will be able to fetch such data. This would also be a consideration, depending on the implemented reputation system, where the oracle/s would be delegated the computation of the reputation in order to remove some of the load of the blockchain. However, as mentioned, this would affect the trust in the system, which is why there needs to be a mechanism that establishes trust of the oracle results. There are several approaches where decentralized oracles can provide results and a certain selection algorithm would be used in order to select the result, as it is fit for the application. The results can also have a signed message, while using the many existing algorithms, which ensures that the data have not been tampered with.
3.2. Establishing Trust
In reputation systems, trust is the essential component to be preserved, and to ensure that, we must authenticate service providers. A centralized authenticating entity would be counterproductive to the goal of the system. With the use of oracles and smart contracts, the process of authentication can both be managed and executed in a decentralized manner. The smart contract would govern the oracle interactions, while the oracles themselves will execute the authentication method. Figure 2 shows a simple example that uses a unique identifier (UID) to authenticate the service provider, which is an Internet of Things (IoT) device in this case. Instead of having a central entity check that the UID is valid, decentralized oracles will compare the given ID with the valid ID. Additionally, then, each oracle submits a vote that is aggregated by the smart contract. The smart contract processes the result and determines the authenticity of the device based on the aggregate. The oracles can be managed by an independent smart contract that is only tasked with handling the oracles. This oracle management smart contract handles the authentication and only notifies the main contract of the result once the authentication is done.

Figure 2.
Authentication implementation example.
Oraclize or Provable is one of the most popular platforms that offer oracle services and it is adopted by the main blockchain technologies. It utilizes authenticity proof to verify data []. Another such service is chainLink, which relies on a highly reliable decentralized oracle network in order to provide the services []. Whether it is a traditional approach that is similar to authenticity proofs or one that utilizes consensus of decentralized dependable oracles, the goal is to maintain the relative trust of the external entities. It is possible to rely on existing oracle services or to create a custom oracle management smart contract for a consortium, depending on the use case. An important point to consider when designing such systems is the decentralized nature of the network that should be preserved for a trustless system. This is possible beyond the blockchain, where the results are aggregated from a network of oracles on a smart contract. Storage can further complement the scheme with decentralized/distributed storage systems. Two of the most popular said storage networks are the Ethereum supported decentralized storage Swarm and the Inter-Planetary File System (IPFS) [,]. Connecting all of the mentioned schemes and approaches, a general example of a system with such a model can be seen in Figure 3. The figure shows an overview of the architecture without delving into the underlying authentication methods of data or the management of oracle interactions.
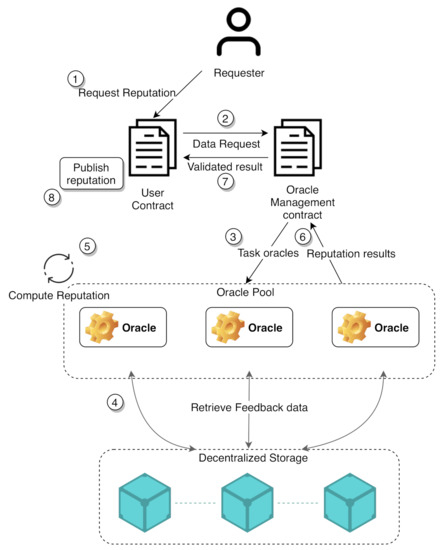
Figure 3.
Oracle utilization model.
It is important to understand why a smart contract has such restrictions to be able to resolve them in a proper manner. However, resolving the issue should not conflict with the workings of the blockchain. It is the case that the nature of the blockchain does not allow for such operations, as will be discussed in the next section.
4. The Requirement of Deterministic Results
Blockchain is updated only after there is a consensus across the network. As such, if anything hinders such consensus, it would be interfering with the functionality of the technology. In a large permissionless blockchain, conflicts regarding the version or the blocks occur; they are sometimes referred to as forks [].
This occurs when two competing miners propagate the blocks; what happens is that one node receives a block that is different than the other. The fork occurs when two miners are successful in solving two different puzzles simultaneously, and the new potential blocks are propagated to the network nodes. The nodes will receive different blocks, thus creating two concurrent chains in the network.
4.1. The Rationale of Determinism
The occurrence of forks in the chain can be seen as non-determinism, and to force determinism the chain that will be adopted in the blockchain is the longest chain. Accordingly, eventually only one chain will survive while the forked chains are dropped, and there is no means to determine which chain continues before that happens. That is why usually in blockchains, such as bitcoin, the network waits for the block to be “a couple of blocks deep” before accepting it as the final result. This is done to avoid having that block being dropped and losing the changes if there was a competing longest chain []. This approach allows the blockchain to continue without hindering its functionality, but its inefficient aspect is in dropping the blocks that have already been mined back to the transaction pool. The deterministic aspect in the network is enforced by the consensus, which converges with certainty to a single result. This result is eligible to be used as soon as it is mined, because it is deterministic. This is the case for smart contracts, the results of smart contracts need to be deterministic, so that their execution yields results that are consistent across all nodes. This is important, since the results do not pass unless they have the consensus of the executing nodes. The yielded results change ledger states, which could be relied on for further operations, so it is critical that they are final. Hence, smart contracts cannot rely on non-deterministic results, and they must strictly produce the same output given the same input []. This leads to the need for oracles to fetch off-chain data, which also need to be deterministic. To achieve that, decentralized oracles need to have a consensus over the result, before submitting it to the smart contract. On the other hand, a method to authenticate the result from a single oracle can be used, but it might not achieve the same level of trust as the former approach. The generation of a random number is a direct example that portrays the limits of determinism. Changing variables, such as time, block number, or a nonce, can be used to generate a number, but the result is not truly random. Because all of the variables and states are visible and, thus, the algorithm can be figured out. Hence, to produce a truly random result, the random generator produces randomness off-chain and inserts the result into the smart contract, so that it is unpredictable. A convenient out of the box solution is offered by Chainlink, with their Chainlink VRF service that generates random numbers for smart contracts [].
4.2. The Impact on Smart Contract Operations
The mentioned issue extends to another problem, since smart contracts cannot rely on non-deterministic data, it has to be ensured that all data passing through smart contracts are deterministic. Floating points are an arithmetic representation proposed by the IEEE 754 standard and it is mainly to be used to represent huge or minuscule numbers. Floating point is one of the most common formats used in computers for representation and computation, but computers can only represent a finite number of digits. Accordingly, it is not feasible to precisely represent repeating binary representation values while using floating point representation, so, generally, floating point can be considered as unstable and not fully deterministic []. This would lead to the issue of not being able to do floating point operations on smart contracts due to their non-deterministic nature. Figure 4 shows an example of an arithmetic operation where the given result is not as expected. The result is limited to being an integer, and even any inner intermediary operation result is converted to an integer. For example, assume that we want to compute the value of the following term . The term should result in (where the horizontal line is a vinculum indicating a repeating decimal value); however, the result here is 1. Multiplying 5 with the original intermediary result should yield , which will be displayed as 8, but the result here is 5, since the multiplication was essentially instead of .
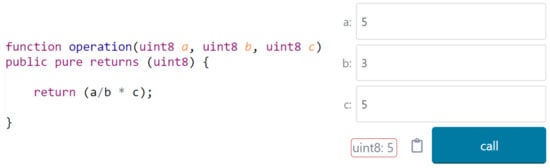
Figure 4.
Arithmetic operation result in solidity.
This greatly limits the computational capabilities of smart contracts, as it would be difficult to implement certain functions, such as logarithmic and exponential functions. Even though it could be done, it would be costly and most likely be an approximation, and, as such, this is a limitation that needs to be worked around when dealing with smart contracts. Vitalik, the founder of Ethereum, has previously suggested in a Reddit forum to use Taylor series to approximate a logarithmic function. Another aspect to take into consideration is the overflow and underflow of integers. However, it will not be discussed moving on, as it is a persistent issue with programming languages and solutions exist, even for a smart contract, such as the library SafeMath [].
Information is lost when resorting to fractions, since what follows the decimal point is not being kept track of, as previously discussed. A range expansion could be a remedy for such an issue, such that minimal information is lost. Increasing the range of the dividend will result in a larger number, which would include a portion of the fractional part (after the decimal point) as a whole number. A simple linear mapping would be the most convenient to follow, as shown in Equation (1) :
where represents the input range and represents the output range. The ranges used should be chosen based on the desired precision, with higher ranges giving you more values of the fractional part. Furthermore, it is generally best to postpone any division operations until the end of the expression in order to avoid any intermediary losses. Now, assuming that the system is computing a reputation, the result is adjusted to a user-friendly range on the user’s client, which would usually be the decentralized application (Dapp), an application that is used to interact with the blockchain network. Going back to the example, the Dapp will receive the data 8333, but adjust it to its original range, displaying it as or rounding it to , since Dapps do not have the same restrictions as smart contracts.
Other mappings could be more apt for computation of reputation, such as exponential growth and decay, or logarithmic functions, but, in the context of smart contract computation, a linear function would be most suitable. A smoother solution would be already having the reputation equation parameters, such as the feedback of the user, in a large range, and the final result would either be interpreted by the users or adjusted on the Dapp, as such there would be no need for a mapping or auxiliary calculations. Again, this complexity could be seen as a representation issue, but it extends to a more critical issue by the fact that it affects intermediary operations, as such it should be tackled carefully. Several libraries implement different methods to force the representation of floating-point or fixed-point, but it introduces complexity in computation and needs awareness of the gas to be consumed, which would vary based on the operations. Gas is a measurement unit in Ethereum that quantifies the work done by the network [], while, in other blockchain platforms, different units are used. Third party libraries, such as ABDK Math [] and Bankex [], offer floating-point contracts for arithmetic operations, while ABDK, also along with Exponential [] and Fixidity [], offer fixed-point libraries, which either utilize the integer range or deal with bytes rather than numbers to represent a fractional number. While the mentioned libraries offer workarounds, they are expanding on the same concept of using a larger range to represent the fractional part and, as such, the mentioned approach of scaling the numbers would be the simple straightforward approach. All of the solutions are workarounds that will not overcome the issue of native support for such formats, fixed-point representation is something that Ethereum has been working on for a while, but as of this date is still not yet supported either [].
5. Time Management in the Context of Smart Contracts
Time is almost always a critical factor in systems, even if not used directly in development. The introduction of time into a system brings up a new dimension of restriction, but also a dimension of dynamicity. This is not different in blockchain, while using time for certain operations is crucial for certain applications. However, due to the nature of time accuracy being critical, and doing that through code needs meticulous implementation. Smart contracts allow for such possibilities, time needs to be adapted to the smart contract environment. To do so, the common conventional representation will raise difficulties; on the other hand, numbers are a more natural form for programming languages to store and deal with. For this reason, Unix epoch time has been designed for use in computer systems, and it represents the time elapsed since 1 January 1970, in a number format, as specified in the Unix programmers manual []. Figure 5 represents the Unix epoch time format with its corresponding time and date. Accordingly, this not only allows for time to be used in smart contracts, but the contracts provide native support for this format to keep track of block timestamps and other built-in functions that are accessible by the developer. For example, in Ethereum, a simple “now” function returns the current time, and units of seconds, minutes, hours, days, weeks, months, years are supported.

Figure 5.
Unix Epoch Time format and corresponding time and date.
In RMSs, feedback contains valuable information that needs to be taken into account, one of which is time. It is crucial to take into account the most recent and important interactions due to the possibility of the changing behavior of an entity over time. Change is a natural process and an entity with bad behavior could have a good one after a while and vice versa. Accordingly, it would make sense that recent feedbacks would hold more weight than older feedbacks. Thus, we need to use “Aging” or time-decay in computing the reputation of a service provider, and this is where the use of time comes in. Time would be used as a weight to compute the feedbacks received and come up with a more representative trust value. Furthermore, using aging would combat the sudden behavior change as the recent transactions contribute the most, thus an entity will be deterred from misbehavior. On the other hand, the entity would be motivated to offer better service, since old misbehavior or bad transactions can be forgotten with recent good transactions. The aging mechanism can be tuned to be responsive to sudden behavior changes, by adjusting the weight that is given to new transactions appropriately.
Temporal Adaptability in Reputation
A study conducted by [] shows how it is unreasonable that old transactions and new transactions have equal weights by illustrating its effects on the services and the buyer decisions. Several approaches implementing time-decay have been pursued to establish the required feature. A linear approach is simpler, but, in reputation systems, non-linear computation models are more prevalent. The authors in [] proposed a linear discount function that is simply controlled by a decay rate and divided by the months that passed, disregarding the first month. Another approach that some solutions referred to as aging is based on order, taking the most recent transactions, regardless of the time window between them [,,]. Several approaches use a non-linear function, commonly an aging factor is used in the form of an inclusion/fading variable that is a non-linear component in the works of [,,]. The general function can be seen in Equation (2), where R is the reputation, is the feedback, and is the inclusion/fading factor with exponent t being the time difference between the last two ratings. A variation can be seen in the work [], which uses discrete time periods, and a “longevity” variable that is similar to the aging factors mentioned. The function is a multiplication of the aging factor and the old recent feedbacks, summed with the new ratings. Another non-linear function is proposed in collaborative filtering systems, which predicts and adjusts ratings based on the nearest neighbours []. It utilizes Euler’s number as a factor with an appropriate weight being the exponent.
Implicit aging mechanisms that require computing statistics are impractical, since smart contracts are not able to query the blockchain-like querying a normal database system. For example, Wikipedia’s item reliability is determined by the frequency of writes to a certain item, and the modification count is correlated to the trustworthiness of the item. Trying to fetch from the blockchain meta-information, such as how many times something was modified would be inefficient, as the recomputation of the transactions needs to be done in order to find the final state. Explicit aging is a more efficient approach, especially since the smart contracts support the use of Unix Epoch time.
The mentioned approaches would not be ideal in an environment where determinism is required and complex mathematical models are costly. Thus, functions of observable functions are not favored. The weights of feedbacks can be adjusted according to the order they came in or based on the timestamp of their submission. The difference between two transactions is variable to a large degree, so, if two transactions had a difference of six months between them, it would not be accurate to consider those last two transactions as “recent”. It would be much more accurate to rely on time to precisely give weights to the feedbacks, but dealing with time is more complex to design and implement. One of the difficulties that could be faced is the incorporation of time itself as a weight. The time could be taken relative to a certain fixed point or it could be the difference between timestamps.
Using the timestamps themselves as pure weights would also give the same result, but the timestamps need to be saved and the equation would need to be computed every time that a feedback arrives. Such an equation might be seen as a more direct representation of the time weights, but ultimately both approaches achieve the same goal, an example of such a function could be seen in Equation (3). This represents a tailored time weighted mean, where is the time weight and is the corresponding feedback. It would depend on the use case to determine which function is more fit, as the first is simpler, while the second function, as shown in Equation (4), is efficient.
Using the difference would relieve the system from having to save all of the corresponding timestamps, as the current and previous timestamps are what is needed. However, cases where the difference is zero or the difference is always constant need to be taken into consideration, which is why using a recursive decaying equation might prove to be a more solid approach. A representation of such an equation can be seen in Equation (4).
It is important to note that, even though we are focusing on time, the weight itself can be adjusted to suit the use case, things, such as the importance and type of feedback, can be factored into the weight along with time. Furthermore, the weight can be simply held constant and, as such, the equation would take into account order rather than raw time. Accordingly, w is a dynamic variable that could represent an aggregate weight, while f represents the individual feedbacks.
When comparing Equation (4) to the discussed approaches in literature and the provided analysis, we summarize the benefit of using such a mechanism in the following three points:
- The equation is recursive and does not require the aggregation of past feedbacks to generate the new reputation, but it is computed only while using the currently provided feedback.
- Time is explicitly incorporated by utilizing the smart contract supported Unix Epoch clock.
- A simple linear equation is used as opposed to a complex non-linear equation, in order to accommodate for the smart contract computation capabilities in a practical manner.
While Equation (4) shows the general form where the range would be from 0 to 1, the weight can be subtracted from the maximum of the scaled range rather than 1. As mentioned, using this equation previous feedbacks are not needed and, with every new feedback, the previous accumulative reputation is decreased by the multiplication of . Equation (3), on the other hand, would use the general weight average form where the summation of x in the denominator would be the sum of all the weights used.
Note that, in the case where all the weight are equal, i.e., , Equation (4) can be simplified and expended to:
Equation (5) clarifies that the old feedbacks become less significant with every new feedback, due to being multiplied by a decaying factor.
6. The Impact on Reputation Update
With respect to the reputation updates, two approaches can be considered: proactive and reactive.
6.1. Proactive Updates
Having the system “always updated” is convenient and reassuring for the user. When a feedback is submitted, the reputation is updated across the system. Even though the transaction will be executed instantly, the process of displaying the result will actually take time as it has to be mined and propagated through the network. What is referred to here is the proactive execution of the whole process, but not the instant publishing of the result on the blockchain. This approach is appealing, as it does not necessarily require storing heaps of data, since it is processed and used in order to update the final result proactively without saving the intermediary data on the smart contract. This would surely need the appropriate computation model, which only requires data that are currently present to avoid storing the data. The previous feedbacks be updated without accessing them, the flow of such a process can be seen in Figure 6a. It is possible to use a decaying function, as mentioned previously, which is recursive with each feedback. While using this approach, users can check the reputation at any point in time and be assured that it is up to date, it would also relieve the system from having the load of processing a group of feedbacks concurrently. If the reputation is computed at a certain point, while a lot of feedbacks have accumulated, the chain has to process all of the available feedbacks to compute the reputation. This would concentrate the load at a certain point of time, rather than a constant or regular flow of transactions, which might congest the system and possibly cause delays.
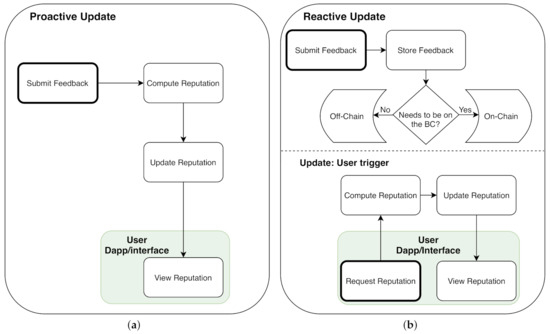
Figure 6.
Proactive and Reactive Updates Overview.
This approach of proactive computation would be appropriate in a fast-paced environment, where all of the users are constantly active and transacting. However, depending on the type of reputation system, some users might be active, while others are not. Extra computation would be done and a larger pool of transactions would be created, where users are not interested in or in need of the computed results. This is even magnified when other operations are done, such as updating credibility, updating oracle reputation, and storing off-chain data. In this case, a reactive approach would be more appropriate for avoiding continuous fruitless computation. The proactive approach would also not be a viable option if a huge database has to be maintained for the computations.
6.2. Reactive Updates
In the case that the system follows the approach of reactive updates, the system reacts to triggers and events. The update could be executed based on a user request, requesting the reputation which would trigger its computation and update, the user can then simply view the reputation. The trigger event could also be temporally triggered, where the computation starts at a certain specified time or after certain time intervals. Furthermore, it can be triggered by logical events, such as reaching a set number of new feedbacks, by keeping a counter of the feedbacks, and starting the update when the statement is fulfilled. Using such approaches where the user is not in control eliminates reliance on the user, which is an uncontrolled factor of the system. The different trigger cases would make sense, depending on the application, but even better is that there could be more than one trigger event, thus having a more robust and extensive model. This approach would postpone the computation to a certain point, which might take some time, but would surely be something of need, as the user requested it, as shown in Figure 6b. This would avoid unnecessary computation and this would also remove the constant small delay that is posed by the proactive update of the system. However, in this case, whatever data are going to be used in computation at that point need to be stored, so that they can be used in computation when requested. Accordingly, the storage needs to be considered and taken care of in a way where it does not drastically affect the computational functionalities of the system. Hence, depending on the nature of the system, it is important to assess whether the system needs to always be up to date or updated when needed.
6.3. Delay
Furthermore, the latency of the network is an important aspect of the update flow to carefully consider in the design, since the time to mine a block varies, as it could take a minute or ten minutes based on the network technology. Even in the described proactive case, the transactions have to wait until they are chosen from the transaction pool and assembled in a block, and then a consensus on the validity of the block at which point the transaction appears on the blockchain. If a user’s transaction is aggregated in the first block to be mined, then it will only be the block time delay; however, the user might wait for a couple of blocks for the transaction to be mined, thus waiting the time of several blocks. Adding up to this is the propagation time that is also affected by the network size and block size. Hence, it is important to realize and assess the time frame that is allowed for the data to be published. The main delay comes from the consensus algorithm, where consensus is usually done by PoW, which consumes a lot of resources and time. However, a lot of other consensus algorithms exist, but not as commonly used, where they also provide fast consensus, but might offer less security, such as Proof-of-Stake (PoS) and Byzantine Fault Tolerance (BFT) []. However, there have been advancements in consensus algorithms that offer the same security for much less time and energy consumption, such as Ouroboros, the system that is built on PoS []. However, consensus still does take time and the delay window is something to be taken into account in the framework.
7. Reducing Smart Contract Storage Requirements
The paper has grappled with the issues of a blockchain-based reputation system and discussed methods of going around them. Even though off-chain storage is helping off-load some of the storage requirements on the blockchain, and oracles off-loading some of the computation requirements. The blockchain, which is managed by the smart contracts, still execute a considerable amount of the operations. In order to efficiently manage a system, it is of great importance to reduce the consumption of resources and time when possible without compromising the functionality of the system. A promising approach would be to limit the amount of data that need to be stored in a smart contract. It is counter-intuitive to base the reputation of a service provider while taking all of the transactions they did in the past into account []. Giving more weight to newer feedbacks would give an implication of their recent behavior, while also taking their history into account, but with less weight. As such, having the most recent feedbacks, we can get the real reputation of a provider without keeping track of every single review that they have received. This will greatly decrease the computation and storage that the smart contract bears, without losing on the accuracy of reputation. Being able to get a representative trust value with minimal computation and storage will also allow for a scalable solution.
7.1. Simulation
The goal of the experiment is to see the effects of dropping less relevant reviews and focusing on the more significant ones for a certain service, based on time. We would like to highlight that this test pertains to the mentioned reactive reputation update, as the feedbacks need to be stored until computation time. In order to carry out our test, we have used a publicly available dataset of Amazon product reviews (Available online: https://jmcauley.ucsd.edu/data/amazon/), which has a substantial amount of ratings with their metadata []. The Amazon products serve as our “services” that the users rate. Specifically, we use the category of instant videos with total ratings above 10,000. The typical amazon rating system is in the range of , which we normalized to the range of for our computation model. Taking the resource consumption on a public blockchain into account, the computational cost and storage requirements of the mechanism have been summarized in Table 1. If a reputation state variable is not being updated, then this function would cost no gas, e.g., a user reading an updated reputation without changing a state in the blockchain. The experiment was performed on Remix, an Ethereum IDE, with the current average gas price of 39 Gwei (as of 14 December 2020). The mechanism was implemented according to Equation (4), which would take the feedback as an input parameter and update the existing reputation. For our experiments, we chose three different products with 10,000 ratings each.

Table 1.
Transaction Resource Consumption.
We considered in our experiments the following three test scenarios :
- Scenario 1: the goal of this scenario is to assess the impact of the number of considered feedbacks on the reputation value. In this scenario, we consider the feedbacks regarding a specific product. The number of total feedbacks is set to the following values . From the 10,000 feedbacks, the 100 and 1000 feedbacks are chosen as the oldest 100 and 1000 feedbacks, respectively. These may represent the evolution of the feedbacks that are received over time. The reputation values are computed while using Equation (4). Equation (6) is used in order to compute the percentage error incurred if we only consider a specific number of recent feedbacks (i.e., truncated reputation) out of the total number of feedbacks (i.e., original reputation). The weights of Equation (4) were held constant at .
- Scenario 2: the goal of this scenario is to assess the impact of the weights on the reputation value. The number of considered feedbacks is set to 10,000. The considered weight values are .
- Scenario 3: the goal of this scenario is to confirm that the behavior of the error with respect to the number of considered feedbacks is the same for any product. Three instant videos were randomly selected from the Amazon dataset. The total number of feedbacks was set to 10,000 as in the previous scenario, and the weight was similar to Scenario 1, being at .
The percentage error is computed, as follows
where is the truncated reputation value and is the original reputation value.
7.2. Analysis
In the following figures, the X-Axis represents the number of feedbacks used in order to compute the reputation. These feedbacks are the most recent ones, as they contribute the most to the reputation with their high weights. The Y-Axis represents the percentage error of the original reputation, which would have been the result of all the feedbacks, and the truncated reputation, which includes a set of the recent feedbacks.
Figure 7 depitcts the results obtained in Scenario 1. The results show that the error percentage converges to zero when a certain number of feedbacks are retained, regardless of the total number of feedbacks. The fluctuation only occurs at the start, since the latest feedbacks differ in value between each set. The results conform with Equation (4), which is essentially multiplying all of the feedbacks with their weight in every iteration. Thus, the old feedbacks are adjusted accordingly to contribute less and less as time goes by. As such, at one point, these old reputations contribution is almost negligible, regardless of their number. The simplified Equation (5) shows how the previous reputation decays exactly.
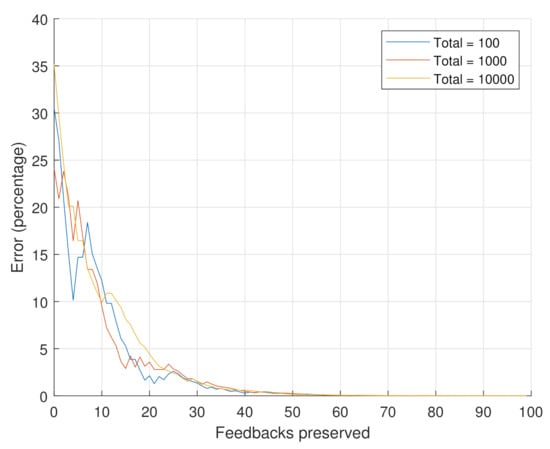
Figure 7.
Error percentage for varying total number of feedbacks.
Figure 8 shows the obtained results of Scenario 2. We can observe that the controlling variable of the number of feedbacks needed to preserve the accuracy of the reputation also depends on the weights.
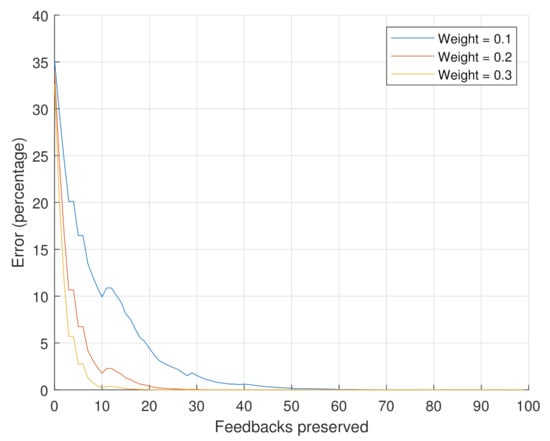
Figure 8.
Error percentage for varying weights.
Because we are using the same exact feedbacks, the three curves show a similar trend, in that they decrease while the number of preserved feedbacks increases. However, the decrease is sharper with larger weights. This means that the higher the weight is for recent feedbacks, the lower the number of feedbacks that need to be retained.
Figure 9 depicts the results of Scenario 3. In this case, different products have different feedback sets. The typical pattern of error decrease occurs, with some variations being seen at the start, which is due to the limited number of considered ratings. Eventually, the error percentage converges to zero as the decay component gains momentum.
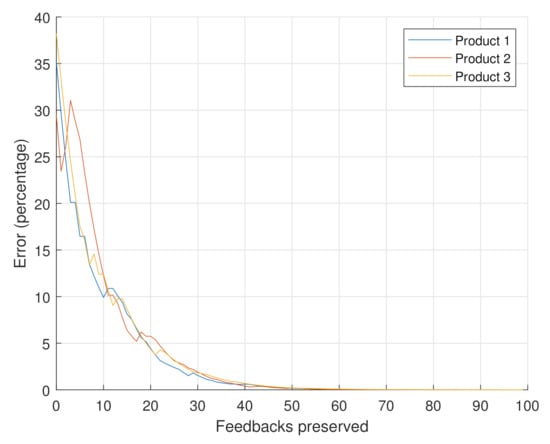
Figure 9.
Error percentage for varying products.
Based on the results from the previous three test scenarios, we can conclude that the main factors for choosing the required number of retained feedbacks to obtain an accurate estimate of the reputation are the weights. Even though the variation of feedbacks affects the reputation, the effect on the difference of the truncated reputation as compared to the original reputation can be made minimal. In general, the error decreases consistently to eventually converge to zero, despite the minor fluctuations.
The fruition of these results is in being able to work with a fraction of the data and provide accurate reputation values. This has the benefit of decreasing the network load and computation demands. These benefits can help to improve the system’s non-functional requirements whether it is using on-chain or off-chain storage and computation alternatives. In the case of an on-chain scenario, less computation is done on the smart contract, which will save both gas and resources. Additionally, saving less amount of data by the smart contract will reduce the chain size requirements. In the off-chain scenario, only recent feedbacks need to be fetched, which reduces the load on the network. Additionally, the requirements on the smart contract-governed computation modules are reduced.
8. Conclusions
RMSs are imperative for establishing trust for the unreliable entities of the virtual domain. However, there is yet to be an impervious system that solves the matter. The potential of DLT has become clear after years of its formation, and its feasibility in RMSs is evident, with it catering to the requirements of the integrity of data, transparency of transaction, and anonymity of users. However, the proposed solutions have shown that its consolidation into RMSs is a rocky process. Several challenges are faced in developing such solutions that are evident once the implementation of the system is undertaken. Our goal is to identify the challenges and pitfalls that would hinder the realization of such a system, and offer clarifications and recommendations that could help to tackle them.
The scalability of the blockchain is one of the main challenges that has garnered research attention. Using the blockchain to govern all of the interactions in a system would be impractical in most cases, and selective diversion of some interactions of the blockchain under provision would be more applicable. Such logic is facilitated by smart contracts, which allow for complex operations on the chain. However, a smart contract is still bounded in what it can achieve, such as initiating interaction with the outside environment and requiring the determinism of results. Such requirements demand the utilization of external aid through oracles, which call for the enforcement of trust on the oracle level. Additionally, the need for determinism limit the scope of arithmetic operations and representation. As such, mechanisms to establish trust of oracles are presented, and techniques to efficiently execute reputation computations on the chain are provided.
RMSs are complex systems that contain synchronous and asynchronous functions. We provide insight into the crucial reputation update with its different schemes in the system, where the reputation should be available when needed while maintaining an efficient computation model. Finally, we give a more precise reputation through the inclusion of “aging”. Promoting the use of time, we also provide simulation and analysis on the use of the recent feedbacks to devise an accurate reputation value. Disregarding old feedbacks to reduce storage and computation requirements, we are still able to preserve the original reputation value by using less than 50 feedbacks approximately with an error margin that is lower than . We believe our recommendations would be of interest to all contract-based blockchains.
Author Contributions
Conceptualization, A.B., Y.I. and E.D.; Methodology, A.B., Y.I. and E.D.; Software, A.B.; Validation, A.B.; Formal analysis, A.B., Y.I. and E.D.; Investigation, A.B.; Resources, Y.I. and E.D.; Data curation, A.B.; Writing–original draft preparation, A.B.; Writing–review and editing, A.B., Y.I. and E.D.; Visualization, A.B. and Y.I.; Supervision, Y.I. and E.D.; Project administration, Y.I. and E.D.; Funding acquisition, Y.I. and E.D. All authors have read and agreed to the published version of the manuscript.
Funding
This work has been partly funded by the European Commission within the H2020 Framework Programme under the H2020 project CONCORDIA (contract n. 830927).
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| BFT | Byzantine Fault Tolerance |
| DL | Distributed Ledger |
| DLT | Distributed Ledger Technology |
| PoS | Proof-of-Stake |
| PoW | Proof-of-Work |
| RMS | Reputation Management System |
References
- Mekouar, L.; Iraqi, Y.; Boutaba, R. Reputation-Based Trust Management in Peer-to-Peer Systems: Taxonomy and Anatomy. In Handbook of Peer-to-Peer Networking; Springer: Berlin/Heidelberg, Germany, 2010; pp. 689–732. [Google Scholar]
- Ruan, Y.; Durresi, A. A Survey of Trust Management Systems for Online Social Communities—Trust Modeling, Trust Inference and Attacks. Knowl.-Based Syst. 2016, 106, 150–163. [Google Scholar] [CrossRef]
- Belotti, M.; Božić, N.; Pujolle, G.; Secci, S. A Vademecum on Blockchain Technologies: When, Which, and How. IEEE Commun. Surv. Tutor. 2019, 21, 3796–3838. [Google Scholar] [CrossRef]
- Bellini, E.; Iraqi, Y.; Damiani, E. Blockchain-Based Distributed Trust and Reputation Management Systems: A Survey. IEEE Access 2020, 8, 21127–21151. [Google Scholar] [CrossRef]
- Dennis, R.; Owen, G. Rep on the Block: A Next Generation Reputation System Based on the Blockchain. In Proceedings of the 2015 10th International Conference for Internet Technology and Secured Transactions (ICITST), London, UK, 14–16 December 2015; pp. 131–138. [Google Scholar] [CrossRef]
- Careem, M.A.A.; Dutta, A. SenseChain: Blockchain Based Reputation System for Distributed Spectrum Enforcement. In Proceedings of the 2019 IEEE International Symposium on Dynamic Spectrum Access Networks (DySPAN), Newark, NJ, USA, 11–14 November 2019; pp. 1–10. [Google Scholar]
- Lu, Z.; Wang, Q.; Qu, G.; Liu, Z. Bars: A Blockchain-Based Anonymous Reputation System for Trust Management in VANETS. In Proceedings of the 2018 17th IEEE International Conference On Trust, Security And Privacy In Computing And Communications/12th IEEE International Conference On Big Data Science And Engineering (TrustCom/BigDataSE), New York, NY, USA, 1–3 August 2018; pp. 98–103. [Google Scholar]
- Dorigo, M. Blockchain Technology for Robot Swarms: A Shared Knowledge and Reputation Management System for Collective Estimation. In Proceedings of the Swarm Intelligence: 11th International Conference, ANTS 2018, Rome, Italy, 29–31 October 2018; Springer: Berlin/Heidelberg, Germany, 2018; Volume 11172, p. 425. [Google Scholar]
- Smith, T.D. The Blockchain Litmus Test. In Proceedings of the 2017 IEEE International Conference on Big Data (Big Data), Boston, MA, USA, 11–14 December 2017; pp. 2299–2308. [Google Scholar]
- Why New Off-Chain Storage Is Required for Blockchains Document Version 4.1. Technical Report. Available online: https://www.ibm.com/downloads/cas/RXOVXAPM (accessed on 17 September 2020).
- Zheng, Z.; Xie, S.; Dai, H.; Chen, X.; Wang, H. An Overview of Blockchain Technology: Architecture, Consensus, and Future Trends. In Proceedings of the 2017 IEEE International Congress on Big Data (BigData Congress), Honolulu, HI, USA, 25–30 June 2017; pp. 557–564. [Google Scholar]
- Zhou, Q.; Huang, H.; Zheng, Z.; Bian, J. Solutions to Scalability of Blockchain: A Survey. IEEE Access 2020, 8, 16440–16455. [Google Scholar] [CrossRef]
- Göbel, J.; Krzesinski, A.E. Increased Block Size and Bitcoin Blockchain Dynamics. In Proceedings of the 2017 27th International Telecommunication Networks and Applications Conference (ITNAC), Melbourne, VIC, Australia, 22–24 November 2017; pp. 1–6. [Google Scholar]
- Eberhardt, J.; Heiss, J. Off-Chaining Models and Approaches to Off-Chain Computations. In Proceedings of the 2ndWorkshop on Scalable and Resilient Infrastructures for Distributed Ledgers; Association for Computing Machinery, SERIAL’18, New York, NY, USA, 10–14 December 2018; pp. 7–12. [Google Scholar] [CrossRef]
- Bitcoin Blocks-Size. Available online: https://www.blockchain.com/charts/blocks-size (accessed on 14 November 2020).
- Acharjamayum, I.; Patgiri, R.; Devi, D. Blockchain: A Tale of Peer to Peer Security. In Proceedings of the 2018 IEEE Symposium Series on Computational Intelligence (SSCI), Bangalore, India, 18–21 November 2018; pp. 609–617. [Google Scholar]
- Bitansky, N.; Canetti, R.; Chiesa, A.; Goldwasser, S.; Lin, H.; Rubinstein, A.; Tromer, E. The Hunting of the SNARK. J. Cryptol. 2017, 30, 989–1066. [Google Scholar] [CrossRef]
- Bünz, B.; Bootle, J.; Boneh, D.; Poelstra, A.; Wuille, P.; Maxwell, G. Bulletproofs: Short Proofs for Confidential Transactions and More. In Proceedings of the 2018 IEEE Symposium on Security and Privacy (SP), San Francisco, CA, USA, 20–24 May 2018; pp. 315–334. [Google Scholar]
- Konda, C.; Connor, M.; Westland, D.; Drouot, Q.; Brody, P. Nightfall. Available online: https://img.learnblockchain.cn/pdf/nightfall-v1.pdf (accessed on 17 September 2020).
- Zheng, Z.; Xie, S.; Dai, H.N.; Chen, W.; Chen, X.; Weng, J.; Imran, M. An Overview on Smart Contracts: Challenges, Advances and Platforms. Future Gener. Comput. Syst. 2020, 105, 475–491. [Google Scholar] [CrossRef]
- Szabo, N. Smart Contracts. Phonetic Sciences. Available online: https://www.fon.hum.uva.nl/rob/Courses/InformationInSpeech/CDROM/Literature/LOTwinterschool2006/szabo.best.vwh.net/smart.contracts.html (accessed on 14 November 2020).
- Beniiche, A. A Study of Blockchain Oracles. arXiv 2020, arXiv:2004.07140. [Google Scholar]
- Provable. Blockchain Oracle Service, Enabling Data-Rich Smart Contracts. Available online: https://provable.xyz/ (accessed on 14 November 2020).
- Ellis, S.; Juels, A.; Nazarov, S. ChainLink: A Decentralized Oracle Network. White Paper. Available online: https://link.smartcontract.com/whitepaper (accessed on 17 September 2020).
- Swarm. Swarm 0.5 Documentation. Available online: https://swarm-guide.readthedocs.io/en/latest/introduction.html (accessed on 14 November 2020).
- Benet, J. IPFS-Content Addressed, Versioned, P2P File System. arXiv 2014, arXiv:1407.3561. [Google Scholar]
- Yaga, D.; Mell, P.; Roby, N.; Scarfone, K. Blockchain Technology Overview. arXiv 2019, arXiv:1906.11078. [Google Scholar]
- Nakamoto, S. Bitcoin: A Peer-to-Peer Electronic Cash System. Technical Report. Available online: https://bitcoin.org/bitcoin.pdf (accessed on 17 September 2020).
- Chainlink. Generate Random Numbers for Smart Contracts Using Chainlink VRF. Available online: https://docs.chain.link/docs/chainlink-vrf (accessed on 14 November 2020).
- Sanchez-Stern, A.; Panchekha, P.; Lerner, S.; Tatlock, Z. Finding Root Causes of Floating Point Error. In Proceedings of the 39th ACM SIGPLAN Conference on Programming Language Design and Implementation, Philadelphia, PA, USA, 18–22 June 2018; pp. 256–269. [Google Scholar]
- OpenZeppelin. OpenZeppelin-Contracts-SafeMath. Available online: https://github.com/OpenZeppelin/openzeppelin-contracts/blob/master/contracts/math/SafeMath.sol (accessed on 19 November 2020).
- Ethereum Homestead 0.1 Documentation. Account Types, Gas, and Transactions. Available online: https://ethdocs.org/en/latest/contracts-and-transactions/account-types-gas-and-transactions.html (accessed on 14 November 2020).
- ABDK-Consulting. Abdk-Consulting/Abdk-Libraries-Solidity. Available online: https://github.com/abdk-consulting/abdk-libraries-solidity (accessed on 14 November 2020).
- BANKEX. Solidity-Float-Point-Calculation. Available online: https://github.com/BankEx/solidity-float-point-calculation (accessed on 14 November 2020).
- Compound-Finance. Compound-Protocol/Exponential.sol. Available online: https://github.com/compound-finance/compound-protocol/blob/v2.6/contracts/Exponential.sol (accessed on 14 November 2020).
- Cement Meta-Stable Coin. CementDAO/Fixidity. Available online: https://github.com/CementDAO/Fixidity (accessed on 14 November 2020).
- Buterin, V. A Next-Generation Smart Contract and Decentralized Application Platform. White Paper. Available online: https://blockchainlab.com/pdf/Ethereum_white_paper-a_next_generation_smart_contract_and_decentralized_application_platform-vitalik-buterin.pdf (accessed on 17 September 2020).
- Unix Manual, First Edition. Unix Programmer’s Manual. Available online: https://www.bell-labs.com/usr/dmr/www/1stEdman.html (accessed on 14 November 2020).
- Jøsang, A.; Hird, S.; Faccer, E. Simulating the Effect of Reputation Systems on e-Markets. In Proceedings of the International Conference on Trust Management, Crete, Greece, 28–30 May 2003; Springer: Berlin/Heidelberg, Germany, 2003; pp. 179–194. [Google Scholar]
- Mu, P.; Chang, M. Time-Decay-Based Reputation Method for Buyers Making Decisions in Online Shopping. In Proceedings of the 9th International Conference on Electronic Business, Macau, China, 30 November–4 December 2009; pp. 855–863. [Google Scholar]
- Alswailim, M.A.; Hassanein, H.S.; Zulkernine, M. A Reputation System to Evaluate Participants for Participatory Sensing. In Proceedings of the 2016 IEEE Global Communications Conference (GLOBECOM), Washington, DC, USA, 4–8 December 2016; pp. 1–6. [Google Scholar]
- Huynh, T.D.; Jennings, N.R.; Shadbolt, N.R. An Integrated Trust and Reputation Model for Open Multi-Agent Systems. Auton. Agents-Multi-Agent Syst. 2006, 13, 119–154. [Google Scholar] [CrossRef]
- Michiardi, P.; Molva, R. Core: A Collaborative Reputation Mechanism to Enforce Node Cooperation in Mobile Ad Hoc Networks. In Advanced Communications and Multimedia Security; Springer: Berlin/Heidelberg, Germany, 2002; pp. 107–121. [Google Scholar]
- Ayday, E.; Lee, H.; Fekri, F. An Iterative Algorithm for Trust and Reputation Management. In Proceedings of the 2009 IEEE International Symposium on Information Theory, Seoul, Korea, 28 June–3 July 2009; pp. 2051–2055. [Google Scholar]
- Xu, Z.; Martin, P.; Powley, W.; Zulkernine, F. Reputation-Enhanced QoS-Based Web Services Discovery. In Proceedings of the IEEE International Conference on Web Services (ICWS 2007), Salt Lake City, UT, USA, 9–13 July 2007; pp. 249–256. [Google Scholar]
- Wishart, R.; Robinson, R.; Indulska, J.; Jøsang, A. SuperstringRep: Reputation-Enhanced Service Discovery. In Proceedings of the Twenty-eighth Australasian conference on Computer Science, Newcastle, NSW, Australia, 31 January–3 February 2005; Volume 38, pp. 49–57. [Google Scholar]
- Josang, A.; Haller, J. Dirichlet Reputation Systems. In Proceedings of the Second International Conference on Availability, Reliability and Security (ARES’07), Vienna, Austria, 10–13 April 2007; pp. 112–119. [Google Scholar]
- Margaris, D.; Vassilakis, C. Pruning and Aging for User Histories in Collaborative Filtering. In Proceedings of the 2016 IEEE Symposium Series on Computational Intelligence (SSCI), Athens, Greece, 6–9 December 2016; pp. 1–8. [Google Scholar]
- Kiayias, A.; Russell, A.; David, B.; Oliynykov, R. Ouroboros: A Provably Secure Proof-of-Stake Blockchain Protocol. In Proceedings of the Annual International Cryptology Conference, Santa Barbara, CA, USA, 20–24 August 2017; Springer: Berlin/Heidelberg, Germany, 2017; pp. 357–388. [Google Scholar]
- Josang, A.; Ismail, R. The Beta Reputation System. In Proceedings of the 15th Bled Electronic Commerce Conference, Bled, Slovenia, 17–19 June 2002; Volume 5, pp. 2502–2511. [Google Scholar]
- He, R.; McAuley, J. Ups and Downs: Modeling the Visual Evolution of Fashion Trends with One-Class Collaborative Filtering. In Proceedings of the 25th International Conference on World Wide Web, Montreal, QC, Canada, 11–15 May 2016; pp. 507–517. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).