Competitive Game Theoretic Clustering-Based Multiple UAV-Assisted NB-IoT Systems
Abstract
:1. Introduction
- Based on the assumption that a UAV is placed at the center of the IoT cluster within its coverage area, we developed a competitive clustering algorithm for all the UAVs and IoT devices in the network. The IoT devices determine the UAV that can maximize the transmission throughput. The UAV simultaneously calculates the optimal placement in order to minimize the power consumption (i.e., the maximum operation time) when all the IoT devices within the coverage area are considered. Therefore, the challenges of joint optimization of UAV-related problems can be resolved based on Stackelberg game theoretic approach in competitive environment.
- The adjacent clusters are then heuristically calculating to contain the non-clustered IoT devices so as to obtain the optimal system capacity maximization. The distance between the UAV and the non-clustered IoT devices is calculated, the UAV energy consumption and system capacity maximization are considered, and the non-clustered IoT devices are assigned to the appropriate cluster based on Stackelberg game theoretic approach based on Nash equilibrium.
- The simulation results demonstrate that the proposed algorithm exhibits rapid convergence to the suboptimal solution and is observed to significantly increase the system performance by approximately 28% when compared to the existing methods.
2. System Model and Problem Formulation
2.1. System Model
2.2. Problem Formulation
3. Competitive Clustering-Based Uav Placement with Stackelberg Game Theoretic Approach
3.1. Initial Uavs and Iot Nodes Deployment
| Algorithm 1 Stackelberg Game Theoretic Clustering Algorithm |
Step 1: Initiation state information of UAVs and IoT nodes
|

3.2. Optimization of Uav Placement
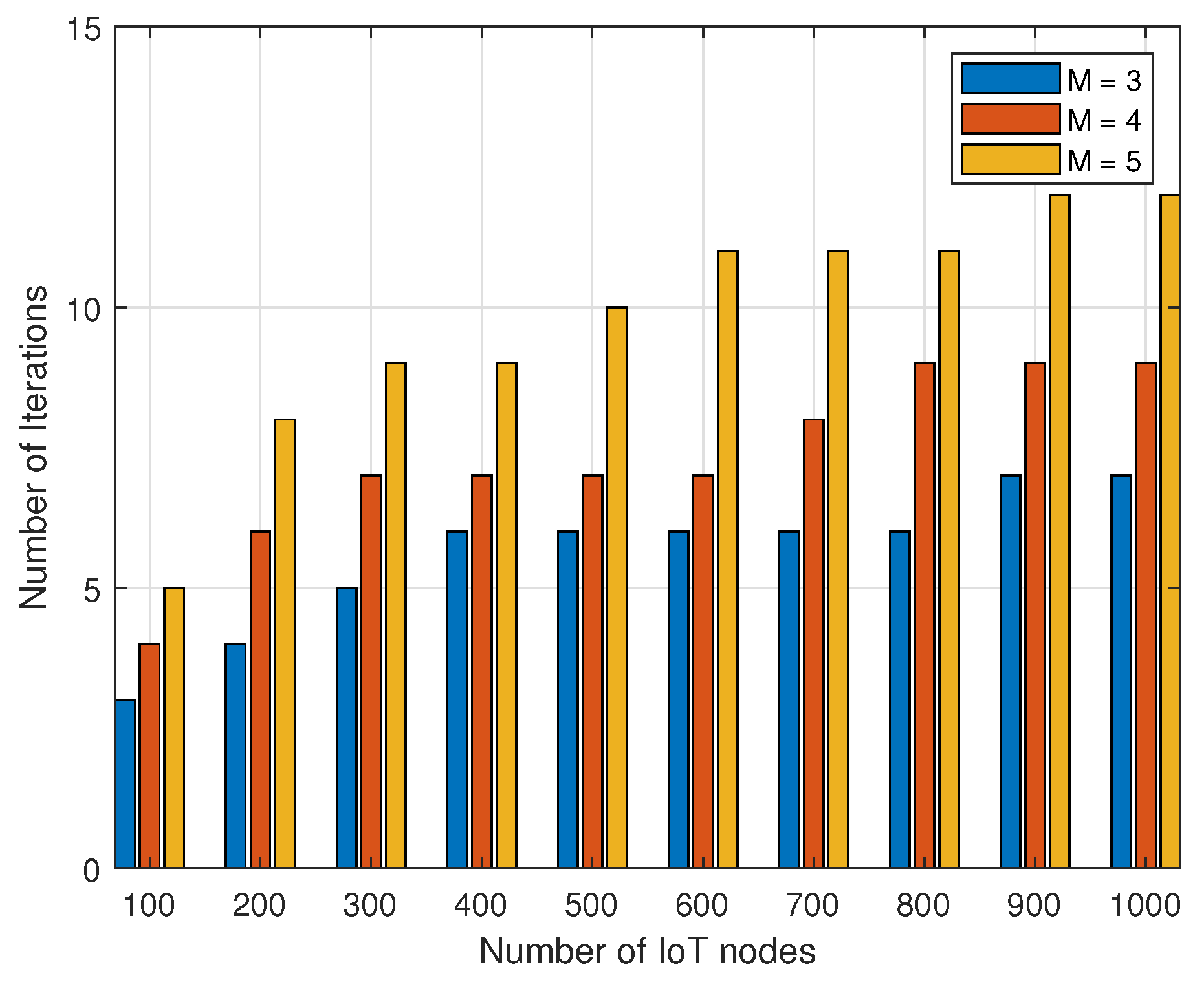
4. Simulation Results
5. Discussion
6. Concluding Remarks
Author Contributions
Funding
Conflicts of Interest
References
- Lin, X.; Yajnanarayana, V.; Muruganathan, S.D.; Gao, S.; Asplund, H.; Maattanen, H.-L.; Bergstrom, M.; Euler, S.; Wang, Y.-P.E. The sky is not the limit: LTE for unmanned aerial vehicles. IEEE Commun. Mag. 2018, 56, 204–210. [Google Scholar] [CrossRef] [Green Version]
- Perz, R.; Wronowski, K. UAV application for precision agriculture. Aircr. Eng. Aerosp. Technol. 2018, 91, 257–263. [Google Scholar] [CrossRef]
- Pouya, B.; Mehdi, F.; Kate, S.-M.; Vladimir, E. A transformation technique for the clustered generalized traveling salesman problem with applications to logistics. Eur. J. Oper. Res. 2020, 285, 444–457. [Google Scholar]
- Atzori, L.; Iera, A.; Morabito, G. The Internet of Things: A survey. Comput. Netw. 2010, 54, 2787–2805. [Google Scholar] [CrossRef]
- Dao, N.-N.; Na, W.; Tran, A.-T.; Nguyen, D.N.; Cho, S. Energy-efficient spectrum sensing for IoT devices. IEEE Syst. J. 2020. [Google Scholar] [CrossRef]
- Chandrasekharan, S.; Gomez, K.; Al-Hourani, A.; Kandeepan, S.; Rasheed, T.; Goratti, L.; Reynaud, L.; Grace, D.; Bucaille, I.; Wirth, T.; et al. Designing and implementing future aerial communication networks. IEEE Commun. Mag. 2016, 54, 26–34. [Google Scholar] [CrossRef] [Green Version]
- Zeng, Y.; Zhang, R.; Lim, T.J. Wireless communications with unmanned aerial vehicles: Opportunities and challenges. IEEE Commun. Mag. 2016, 54, 36–42. [Google Scholar] [CrossRef] [Green Version]
- Gupita, L.; Jain, R.; Vaszkun, G. Survey of important issues in UAV communication networks. IEEE Commun. Surv. Tutor. 2015, 18, 1123–1152. [Google Scholar] [CrossRef] [Green Version]
- Lakew, D.S.; Sa’ad, U.; Dao, N.-N.; Na, W.; Cho, S. Routing in flying ad hoc networks: A comprehensive survey. IEEE Commun. Surv. Tutor. 2020, 22, 1071–1120. [Google Scholar] [CrossRef]
- Dao, N.-N.; Park, M.; Kim, J.; Cho, S. Adaptive MCS selection and resource planning for energy-efficient communication in LTE-M based IoT sensing platform. PLoS ONE 2017, 12, e0182527. [Google Scholar] [CrossRef] [Green Version]
- Sharama, V.; Kumar, R.; Kaur, R. UAV-assisted content-based sensor search in IoTs. Electron. Lett. 2017, 53, 724–726. [Google Scholar] [CrossRef]
- Motlagh, N.H.; Bagaa, M.; Taleb, T. UAV-based IoT platform: A crowd surveillance use case. IEEE Commun. Mag. 2017, 55, 128–134. [Google Scholar] [CrossRef] [Green Version]
- He, H.; Zhang, S.; Zeng, Y.; Zhang, R. Joint altitude and beamwidth optimization for UAV-enabled multiuser communications. IEEE Commun. Lett. 2017, 22, 344–347. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Liu, M.; Sun, J.; Gui, G.; Gacanin, H.; Sari, H.; Adachi, F. Multiple unmanned aerial vehicles deployment and user pairing for non-orthogonal multiple access schemes. IEEE Internet Things J. 2020, 22, 1071–1120. [Google Scholar] [CrossRef]
- Duan, R.; Wnag, J.; Jiang, C.; Yao, H.; Ren, Y.; Qian, Y. Resource allocation for multi-UAV aided IoT NOMA uplink transmission systems. IEEE Internet Things J. 2019, 6, 7025–7037. [Google Scholar] [CrossRef]
- Jiang, B.; Yang, J.; Xu, H.; Song, H.; Zheng, G. Multimedia data throughput maximization in Internet-of-Things system based on optimization of cache-enabled UAV. IEEE Internet Things J. 2018, 6, 3525–3532. [Google Scholar] [CrossRef]
- Mozaffari, M.; Saad, W.; Bennis, M.; Debbah, M. Efficient deployment of multiple unmanned aerial vehicles for optimal wireless coverage. IEEE Commun. Lett. 2016, 20, 1647–1650. [Google Scholar] [CrossRef]
- Tuyishimire, E.; Bagula, B.A.; Ismail, A. Optimal clustering for efficient data muling in the Internet-of-Things in motion. In Proceedings of the International Symposium on Ubiquitous Networking, Hammamet, Tunisia, 2–5 May 2018; pp. 359–371. [Google Scholar]
- Ebrahimi, D.; Sharafeddine, S.; Ho, P.-H.; Assi, C. UAV-aided projection-based compressive data gathering in wireless sensor networks. IEEE Internet Things J. 2018, 6, 1893–1905. [Google Scholar] [CrossRef]
- Mozaffari, M.; Saad, W.; Bennis, M.; Debbah, M. Mobile Internet of Things: Can UAVs provide an energy-efficient mobile architecture? In Proceedings of the Global communications conference (GLOBECOM), Washington, DC, USA, 4–8 December 2016; pp. 1–6. [Google Scholar]
- Gibbons, R. A Primer in Game Theory; Harvester Wheatshead: New York, NY, USA, 1992. [Google Scholar]
- Lee, C.; Park, L.; Cho, S. Light-Weight Stackelberg Game Theoretic Demand Response Scheme for Massive Smart Manufacturing Systems. IEEE Access 2018, 6, 23316–23324. [Google Scholar] [CrossRef]
- Luan, H.; Xu, Y.; Liu, D.; Du, Z.; Qian, H.; Liu, X.; Tong, X. Energy Efficient Task Cooperation for Multi-UAV Networks: A Coalition Formation Game Approach. IEEE Access 2020, 8, 149372–149384. [Google Scholar] [CrossRef]
- Zhu, S.; Gui, L.; Cheng, N.; Sun, F.; Zhang, Q. Joint Design of Access Point Selection and Path Planning for UAV-Assisted Cellular Networks. IEEE Inernet Things J. 2020, 7, 220–223. [Google Scholar] [CrossRef]
- Bor-Yaliniz, R.I.; El-Keyi, A.; Yanikomeroglu, H. Efficient 3-D placement of an aerial base station in next generation cellular networks. In Proceedings of the International Conference on Communications (ICC), KualaLumpur, Malaysia, 22–27 May 2016; pp. 1–5. [Google Scholar]
- Wang, J.; Jiang, C.; Wei, Z.; Pan, C.; Zhang, H.; Ren, Y. Joint UAV hovering altitude and power control for space-air-ground IoT networks. IEEE Internet Things J. 2018, 6, 1741–1753. [Google Scholar] [CrossRef] [Green Version]
- Wu, Q.; Zeng, Y.; Zhang, R. Joint trajectory and communication design for multi-UAV enabled wireless networks. IEEE Trans. Wirel. Commun. 2018, 17, 2109–2121. [Google Scholar] [CrossRef] [Green Version]
- Karp, R.M. Reducibility among combinatorial problems. In Proceedings of the a Symposium on the Complexity of Computer Computations, Yorktown Heights, New York, 20–22 March 1972; pp. 85–103. [Google Scholar]
- Boyd, S.; Boyd, S.P.; Vandenberghe, L. Convex Optimization; Cambridge University Press: Cambridge, UK, 2004; ISBN 978-051-180-444-1. [Google Scholar]




| Parameters | Value |
|---|---|
| Field Size | 1000 m × 1000 m |
| Beamwidth of Antenna | |
| 500 m | |
| 50 m | |
| 50 m | |
| 10 kbps | |
| 50 kbps | |
| B | 20 MHz |
| , | [0, 1] |
| K | 100 |
| dBm | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, C.; Jang, G.; Dao, N.-N.; Lakew, D.S.; Lee, C.; Cho, S. Competitive Game Theoretic Clustering-Based Multiple UAV-Assisted NB-IoT Systems. Electronics 2021, 10, 356. https://doi.org/10.3390/electronics10030356
Lee C, Jang G, Dao N-N, Lakew DS, Lee C, Cho S. Competitive Game Theoretic Clustering-Based Multiple UAV-Assisted NB-IoT Systems. Electronics. 2021; 10(3):356. https://doi.org/10.3390/electronics10030356
Chicago/Turabian StyleLee, Chunghyun, Gunhee Jang, Nhu-Ngoc Dao, Demeke Shumeye Lakew, Cheol Lee, and Sungrae Cho. 2021. "Competitive Game Theoretic Clustering-Based Multiple UAV-Assisted NB-IoT Systems" Electronics 10, no. 3: 356. https://doi.org/10.3390/electronics10030356
APA StyleLee, C., Jang, G., Dao, N.-N., Lakew, D. S., Lee, C., & Cho, S. (2021). Competitive Game Theoretic Clustering-Based Multiple UAV-Assisted NB-IoT Systems. Electronics, 10(3), 356. https://doi.org/10.3390/electronics10030356








