Model Predictive Current Control with Fixed Switching Frequency and Dead-Time Compensation for Single-Phase PWM Rectifier
Abstract
:1. Introduction
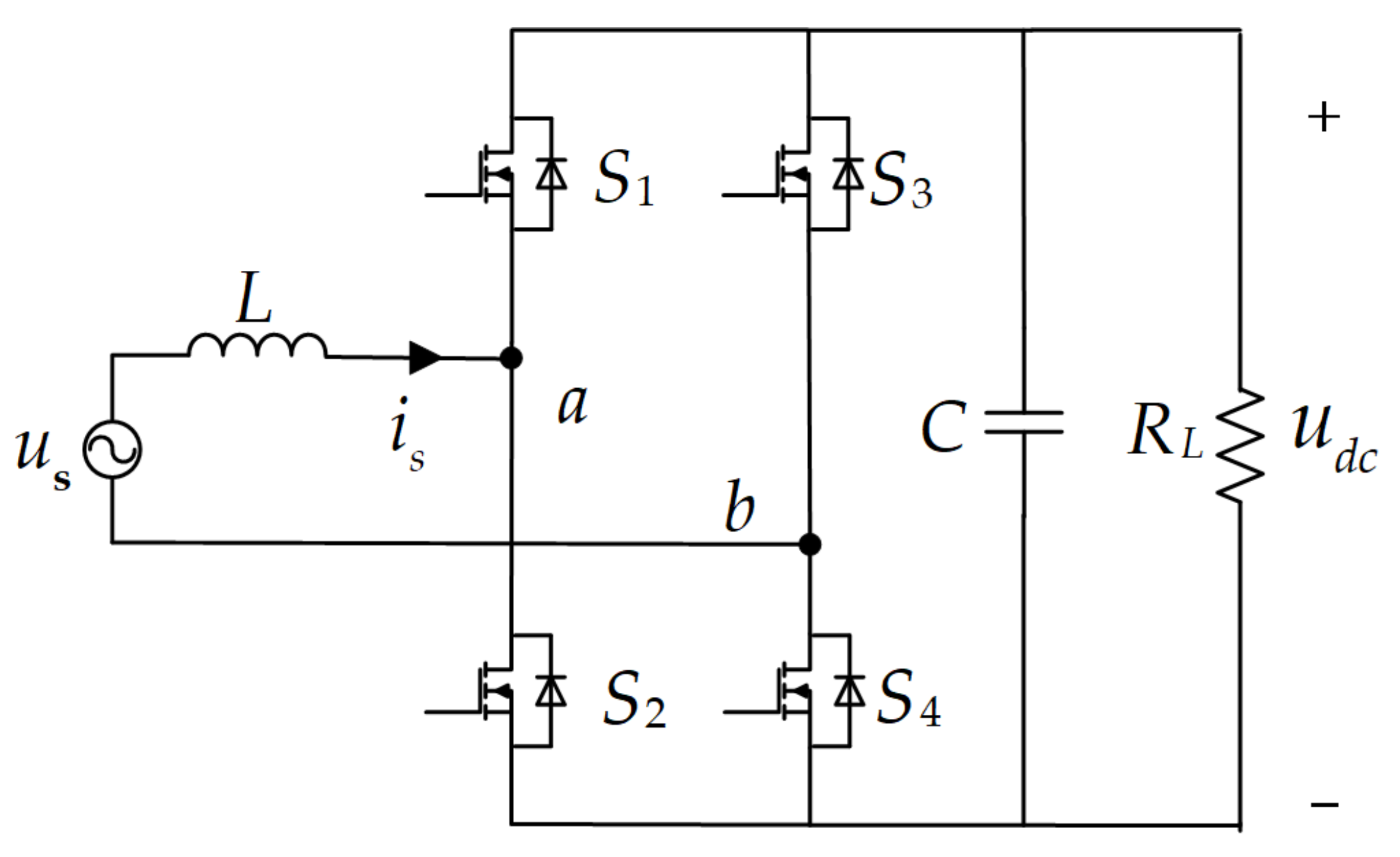
2. Mathematical Model of Single-Phase PWM Rectifiers
3. The Principle of Model Predictive Current Control with Fixed Switching Frequency
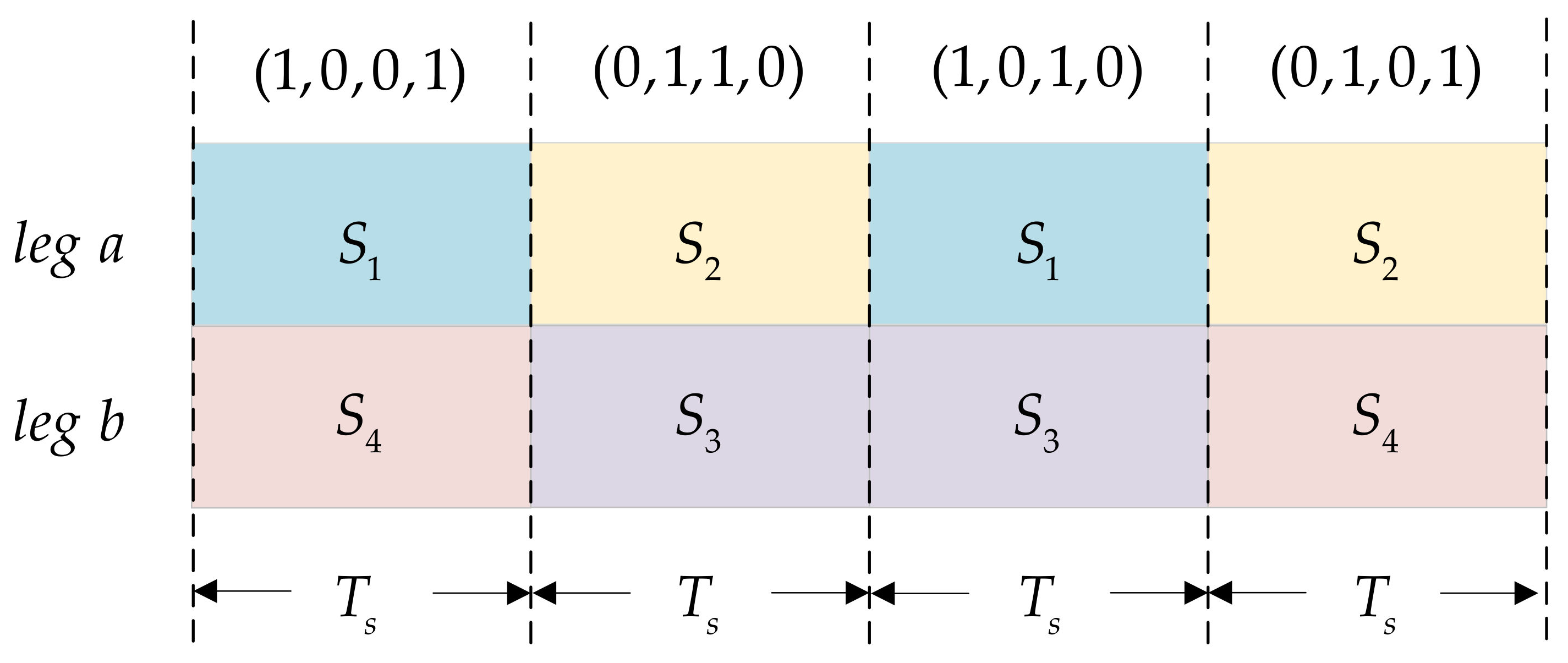
3.1. The Principle of Fixed Switching Frequency Control
3.2. Current Prediction Equation
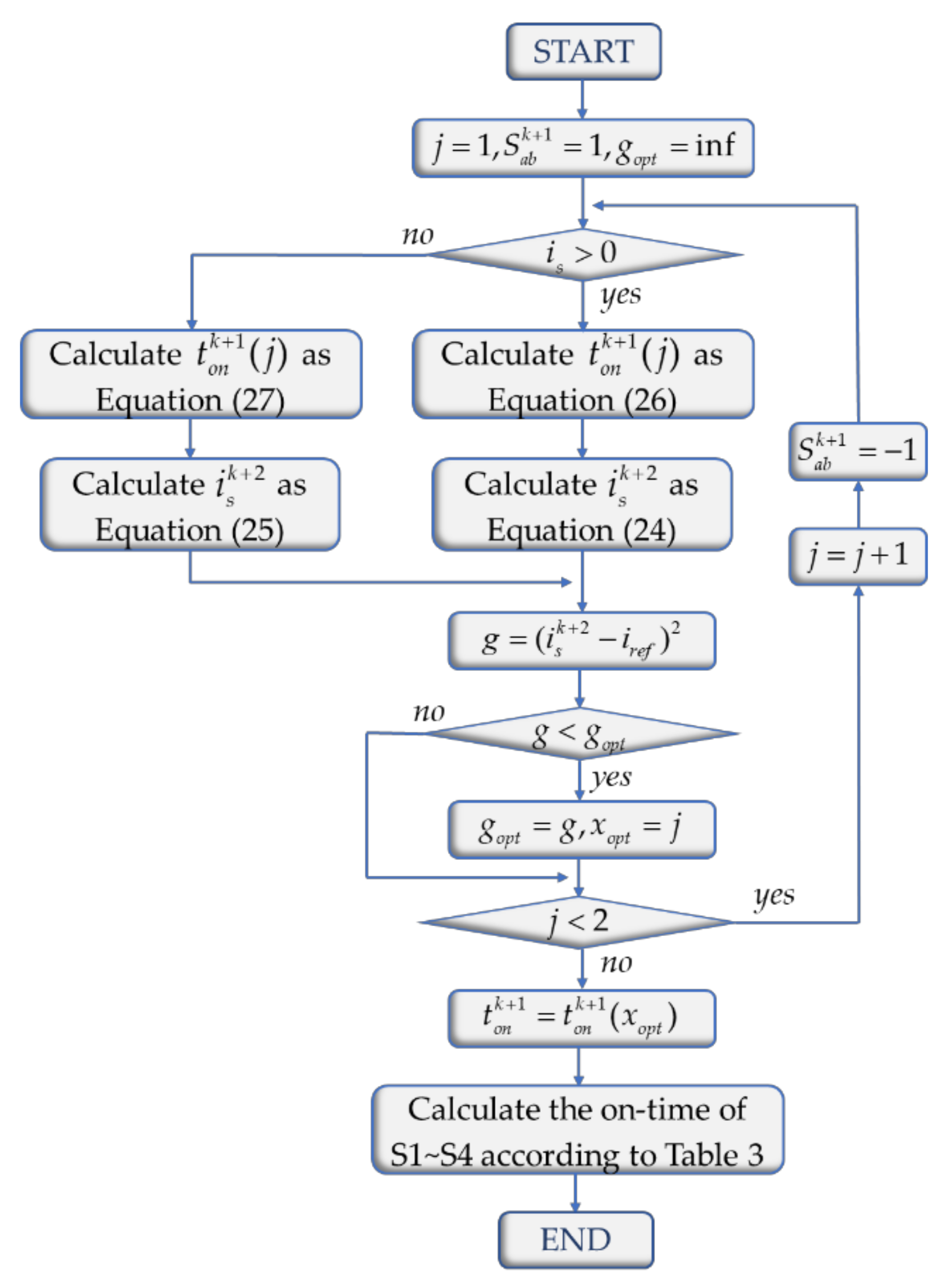
3.3. Cost Function and the Optimal Action Time of the Effective Vector
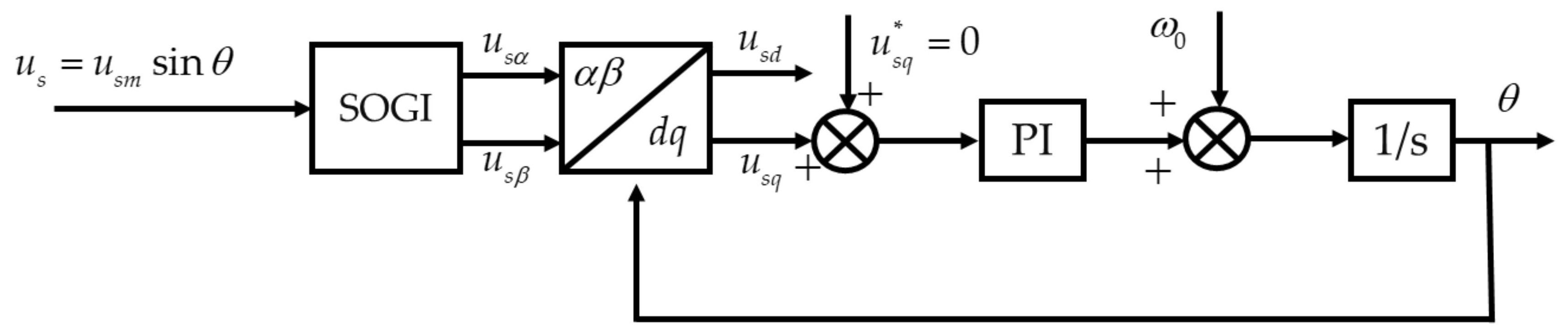
3.4. Implementation Scheme of Phase-Locked Loop
3.5. The Control System of the Proposed MPCC
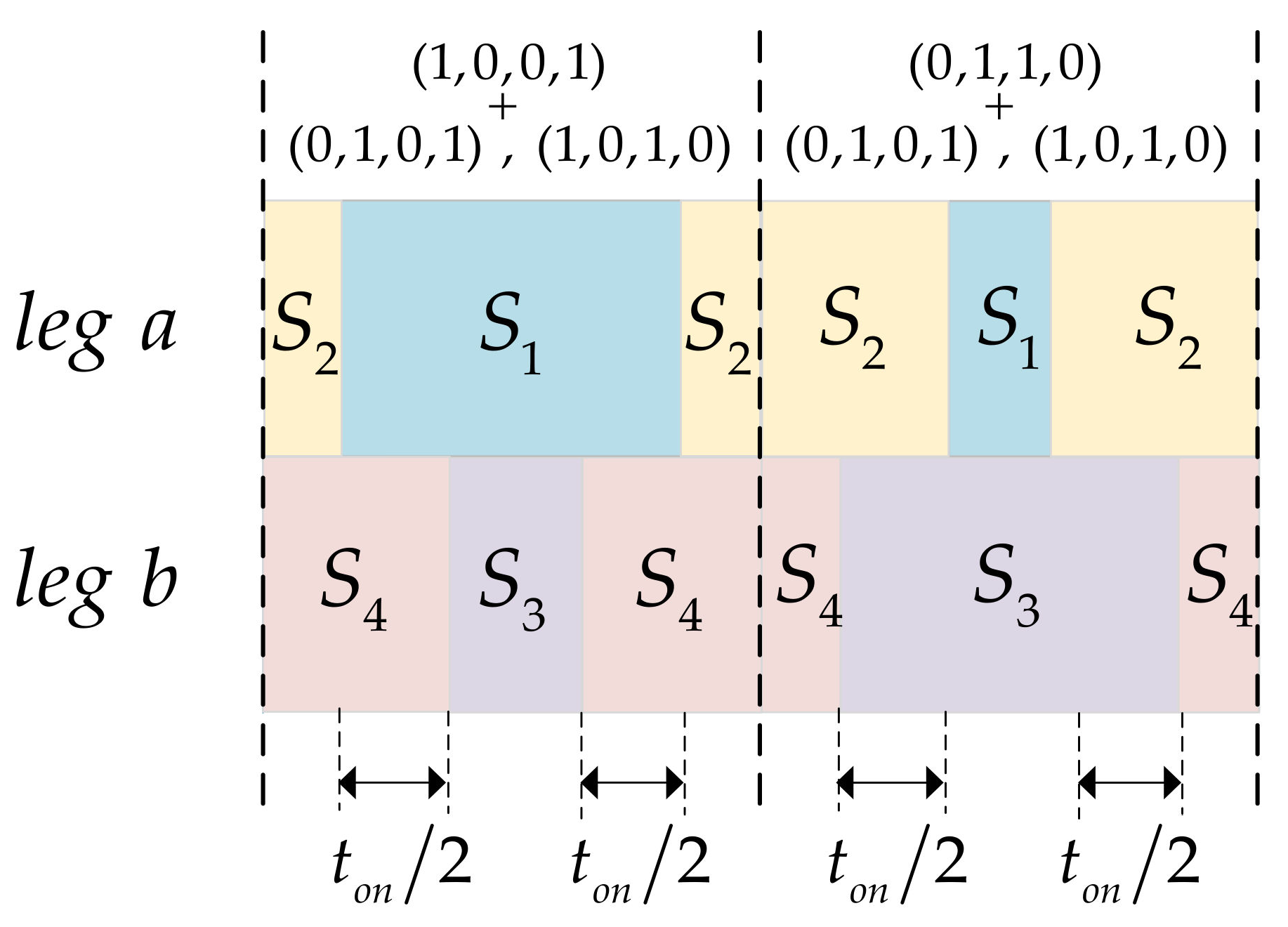
4. Dead-Time Compensation
5. Simulation Results
6. Experimental Results
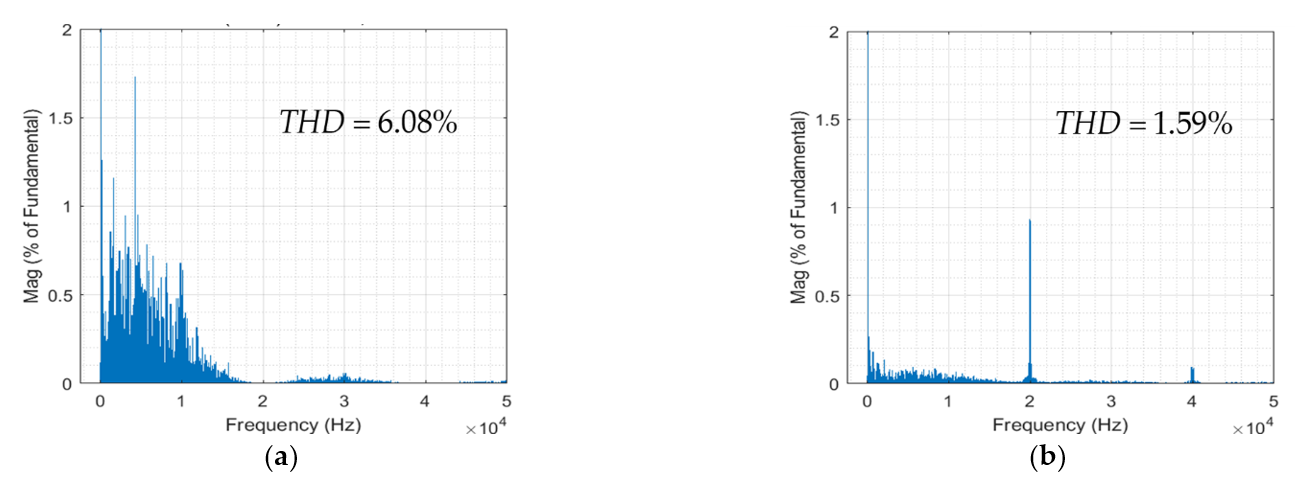
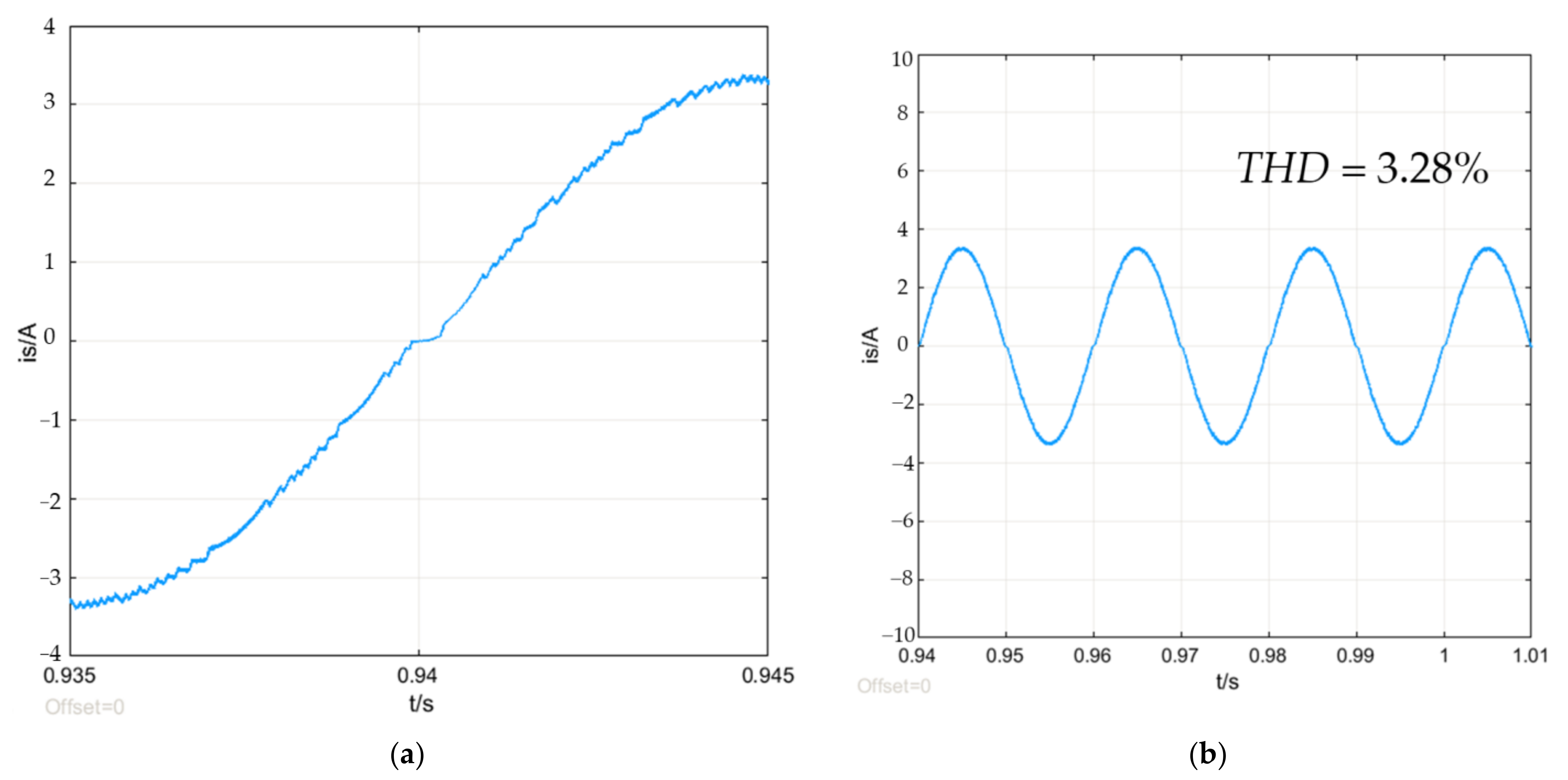
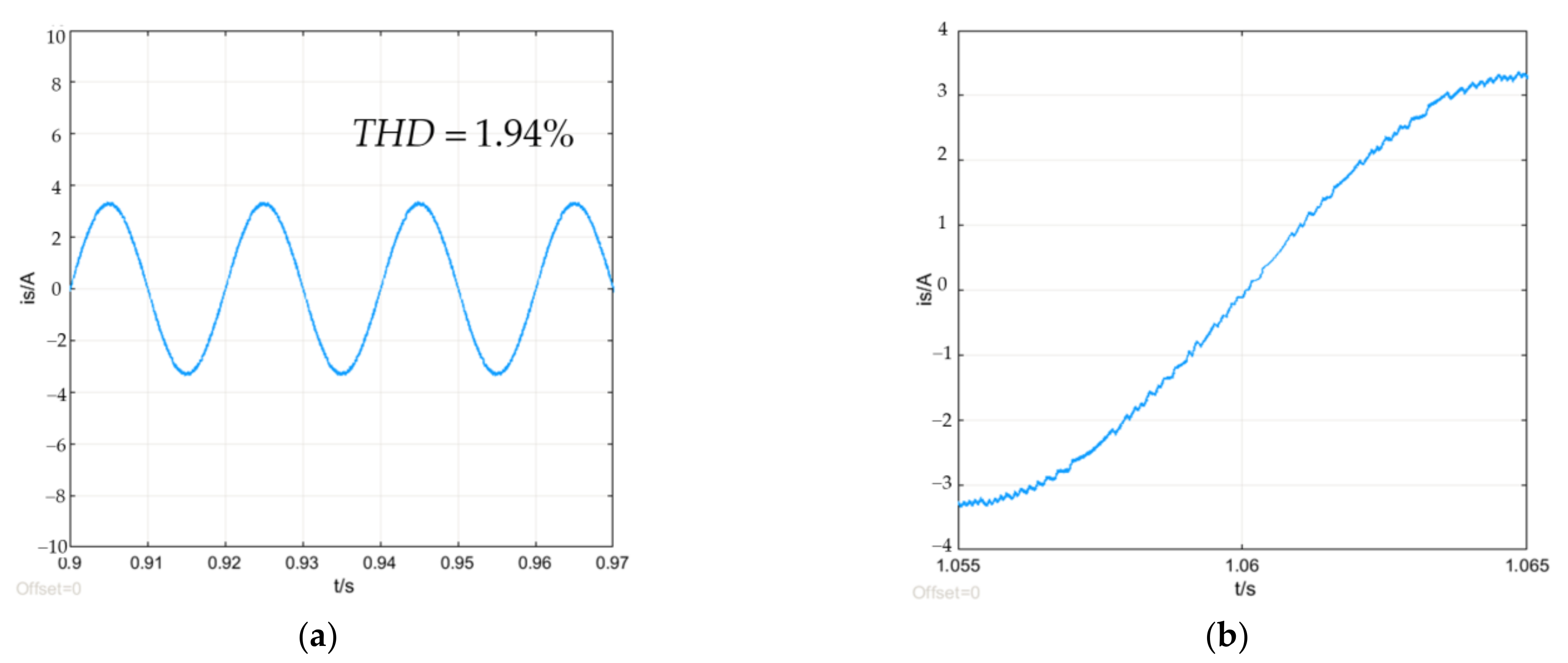
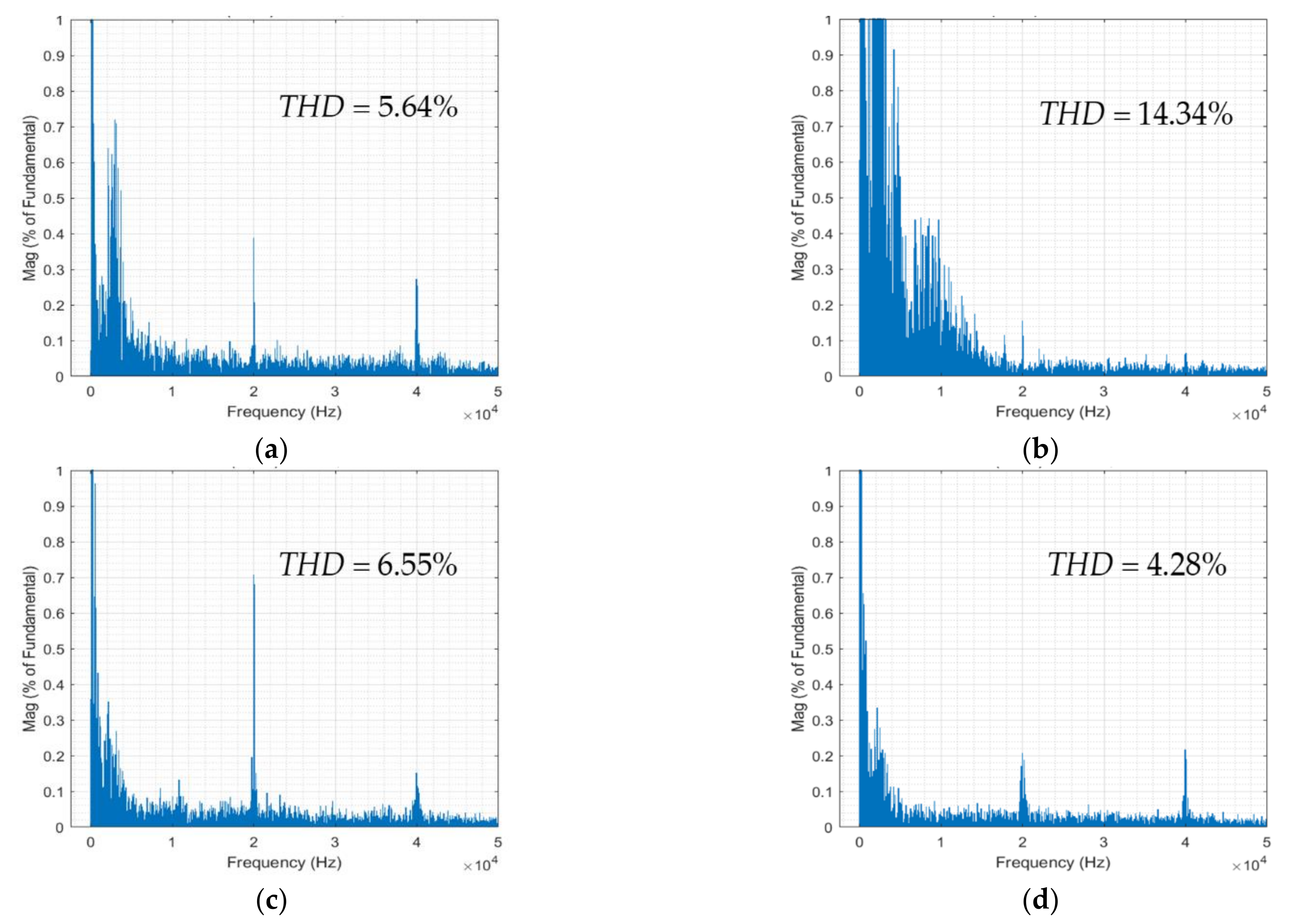
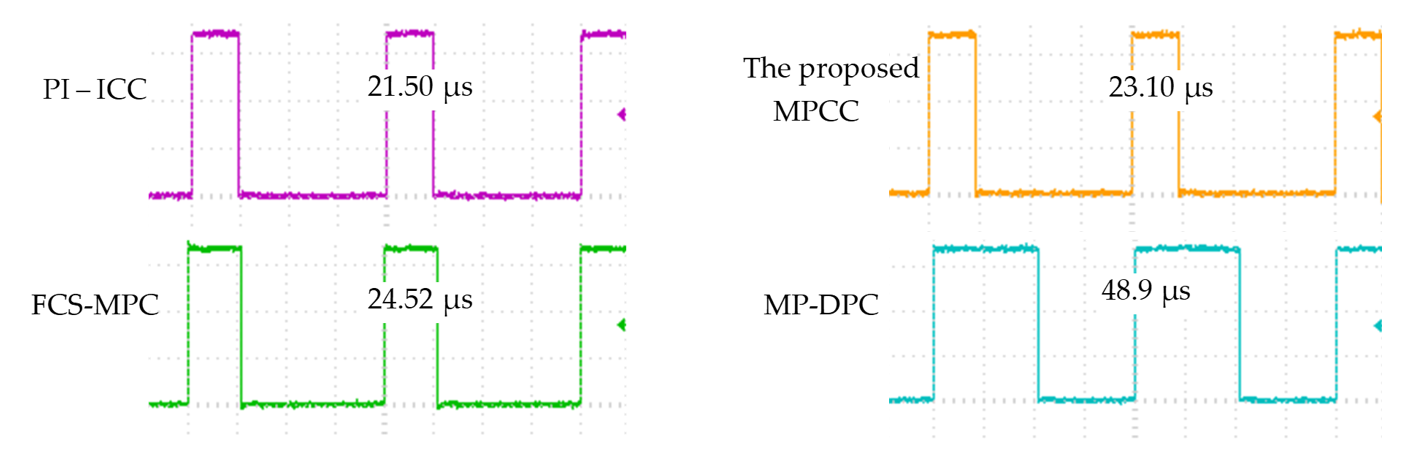
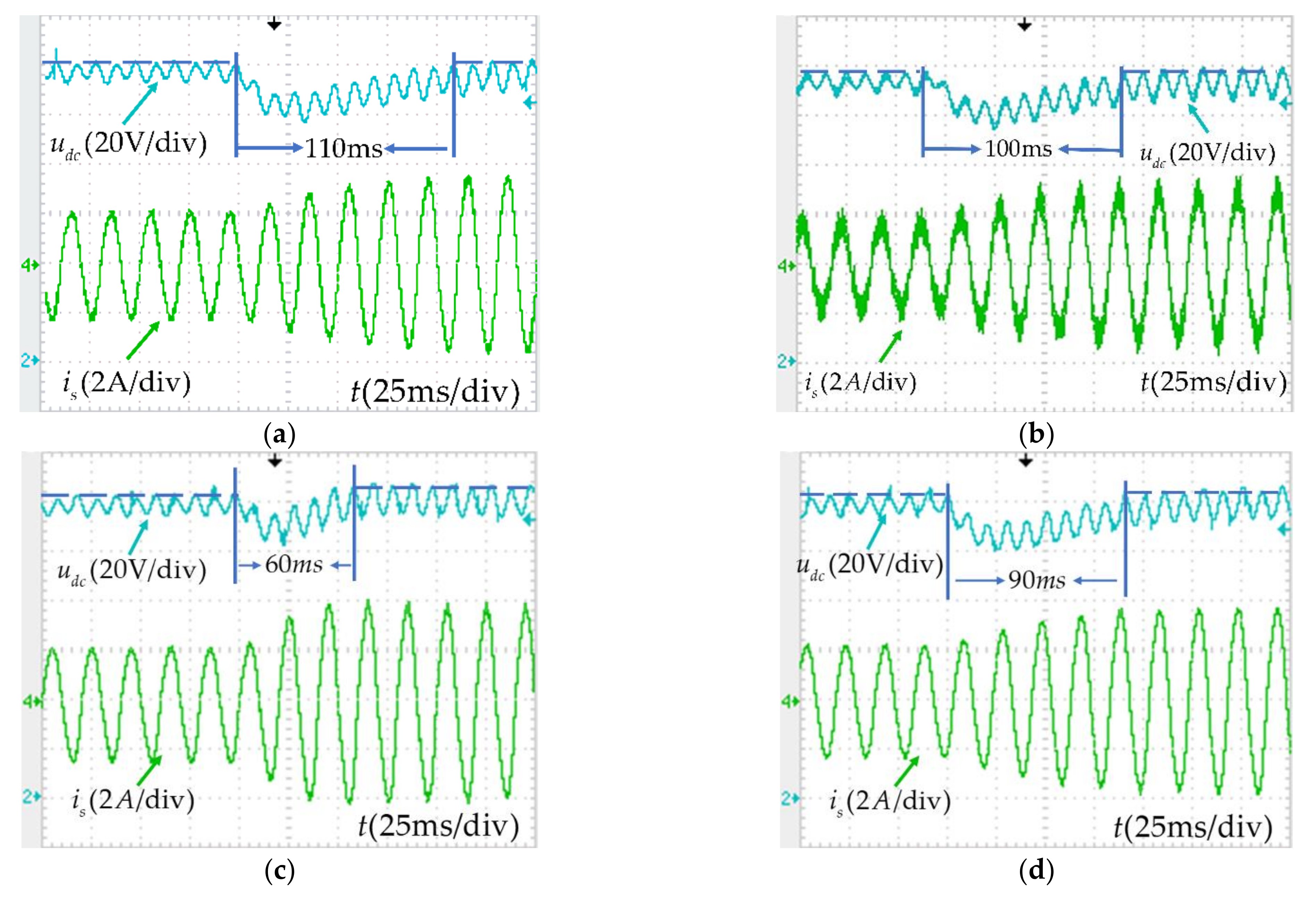
6.1. Performance Comparison with Other Algorithms
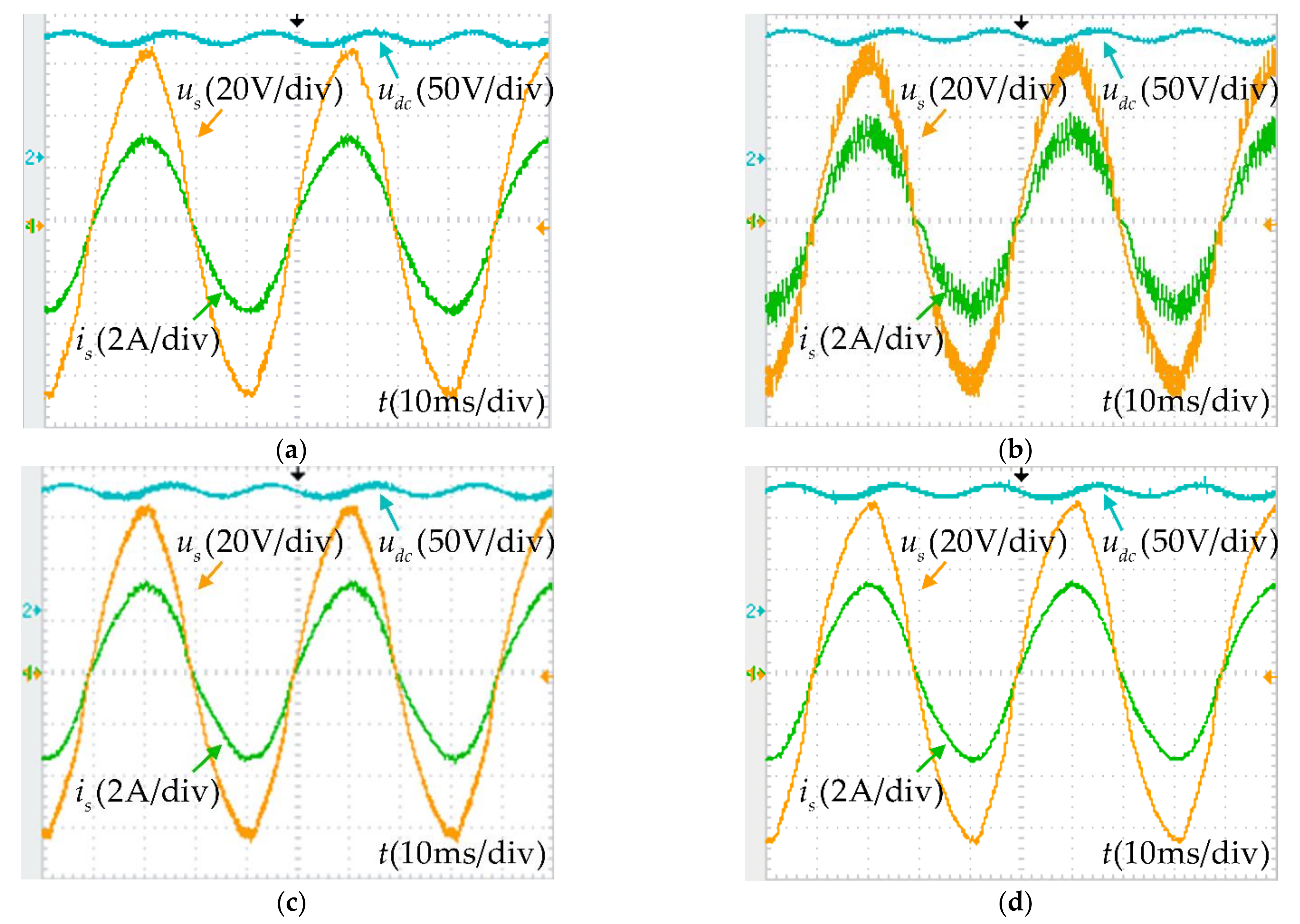
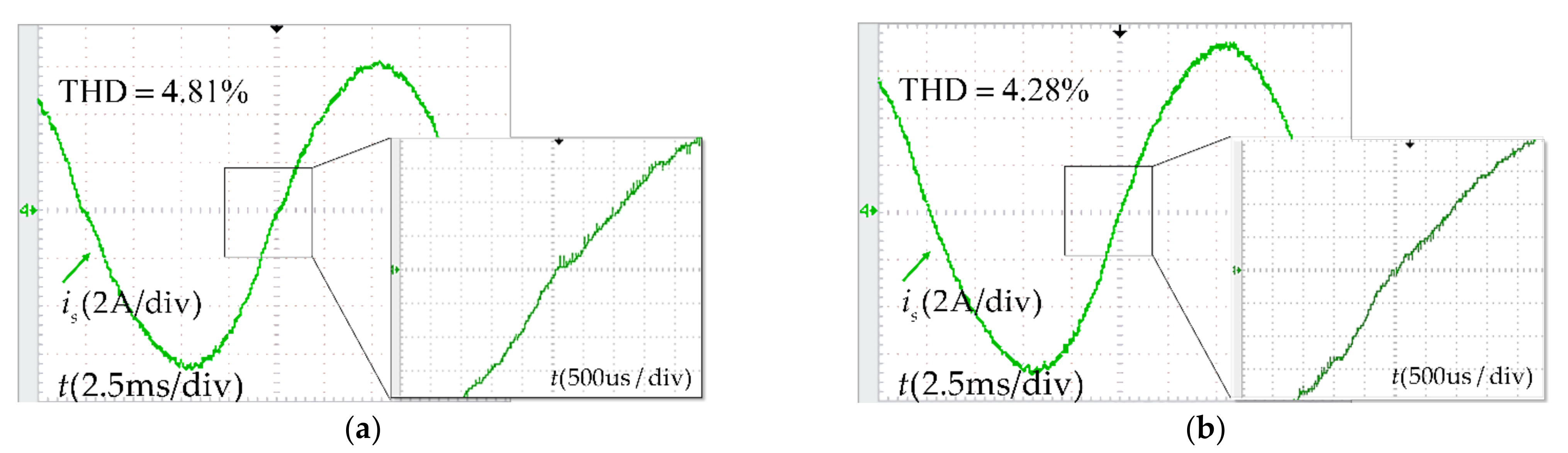
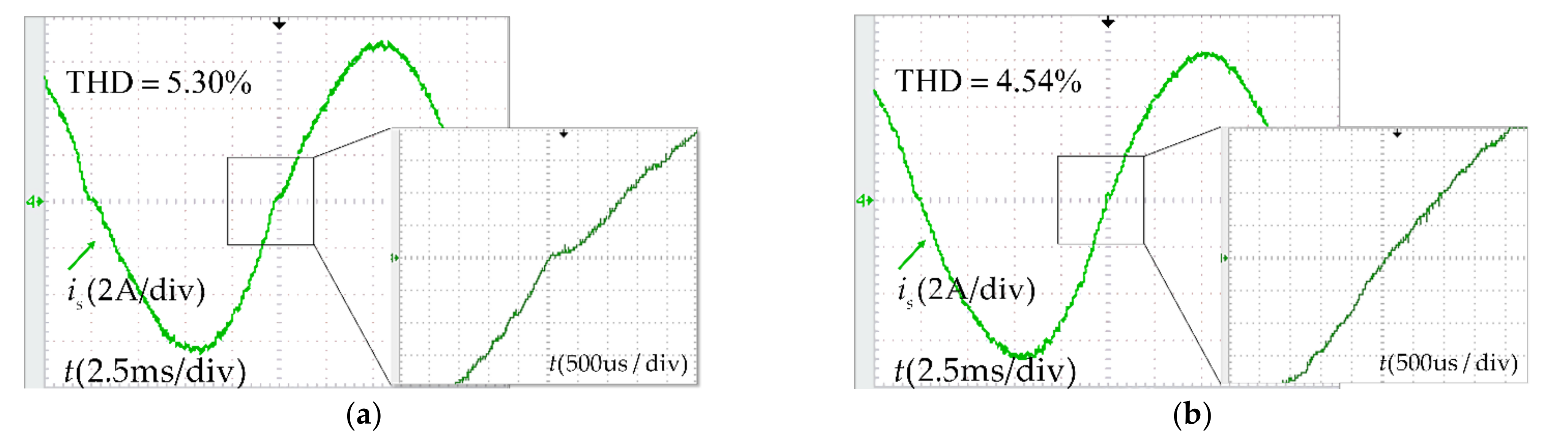
6.2. Experiment of Dead-Time Compensation
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Krein, P.T.; Balog, R.S.; Mirjafari, M. Minimum Energy and Capacitance Requirements for Single-Phase Inverters and Rectifiers Using a Ripple Port. IEEE Trans. Power Electron. 2012, 27, 4690–4698. [Google Scholar] [CrossRef]
- Youssef, A.B.; El Khil, S.K.; Slama-Belkhodja, I. State Observer-Based Sensor Fault Detection and Isolation, and Fault Tolerant Control of a Single-Phase PWM Rectifier for Electric Railway Traction. IEEE Trans. Power Electron. 2013, 28, 5842–5853. [Google Scholar] [CrossRef]
- Komurcugil, H.; Altin, N.; Ozdemir, S.; Sefa, I. An Extended Lyapunov-Function-Based Control Strategy for Single-Phase UPS Inverters. IEEE Trans. Power Electron. 2015, 30, 3976–3983. [Google Scholar] [CrossRef]
- Dixon, J.W.; Ooi, B. Indirect Current Control of a Unity Power Factor Sinusoidal Current Boost Type Three-Phase Rectifier. IEEE Trans. Ind. Electron. 1988, 35, 508–515. [Google Scholar] [CrossRef]
- Albanna, A.Z.; Hatziadoniu, C.J. Harmonic Modeling of Hysteresis Inverters in Frequency Domain. IEEE Trans. Power Electron. 2010, 25, 1110–1114. [Google Scholar] [CrossRef]
- Viswadev, R.; Mudlapur, A.; Ramana, V.V.; Venkatesaperumal, B.; Mishra, S. A Novel AC Current Sensorless Hysteresis Control for Grid-Tie Inverters. IEEE Trans Circuits Syst. II Express Briefs 2020, 67, 2577–2581. [Google Scholar] [CrossRef]
- Brenna, M.; Foiadelli, F.; Zaninelli, D. New Stability Analysis for Tuning PI Controller of Power Converters in Railway Application. IEEE Trans. Ind. Electron. 2011, 58, 533–543. [Google Scholar] [CrossRef]
- Song, H.; Keil, R.; Mutschler, P.; van der Weem, J.; Nam, K. Advanced Control Scheme for a Single-Phase PWM Rectifier in Traction Applications. In Proceedings of the 38th IAS Annual Meeting on Conference Record of the Industry Applications Conference, Salt Lake City, UT, USA, 12–16 October 2003; pp. 1558–1565. [Google Scholar]
- Husev, O.; Roncero-Clemente, C.; Makovenko, E.; Pimentel, S.P.; Vinnikov, D.; Martins, J. Optimization and Implementation of the Proportional-Resonant Controller for Grid-Connected Inverter with Significant Computation Delay. IEEE Trans. Ind. Electron. 2020, 67, 1201–1211. [Google Scholar] [CrossRef]
- Mateev, V.; Ralchev, M.; Marinova, I. Current Sensor Accuracy Enhancement by Harmonic Spectrum Analysis. In Proceedings of the 13th International Conference on Sensing Technology (ICST), Sydney, Australia, 2–4 December 2019; pp. 1–4. [Google Scholar]
- Berg, M.; Roinila, T. Dynamic Effect of Input-Voltage Feedforward in Three-Phase Grid-Forming Inverters. Energies 2020, 13, 2923. [Google Scholar] [CrossRef]
- Kwak, S.; Moon, U.; Park, J. Predictive-Control-Based Direct Power Control with an Adaptive Parameter Identification Technique for Improved AFE Performance. IEEE Trans. Power Electron. 2014, 29, 6178–6187. [Google Scholar] [CrossRef]
- Panten, N.; Hoffmann, N.; Fuchs, F.W. Finite Control Set Model Predictive Current Control for Grid-Connected Voltage-Source Converters with LCL Filters: A Study Based on Different State Feedbacks. IEEE Trans. Power Electron. 2016, 31, 5189–5200. [Google Scholar] [CrossRef]
- Ahmed, A.A.; Koh, B.K.; Lee, Y.I. A Comparison of Finite Control Set and Continuous Control Set Model Predictive Control Schemes for Speed Control of Induction Motors. IEEE Trans. Ind. Inform. 2018, 14, 1334–1346. [Google Scholar] [CrossRef]
- Wang, W.; Fan, Y.; Chen, S.; Zhang, Q. Finite Control Set Model Predictive Current Control of a Five-Phase PMSM with Virtual Voltage Vectors and Adaptive Control Set. CES Trans. Electr. Mach. Syst. 2018, 2, 136–141. [Google Scholar] [CrossRef]
- Zhang, Y.; Peng, Y.; Yang, H. Performance Improvement of Two-Vectors-Based Model Predictive Control of PWM Rectifier. IEEE Trans. Power Electron. 2016, 31, 6016–6030. [Google Scholar] [CrossRef]
- Nikhil, P.; Sonam, K.; Monika, M.; Wagh, S. Finite Control Set Model Predictive Control for Two Level Inverter with Fixed Switching Frequency. In Proceedings of the 2018 SICE International Symposium on Control Systems (SICE ISCS), Tokyo, Japan, 9–11 March 2018; pp. 74–81. [Google Scholar]
- Malinowski, M.; Jasinski, M.; Kazmierkowski, M.P. Simple Direct Power Control of Three-Phase PWM Rectifier Using Space-Vector Modulation (DPC-SVM). IEEE Trans. Ind. Electron. 2004, 51, 447–454. [Google Scholar] [CrossRef]
- Bouafia, A.; Gaubert, J.P.; Krim, F. Predictive Direct Power Control of Three-Phase Pulsewidth Modulation (PWM) Rectifier Using Space-Vector Modulation (SVM). IEEE Trans. Power Electron. 2010, 25, 228–236. [Google Scholar] [CrossRef]
- Tarisciotti, L.; Zanchetta, P.; Watson, A.; Clare, J.C.; Degano, M.; Bifaretti, S. Modulated Model Predictive Control for a Three-Phase Active Rectifier. IEEE Trans. Ind. Appl. 2015, 51, 1610–1620. [Google Scholar] [CrossRef]
- Antoniewicz, P.; Kazmierkowski, M.P. Virtual-Flux-Based Predictive Direct Power Control of AC/DC Converters with Online Inductance Estimation. IEEE Trans. Ind. Electron. 2008, 55, 4381–4390. [Google Scholar] [CrossRef]
- Hu, B.; Kang, L.; Liu, J.; Zeng, J.; Wang, S.; Zhang, Z. Model Predictive Direct Power Control with Fixed Switching Frequency and Computational Amount Reduction. IEEE J. Emerg. Sel. Top. Power Electron. 2019, 7, 956–966. [Google Scholar] [CrossRef]
- Ramirez, R.O.; Espinoza, J.R.; Villarroel, F.; Maurelia, E.; Reyes, M.E. A Novel Hybrid Finite Control Set Model Predictive Control Scheme with Reduced Switching. IEEE Trans. Ind. Electron 2014, 61, 5912–5920. [Google Scholar] [CrossRef]
- Kang, L.; Cheng, J.; Hu, B.; Luo, X.; Zhang, J. A Simplified Optimal-Switching-Sequence MPC with Finite-Control-Set Moving Horizon Optimization for Grid-Connected Inverter. Electronics 2019, 8, 457. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.; Cheng, S.; Liu, Y.; Shen, A. FCS-MPC for a Single-Phase Two-Stage Grid-Connected PV Inverter. IET Power Electron. 2019, 12, 915–922. [Google Scholar] [CrossRef]
- Azab, M. Performance of Model Predictive Control Approach for Single-Phase Distributed Energy Grid Integration with PQ Control. IET Energy Syst. Integr. 2019, 1, 121–132. [Google Scholar] [CrossRef]
- Yang, Y.; Wen, H.; Fan, M.; Xie, M.; Chen, R.; Wang, Y. A Constant Switching Frequency Model Predictive Control without Weighting Factors for T-Type Single-Phase Three-Level Inverters. IEEE Trans. Ind. Electron. 2019, 66, 5153–5164. [Google Scholar] [CrossRef]
- Song, W.; Deng, Z.; Wang, S.; Feng, X. A Simple Model Predictive Power Control Strategy for Single-Phase PWM Converters with Modulation Function Optimization. IEEE Trans. Power Electron. 2016, 31, 5279–5289. [Google Scholar] [CrossRef]
- Herran, M.A.; Fischer, J.R.; Gonzalez, S.A.; Judewicz, M.G.; Carrica, D.O. Adaptive Dead-Time Compensation for Grid-Connected PWM Inverters of Single-Stage PV Systems. IEEE Trans. Power Electron. 2013, 28, 2816–2825. [Google Scholar] [CrossRef]
- Mora, A.; Juliet, J.; Santander, A.; Lezana, P. Dead-Time and Semiconductor Voltage Drop Compensation for Cascaded H-Bridge Converters. IEEE Trans. Ind. Electron. 2016, 63, 7833–7842. [Google Scholar] [CrossRef]
- Liu, G.; Wang, D.; Jin, Y.; Wang, M.; Zhang, P. Current-Detection-Independent Dead-Time Compensation Method Based on Terminal Voltage A/D Conversion for PWM VSI. IEEE Trans. Ind. Electron. 2017, 64, 7689–7699. [Google Scholar] [CrossRef]
- Kim, E.; Seong, U.; Lee, J.; Hwang, S. Compensation of Dead Time Effects in Grid-Tied Single-Phase Inverter Using SOGI. In Proceedings of the IEEE Applied Power Electronics Conference and Exposition (APEC), Tampa, FL, USA, 26–30 March 2017; pp. 2633–2637. [Google Scholar]
- Li, X.; Akin, B.; Rajashekara, K. Vector Based Dead-Time Compensation for Three-Level T-type Converters. IEEE Trans. Ind. Appl. 2016, 52, 1597–1607. [Google Scholar]
- Hu, B.; Kang, L.; Cheng, J.; Linghu, J.; Zhang, Z. Integrated Dead-Time Compensation and Elimination Approach for Model Predictive Power Control with Fixed Switching Frequency. IET Power Electron. 2019, 12, 1220–1228. [Google Scholar] [CrossRef]
- Lin, Y.; Lai, Y. Dead-Time Elimination of PWM-Controlled Inverter/Converter without Separate Power Sources for Current Polarity Detection Circuit. IEEE Trans. Ind. Electron. 2009, 56, 2121–2127. [Google Scholar]
- Chen, L.; Peng, F.Z. Dead-Time Elimination for Voltage Source Inverters. IEEE Trans. Power Electron. 2008, 23, 574–580. [Google Scholar] [CrossRef]


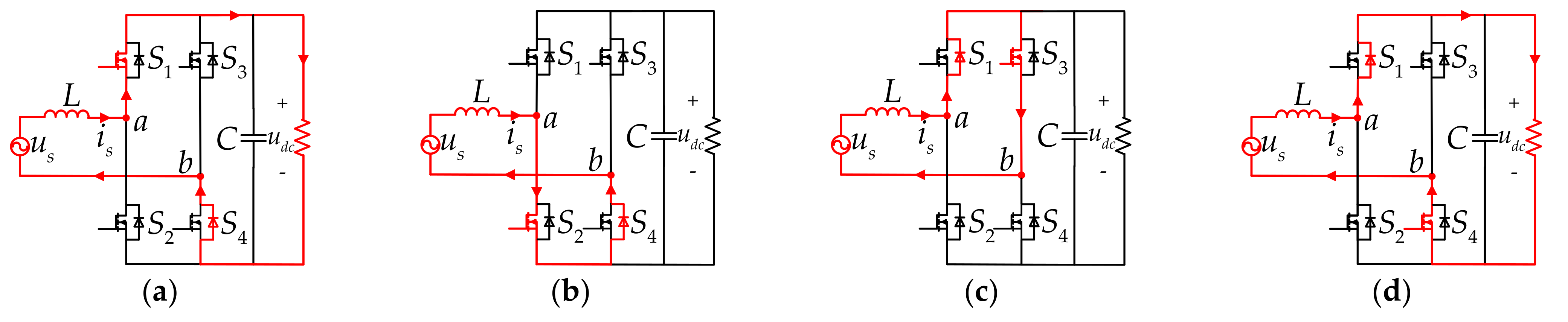
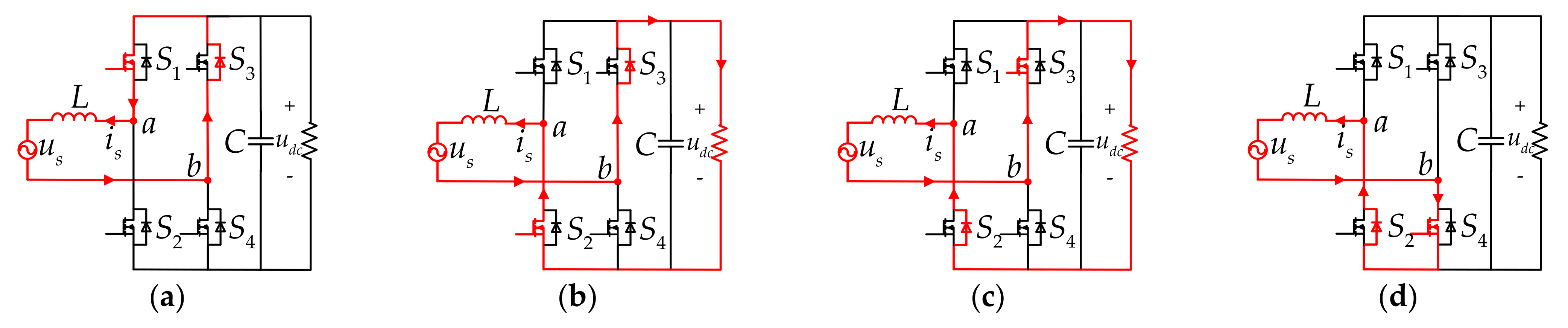



| 1 | 0 | 0 | 1 | |
| 1 | 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 | |
| 0 | 1 | 0 | 1 | 0 |
| Vectors | (1,0,0,1) | (0,1,1,0) | (1,0,1,0) | (0,1,0,1) |
|---|---|---|---|---|
| Switches | ||||
| 0 | 0 | |||
| 0 | 0 | |||
| 0 | 0 | |||
| 0 | 0 |
| Combinations | (1,0,0,1) (1,0,1,0), (0,1,0,1) | (0,1,0,1) (1,0,1,0), (0,1,0,1) |
|---|---|---|
| Switches | ||
| (1,0,0,0) | (0,1,0,0) | (0,0,1,0) | (0,0,0,1) | |
|---|---|---|---|---|
| System Parameters | Symbol | Value |
|---|---|---|
| Filter inductance | L | 10 mH |
| DC-link capacitor | C | 220 µF |
| DC-link voltage | 120 V | |
| AC Voltage peak | 60 V | |
| Load resistance | 150 Ω | |
| Sampling frequency | 20 kHz | |
| Dead-time | 2 µs |
| Performance | PI-ICC | FCS-MPC | MP-DPC | The Proposed MPCC |
|---|---|---|---|---|
| THD | 5.64% | 14.34% | 6.55% | 4.28% |
| Execution time | 21.50 µs | 24.52 µs | 48.9 µs | 23.10 µs |
| Settling time of DC voltage | 110 ms | 100 ms | 60 ms | 90 ms |
| PI controller number | 2 | 1 | 1 | 1 |
| Inner controller | current | current | power | current |
| Dead-Time | 2 µs | 4 µs | 6 µs | |||
|---|---|---|---|---|---|---|
| Performance | ||||||
| Is There Compensation (yes or no) | no | yes | no | yes | no | yes |
| Clamping time | 200 µs | none | 300 µs | none | 500 µs | none |
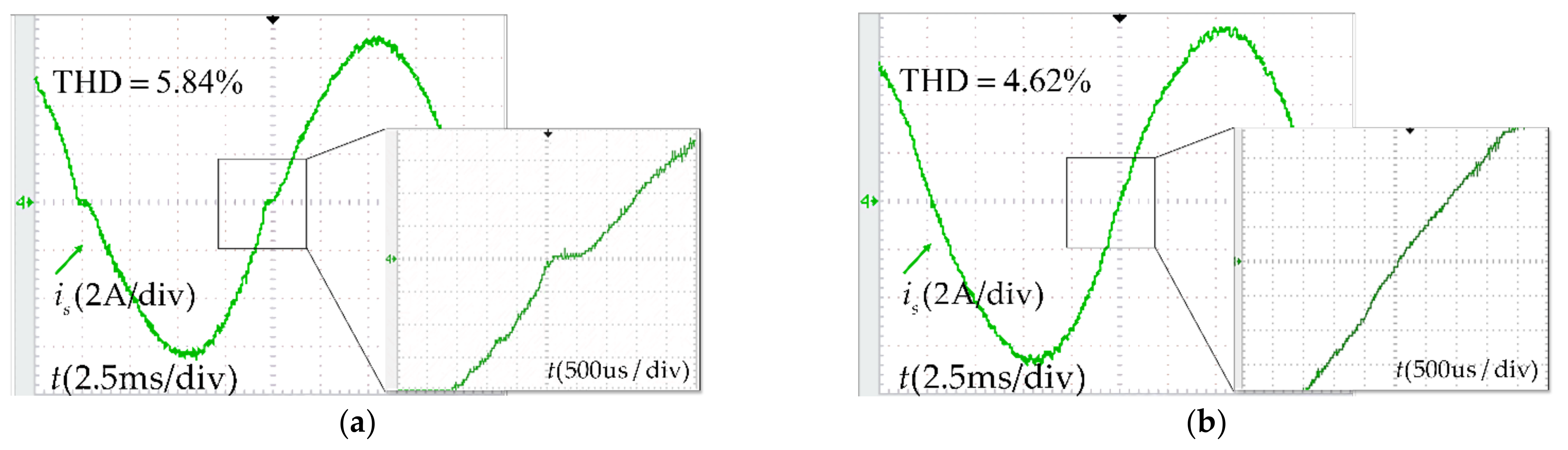
| THD | 4.81% | 4.28% | 5.30% | 4.54% | 5.84% | 4.62% |
| PF | 1.000 | 1.000 | 1.000 | 1.000 | 0.991 | 1.000 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kang, L.; Zhang, J.; Zhou, H.; Zhao, Z.; Duan, X. Model Predictive Current Control with Fixed Switching Frequency and Dead-Time Compensation for Single-Phase PWM Rectifier. Electronics 2021, 10, 426. https://doi.org/10.3390/electronics10040426
Kang L, Zhang J, Zhou H, Zhao Z, Duan X. Model Predictive Current Control with Fixed Switching Frequency and Dead-Time Compensation for Single-Phase PWM Rectifier. Electronics. 2021; 10(4):426. https://doi.org/10.3390/electronics10040426
Chicago/Turabian StyleKang, Longyun, Jianbin Zhang, Hailan Zhou, Zixian Zhao, and Xinwei Duan. 2021. "Model Predictive Current Control with Fixed Switching Frequency and Dead-Time Compensation for Single-Phase PWM Rectifier" Electronics 10, no. 4: 426. https://doi.org/10.3390/electronics10040426





