Prediction Model for Random Variation in FinFET Induced by Line-Edge-Roughness (LER)
Abstract
1. Introduction
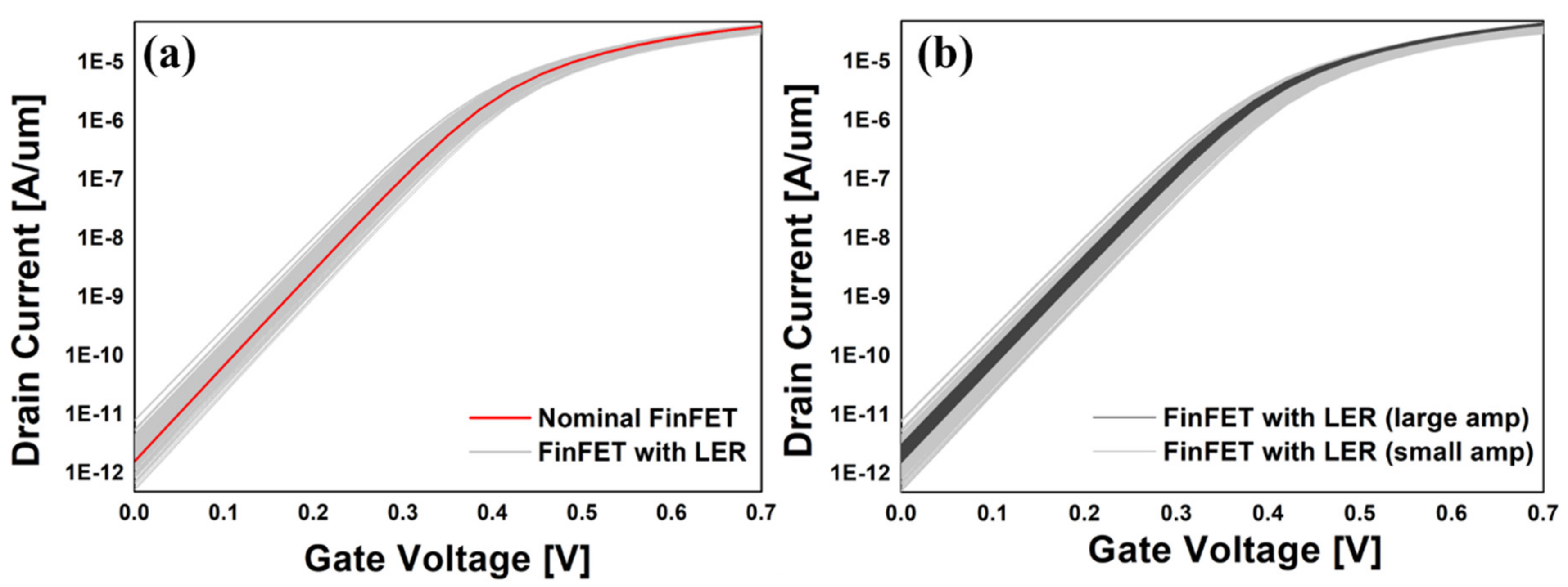
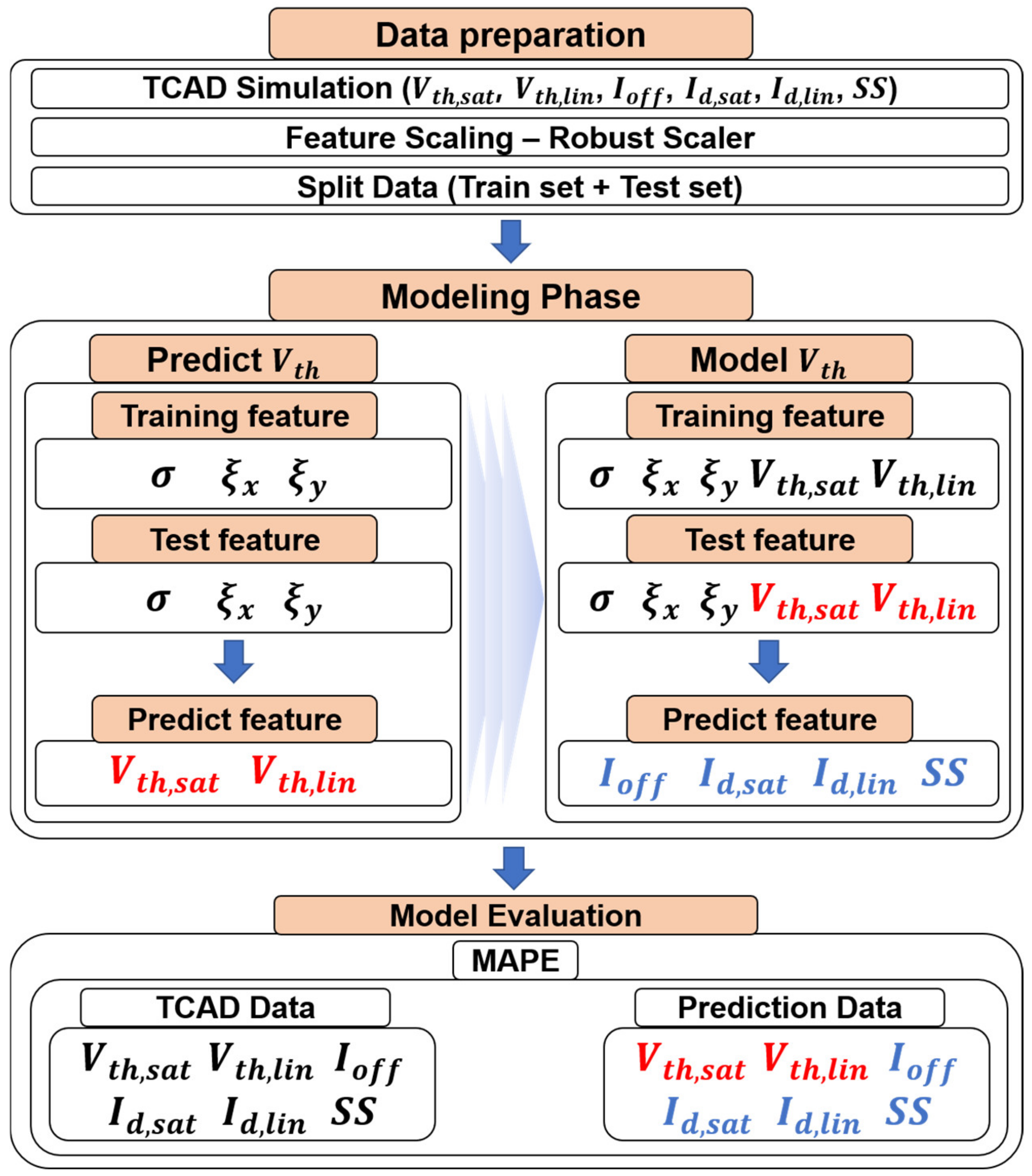
2. Simulation
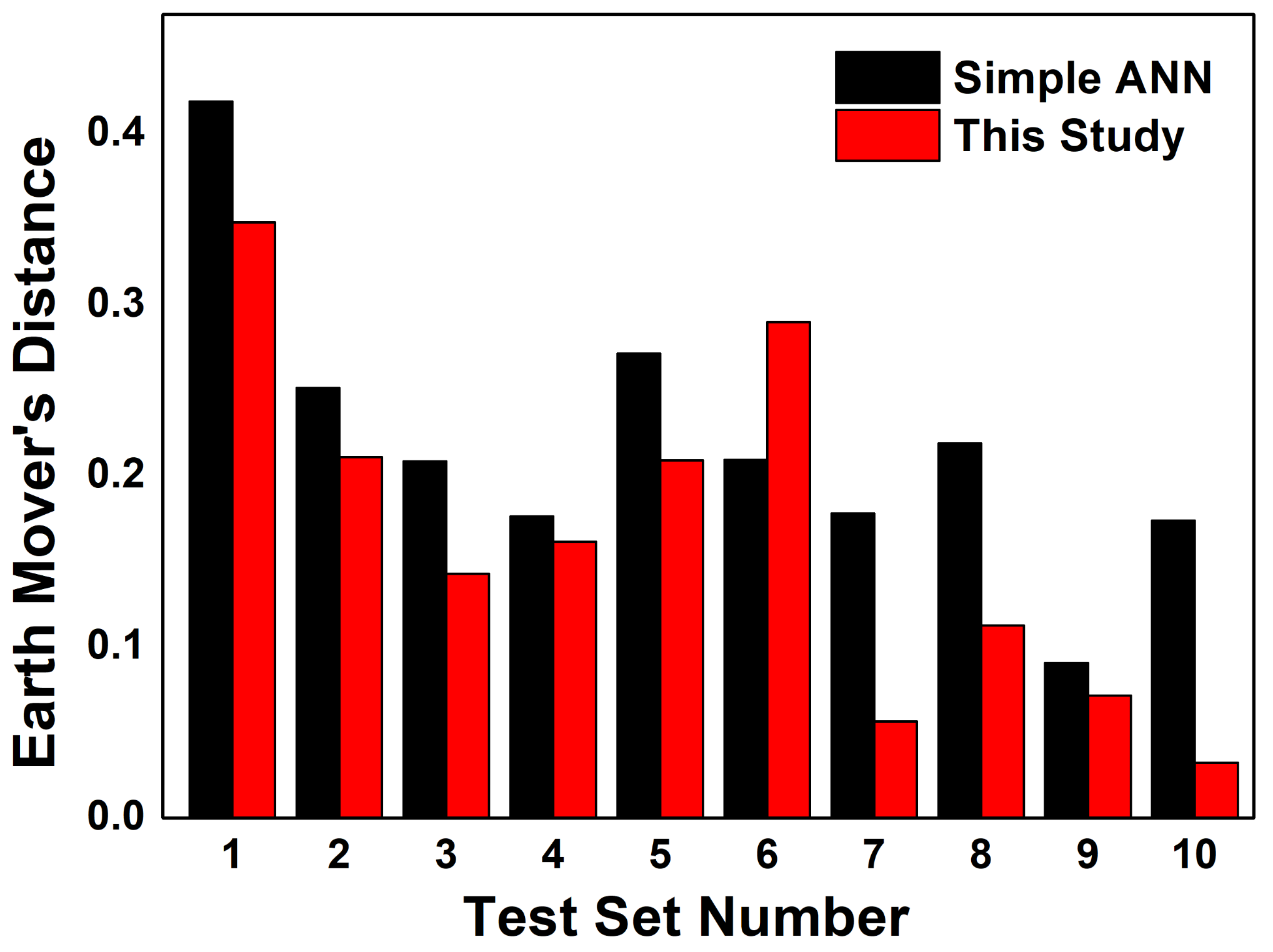
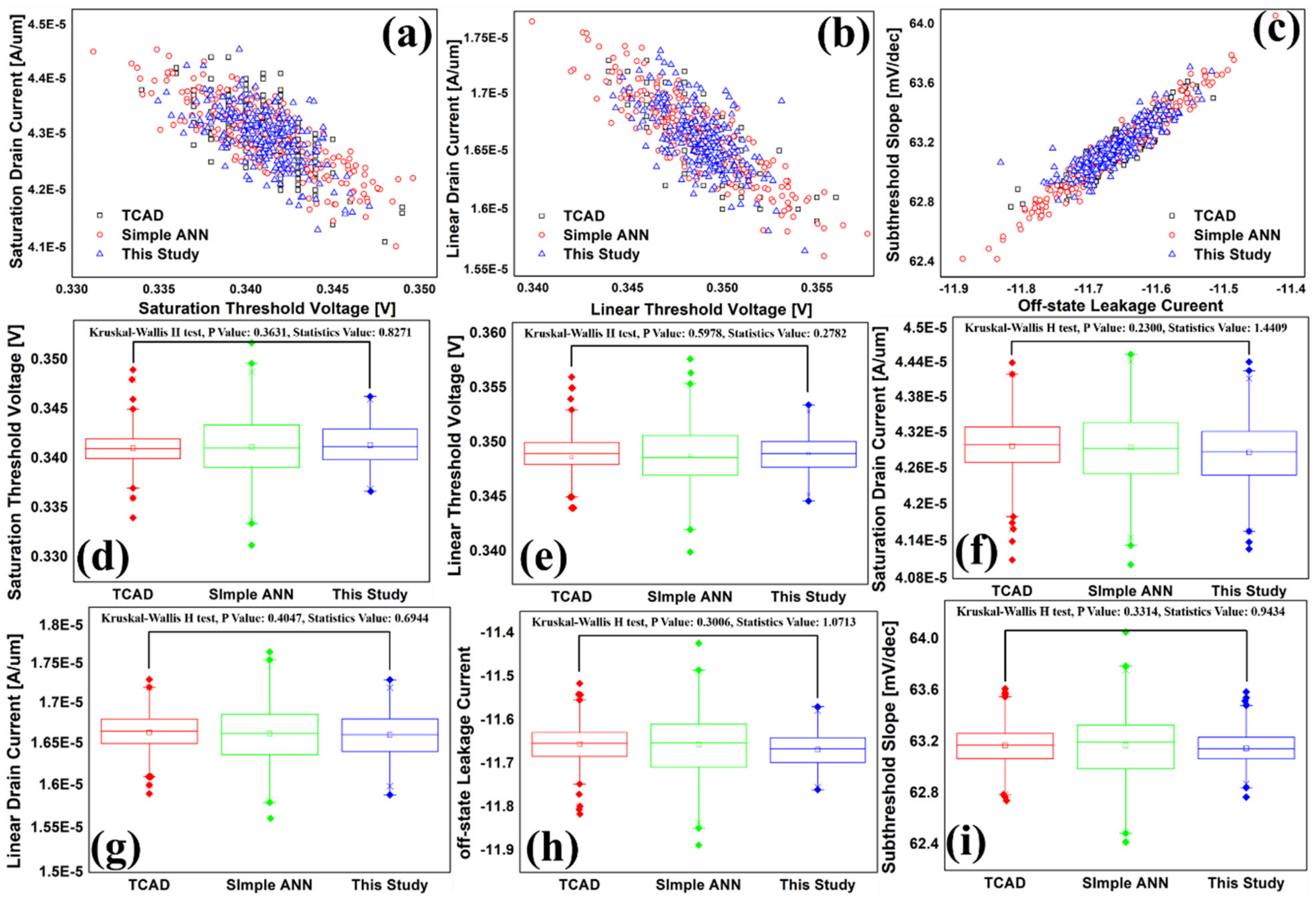
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Asenov, A.; Kaya, S.; Brown, A.R. Intrinsic parameter fluctuations in decananometer MOSFETs introduced by gate line edge roughness. IEEE Trans. Electron Devices 2003, 50, 1254–1260. [Google Scholar] [CrossRef]
- Asenov, A. Random dopant induced threshold voltage lowering and fluctuations in sub-0.1/spl mu/m MOSFET’s: A 3-D “atomistic” simulation study. IEEE Trans. Electron Devices 1998, 45, 2505–2513. [Google Scholar] [CrossRef]
- Brown, A.R.; Roy, G.; Asenov, A. Poly-Si-gate-related variability in decananometer MOSFETs with conventional architecture. IEEE Trans. Electron Devices 2007, 54, 3056–3063. [Google Scholar] [CrossRef]
- Tsubaki, H.; Yamanaka, T.; Nishiyama, F.; Shitabatake, K. A study on the material design for the reduction of LWR. In Proceedings of the Advances in Resist Materials and Processing Technology XXIV, San Jose, CA, USA, 26–28 February 2007; p. 651918. [Google Scholar]
- Tagawa, S.; Nagahara, S.; Iwamoto, T.; Wakita, M.; Kozawa, T.; Yamamoto, Y.; Werst, D.; Trifunac, A.D. Radiation and photochemistry of onium salt acid generators in chemically amplified resists. In Proceedings of the Advances in Resist Technology and Processing XVII, Santa Clara, CA, USA, 28 February–1 March 2000; pp. 204–213. [Google Scholar]
- Prabhu, V.M.; Vogt, B.D.; Kang, S.; Rao, A.; Lin, E.K.; Satija, S.K.; Turnquest, K. Direct measurement of the in-situ developed latent image: The residual swelling fraction. In Proceedings of the Advances in Resist Materials and Processing Technology XXIV, San Jose, CA, USA, 26–28 February 2007; p. 651910. [Google Scholar]
- Constantoudis, V.; Patsis, G.; Tserepi, A.; Gogolides, E. Quantification of line-edge roughness of photoresists. II. Scaling and fractal analysis and the best roughness descriptors. J. Vac. Sci. Technol. B Microelectron. Nanometer Struct. Process. Meas. Phenom. 2003, 21, 1019–1026. [Google Scholar] [CrossRef]
- Patsis, G.P.; Constantoudis, V.; Tserepi, A.; Gogolides, E.; Grozev, G.; Hoffmann, T. Roughness analysis of lithographically produced nanostructures: Off-line measurement and scaling analysis. Microelectron. Eng. 2003, 67, 319–325. [Google Scholar] [CrossRef]
- Constantoudis, V.; Patsis, G.P.; Gogolides, E. Photoresist line-edge roughness analysis using scaling concepts. J. Micro/Nanolithogr. MEMS MOEMS 2004, 3, 429–436. [Google Scholar] [CrossRef]
- Yamaguchi, A.; Tsuchiya, R.; Fukuda, H.; Komuro, O.; Kawada, H.; Iizumi, T. Characterization of line-edge roughness in resist patterns and estimations of its effect on device performance. In Proceedings of the Metrology, Inspection, and Process Control for Microlithography XVII, Santa Clara, CA, USA, 24–27 February 2003; pp. 689–698. [Google Scholar]
- Bunday, B.D.; Bishop, M.; Villarrubia, J.S.; Vladar, A.E. CD-SEM measurement line-edge roughness test patterns for 193-nm lithography. In Proceedings of the Metrology, Inspection, and Process Control for Microlithography XVII, Santa Clara, CA, USA, 24–27 February 2003; pp. 674–688. [Google Scholar]
- Wang, X.-B.; Ferris, K.; Wang, L.-S. Photodetachment of gaseous multiply charged anions, copper phthalocyanine tetrasulfonate tetraanion: Tuning molecular electronic energy levels by charging and negative electron binding. J. Phys. Chem. A 2000, 104, 25–33. [Google Scholar] [CrossRef]
- Stewart, M.D.; Tran, H.V.; Schmid, G.M.; Stachowiak, T.B.; Becker, D.J.; Willson, C.G. Acid catalyst mobility in resist resins. J. Vac. Sci. Technol. B Microelectron. Nanometer Struct. Process. Meas. Phenom. 2002, 20, 2946–2952. [Google Scholar] [CrossRef]
- Oh, S.; Shin, C. 3-D quasi-atomistic model for line edge roughness in nonplanar MOSFETs. IEEE Trans. Electron Devices 2016, 63, 4617–4623. [Google Scholar] [CrossRef]
- Burke, S. Missing values, outliers, robust statistics & non-parametric methods. Sci. Data Manag. 1998, 1, 32–38. [Google Scholar]
- Baravelli, E.; Dixit, A.; Rooyackers, R.; Jurczak, M.; Speciale, N.; De Meyer, K. Impact of line-edge roughness on FinFET matching performance. IEEE Trans. Electron Devices 2007, 54, 2466–2474. [Google Scholar] [CrossRef]
- Chen, Y.-N.; Chen, C.-J.; Fan, M.-L.; Hu, V.P.-H.; Su, P.; Chuang, C.-T. Impacts of work function variation and line-edge roughness on TFET and FinFET devices and 32-bit CLA circuits. J. Low Power Electron. Appl. 2015, 5, 101–115. [Google Scholar] [CrossRef]
- Bircanoğlu, C.; Arıca, N. A comparison of activation functions in artificial neural networks. In Proceedings of the 2018 26th Signal Processing and Communications Applications Conference (SIU), Izmir, Turkey, 2–5 May 2018; pp. 1–4. [Google Scholar]
- Ioffe, S.; Szegedy, C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. arXiv 2015, arXiv:1502.03167. [Google Scholar]
- Rubner, Y.; Tomasi, C.; Guibas, L.J. A metric for distributions with applications to image databases. In Proceedings of the Sixth International Conference on Computer Vision (IEEE Cat. No. 98CH36271), Bombay, India, 7 January 1998; 56, pp. 59–66. [Google Scholar]


| Device Parameters | |||
|---|---|---|---|
| Symbol | Description | Unit | Value |
| Lg | Gate length | nm | 20 |
| Tox | Equivalent oxide thickness (HfO2) | nm | 0.3 |
| Wfin | Fin width | nm | 7 |
| Hfin | Fin height | nm | 50 |
| VDD | Power supply voltage | V | 0.7 |
| IVti | Constant current | A/um | 5.35 × 10−7 |
| σ | RMS amplitude | nm | 0.1~0.8 |
| ξx | x-axis correlation length | nm | 10~100 |
| ξy | y-axis correlation length | nm | 20~200 |
| Model | Time | |
|---|---|---|
| Simple ANN | 450 s (15,000 epoch) | |
| This study | Predict Vth | 100 s (5000 epoch) |
| Model Vth | 175 s (5000 epoch) | |
| TEST SET | Amp. | Corr. x | Corr. y | EMD | |
|---|---|---|---|---|---|
| Simple ANN | 1 | 0.6248 | 17.0074 | 173.8572 | 0.419317 |
| 2 | 0.5565 | 80.9191 | 80.5699 | 0.251837 | |
| 3 | 0.5047 | 48.6240 | 67.9938 | 0.208757 | |
| 4 | 0.5605 | 25.4287 | 69.3974 | 0.176496 | |
| 5 | 0.6373 | 69.1486 | 65.3304 | 0.271804 | |
| 6 | 0.7295 | 89.3916 | 195.6248 | 0.209605 | |
| 7 | 0.1527 | 23.3264 | 51.2533 | 0.178308 | |
| 8 | 0.6899 | 85.0886 | 80.9837 | 0.219300 | |
| 9 | 0.2593 | 78.1265 | 28.0868 | 0.090672 | |
| 10 | 0.1411 | 96.7100 | 186.6837 | 0.174057 | |
| Average EMD | 0.220015 | ||||
| This Study | 1 | 0.6248 | 17.0074 | 173.8572 | 0.348625 |
| 2 | 0.5565 | 80.9191 | 80.5699 | 0.211269 | |
| 3 | 0.5047 | 48.6240 | 67.9938 | 0.143110 | |
| 4 | 0.5605 | 25.4287 | 69.3974 | 0.161759 | |
| 5 | 0.6373 | 69.1486 | 65.3304 | 0.209351 | |
| 6 | 0.7295 | 89.3916 | 195.6248 | 0.290165 | |
| 7 | 0.1527 | 23.3264 | 51.2533 | 0.056710 | |
| 8 | 0.6899 | 85.0886 | 80.9837 | 0.112868 | |
| 9 | 0.2593 | 78.1265 | 28.0868 | 0.071807 | |
| 10 | 0.1411 | 96.7100 | 186.6837 | 0.032418 | |
| Average EMD | 0.163808 | ||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, J.; Park, T.; Ahn, H.; Kwak, J.; Moon, T.; Shin, C. Prediction Model for Random Variation in FinFET Induced by Line-Edge-Roughness (LER). Electronics 2021, 10, 455. https://doi.org/10.3390/electronics10040455
Lee J, Park T, Ahn H, Kwak J, Moon T, Shin C. Prediction Model for Random Variation in FinFET Induced by Line-Edge-Roughness (LER). Electronics. 2021; 10(4):455. https://doi.org/10.3390/electronics10040455
Chicago/Turabian StyleLee, Jinwoong, Taeeon Park, Hongjoon Ahn, Jihwan Kwak, Taesup Moon, and Changhwan Shin. 2021. "Prediction Model for Random Variation in FinFET Induced by Line-Edge-Roughness (LER)" Electronics 10, no. 4: 455. https://doi.org/10.3390/electronics10040455
APA StyleLee, J., Park, T., Ahn, H., Kwak, J., Moon, T., & Shin, C. (2021). Prediction Model for Random Variation in FinFET Induced by Line-Edge-Roughness (LER). Electronics, 10(4), 455. https://doi.org/10.3390/electronics10040455








