Design of Cut Off-Frequency Fixing Filters by Error Compensation of MAXFLAT FIR Filters
Abstract
1. Introduction
2. Closed-Form Chebyshev Polynomial for Cutoff-Frequency Fixing Filter Design
3. The Order of Flatness (K)
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhao, H.; Zhang, L.; Liu, J.; Zhang, C.; Cai, J.; Shen, L. Design of a Low-Order FIR Filter for a High-Frequency Square-Wave Voltage Injection Method of the PMLSM Used in Maglev Train. Electronics 2020, 9, 729. [Google Scholar] [CrossRef]
- Kalpun, D.; Butusov, D.; Ostrovskii, V.; Veligosha, A.; Gulvanskii, V. Optimization of the FIR filter structure in finite residue field algebra. Electronics 2018, 7, 372. [Google Scholar]
- Vaidyanathan, P. Efficient and multiplierless design of FIR filters with very sharp cutoff via maximally flat building blocks. IEEE Trans. Circuits Syst. 1985, 32, 236–244. [Google Scholar] [CrossRef]
- Vaidyanathan, P. Optimal design of linear phase FIR digital filters with very flat passbands and equiripple stopbands. IEEE Trans. Circuits Syst. 1985, 32, 904–917. [Google Scholar] [CrossRef]
- Samadi, S.; Nishihara, A. The world of flatness. IEEE Circuits Syst. Mag. 2007, 7, 38–44. [Google Scholar] [CrossRef]
- Ping, Z.; Chun, Z. Four-Channel Tight Wavelet Frames Design Using Bernstein Polynomial. Circuits Syst. Signal Process. 2012, 31, 1847–1861. [Google Scholar]
- Huang, X.; Jing, S.; Wang, Z.; Xu, Y.; Zheng, Y. Closed-form FIR filter design based on convolution window spectrum interpolation. IEEE Trans. Signal Process. 2015, 64, 1173–1186. [Google Scholar] [CrossRef]
- Huang, X.; Wang, Y.; Yan, Z.; Xian, H.; Liu, M. Closed-form FIR filter design with accurately controllable cut-off frequency. Circuits Syst. Signal Process. 2017, 36, 721–741. [Google Scholar] [CrossRef]
- Tseng, C.C.; Lee, S.L. Closed-form designs of digital fractional order Butterworth filters using discrete transforms. Signal Process. 2017, 137, 80–97. [Google Scholar] [CrossRef]
- Roy, S.; Chandra, A. On the Order Minimization of interpolated Bandpass Method Based Narrow Transition Band FIR Filter Design. IEEE Trans. Circuits Syst. I Reg. Pap. 2019, 66, 4287–4295. [Google Scholar] [CrossRef]
- Huang, X.; Zhang, B.; Qin, H.; An, W. Closed-form design of variable fractional-delay FIR filters with low or middle cutoff frequencies. IEEE Trans. Circuits Syst. I Reg. Pap. 2017, 65, 628–637. [Google Scholar] [CrossRef]
- Kušljević, M.D.; Tomić, J.J.; Poljak, P.D. Maximally Flat-Frequency-Response Multiple-Resonator-Based Harmonic Analysis. IEEE Trans. Instrum. Meas. 2017, 66, 3387–3398. [Google Scholar] [CrossRef]
- Yoshida, T.; Aikawa, N. Low-Delay Band-Pass Maximally Flat FIR Digital Differentiators. Circuits Syst. Signal Process. 2018, 37, 3576–3588. [Google Scholar] [CrossRef]
- Roy, S.; Chandra, A. Design of narrow transition band variable bandwidth digital filter. IET Circuits Devices Syst. 2020, 14, 750–757. [Google Scholar] [CrossRef]
- Herrmann, O. On the approximation problem in nonrecursive digital filter design. IEEE Trans. Circ. Theory 1971, 18, 411–413. [Google Scholar] [CrossRef]
- Miller, J.A. Maximally flat nonrecursive digital filters. Electron. Lett. 1972, 8, 157–158. [Google Scholar] [CrossRef]
- Rajagpoal, L.; Roy, S.C.D. Design of maximally-flat FIR filters using the Bernstein polynomial. IEEE Trans. Circuits Syst. 1987, 34, 1587–1590. [Google Scholar]
- Fahmy, M.F. Maximally flat non-recursive digital filters. Int. J. Circuit Theory Appl. 1976, 4, 311–313. [Google Scholar] [CrossRef]
- Bromba, M.U.A.; Ziegler, H. Explicit formula for filter function of maximally flat nonrecursive digital filters. Electron Lett. 1980, 16, 905–906. [Google Scholar] [CrossRef]
- Thajchayapong, P.; Puangpool, M.; Banjongjit, S. Maximally Flat FIR filters with prescribed cut-off frequency. Electron. Lett. 1980, 16, 514–515. [Google Scholar] [CrossRef]
- Roy, S.C.D. A New Chebyshev-like Low-pass Filter Approximation. Circuits Syst. Signal Process. 2010, 29, 629–636. [Google Scholar]
- Rajagpoal, L.; Roy, S.C.D. Optimal design of maximally flat FIR filters with arbitrary magnitude specifications. IEEE Trans. Acoust. Speech Signal Process. 1989, 37, 512–518. [Google Scholar] [CrossRef]
- Jeon, J.; Kim, D. Design of nonrecursive FIR filters with simultaneously MAXFLAT magnitude and prescribed cutoff frequency. Digital Signal Process. 2012, 22, 1085–1094. [Google Scholar] [CrossRef]
- Lian, Y.; Yu, Y.J. Guest Editorial: Low-Power Digital Filter Design Techniques and Their Applications. Circuits Syst Signal Process. 2010, 29, 1–5. [Google Scholar] [CrossRef][Green Version]
- Vlcek, M.; Unbehauen, R. Analytical solution of design for IIR equiripple filters. IEEE Trans. Acoust. Speech Signal Process. 1989, 37, 1518–1531. [Google Scholar] [CrossRef]
- Kaiser, J.F. Comments on maximally flat nonrecursive digital filters. Int. J. Circuit Theory Appl. 1977, 5, 103. [Google Scholar] [CrossRef]
- Jinaga, B.C.; Roy, S.C.D. Explicit formulas for the Weighting coefficients of maximally flat nonrecursive digital filters. Proc. IEEE. 1984, 72, 1092. [Google Scholar] [CrossRef]
- Jinaga, B.C.; Roy, S.C.D. Explicit formula for the coefficients of maximally flat nonrecursive digital filter transfer function expressed in powers of cos w. Proc. IEEE. 1985, 73, 1135–1136. [Google Scholar] [CrossRef]
- Kumar, B.; Kumar, A. Efficient linear-phase FIR, maximally flat error approximations for the amplitude response |1/ωr|, r = 1, 2, 3, …, and a versatile realization. Circuits Syst. Signal Process. 2000, 19, 567–580. [Google Scholar] [CrossRef]
- Vesma, J.; Saramaki, T. Polynomial-Based Interpolation Filters—Part I: Filter Synthesis. Circuits Syst. Signal Process. 2007, 26, 115–146. [Google Scholar] [CrossRef]
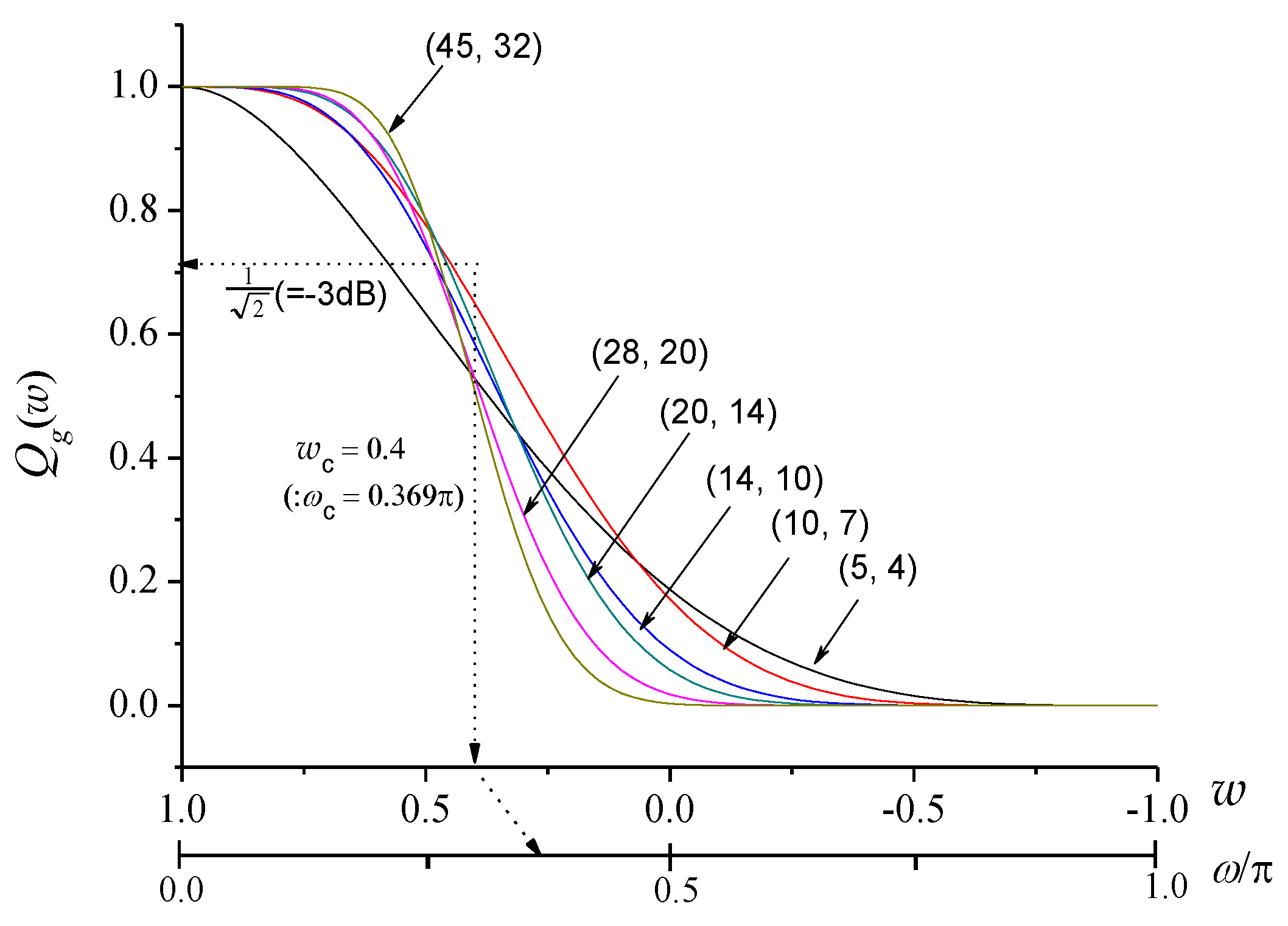
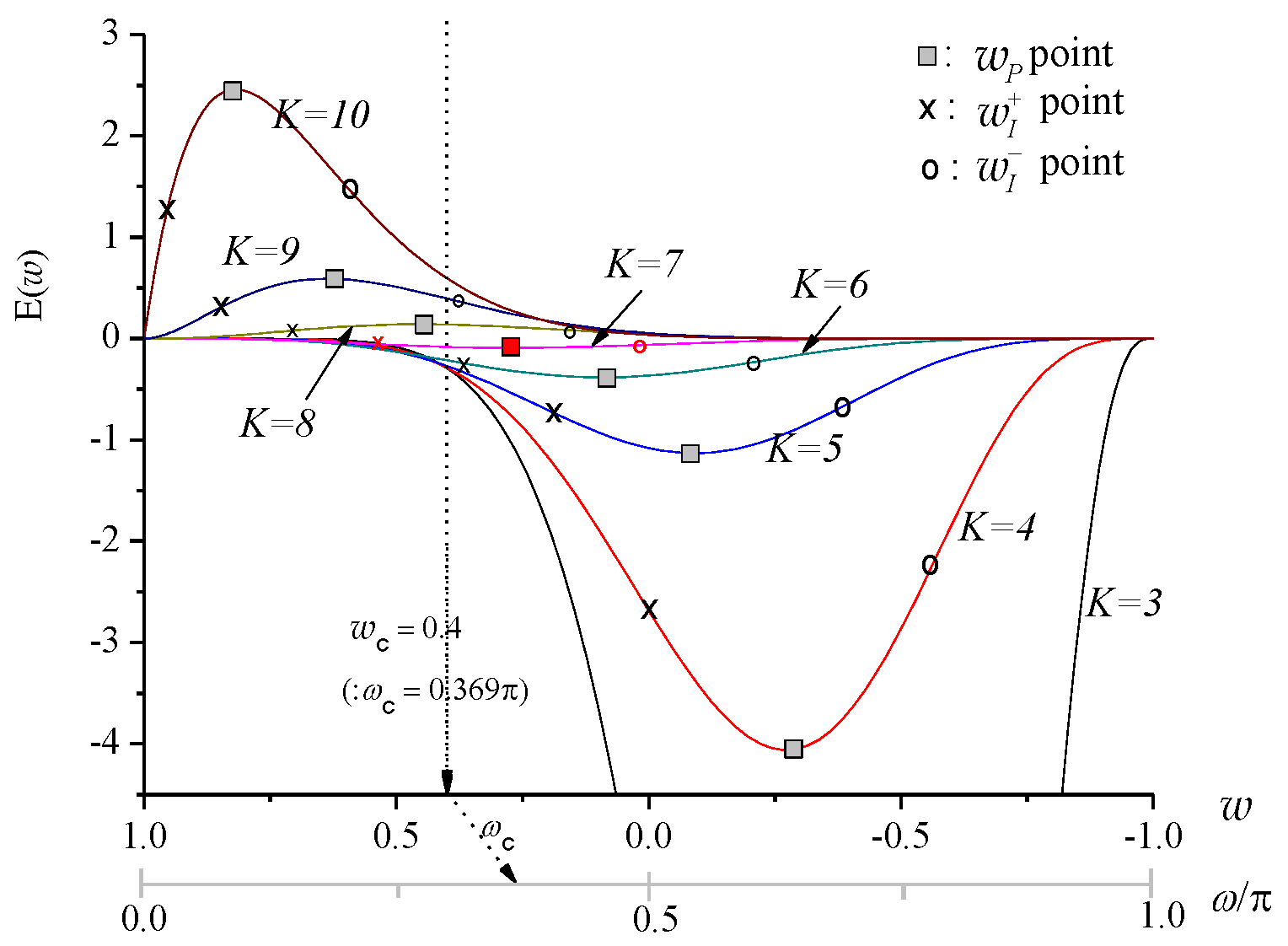
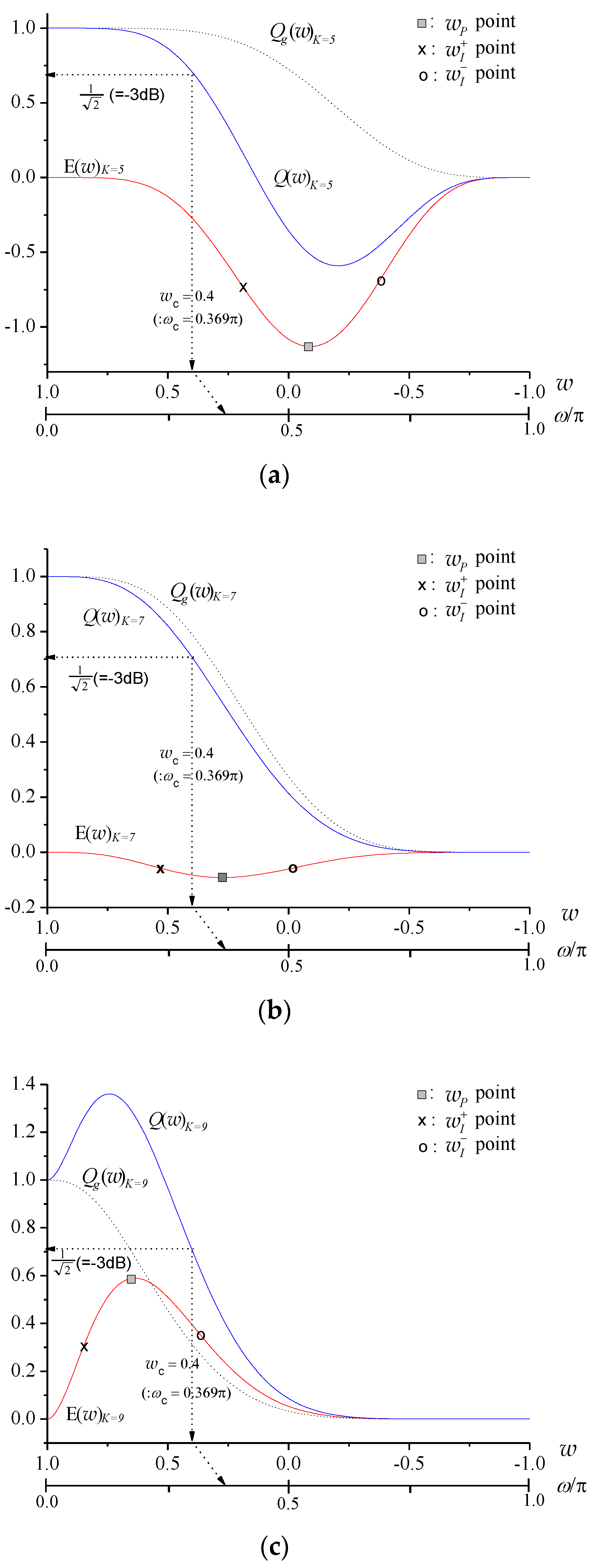

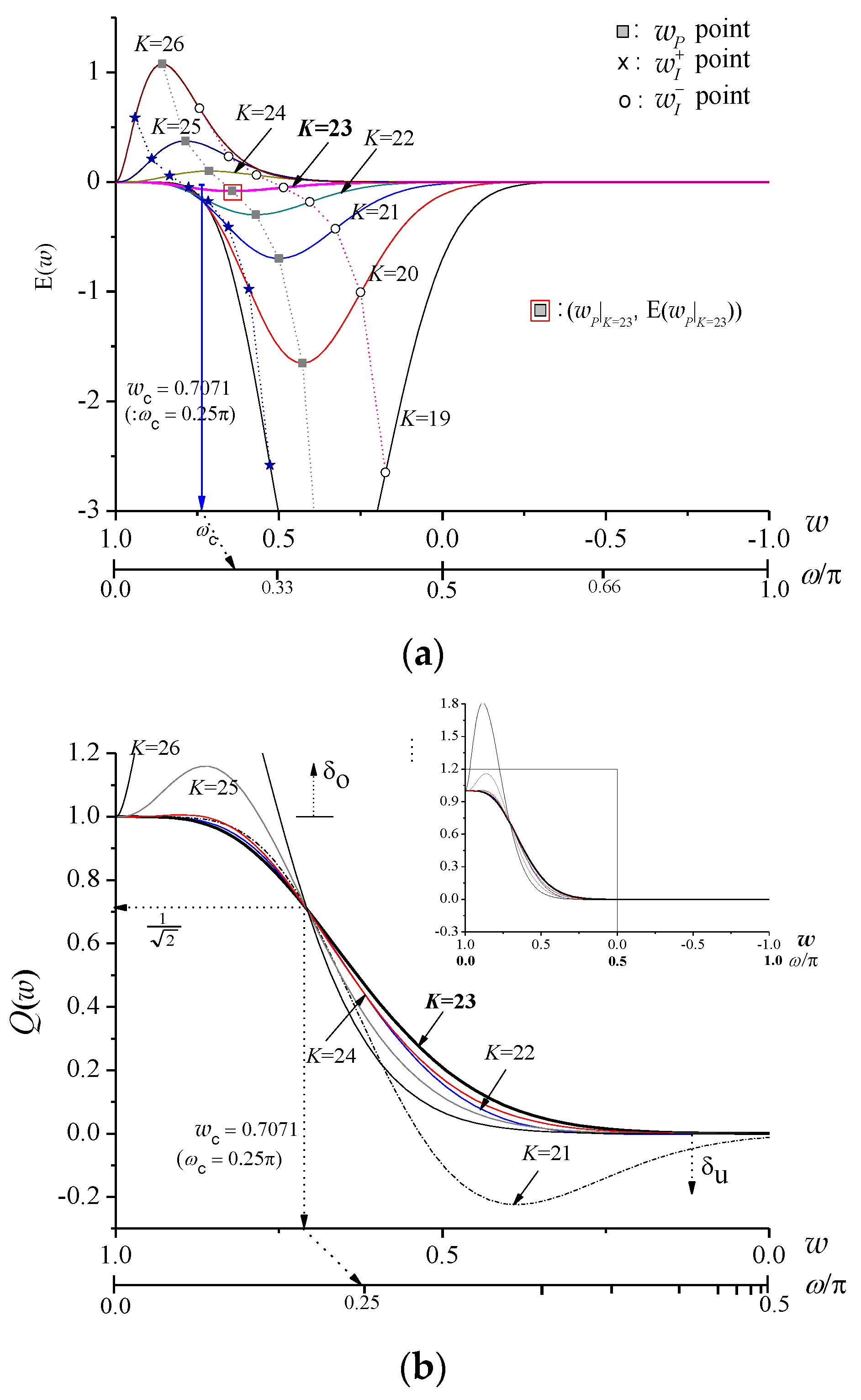



| Parameters | ||||||||
|---|---|---|---|---|---|---|---|---|
| 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| CK | −0.1982 | −0.3355 | −0.5405 | −0.7333 | −0.4836 | 1.3807 | 6.7866 | 17.5271 |
| −0.7032 | −0.5507 | −0.3871 | −0.2135 | −0.0300 | 0.1645 | 0.3731 | 0.6037 | |
| −0.4545 | −0.2727 | −0.0909 | 0.0909 | 0.2727 | 0.4545 | 0.6364 | 0.8182 | |
| −0.1645 | 0.0300 | 0.2135 | 0.3871 | 0.5507 | 0.7032 | 0.8418 | 0.9583 | |
| −0.2923 | −0.2886 | −0.2713 | −0.2147 | −0.0826 | 0.1375 | 0.3944 | 0.5941 | |
| −11.7403 | −2.3584 | −0.6661 | −0.2284 | −0.0550 | 0.0851 | 0.3615 | 1.5264 | |
| −20.6230 | −4.0613 | −1.1314 | −0.3837 | −0.0915 | 0.1403 | 0.5898 | 2.4573 | |
| −12.5099 | −2.4404 | −0.6733 | −0.2259 | −0.0531 | 0.0799 | 0.3236 | 1.1842 | |
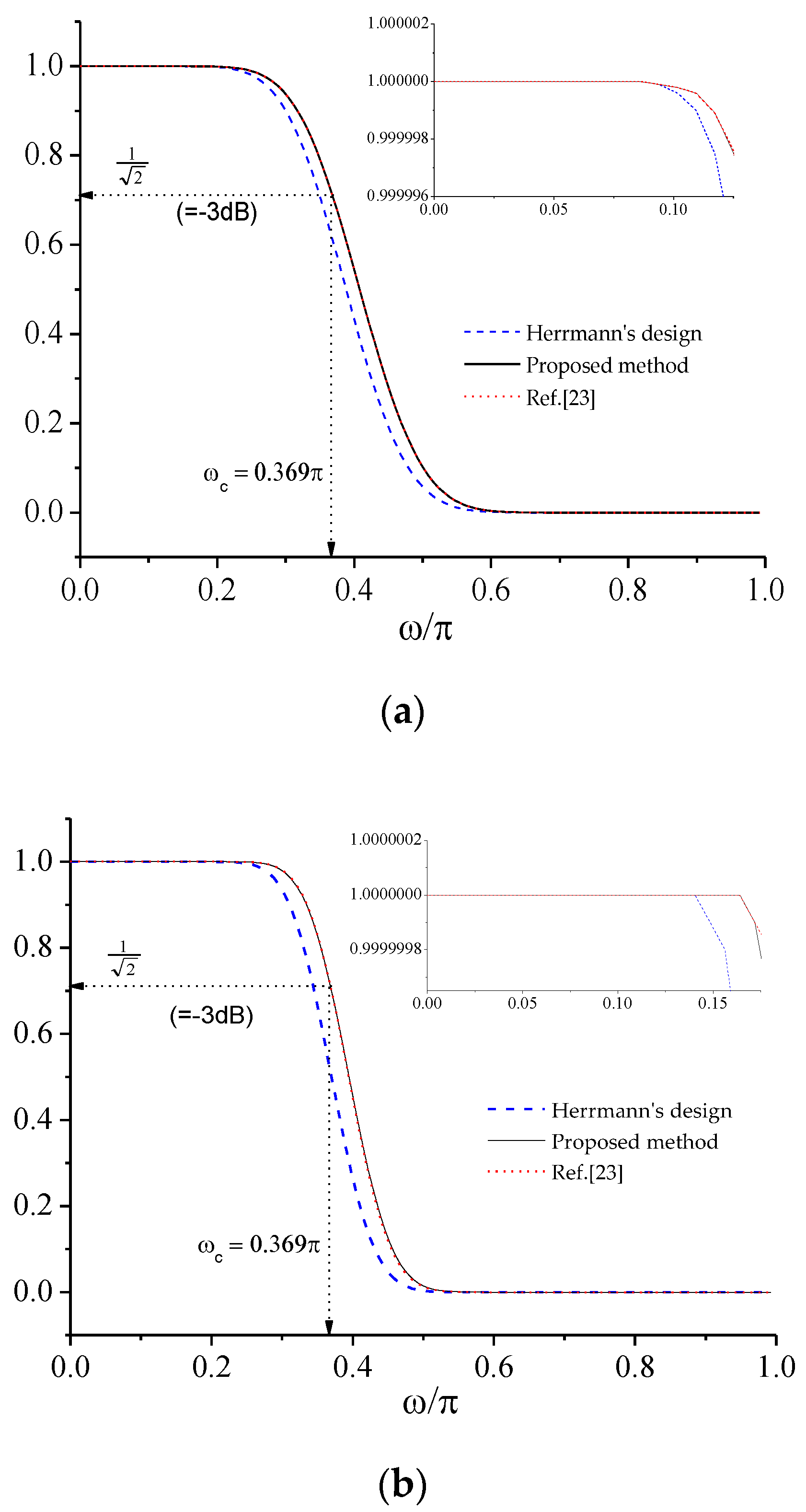
| Example | - | - | Figure 3a | - | Figure 3b | - | Figure 3c | Figure 3d |
| Parameters | ||||||||
|---|---|---|---|---|---|---|---|---|
| 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | |
| CK | −718.85 | −475.26 | −293.62 | −151.91 | −41.13 | 37.64 | 80.72 | 90.53 |
| 0.1741 | 0.2500 | 0.3272 | 0.4058 | 0.4862 | 0.5687 | 0.6539 | 0.7433 | |
| 0.3571 | 0.4286 | 0.5000 | 0.5714 | 0.6429 | 0.7143 | 0.7857 | 0.8571 | |
| 0.5274 | 0.5918 | 0.6550 | 0.7166 | 0.7766 | 0.8344 | 0.8894 | 0.9404 | |
| −0.2882 | −0.2776 | −0.2499 | −0.1884 | −0.0743 | 0.0991 | 0.3097 | 0.5061 | |
| −2.6494 | −1.0075 | −0.4267 | −0.1832 | −0.0510 | 0.0612 | 0.2316 | 0.6708 | |
| −4.3577 | −1.6531 | −0.6983 | −0.2990 | −0.0829 | 0.0993 | 0.3738 | 1.0761 | |
| −2.5816 | −0.9755 | −0.4101 | −0.1746 | −0.0480 | 0.0569 | 0.2106 | 0.5861 | |
| 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0058 | 0.1594 | 0.8101 | |
| −3.7859 | −1.1088 | −0.2241 | −0.0021 | 0.0 | 0.0 | 0.0 | 0.0 | |
| Parameters | |||||||
|---|---|---|---|---|---|---|---|
| MAXFLAT Filters of Equation (10) | Reference [23] | Cutoff Fixing Filters of Equation (18) | MAXFLAT Filters of Equation (10) | Reference [23] | Cutoff Fixing Filters of Equation (18) | ||
| 0.3502π | 0.3690π | 0.3690π | 0.2419π | 0.25π | 0.25π | ||
| 2 | 0.0188 | 2.14 × 10−5 | 0.0 | 0.0081 | 0.0 | 0.0 | |
| 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | ||
| 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | ||
| K decision | Equation (15) | training (13 iteration) | Equation (28) | Equation (15) | training (16 iterations) | Equation (28) | |
| accuracy/complexity 4 | low/low | high/very high | high/low | low/low | high/very high | high/low | |
| 0.3445π | 0.3690π | 0.3690π | 0.2445π | 0.25π | 0.25π | ||
| π | 0.0245 | 3.14 × 10−7 | 0.0 | 0.0055 | 1.83 × 10−12 | 0.0 | |
| 0.0 | 0.0 | 3.11× 10−15 | 0.0 | 0.0 | 4.44 × 10−16 | ||
| 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | ||
| K decision | Equation (15) | training (30 iteration) | Equation (28) | Equation (15) | training (37 iterations) | Equation (28) | |
| accuracy/complexity 4 | low/low | high/very high | high/low | low/low | high/very high | high/low | |
| Parameters | N | |||||
|---|---|---|---|---|---|---|
| 10 | 14 | 20 | 28 | 45 | 63 | |
| 6 | 9 | 13 | 18 | 30 | 42 | |
| −0.5846 | −0.7311 | −1.8770 | −10.073 | −112.62 | −4055.5 | |
| 0.2000 | 0.2857 | 0.3000 | 0.2857 | 0.3333 | 0.3333 | |
| 0.5000 | 0.5318 | 0.5059 | 0.4618 | 0.4702 | 0.4495 | |
| = −1.198409231 | h0 = −0.000000018 | h11 = −0.003859813 |
| = 21.309955797 | h1 = −0.000000147 | h12 = −0.005450869 |
| = −169.484927527 | h2 = −0.000000073 | h13 = 0.005958058 |
| = 802.886975733 | h3 = 0.000003072 | h14 = 0.020963265 |
| = −2532.615452798 | h4 = 0.000011169 | h15 = 0.004171941 |
| = 5615.229929033 | h5 = −0.000003022 | h16 = −0.048651840 |
| = −8988.135420893 | h6 = −0.000097254 | h17 = −0.055049249 |
| = 10,505.014699770 | h7 = −0.000159706 | h18 = 0.078213381 |
| h8 = 0.000280582 | h19 = 0.297774354 | |
| h9 = 0.001164512 | h20 = 0.408751644 | |
| h10 = 0.000355835 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chung, D.; Cho, W.; Jeong, I.; Jeon, J. Design of Cut Off-Frequency Fixing Filters by Error Compensation of MAXFLAT FIR Filters. Electronics 2021, 10, 553. https://doi.org/10.3390/electronics10050553
Chung D, Cho W, Jeong I, Jeon J. Design of Cut Off-Frequency Fixing Filters by Error Compensation of MAXFLAT FIR Filters. Electronics. 2021; 10(5):553. https://doi.org/10.3390/electronics10050553
Chicago/Turabian StyleChung, Daewon, Woon Cho, Inyeob Jeong, and Joonhyeon Jeon. 2021. "Design of Cut Off-Frequency Fixing Filters by Error Compensation of MAXFLAT FIR Filters" Electronics 10, no. 5: 553. https://doi.org/10.3390/electronics10050553
APA StyleChung, D., Cho, W., Jeong, I., & Jeon, J. (2021). Design of Cut Off-Frequency Fixing Filters by Error Compensation of MAXFLAT FIR Filters. Electronics, 10(5), 553. https://doi.org/10.3390/electronics10050553






