Abstract
Rotation-Invariant Face Detection (RIPD) has been widely used in practical applications; however, the problem of the adjusting of the rotation-in-plane (RIP) angle of the human face still remains. Recently, several methods based on neural networks have been proposed to solve the RIP angle problem. However, these methods have various limitations, including low detecting speed, model size, and detecting accuracy. To solve the aforementioned problems, we propose a new network, called the Searching Architecture Calibration Network (SACN), which utilizes architecture search, fully convolutional network (FCN) and bounding box center cluster (CC). SACN was tested on the challenging Multi-Oriented Face Detection Data Set and Benchmark (MOFDDB) and achieved a higher detecting accuracy and almost the same speed as existing detectors. Moreover, the average angle error is optimized from the current 12.6° to 10.5°.
1. Introduction
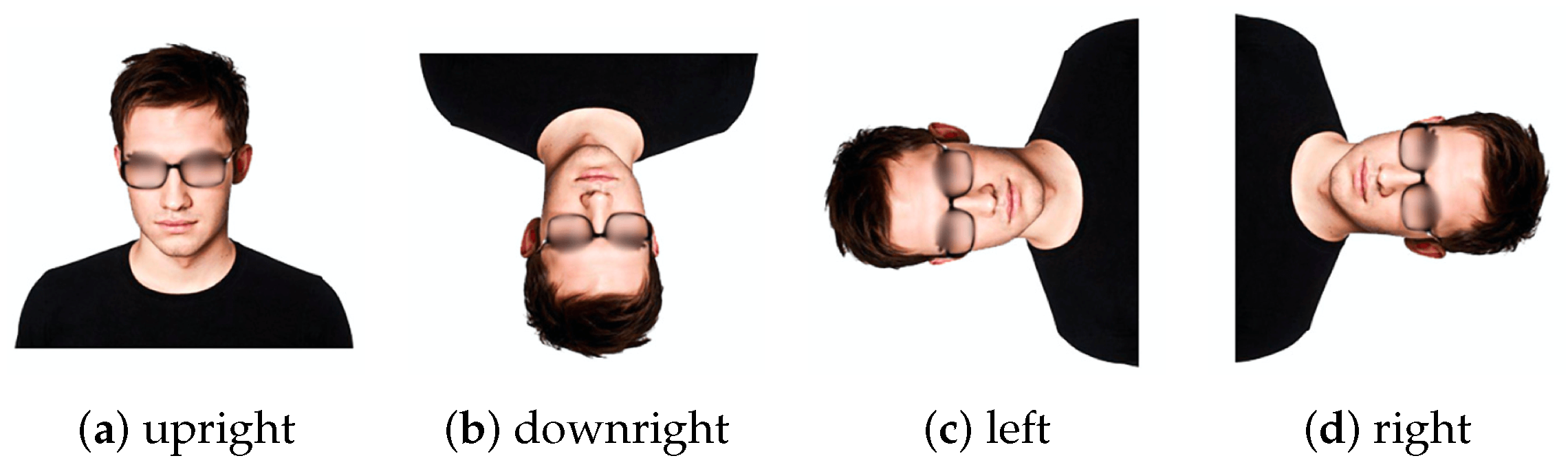
Face recognition [1,2,3] has played an important role in the field of computer vision. Currently, most facial recognition systems are designed with a Convolutional Neural Network (CNN) model, such as the Multitask Cascaded Convolutional Networks (MTCNNs) [4], Cascading networks [5,6,7], Fully Convolutional Networks (FCNs) [8,9,10,11], Feature Pyramid Networks (FPNs) [12,13], and Deep Convolutional Neural Networks (DCNNs) [14,15]. In addition to their accuracy issues, these facial detector networks can only work on upright faces. Fortunately, Direction-Sensitivity Feature Ensemble Networks (DFENs) [16], Angle-Sensitivity Cascaded Networks (ASCNs) [17], Rotational Regression [18], Progressive Calibration Networks (PCNs) [19], and Multi-task Progressive Calibration Networks (MTPCNs) [20] are proposed for Rotation-Invariant Face Detection (RIPD) at different angles, as shown in Figure 1.
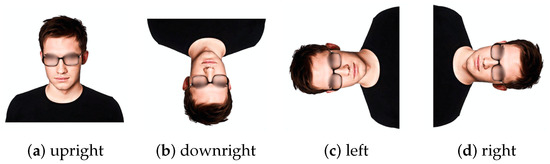
Figure 1.
The definition of facial orientation: (a) upright at 0°; (b) downright at −180°; (c) left at −90°; and (d) right at 90°.
To solve the problem of RIPD, we propose a novel network, called Searching Architecture Calibration Network (SACN), based on architecture search. SACN has three stages, constructed by CNN, and each stage involves three tasks: face or non-face classification, bounding box regression, and angle calibration. In the first stage, we utilize FCN to process multi-scale images instead of fixed-size images. In the second and third stages, we utilize architecture search to construct the network automatically. Finally, the task of angle regression, ranging from −180° to 180°, can be optimized from −45° to 45° using our network. The source code is available at https://github.com/Boooooram/SACN (accessed on 1 February 2021).
We summarize the contributions of this article as follows:
- We introduce architecture search to construct the network structure, which can reduce the angle error and the size of the model.
- We propose CC instead of non-maximum suppression (NMS). CC is a cluster method based on mean shift and can improve the accuracy of angle classification.
- Experiments were conducted on MOFDDB, which proved that the proposed approach provides a performance improvement compared to the state-of-the-art techniques in terms of angle error.
2. Related Work
2.1. Rotation-Invariance Face Detector
2.1.1. DFEN
DFEN utilizes a normal convolutional model to detect the rotation-invariant face from coarse to fine. It changes the bounding box regression by introducing angle prediction processed by a Single Shot Detector (SSD). DFEN also introduces an angle module to the network to extract the face angle features. Although their method achieves excellent accuracy in face detection, the detecting speed is not satisfactory due to the size of the SSD, which is almost 100 Megabytes.
2.1.2. ASCN
ASCN is a joint framework that consists of RIPD and face alignment, which can predict bounding boxes, face landmarks, and RIP angles simultaneously through a cascaded network. ASCN also introduces an innovative pose-equitable loss to improve the detecting accuracy.
2.1.3. Rotational Regression
Rotational regression detects the angle of the human face by training the neural network with a regression angle. This method requires a particularly complex network to ensure that the detecting angle does not suffer from too large a deviation, leading to the training network being a time-consuming process. The network can ensure that the angle of regression will not be greatly different. If the angle of regression is not correct, it will cause a large deviated range. In this case, the prediction of the RIP angle may affect the error prediction of the face, so as to improve the recall rate of the facial detector.
2.1.4. PCN
PCN offers an improvement of the rotation regression algorithm. By training the three-stage progressive calibration network, the angles of the three stages are detected, and the position of the face is located by the bounding box regression method; finally, these three angles are added to obtain the regression angle of the face. The PCN network uses three small networks to ensure the detecting speed. The PCN predicts the angle step by step, thus ensuring that the multi-stage edge regression errors are limited. However, due to the limitation of the network structure of the PCN, the accuracy of the training is not high. Furthermore, the input size needs to be fixed because of the full connection layer, which leads to a low detecting speed.
2.1.5. MTPCN
MTPCN offers an improvement on PCN. It introduces the explicit geometric structure representation into PCN to reserve the important information for precise calibration. Thus, MTPCN performs almost the same way as PCN.
2.2. Architecture Search
Differentiable ARchiTecture Search (DARTS) [21] is a framework for searching the network architecture on a small dataset and then transferring the learned architecture to the target dataset. Most of the existing models based on CNN are manually predetermined. However, DARTS introduces two types of convolutional blocks, which make it easier to build the architecture. The first one is the Normal Block, which returns a feature map of the same dimension. The second is the Reduction Block, which returns a feature map where the feature map height and width are reduced by a factor of two. The structure of these two blocks are searched by the Recurrent Neural Network (RNN) controller within the search space. In the search space, the block takes two states, and , as inputs, which are the outputs of previous blocks or the input data. The controller RNN will construct the structure of the other convolutional block according to these two states. The structures of each block are grouped into five blocks, where each block has five searching steps evaluated by five distinct SoftMax classifiers. The searching step is defined as follows:
- Select a state from and or from the set of states created by previous blocks.
- Select a second hidden state from the same options as in Step 1.
- Select an operation from the operation set to process the state selected in Step 1.
- Select an operation from the operation set to process the state selected in Step 2.
- Select a method from element-wise summation, element-wise multiplication or element-wise concatenation to combine the outputs of Steps 3 and 4 to create a new state.
In Steps 3 and 4, some common operations are listed as follows:
| a) 1 × 3 then 3 × 1 conv | b) 1 × 5 then 5 × 1 conv |
| c) 1 × 7 then 7 × 1 conv | d) 3 × 3 dilated conv |
| e) 5 × 5 dilated conv | f) 7 × 7 dilated conv |
| g) 3 × 3 average pooling | h) 5 × 5 average pooling |
| i) 7 × 7 average pooling | j) 3 × 3 max pooling |
| k) 5 × 5 max pooling | l) 7 × 7 max pooling |
| m) 3 × 3 depth-sep conv | n) 5 × 5 depth-sep conv |
| o) 7 × 7 depth-sep conv | p) 1 × 1 convolution |
| q) 3 × 3 convolution | r) skip connect |
In Step 5, all the unused states in the current block are concatenated to create the final output of the current block.
3. Searching Architecture Calibration Network
3.1. Motivation of this Approach
Since the detecting accuracy of current facial detectors is generally improved by manually adjusting the model structure, it seems possible to improve the angle prediction problem by using an appropriate network structure. Inspired by Liu et al. [21], a new structure can be learned in continuous space, which solves the problem of adjusting the precision of the RIP angle.
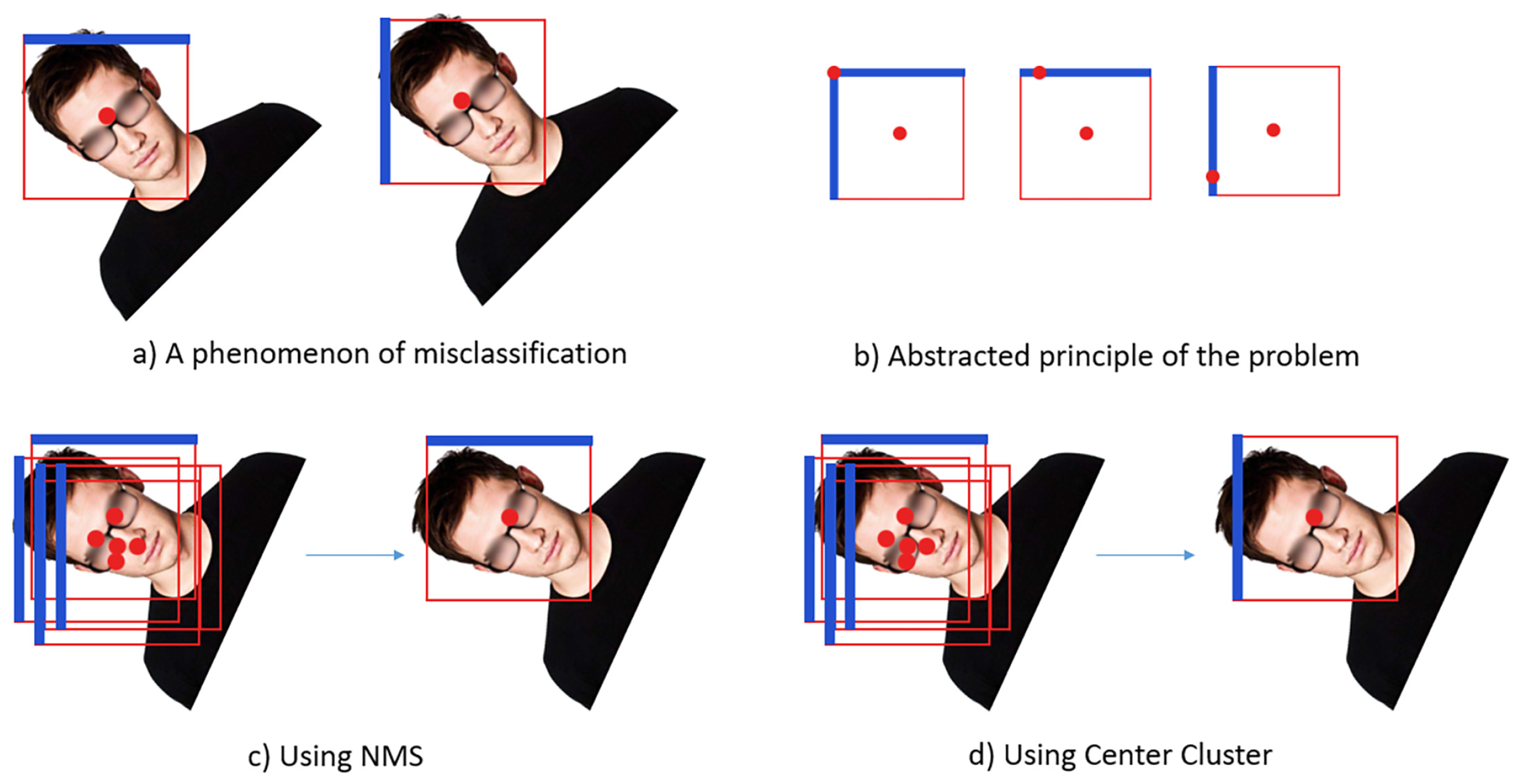
To enhance the model structure, we assumed that the non-maximum suppression [22] mainly concentrates on the maximum confidence score region, which may lead to the suppression of other information around the bounding box. Although NMS seems to be superior to other suppressing methods, such as mean shift clusters [23] in upright face detection, as shown in Figure 1a, this ignores the information of the surrounding box angle, which results in the inferior performance of rotating face detection compared to cluster detection. To detect RIP errors more accurately, a new method, called CC, is proposed.
3.2. Hypothesis of Center Cluster
Experimentally, a phenomenon was accidentally discovered, as shown in Figure 2a. When using NMS, the edge of the rotation type was always at risk of being misclassified, as shown in Figure 2c, which increased the error of the face detector. According to the abstracted principle of Figure 2b, it is concluded that the NMS is too sensitive to the position of the maximum confidence interval, which may increase the risk of misclassification. Therefore, the idea of modifying angle classification by using the angle information of the surrounding bounding box is proposed, which is called CC, as shown in Figure 2d.
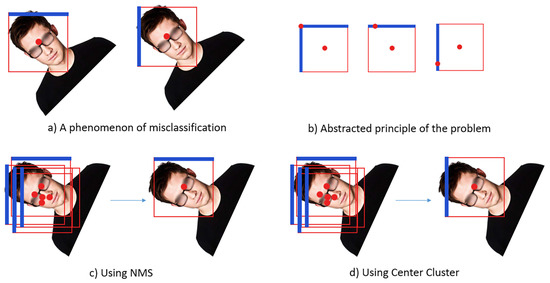
Figure 2.
(a) Phenomenon of misclassification under a boundary where the blue line represents the upright orientation predicted by the detector and the red point represents the center of the bounding box. (b) The red point on the border represents the true orientation of the face. (c) The surrounding bounding boxes’ information is ignored when using non-maximum suppression (NMS) method. (d) The surrounding bounding boxes’ information, captured by CC.
3.3. Overall Processing
As shown in Figure 3, the SACN detector is implemented as follows: images of different scales are passed through the SACN three-stage detector, and the first stage of the detector is intuitively utilized to generate sliding windows through an image pyramid method and deconvolution operation. While detecting the bounding boxes, the detector will generate face candidate regions and obtain the predicted angle. Then, CC was proposed to calibrate the obtained angle. Some low and high overlap bounding boxes were removed by CC. By reducing the angle error in the cluster and the number of bounding boxes, detecting time can be saved, and the angle error can be calibrated to suppress the bounding boxes in each stage. The final calibrated angle can be obtained through the different calibrations of each stage of the network.

Figure 3.
The Searching Architecture Calibration Network (SACN) process.
3.4. Center Cluster Calibration
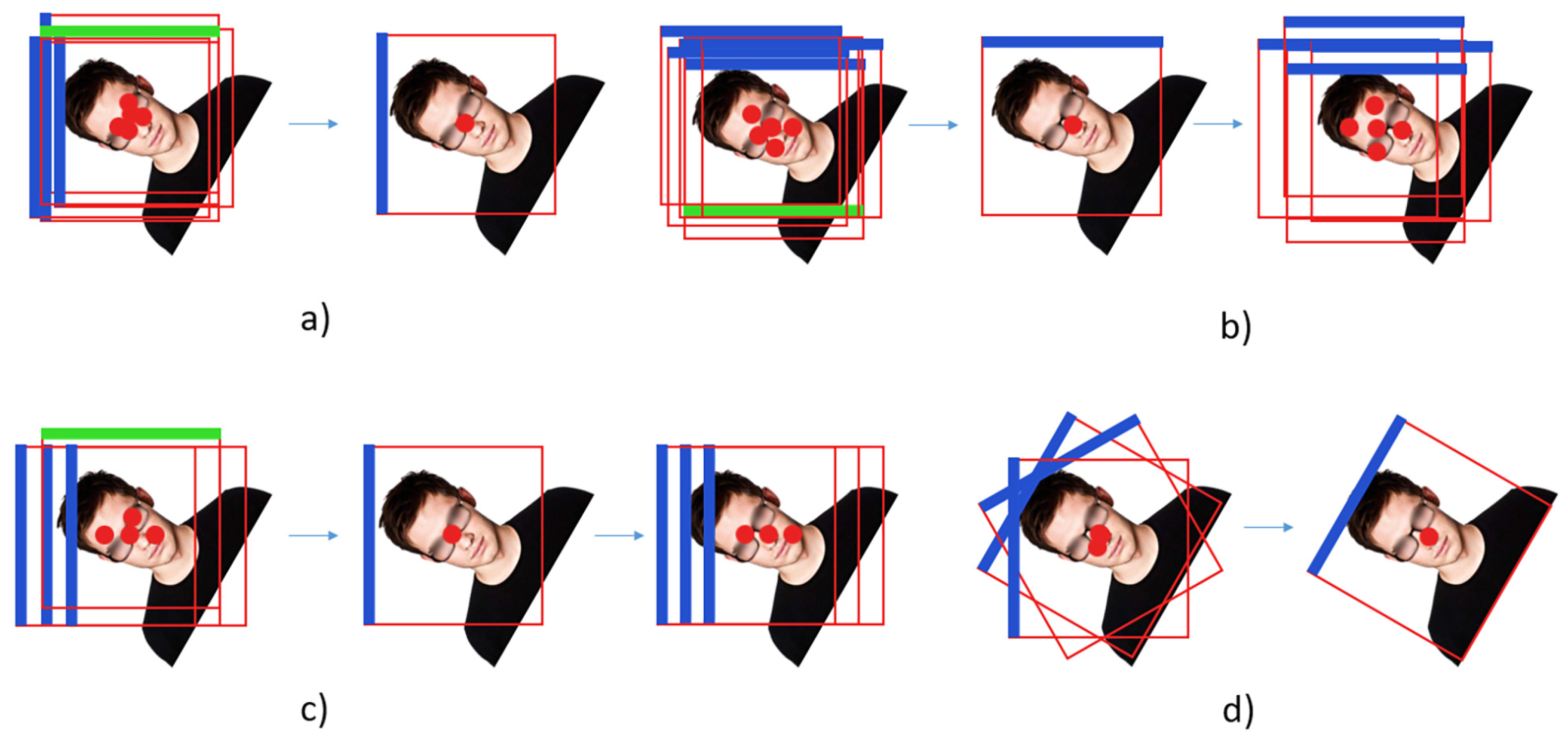
First, due to the high similarity of human faces, we assumed that the proportion of human faces in each image is almost the same. Then, for the center point of each character, the idea proposed by NMS is removing the bounding boxes with inaccurate detection. However, the classification information contains an angle error. In fact, this angle information is also valuable to the detector. On this basis, a cluster method based on mean shift is designed, as shown in Figure 4a. The distance between the center points in the experiment was defined as , where is the average width of the current cluster, is the width controller, and the is defined as:
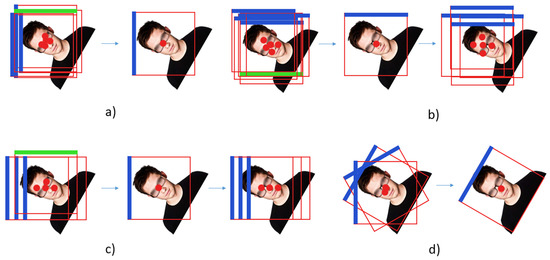
Figure 4.
The process of CC, where the red dot represents the center of the bounding box, the blue line represents the true direction predicted by the detector, and the green line represents the error direction predicted by the detector: (a) the cluster method at the center of the bounding box; (b) the first stage of the network in order to correct all the angles of the output of the first stage by accumulating the most detected angles in the cluster; (c) the second stage of the network; and (d) the third stage of the display network, where the angle of the final prediction is calibrated by finding the most reliable position of the detector.
For the first and second stages, the bounding boxes obtained at each stage are clustered and calibrated. The mean shift method is adopted and the parameter bandwidth is . For the bandwidth of each stage, the average width of the cluster side length is obtained, as shown in (1). Then, the angle values of the first and second stages are set, and the maximum value of the category calibrates the angle within the cluster. The formula is defined as:
where represents the ith predicted rig in the cluster and is the function that computes the summation of the number of classified rig angles—for example, max is 0°.
3.5. SACN in First Stage
For each image of any size, FCN has three goals: face and non-face classification, bounding box regression, and angular calibration classification. The formula is defined as:
where is the first stage output detector composed of the first stage of the minimal convolutional network; f is the confidence score, indicating whether the face is or is not included; t is a one-dimensional vector, including the regression value of each bounding box, such as the coordinate of left-top point and the width of the bounding box; and g is the classified value of the RIP angle of the face.
The main purpose of the first parameter f is to distinguish the cross-entropy loss function of the face and non-face through the following formula:
where equals 1 if facial information is considered to be included; otherwise, it equals 0.
The main task of the second parameter t is to find the regression formula of the bounding boxes as follows:
where t and represent the regression value of the prediction and the ground truth, respectively, and S represents the Smooth L1 loss in faster-RCNN [24]. Furthermore, t contains three parameters:
where a and b are the coordinates of the top left corner of the facial image and w is the width of the facial image. a and represent the prediction and the ground truth, respectively; likewise, b and represent the prediction and the ground truth, respectively. For the classification of the last correction angle, the binary solutions of 0–1 are obtained by the cross entropy loss function.
where equals 0 if it is upright; otherwise, it is downright. Finally, the following cascade loss function for convex optimization is used:
where and are weight factors used to balance each loss function. In the experiment, equals 0.8 and equals 1. The loss function is minimized by optimizing the parameters of . Finally, the calibrated angle of the first stage is classified according to the threshold value:
Finally, the RIP angle will be changed from [−180°, 180°] to [−90°, 90°]. Bounding boxes with an Intersection over Union (IoU) greater than 0.7 are positive examples. Those with an IoU between 0.4 and 0.7 are suspicious examples. Those with an IoU less than 0.4 are negative examples. To reduce the cost of the edge of the classification error, examples are used for the training network within the ranges of [−180°, −115°] ∪ [115°, 180°] and [−45°, 45°], which represents facing down and facing up.
3.6. SACN in Second Stage
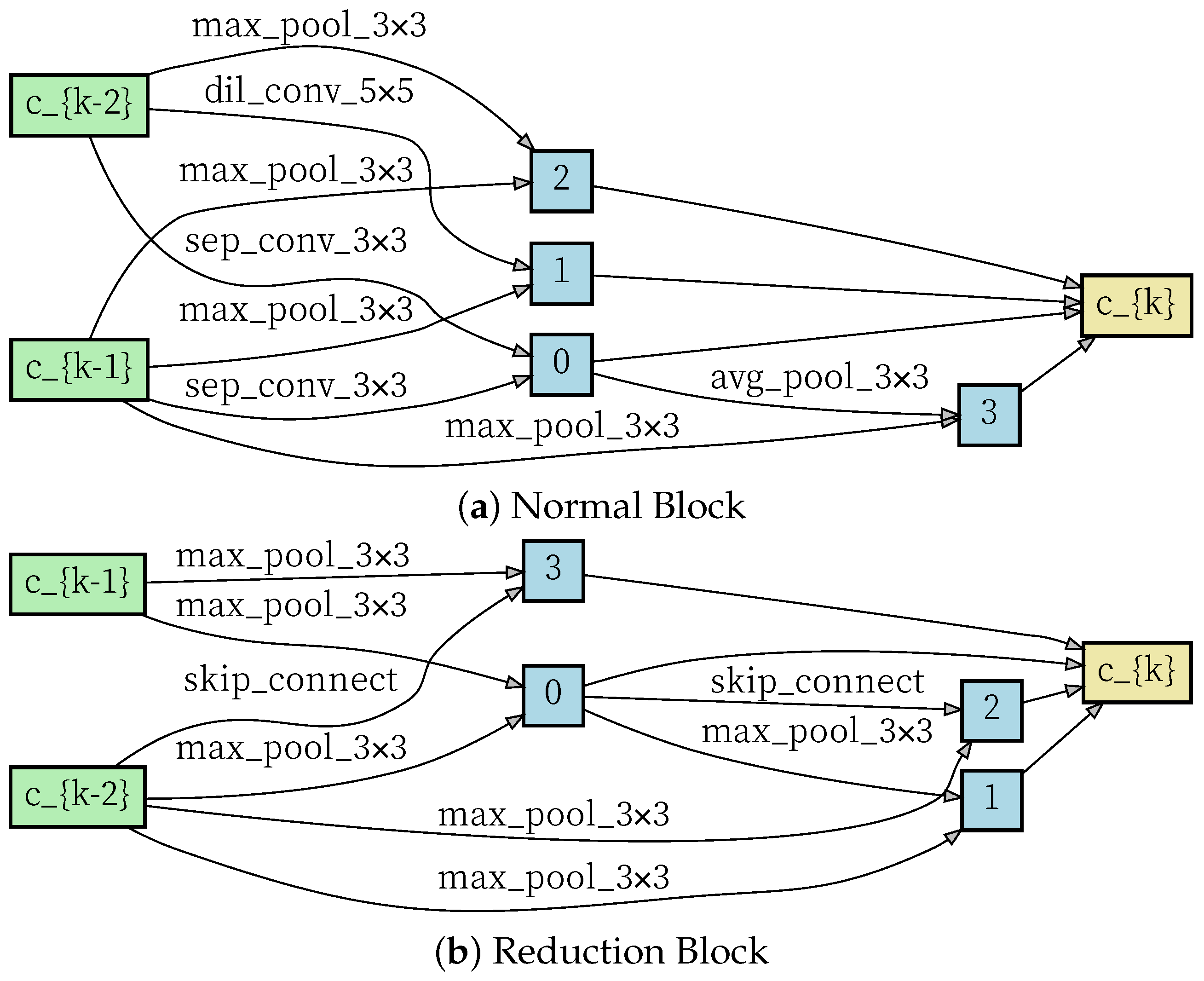
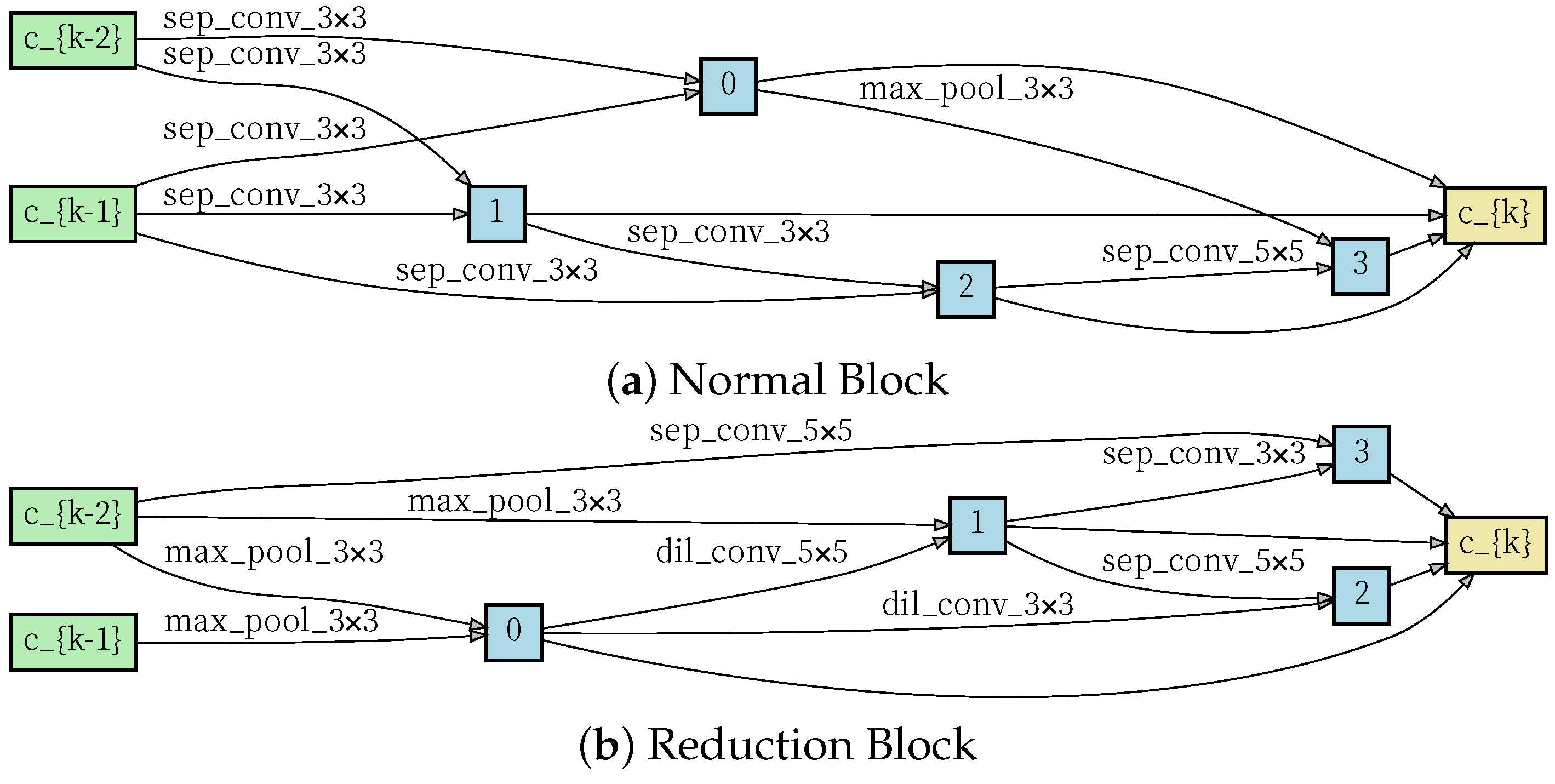
Inspired by Liu et al. [21], four nodes are set in the continuous relaxation space, and then the operation between each node is learned separately. A value for each operation is set and, finally, the connection for the operation is selected by changing the value. After that, an RNN controller, such as that used in [25], is used to optimize the dual optimization problem. On this basis, a bivariate optimization strategy is proposed to optimize both model precision and architecture precision. A conventional type of block structure is designed to handle information of the same size, and a reduced type is designed to reduce the size to half of its original size, which reduces redundant information. The results are shown in Figure 5.
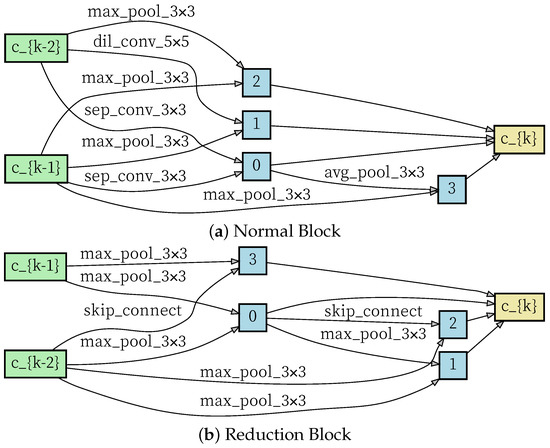
Figure 5.
The normal and reduction block learned by SACN in the second stage.
Finally, architecture search is applied for constructing the network and the parameters of the model are relearned. As such, the second stage of SACN is similar to the first stage. The second stage also performs three tasks at the same time, including the face and non-face tasks, bounding box regression, and the classification of angle correction. The formula is defined as follows:
where is the detector of the second stage, structured by architecture search. x represents the image through the first stage of cutting and correction, f represents the facial confidence score, t represents the regression of the boundary box, and g represents the confidence score of angular classification.
Based on the first stage, the angle that has been fixed by the second stage can be divided into [−90°, −45°], [−45°, 45°], and [45°, 90°]. The SoftMax function used to classify the above angle is defined as follows:
where equals the ith index of the predicted max angular confidence score and equals the second refined RIP angle.
In the boundary of the training, to avoid the misclassification problem, the angle range reduction degrees [−90°, −60°], [−30°, 30°], and [60°, 90°] and the three angles correspond to the three values of 0, 1, and 2, respectively.
3.7. SACN in Third Stage
Similar to the second stage, architecture search is also carried out in the third stage, and the structure of the third stage is shown in Figure 6.
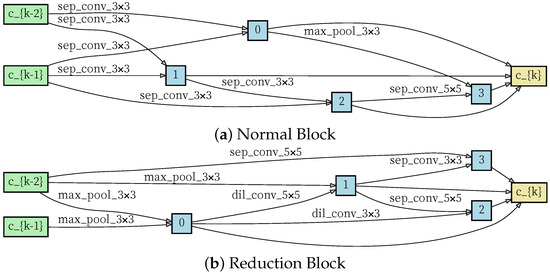
Figure 6.
The normal and reduction block learned by SACN in third stage.
Additionally, a cascade of three tasks is carried out, including facial prediction, the regression of the bounding box, and the calculation of the regression value of the third angle.
where f is the facial classification function, t is a one-dimensional vector which is used to regress the bounding boxes, and is the angular regression, which ranges [−45°, 45°]. is the detector of the third-stage output. x represents the face that was clipped and calibrated by the second stage.
An example of SACN is shown in Figure 7, and the final RIP angle is defined as follows:

Figure 7.
The final rotated angle is calculated by the sum of three stages.
4. Experiments
In the following sections, the implementation details of SACN are introduced. Then, some experiments that were conducted on the challenging datasets of wide rotating faces, named multi-oriented FDDB [26], are described. The results of these experiments prove that our method has a better performance in terms of accuracy than most state-of-the-art methods.
4.1. Implementation Details
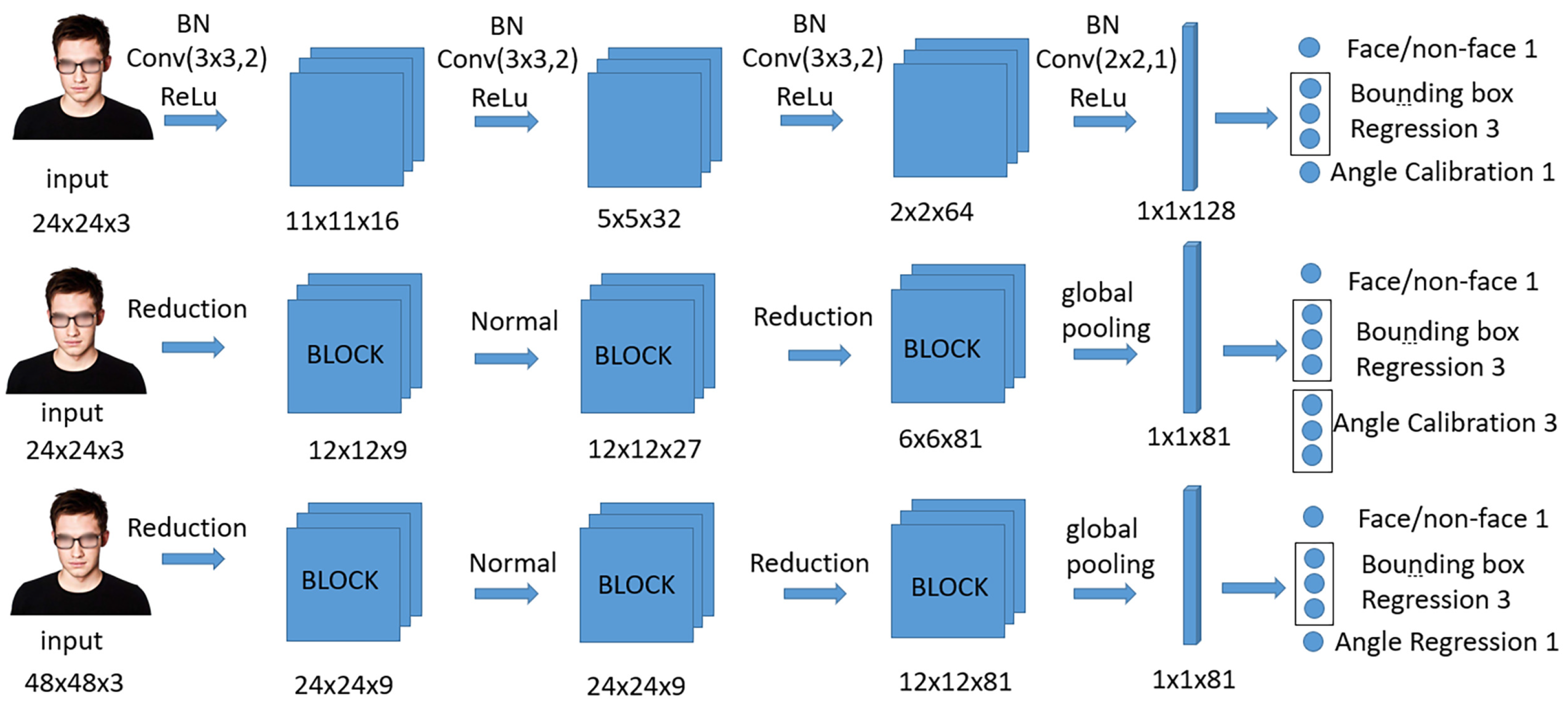
The designed network structure is shown in Figure 8. In the first two stages of our SACN, we only need to conduct some coarse calibrations, such as calibrations from downright to upright, and from left or right to upright. Furthermore, we can easily obtain the coarse angle calibrations by combining the calibration task with the classification task and the bounding regression task. In the third stage of SACN, we attempt to directly regress the precise RIP angles of face candidates instead of coarse orientations due to the fact that the RIP angle has been reduced to a small range in previous stages. We apply FCN in the first stage to process the multi-scale inputs. In the second and third stages, we replace traditional CNN with a Normal Block and a Reduction Block.

Figure 8.
The structure of the SACN, Conv, BN, ReLU, global pooling mean convolution layer, Batch Normalization, ReLU activation layer, and global pooling layer, respectively. (k,k,s) indicates that the kernel size is and the stride is s. Reduction and Normal operations were learned by SACN, as shown in Figure 5 and Figure 6.
We utilized the stochastic gradient descent method (SGD) and backpropagation method in the training stage. We also set the maximum number of iterations to . The learning rate was adjusted according to the number of iterations. The initial learning rate was 0.025, the weight attenuation rate was 3 × 10, and the momentum was 0.9. To prevent a gradient explosion, five gradient cutters were set. All variables start with a Gaussian distribution of 0.001 to accelerate convergence.
4.2. Benchmark Datasets
The FDDB dataset contains 5171 labeled faces. However, most faces in FDDB are upright. To better evaluate the performance of models on rotation invariance, we rotated these images by −180°, 90°, and −900°, so as to form a multi-oriented version of FDDB. We renamed the initial FDDB as FDDB-up in this work, and we renamed the others as FDDB-left, FDDB-right, and FDDB-down, according to their rotated angles. Several state-of-the-art methods and our methods were evaluated on MOFDDB.
4.3. Evaluation Results
4.3.1. Results of Rotation Calibration
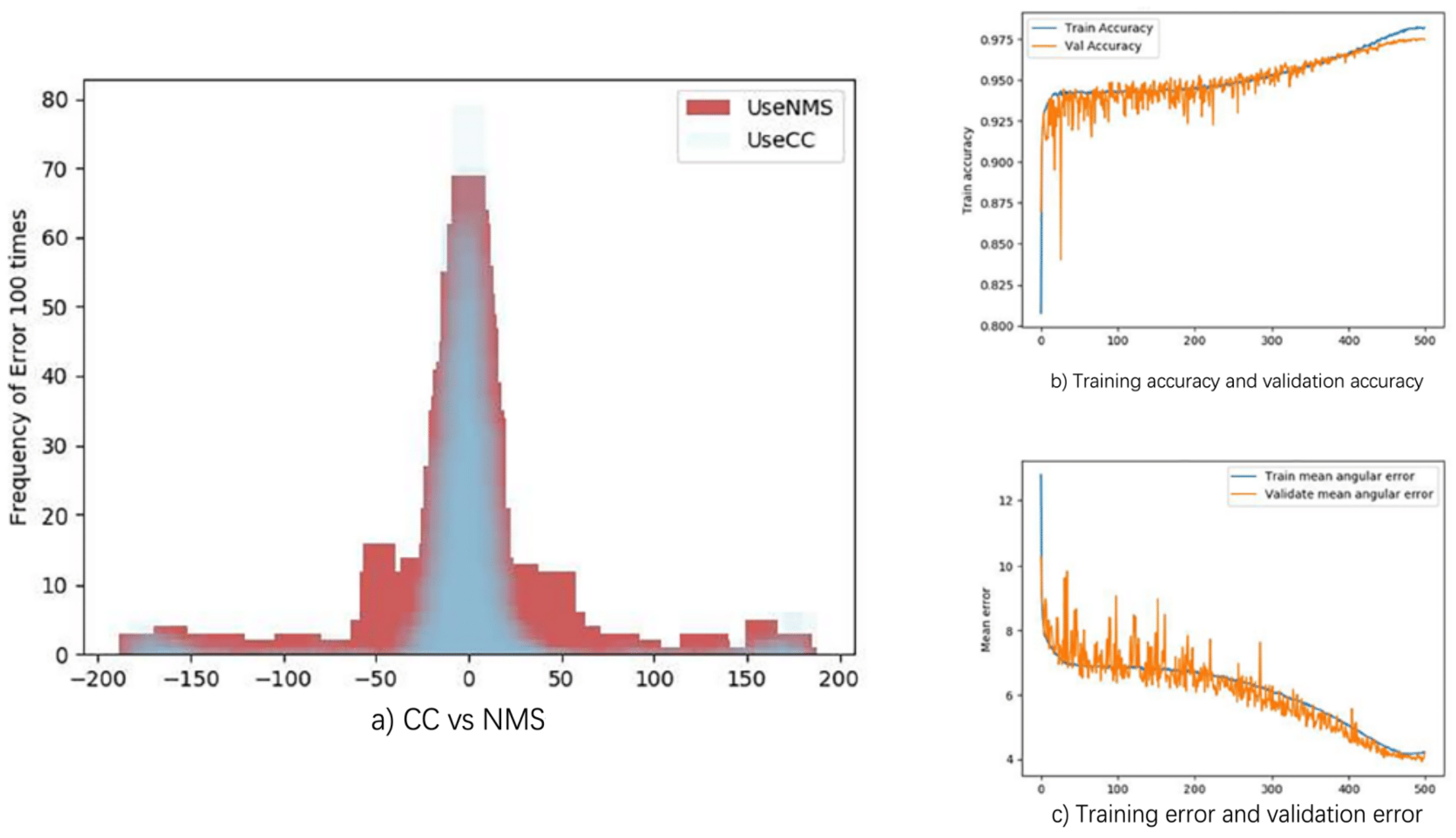
As shown in Figure 9b, the accuracy of SACN is 97%, which is improved from 96% with PCN. Although the average angular error of the third stage was reduced from 8° for PCN to 4.5°, as shown in Figure 9c, the average error is still quite high, because the regression of the angle is complex. After applying CC, we found that the detected error of the SACN is narrow, as shown in Figure 9a.
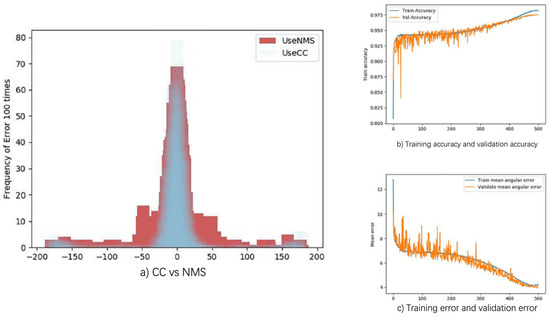
Figure 9.
(a) The frequency of the angular detection error with CC and NMS; (b) the training accuracy and validation accuracy of SACN, converging at 97% with 500 epochs; and (c) the regressive average angular error, which is predicted by the third stage, converging at 4.5° with 500 epochs.
4.3.2. Accuracy Comparison
As mentioned above, SACN aims to achieve accurate rotating-invariant face detection in a short amount of time. Several models were evaluated using 640 × 480 images and 40 × 40 minimum face images. The recall rate of 100 false positives on multi-oriented FDDB is shown in Table 1. Compared with other methods, SACN reduces the average angular error and has almost the same detecting speed and recall rate. The results of Faster R-CNN, Cascade CNN, PCN, and SACN are shown in Figure 10.

Table 1.
Performance comparisons with other methods.

Figure 10.
The detecting results of Faster R-CNN, Cascade CNN, PCN, and SACN.
4.3.3. Problems and Limitations
As shown in Figure 9a, the error of CC with 180° is higher than NMS, which may decrease the performance of detection on the dataset FDDB-down. We believe that the structure of the first stage of SACN and the parameter bandwidth of CC are responsible for this result.
Furthermore, we found that the detecting speed of SACN is not satisfied. We think that the reason that the detecting speed is lower than PCN is because PCN is implemented in Caffe (c++), while SACN is implemented in Pytorch (Python). The difference in speed largely comes from c++ and Python.
Finally, we found that our dataset was not balanced in terms of race, which is a key point for face detection, as mentioned in [27,28]. The authors of [28] constructed a balanced race dataset, including White, Black, Indian, East Asian, Southeast Asian, Middle East, and Latino faces. However, the RIP angles are not labeled in this dataset.
4.3.4. Ablation Experiment
We set the width controller as different values in the ablation experiment, as shown in Table 2. We found that the model performed better when equaled 0.2. When equaled 0.1, there would be too many clusters because the search radius was too small. The number of cluster affected the classification of angle according to (2) as well as the performance of the model. When equaled 0.3, there would be few clusters because the search radius was large enough. There would even be only one cluster when was too large, which might lead to CC not working well if there were too many wrong predictions.

Table 2.
Ablation experiment on the width controller of bandwidth.
5. Conclusions and Future Works
In this paper, we propose a novel rotation-invariant face detector (SACN). It mainly consists of three stages. In the first stage, the network is constructed by FCN. In the next two stages, the networks are constructed by architecture search based on controller RNN. Furthermore, in the first two stages, the rotation angles and bounding boxes are optimized jointly. After that, the task of RIP angle regression, ranging from −180° to 180°, can be optimized from −45° to 45°. In the third stage, we directly regress the precise RIP angles of face candidates. In addition, we replace non-maximum suppression with a novel suppression method, named CC, which is a cluster method based on mean shift because CC can improve the accuracy of angle classification. As evaluated on public datasets of multi-oriented FDDB, SACN outperforms several state-of-the-art methods in terms of the accuracy of the RIP angle, while maintaining a real-time performance.
In the future, we plan to extend our work in the following aspects: (1) construct a race-balanced dataset with labels for RIP angles; (2) optimize the model in terms of accuracy and detection speed; and (3) compare our method with other state-of-the-art methods on this dataset.
Author Contributions
Conceptualization, A.S.; data curation, X.X.; methodology, A.S.; resources, A.S.; software, X.X.; validation, X.X.; writing—original draft, X.Z.; and writing—review and editing, X.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
FDDB: http://vis-www.cs.umass.edu/fddb/ (accessed on 1 February 2021).
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| RIPD | Rotation-Invariant Face Detection |
| RIP | rotation-in-plane |
| FCN | fully convolutional network |
| CC | center cluster |
| CNN | convolution neural network |
| MTCNN | Multitask Cascaded Convolutional Networks |
| FPN | Feature Pyramid Network |
| DCNN | Deep Convolutional Neural Network |
| DFEN | Direction-Sensitivity Features Ensemble Network |
| MTPCN | Multi-task Progressive Calibration Networks |
| ASCN | Angle-Sensitivity Cascaded Networks |
| PCN | Progressive Calibration Networks |
| SSD | Single Shot Detector |
| NIN | network in network |
| RNN | Recurrent Neural Network |
| NMS | non-maximum suppression |
| SACN | searching architecture calibration network |
| RL | reinforcement learning |
| FDDB | Face Detection Data Set and Benchmark |
| IoU | Intersection over Union |
| SGD | stochastic gradient descent |
References
- Zhao, H.; Ying, X.; Shi, Y.; Tong, X.; Wen, J.; Zha, H. RDCFace: Radial Distortion Correction for Face Recognition. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 14–19 June 2020; pp. 7721–7730. [Google Scholar]
- Deng, J.; Guo, J.; Liu, T.; Gong, M.; Zafeiriou, S. Sub-center arcface: Boosting face recognition by large-scale noisy web faces. In European Conference on Computer Vision; Springer: Cham, Switzerland, 2020; pp. 741–757. [Google Scholar]
- Zhang, Y.; Deng, W.; Wang, M.; Hu, J.; Li, X.; Zhao, D.; Wen, D. Global-local gcn: Large-scale label noise cleansing for face recognition. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 14–19 June 2020; pp. 7731–7740. [Google Scholar]
- Zhang, K.; Zhang, Z.; Li, Z.; Qiao, Y. Joint face detection and alignment using multitask cascaded convolutional networks. IEEE Signal Process. Lett. 2016, 23, 1499–1503. [Google Scholar] [CrossRef]
- Li, H.; Lin, Z.; Shen, X.; Brandt, J.; Hua, G. A convolutional neural network cascade for face detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 5325–5334. [Google Scholar]
- Farfade, S.S.; Saberian, M.J.; Li, L.J. Multi-view face detection using deep convolutional neural networks. In Proceedings of the 5th ACM on International Conference on Multimedia Retrieval, Shanghai, China, 23–26 June 2015; pp. 643–650. [Google Scholar]
- Jaderberg, M.; Simonyan, K.; Zisserman, A.; Kavukcuoglu, K. Spatial transformer networks. Adv. Neural Inf. Process. Syst. 2015, 28, 2017–2025. [Google Scholar]
- Kim, Y.; Park, W.; Roh, M.C.; Shin, J. GroupFace: Learning Latent Groups and Constructing Group-Based Representations for Face Recognition. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 14–19 June 2020. [Google Scholar]
- Dai, J.; Li, Y.; He, K.; Sun, J. R-fcn: Object detection via region-based fully convolutional networks. arXiv 2016, arXiv:1605.06409. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Spatial pyramid pooling in deep convolutional networks for visual recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 37, 1904–1916. [Google Scholar] [CrossRef] [PubMed]
- Long, J.; Shelhamer, E.; Darrell, T. Fully convolutional networks for semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 3431–3440. [Google Scholar]
- Lin, T.Y.; Dollár, P.; Girshick, R.; He, K.; Hariharan, B.; Belongie, S. Feature pyramid networks for object detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 2117–2125. [Google Scholar]
- Wang, Q.; Wu, T.; Zheng, H.; Guo, G. Hierarchical Pyramid Diverse Attention Networks for Face Recognition. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 14–19 June 2020. [Google Scholar]
- Najibi, M.; Singh, B.; Davis, L.S. Fa-rpn: Floating region proposals for face detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–20 June 2019; pp. 7723–7732. [Google Scholar]
- Prasad, S.; Li, Y.; Lin, D.; Sheng, D. maskedFaceNet: A Progressive Semi-Supervised Masked Face Detector. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Waikoloa, HI, USA, 5–9 January 2021; pp. 3389–3398. [Google Scholar]
- Zhou, L.F.; Gu, Y.; Liang, S.; Lei, B.J.; Liu, J. Direction-Sensitivity Features Ensemble Network for Rotation-Invariant Face Detection. In Chinese Conference on Pattern Recognition and Computer Vision (PRCV); Springer: Berlin/Heidelberg, Germany, 2020; pp. 581–590. [Google Scholar]
- Yang, B.; Yang, C.; Liu, Q.; Yin, X.C. Joint rotation-invariance face detection and alignment with angle-sensitivity cascaded networks. In Proceedings of the 27th ACM International Conference on Multimedia, Nice, France, 21–25 October 2019; pp. 1473–1480. [Google Scholar]
- Rowley, H.A.; Baluja, S.; Kanade, T. Rotation invariant neural network-based face detection. In Proceedings of the 1998 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (Cat. No. 98CB36231), Santa Barbara, CA, USA, 25 June 1998; pp. 38–44. [Google Scholar]
- Shi, X.; Shan, S.; Kan, M.; Wu, S.; Chen, X. Real-time rotation-invariant face detection with progressive calibration networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 2295–2303. [Google Scholar]
- Zhou, L.F.; Gu, Y.; Wang, P.S.; Liu, F.Y.; Liu, J.; Xu, T.Y. Rotation-Invariant Face Detection with Multi-task Progressive Calibration Networks. In Proceedings of the International Conference on Pattern Recognition and Artificial Intelligence, Zhongshan, China, 19–23 October 2020; Springer: Berlin/Heidelberg, Germany, 2020; pp. 513–524. [Google Scholar]
- Liu, H.; Simonyan, K.; Yang, Y. Darts: Differentiable architecture search. arXiv 2018, arXiv:1806.09055. [Google Scholar]
- Hosang, J.; Benenson, R.; Schiele, B. Learning non-maximum suppression. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4507–4515. [Google Scholar]
- Dalal, N.; Triggs, B. Histograms of oriented gradients for human detection. In Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05), San Diego, CA, USA, 20–26 June 2005; Volume 1, pp. 886–893. [Google Scholar]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster r-cnn: Towards real-time object detection with region proposal networks. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 39, 1137–1149. [Google Scholar] [CrossRef]
- Zoph, B.; Vasudevan, V.; Shlens, J.; Le, Q.V. Learning transferable architectures for scalable image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 8697–8710. [Google Scholar]
- Jain, V.; Learned-Miller, E. Fddb: A Benchmark for Face Detection in Unconstrained Settings; Technical Report, UMass Amherst Technical Report; UMass Amherst: Amherst, MA, USA, 2010. [Google Scholar]
- Liu, A.; Li, X.; Wan, J.; Liang, Y.; Escalera, S.; Escalante, H.J.; Madadi, M.; Jin, Y.; Wu, Z.; Yu, X.; et al. Cross-ethnicity face anti-spoofing recognition challenge: A review. IET Biom. 2021, 10, 24–43. [Google Scholar] [CrossRef]
- Karkkainen, K.; Joo, J. FairFace: Face Attribute Dataset for Balanced Race, Gender, and Age for Bias Measurement and Mitigation. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Waikoloa, HI, USA, 5–9 January 2021; pp. 1548–1558. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).