Economic and Ecological Design of Hybrid Renewable Energy Systems Based on a Developed IWO/BSA Algorithm
Abstract
:1. Introduction
- We propose a hybrid algorithm called IWO/BSA, with the aim of improving the performance of the original IWO and BSA algorithms by combining their advantages into an algorithm.
- The proposed algorithm is applied to the optimal economic design of a stand-alone hybrid microgrid system in Dakhla (Morocco).
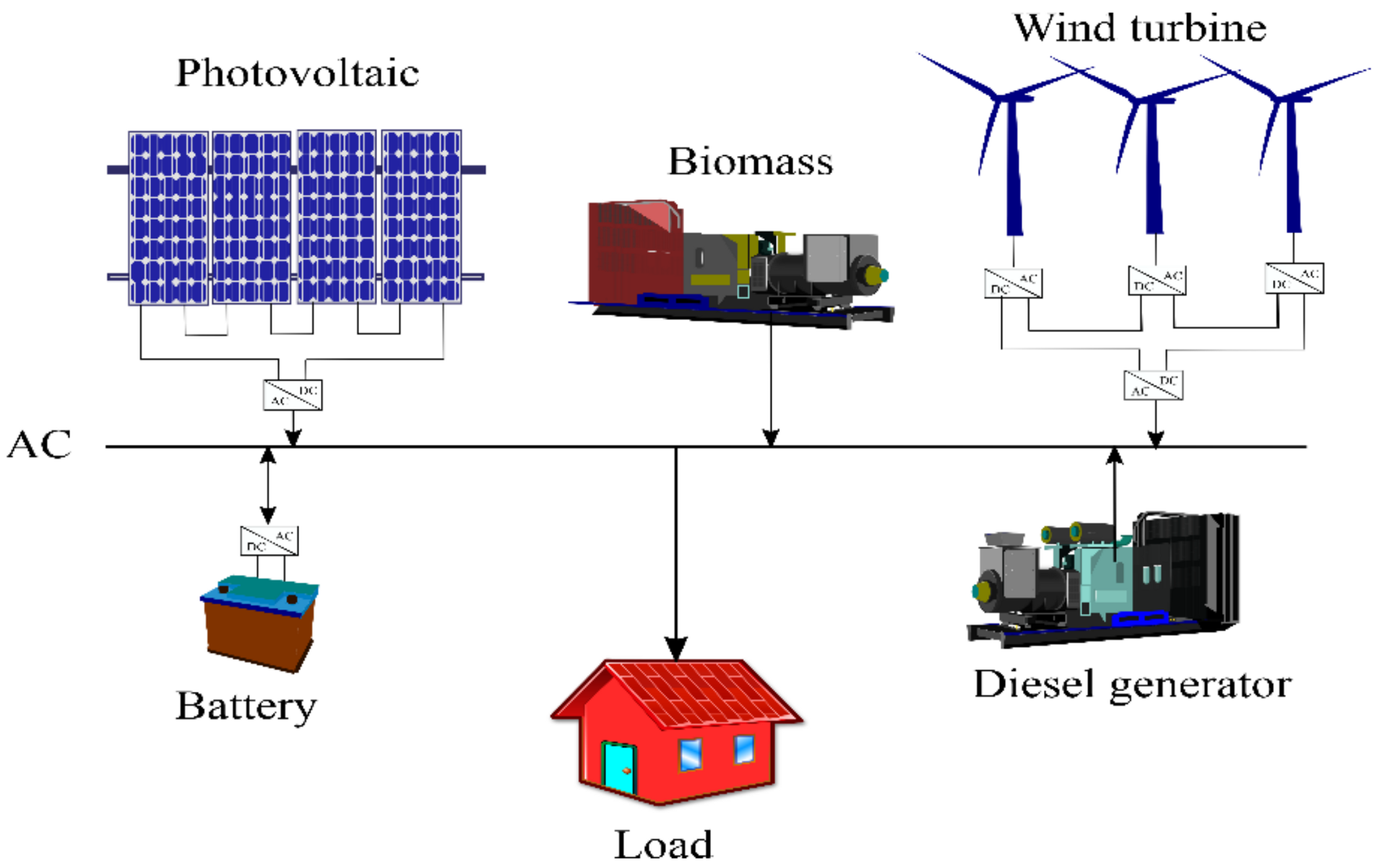
- Four configurations consisting of RES (PV, WT and biomass) with diesel generators and battery storage systems are suggested.
- Comparing the proposed IWO/BSA with artificial electric field (AEFA), GWO, BSA, and IWO algorithms.
2. Mathematical Description of the Proposed Hybrid System Components
- The PV and WT are used firstly as the main power sources to feed the load needs.
- The BESS operates when the PV and WT cannot feed the full load.
- The biomass system starts working when the battery depletes to a minimum permissible power and the load power exceeds 30% of its nominal power.
2.1. PV System
2.2. Wind System
2.3. Biomass System
2.4. Diesel System
2.5. BESS System
3. Formulation of the Optimization Problem
3.1. Net Present Cost
3.1.1. PV and WT Costs
3.1.2. Diesel Costs
3.1.3. BESS Costs
3.1.4. Biomass Costs
3.1.5. Inverter Costs
3.2. Levelized Cost of Energy
3.3. Loss of Power Supply Probability
3.4. Renewable Energy Fraction
3.5. Availability Index Fraction
3.6. Constraints
4. Algorithms
4.1. Invasive Weed Optimization Algorithm
4.1.1. Population Initialization
4.1.2. Reproduction
4.1.3. Spatial Dispersal
4.1.4. Competitive Exclusion
| Algorithm 1: IWO |
| Initialize a set of random weeds, within the limits . |
| Set the IWO’s parameters |
| Evaluate the objective function for all weeds |
| While ( < ) |
| Calculate the best and worst fitness in the colony |
| Calculate the σ |
| for each weed in the colony |
| Calculate the number of seeds following the |
| fitness of each weed |
| Add the seeds to their parents in the colony |
| if |
| Sort the new population according to their fitness |
| Eliminate the worst fitness in order to achieve the allowed |
| end if |
| end for |
| Update iteration |
| end while |
| Return the final best solution |
4.2. Backtracking Search Algorithm
4.2.1. Population Initialization
4.2.2. Selection-I
4.2.3. Mutation
4.2.4. Crossover
4.3. Hybrid IWO/BSA Algorithm
| Algorithm 2: BSA |
| Initialize a set of random population and historical population within the limits . |
| Initialize set the only BSA parameter called the mix rate and take the best fitness at the inf value. |
| Evaluate the objective function for the . |
| While (iter <) |
| Selection-I look at equations 24,25 and 26 |
| Mutation calculates mutant using: where F = 0.6 randn |
| Crossover calculates the trial population T: |
| if (c < d |c, d ) then |
| for i from 1 to N do |
| end |
| else |
| for i from 1 to N do, |
| end |
| Generate the Trial population, T |
| for i from 1 to N do |
| for i from 1 to N do |
| if then |
| end |
| end |
| Appling the Boundary Control Mechanism |
| Selection-II evaluate the objective function of |
| for i from 1 to N do |
| if then |
| end |
| end |
| Comparison between the actual best solutionand |
| end while |
| Return the final best solution |
4.3.1. Initialization
4.3.2. Reproduction
4.3.3. Selection I
4.3.4. Mutation and Crossover
4.3.5. Spatial Dispersal
4.3.6. Competitive Exclusion
4.3.7. Selection II
5. Case Study
6. Results and Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| AEFA | Artificial Electric Field Algorithm |
| ALO | Antlion Optimizer |
| BESS | Battery energy storage system |
| BO | Bonobo Optimizer |
| BOACA | Bi-objective ant colony algorithm |
| BSA | Backtracking Search Algorithm |
| COE | Cost of Energy |
| CS | Cuckoo search |
| CSA | Crow search algorithm |
| DG | Diesel generator |
| FA | Firefly algorithm |
| GA | Genetic algorithm |
| GC | Grid-Connected |
| GOA | Grasshopper Optimization Algorithm |
| GWO | Grey Wolf Optimizer |
| HHO | Harris Hawks optimizer |
| HRES | Hybrid renewable energy system |
| IWO | Invasive Weed Optimization |
| JLBO | Jaya and teaching–learning-based optimization |
| MPPT | Maximum Power Point Tracker |
| MVO | Multi-Verse Optimizer |
| NPC | Net Present Cost |
| PHS | Pumped hydro storage |
| PSO | Particle swarm optimization |
| QOBO | Quasi-Oppositional Bonobo Optimizer |
| RES | Renewable energy sources |
| SA | Stand-Alone |
| SOC | State of charge |
| SSO | Social spider optimizer |
| TORSCHE | Time Optimization of Resources, Scheduling |
| WDO | Wind driven optimization |
| WOA | Whale Optimization Algorithm |
| WT | Wind turbine |
| Symbols | |
| Area of PV and swept area of wind (m2) | |
| , | Constants of the linear consumption of the fuel (L/kW) |
| PV area (m2) | |
| Swept area of the wind turbine (m2) | |
| Capacity of BESS (kWh) | |
| Initial cost of the BESS ($) | |
| Investment cost of PV and wind generators ($) | |
| Calorific value of the organic material (MJ/kg) | |
| Capacity of battery (kWh) | |
| Investment cost of biomass ($) | |
| Cost of the consumed quantity of fuel ($/year) | |
| Inverter investment cost ($) | |
| Maximum power coefficient (%) | |
| Min battery energy in discharge (kWh) | |
| Energy Load (kWh) | |
| Fuel cost ($) | |
| Fuel consumption (L/h) | |
| Consumed quantity of fuel (L) | |
| Diesel run number | |
| O&M (contain the replacement) costs of the BESS ($) | |
| O&M cost of the inverter ($) | |
| Operation & maintenance costs ($) | |
| O&M cost of biomass ($) | |
| Maintenance and Operation cost of diesel generator ($) | |
| Operating hours (hr) | |
| Biomass power (kW) | |
| Rated capacity of biomass (kW) | |
| Output power of diesel generator (kW) | |
| Output power of diesel generator (kW) | |
| Output power of diesel generator (kW) | |
| Rated power of the inverter (kW) | |
| Load power (kW) | |
| Output power of PV (kW) | |
| Rated power (kW) | |
| Output power of renewable energy sources (kW) | |
| Annual working of system (kWh/Year) | |
| Output wind power (kW) | |
| Annual replacement cost of diesel ($) | |
| Diesel replacement cost ($/kW) | |
| Number of seeds that a weed can produce | |
| Maximum allowed number of seeds generated | |
| Minimum allowed number of seeds generated | |
| Total organic material of biomass () | |
| Ambient temperature (°C), | |
| Photovoltaic cell reference temperature (°C). | |
| Fitness of the plant i | |
| Maximum fitness value of the plants in the colony | |
| Minimum fitness value of the plants in the colony | |
| Interest rate (%) | |
| Maximum iteration | |
| Fuel price ($/L) | |
| Cut-in speed (m/s) | |
| Cut-out speed (m/s) | |
| Rated wind speed (m/s) | |
| Biomass efficiency (%) | |
| Efficiency of the battery (%) | |
| Efficiency of the inverter (%) | |
| Efficiency of the PV (%) | |
| Reference efficiency, is the efficiency of the MPPT equipment, | |
| Annual fixed cost of O&M of biomass ($/kW/year) | |
| Variable cost of O&M of biomass ($/kWh) | |
| Annual O&M cost of the inverter ($/year) | |
| Annual operation & maintenance of PV and wind ($/m2/year) | |
| Annual O&M cost of BESS ($/m2/year) | |
| Annual O&M cost of diesel ($/hr) | |
| Initial cost of PV and wind ($/m2) | |
| BESS initial cost ($/kWh) | |
| Biomass initial cost ($/kW) | |
| Diesel initial cost ($/kW) | |
| Inverter initial cost ($/m2) | |
| Initial standard deviation | |
| Final standard deviation | |
| Standard deviation | |
| Availability index (%) | |
| Autonomy daily of the battery (day) | |
| Investment cost ($) | |
| Capital recovery factor | |
| Depth of discharge (%) | |
| Solar irradiation (kW/m2) | |
| Levelized cost of energy ($/kWh) | |
| Loss of power supply probability (%) | |
| Nominal operating cell temperature (°C), | |
| Net Present Cost ($) | |
| Operation and maintenance cost ($) | |
| Replacement cost ($) | |
| Renewable Fraction (%) | |
| Nonlinear modulation index | |
| Wind velocity (m/s) | |
| Temperature coefficient of the efficiency | |
| Inflation rate (%) | |
| Escalation rate (%) | |
| Air density (Kg/m3) |
Appendix A
| Symbol | Quantity | Conversion |
|---|---|---|
| N | Project lifetime | 20 year |
| Interest rate | 13.25% | |
| Escalation rate | 2% | |
| Inflation rate | 12.27% | |
| PV initial cost | 300 $/m2 | |
| Annual O&M cost of PV | $/m2/year | |
| Reference efficiency of the PV | 25% | |
| Efficiency of MPPT | 100% | |
| PV cell reference temperature | 25 °C | |
| Temperature coefficient | 0.005 °C | |
| NOCT | Nominal operating cell temperature | 47 °C |
| PV system lifetime | 20 year | |
| Wind initial cost | 125 $/m2 | |
| Annual O&M cost of wind | $/m2/year | |
| Maximum power coefficient | 48% | |
| Cut-in wind speed | 2.6 m/s | |
| Cut-out wind speed | 25 m/s | |
| Rated wind speed | 9.5 m/s | |
| Wind system lifetime | 20 year | |
| Diesel initial cost | 250 $/kW | |
| Annual O&M cost of diesel | 0.05 $/h | |
| Replacement cost | 210 $/kW | |
| Fuel price in Egypt | 0.43 $/L | |
| Diesel system lifetime | 7 year | |
| Battery initial cost | 100 $/kWh | |
| Annual operation & maintenance cost of Battery | $/m2/year | |
| Depth of discharge | 80% | |
| Battery efficiency | 97% | |
| Minimum state of charge | 20% | |
| Maximum state of charge | 80% | |
| Battery system lifetime | 5 year | |
| Inverter initial cost | 400 $/m2 | |
| Annual O&M cost of inverter | 20 $/year | |
| Inverter efficiency | 97% |
| Algorithms | Parameters |
|---|---|
| AEFA | 500; ⍺ = 30; Population size = 10; Maximum iteration = 100 |
| GWO | a = Linear reduction from 2 to 0; Search agents = 10; Maximum iteration = 100 |
| IWO | 1; 3; 0.5; 0.001; Population Size = 10; Maximum Population Size = 25; Exponent = 1; Maximum iteration = 100 |
| BSA | DIM_RATE = 1; Population size = 10; Maximum iteration = 100 |
| IWO/BSA | 1; 3; 0.5; 0.001; Exponent = 1; DIM_RATE = 1; Population Size = 10; Maximum Population Size = 25; Maximum iteration = 100 |
| System | Datasheet |
|---|---|
| PV | Manufacture: Solar World; Model: Submodule Plus SW 255 poly; Rated power: 255 W; Area: 1.68 m2 |
| Wind Biomass | Manufacture: Siemens; Model: SWT-3.0-113; Rated power: 3 kW; Area: 10,029 m2 Community Power Corporation (CPC) |
| Diesel | Rated power: 140 W |
| Battery | Model: Lead Acid, Rated power: 1.85 kWh |
| Inverter | Manufacture: Sunny Swiss, Model: SB2000HF, Nominal power: 8000 W |
References
- Babatunde, O.M.; Munda, J.L.; Hamam, Y. A Comprehensive State-of-the-Art Survey on Hybrid Renewable Energy System Operations and Planning. IEEE Access 2020, 8, 75313–75346. [Google Scholar] [CrossRef]
- Kharrich, M.; Mohammed, O.H.; Mohammed, Y.S.; Akherraz, M. A Review on Recent Sizing Methodologies for Hybrid Microgrid Systems. Int. J. Energy Convers. 2019, 7, 230–240. [Google Scholar] [CrossRef]
- Zia, M.F.; Benbouzid, M.; Elbouchikhi, E.; Muyeen, S.M.; Techato, K.; Guerrero, J.M. Microgrid Transactive Energy: Review, Architectures, Distributed Ledger Technologies, and Market Analysis. IEEE Access 2020, 8, 19410–19432. [Google Scholar] [CrossRef]
- Mbungu, N.T.; Naidoo, R.M.; Bansal, R.C.; Vahidinasab, V. Overview of the Optimal Smart Energy Coordination for Microgrid Applications. IEEE Access 2019, 7, 163063–163084. [Google Scholar] [CrossRef]
- Gomes, L.; Vale, Z.A.; Corchado, J.M. Multi-Agent Microgrid Management System for Single-Board Computers: A Case Study on Peer-to-Peer Energy Trading. IEEE Access 2020, 8, 64169–64183. [Google Scholar] [CrossRef]
- Shrestha, A.; Bishwokarma, R.; Chapagain, A.; Banjara, S.; Aryal, S.; Mali, B.; Thapa, R.; Bista, D.; Hayes, B.P.; Papadakis, A.; et al. Peer-to-Peer Energy Trading in Micro/Mini-Grids for Local Energy Communities: A Review and Case Study of Nepal. IEEE Access 2019, 7, 131911–131928. [Google Scholar] [CrossRef]
- Mazzeo, D.; Matera, N.; de Luca, P.; Baglivo, C.; Congedo, P.M.; Oliveti, G. A literature review and statistical analysis of photovoltaic-wind hybrid renewable system research by considering the most relevant 550 articles: An upgradable matrix literature database. J. Clean. Prod. 2021, 295, 126070. [Google Scholar] [CrossRef]
- Diab, A.A.Z.; Sultan, H.M.; Mohamed, I.S.; Kuznetsov, O.N.; Do, T.D. Application of Different Optimization Algorithms for Optimal Sizing of PV/Wind/Diesel/Battery Storage Stand-Alone Hybrid Microgrid. IEEE Access 2019, 7, 119223–119245. [Google Scholar] [CrossRef]
- Zhou, Z.; Ge, L. Operation of Stand-Alone Microgrids Considering the Load Following of Biomass Power Plants and the Power Curtailment Control Optimization of Wind Turbines. IEEE Access 2019, 7, 186115–186125. [Google Scholar] [CrossRef]
- Kharrich, M.; Mohammed, O.; Akherraz, M. Design of Hybrid Microgrid PV/Wind/Diesel/Battery System: Case Study for Rabat and Baghdad. EAI Endorsed Trans. Energy Web 2018, 7, 162692. [Google Scholar] [CrossRef]
- Tooryan, F.; HassanzadehFard, H.; Collins, E.R.; Jin, S.; Ramezani, B. Optimization and energy management of distributed energy resources for a hybrid residential microgrid. J. Energy Storage 2020, 30, 101556. [Google Scholar] [CrossRef]
- Bukar, A.L.; Tan, C.W.; Lau, K.Y. Optimal sizing of an autonomous photovoltaic/wind/battery/diesel generator microgrid using grasshopper optimization algorithm. Solar Energy 2019, 188, 685–696. [Google Scholar] [CrossRef]
- Sanajaoba, S. Optimal sizing of off-grid hybrid energy system based on minimum cost of energy and reliability criteria using firefly algorithm. Solar Energy 2019, 188, 655–666. [Google Scholar] [CrossRef]
- Fathy, A.; Kaaniche, K.; Alanazi, T.M. Recent Approach Based Social Spider Optimizer for Optimal Sizing of Hybrid PV/Wind/Battery/Diesel Integrated Microgrid in Aljouf Region. IEEE Access 2020, 8, 57630–57645. [Google Scholar] [CrossRef]
- Saravanan, B.; Vasudevan, E.R.; Kothari, D.P. Unit commitment problem solution using invasive weed optimization algorithm. Int. J. Electr. Power Energy Syst. 2014, 55, 21–28. [Google Scholar] [CrossRef]
- Bhattacharjee, K.; Bhattacharya, A.; Dey, S.H.N. Backtracking search optimization based economic environmental power dispatch problems. Int. J. Electr. Power Energy Syst. 2015, 73, 830–842. [Google Scholar] [CrossRef]
- Panda, M.R.; Das, P.; Pradhan, S. Hybridization of IWO and IPSO for mobile robots navigation in a dynamic environment. J. King Saud Univ. Comput. Inf. Sci. 2020, 32, 1020–1033. [Google Scholar] [CrossRef]
- Mahto, S.K.; Choubey, A. A novel hybrid IWO/WDO algorithm for nulling pattern synthesis of uniformly spaced linear and non-uniform circular array antenna. AEU Int. J. Electron. Commun. 2016, 70, 750–756. [Google Scholar] [CrossRef]
- Lin, Q.; Gao, L.; Li, X.; Zhang, C. A hybrid backtracking search algorithm for permutation flow-shop scheduling problem. Comput. Ind. Eng. 2015, 85, 437–446. [Google Scholar] [CrossRef]
- Khan, A.; Javaid, N. Jaya Learning-Based Optimization for Optimal Sizing of Stand-Alone Photovoltaic, Wind Turbine, and Battery Systems. Engineering 2020, 6, 812–826. [Google Scholar] [CrossRef]
- Kharrich, M.; Mohammed, O.H.; Kamel, S.; Selim, A.; Sultan, H.M.; Akherraz, M.; Jurado, F. Development and Implementation of a Novel Optimization Algorithm for Reliable and Economic Grid-Independent Hybrid Power System. Appl. Sci. 2020, 10, 6604. [Google Scholar] [CrossRef]
- Makhdoomi, S.; Askarzadeh, A. Optimizing operation of a photovoltaic/diesel generator hybrid energy system with pumped hydro storage by a modified crow search algorithm. J. Energy Storage 2020, 27, 101040. [Google Scholar] [CrossRef]
- Abo-Elyousr, F.K.; Elnozahy, A. Bi-objective economic feasibility of hybrid micro-grid systems with multiple fuel options for islanded areas in Egypt. Renew. Energy 2018, 128, 37–56. [Google Scholar] [CrossRef]
- Ming, M.; Wang, R.; Zha, Y.; Zhang, T. Multi-Objective Optimization of Hybrid Renewable Energy System Using an Enhanced Multi-Objective Evolutionary Algorithm. Energies 2017, 10, 674. [Google Scholar]
- Mohamed, A.A.; Ali, S.; Alkhalaf, S.; Senjyu, T.; Hemeida, A.M. Optimal Allocation of Hybrid Renewable Energy System by Multi-Objective Water Cycle Algorithm. Sustainability 2019, 11, 6550. [Google Scholar] [CrossRef] [Green Version]
- Crainz, M.; Curto, D.; Franzitta, V.; Longo, S.; Montana, F.; Musca, R.; Riva Sanseverino, E.; Telaretti, E. Flexibility Services to Minimize the Electricity Production from Fossil Fuels. A Case Study in a Mediterranean Small Island. Energies 2019, 12, 3492. [Google Scholar] [CrossRef] [Green Version]
- Hossain, M.A.; Chakrabortty, R.K.; Ryan, M.J.; Pota, H.R. Energy management of community energy storage in grid-connected microgrid under uncertain real-time prices. Sustain. Cities Soc. 2021, 66, 102658. [Google Scholar] [CrossRef]
- Curto, D.; Franzitta, V.; Viola, A.; Cirrincione, M.; Mohammadi, A.; Kumar, A. A renewable energy mix to supply small islands. A comparative study applied to Balearic Islands and Fiji. J. Clean. Prod. 2019, 241, 118356. [Google Scholar] [CrossRef]
- Tsai, C.-T.; Beza, T.M.; Molla, E.M.; Kuo, C.-C. Analysis and Sizing of Mini-Grid Hybrid Renewable Energy System for Islands. IEEE Access 2020, 8, 70013–70029. [Google Scholar] [CrossRef]
- Rehman, S.; Natrajan, N.; Mohandes, M.; Alhems, L.M.; Himri, Y.; Allouhi, A. Feasibility Study of Hybrid Power Systems for Remote Dwellings in Tamil Nadu, India. IEEE Access 2020, 8, 143881–143890. [Google Scholar] [CrossRef]
- Hossain, M.; Mekhilef, S.; Olatomiwa, L. Performance evaluation of a standalone PV-wind-diesel-battery hybrid system feasible for a large resort center in South China Sea, Malaysia. Sustain. Cities Soc. 2017, 28, 358–366. [Google Scholar] [CrossRef]
- Mazzeo, D.; Baglivo, C.; Matera, N.; Congedo, P.M.; Oliveti, G. A novel energy-economic-environmental multi-criteria decision-making in the optimization of a hybrid renewable system. Sustain. Cities Soc. 2020, 52, 101780. [Google Scholar] [CrossRef]
- Curto, D.; Favuzza, S.; Franzitta, V.; Musca, R.; Navia, M.A.N.; Zizzo, G. Evaluation of the optimal renewable electricity mix for Lampedusa island: The adoption of a technical and economical methodology. J. Clean. Prod. 2020, 263, 121404. [Google Scholar] [CrossRef]
- Ahmad, S.; Ullah, I.; Jamil, F.; Kim, D. Toward the Optimal Operation of Hybrid Renewable Energy Resources in Microgrids. Energies 2020, 13, 5482. [Google Scholar] [CrossRef]
- Heydari, A.; Askarzadeh, A. Optimization of a biomass-based photovoltaic power plant for an off-grid application subject to loss of power supply probability concept. Appl. Energy 2016, 165, 601–611. [Google Scholar] [CrossRef]
- Guangqian, D.; Bekhrad, K.; Azarikhah, P.; Maleki, A. A hybrid algorithm based optimization on modeling of grid independent biodiesel-based hybrid solar/wind systems. Renew. Energy 2018, 122, 551–560. [Google Scholar] [CrossRef]
- Sawle, Y.; Gupta, S.C.; Bohre, A.K. Socio-techno-economic design of hybrid renewable energy system using optimization techniques. Renew. Energy 2018, 119, 459–472. [Google Scholar] [CrossRef]
- Ramli, M.A.M.; Bouchekara, H.R.E.H.; Alghamdi, A.S. Optimal sizing of PV/wind/diesel hybrid microgrid system using multi-objective self-adaptive differential evolution algorithm. Renew. Energy 2018, 121, 400–411. [Google Scholar] [CrossRef]
- Movahediyan, Z.; Askarzadeh, A. Multi-objective optimization framework of a photovoltaic-diesel generator hybrid energy system considering operating reserve. Sustain. Cities Soc. 2018, 41, 1–12. [Google Scholar] [CrossRef]
- Ghiasi, M. Detailed study, multi-objective optimization, and design of an AC-DC smart microgrid with hybrid renewable energy resources. Energy 2019, 169, 496–507. [Google Scholar] [CrossRef]
- Mehrabian, A.R.; Lucas, C. A novel numerical optimization algorithm inspired from weed colonization. Ecol. Inform. 2006, 1, 355–366. [Google Scholar] [CrossRef]
- Civicioglu, P. Backtracking Search Optimization Algorithm for numerical optimization problems. Appl. Math. Comput. 2013, 219, 8121–8144. [Google Scholar] [CrossRef]














| Reference | Year | Hybrid RESs | Algorithm/Tool | OF | Advantages | Potential Improvements |
|---|---|---|---|---|---|---|
| Tooryan et al. [11] | 2020 | PV/wind/diesel/battery | PSO, GA | NPC | Clear and simple study | Classical approach methods are used. |
| Bukar et al. [12] | 2019 | PV/wind/diesel/battery | GOA, CSA, PSO | COE | Application of GOA algorithm | System credibility such as uncertainty and availability should be enhanced. |
| Sanajaoba et al. [13] | 2019 | PV/wind/battery | FA, GA, PSO | COE | The developed model is applied for three remote unelectrified villages | The sensitivity analysis is not included. |
| Fathy et al. [14] | 2020 | PV/wind/battery/diesel | GWO, MVO, ALO, WOA, SSO | COE | Detailed study with many results | The proposed SSO could be further explored |
| Khan and Javaid [20] | 2020 | -PV/wind/battery -PV/battery -Wind/battery | Jaya, TLBO, JLBO, GA | TAC | Proposed a new hybrid algorithm named JLBO | The uncertainty for the wind and PV should be considered. |
| Kharrich et al. [21] | 2020 | -PV/wind/diesel/battery -PV/biomass -PV/diesel/battery -wind/diesel/battery | QOBO, BO, HHO, AEFA, IWO | NPC | Proposed a new developed algorithm called QOBO | The uncertainty parameter is missing. |
| Makhdoomi and Askarzadeh [22] | 2020 | PV/diesel/PHS | GA, PSO, CSA, CSAAC-AP | Fuel consumption | Proposing a modified CSA | The operation time-span of the study is only 24 h. |
| Abo-Elyousr and Nozh [23] | 2018 | PV/wind/biomass/NGFC/NGT | BOACA, GA, PSO, HOMER | -COE -GHG | Developing a BOACA algorithm offers optimal HMG system configuration and sizing | The LPSP results should be further examined and analyzed. |
| Hossain et al. [31] | 2016 | PV/wind/diesel/battery | HOMER | NPC | Performance evaluation of standalone hybrid system | The study is only based on commercial software application. Other meta-heuristic algorithms could be included and examined. |
| Heydari and Askarzadeh [35] | 2016 | PV/biomass | HSA | NPC | Proving the disadvantage of the HOMER software compared to the meta-heuristic algorithms. | Algorithm comparison is required to confirm that the best results could be found from HS algorithm. |
| Guangqian et al. [36] | 2018 | -Wind/PV/diesel/battery -Wind/diesel/battery -PV/diesel/battery | HSA, SAA, HHSSAA | LCC | Proposing a hybrid algorithm for determining the optimal size of grid-independent system. | The reliability and other factors are should be considered. |
| Sawle et al. [37] | 2018 | -PV/biomass/diesel/battery -PV/diesel/battery -Wind/biomass/diesel/battery -Wind/diesel/battery -PV/wind/diesel/battery -PV/wind/biomass/diesel/battery | GA, PSO, BFPSO, TLBO | COEI + LPSPI + (1/RFI) + (1/HDI) + PMI + (1/JCI) | Considering social, technical, and economic indices in only one objective function. | Adding the uncertainty will bonus and improve this study. |
| Ramli et al. [38] | 2018 | PV/wind/diesel/battery | MOSaDE | -COE -LPSP | Detailed study | Comparison with another multi-objective algorithm is necessary. Otherwise, the knee point should be used to define a compromise solution. |
| Movahediyan and Askarzadeh [39] | 2018 | PV/diesel | MO-CSA, MOPSO | -LPSP -NPC-CO2 emission | Considering the operating reserve impact in the sizing problem. | Other systems need to be included in the study. |
| Ghiasi [40] | 2018 | PV/wind/battery grid connected | MOPSO, MOGA | -Availability -Cost | The use of the availability factor in the inter-connected system. | The reliability could be considered for extending this method. |
| Hybrid Power System | Algorithm | PV (m2) | WT (m2) | Diesel (kW) | Battery (kWh) | Biomass (t/Year) |
|---|---|---|---|---|---|---|
| AEFA | 67.5137 | 702.9344 | // | 4.7888 | 32.1741 | |
| GWO | 77.4342 | 780.7906 | // | 9.2082 | 27.5612 | |
| PV/WT/Biomass/Battery | BSA | 75.7053 | 576.7633 | // | 4.8753 | 0.3522 |
| IWO | 234.6187 | 890.4494 | // | 6.8913 | 19.6979 | |
| IWO/BSA | 89.7678 | 554.205 | // | 4.78773 | 0.0000 | |
| AEFA | 355.5057 | // | // | // | 32.3361 | |
| GWO | 357.6068 | // | // | // | 34.2460 | |
| PV/Biomass | BSA | 390.6575 | // | // | // | 0.6572 |
| IWO | 386.4402 | // | // | // | 50.2505 | |
| IWO/BSA | 349.5524 | // | // | // | 18.9940 | |
| AEFA | 414.1790 | // | 0.6979 | 13.1553 | // | |
| GWO | 436.8411 | // | 0.5732 | 21.4832 | // | |
| PV/Diesel/Battery | BSA | 385.4886 | // | 0.5367 | 11.5347 | // |
| IWO | 488.2624 | // | 0.5697 | 27.8874 | // | |
| IWO/BSA | 391.3988 | // | 0.5565 | 12.9746 | // | |
| AEFA | // | 7440.8018 | 0.0949 | 11.9624 | // | |
| GWO | // | 8481.7017 | 0.9766 | 23.9765 | // | |
| WT/Diesel/Battery | BSA | // | 2237.7688 | 48.2904 | 11.9192 | // |
| IWO | // | 2124.2369 | 54.1864 | 29.9514 | // | |
| IWO/BSA | // | 1850.8162 | 20.8737 | 41.5201 | // |
| Hybrid Power System | Algorithm | NPC ($) | LCOE ($/kWh) | LPSP | Availability (%) | Renewable Energy (%) | Battery Autonomy (Day) |
|---|---|---|---|---|---|---|---|
| AEFA | 132,529 | 0.3048 | 0.0487 | 96.7275 | // | 0.5025 | |
| GWO | 147,645 | 0.3395 | 0.0494 | 96.9305 | // | 0.9663 | |
| PV/WT/Biomass/Battery | BSA | 112,324 | 0.2583 | 0.0496 | 95.8039 | // | 0.5116 |
| IWO | 201,912 | 0.4643 | 0.0372 | 97.3849 | // | 0.7232 | |
| IWO/BSA | 111,929 | 0.2574 | 0.0498 | 95.7752 | // | 0.5024 | |
| AEFA | 127,339 | 0.1210 | 0.0484 | 96.0199 | // | // | |
| PV/Biomass | GWO | 128,009 | 0.1216 | 0.0477 | 96.1075 | // | // |
| BSA | 130,611 | 0.1241 | 0.0500 | 95.1179 | // | // | |
| IWO | 136,344 | 0.1295 | 0.0393 | 96.9598 | // | // | |
| IWO/BSA | 124,689 | 0.1184 | 0.0499 | 95.6296 | // | // | |
| AEFA | 164,695 | 0.1565 | 0.0433 | 97.1636 | 98.6270 | 0.5703 | |
| PV/Diesel/Battery | GWO | 166,540 | 0.1582 | 0.0456 | 97.3848 | 98.9496 | 0.9313 |
| BSA | 151,667 | 0.1441 | 0.0498 | 96.6089 | 98.8330 | 0.5000 | |
| IWO | 168,305 | 0.1599 | 0.0278 | 98.7587 | 99.1402 | 1.2089 | |
| IWO/BSA | 142,233 | 0.1354 | 0.0250 | 98.6109 | 98.8330 | 0.5635 | |
| AEFA | 839,754 | 0.7977 | 0.0491 | 95.6578 | 99.9995 | 0.5186 | |
| WT/Diesel/Battery | GWO | 967,611 | 0.9192 | 0.0497 | 96.0061 | 99.9959 | 1.0394 |
| BSA | 1,084,283 | 1.0300 | 0.0494 | 99.6037 | 98.6116 | 0.5167 | |
| IWO | 1,178,630 | 1.1197 | 0.0234 | 99.8091 | 98.2891 | 1.2984 | |
| IWO/BSA | 590,097 | 0.5606 | 0.0128 | 96.5619 | 99.1954 | 1.7999 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kharrich, M.; Kamel, S.; Ellaia, R.; Akherraz, M.; Alghamdi, A.S.; Abdel-Akher, M.; Eid, A.; Mosaad, M.I. Economic and Ecological Design of Hybrid Renewable Energy Systems Based on a Developed IWO/BSA Algorithm. Electronics 2021, 10, 687. https://doi.org/10.3390/electronics10060687
Kharrich M, Kamel S, Ellaia R, Akherraz M, Alghamdi AS, Abdel-Akher M, Eid A, Mosaad MI. Economic and Ecological Design of Hybrid Renewable Energy Systems Based on a Developed IWO/BSA Algorithm. Electronics. 2021; 10(6):687. https://doi.org/10.3390/electronics10060687
Chicago/Turabian StyleKharrich, Mohammed, Salah Kamel, Rachid Ellaia, Mohammed Akherraz, Ali S. Alghamdi, Mamdouh Abdel-Akher, Ahmad Eid, and Mohamed I. Mosaad. 2021. "Economic and Ecological Design of Hybrid Renewable Energy Systems Based on a Developed IWO/BSA Algorithm" Electronics 10, no. 6: 687. https://doi.org/10.3390/electronics10060687
APA StyleKharrich, M., Kamel, S., Ellaia, R., Akherraz, M., Alghamdi, A. S., Abdel-Akher, M., Eid, A., & Mosaad, M. I. (2021). Economic and Ecological Design of Hybrid Renewable Energy Systems Based on a Developed IWO/BSA Algorithm. Electronics, 10(6), 687. https://doi.org/10.3390/electronics10060687











