Performance Analysis of Deep Neural Network Controller for Autonomous Driving Learning from a Nonlinear Model Predictive Control Method

Abstract

Nonlinear model predictive control (NMPC) is based on a numerical optimization method considering the target system dynamics as constraints. This optimization process requires large amount of computation power and the computation time is often unpredictable which may cause the control update rate to overrun. Therefore, the performance must be carefully balanced against the computational time. To solve the computation problem, we propose a data-based control technique based on a deep neural network (DNN). The DNN is trained with closed-loop driving data of an NMPC. The proposed "DNN control technique based on NMPC driving data" achieves control characteristics comparable to those of a well-tuned NMPC within a reasonable computation period, which is verified with an experimental scaled-car platform and realistic numerical simulations.

1. Introduction

Artificial intelligence technology has made great progress owing to the high-performance data processing devices and use of parallel processers with GPU programming. In addition, artificial intelligence technology has been widely used in the field of autonomous driving; in particular, it has helped solve challenging problems that are difficult to solve with the existing rule-based algorithms.

A level three or higher autonomous driving system based on the autonomous driving standards of the Society of Automated Engineers must handle various driving situations. Many researchers have studied control methods based on Deep neural network (DNN) to develop higher level autonomous driving systems that approach human driving characteristics. Therefore, data-based approaches have become the focus of control methods and have been investigated by many researchers. In particular, inverse reinforcement learning is used to solve the trajectory planning problem of autonomous vehicles [1]. Moreover, a cooperative steering control method was developed with driving data of human drivers for semi-autonomous vehicles [2]. In [3], a supervised learning technique was applied for policy learning for model predictive control (MPC) to solve the integrated chassis control problem; in addition, many researchers have applied neural networks to develop data-driven control methods suitable for diverse environments and model changes [4,5,6].

In this study, a data-driven control method is developed with closed-loop data of the nonlinear model predictive control (NMPC) method as the reference data. The numerical optimization process in the NMPC method optimizes the current driving states, and predicts the future states over the receding horizon steps. The future vehicle states are computed with the vehicle dynamics equation, and the best control inputs within the acceptable control inputs and state limits are determined.

However, the optimization process that derives the best results cannot usually sustain a stable computation time (see Figure 1). Moreover, the performance of a state prediction process based on the vehicle model may be degraded by uncertainty in the model. Researchers are trying to improve the performance of the NMPC method with driving data. In particular, a computationally efficient approach for learning from a model predictive controller was proposed in [7], and a data-driven MPC method for unknown environments was proposed in [8]. Finally, many researchers have applied data-driven approaches to improve the performance of the MPC method [9,10,11,12,13,14,15,16,17].

In this study, we generated closed-loop data with the MPC technique. The proposed deep neural network (DNN)-based controller learns the autonomy implemented in the control algorithm. The lighter neural network computation replaces the sophisticated numerical optimization process. Subsequently, the performance of the developed controller was verified with numerical simulations and an experimental platform. We developed a test environment with a 1:43 scale remotely controlled autonomous vehicle and evaluated the real-time performance of the developed control algorithm.

The nonlinear model predictive controller is presented in Section 2; Section 3 presents the development of the DNN to be trained with data generated from the reference NMPC method in Section 3. In Section 4, the simulation results of the developed controller are presented, and the performance characteristics of the NMPC method and trained ANN are compared. In Section 5, the real-time control performance of the developed DNN controller is verified in test scenarios of scaled-car experiments.

2. Design of Nonlinear Model Predictive Controller

2.1. Nonlinear Model Predictive Control (NMPC)

The presented NMPC technique was developed to train DNN. The controller predicts the vehicle states within a pre-specified prediction interval (N steps) and the best control input for a certain route through numerical optimization (Figure 2).

The optimization process considers the dynamic characteristics of the vehicle under the specified constraints. Therefore, its control inputs are better optimized to the vehicle characteristics than those of other path tracking algorithms [18,19]; in addition, the risk of slipping, rollover, and control failure in following the path is reduced. These problems arise owing to an excessive control input during obstacle avoidance or a sudden turn.

2.2. Vehicle Maneuver Predictive Model

The vehicle prediction model of the NMPC method uses a four-state kinematic model constructed in the global coordinate system (x,y). The states $\xi , \eta , \theta \mathrm{and} v$ are defined in Figure 3:

$$X=\left(\xi ,\eta ,\theta ,v\right).$$

(1)

The control inputs $\left(u\right)$ are the acceleration input $\left(a_{cmd}\right)$ and steering input $\left({\delta }_{cmd}\right)$:

$$u=\left(a_{cmd},{\delta }_{cmd}\right).$$

(2)

The kinematic model is composed of vehicle states; its controller inputs are as follows:

$$\begin{gathered} {\xi }_{k+1}=v_k\ast \cos \left({\theta }_k\right), \\ {\eta }_{k+1}=v_k\ast \sin \left({\theta }_k\right), \\ {\theta }_{k+1}=\frac{v_k}{L}\ast \tan \left({\theta }_k\right), \\ {v}_{k+1}=v_k+\Delta T\left(a_{cmd}-\frac{\sin \left(\theta \right)\ast F_{yf}}{m}\right), \end{gathered}$$

(3)

where L, ΔT, and m denote the vehicle length, control period, and vehicle mass, respectively. Moreover, $F_{yf}$ is the decelerating lateral force acting on the front wheel when the vehicle is turning. This term reduces the longitudinal velocity by $\frac{\sin \left(\theta \right)\ast F_{yf}}{m}$.

2.3. Optimization Process of NMPC Method

To design the model prediction control technique, the cost function must be configured. Our cost function computes the state error $(X^e)$ between the target reference points $\left(X^r\right)$ and predicted vehicle states:

$$X^r=\left({\xi }^r,{\eta }^r,{\theta }^r,v^r\right),$$

(4)

$$\begin{gathered} X^e=X-X^r, \\ =\left(\xi -{\xi }^r,\eta -{\eta }^r,\theta -{\theta }^r,v-v^r\right), \\ =[e_1,e_2,e_3,\cdots ,e_N]. \end{gathered}$$

(5)

N = Number of receding horizons of the NMPC (30 steps)

The cost function $J$ of the NMPC method is defined based on the error vector (Equation (5)) and the matrix of weights of each term:

$$J=\frac{1}{2}{e}_N^{T}P{e}_N+\frac{1}{2}{\displaystyle \sum }_{k=0}^{N-1}(e_k^{T}Q{e}_k+u_k^{T}R{u}_k).$$

(6)

where P, Q and R are weight matrices, and N represents the number of receding horizon steps. The designed cost function is minimized with a numerical optimization method based on the conjugate descent approach.

3. Deep Neural Network (DNN) Controller

3.1. Design of Deep Neural Network (DNN)

In this study, the control strategy of the NMPC method is learned with Artificial Neural Network (ANN) techniques. This technique includes one input layer, one or more hidden layers, and one output layer. Because the data propagate from the input to the output layers, our strategy is called “a feed-forward neural network”.

The feed-forward structure is commonly adopted in ANNs, there are two types: shallow neural networks with one hidden layer and deep neural networks (DNNs) with multiple hidden layers.

In this study, a DNN with five hidden layers (each with 20 artificial neurons) is used to stabilize the control inputs of the various input data (see Figure 4).

The designed network accepts 120 inputs and generates 60 outputs (see

Table 1. Training data of deep neural network (DNN).

Network Input Dataset (Network Input, Vehicle State)
Information		Number of Data	Number of Network Total Input Data
Local position	$x$	2N 1 (60)	4N (120)
	$y$
Driving direction	$\theta$	N (30)
Vehicle velocity	$v$	N (30)
Network Input Dataset (Network Output, Control Command)
Information		Number of Data	Number of Network Total Input Data
Acceleration command	$a^{cmd}$	N (30)	2N (60)
Steering command	$s^{cmd}$	N (30)

¹N = Number of receding horizons of the nonlinear model predictive control (NMPC) with 30 steps.

). These data are defined in Section 3.2.

3.2. Design of Input and Output Data of Deep Neural Network

To train the DNN controller with control performance characteristics similar to those of the NMPC method, the reference path point $\left(X^r\right)$ used in the NMPC method is used as the input datum. However, because the DNN control method cannot predict the behavior of the control vehicle, only the current vehicle state $(X_c)$ without the predicted state is used. The input data $I$ of the DNN control system are defined in Equations (7)–(9):

$$I_n=\left[x_n^I,y_n^I,{\theta }_n^I,v_n^I\right], (n=1, 2, 3, \dots , N),$$

(7)

with

$$\begin{gathered} x_n^I=\left({\xi }_n^r-{\xi }_c\right)\ast \cos \left({\theta }_c\right)+\left({\eta }_n^r-{\eta }_n\right)\ast \sin \left({\theta }_c\right), \\ {y}_n^I=-\left({\xi }_n^r-{\xi }_c\right)\ast \sin \left({\theta }_c\right)+\left({\eta }_n^r-{\eta }_n\right)\ast \cos \left({\theta }_c\right), \\ {\theta }_n^I={\theta }_n^r-{\theta }_c, \\ {v}_n^I=v_n^r-v_c, \end{gathered}$$

(8)

$$I=\left[I_1, I_2, I_3,\cdots ,I_N\right].$$

(9)

The vehicle state ($X$) is illustrated in Figure 5.

The target data of the DNN training are the input data of the NMPC command data with a prediction step size of N. They are defined as follows:

$$T_n=\left[a_n^{cmd},{\delta }_n^{cmd}\right], (n=1, 2, 3, \dots , N),$$

(10)

$$T=\left[T_1,T_2,T_3,\cdots ,T_N\right].$$

(11)

4. Simulation Test

The performance of the developed ANN-based controller was evaluated in realistic simulation tests.

4.1. Obtaining Training Dataset

The simulations were performed in a 1:43-scale vehicle model on an experimental platform. The simulation environment is presented in

Table 2. Simulation environment for data acquisition.

Target Vehicle (dNano 1:43 Scale Car)		Model Predictive Control
Mass	40 g	Control period	20 ms
Length	108.8 mm	Receding horizon	30 steps
Width	45.2 mm	Target velocity	0.6 m/s
Wheelbase	61.9 mm	Lateral acceleration constraint	$2 \mathrm{m}/{\mathrm{s}}^2$

. The control period was 20 ms, the NMPC prediction size was N = 30 steps, and the target reference velocity was 0.6 m/s. The reference path included four 90° corners and two “U” bends, as shown in Figure 6.

To generate diverse training data, the position and direction of the initial vehicle were randomly determined with a uniform distribution. After approximately 13 min of simulation, a rich-diversity 39,000 training dataset was obtained. The driving trajectory of the simulation for data acquisition is shown in Figure 7.

4.2. Simulation Scenarios

The performance of the DNN control technique was verified in three simulation scenarios.

The driving path in the first scenario was used to generate the training data in Figure 7. The similarity between the trajectories of the trained DNN controller and the NMPC method will be presented.

The second and third scenarios were designed to check whether the DNN controller can drive along routes different from that during data acquisition. Figure 8 shows the target reference paths in the second and third scenarios.

4.3. Simulation Results

4.3.1. Results of Scenario 1

The simulation results of scenario 1 are shown in Figure 9. The trajectory of the vehicle controlled by the DNN controller was very similar to that of the NMPC method. The NMPC method is advantageous because the optimal control input follows the target trajectory by predicting the future trajectories. Therefore, the vehicle can smoothly follow the desired path around the sharp corner by changing the driving direction before entering the corner.

These driving features of the NMPC method are inherited by the DNN controller, thereby enabling smooth driving around a corner.

Panels (b) and (c) of Figure 9 present the acceleration and steering-angle control inputs computed by the NMPC and DNN controllers. Overall, the commands generated by the DNN were very similar to those of the NMPC method, in particular, those of the steering input. In addition, the steering-angle error between the two controllers was 0.005 radian (0.28°) on average.

Unlike the steering angle, the acceleration input presented relatively large errors in sections with great acceleration changes. In section ①, the acceleration error reached $0.0358$ m/s² at the greatest deceleration, when the speed needed to be reduced before turning around the corner. Panel (d) of Figure 9 shows the differences in the vehicle velocities of two controllers. The velocities differed by $0.0132 \mathrm{m}/\mathrm{s}$ in section ④ immediately after the U-turn; however, the differences across the entire course were very small (0.0064 m/s on average).

4.3.2. Results of Scenario 2

In the second scenario, the vehicle drove along a path with eight consecutive right-angled turns. In this scenario, the DNN controller was trained with driving data obtained from scenario 1. The second simulation assessed whether the DNN controller can robustly handle general driving scenarios and whether the controller requires individual training for all possible driving situations.

Figure 10 shows the control inputs generated with the NMPC method by the DNN controller in the second scenario. As observed in scenario 1, the accelerations and steering inputs of the DNN controller were very similar to those of the NMPC method. The acceleration inputs showed larger differences at the sharp turnaround point than in scenario 1, because the DNN controller was not trained along the same path. Although the control performance was slightly degraded, the tracking performance of the DNN controller remained similar to that of the NMPC method in this scenario.

4.3.3. Results of Scenario 3

In scenario 3, the vehicle drove around corners with curvatures not included in the training data. The error in the accelerated input at the corner was slightly increased with respect to those of the previous scenarios. The steering control inputs were similar to those of scenario 1; however, the maximal and average errors were 0.0561 radian (3.22°) and 0.010 radian (0.63°), respectively. Moreover, the average error was 2.2 times that of scenario 1. The error was particularly large in sections ② and ③, in which the curvatures of the corners differed from those in the training dataset.

The simulation test results are shown in Figure 11. Such as in the other cases, the differences between the control inputs are due to the lack of training data; nevertheless, the DNN controller guided the vehicle along the path without significant errors.

5. Scaled-Car Test

5.1. Test Environment

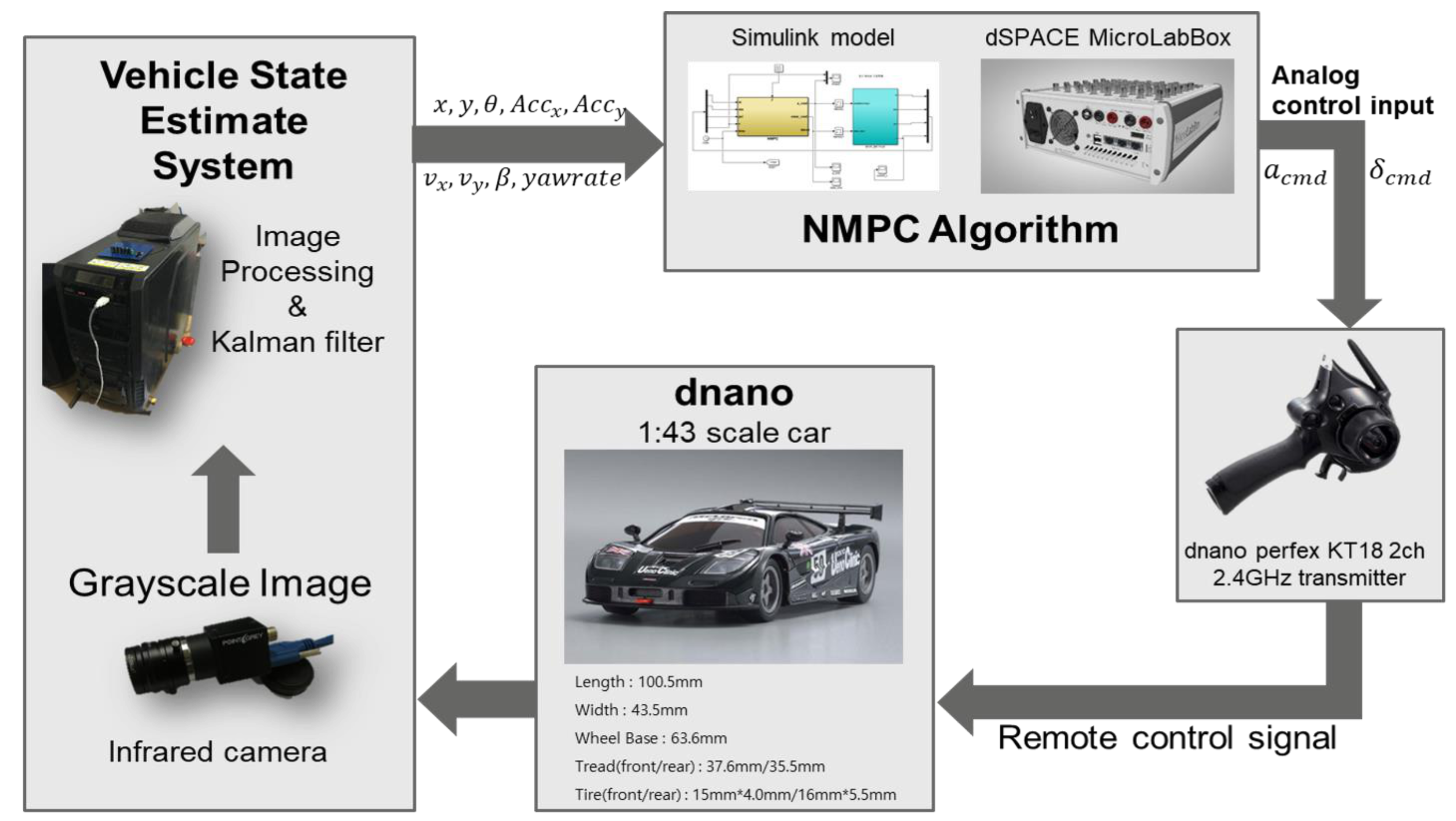
The developed control algorithm is difficult to validate with real experimental vehicles for cost and safety reasons. Instead, we developed a 1:43-scale car as an experimental platform.

The test environment is shown in Figure 12. The vehicle posture $\left(\xi ,\eta ,\theta \right)$ was obtained by processing the images obtained with an infrared camera at the top of the test track. The NMPC and DNN controllers were implemented on a real-time computing platform, thereby enabling vehicle control with wireless controllers.

The data acquisition scenario in the scaled-car test is shown in Figure 13. The NMPC control period, number of receding horizon steps, and target velocity were 20 ms, 30, and 1.0 m/s, respectively. The data were acquired along the path in simulation scenario 1.

5.2. Results of Scaled-Car Test

5.2.1. Trajectory Result

The driving trajectories of the DNN controller and the NMPC were very similar in the scaled-car environment test (see Figure 14).

5.2.2. Control Input Analysis

The acceleration and steering control distributions in each driving interval of the scaled-car test environment were analyzed, and the similarity between the DNN controller and NMPC command inputs was analyzed.

Table 3. Analysis of acceleration command.

Acc. Max	NMPC	DNN	Difference
Acc. Min
Section ①	0.5303	0.5084	−0.0219
	0.3964	0.4232	0.0268
Section ②	0.5094	0.5430	0.0336
	0.4420	0.4512	0.0092
Section ③	0.5153	0.5691	0.0538
	0.4372	0.4693	0.0322
Section ④	0.4517	0.4787	0.0271
	0.3540	0.3893	0.0353
Section ⑤	0.0560	0.6102	0.0542
	0.4026	0.4285	0.0258
Average maximal difference			0.0381
Average minimal difference			0.0259
			$\mathrm{unit}: \mathrm{m}/{\mathrm{s}}^2$

shows the maximal and minimal acceleration control inputs of both controllers for sections ① to ⑤ of the driving trajectory shown in Figure 13. The scale car made several laps of the entire track and the highest and lowest commands are listed in the Table 3. Figure 15 presents the values in Table 3 to show the similarity between the NMPC and DNN controllers. Although the acceleration inputs were not exactly identical, the acceleration commands showed similar patterns along the section; in addition, the overall acceleration control inputs of the DNN controller were slightly higher than those of the NMPC.

Table 4. Analysis of steering command.

Str. Max	NMPC	DNN	Difference
Str. Min
Section ①	−0.0835	−0.0586	0.0250
	−0.2608	−0.2632	−0.0024
Section ②	−0.0992	−0.0992	0
	−0.2623	−0.2406	0.0217
Section ③	0.0796	0.0160	−0.0636
	−0.3543	−0.3639	−0.0096
Section ④	−0.3869	−0.3658	−0.0211
	−0.3694	−0.3953	−0.0259
Section ⑤	−0.0728	−0.0485	0.0244
	−0.4167	−0.4576	−0.0409
Average Maximal Difference			0.0268
Average Minimal Difference			0.0201
			$\mathrm{unit}: radian$

shows the maximal and minimal steering control inputs in sections ① to ⑤ of the driving trajectory. Figure 16 shows the values presented in Table 4. Moreover, Figure 16, shows that the steering control inputs calculated by the NMPC and DNN controllers along the sections were similar; thus, the DNN controller was well trained and exhibited performance characteristics similar to those of the NMPC method.

Figure 17 presents the acceleration input versus the steering input according to the driving sections. The graphs of the NMPC and DNN controllers showed similar patterns that followed the corner sequence; this confirms that the control strategy of the NMPC is inherited by the DNN controller through learning.

5.2.3. Comparison of Computation Times

One of the main goal of this study was to reduce the uncertainty in the computation time of the NMPC method. Consequently, we replaced the NMPC method with the DNN-based control method. The computation times of the two controllers were analyzed in the scaled-car environment; the results are shown in Figure 18.

The computation time of the NMPC method was typically approximately 7 ms, which increased to more than 40 ms in sections ①, ②, and ③, when the vehicle entered the corner section at a high speed. The NMPC method required more computation time when encountering a sudden change in its desired path. By contrast, the computation time of the DNN control method varied only by 0.07–0.08 ms with no significant changes along the path.

These results confirm that the computation time of the DNN-based method is shorter and more stable than of the NMPC method.

6. Conclusions

We developed a data-driven control method based on ANNs, which aims to improve the real-time performance of the NMPC method. Therefore, we acquired driving data of the NMPC, trained the DNN on the NMPC data, and conducted driving tests in a simulation environment. The autonomous driving results of the well-trained DNN controller approximately match those of the NMPC.

To evaluate the real-time performance of the developed controller, we performed a scaled-car test and simulated a real-world autonomous driving control environment. On the autonomous driving test platform, the control performance characteristic were similar to those of NMPC method, and the computation time was dramatically improved. In particular, the data-based DNN controller stabilized the computation time, which is unstable in the NMPC method. The results demonstrate the applicability of the DNN controller to real-time platforms.

The developed control method can help implement an autonomous driving control method which, learns the existing rule-based control algorithm and human driving strategy.