Parallel Computation of CRC-Code on an FPGA Platform for High Data Throughput
Abstract
:1. Introduction
2. CRC Background
3. CRC Computational Process
3.1. Serial CRC Generation Process
| Algorithm 1. Bitwise CRC. |
| 1: Input: Byte Array Data |
| 2: Crc = 0XFFFFFFFF |
| 3: While index < size of data do |
| 4: CRC = CRC XOR data[index] |
| 5: for j = 0; j < 8; j++ do |
| 6: CRC = (CRC >> 1) XOR -(CRC AND 1) AND G(x) |
| 7: end for |
| 8: index + 1 |
| 9: end while |
| 10: Return CRC XOR 0XFFFFFFFF |
3.2. The Sarwate’s Algorithm and Slicing by an N Algorithm
| Algorithm 2. Sarwate Algorithm. |
| 1: Input: Byte Array Data |
| 2: Crc = 0XFFFFFFFF |
| 3: While index < size of data do |
| 4: CRC = (CRC >> 8) XOR TABLE[(CRC AND 0xFF) XOR data[index]] |
| 5: index + 1 |
| 6: end while |
| 7: Return CRC XOR 0XFFFFFFFF |
| Algorithm 3. Slicing by 4 Algorithm. |
| 1: Input: Byte Array Data |
| 2: Crc = 0XFFFFFFFF |
| 3: While index < size of data do |
| 4: CRC = CRC XOR data[index:index+3] |
| 5: XOR TABLE1[(CRC AND 0xFF)] |
| 6: XOR TABLE2[((CRC >> 8) AND 0xFF)] |
| 7: XOR TABLE3[((CRC >> 16) AND 0xFF)] |
| 8: XOR TABLE4[((CRC >> 24) AND 0xFF)] |
| 9: index + 4 |
| 10: end while |
| 11: Return CRC XOR 0XFFFFFFFF |
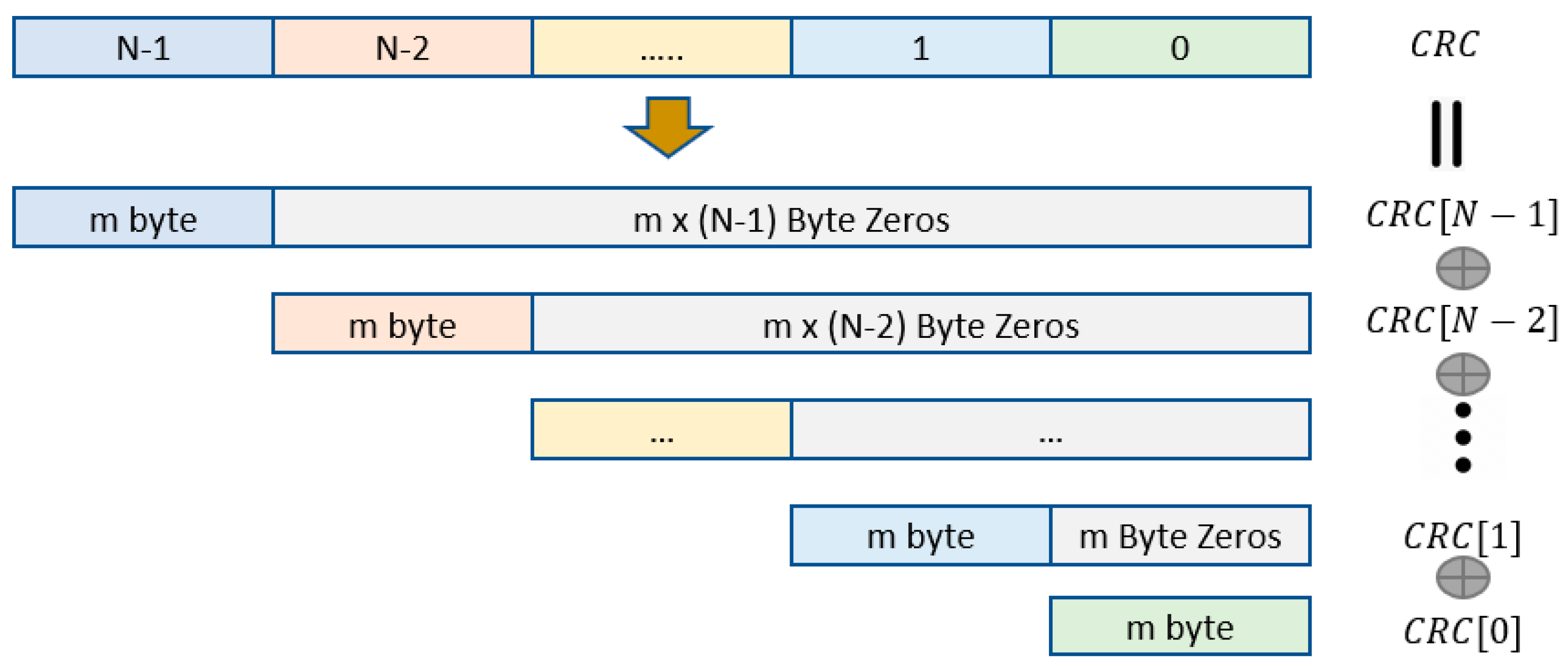
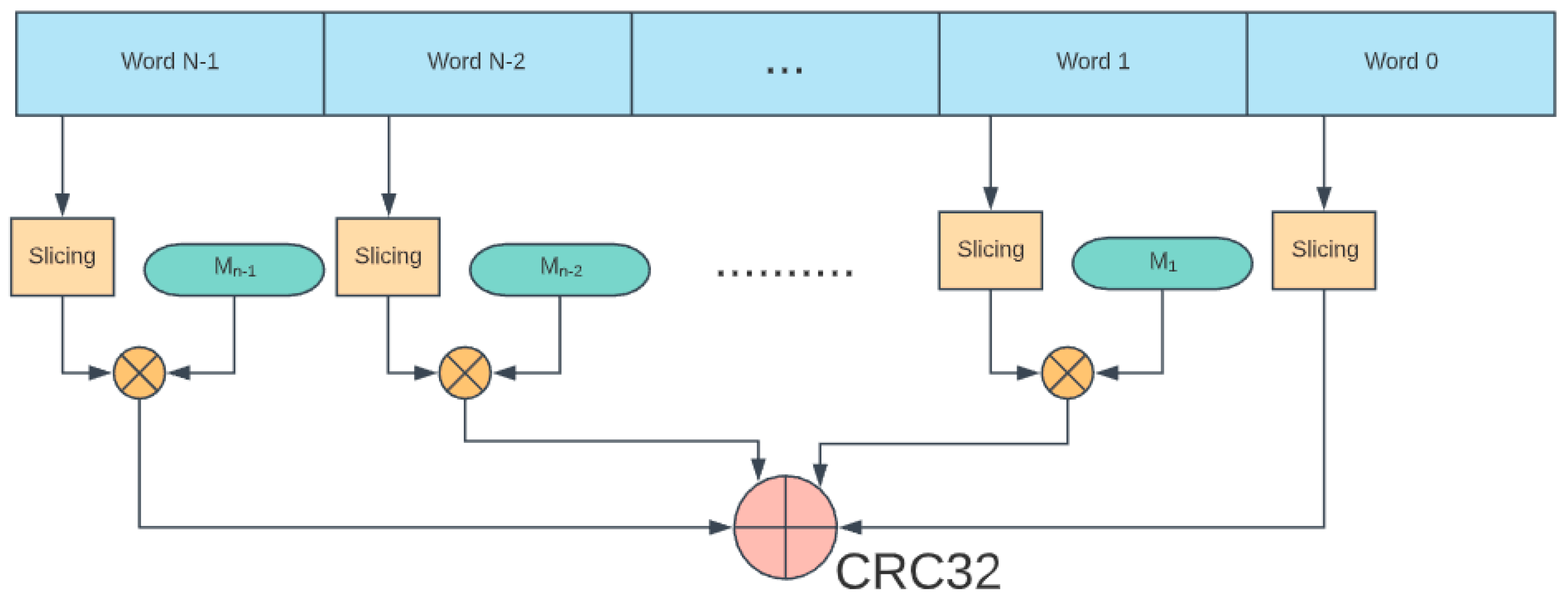
3.3. Matrix Transformation
3.4. Hybrid Method
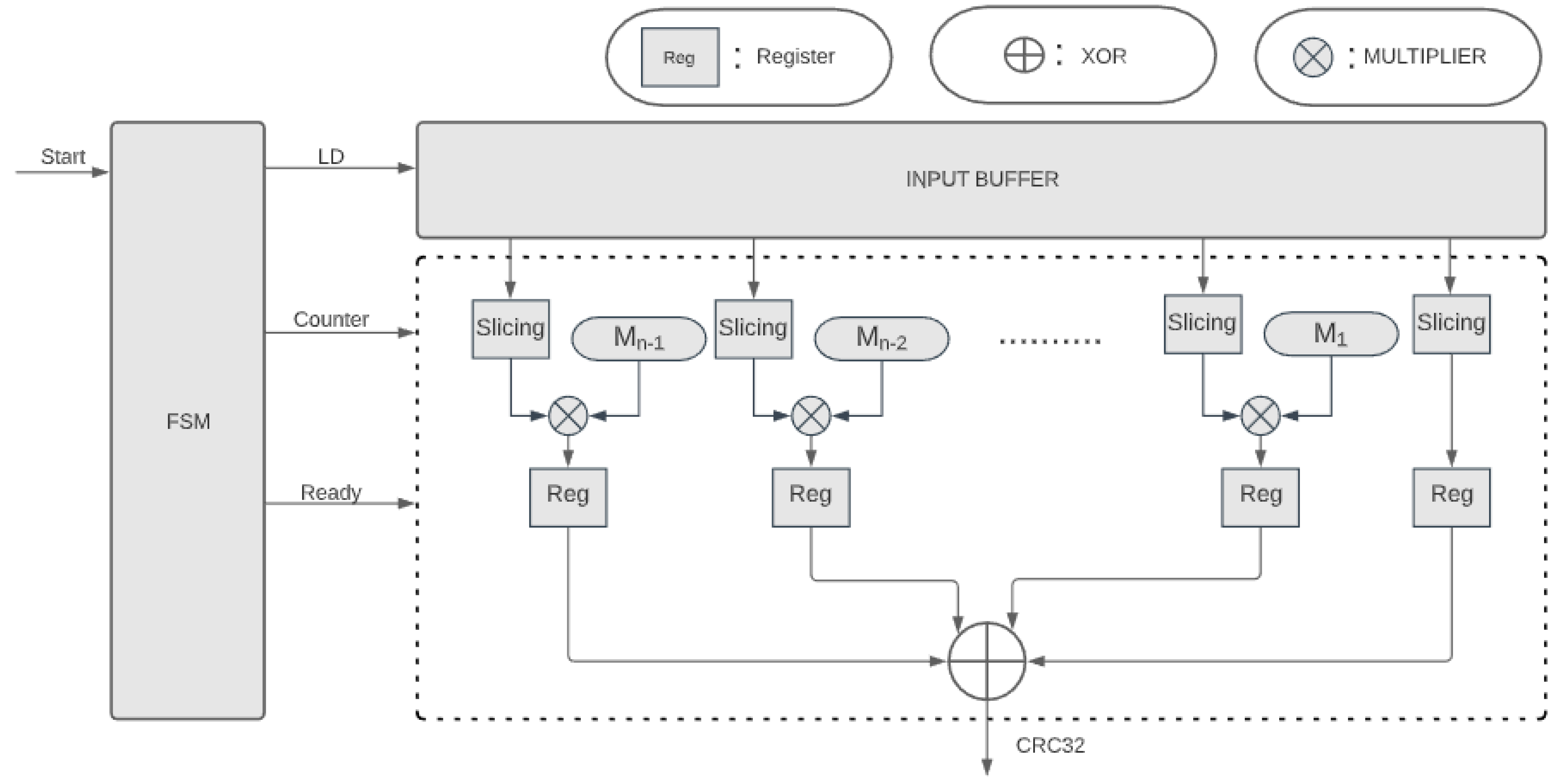
4. FPGA Implementation
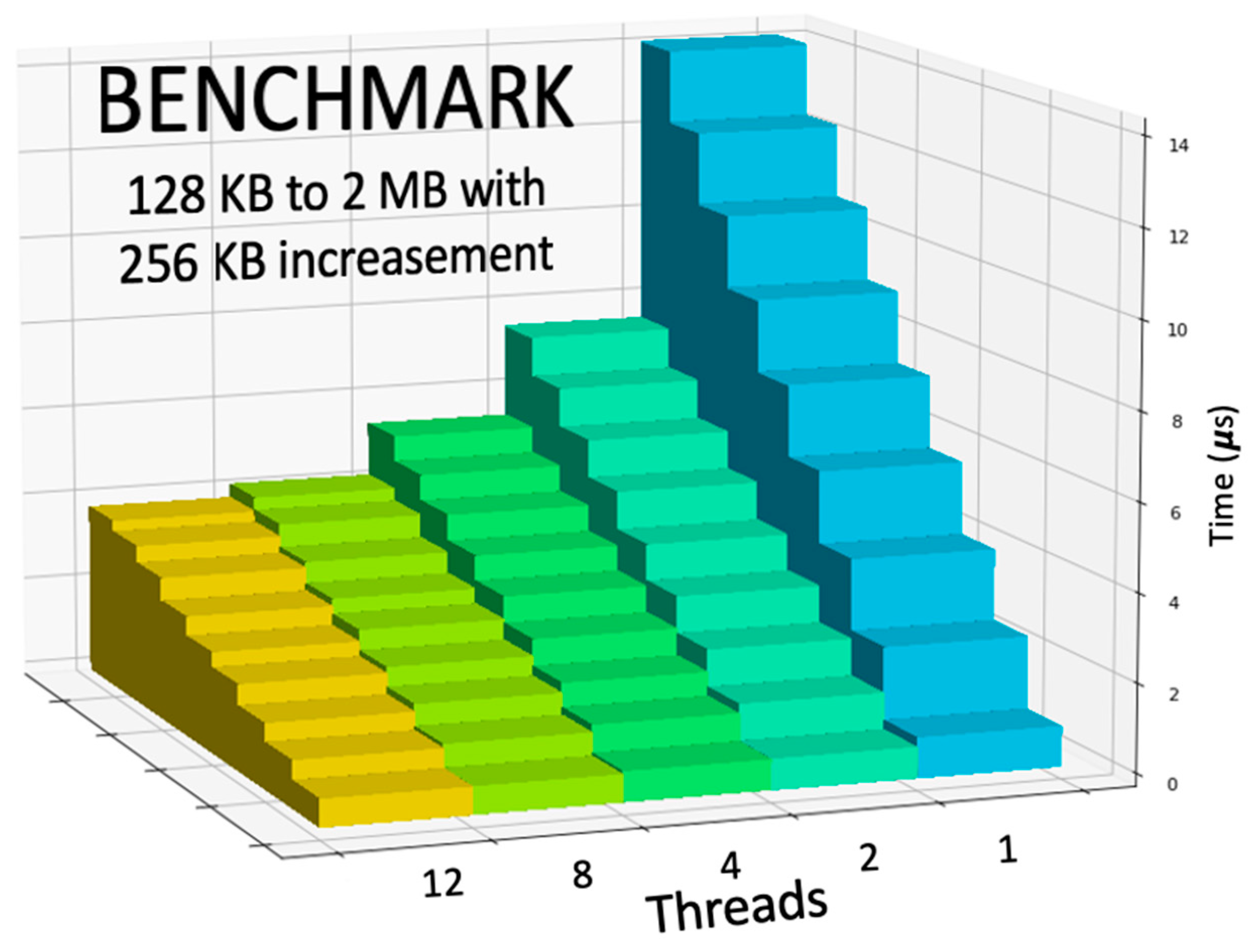
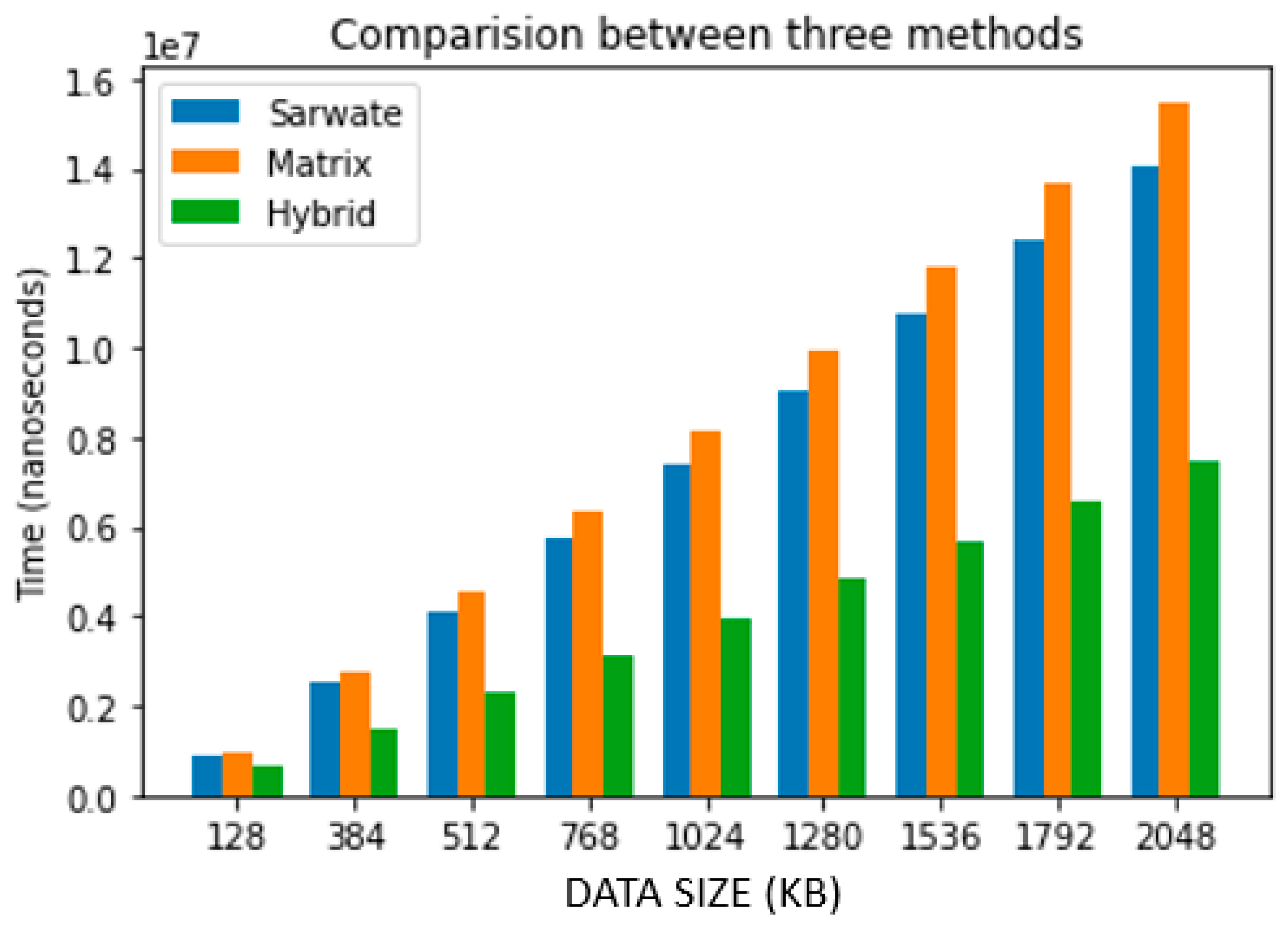
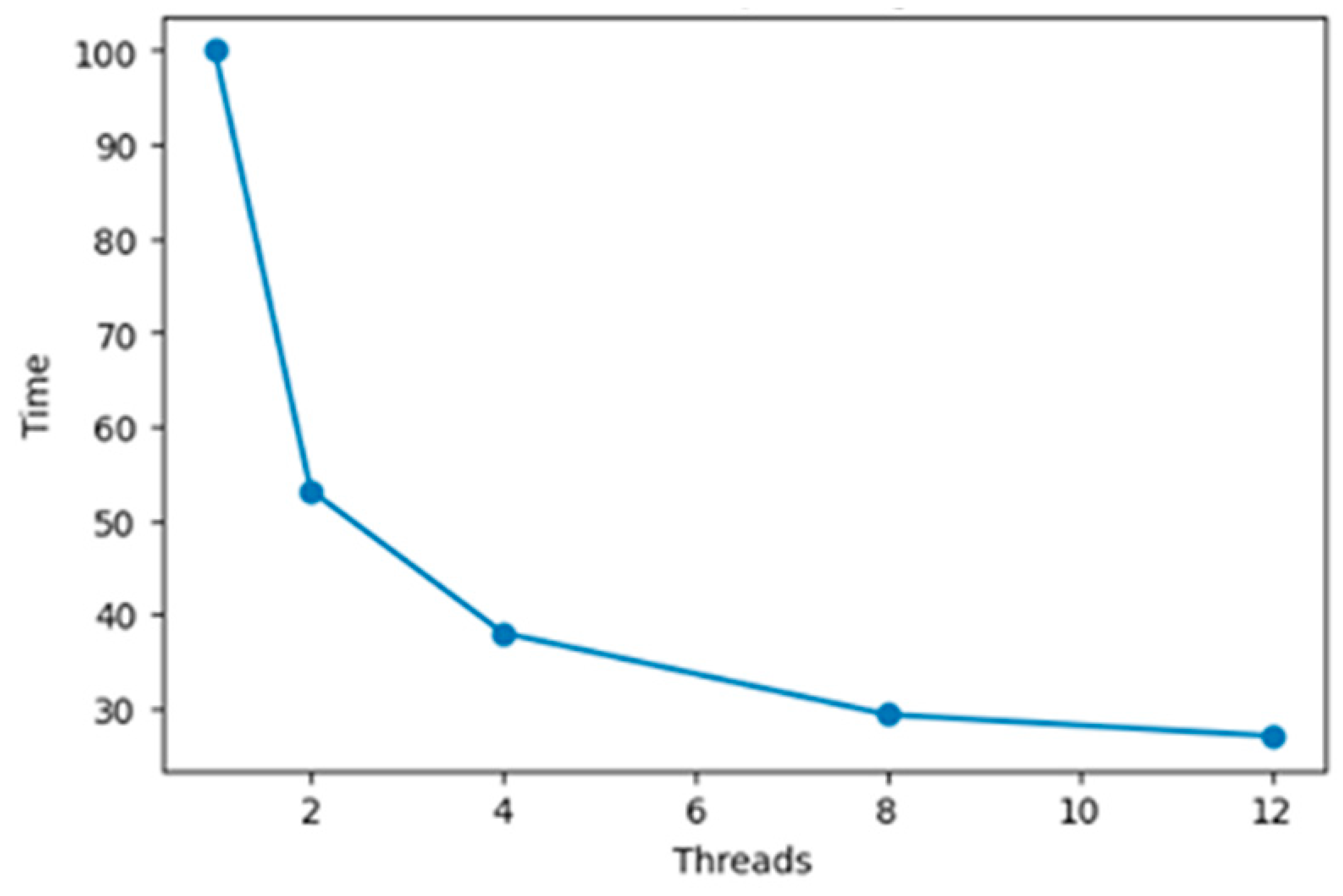
5. Experimental Results
6. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
References
- Aslam, S.; Amato, M.; Bowles, N.; Calcutt, S.; Hewagama, T.; Howard, J.; Howett, C.; Hsieh, W.-T.; Hurford, T.; Hurley, J.; et al. Dual-telescope multi-channel thermal-infrared radiometer for outer planet fly-by missions. Acta Astronautica 2016, 128, 628–639. [Google Scholar] [CrossRef]
- Aslam, S.; Achterberg, R.K.; Calcutt, S.B.; Cottini, V.; Gorius, N.J.; Hewagama, T.; Irwin, P.G.; Nixon, C.A.; Quilligan, G.; Roos-Serote, M.; et al. Advanced Net Flux Radiometer for the Ice Giants. Space Sci. Rev. 2020, 216, 11. [Google Scholar] [CrossRef]
- Mousis, O.; Atkinson, D.H.; Cavalié, T.; Fletcher, L.N.; Amato, M.J.; Aslam, S.; Ferri, F.; Renard, J.-B.; Spilker, T.; Venkatapathy, E.; et al. Scientific rationale for Uranus and Neptune in situ explorations. Planet. Space Sci. 2018, 155, 12–40. [Google Scholar] [CrossRef] [Green Version]
- Lin, B.-C. System and Method for Storing a Data File Backup. U.S. Patent US7533291B2, 12 May 2009. [Google Scholar]
- Hu, T.; Zheng, M.; Tan, J.; Zhu, L.; Miao, W. Intelligent photovoltaic monitoring based on solar irradiance big data and wireless sensor networks. Ad. Hoc. Netw. 2015, 35, 127–136. [Google Scholar] [CrossRef]
- Elahi, A.; Gschwender, A. Zigbee Wireless Sensor and Control Network; Prentice Hall Press: Upper Saddle River, NJ, USA, 2009. [Google Scholar]
- Berger, C. Automating Acceptance Tests for Sensor- and Actuator-Based Systems on the Example of Autonomous Vehicles; Shaker Verlag Gmbh: Aachen, Germany, 2010. [Google Scholar]
- Brito, J.; Gomes, T.; Miranda, J.; Monteiro, L.; Cabral, J.; Mendes, J.; Monteiro, J.L. An Intelligent Home Automation Control System Based on a Novel Heat Pump and Wireless Sensor Networks. In Proceedings of the 2014 IEEE 23rd International Symposium on Industrial Electronics (ISIE), Istanbul, Turkey, 1–4 June 2014; pp. 1448–1453. [Google Scholar] [CrossRef]
- Küçük, G.; Başaran, C. Reducing Energy Consumption of Wireless Sensor Networks through Processor Optimizations. J. Comput. 2007, 2, 67–74. [Google Scholar] [CrossRef]
- Wu, H. A Brief Overview of CRC Implementation for 5G NR. Available online: https://www.intechopen.com/online-first/a-brief-overview-of-crc-implementation-for-5g-nr (accessed on 20 October 2020).
- Wesley Peterson, W. Available online: https://en.wikipedia.org/wiki/W._Wesley_Peterson (accessed on 20 October 2020).
- Sarwate, D.V. Computation of cyclic redundancy checks via table look-up. Commun. ACM 1988, 31, 1008–1013. [Google Scholar] [CrossRef]
- Kounavis, M.E.; Berry, F.L. Novel Table Lookup-Based Algorithms for High-Performance CRC Generation. IEEE Trans. Comput. 2008, 57, 1550–1560. [Google Scholar] [CrossRef]
- Derby, J. High-speed CRC computation using state-space transformations. In Proceedings of the GLOBECOM’01. IEEE Global Telecommunications Conference (Cat. No.01CH37270), San Antonio, TX, USA, 25–29 November 2001; pp. 166–170. [Google Scholar] [CrossRef]
- Kounavis, M.E.; Berry, F.L. A Systematic Approach to Building High Performance Software-Based CRC Generators. In Proceedings of the 10th IEEE Symposium on Computers and Communications (ISCC’05), Cartagena, Murcia, Spain, 27–30 June 2005; pp. 855–862. [Google Scholar] [CrossRef]
- Mitra, J.; Nayak, T. Reconfigurable very high throughput low latency VLSI (FPGA) design architecture of CRC 32. Integration 2017, 56, 1–14. [Google Scholar] [CrossRef]
- Henriksson, T.; Eriksson, H.; Nordqvist, U.; Larsson-Edefors, P.; Liu, D. VLSI implementation of CRC-32 for 10 Gigabit Ethernet. In Proceedings of the ICECS 2001, 8th IEEE International Conference on Electronics, Circuits and Systems (Cat. No.01EX483), Malta, Malta, 2–5 September 2001; p. 4. [Google Scholar]
- Chi, M.; He, D.; Liu, J. Exploring Various Levels of Parallelism in High-Performance CRC Algorithms. IEEE Access 2019, 7, 32315–32326. [Google Scholar] [CrossRef]

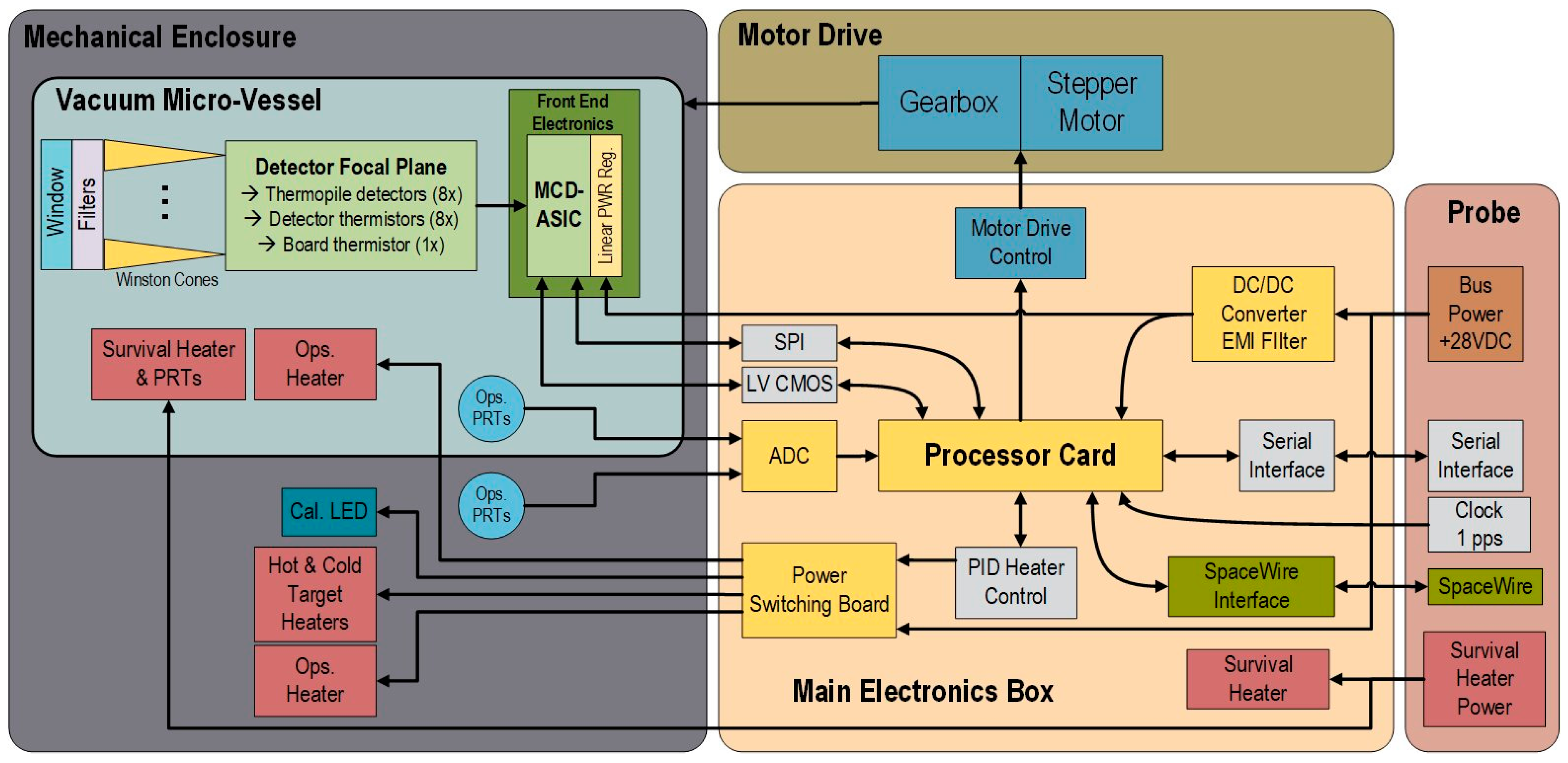




| Name | Number of Bits | Number of Channels | Total | Comment |
|---|---|---|---|---|
| Thermopile Data + Time Stamp Thermistor data on thermopile Hot Target Temperature | 32 | 8 | 256 | Science Data |
| 16 | 8 | 128 | Science Data | |
| 12 | 1 | 12 | Thermal data | |
| Fan-out board Temperature Vessel Temperature | 12 | 1 | 12 | Thermal data |
| 12 | 1 | 12 | Thermal data | |
| Windows Temperature Cold Target Temperature LED status Motor Position | 12 | 1 | 12 | Thermal data |
| 12 | 1 | 12 | Thermal data | |
| 1 | 1 | 1 | Auxiliary data, 1 bit for ON/OFF | |
| 3 | 1 | 3 | Auxiliary data, 3 bits for 7 positions | |
| Survival Heater Status Thermopile Data + Time Stamp | 1 | 1 | 1 | Auxiliary data, 1 bit for ON/OFF |
| 32 | 8 | 256 | Science Data |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tran, D.; Aslam, S.; Gorius, N.; Nehmetallah, G. Parallel Computation of CRC-Code on an FPGA Platform for High Data Throughput. Electronics 2021, 10, 866. https://doi.org/10.3390/electronics10070866
Tran D, Aslam S, Gorius N, Nehmetallah G. Parallel Computation of CRC-Code on an FPGA Platform for High Data Throughput. Electronics. 2021; 10(7):866. https://doi.org/10.3390/electronics10070866
Chicago/Turabian StyleTran, Dat, Shahid Aslam, Nicolas Gorius, and George Nehmetallah. 2021. "Parallel Computation of CRC-Code on an FPGA Platform for High Data Throughput" Electronics 10, no. 7: 866. https://doi.org/10.3390/electronics10070866
APA StyleTran, D., Aslam, S., Gorius, N., & Nehmetallah, G. (2021). Parallel Computation of CRC-Code on an FPGA Platform for High Data Throughput. Electronics, 10(7), 866. https://doi.org/10.3390/electronics10070866







