Optimization of Two-Stage IPD-(1+I) Controllers for Frequency Regulation of Sustainable Energy Based Hybrid Microgrid Network
Abstract
:1. Introduction
- (a)
- Design and implementation of a (IPD-(1+I)) controller and development of it’s transfer function for a multi-source islanded micro grid system’s (MS-IμGS) frequency response model.
- (b)
- Performing different simulation case studies to test the dynamic performance of the proposed control stratagem and analysed the results for frequency deviation and power sharing characteristics of other subsystems. The performance of the study is reported via the measurement of performance indices (J), JFOD, settling time, undershoot, and overshoot.
- (c)
- The performance of the proposed stratagem is validated using real-time wind data.
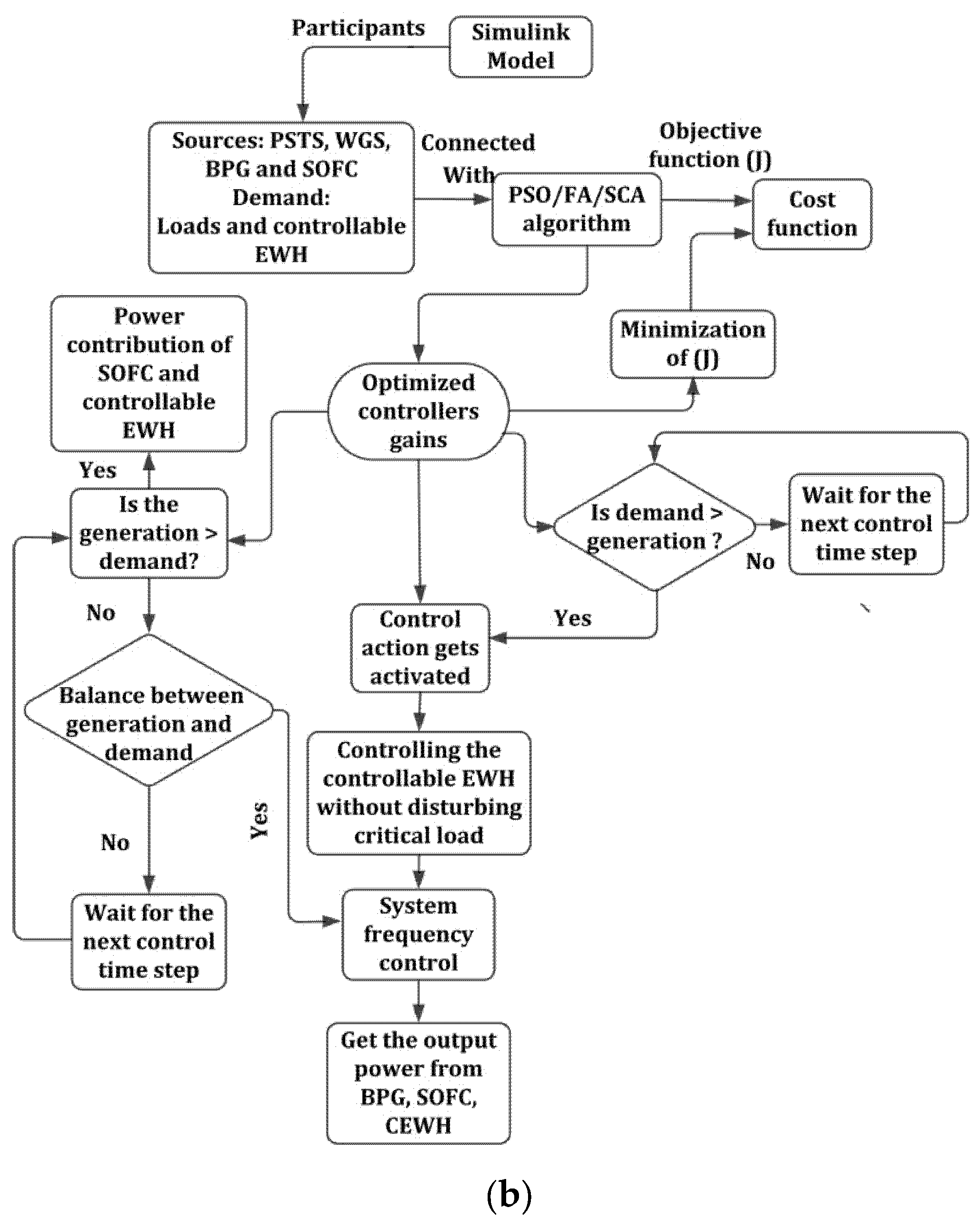
2. Details of the Proposed Frequency Response Model
2.1. Dynamic Modeling of Generation Units
2.1.1. Wind Generation System (WGS)
2.1.2. Parabolic Trough Solar Thermal System (PSTS)
2.1.3. Bio-Diesel Power Generation (BPG)
2.1.4. Solid-Oxide Fuel Cell (SOFC)
2.2. Dynamic Modeling of Controllable Electric Water Heater
2.3. Dynamic Modeling of Power System and Load
3. Designed of Two-Stage (IPD-(1+I)) Controller Model
4. Detail of Sine-Cosine Algorithmic Technique (SCA)
5. Simulation Results and System Validation
5.1. Case 1: Frequency Response Study under Non-Accessibility of All RUs
5.2. Case 2: Frequency Response Study under Concurrent Random Change in RU’s Generation and Load
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- Almeshqab, F.; Ustun, T.S. Lessons learned from rural electrification initiatives in developing countries: Insights for technical, social, financial and public policy aspects. Renew. Sustain. Energy Rev. 2019, 102, 35–53. [Google Scholar] [CrossRef]
- The Sustainable Development Goals Report 2019. United Nations 2019. Available online: https://unstats.un.org/sdgs/report/2019/The-Sustainable-Development-Goals-Report-2019.pdf (accessed on 11 April 2021).
- Tabak, A.; Özkaymak, M.; Tahir, M.; Oktay, H. Optimization and Evaluation of Hybrid PV/WT/BM System in Different Initial Costs and LPSP Conditions. Int. J. Adv. Comput. Sci. Appl. 2017, 8, 123–131. [Google Scholar] [CrossRef] [Green Version]
- Boukelia, T.; Mecibah, M. Parabolic trough solar thermal power plant: Potential, and projects development in Algeria. Renew. Sustain. Energy Rev. 2013, 2, 288–297. [Google Scholar] [CrossRef]
- Rakhshani, E.; Remon, D.; Cantarellas, A.M.; Rodriguez, P. Analysis of derivative control based virtual inertia in multi-area high-voltage direct current interconnected power systems. IET Gener. Transm. Distrib. 2016, 10, 1458–1469. [Google Scholar] [CrossRef] [Green Version]
- Ustun, T.S.; Aoto, Y. Analysis of Smart Inverter’s Impact on the Distribution Network Operation. IEEE Access 2019, 7, 9790–9804. [Google Scholar] [CrossRef]
- Latif, A.; Hussain, S.M.S.; Das, D.C.; Ustun, T.S. State-of-the-art of controllers and soft computing techniques for regulated load frequency management of single/multiarea traditional and renewable energy based power systems. Appl. Energy 2020, 266, 114858. [Google Scholar] [CrossRef]
- Hosseinzadeh, M.; Salmasi, F.R. Robust Optimal Power Management System for a Hybrid AC/DC Micro-Grid. IEEE Trans. Sustain. Energy 2015, 6, 675–687. [Google Scholar] [CrossRef]
- Schonbergerschonberger, J.; Duke, R.; Round, S.D. DC-Bus Signaling: A Distributed Control Strategy for a Hybrid Renewable Nanogrid. IEEE Trans. Ind. Electron. 2006, 53, 1453–1460. [Google Scholar] [CrossRef]
- Jiayi, H.; Chuanwen, J.; Rong, X. A review on distributed energy resources and MicroGrid. Renew. Sustain. Energy Rev. 2008, 12, 2472–2483. [Google Scholar] [CrossRef]
- Alhelou, H.H.; Hamedani-Golshan, M.E.; Zamani, R.; Heydarian-Forushani, E.; Siano, P. Challenges and opportunities of load frequency control in conventional, modern and future smart power systems: A comprehensive review. Energies 2018, 11, 2497. [Google Scholar] [CrossRef] [Green Version]
- Das, D.C.; Roy, A.K.; Sinha, N. GA based frequency controller for solar thermal–diesel–wind hybrid energy generation/energy storage system. Int. J. Electr. Power Energy Syst. 2012, 43, 262–279. [Google Scholar] [CrossRef]
- Rout, U.K.; Sahu, R.K.; Panda, S. Design and analysis of differential evolution algorithm based automatic generation control for interconnected power system. Ain Shams Eng. J. 2013, 4, 409–421. [Google Scholar] [CrossRef] [Green Version]
- Dash, P.; Saikia, L.C.; Sinha, N. Flower Pollination Algorithm Optimized PI-PD Cascade Controller in Automatic Generation Control of a Multi-area Power System. Int. J. Electr. Power Energy Syst. 2016, 82, 19–28. [Google Scholar] [CrossRef]
- Hussain, I.; Ranjan, S.; Das, D.C.; Sinha, N. Performance analysis of flower pollination algorithm optimized PID controller for wind-PV-SMES-BESS-diesel autonomous hybrid power system. Int. J. Renew. Energy Res. 2017, 7, 643–651. [Google Scholar]
- Hussain, I.; Das, D.C.; Sinha, N.; Latif, A.; Hussain, S.M.S.; Ustun, T.S. Performance Assessment of an Islanded Hybrid Power System with Different Storage Combinations Using an FPA-Tuned Two-Degree-of-Freedom (2DOF) Controller. Energies 2020, 13, 5610. [Google Scholar] [CrossRef]
- Latif, A.; Das, D.C.; Ranjan, S.; Hussain, I. Integrated demand side management and generation control for frequency control of a microgrid using PSO and FA based controller. Int. J. Renew. Energy Res. 2018, 8, 188–199. [Google Scholar]
- Latif, A.; Pramanik, A.; Das, D.C.; Hussain, I.; Ranjan, S. Plug in hybrid vehicle-wind-diesel autonomous hybrid power system: Frequency control using FA and CSA optimized controller. Int. J. Syst. Assur. Eng. Manag. 2018, 9, 1147–1158. [Google Scholar] [CrossRef]
- Gorripotu, T.S.; Ramana, P.; Sahu, R.K.; Panda, S. Sine Cosine Optimization Based Proportional Derivative-Proportional Integral Derivative Controller for Frequency Control of Hybrid Power System. In Computational Intelligence in Data Mining; Springer: Singapore, 2020; pp. 789–797. [Google Scholar]
- Alattar, A.H.; Selem, S.I.; Metwally, H.; Ibrahim, A.; Aboelsaud, R.; Tolba, M.A.; El-Rifaie, A.M. Performance enhancement of micro grid system with SMES storage system based on mine blast optimization algorithm. Energies 2019, 12, 3110. [Google Scholar] [CrossRef] [Green Version]
- Wang, H.; Zeng, G.; Dai, Y.; Bi, D.; Sun, J.; Xie, X. Design of a fractional order frequency PID controller for an islanded microgrid: A multi-objective extremal optimization method. Energies 2017, 10, 1052. [Google Scholar] [CrossRef] [Green Version]
- Pan, I.; Das, S. Kriging based surrogate modeling for fractional order control of microgrids. IEEE Trans. Smart Grid. 2015, 6, 36–44. [Google Scholar] [CrossRef] [Green Version]
- Guha, D.; Roy, P.K.; Banerjee, S. Equilibrium optimizer-tuned cascade fractional-order 3DOF-PID controller in load frequency control of power system having renewable energy resource integrated. Int. Trans. Electr. Energy Syst. 2021, 31, e12702. [Google Scholar] [CrossRef]
- Karimipouya, A.; Abdi, H. Microgrid frequency control using the virtual inertia and ANFIS-based Controller. Int. J. Ind. Electron. Control Optim. 2019, 2, 145–154. [Google Scholar]
- Lal, D.K.; Barisal, A.K.; Tripathy, M. Load frequency control of multi area interconnected microgrid power system using grasshopper optimization algorithm optimized fuzzy PID controller. In Proceedings of the 2018 Recent Advances on Engineering, Technology and Computational Sciences (RAETCS), Allahabad, India, 6–8 February 2018; pp. 1–6. [Google Scholar]
- Mirjalili, S. SCA: A sine cosine algorithm for solving optimization problems. Knowl. Based Syst. 2016, 96, 120–133. [Google Scholar] [CrossRef]
- Shang-Guan, X.; He, Y.; Zhang, C.; Jiang, L.; Spencer, J.W.; Wu, M. Sampled-data based discrete and fast load frequency control for power systems with wind power. Appl. Energy 2020, 259, 114202. [Google Scholar] [CrossRef]
- Khooban, M.H.; Dragicevic, T.; Blaabjerg, F.; Delimar, M. Shipboard microgrids: A novel approach to load frequency control. IEEE Trans. Sustain. Energy 2018, 9, 843–852. [Google Scholar] [CrossRef]
- Kuravi, S.; Trahan, J.; Goswami, D.Y. Thermal energy storage technologies and systems for concentrating solar power plants. Prog. Energy Combust. Sci. 2013, 39, 285–319. [Google Scholar] [CrossRef]
- Latif, A.; Hussain, S.M.S.; Das, D.C.; Ustun, T.S. Double stage controller optimization for load frequency stabilization in hybrid wind-ocean wave energy based maritime microgrid system. Appl. Energy 2021, 282, 116171. [Google Scholar] [CrossRef]
- Taghizadeh, M.; Hoseintabar, M.; Faiz, J. Frequency control of isolated WT/PV/SOFC/UC network with new control strategy for improving SOFC dynamic response. Int. Trans. Electr. Energy Syst. 2015, 25, 1748–1770. [Google Scholar] [CrossRef]







| Symbol | Nomenclature | Value |
|---|---|---|
| ΔPld | Net load demand of MS-IμGS | - |
| ∆f | frequency deviation (Hz) of MS-IμGS | - |
| ΔPg | Net generated power of MS-IμGS | - |
| D | Microgrid damping co-efficient | 0.1 |
| M | Microgrid inertia constant | 0.12 |
| KCEx | Gain of engine delay of BPG | 1 |
| TCEx | Constant time engine delay of BPG | 0.4 s |
| KWGSx | Gain of wind | 1 |
| TWGSx | Time constant wind | 5 s |
| KCx, KGx, KTx | Gain of collector, governor and turbine of PSTS | 1.8, 1, 1 |
| TCx, TGx, TTx | Constant time of collector, governor and turbine of PSTS | 1.8 s, 1 s, 3 s |
| KSOFCx | Gain of SOFC | 1 |
| TSOFCx | Time constant of SOFC | 0.2 s |
| KCEWHx | Gain of CEWH | 1 |
| TCEWHx | Time constant of CEWH | 0.1 s |
| tsim | Simulated run time of MS-IμGS | 100 s |
| Controllers | PI | PID | (IPD-(1+I)) | |
|---|---|---|---|---|
| Maximum Overshoot (+MXO) | ||||
| Δf (in Hz) | 0.0551 | 0.0008 | 0.00003 | |
| Maximum Undershoot (-MXU) | ||||
| Δf (in Hz) | 0.0480 | 0.0025 | 0.0023 | |
| Settling time (TST) | ||||
| Δf (in s) | 5.468 | 4.075 | 1.825 | |
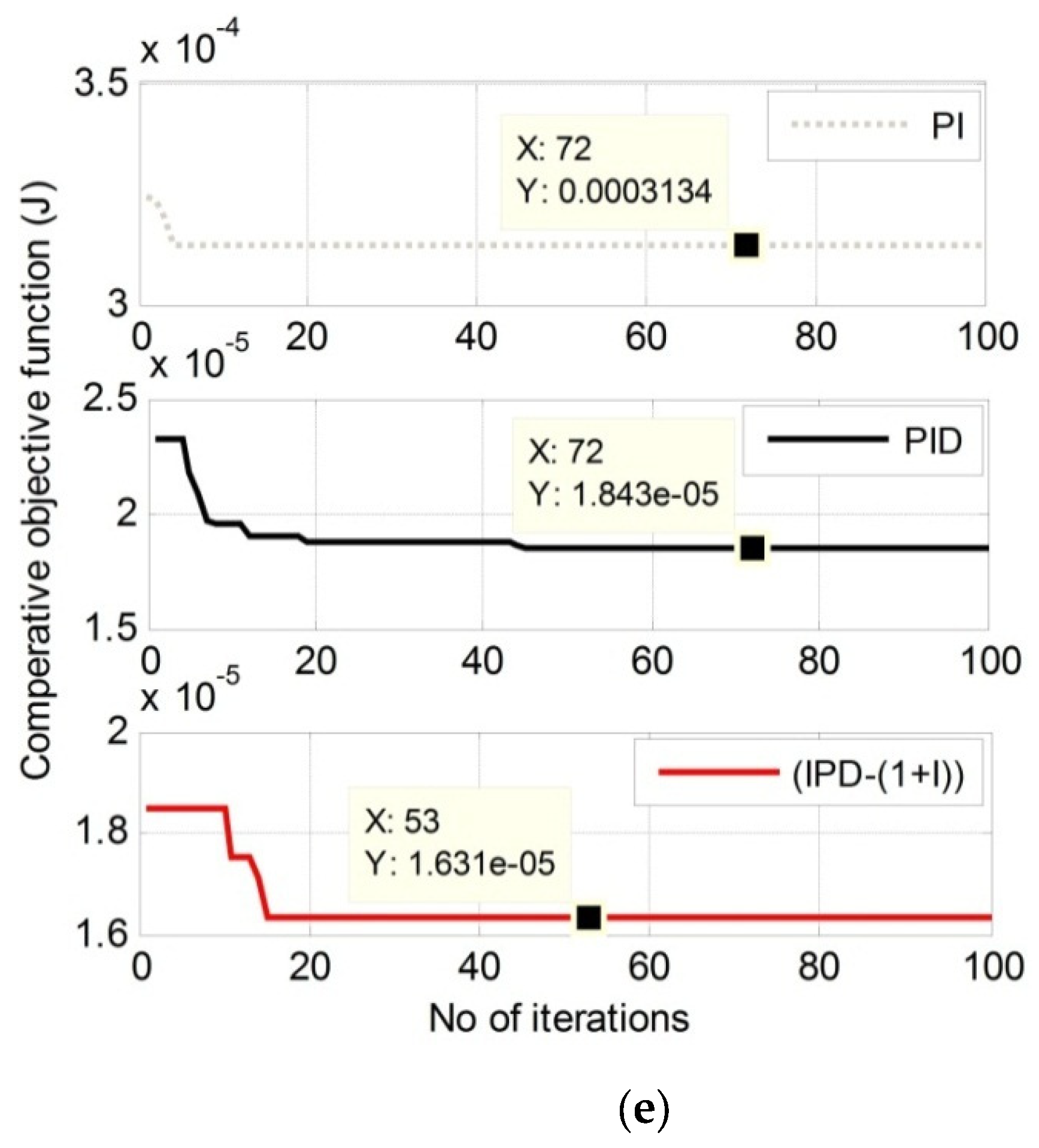
| Minimum value of J (Jmin) | ||||
| 3.13 × 10−4 | 1.84 × 10−5 | 1.63 × 10−5 | ||
| Figure of demerits (JFOD) | ||||
| 29.904 | 16.605 | 3.330 | ||
| Optimized controllers’ values | ||||
| Controller-1 | KP1 | 39.60 | 0.00091 | 39.48 |
| KI11 | 32.46 | 39.06 | 46.67 | |
| KD1 | - | 22.02 | 39.92 | |
| KI12 | - | - | 14.27 | |
| Controller-2 | KP2 | 49.58 | 49.97 | 4.28 |
| KI21 | 30.18 | 48.75 | 14.40 | |
| KD2 | - | 49.08 | 15.81 | |
| KI22 | - | - | 40.34 | |
| Techniques | PSO | FA | SCA | |
|---|---|---|---|---|
| Optimized Controllers’ Values | ||||
| Controller-1 | KP1 | 48.12 | 24.45 | 49.87 |
| KI11 | 18.46 | 40.41 | 49.99 | |
| KD1 | 20.89 | 18.28 | 18.30 | |
| KI12 | 44.86 | 39.60 | 42.48 | |
| Controller-2 | KP2 | 49.87 | 35.95 | 47.77 |
| KI21 | 39.11 | 39.86 | 37.76 | |
| KD2 | 20.05 | 25.32 | 21.59 | |
| KI22 | 49.53 | 49.89 | 49.96 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Latif, A.; Hussain, S.M.S.; Das, D.C.; Ustun, T.S. Optimization of Two-Stage IPD-(1+I) Controllers for Frequency Regulation of Sustainable Energy Based Hybrid Microgrid Network. Electronics 2021, 10, 919. https://doi.org/10.3390/electronics10080919
Latif A, Hussain SMS, Das DC, Ustun TS. Optimization of Two-Stage IPD-(1+I) Controllers for Frequency Regulation of Sustainable Energy Based Hybrid Microgrid Network. Electronics. 2021; 10(8):919. https://doi.org/10.3390/electronics10080919
Chicago/Turabian StyleLatif, Abdul, S. M. Suhail Hussain, Dulal Chandra Das, and Taha Selim Ustun. 2021. "Optimization of Two-Stage IPD-(1+I) Controllers for Frequency Regulation of Sustainable Energy Based Hybrid Microgrid Network" Electronics 10, no. 8: 919. https://doi.org/10.3390/electronics10080919







