Accelerating Neural Network Inference on FPGA-Based Platforms—A Survey
Abstract
:1. Introduction
2. Architecture of Deep Neural Network
2.1. Convolutional Neural Network
2.2. Recurrent Neural Network
2.3. Implementation Requirements
3. Resource-Limited Platform
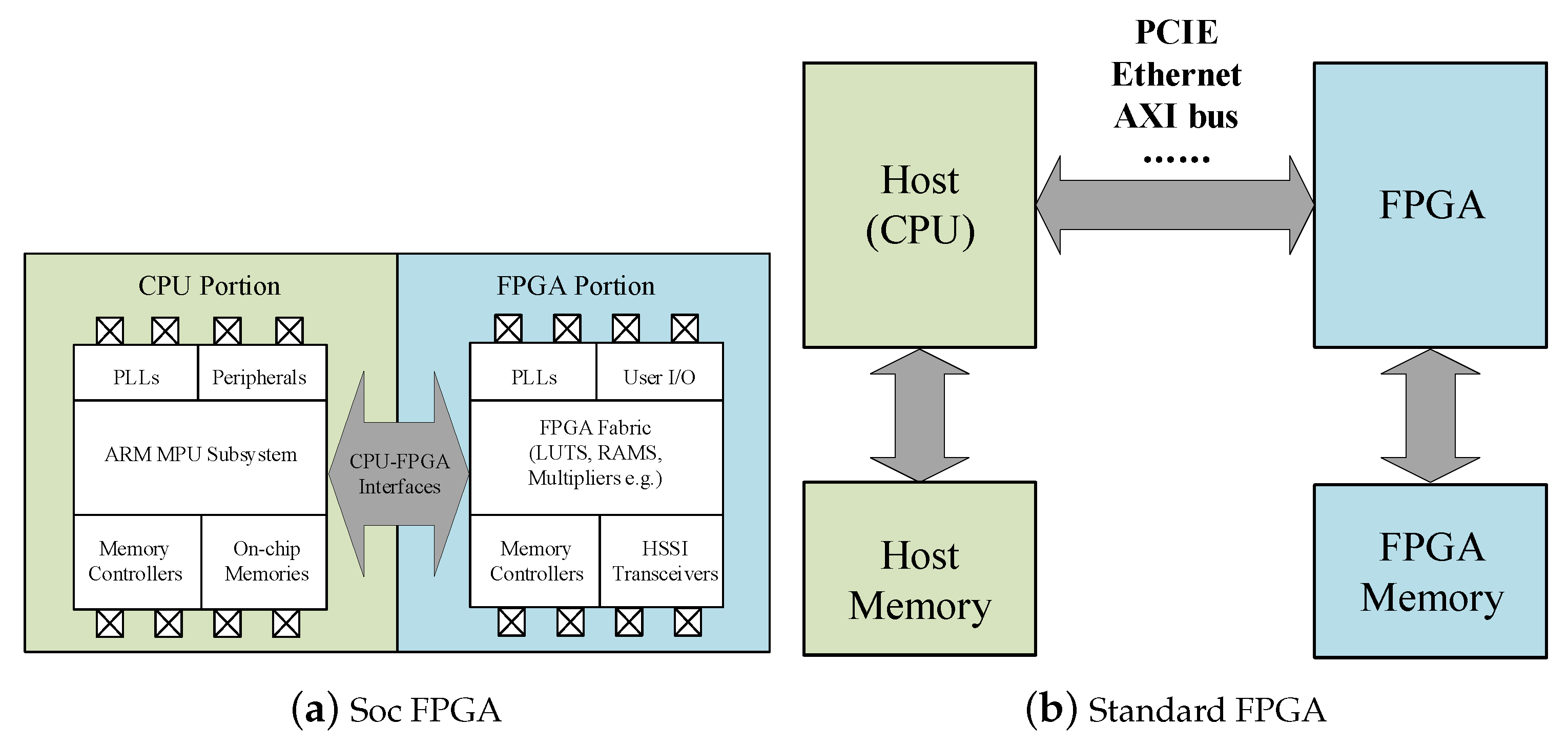
3.1. FPGA-Based Acceleration
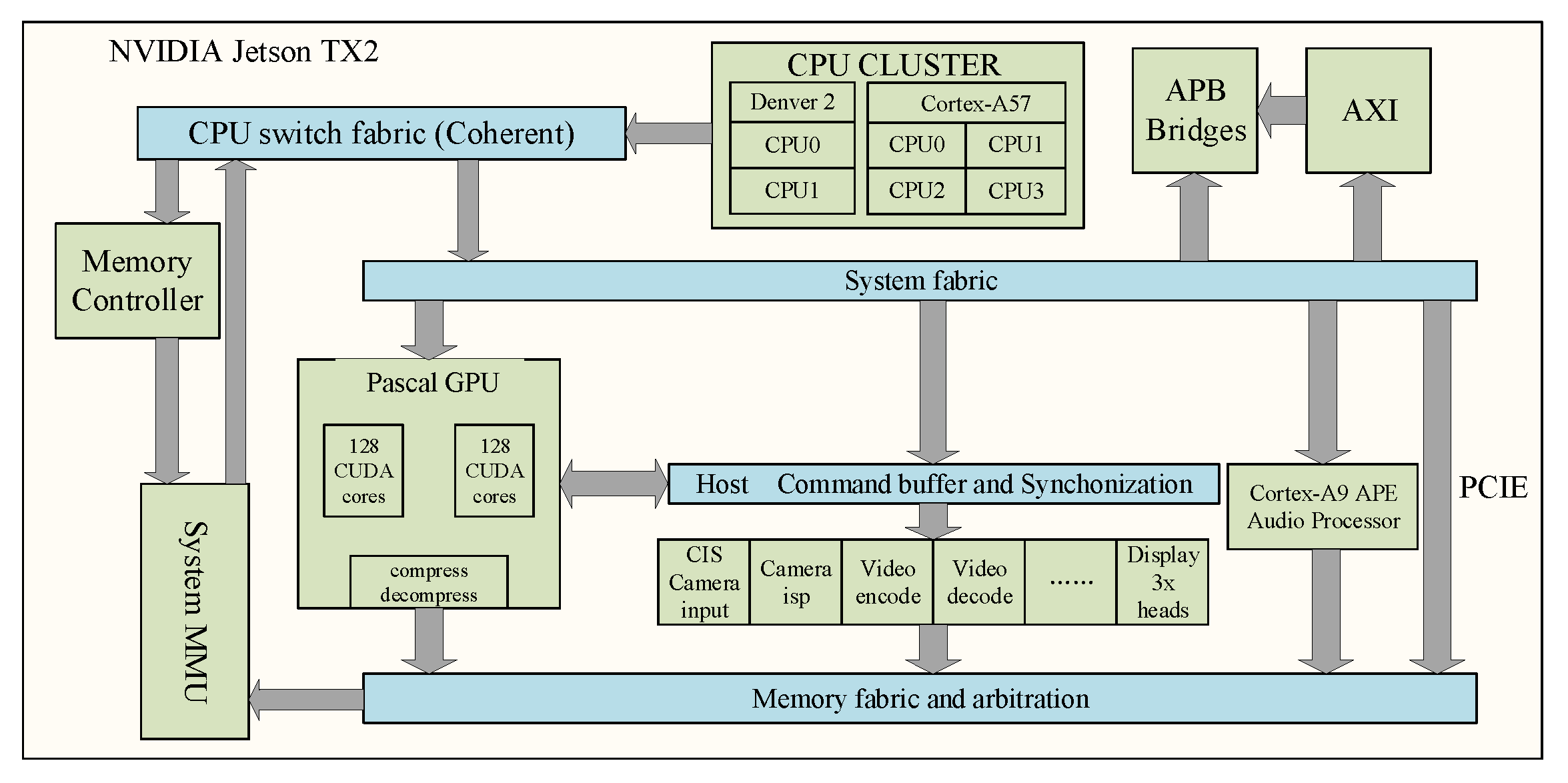
3.2. GPU-Based Acceleration
3.3. ASIC Acceleration
3.4. Microprogrammed Control Unit Acceleration
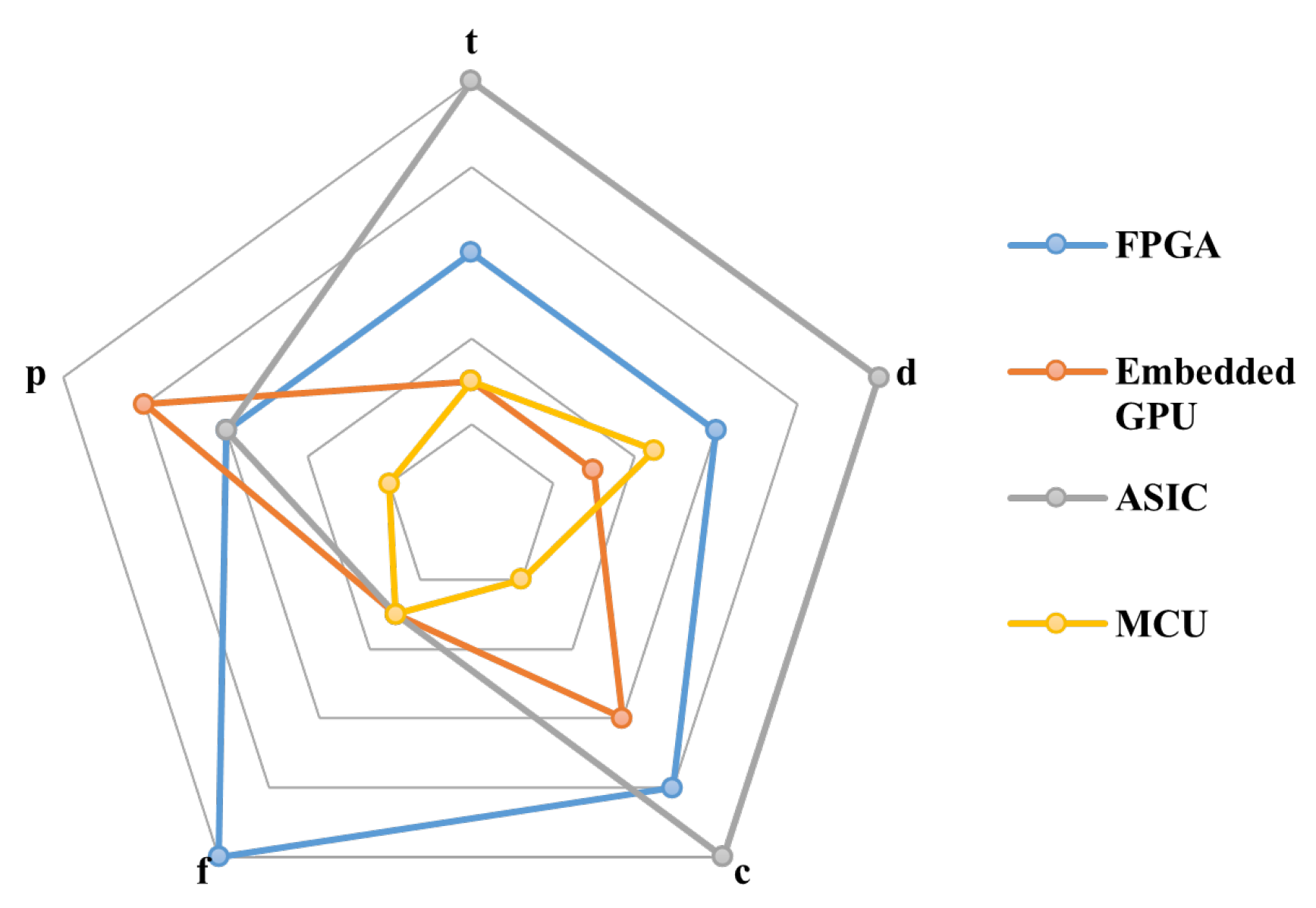
3.5. Why Choose FPGA
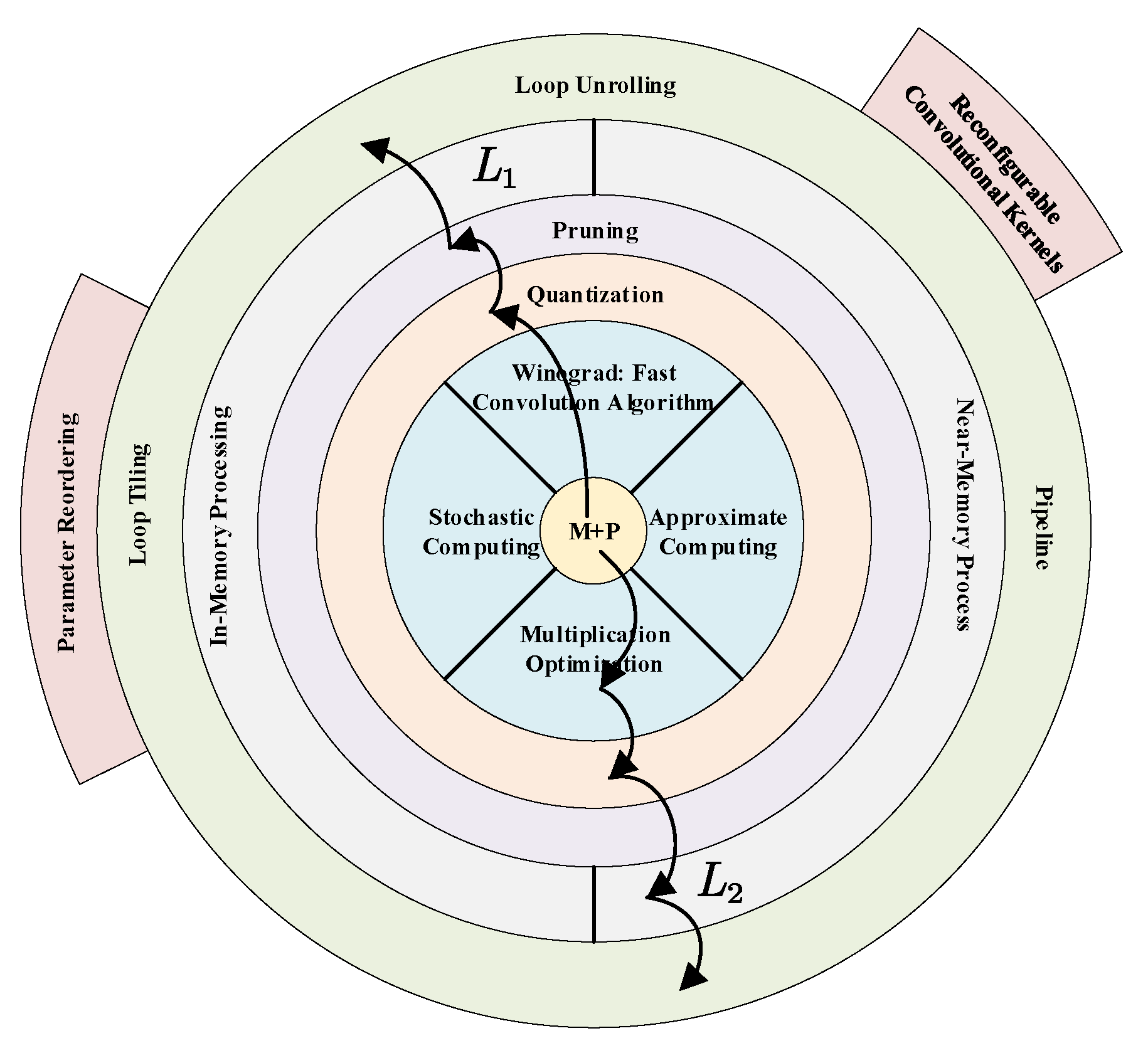
4. Computing and Memory Oriented Accelerating
4.1. Reducing Computing Complexity
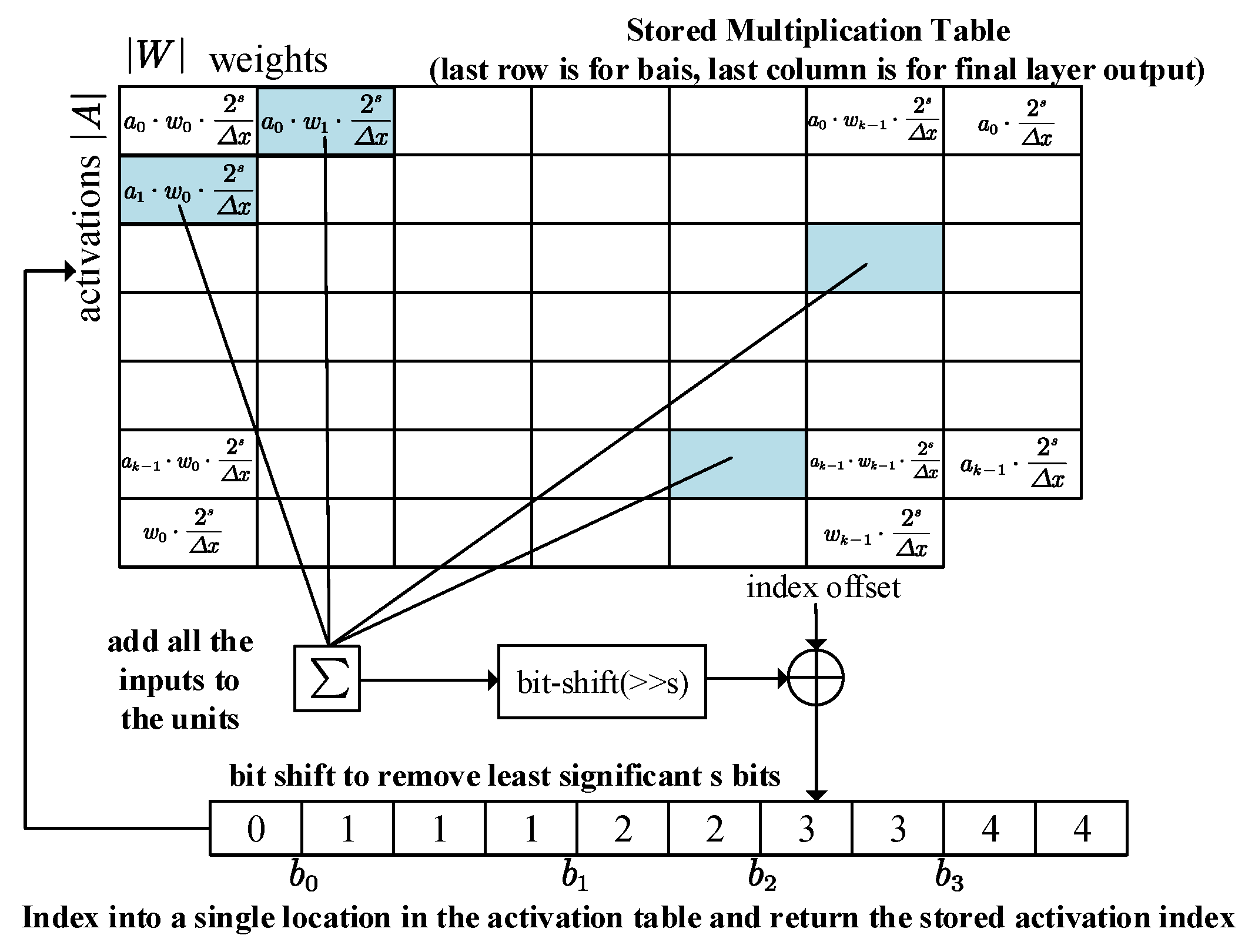
4.1.1. Multiplication Optimization
4.1.2. Approximate Computing
4.1.3. Stochastic Computing
4.1.4. Winograd: Fast Convolution Algorithm
4.2. Increasing Computing Parallelism
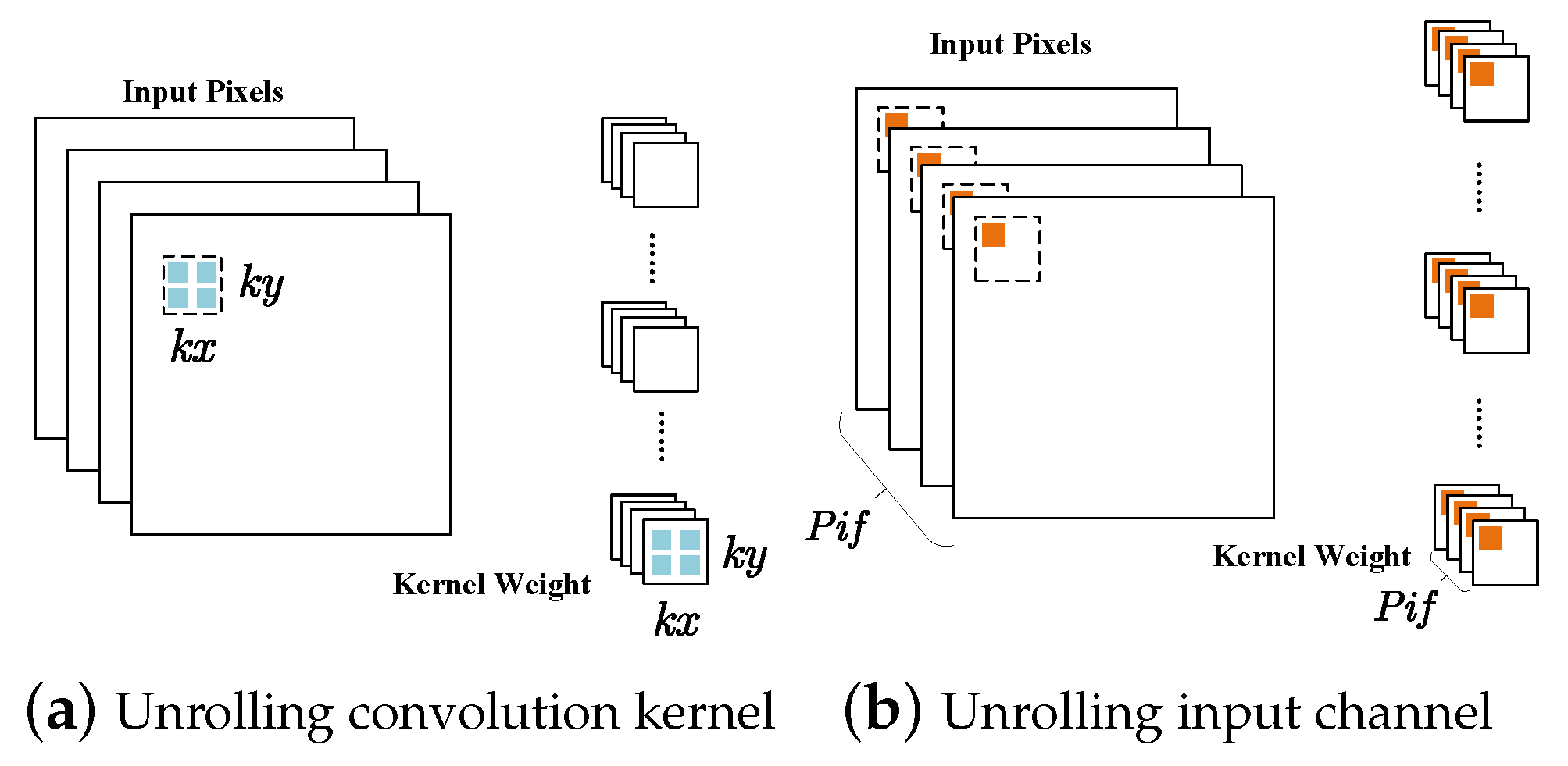
4.2.1. Loop Unrolling
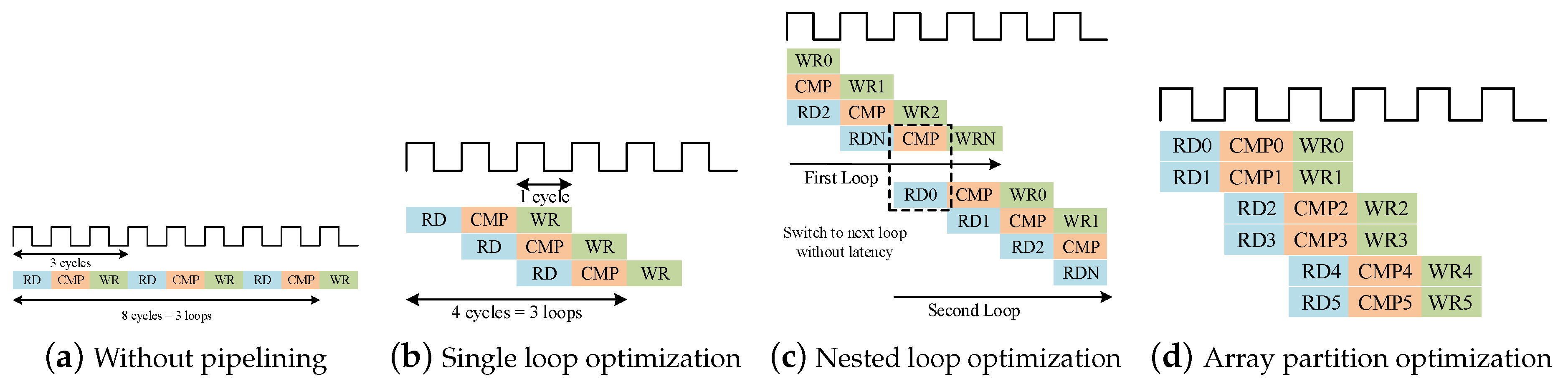
4.2.2. Pipeline
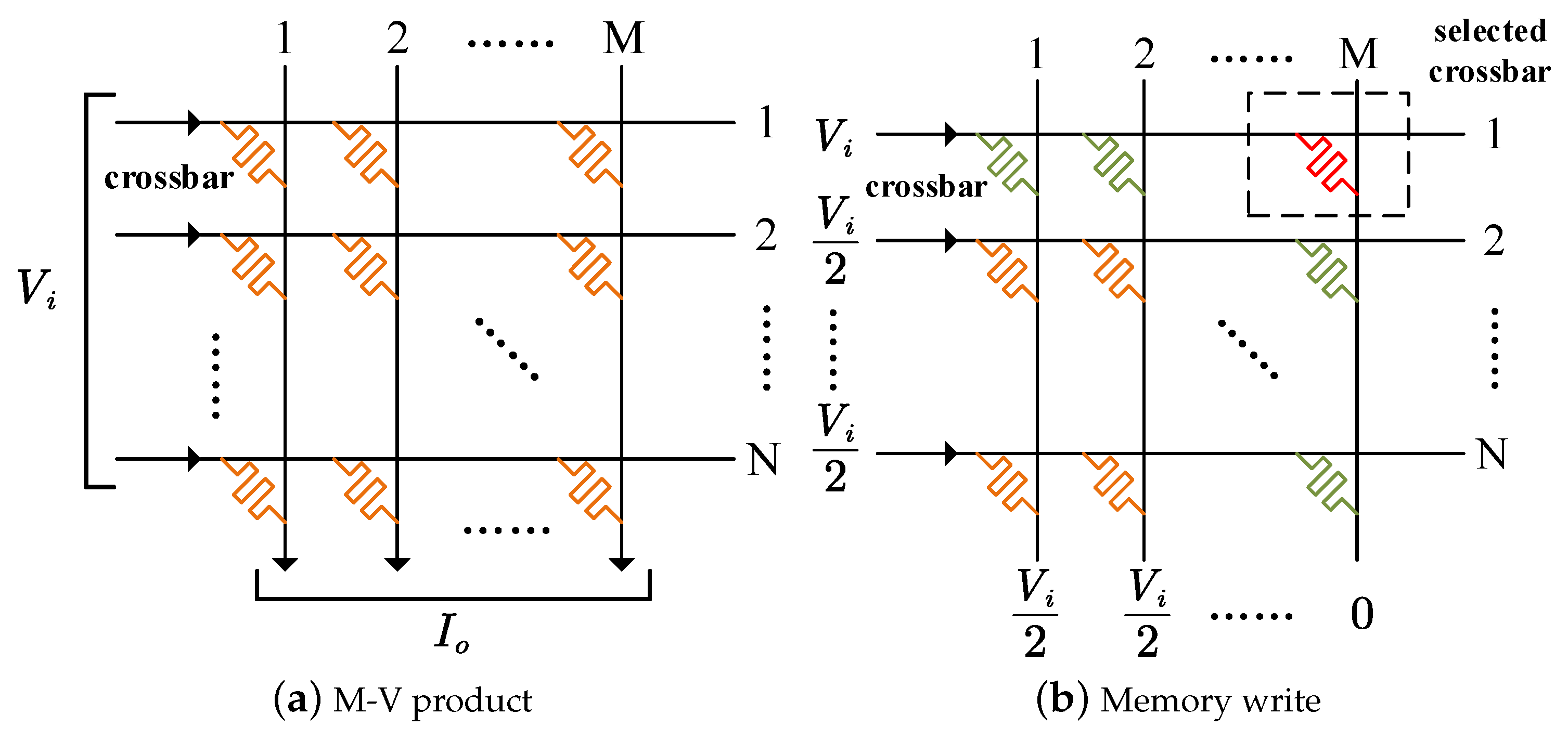
4.2.3. In-Memory Processing
4.3. Data Reuse
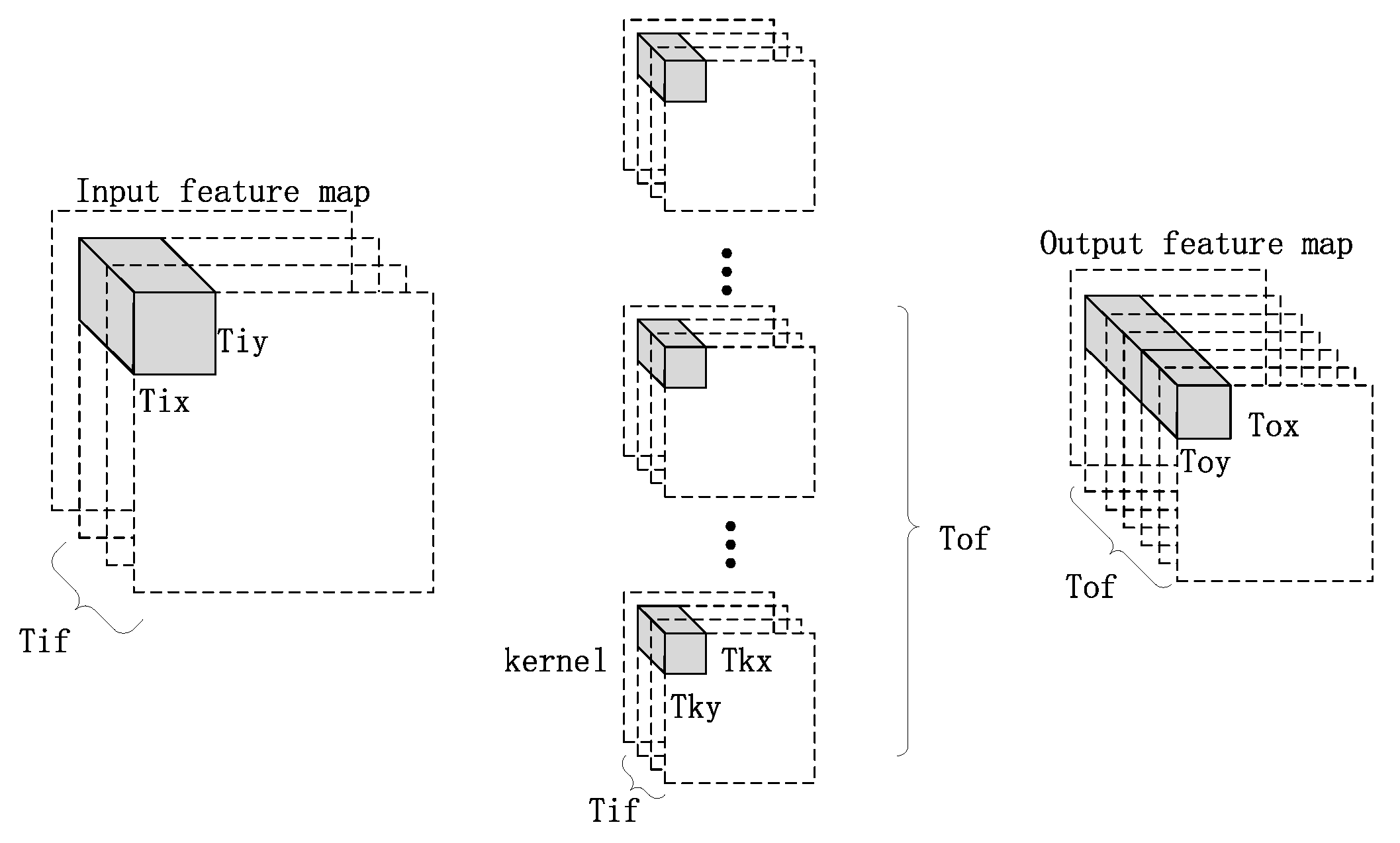
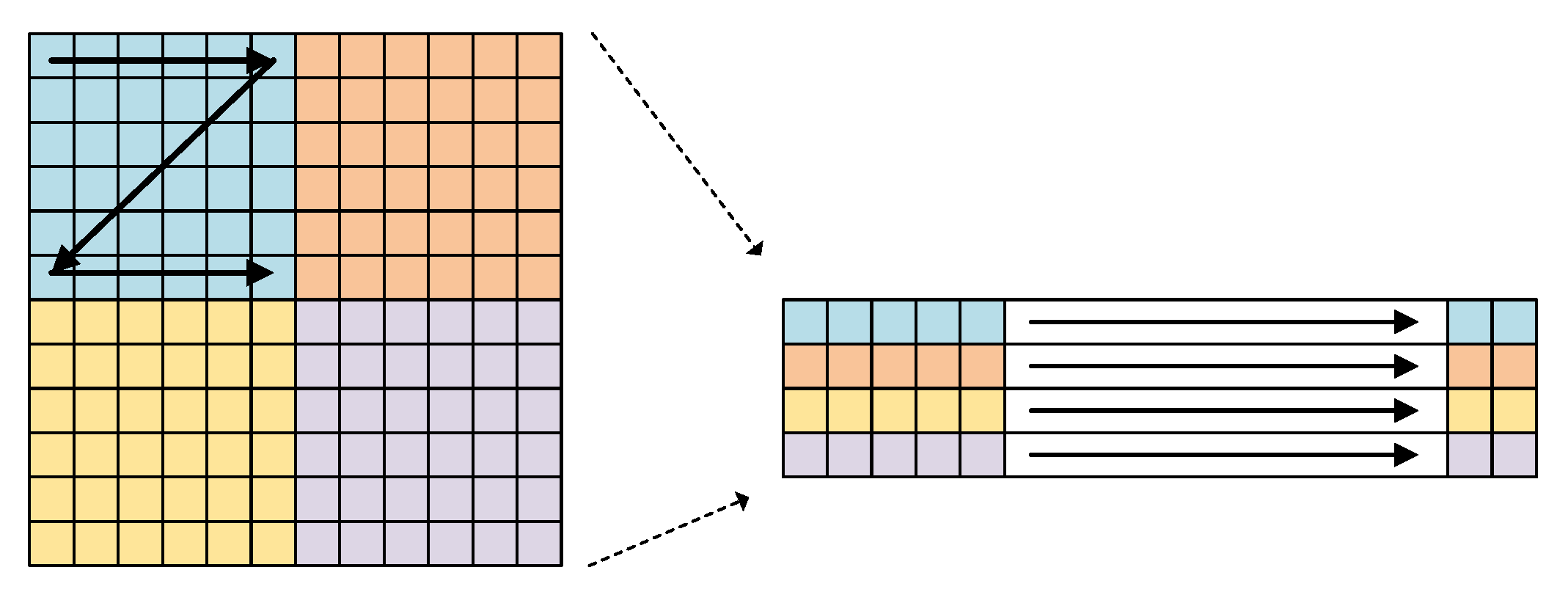
4.3.1. Loop Tiling
4.3.2. Parameter Reordering
4.3.3. Near-Memory Process
4.3.4. Reconfigurable Convolutional Kernels
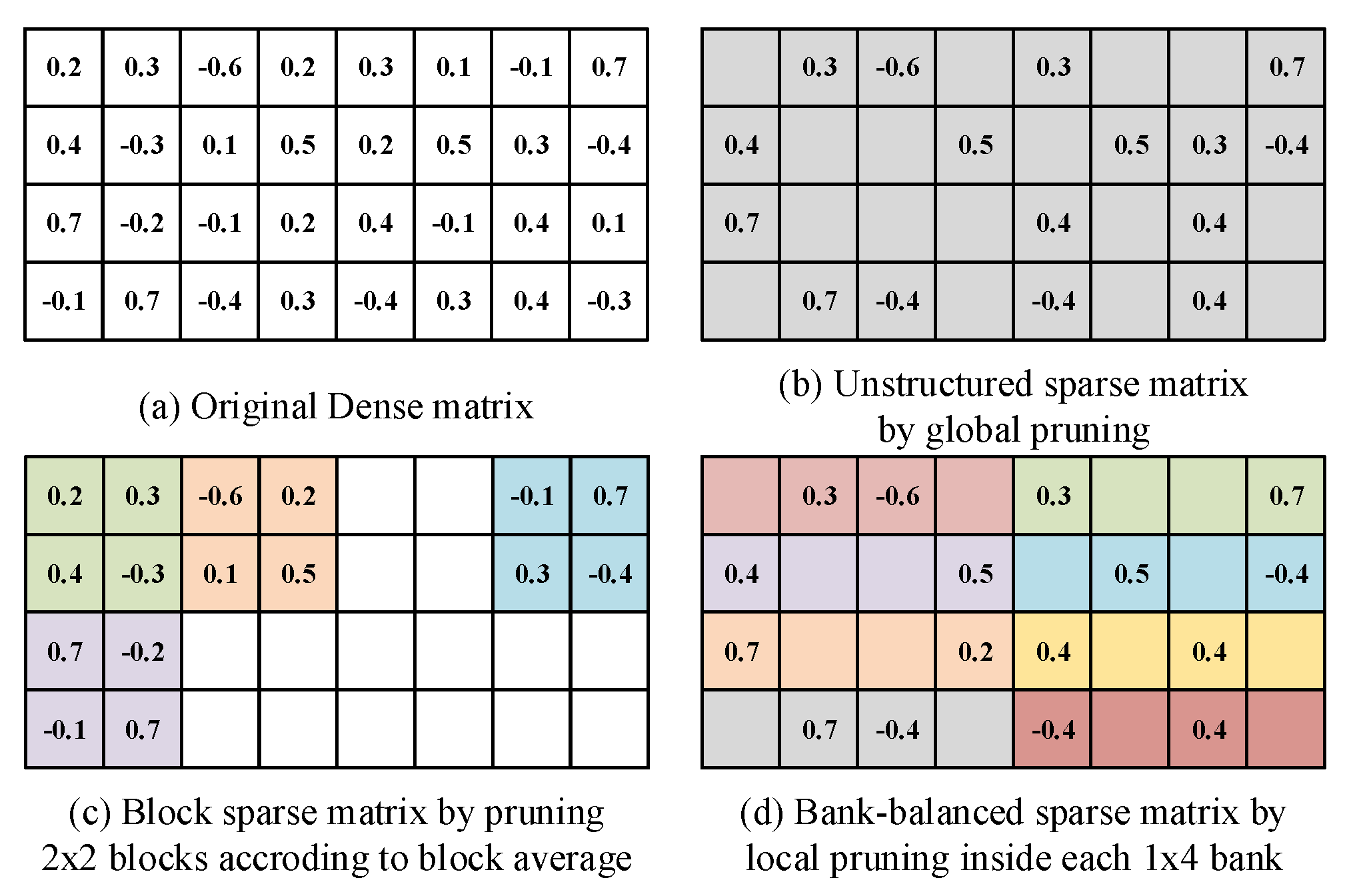
4.4. Pruning
4.5. Quantization
5. Technique Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| FPGA | Field Programmable Gata Array |
| GPU | Graphics Processing Unit |
| MCU | Microprogrammed Control Unit |
| ASIC | Application Specific Integrated Circuit |
| DNN | Deep Neural Network |
| CNN | Convolutional Neural Network |
| RNN | Recurrent Neural Network |
| ReRAM/RRAM | Resistance Random Access Memory |
References
- Guo, K.; Zeng, S.; Yu, J.; Wang, Y.; Yang, H. A survey of fpga-based neural network accelerator. arXiv 2017, arXiv:1712.08934. [Google Scholar]
- Lacey, G.; Taylor, G.W.; Areibi, S. Deep learning on fpgas: Past, present, and future. arXiv 2016, arXiv:1602.04283. [Google Scholar]
- Marchisio, A.; Hanif, M.A.; Khalid, F.; Plastiras, G.; Kyrkou, C.; Theocharides, T.; Shafique, M. Deep learning for edge computing: Current trends, cross-layer optimizations, and open research challenges. In Proceedings of the 2019 IEEE Computer Society Annual Symposium on VLSI (ISVLSI), Miami, FL, USA, 15–17 July 2019; pp. 553–559. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Redmon, J.; Farhadi, A. Yolov3: An incremental improvement. arXiv 2018, arXiv:1804.02767. [Google Scholar]
- Howard, A.G.; Zhu, M.; Chen, B.; Kalenichenko, D.; Wang, W.; Weyand, T.; Andreetto, M.; Adam, H. Mobilenets: Efficient convolutional neural networks for mobile vision applications. arXiv 2017, arXiv:1704.04861. [Google Scholar]
- Sandler, M.; Howard, A.; Zhu, M.; Zhmoginov, A.; Chen, L.C. Mobilenetv2: Inverted residuals and linear bottlenecks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 4510–4520. [Google Scholar]
- Howard, A.; Sandler, M.; Chu, G.; Chen, L.C.; Chen, B.; Tan, M.; Wang, W.; Zhu, Y.; Pang, R.; Vasudevan, V.; et al. Searching for mobilenetv3. In Proceedings of the IEEE International Conference on Computer Vision, Seoul, Korea, 27 October–2 November 2019; pp. 1314–1324. [Google Scholar]
- Zhang, X.; Zhou, X.; Lin, M.; Sun, J. Shufflenet: An extremely efficient convolutional neural network for mobile devices. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 6848–6856. [Google Scholar]
- Ma, N.; Zhang, X.; Zheng, H.T.; Sun, J. Shufflenet v2: Practical guidelines for efficient cnn architecture design. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 116–131. [Google Scholar]
- Khan, A.; Sohail, A.; Zahoora, U.; Qureshi, A.S. A survey of the recent architectures of deep convolutional neural networks. Artif. Intell. Rev. 2020, 53, 5455–5516. [Google Scholar] [CrossRef] [Green Version]
- Lee, C.Y.; Gallagher, P.W.; Tu, Z. Generalizing pooling functions in convolutional neural networks: Mixed, gated, and tree. Artif. Intell. Stat. 2016, 51, 464–472. [Google Scholar]
- Ioffe, S.; Szegedy, C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. arXiv 2015, arXiv:1502.03167. [Google Scholar]
- Lin, M.; Chen, Q.; Yan, S. Network in network. arXiv 2013, arXiv:1312.4400. [Google Scholar]
- Lipton, Z.C.; Berkowitz, J.; Elkan, C. A critical review of recurrent neural networks for sequence learning. arXiv 2015, arXiv:1506.00019. [Google Scholar]
- Han, S.; Kang, J.; Mao, H.; Hu, Y.; Li, X.; Li, Y.; Xie, D.; Luo, H.; Yao, S.; Wang, Y.; et al. Ese: Efficient speech recognition engine with sparse lstm on fpga. In Proceedings of the 2017 ACM/SIGDA International Symposium on Field-Programmable Gate Arrays, Monterey, CA, USA, 22–24 February 2017; pp. 75–84. [Google Scholar]
- Wang, S.; Li, Z.; Ding, C.; Yuan, B.; Qiu, Q.; Wang, Y.; Liang, Y. C-LSTM: Enabling efficient LSTM using structured compression techniques on FPGAs. In Proceedings of the 2018 ACM/SIGDA International Symposium on Field-Programmable Gate Arrays, Monterey, CA, USA, 25–27 February 2018; pp. 11–20. [Google Scholar]
- Gao, C.; Neil, D.; Ceolini, E.; Liu, S.C.; Delbruck, T. DeltaRNN: A power-efficient recurrent neural network accelerator. In Proceedings of the 2018 ACM/SIGDA International Symposium on Field-Programmable Gate Arrays, Monterey, CA, USA, 25–27 February 2018; pp. 21–30. [Google Scholar]
- Cao, S.; Zhang, C.; Yao, Z.; Xiao, W.; Nie, L.; Zhan, D.; Liu, Y.; Wu, M.; Zhang, L. Efficient and effective sparse LSTM on fpga with bank-balanced sparsity. In Proceedings of the 2019 ACM/SIGDA International Symposium on Field-Programmable Gate Arrays, Seaside, CA, USA, 24–26 February 2019; pp. 63–72. [Google Scholar]
- Yang, Y.; Huang, Q.; Wu, B.; Zhang, T.; Ma, L.; Gambardella, G.; Blott, M.; Lavagno, L.; Vissers, K.; Wawrzynek, J.; et al. Synetgy: Algorithm-hardware co-design for convnet accelerators on embedded fpgas. In Proceedings of the 2019 ACM/SIGDA International Symposium on Field-Programmable Gate Arrays, Seaside, CA, USA, 24–26 February 2019; pp. 23–32. [Google Scholar]
- Zhou, S.; Wu, Y.; Ni, Z.; Zhou, X.; Wen, H.; Zou, Y. Dorefa-net: Training low bitwidth convolutional neural networks with low bitwidth gradients. arXiv 2016, arXiv:1606.06160. [Google Scholar]
- Rastegari, M.; Ordonez, V.; Redmon, J.; Farhadi, A. Xnor-net: Imagenet classification using binary convolutional neural networks. In European Conference on Computer Vision; Springer: Amsterdam, The Netherlands, 2016; pp. 525–542. [Google Scholar]
- Jouppi, N.P.; Young, C.; Patil, N.; Patterson, D.; Agrawal, G.; Bajwa, R.; Bates, S.; Bhatia, S.; Boden, N.; Borchers, A.; et al. In-datacenter performance analysis of a tensor processing unit. In Proceedings of the 44th Annual International Symposium on Computer Architecture, Toronto, ON, Canada, 24–28 June 2017; pp. 1–12. [Google Scholar]
- Chen, T.; Du, Z.; Sun, N.; Wang, J.; Wu, C.; Chen, Y.; Temam, O. Diannao: A small-footprint high-throughput accelerator for ubiquitous machine-learning. ACM Sigarch Comput. Archit. News 2014, 42, 269–284. [Google Scholar] [CrossRef]
- Chen, Y.; Luo, T.; Liu, S.; Zhang, S.; He, L.; Wang, J.; Li, L.; Chen, T.; Xu, Z.; Sun, N.; et al. Dadiannao: A machine-learning supercomputer. In Proceedings of the 2014 47th Annual IEEE/ACM International Symposium on Microarchitecture, Cambridge, UK, 13–17 December 2014; pp. 609–622. [Google Scholar]
- Du, Z.; Fasthuber, R.; Chen, T.; Ienne, P.; Li, L.; Luo, T.; Feng, X.; Chen, Y.; Temam, O. ShiDianNao: Shifting vision processing closer to the sensor. In Proceedings of the 42nd Annual International Symposium on Computer Architecture, Portland, OR, USA, 13–17 June 2015; pp. 92–104. [Google Scholar]
- Liu, D.; Chen, T.; Liu, S.; Zhou, J.; Zhou, S.; Teman, O.; Feng, X.; Zhou, X.; Chen, Y. Pudiannao: A polyvalent machine learning accelerator. ACM Sigarch Comput. Archit. News 2015, 43, 369–381. [Google Scholar] [CrossRef]
- Han, D.; Lee, J.; Lee, J.; Yoo, H.J. A low-power deep neural network online learning processor for real-time object tracking application. IEEE Trans. Circuits Syst. Regul. Pap. 2018, 66, 1794–1804. [Google Scholar] [CrossRef]
- Han, D.; Lee, J.; Lee, J.; Yoo, H.J. A 1.32 TOPS/W Energy Efficient Deep Neural Network Learning Processor with Direct Feedback Alignment based Heterogeneous Core Architecture. In Proceedings of the 2019 Symposium on VLSI Circuits, Kyoto, Japan, 9–14 June 2019; pp. C304–C305. [Google Scholar]
- Chen, Y.H.; Krishna, T.; Emer, J.S.; Sze, V. Eyeriss: An energy-efficient reconfigurable accelerator for deep convolutional neural networks. IEEE J. Solid-State Circuits 2016, 52, 127–138. [Google Scholar] [CrossRef] [Green Version]
- Moons, B.; Uytterhoeven, R.; Dehaene, W.; Verhelst, M. 14.5 envision: A 0.26-to-10tops/w subword-parallel dynamic-voltage-accuracy-frequency-scalable convolutional neural network processor in 28nm fdsoi. In Proceedings of the 2017 IEEE International Solid-State Circuits Conference (ISSCC), San Francisco, CA, USA, 5–9 February 2017; pp. 246–247. [Google Scholar]
- Lee, J.; Kim, C.; Kang, S.; Shin, D.; Kim, S.; Yoo, H.J. UNPU: A 50.6 TOPS/W unified deep neural network accelerator with 1b-to-16b fully-variable weight bit-precision. In Proceedings of the 2018 IEEE International Solid-State Circuits Conference-(ISSCC), San Francisco, CA, USA, 11–15 February 2018; pp. 218–220. [Google Scholar]
- Yuan, Z.; Yue, J.; Yang, H.; Wang, Z.; Li, J.; Yang, Y.; Guo, Q.; Li, X.; Chang, M.F.; Yang, H.; et al. Sticker: A 0.41-62.1 TOPS/W 8Bit neural network processor with multi-sparsity compatible convolution arrays and online tuning acceleration for fully connected layers. In Proceedings of the 2018 IEEE Symposium on VLSI Circuits, Honolulu, HI, USA, 18–22 June 2018; pp. 33–34. [Google Scholar]
- Zhang, J.F.; Lee, C.E.; Liu, C.; Shao, Y.S.; Keckler, S.W.; Zhang, Z. SNAP: A 1.67—21.55 TOPS/W Sparse Neural Acceleration Processor for Unstructured Sparse Deep Neural Network Inference in 16nm CMOS. In Proceedings of the 2019 Symposium on VLSI Circuits, Kyoto, Japan, 9–14 June 2019; pp. C306–C307. [Google Scholar]
- Ma, J. Neural Network on Microcontroller. Available online: https://github.com/majianjia/nnom (accessed on 9 November 2020).
- Baluja, S.; Marwood, D.; Covell, M.; Johnston, N. No Multiplication? No Floating Point? No Problem! Training Networks for Efficient Inference. arXiv 2018, arXiv:1809.09244. [Google Scholar]
- Mittal, S. A survey of techniques for approximate computing. ACM Comput. Surv. 2016, 48, 1–33. [Google Scholar] [CrossRef] [Green Version]
- Esmaeilzadeh, H.; Sampson, A.; Ceze, L.; Burger, D. Neural acceleration for general-purpose approximate programs. In Proceedings of the 2012 45th Annual IEEE/ACM International Symposium on Microarchitecture, Vancouver, BC, Canada, 1–5 December 2012; pp. 449–460. [Google Scholar]
- St. Amant, R.; Yazdanbakhsh, A.; Park, J.; Thwaites, B.; Esmaeilzadeh, H.; Hassibi, A.; Ceze, L.; Burger, D. General-purpose code acceleration with limited-precision analog computation. ACM Sigarch Comput. Archit. News 2014, 42, 505–516. [Google Scholar] [CrossRef]
- Zhang, Q.; Wang, T.; Tian, Y.; Yuan, F.; Xu, Q. ApproxANN: An approximate computing framework for artificial neural network. In Proceedings of the 2015 Design, Automation & Test in Europe Conference & Exhibition (DATE), Grenoble, France, 9–13 March 2015; pp. 701–706. [Google Scholar]
- Venkataramani, S.; Ranjan, A.; Roy, K.; Raghunathan, A. AxNN: Energy-efficient neuromorphic systems using approximate computing. In Proceedings of the 2014 IEEE/ACM International Symposium on Low Power Electronics and Design (ISLPED), La Jolla, CA, USA, 11–13 August 2014; pp. 27–32. [Google Scholar]
- Xu, C.; Wu, X.; Yin, W.; Xu, Q.; Jing, N.; Liang, X.; Jiang, L. On quality trade-off control for approximate computing using iterative training. In Proceedings of the 2017 54th ACM/EDAC/IEEE Design Automation Conference (DAC), Austin, TX, USA, 18–22 June 2017; pp. 1–6. [Google Scholar]
- Moons, B.; Uytterhoeven, R.; Dehaene, W.; Verhelst, M. DVAFS: Trading computational accuracy for energy through dynamic-voltage-accuracy-frequency-scaling. In Proceedings of the Design, Automation & Test in Europe Conference & Exhibition (DATE), Lausanne, Switzerland, 27–31 March 2017; pp. 488–493. [Google Scholar]
- Alaghi, A.; Hayes, J.P. Survey of stochastic computing. ACM Trans. Embed. Comput. Syst. 2013, 12, 1–19. [Google Scholar] [CrossRef]
- Li, J.; Yuan, Z.; Li, Z.; Ren, A.; Ding, C.; Draper, J.; Nazarian, S.; Qiu, Q.; Yuan, B.; Wang, Y. Normalization and dropout for stochastic computing-based deep convolutional neural networks. Integration 2019, 65, 395–403. [Google Scholar] [CrossRef]
- Ren, A.; Li, Z.; Ding, C.; Qiu, Q.; Wang, Y.; Li, J.; Qian, X.; Yuan, B. Sc-dcnn: Highly-scalable deep convolutional neural network using stochastic computing. ACM SIGPLAN Not. 2017, 52, 405–418. [Google Scholar] [CrossRef]
- Kim, K.; Kim, J.; Yu, J.; Seo, J.; Lee, J.; Choi, K. Dynamic energy-accuracy trade-off using stochastic computing in deep neural networks. In Proceedings of the 53rd Annual Design Automation Conference, Austin, TX, USA, 5–9 June 2016; pp. 1–6. [Google Scholar]
- Sim, H.; Lee, J. A new stochastic computing multiplier with application to deep convolutional neural networks. In Proceedings of the 54th Annual Design Automation Conference 2017, Austin, TX, USA, 18–22 June 2017; pp. 1–6. [Google Scholar]
- Sim, H.; Lee, J. Log-quantized stochastic computing for memory and computation efficient DNNs. In Proceedings of the 24th Asia and South Pacific Design Automation Conference, Tokyo, Japan, 21–24 January 2019; pp. 280–285. [Google Scholar]
- Hojabr, R.; Givaki, K.; Tayaranian, S.R.; Esfahanian, P.; Khonsari, A.; Rahmati, D.; Najafi, M.H. Skippynn: An embedded stochastic-computing accelerator for convolutional neural networks. In Proceedings of the 2019 56th ACM/IEEE Design Automation Conference (DAC), Las Vegas, NV, USA, 2–6 June 2019; pp. 1–6. [Google Scholar]
- Toom, A.L. The complexity of a scheme of functional elements realizing the multiplication of integers. Sov. Math. Dokl. 1963, 3, 714–716. [Google Scholar]
- Cook, S. On the Minimum Computation Time for Multiplication. Ph.D. Thesis, Harvard University, Cambridge, MA, USA, 1966. [Google Scholar]
- Winograd, S. Arithmetic Complexity of Computations; Siam: Philadelphia, PA, USA, 1980; Volume 33. [Google Scholar]
- Lavin, A.; Gray, S. Fast algorithms for convolutional neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 4013–4021. [Google Scholar]
- Lu, L.; Liang, Y.; Xiao, Q.; Yan, S. Evaluating fast algorithms for convolutional neural networks on FPGAs. In Proceedings of the 2017 IEEE 25th Annual International Symposium on Field-Programmable Custom Computing Machines (FCCM), Napa, CA, USA, 30 April–2 May 2017; pp. 101–108. [Google Scholar]
- Kala, S.; Mathew, J.; Jose, B.R.; Nalesh, S. UniWiG: Unified winograd-GEMM architecture for accelerating CNN on FPGAs. In Proceedings of the 2019 32nd International Conference on VLSI Design and 2019 18th International Conference on Embedded Systems (VLSID), Delhi, India, 5–9 January 2019; pp. 209–214. [Google Scholar]
- Li, H.; Fan, X.; Jiao, L.; Cao, W.; Zhou, X.; Wang, L. A high performance FPGA-based accelerator for large-scale convolutional neural networks. In Proceedings of the 2016 26th International Conference on Field Programmable Logic and Applications (FPL), Lausanne, Switzerland, 29 August–2 September 2016; pp. 1–9. [Google Scholar]
- Motamedi, M.; Gysel, P.; Akella, V.; Ghiasi, S. Design space exploration of FPGA-based deep convolutional neural networks. In Proceedings of the 2016 21st Asia and South Pacific Design Automation Conference (ASP-DAC), Macao, China, 25–28 January 2016; pp. 575–580. [Google Scholar]
- Wu, R.; Liu, B.; Fu, J.; Xu, M.; Fu, P.; Li, J. Research and Implementation of ε-SVR Training Method Based on FPGA. Electronics 2019, 8, 919. [Google Scholar] [CrossRef] [Green Version]
- Khoram, S.; Zha, Y.; Zhang, J.; Li, J. Challenges and opportunities: From near-memory computing to in-memory computing. In Proceedings of the 2017 ACM on International Symposium on Physical Design, Portland, OR, USA, 19–22 March 2017; pp. 43–46. [Google Scholar]
- Lee, B.C.; Ipek, E.; Mutlu, O.; Burger, D. Architecting phase change memory as a scalable dram alternative. In Proceedings of the 36th Annual International Symposium on Computer Architecture, Austin, TX, USA, 20–24 June 2009; pp. 2–13. [Google Scholar]
- Wong, H.S.P.; Lee, H.Y.; Yu, S.; Chen, Y.S.; Wu, Y.; Chen, P.S.; Lee, B.; Chen, F.T.; Tsai, M.J. Metal–oxide RRAM. Proc. IEEE 2012, 100, 1951–1970. [Google Scholar] [CrossRef]
- Cheng, M.; Xia, L.; Zhu, Z.; Cai, Y.; Xie, Y.; Wang, Y.; Yang, H. Time: A training-in-memory architecture for memristor-based deep neural networks. In Proceedings of the 2017 54th ACM/EDAC/IEEE Design Automation Conference (DAC), Austin, TX, USA, 18–22 June 2017; pp. 1–6. [Google Scholar]
- Xia, L.; Tang, T.; Huangfu, W.; Cheng, M.; Yin, X.; Li, B.; Wang, Y.; Yang, H. Switched by input: Power efficient structure for RRAM-based convolutional neural network. In Proceedings of the 53rd Annual Design Automation Conference, Austin, TX, USA, 5–9 June 2016; pp. 1–6. [Google Scholar]
- Chen, L.; Li, J.; Chen, Y.; Deng, Q.; Shen, J.; Liang, X.; Jiang, L. Accelerator-friendly neural-network training: Learning variations and defects in RRAM crossbar. In Proceedings of the Design, Automation & Test in Europe Conference & Exhibition (DATE), Lausanne, Switzerland, 27–31 March 2017; pp. 19–24. [Google Scholar]
- Asenov, A.; Kaya, S.; Brown, A.R. Intrinsic parameter fluctuations in decananometer MOSFETs introduced by gate line edge roughness. IEEE Trans. Electron Devices 2003, 50, 1254–1260. [Google Scholar] [CrossRef] [Green Version]
- Xia, L.; Liu, M.; Ning, X.; Chakrabarty, K.; Wang, Y. Fault-tolerant training with on-line fault detection for RRAM-based neural computing systems. In Proceedings of the 54th Annual Design Automation Conference 2017, Austin, TX, USA, 18–22 June 2017; pp. 1–6. [Google Scholar]
- Wang, P.; Ji, Y.; Hong, C.; Lyu, Y.; Wang, D.; Xie, Y. SNrram: An efficient sparse neural network computation architecture based on resistive random-access memory. In Proceedings of the 2018 55th ACM/ESDA/IEEE Design Automation Conference (DAC), San Francisco, CA, USA, 24–28 June 2018; pp. 1–6. [Google Scholar]
- Pentecost, L.; Donato, M.; Reagen, B.; Gupta, U.; Ma, S.; Wei, G.Y.; Brooks, D. MaxNVM: Maximizing DNN storage density and inference efficiency with sparse encoding and error mitigation. In Proceedings of the 52nd Annual IEEE/ACM International Symposium on Microarchitecture, Columbus, OH, USA, 12–16 October 2019; pp. 769–781. [Google Scholar]
- Kogge, P.M. EXECUBE-a new architecture for scaleable MPPs. In Proceedings of the 1994 International Conference on Parallel Processing Vol. 1., Raleigh, NC, USA, 15–19 August 1994; Volume 1, pp. 77–84. [Google Scholar]
- Hall, M.; Kogge, P.; Koller, J.; Diniz, P.; Chame, J.; Draper, J.; LaCoss, J.; Granacki, J.; Brockman, J.; Srivastava, A.; et al. Mapping irregular applications to DIVA, a PIM-based data-intensive architecture. In Proceedings of the 1999 ACM/IEEE Conference on Supercomputing, Portland, OR, USA, 13–19 November 1999; p. 57. [Google Scholar]
- Kwon, Y.; Lee, Y.; Rhu, M. TensorDIMM: A Practical Near-Memory Processing Architecture for Embeddings and Tensor Operations in Deep Learning. In Proceedings of the 52nd Annual IEEE/ACM International Symposium on Microarchitecture, Columbus, OH, USA, 12–16 October 2019; pp. 740–753. [Google Scholar]
- Schuiki, F.; Schaffner, M.; Gürkaynak, F.K.; Benini, L. A scalable near-memory architecture for training deep neural networks on large in-memory datasets. IEEE Trans. Comput. 2018, 68, 484–497. [Google Scholar] [CrossRef]
- Hardieck, M.; Kumm, M.; Möller, K.; Zipf, P. Reconfigurable convolutional kernels for neural networks on FPGAs. In Proceedings of the 2019 ACM/SIGDA International Symposium on Field-Programmable Gate Arrays, Seaside, CA, USA, 24–26 February 2019; pp. 43–52. [Google Scholar]
- Chapman, K.D. Fast Integer Multipliers Fit in FPGAs. EDN 1994, 39, 80. [Google Scholar]
- Kumm, M.; Möller, K.; Zipf, P. Dynamically reconfigurable FIR filter architectures with fast reconfiguration. In Proceedings of the 2013 8th International Workshop on Reconfigurable and Communication-Centric Systems-on-Chip (ReCoSoC), Darmstadt, Germany, 10–12 July 2013; pp. 1–8. [Google Scholar]
- Wiatr, K.; Jamro, E. Constant coefficient multiplication in FPGA structures. In Proceedings of the 26th Euromicro Conference, EUROMICRO 2000, Informatics: Inventing the Future, Maastricht, The Netherlands, 5–7 September 2000; Volume 1, pp. 252–259. [Google Scholar]
- Brunie, N.; De Dinechin, F.; Istoan, M.; Sergent, G.; Illyes, K.; Popa, B. Arithmetic core generation using bit heaps. In Proceedings of the 2013 23rd International Conference on Field programmable Logic and Applications, Porto, Portugal, 2–4 September 2013; pp. 1–8. [Google Scholar]
- Kumm, M.; Zipf, P. Pipelined compressor tree optimization using integer linear programming. In Proceedings of the 2014 24th International Conference on Field Programmable Logic and Applications (FPL), Munich, Germany, 2–4 September 2014; pp. 1–8. [Google Scholar]
- De Dinechin, F.; Istoan, M.; Massouri, A. Sum-of-product architectures computing just right. In Proceedings of the 2014 IEEE 25th International Conference on Application-Specific Systems, Architectures and Processors, Zurich, Switzerland, 18–20 June 2014; pp. 41–47. [Google Scholar]
- Qiu, J.; Wang, J.; Yao, S.; Guo, K.; Li, B.; Zhou, E.; Yu, J.; Tang, T.; Xu, N.; Song, S.; et al. Going deeper with embedded fpga platform for convolutional neural network. In Proceedings of the 2016 ACM/SIGDA International Symposium on Field-Programmable Gate Arrays, Monterey, CA, USA, 21–23 February 2016; pp. 26–35. [Google Scholar]
- Swaminathan, S.; Garg, D.; Kannan, R.; Andres, F. Sparse low rank factorization for deep neural network compression. Neurocomputing 2020, 398, 185–196. [Google Scholar] [CrossRef]
- Lee, D.; Kwon, S.J.; Kim, B.; Wei, G.Y. Learning Low-Rank Approximation for CNNs. arXiv 2019, arXiv:1905.10145. [Google Scholar]
- Long, X.; Ben, Z.; Zeng, X.; Liu, Y.; Zhang, M.; Zhou, D. Learning sparse convolutional neural network via quantization with low rank regularization. IEEE Access 2019, 7, 51866–51876. [Google Scholar] [CrossRef]
- Dai, X.; Yin, H.; Jha, N.K. NeST: A neural network synthesis tool based on a grow-and-prune paradigm. IEEE Trans. Comput. 2019, 68, 1487–1497. [Google Scholar] [CrossRef] [Green Version]
- Noy, A.; Nayman, N.; Ridnik, T.; Zamir, N.; Doveh, S.; Friedman, I.; Giryes, R.; Zelnik-Manor, L. Asap: Architecture search, anneal and prune. arXiv 2019, arXiv:1904.04123. [Google Scholar]
- Dai, X.; Yin, H.; Jha, N.K. Incremental learning using a grow-and-prune paradigm with efficient neural networks. arXiv 2019, arXiv:1905.10952. [Google Scholar]
- Zhu, M.; Zhang, T.; Gu, Z.; Xie, Y. Sparse tensor core: Algorithm and hardware co-design for vector-wise sparse neural networks on modern gpus. In Proceedings of the 52nd Annual IEEE/ACM International Symposium on Microarchitecture, Columbus, OH, USA, 12–16 October 2019; pp. 359–371. [Google Scholar]
- Yang, T.H.; Cheng, H.Y.; Yang, C.L.; Tseng, I.C.; Hu, H.W.; Chang, H.S.; Li, H.P. Sparse ReRAM engine: Joint exploration of activation and weight sparsity in compressed neural networks. In Proceedings of the 46th International Symposium on Computer Architecture, Phoenix, AZ, USA, 22–26 June 2019; pp. 236–249. [Google Scholar]
- Ji, H.; Song, L.; Jiang, L.; Li, H.H.; Chen, Y. ReCom: An efficient resistive accelerator for compressed deep neural networks. In Proceedings of the 2018 Design, Automation & Test in Europe Conference & Exhibition (DATE), Dresden, Germany, 19–23 March 2018; pp. 237–240. [Google Scholar]
- Lin, J.; Zhu, Z.; Wang, Y.; Xie, Y. Learning the sparsity for ReRAM: Mapping and pruning sparse neural network for ReRAM based accelerator. In Proceedings of the 24th Asia and South Pacific Design Automation Conference, Tokyo, Japan, 21–24 January 2019; pp. 639–644. [Google Scholar]
- Chen, X.; Zhu, J.; Jiang, J.; Tsui, C.Y. CompRRAE: RRAM-based convolutional neural network accelerator with r educed computations through ar untime a ctivation e stimation. In Proceedings of the 24th Asia and South Pacific Design Automation Conference, Tokyo, Japan, 21–24 January 2019; pp. 133–139. [Google Scholar]
- Shin, S.; Cox, G.; Oskin, M.; Loh, G.H.; Solihin, Y.; Bhattacharjee, A.; Basu, A. Scheduling page table walks for irregular GPU applications. In Proceedings of the 2018 ACM/IEEE 45th Annual International Symposium on Computer Architecture (ISCA), Los Angeles, CA, USA, 1–6 June 2018; pp. 180–192. [Google Scholar]
- Li, J.; Sun, J.; Vuduc, R. HiCOO: Hierarchical storage of sparse tensors. In Proceedings of the SC18: International Conference for High Performance Computing, Networking, Storage and Analysis, Dallas, TX, USA, 11–16 November 2018; pp. 238–252. [Google Scholar]
- Wang, J.; Yuan, Z.; Liu, R.; Yang, H.; Liu, Y. An N-way group association architecture and sparse data group association load balancing algorithm for sparse CNN accelerators. In Proceedings of the 24th Asia and South Pacific Design Automation Conference, Tokyo, Japan, 21–24 January 2019; pp. 329–334. [Google Scholar]
- Chen, Y.H.; Yang, T.J.; Emer, J.; Sze, V. Eyeriss v2: A flexible accelerator for emerging deep neural networks on mobile devices. IEEE J. Emerg. Sel. Top. Circuits Syst. 2019, 9, 292–308. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Lou, Q.; Zhang, X.; Zhu, C.; Lin, Y.; Chen, D. Design flow of accelerating hybrid extremely low bit-width neural network in embedded FPGA. In Proceedings of the 2018 28th International Conference on Field Programmable Logic and Applications (FPL), Dublin, Ireland, 27–31 August 2018; pp. 163–1636. [Google Scholar]
- Lascorz, A.D.; Sharify, S.; Edo, I.; Stuart, D.M.; Awad, O.M.; Judd, P.; Mahmoud, M.; Nikolic, M.; Siu, K.; Poulos, Z.; et al. ShapeShifter: Enabling Fine-Grain Data Width Adaptation in Deep Learning. In Proceedings of the 52nd Annual IEEE/ACM International Symposium on Microarchitecture, Columbus, OH, USA, 12–16 October 2019; pp. 28–41. [Google Scholar]
- Ding, C.; Wang, S.; Liu, N.; Xu, K.; Wang, Y.; Liang, Y. REQ-YOLO: A resource-aware, efficient quantization framework for object detection on FPGAs. In Proceedings of the 2019 ACM/SIGDA International Symposium on Field-Programmable Gate Arrays, Seaside, CA, USA, 24–26 February 2019; pp. 33–42. [Google Scholar]
- Vogel, S.; Liang, M.; Guntoro, A.; Stechele, W.; Ascheid, G. Efficient hardware acceleration of CNNs using logarithmic data representation with arbitrary log-base. In Proceedings of the International Conference on Computer-Aided Design, San Diego, CA, USA, 5–8 November 2018; pp. 1–8. [Google Scholar]
- Chen, W.; Wilson, J.; Tyree, S.; Weinberger, K.; Chen, Y. Compressing neural networks with the hashing trick. Int. Conf. Mach. Learn. 2015, 37, 2285–2294. [Google Scholar]
- Han, S.; Mao, H.; Dally, W.J. Deep compression: Compressing deep neural networks with pruning, trained quantization and huffman coding. arXiv 2015, arXiv:1510.00149. [Google Scholar]
- Covell, M.; Marwood, D.; Baluja, S.; Johnston, N. Table-Based Neural Units: Fully Quantizing Networks for Multiply-Free Inference. arXiv 2019, arXiv:1906.04798. [Google Scholar]
- Yang, J.; Shen, X.; Xing, J.; Tian, X.; Li, H.; Deng, B.; Huang, J.; Hua, X.s. Quantization networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 7308–7316. [Google Scholar]
- Qin, H.; Gong, R.; Liu, X.; Bai, X.; Song, J.; Sebe, N. Binary neural networks: A survey. Pattern Recognit. 2020, 105, 107281. [Google Scholar] [CrossRef] [Green Version]
- Liu, Z.; Wu, B.; Luo, W.; Yang, X.; Liu, W.; Cheng, K.T. Bi-real net: Enhancing the performance of 1-bit cnns with improved representational capability and advanced training algorithm. In Proceedings of the European conference on computer vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 722–737. [Google Scholar]
- Zhu, S.; Dong, X.; Su, H. Binary ensemble neural network: More bits per network or more networks per bit? In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 4923–4932. [Google Scholar]
- Liu, S.; Zhu, H. Binary Convolutional Neural Network with High Accuracy and Compression Rate. In Proceedings of the 2019 2nd International Conference on Algorithms, Computing and Artificial Intelligence, Sanya, China, 20–22 December 2019; pp. 43–48. [Google Scholar]
- Liu, R.; Peng, X.; Sun, X.; Khwa, W.S.; Si, X.; Chen, J.J.; Li, J.F.; Chang, M.F.; Yu, S. Parallelizing SRAM arrays with customized bit-cell for binary neural networks. In Proceedings of the 2018 55th ACM/ESDA/IEEE Design Automation Conference (DAC), San Francisco, CA, USA, 24–28 June 2018; pp. 1–6. [Google Scholar]
- Agrawal, A.; Jaiswal, A.; Roy, D.; Han, B.; Srinivasan, G.; Ankit, A.; Roy, K. Xcel-RAM: Accelerating binary neural networks in high-throughput SRAM compute arrays. IEEE Trans. Circuits Syst. Regul. Pap. 2019, 66, 3064–3076. [Google Scholar] [CrossRef] [Green Version]


| Models | Quantization | Speed (GOPS) | Energy Efficiency (GOPS/W) | Platform |
|---|---|---|---|---|
| ESE [16] | 12b | 282.2 | 6.9 | XCKU060 |
| C-LSTM [17] | 16b | 131.1 | 6.0 | Virtex-7 |
| DeltaRNN [18] | 16b | 192.0 | 26.3 | XC7Z100 |
| BBS-LSTM [19] | 16b | 304.1 | 15.9 | Arria 10 GX1150 |
| Synetgy [20] | 4-4b | 47.09 | 8.56 | Zynq ZU3EG |
| DoReFa-Net [21] | 2b | 410.2 | 181.5 | ZC702 |
| XNOR-Net [22] | 1b | 207.8 | 44.2 | ZC702 |
| D.Han [28] | TPU-V2 | PDFA [29] | Eyeriss [30] | Envision [31] | UNPU [32] | Sticker [33] | SNAP [34] | |
|---|---|---|---|---|---|---|---|---|
| Technology (nm) | 65 | 20 | 65 | 65 | 28 | 65 | 65 | 16 |
| Frequency (MHz) | 200 | \ | 50–200 | 100–250 | 200 | 5–200 | 20–200 | 33–480 |
| Power (mW) | 126 | 225,000 | 168 | 235–332 | 7.5–300 | 3.2–297 | 20.5–248.4 | 16.3–364 |
| Data Width | INT13,16 | bfloat16 | INT13,16 | INT16 | INT1-16 | INT1-16 | INT8 | INT16 |
| Peak Throughput (GOPS) | 51.2 | 45,000 | 129.5 | 42.0 | 408 | 345.6 | 102–5638 | \ |
| Area (mm) | 3.52 | \ | 5.76 | 12.25 | 1.87 | 16 | 7.8 | 2.4 |
| Energy Efficiency (GOPS/W) | 406.4 | 200 | 770.8–1321 | 126.5 | 260–10,000 | 3080 | 411–62,100 | 21,550 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, R.; Guo, X.; Du, J.; Li, J. Accelerating Neural Network Inference on FPGA-Based Platforms—A Survey. Electronics 2021, 10, 1025. https://doi.org/10.3390/electronics10091025
Wu R, Guo X, Du J, Li J. Accelerating Neural Network Inference on FPGA-Based Platforms—A Survey. Electronics. 2021; 10(9):1025. https://doi.org/10.3390/electronics10091025
Chicago/Turabian StyleWu, Ran, Xinmin Guo, Jian Du, and Junbao Li. 2021. "Accelerating Neural Network Inference on FPGA-Based Platforms—A Survey" Electronics 10, no. 9: 1025. https://doi.org/10.3390/electronics10091025
APA StyleWu, R., Guo, X., Du, J., & Li, J. (2021). Accelerating Neural Network Inference on FPGA-Based Platforms—A Survey. Electronics, 10(9), 1025. https://doi.org/10.3390/electronics10091025







