Wavelet Transform Based Fault Identification and Reconfiguration for a Reduced Switch Multilevel Inverter Fed Induction Motor Drive
Abstract
:1. Introduction
2. Materials and Methods
2.1. Proposed 5-Level Symmetrical RSMLI Structure under Healthy Conditions
2.2. Proposed 5-Level Symmetrical RSMLI Structure under Faulty Conditions
2.3. Fault Identification Using a Discrete Wavelet Transform (DWT) Analysis
2.4. Fault-Reconfiguration Technique Using Auxiliary Switching Cells
3. Results
3.1. Simulation Results
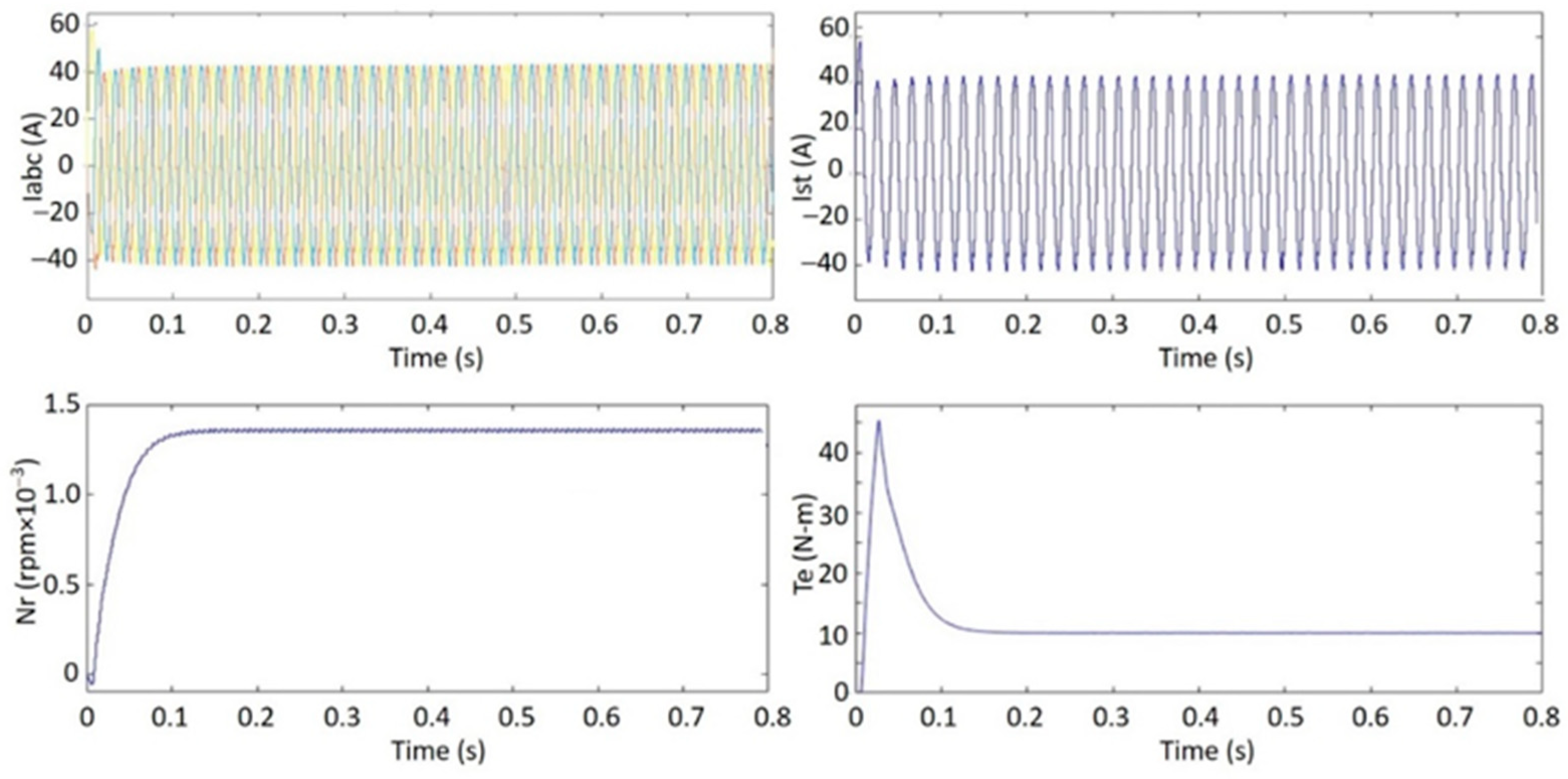
3.1.1. Case A: Evaluation for a Healthy State
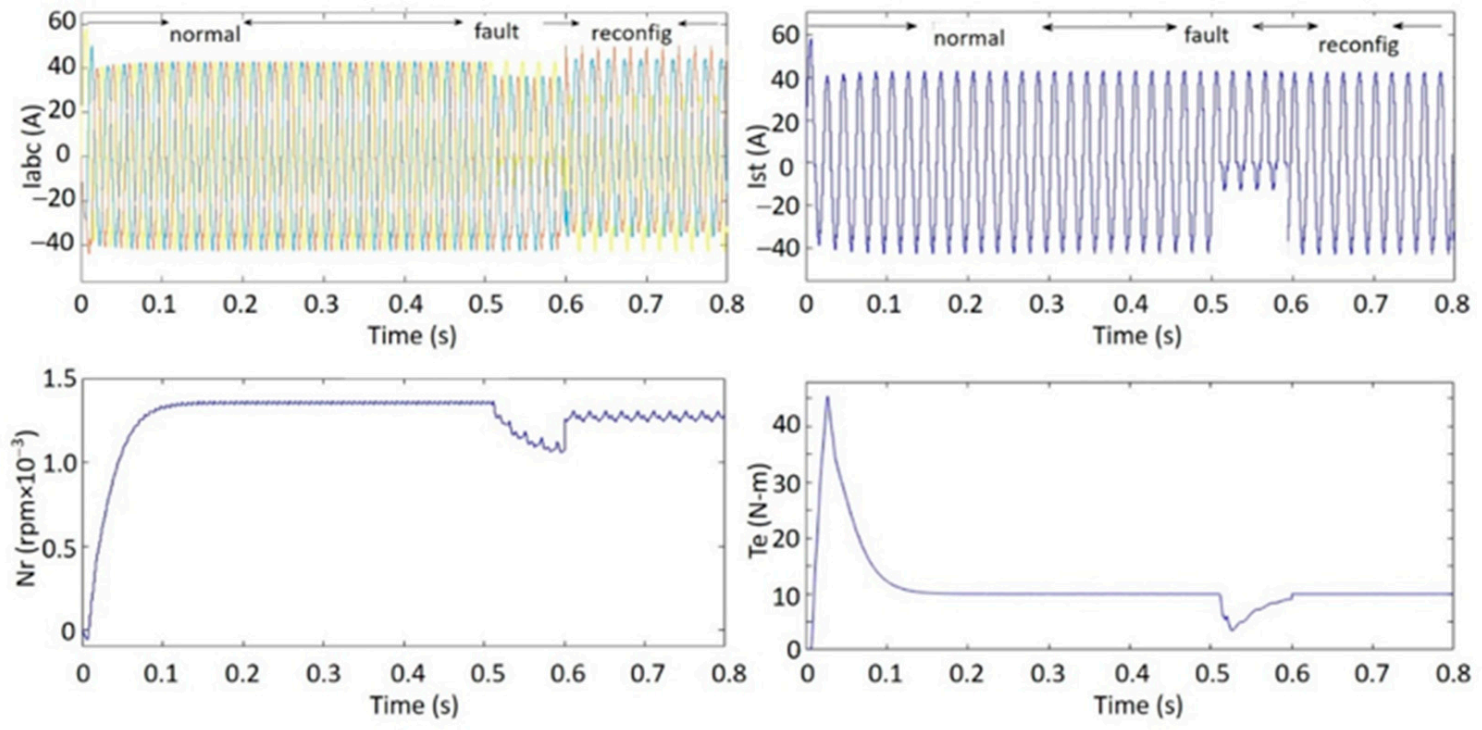
3.1.2. Case B: Performance during GOC Fault and Fault Reconfiguration States
3.1.3. Case C: Performance during GSC Fault and Fault Reconfiguration States
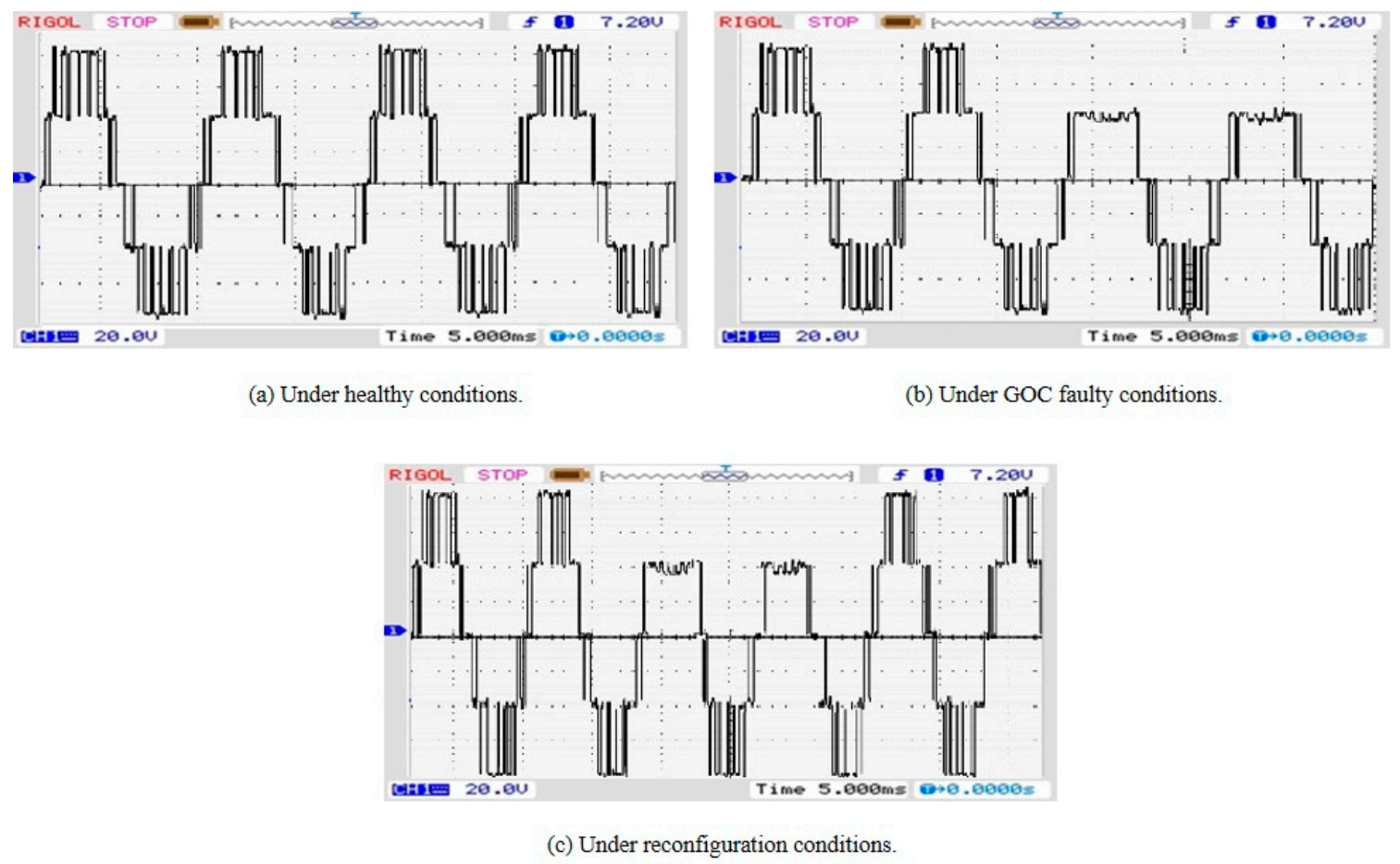
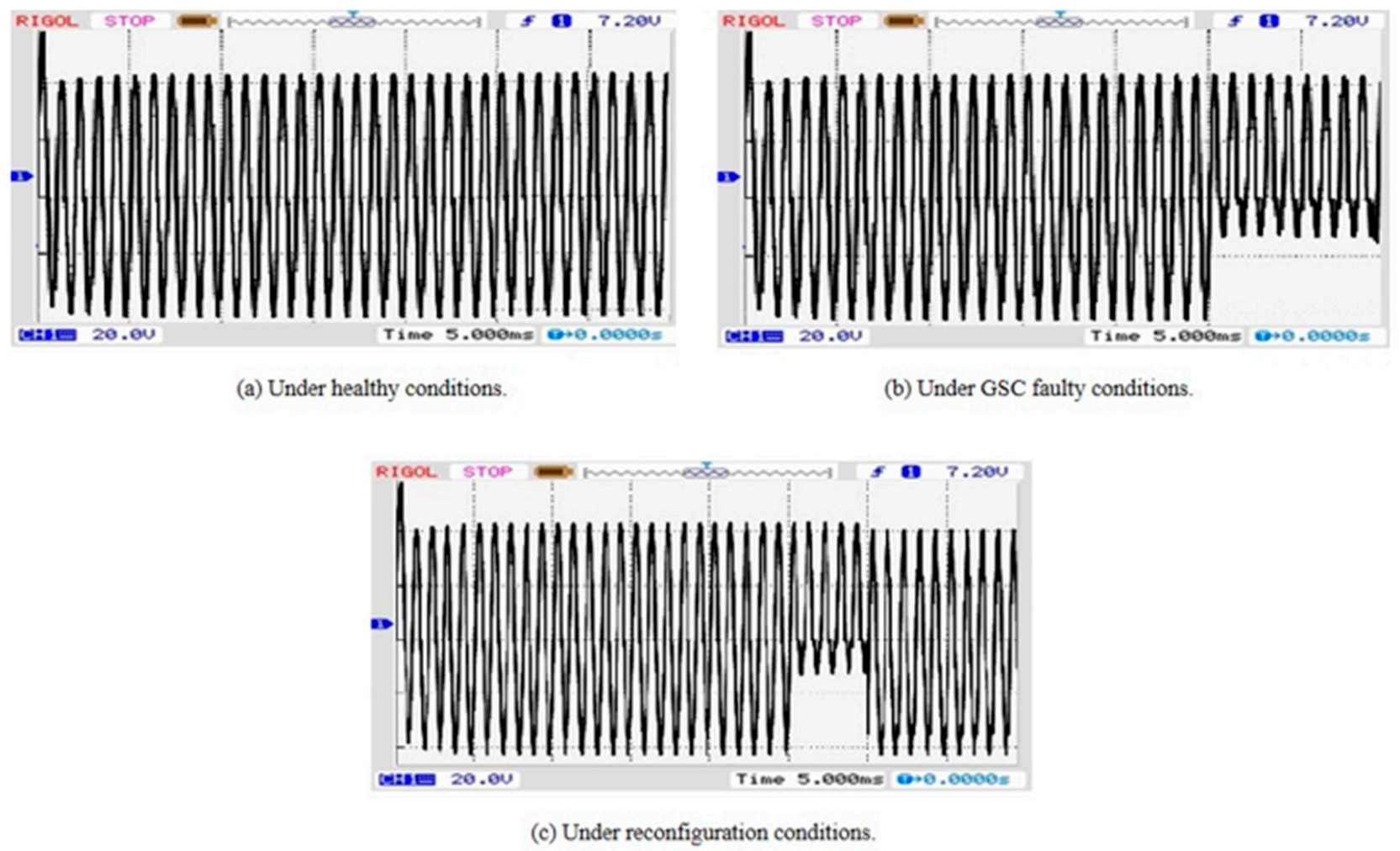
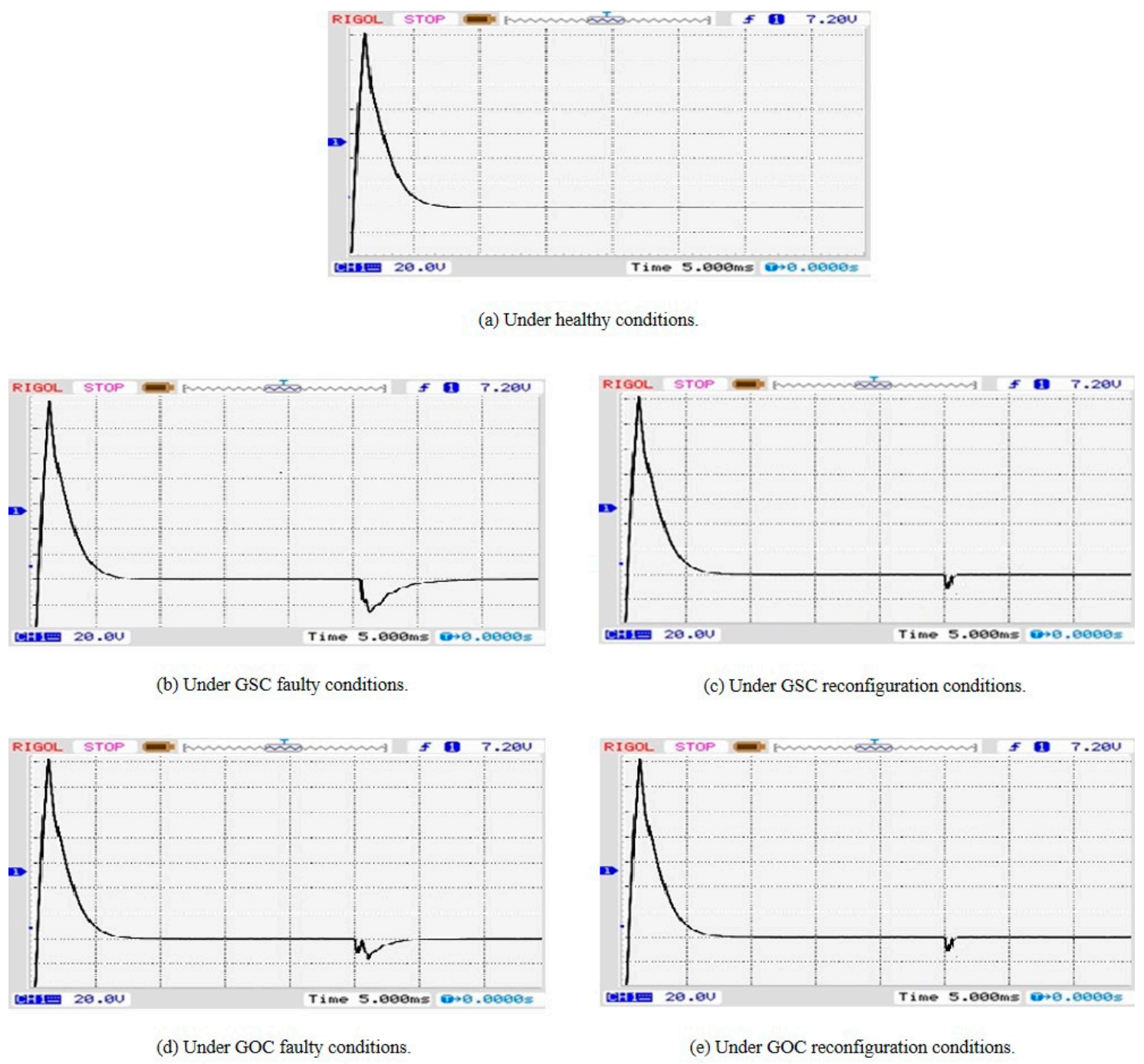
3.2. Experimental Results
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ojha, A.; Chaturvedi, P.; Mittal, A.; Jain, S. Carrier Based Common Mode Voltage Reduction Techniques in Neutral Point Clamped Inverter Based AC-DC-AC Drive System. J. Power Electron. 2016, 16, 142–152. [Google Scholar] [CrossRef] [Green Version]
- Mahato, B.; Raushan, R.; Jana, K.C. Modulation and control of multilevel inverter for an open-end winding induction motor with constant voltage levels and harmonics. IET Power Electron. 2017, 10, 71–79. [Google Scholar] [CrossRef]
- Sankala, A.; Korhonen, J.; Ström, J.; Luukko, J.; Silventoinen, P.; Komulainen, R.; Sarén, H.; Södö, N.; Isaksson, D. Modular double-cascade converter for high-power medium-voltage drives. IET Power Electron. 2015, 8, 1661–1669. [Google Scholar] [CrossRef]
- Chandran, B.P.; Selvakumar, A.I.; Mathew, F.M. Integrating multilevel converters application on renewable energy sources—A survey. J. Renew. Sustain. Energy 2018, 10, 065502. [Google Scholar] [CrossRef]
- Porru, M.; Serpi, A.; Marongiu, I.; Damiano, A. Suppression of DC-link voltage unbalance in three-level neutral-point clamped converters. J. Frankl. Inst. 2018, 355, 728–752. [Google Scholar] [CrossRef]
- Abdullah, R.; Rahim, N.A.; Raihan, S.R.S.; Ahmad, A.Z. Five-Level Diode-Clamped Inverter with Three-Level Boost Converter. IEEE Trans. Ind. Electron. 2014, 61, 5155–5163. [Google Scholar] [CrossRef] [Green Version]
- Raj, M.M.P.; Sundaram, S.S.M. Cascaded H-Bridge Five-Level Inverter for Grid-Connected Photovoltaic System Using Proportional–Integral Controller. Meas. Control. 2016, 49, 33–41. [Google Scholar] [CrossRef] [Green Version]
- Matos, D.M.B.; Estima, J.O.; Cardoso, A.J.M. Fault Analysis of Three-Level NPC Inverters in Synchronous Reluctance Motor Drives. In Privacy and Identity Management. Facing up to Next Steps; Springer: Berlin, Germany, 2016; Volume 470, pp. 206–216. [Google Scholar]
- Veerendra, A.S.; Mohamed, M.R.; Sulaiman, M.H.; Sudhakar, K.; Peddakapu, K. Modelling and simulation of dual sourced front-end converter for hybrid electric vehicles. Int. J. Ambient. Energy 2020, 1–8. [Google Scholar] [CrossRef]
- D′Aversa, A.; Hughes, B.; Patel, S. Challenges and Solutions of Protecting Variable Speed Drive Motors. In Proceedings of the 66th Annual Conference on Protective Relay Engineers, College Station, TX, USA, 8–11 April 2013; pp. 250–256. [Google Scholar]
- Lezana, P.; Pou, J.; Meynard, T.A.; Rodriguez, J.; Ceballos, S.; Richardeau, F. Survey on Fault Operation on Multilevel Inverters. IEEE Trans. Ind. Electron. 2010, 57, 2207–2218. [Google Scholar] [CrossRef] [Green Version]
- Priya, Y.K.; Kumar, M.V. Analysis of various switch faults of the Three level Neutral point clamped inverter feeding induction motor drive. In Proceedings of the 2016 2nd International Conference on Advances in Electrical, Electronics, Information, Communication and Bio-Informatics (AEEICB), Chennai, India, 27–28 February 2016; pp. 580–586. [Google Scholar]
- Trabelsi, M.; Boussak, M.; Gossa, M. Multiple IGBTs open circuit faults diagnosis in voltage source inverter fed induction motor using modified slope method. In Proceedings of the The XIX International Conference on Electrical Machines—ICEM 2010, Rome, Italy, 6–8 September 2010; pp. 1–6. [Google Scholar]
- Estima, J.O.; Cardoso, A.J.M. A New Algorithm for Real-Time Multiple Open-Circuit Fault Diagnosis in Voltage-Fed PWM Motor Drives by the Reference Current Errors. IEEE Trans. Ind. Electron. 2013, 60, 3496–3505. [Google Scholar] [CrossRef]
- Romero-Troncoso, R.D.J. Multirate Signal Processing to Improve FFT-Based Analysis for Detecting Faults in Induction Motors. IEEE Trans. Ind. Inf. 2016, 13, 1291–1300. [Google Scholar] [CrossRef]
- Moussa, M.A.; Boucherma, M.; Khezzar, A. A Detection Method for Induction Motor Bar Fault Using Sidelobes Leakage Phenomenon of the Sliding Discrete Fourier Transform. IEEE Trans. Power Electron. 2016, 32, 5560–5572. [Google Scholar] [CrossRef]
- Corral-Hernández, J.A.; Antonino-Daviu, J.A. Influence of the Start-up System in the Diagnosis of Faults in the Rotor of Induction Motors using the Discrete Wavelet Transform. Procedia Comput. Sci. 2016, 83, 807–815. [Google Scholar] [CrossRef] [Green Version]
- Moosavi, S.; Kazemi, A.; Akbari, H. A comparison of various open-circuit fault detection methods in the IGBT-based DC/AC inverter used in electric vehicle. Eng. Fail. Anal. 2019, 96, 223–235. [Google Scholar] [CrossRef]
- Wu, F.; Hao, Y.; Zhao, J.; Liu, Y. Current similarity based open-circuit fault diagnosis for induction motor drives with discrete wavelet transform. Microelectron. Reliab. 2017, 75, 309–316. [Google Scholar] [CrossRef]
- Cheon, J.-M.; Kim, C.-K.; Lee, J.-M.; Kim, S.-J.; Kwon, S. A New Fault Detectior for Three-Phase Half-Wave Converter Using Wavelet Transform. IFAC Proc. Vol. 2003, 36, 945–950. [Google Scholar] [CrossRef]
- Balamurugan, C.R.; Natarajan, S.; Bensraj, R.; Shanthi, B. A Review on Modulation Strategies of Multi Level Inverter. Indones. J. Electr. Eng. Comput. Sci. 2016, 3, 681. [Google Scholar] [CrossRef]
- Xiao, M.; Xu, Q.; Ouyang, H. An Improved Modulation Strategy Combining Phase Shifted PWM and Phase Disposition PWM for Cascaded H-Bridge Inverters. Energies 2017, 10, 1327. [Google Scholar] [CrossRef] [Green Version]
- Chavali, P.S.; Rao, P.V.R.; Vani, M.U. A Novel Multilevel Inverter with Reduced Number of Switches Using Simplified PWM Technique. J. Inst. Eng. Ser. B 2020, 101, 203–216. [Google Scholar] [CrossRef]
- Ahmed, I.; Borghate, V.B. Simplified space vector modulation technique for seven-level cascaded H-bridge inverter. IET Power Electron. 2014, 7, 604–613. [Google Scholar] [CrossRef]
- Gaeid, K.S.; Maher, R.A.; Lazim, A.J. Multilevel Inverter Fault-Tolerant Control with Wavelet Index in Induction Motor. J. Electr. Eng. Technol. 2019, 14, 1179–1191. [Google Scholar] [CrossRef]
- Bialasiewicz, J.T.; Gonzalez, D.; Balcells, J.; Gago, J. Wavelet-Based Approach to Evaluation of Signal Integrity. IEEE Trans. Ind. Electron. 2012, 60, 4590–4598. [Google Scholar] [CrossRef] [Green Version]
- Keswani, R.A.; Suryawanshi, H.M.; Ballal, M.S. Multi-resolution analysis for converter switch faults identification. IET Power Electron. 2015, 8, 783–792. [Google Scholar] [CrossRef]
- Ananthan, S.N.; Padmanabhan, R.; Meyur, R.; Mallikarjuna, B.; Reddy, M.J.B.; Mohanta, D.K. Real-time fault analysis of transmission lines using wavelet multi-resolution analysis based frequency-domain approach. IET Sci. Meas. Technol. 2016, 10, 693–703. [Google Scholar] [CrossRef]
- Jung, S.-M.; Park, J.-S.; Kim, H.-W.; Cho, K.-Y.; Youn, M.-J. An MRAS-Based Diagnosis of Open-Circuit Fault in PWM Voltage-Source Inverters for PM Synchronous Motor Drive Systems. IEEE Trans. Power Electron. 2012, 28, 2514–2526. [Google Scholar] [CrossRef]
- Kompella, K.D.; Mannam, V.G.R.; Rayapudi, S.R. DWT based bearing fault detection in induction motor using noise cancellation. J. Electr. Syst. Inf. Technol. 2016, 3, 411–427. [Google Scholar] [CrossRef] [Green Version]
- Kim, I.-S. On-line fault detection algorithm of a photovoltaic system using wavelet transform. Sol. Energy 2016, 126, 137–145. [Google Scholar] [CrossRef]
- Lopez-Hernandez, M.; Rangel-Magdaleno, J.; Peregrina-Barreto, H.; Ramirez-Cortes, J. Detection of broken bars on induction motors using MODWT. In Proceedings of the 2018 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Houston, TX, USA, 14–17 May 2018; pp. 1–5. [Google Scholar]
- Chen, W.; Bazzi, A.M. Logic-Based Methods for Intelligent Fault Diagnosis and Recovery in Power Electronics. IEEE Trans. Power Electron. 2017, 32, 5573–5589. [Google Scholar] [CrossRef]
- AbdelGhani, A.B.-B.; Ben-Abdelghani, H.; Richardeau, F.; Blaquiere, J.-M.; Mosser, F.; Slama-Belkhodja, I. Versatile Three-Level FC-NPC Converter with High Fault-Tolerance Capabilities: Switch Fault Detection and Isolation and Safe Postfault Operation. IEEE Trans. Ind. Electron. 2017, 64, 6453–6464. [Google Scholar] [CrossRef]
- Chen, W.; Hotchkiss, E.; Mademlis, C.; Bazzi, A.M. Integrated fault diagnosis and recovery in NPC multi-level inverters. In Proceedings of the 2017 IEEE 11th International Symposium on Diagnostics for Electrical Machines, Power Electronics and Drives (SDEMPED), Tinos, Greece, 29 August–1 September 2017; pp. 415–421. [Google Scholar] [CrossRef]
- Chen, W.; Hotchkiss, E.; Bazzi, A. Reconfiguration of NPC multi-level inverters to mitigate short circuit faults using back-to-back switches. CPSS Trans. Power Electron. Appl. 2018, 3, 46–55. [Google Scholar] [CrossRef]
- Shen, Y.; Miao, B.; Wu, D.; Ibrahim, K.A. Fault-Tolerant Control Strategy for Neutral-Point-Clamped Three-Level Inverter. J. Control. Sci. Eng. 2018, 2018, 1–9. [Google Scholar] [CrossRef] [Green Version]


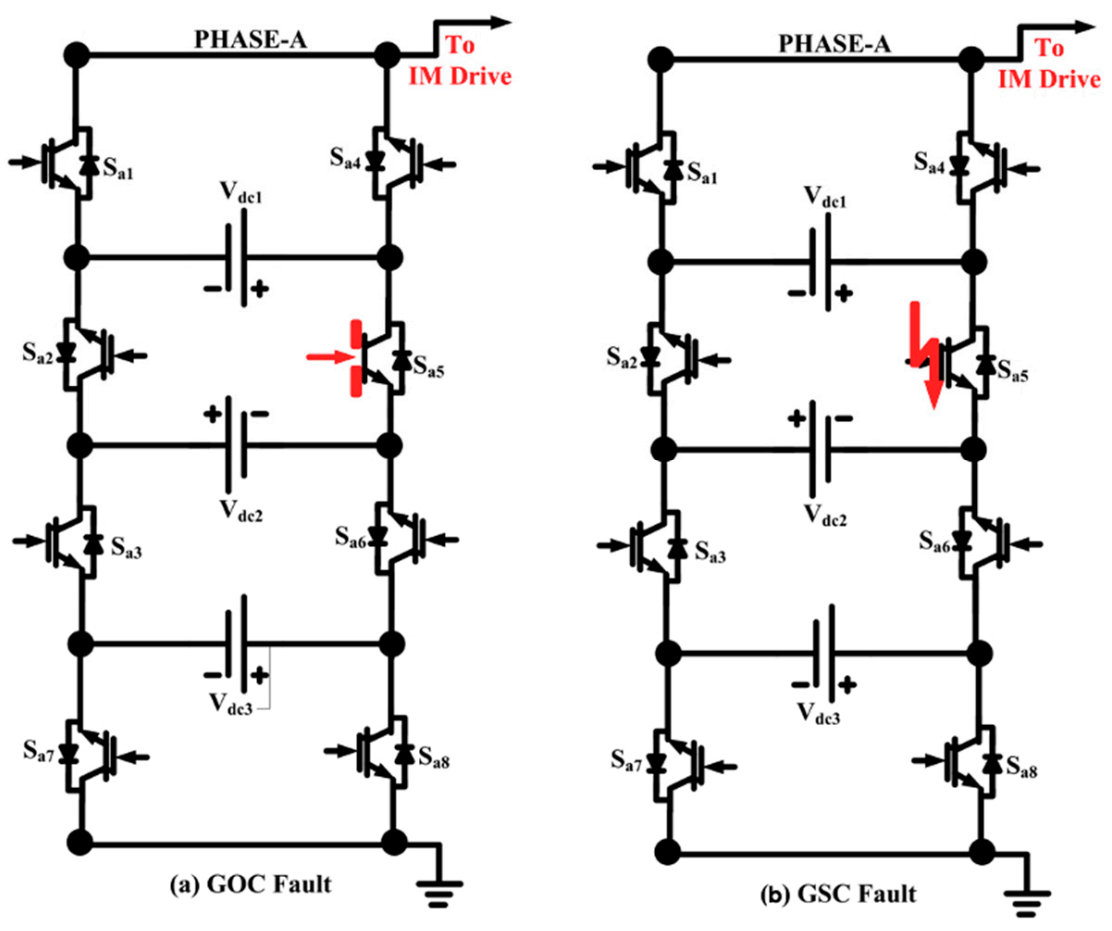






| Outcome Voltages | Sa1 | Sa2 | Sa3 | Sa4 | Sa5 | Sa6 | Sa7 | Sa8 |
|---|---|---|---|---|---|---|---|---|
| Vdc | C | NC | NC | NC | C | C | - | - |
| 2 Vdc | C | NC | C | NC | C | NC | - | - |
| −Vdc | NC | C | C | C | NC | NC | - | - |
| −2 Vdc | NC | C | NC | C | NC | C | - | - |
| 0 Vdc | C | C | C | NC | NC | NC | - | - |
| Outcome Voltages | Sa1 | Sa2 | Sa3 | Sa4 | Sa5 | Sa6 | Sa7 | Sa8 |
|---|---|---|---|---|---|---|---|---|
| Vdc | NC | C | C | C | - | NC | C | NC |
| 2 Vdc | NC | C | NC | C | - | C | NC | C |
| −Vdc | C | C | C | NC | - | NC | NC | C |
| −2 Vdc | NC | NC | C | C | - | NC | NC | C |
| 0 Vdc | C | C | C | NC | - | NC | C | NC |
| Parameters | Values |
|---|---|
| AC Source | Vsa = 230 V, F = 50 Hz |
| Inductors | Lb1 = Lb2 = Lb3 = 1.2 mH |
| DC-Link Capacitor | Cdc = 690 µF, Vdc1 = Vdc2 = Vdc3 = 200 V |
| Switching Frequency | Fs = 3050 Hz |
| Induction Motor | Vo = 400 V, Pm = 10 HP, Tm = 10 N-m |
| Level of Decomposition | |||||||||
| Under healthy conditions | |||||||||
| Mean | −0.46 | −0.52 | −0.29 | −0.93 | −0.53 | −0.82 | −0.38 | −0.29 | −0.33 |
| Median | −3.59 | −3.36 | −2.72 | −3.82 | −3.12 | −3.59 | −3.12 | −3.13 | −2.72 |
| Standard Deviation | 30.06 | 30.11 | 30.18 | 29.96 | 30.12 | 29.97 | 30.15 | 30.14 | 30.15 |
| Median Absolute Deviation | 29.97 | 30.15 | 30.73 | 29.74 | 30.37 | 29.97 | 30.45 | 30.45 | 30.73 |
| Under GOC faulty conditions | |||||||||
| Mean | 11.84 | 11.43 | 11.64 | 11.74 | 11.56 | 11.35 | 12.06 | 11.74 | 11.35 |
| Median | 0.49 | 0.04 | 0.05 | 0.05 | 0.04 | 0.04 | 0.75 | 0.05 | 0.04 |
| Standard Deviation | 19.38 | 19.42 | 19.36 | 19.26 | 19.33 | 19.32 | 19.43 | 19.26 | 19.32 |
| Median Absolute Deviation | 11.63 | 11.12 | 11.17 | 10.98 | 11.12 | 10.94 | 11.82 | 10.98 | 10.94 |
| Under GSC faulty conditions | |||||||||
| Mean | −9.17 | −8.83 | −9.01 | −10.09 | −9.62 | −10.19 | −8.91 | −9.48 | −9.19 |
| Median | −13.4 | −12.95 | −12.95 | −13.69 | −13.57 | −13.81 | −13.11 | −13.52 | −13.28 |
| Standard Deviation | 24.44 | 24.61 | 24.61 | 24.61 | 24.51 | 24.58 | 24.42 | 24.51 | 24.65 |
| Median Absolute Deviation | 21.71 | 22.08 | 22.07 | 21.62 | 21.61 | 21.45 | 21.78 | 21.64 | 21.92 |
| Under GOC fault reconfiguration conditions | |||||||||
| Mean | 4.85 | 4.61 | 4.64 | 4.54 | 4.88 | 4.56 | 4.71 | 4.57 | 4.65 |
| Median | 10.23 | 10.12 | 10.07 | 9.92 | 10.25 | 9.93 | 10.1 | 9.83 | 10.01 |
| Standard Deviation | 28.19 | 28.15 | 28.22 | 28.26 | 28.15 | 28.21 | 28.16 | 28.11 | 28.13 |
| Median Absolute Deviation | 24.87 | 25.02 | 24.99 | 25.16 | 24.81 | 25.12 | 24.95 | 25.21 | 25.02 |
| Under GSC fault reconfiguration conditions | |||||||||
| Mean | −5.12 | −5.22 | −5.21 | −5.31 | −5.13 | −5.25 | −5.41 | −5.22 | −5.41 |
| Median | −10.1 | −10.4 | −10.5 | −10.6 | −10.1 | −10.5 | −10.7 | −10.4 | −10.7 |
| Standard Deviation | 27.77 | 27.79 | 27.84 | 27.81 | 27.82 | 27.85 | 27.79 | 27.87 | 27.79 |
| Median Absolute Deviation | 24.93 | 24.80 | 24.75 | 24.64 | 24.97 | 24.75 | 24.64 | 24.80 | 24.64 |
| Healthy | Under Fault Condition | Under Fault Reconfiguration | |||
| GOC | GSC | GOC | GSC | ||
| 1 | 0.6427 | 0.8159 | 0.9364 | 0.9250 | |
| Average Mad () | 30.27 | 11.16 | 21.75 | 25.03 | 27.76 |
| Faulty Phase Leg Isolation Method | Isolating a Faulty Device Using Fuses | Faulty Cell Isolation Method | ANPC Fault-Tolerant Inverter | Proposed Method | |
|---|---|---|---|---|---|
| Extra Stress on Devices | ✓ | ✓ | |||
| Unbalanced Per-phase Condition | ✓ | ✓ | |||
| Reduced Peak Value | ✓ | ✓ | |||
| Excessive Complexity of Control | ✓ | ✓ | |||
| Excessive Add-on Components | ✓ | ✓ | ✓ | ||
| Not Applicable to Different Inverters | ✓ | ||||
| Not Applicable to Different Levels | ✓ |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Veerendra, A.S.; Shah, A.A.; Mohamed, M.R.; Sekhar, C.P.; Leung, P. Wavelet Transform Based Fault Identification and Reconfiguration for a Reduced Switch Multilevel Inverter Fed Induction Motor Drive. Electronics 2021, 10, 1023. https://doi.org/10.3390/electronics10091023
Veerendra AS, Shah AA, Mohamed MR, Sekhar CP, Leung P. Wavelet Transform Based Fault Identification and Reconfiguration for a Reduced Switch Multilevel Inverter Fed Induction Motor Drive. Electronics. 2021; 10(9):1023. https://doi.org/10.3390/electronics10091023
Chicago/Turabian StyleVeerendra, Arigela Satya, Akeel A. Shah, Mohd Rusllim Mohamed, Chavali Punya Sekhar, and Puiki Leung. 2021. "Wavelet Transform Based Fault Identification and Reconfiguration for a Reduced Switch Multilevel Inverter Fed Induction Motor Drive" Electronics 10, no. 9: 1023. https://doi.org/10.3390/electronics10091023






