A Novel Method for Establishing an Efficiency Map of IPMSMs for EV Propulsion Based on the Finite-Element Method and a Neural Network
Abstract
:1. Introduction
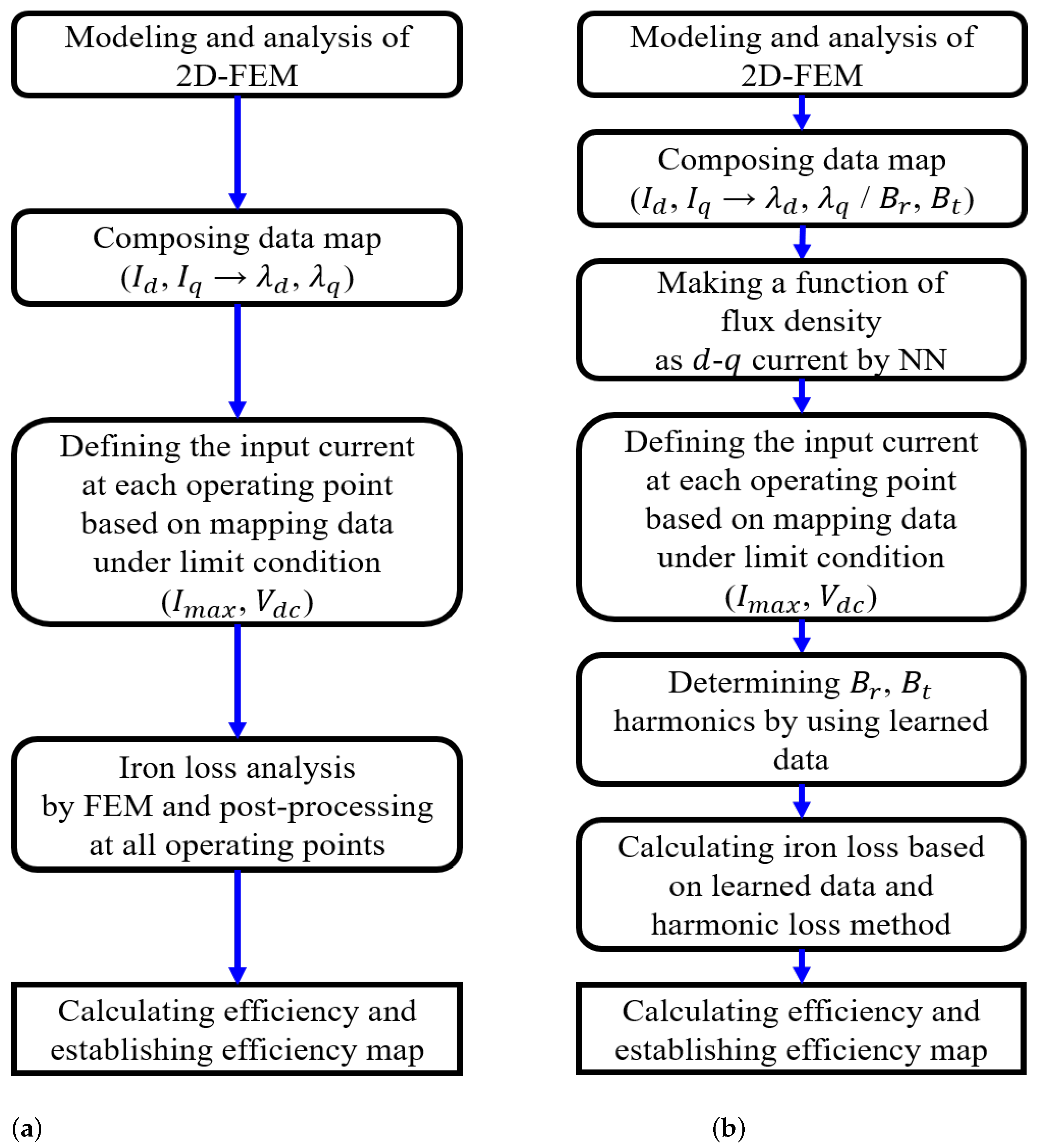
2. The Process of the Proposed Method
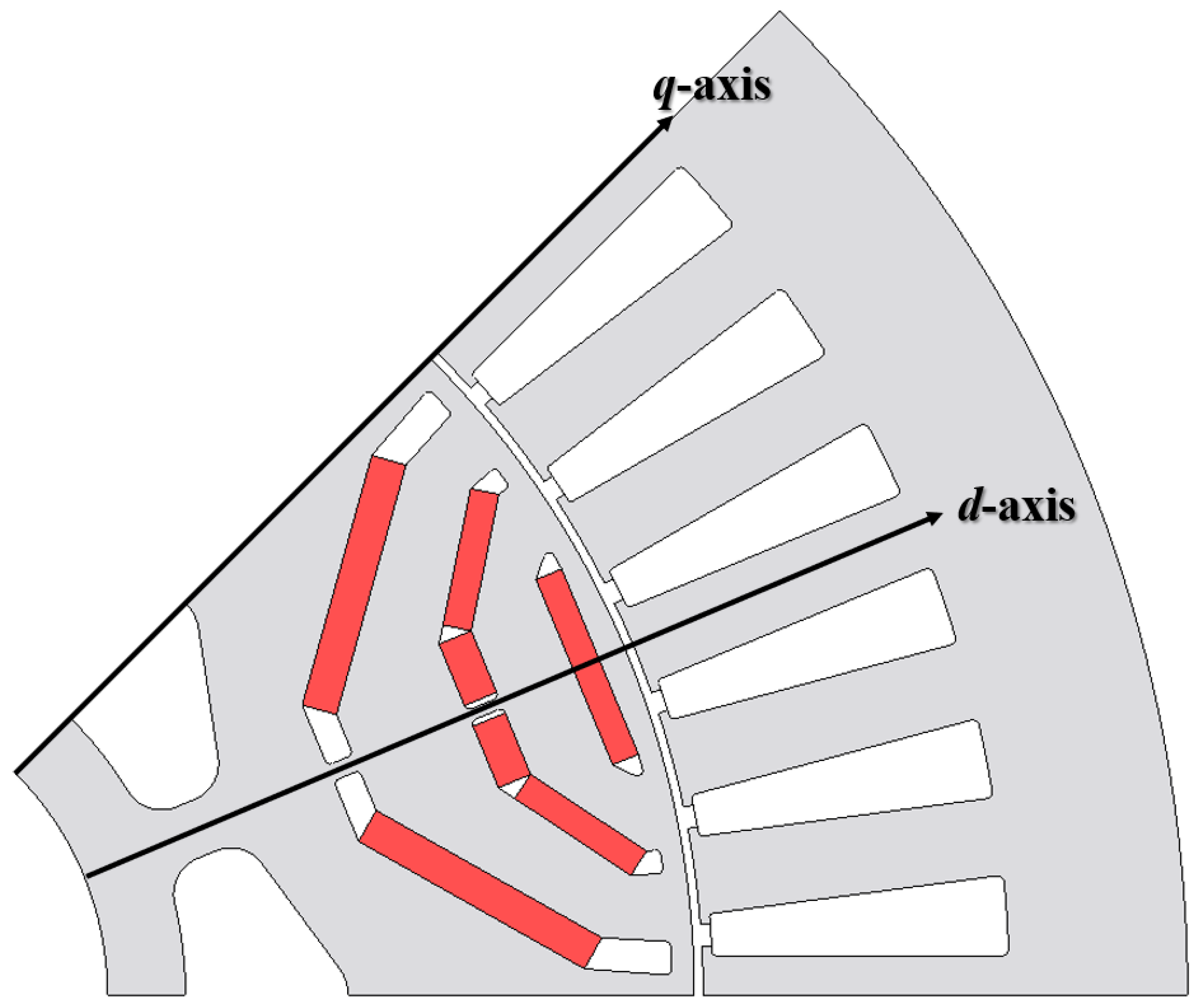
3. Establishing an Efficiency Map of a Propulsion Motor Using the Proposed Method
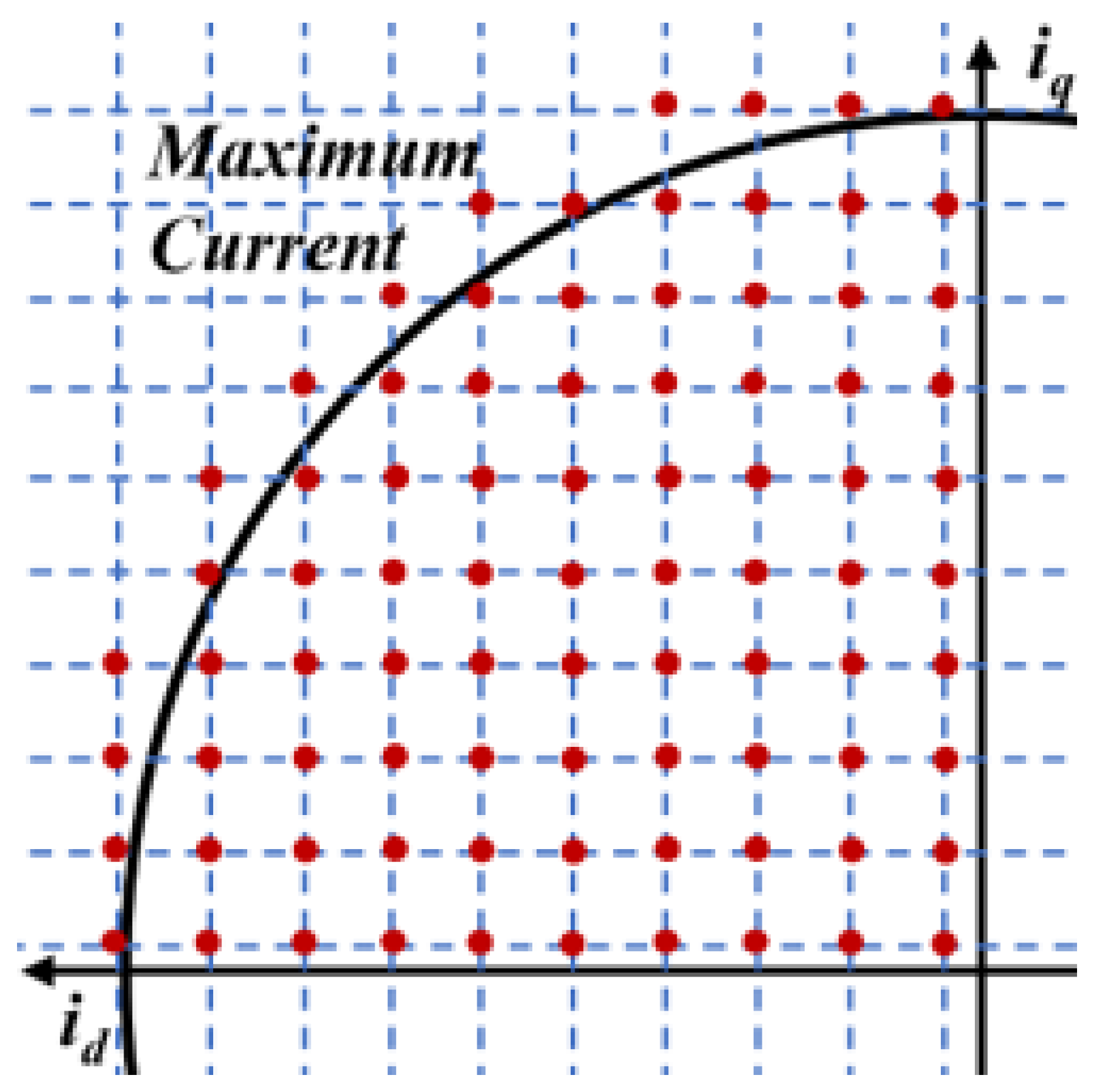
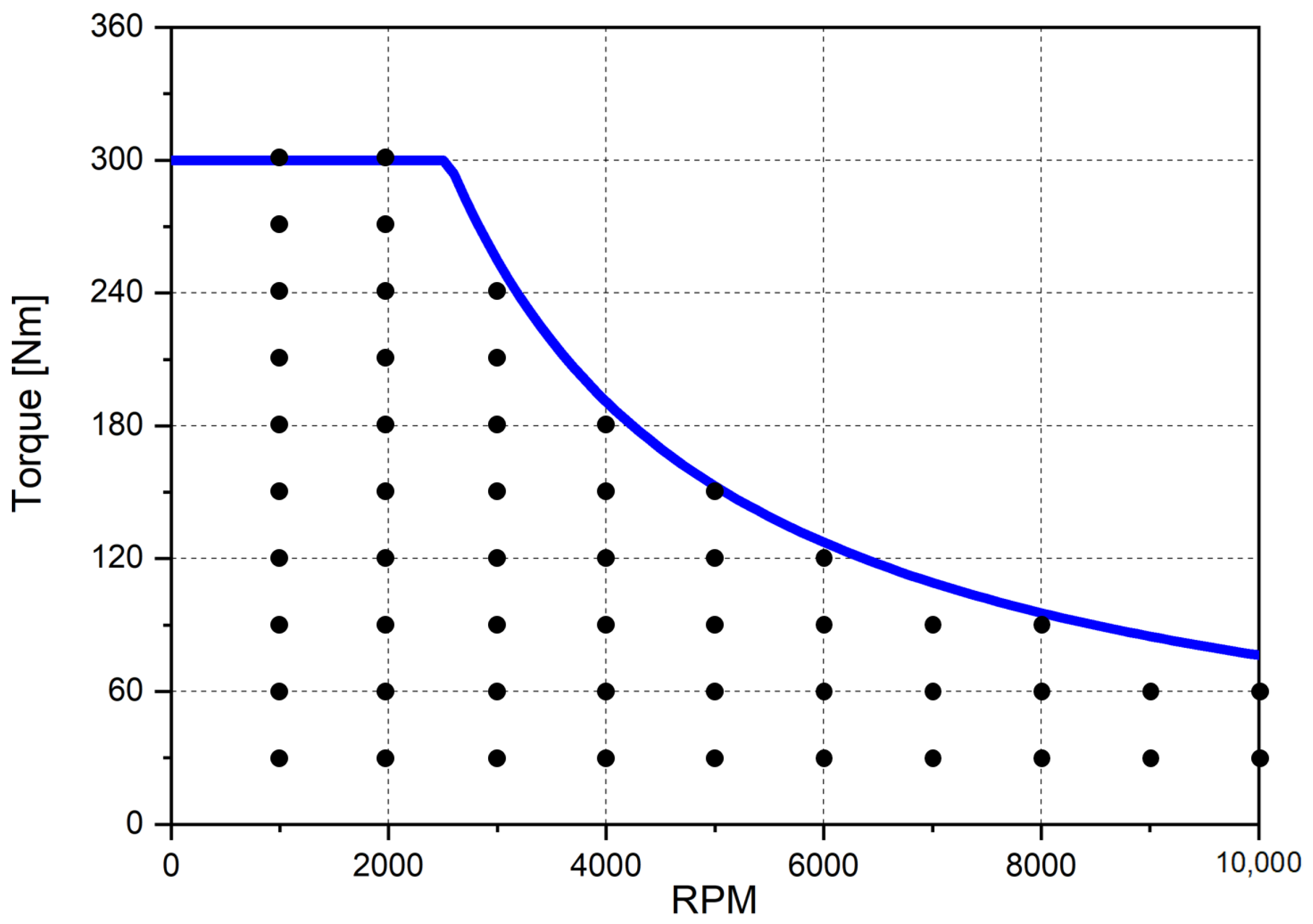
3.1. Composing a Data Map of the Analyzed Motor
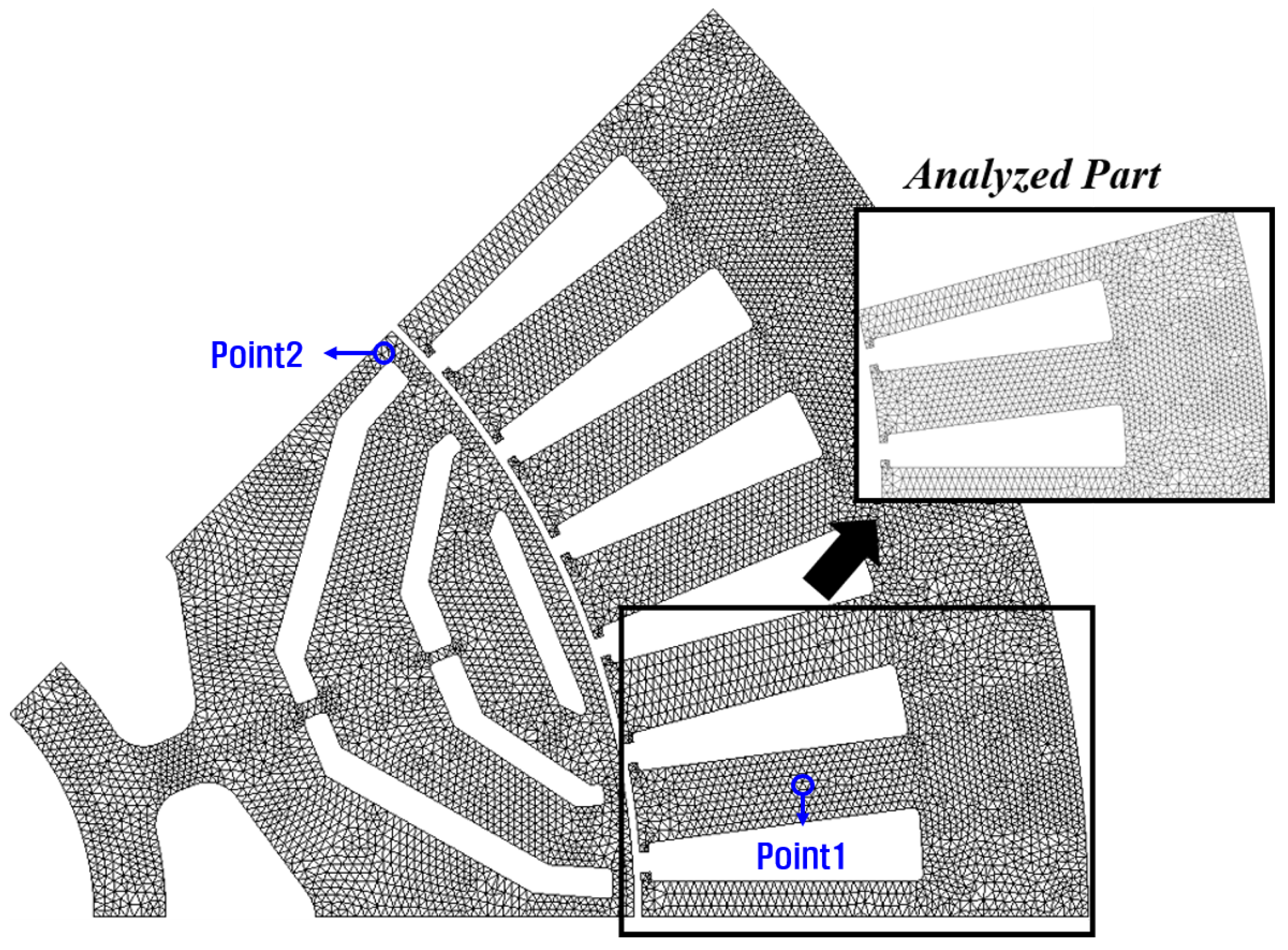
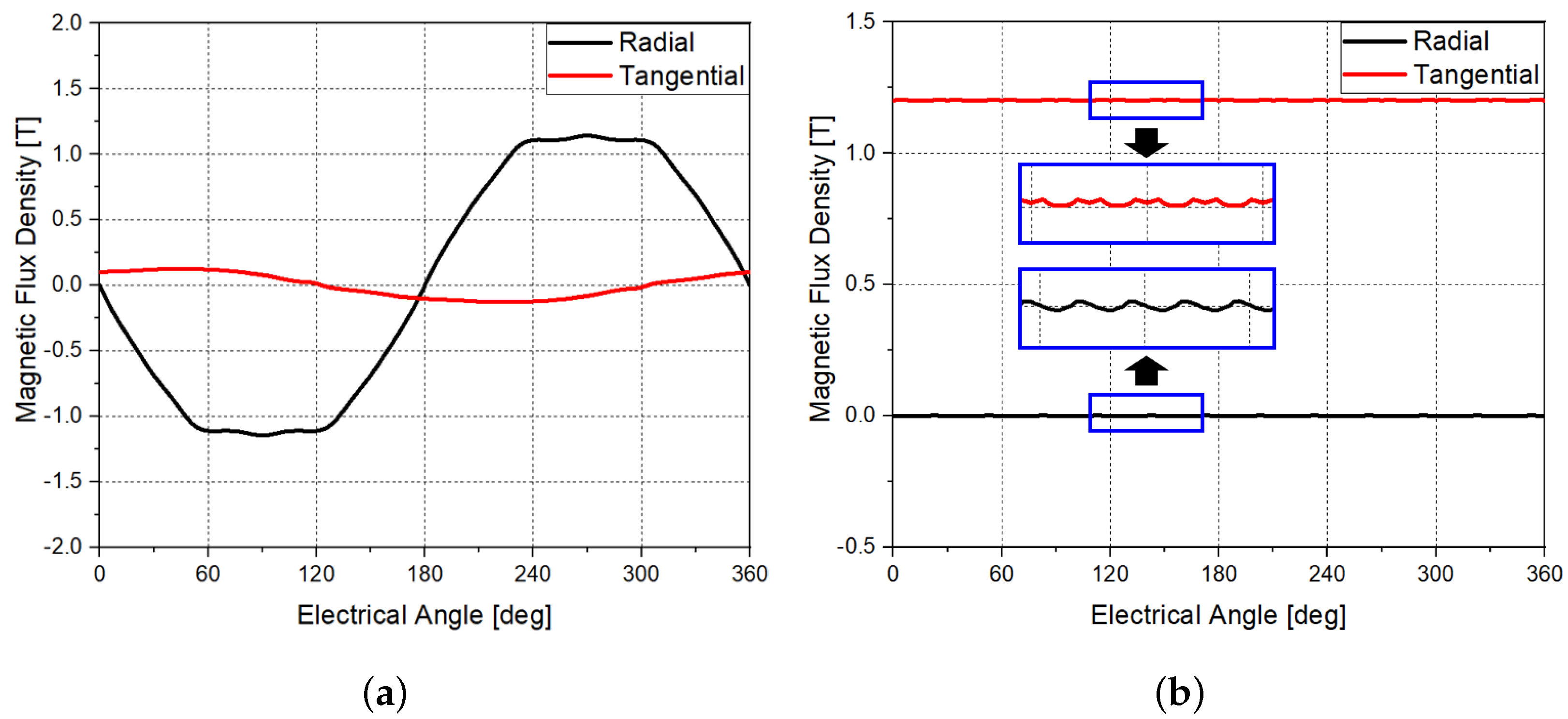
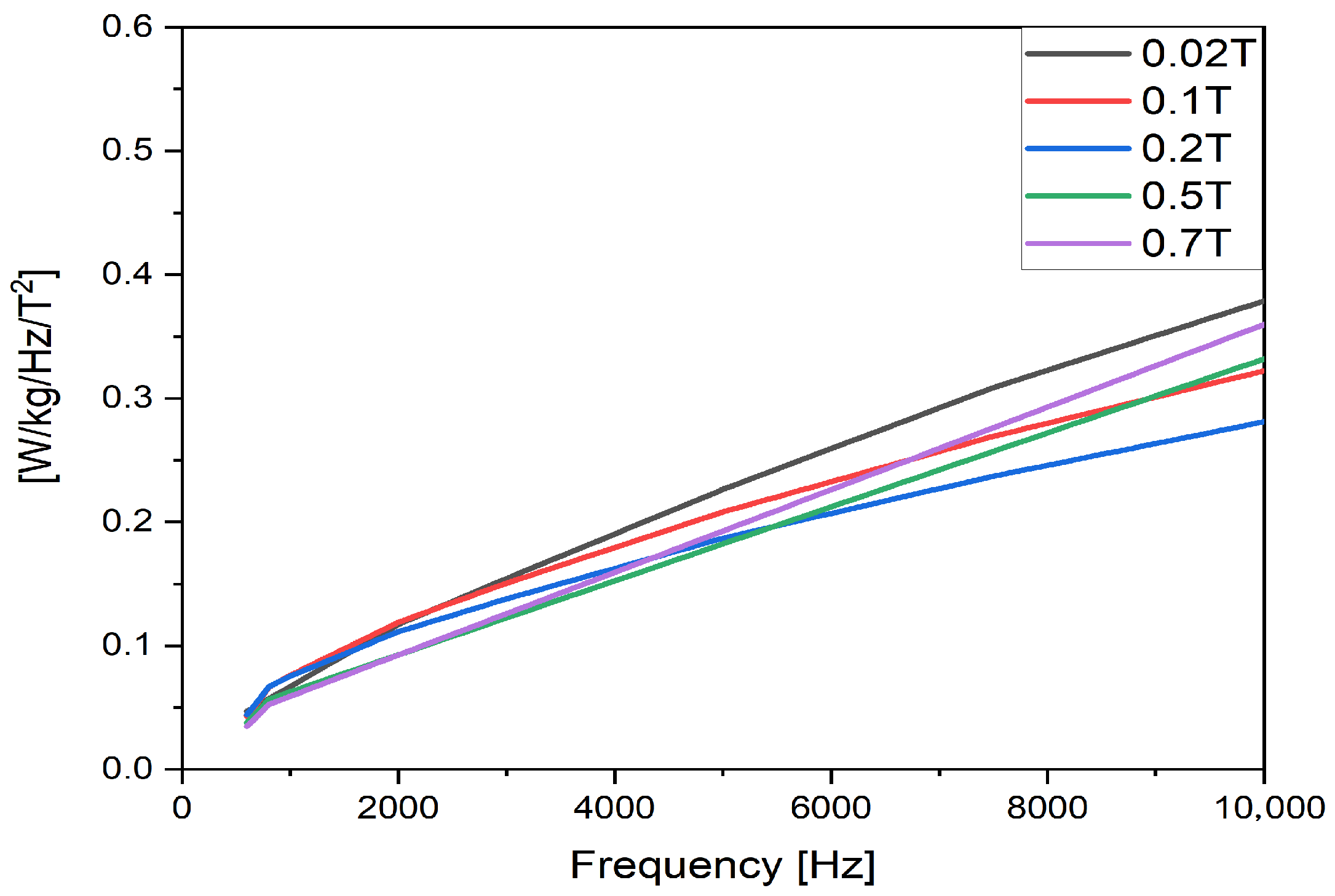
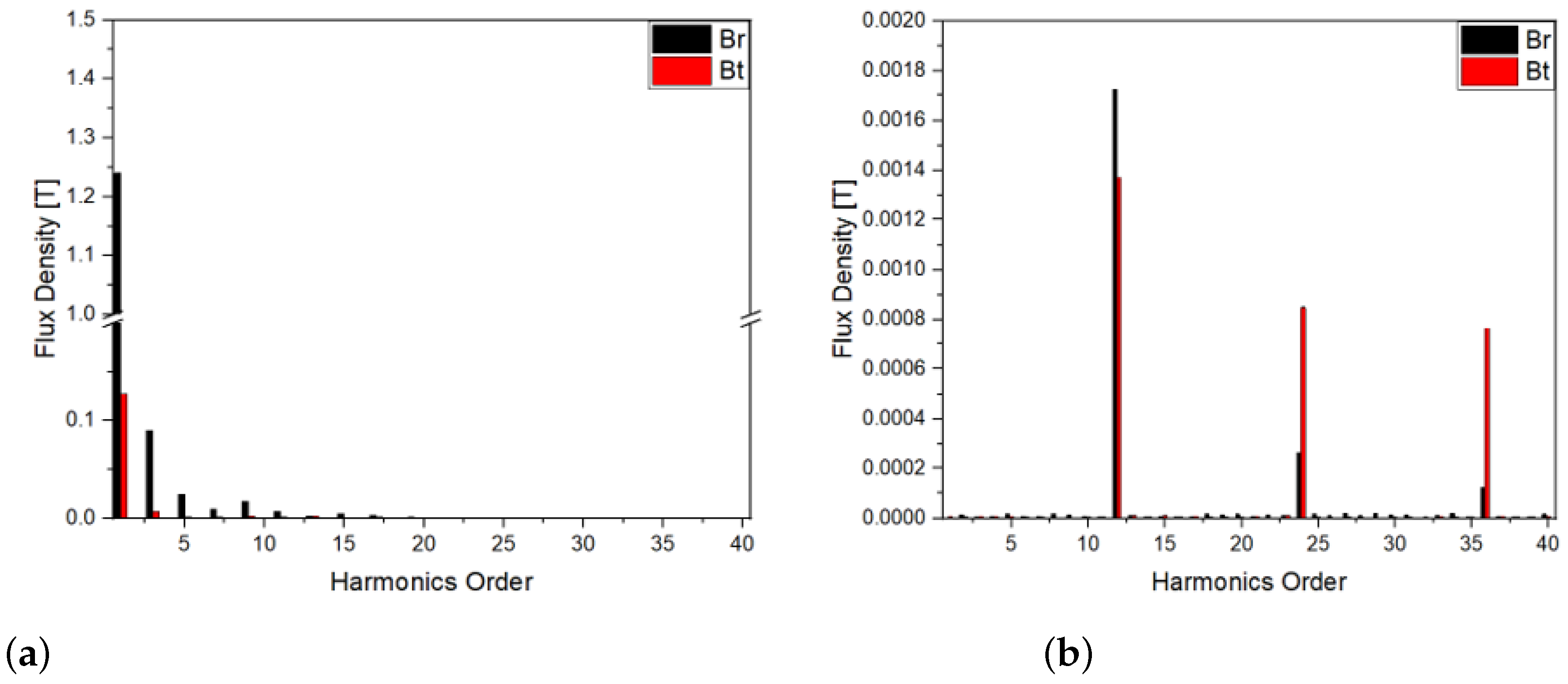
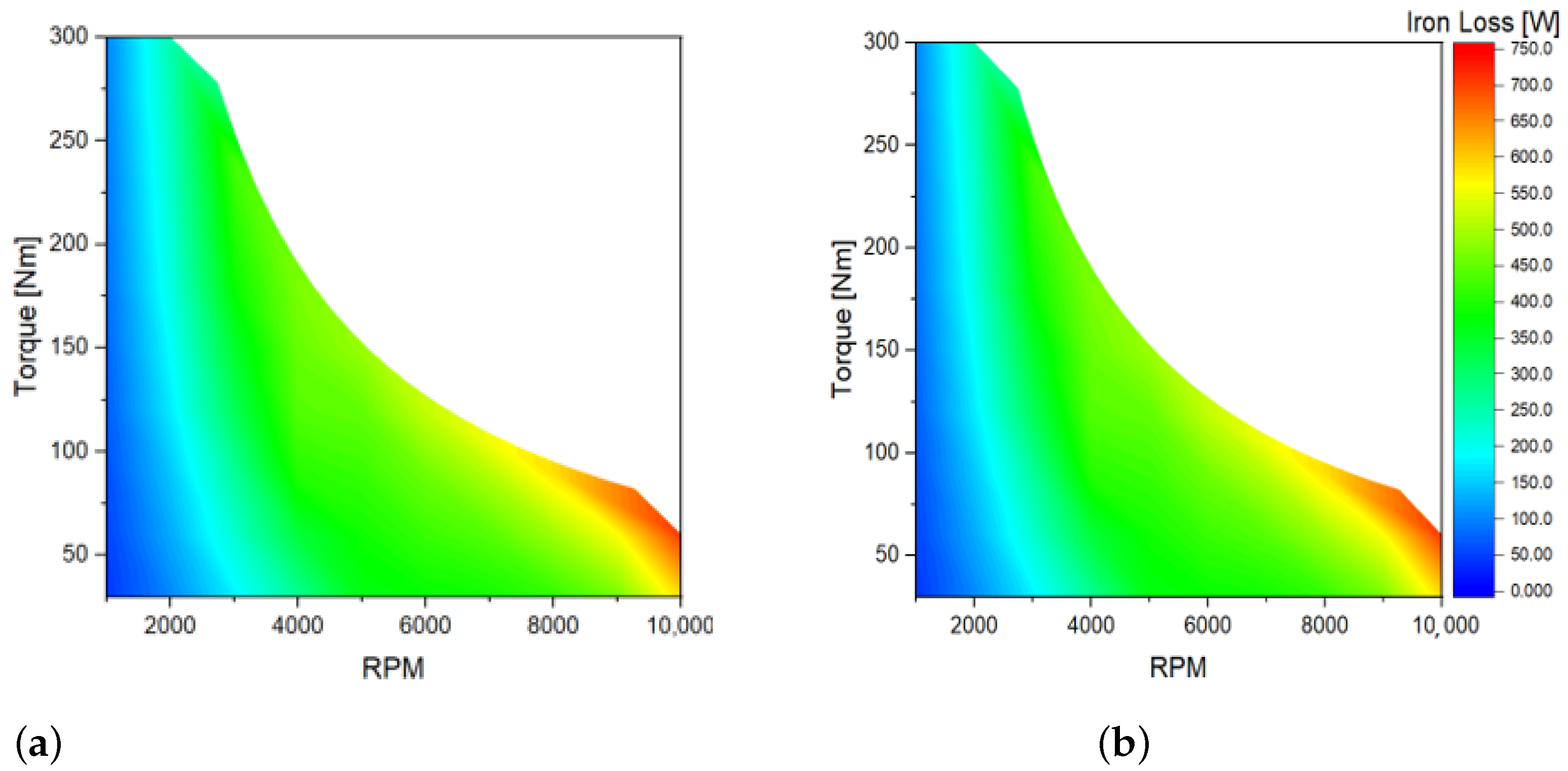
3.2. Calculating Iron Loss Using the Harmonic Loss Method
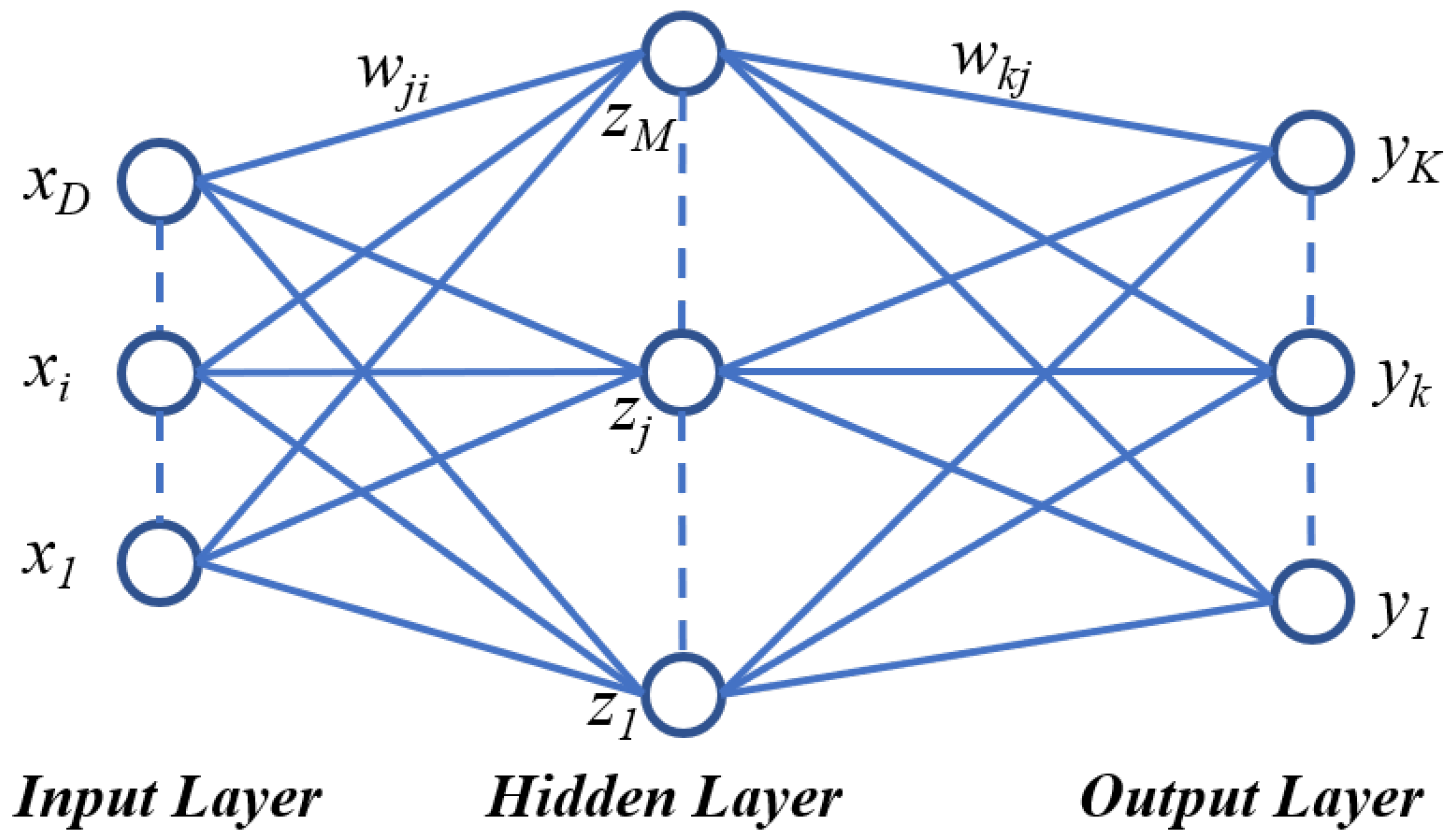
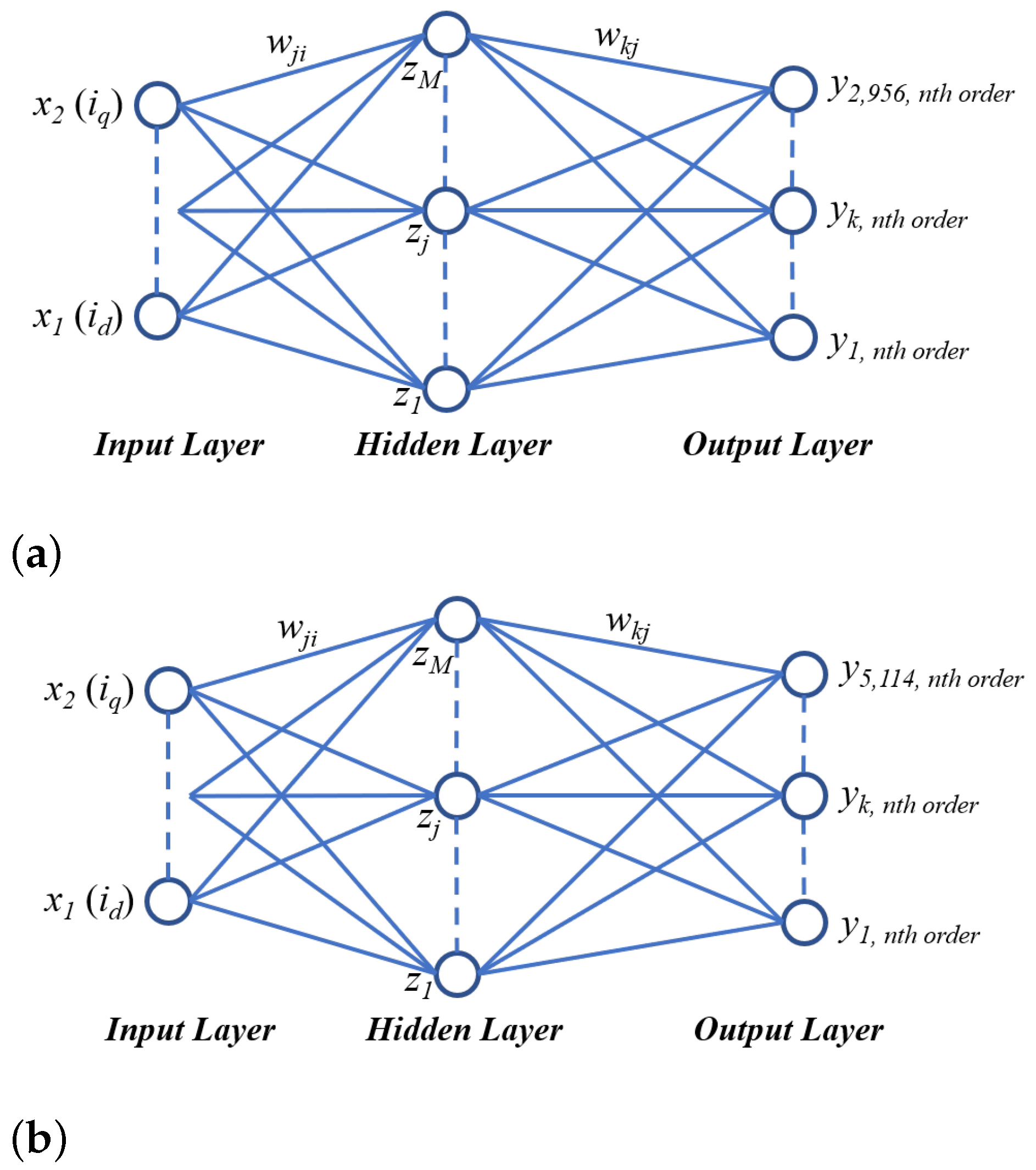
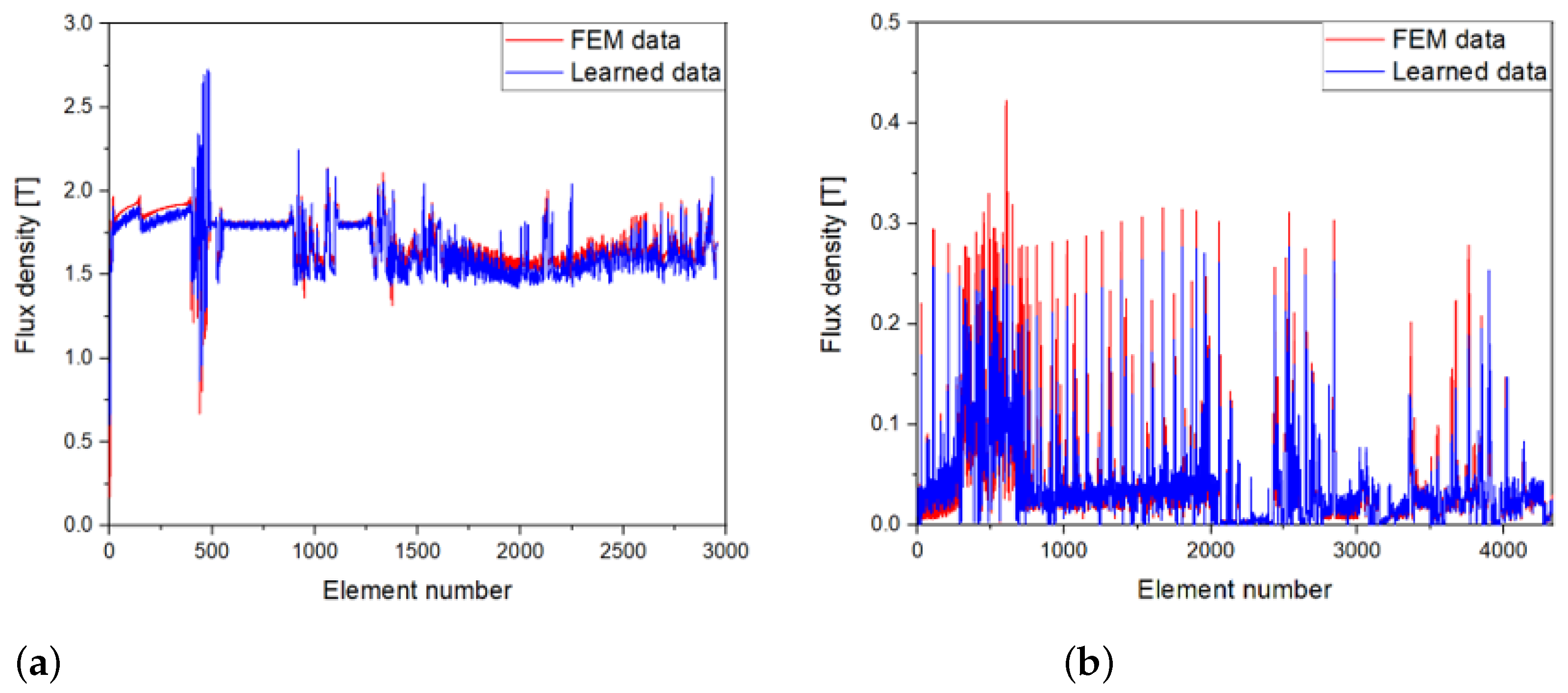
3.3. Learning Process for Flux Density Based on the NN
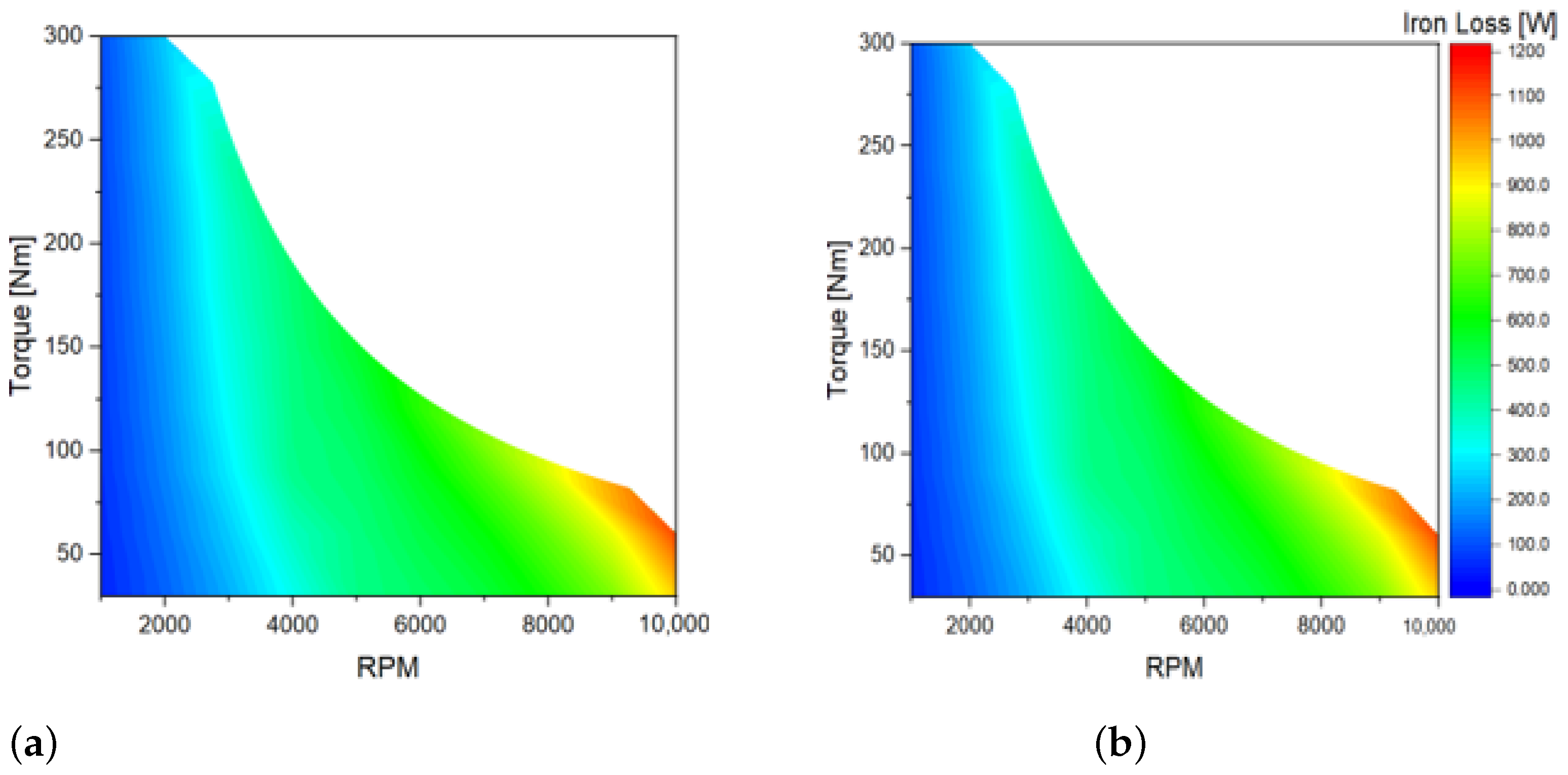
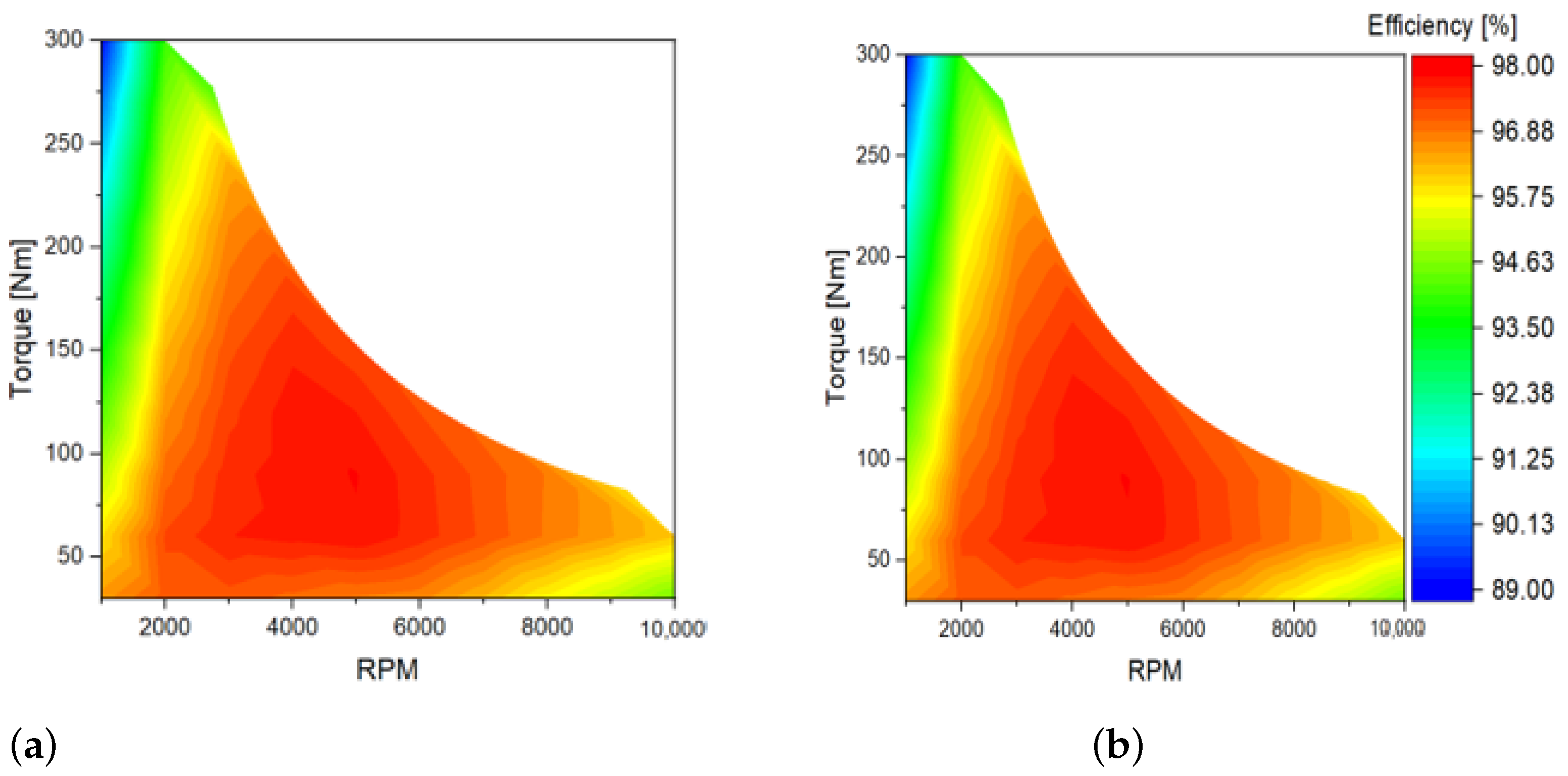
4. Results of the Proposed Method
5. Additional Analysis for Validation of the Proposed Method by Applying Modified Model
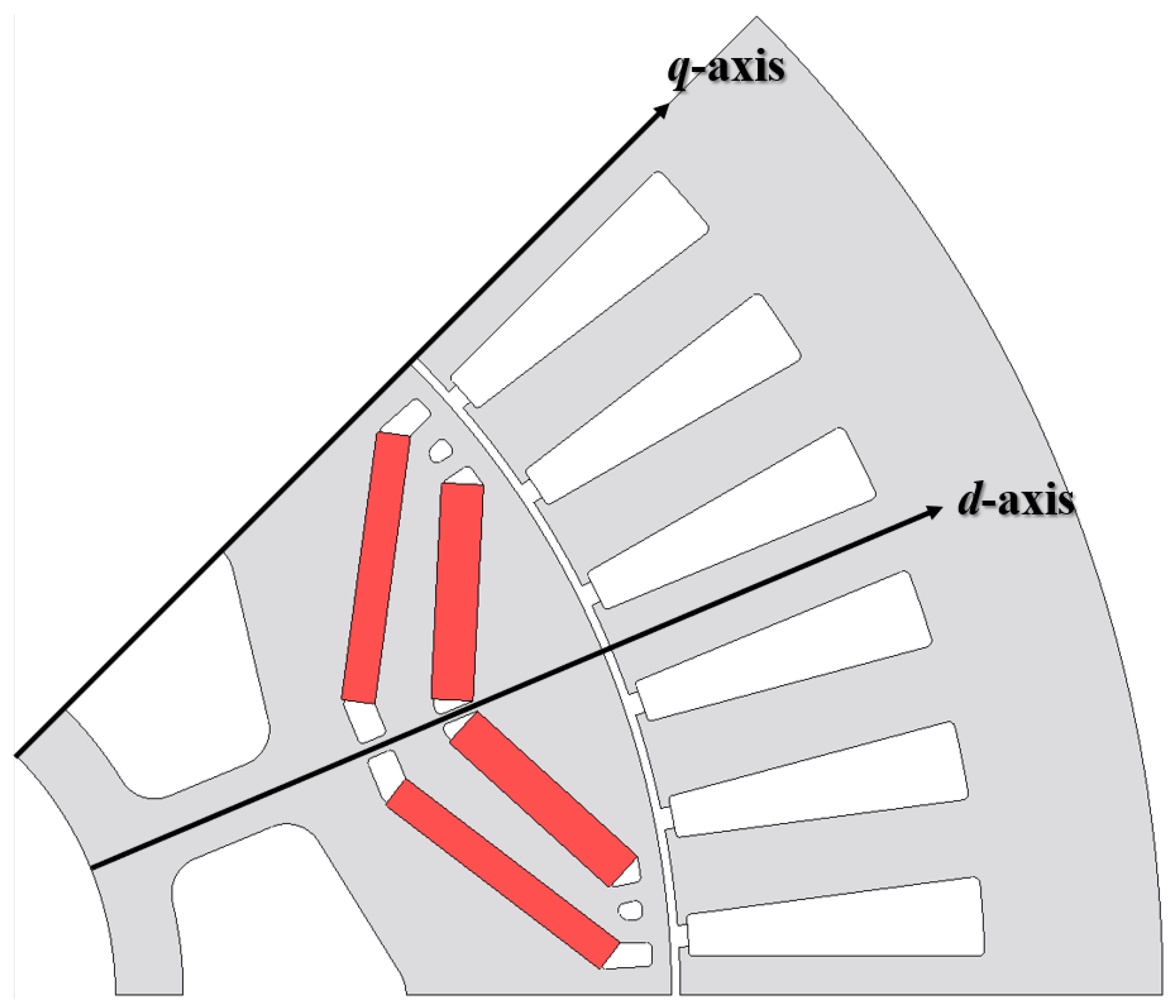
5.1. Configuration of Modified Model
5.2. Analysis and Validation of the Proposed Method
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Chau, K.T.; Chan, C.C.; Liu, C. Overview of permanent-magnet brushless drives for electric and hybrid electric vehicles. IEEE Trans. Ind. Electron. 2008, 55, 2246–2257. [Google Scholar] [CrossRef] [Green Version]
- Seo, J.H.; Kwak, S.Y.; Jung, S.Y.; Lee, C.G.; Chung, T.K.; Jung, H.K. A Research on Iron Loss of IPMSM With a Fractional Number of Slot Per Pole. IEEE Trans. Magn. 2009, 45, 1824–1827. [Google Scholar] [CrossRef]
- Dutta, R.; Rahman, M.F. Design and analysis of an interior permanent magnet (IPM) machine with very wide constant power operation range. IEEE Trans. Energy Convers. 2008, 23, 25–33. [Google Scholar] [CrossRef]
- Jung, H.C.; Park, G.J.; Kim, D.J.; Jung, S.Y. Optimal Design and Validation of IPMSM for Maximum Efficiency Distribution Compatible to Energy Consumption Areas of HD-EV. IEEE Trans. Magn. 2017, 53. [Google Scholar] [CrossRef]
- Chen, X.; Wang, J.B.; Sen, B.; Lazari, P.; Sun, T.F. A High-Fidelity and Computationally Efficient Model for Interior Permanent-Magnet Machines Considering the Magnetic Saturation, Spatial Harmonics, and Iron Loss Effect. IEEE Trans. Ind. Electron. 2015, 62, 4044–4055. [Google Scholar] [CrossRef]
- Zhu, S.; Wang, H.; Zhang, J.W.; Lu, Z.P.; Cheng, M. Fast Calculation of Carrier Harmonic Loss in Permanent Magnet of IPMSM Under PWM VSI Supply Over Entire Working Range. IEEE Trans. Energy Convers. 2019, 34, 1581–1592. [Google Scholar] [CrossRef]
- Krasopoulos, C.T.; Beniakar, M.E.; Kladas, A.G. Multicriteria PM Motor Design Based on ANFIS Evaluation of EV Driving Cycle Efficiency. IEEE Trans. Transport. Electrific. 2018, 4, 525–535. [Google Scholar] [CrossRef]
- Mohammadi, M.H.; Lowther, D.A. A Computational Study of Efficiency Map Calculation for Synchronous AC Motor Drives Including Cross-Coupling and Saturation Effects. IEEE Trans. Magn. 2017, 53. [Google Scholar] [CrossRef]
- Stipetic, S.; Goss, J.; Zarko, D.; Popescu, M. Calculation of Efficiency Maps Using a Scalable Saturated Model of Synchronous Permanent Magnet Machines. IEEE Trans. Ind. Appl. 2018, 54, 4257–4267. [Google Scholar] [CrossRef]
- Asanuma, J.; Doi, S.; Igarashi, H. Transfer Learning through Deep Learning: Application to Topology Optimization of Electric Motor. IEEE Trans. Magn. 2020, 56. [Google Scholar] [CrossRef]
- Qian, W.; Panda, S.K.; Xu, J.X. Speed ripple minimization in PM synchronous motor using iterative learning control. IEEE Trans. Energy Convers. 2005, 20, 53–61. [Google Scholar] [CrossRef]
- Kao, I.H.; Wang, W.J.; Lai, Y.H.; Perng, J.W. Analysis of Permanent Magnet Synchronous Motor Fault Diagnosis Based on Learning. IEEE Trans. Instrum. Meas 2019, 68, 310–324. [Google Scholar] [CrossRef]
- Zaman, S.M.K.; Liang, X.D. An Effective Induction Motor Fault Diagnosis Approach Using Graph-Based Semi-Supervised Learning. IEEE Access 2021, 9, 7471–7482. [Google Scholar] [CrossRef]
- Ionel, D.M.; Popescu, M.; McGilp, M.I.; Miller, T.J.E.; Dellinger, S.J.; Heideman, R.J. Computation of core losses in electrical machines using improved models for laminated steel. IEEE Trans. Ind. Appl. 2007, 43, 1554–1564. [Google Scholar] [CrossRef] [Green Version]
- Yamazaki, K.; Kato, Y. Iron loss analysis of interior permanent-magnet synchronous motors-variation of main loss factors due to driving condition. IEEE Trans. Ind. Appl 2006, 42, 1045–1052. [Google Scholar] [CrossRef]
- Sul, S.K. Control of Electric Machine Drive System; IEEE Press Series on Power Engineering; Wiley-IEEE: Hoboken, NJ, USA, 2011. [Google Scholar]
- Park, G.J.; Son, B.; Kim, Y.J.; Jung, S.Y. Reducing computational time strategy for estimating core loss with spatial and temporal periodicity. In Proceedings of the 2016 IEEE Transportation Electrification Conference and Expo, Asia-Pacific (ITEC Asia-Pacific), Busan, Korea, 1–4 June 2016; pp. 460–464. [Google Scholar]
- Bishop, C.M. Pattern Recognition and Machine Learning; Information Science and Statistics; Springer: New York, NY, USA, 2006; pp. 225–290. [Google Scholar]
- Nicolas, P.R. Scala for Machine Learning, 2nd ed.; Build Systems for Data Processing, Machine Learning, and Deep Learning; Packt: Birmingham, UK, 2017. [Google Scholar]
- Lin, F.J.; Shen, P.H.; Yang, S.L.; Chou, P.H. Recurrent radial basis function network-based fuzzy neural network control for permanent-magnet linear synchronous motor Servo drive. IEEE Trans. Magn. 2006, 42, 3694–3705. [Google Scholar] [CrossRef]
- Lin, F.J.; Wai, R.J.; Duan, R.Y. Neural-network controller for parallel-resonant ultrasonic motor drive. IEEE Trans. Control Syst. Technol. 1999, 7, 494–501. [Google Scholar]
- Wai, R.J.; Yao, J.X.; Lee, J.D. Backstepping Fuzzy-Neural-Network Control Design for Hybrid Maglev Transportation System. IEEE Trans. Neural Netw. Learn. Syst. 2015, 26, 302–317. [Google Scholar] [PubMed]




| Parameter | Value |
|---|---|
| Poles & slots | 8 & 48 |
| Stack length [mm] | 117.2 |
| Outer diameter [mm] | 250 |
| Steel of stator & rotor | 30PNF1600 |
| Magnet grade | N46UH |
| Max. current density [A/mm] | 15 |
| Current limit [A] | 640 |
| Battery voltage [V] | 265 |
| Max. speed [rpm] | 10,000 |
| Parameter | Conventional Method | Proposed Method |
|---|---|---|
| Analyzed Points | 83 | |
| Analysis Step | 21 (1/6 Period) | 61 (1/2 Period) |
| Analysis Time (s) | 10 | 23 |
| Total Time (s) | 830 | 1909 |
| Parameters | Value | |
|---|---|---|
| Training set | 83 | |
| Activation function | Logistic sigmoid | |
| Input unit (d-q currents) | 2 | |
| Output unit (Mesh elements) | Stator | 2956 |
| Rotor | 5114 | |
| Performance | Conventional Method | Proposed Method | |
|---|---|---|---|
| Data map Analysis (s) | 830 | 1909 | |
| Analyzed Points | 53 Points | ||
| Learning Time (s) | - | 420 | |
| Analysis Time (s) | 95 | 5 | |
| Total Time (s) | 5865 | 2594 | |
| Max. Error (%) | Iron Loss | - | 7.3 |
| Efficiency | - | 0.096 | |
| Performance | Conventional Method | Proposed Method | |
|---|---|---|---|
| Data map Analysis (s) | 747 | 1660 | |
| Analyzed Points | 53 Points | ||
| Learning Time (s) | - | 397 | |
| Analysis Time (s) | 92 | 5 | |
| Total Time (s) | 5623 | 2322 | |
| Max. Error (%) | Iron Loss | - | 6.5 |
| Efficiency | - | 0.10 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jun, S.-B.; Kim, C.-H.; Cha, J.; Lee, J.H.; Kim, Y.-J.; Jung, S.-Y. A Novel Method for Establishing an Efficiency Map of IPMSMs for EV Propulsion Based on the Finite-Element Method and a Neural Network. Electronics 2021, 10, 1049. https://doi.org/10.3390/electronics10091049
Jun S-B, Kim C-H, Cha J, Lee JH, Kim Y-J, Jung S-Y. A Novel Method for Establishing an Efficiency Map of IPMSMs for EV Propulsion Based on the Finite-Element Method and a Neural Network. Electronics. 2021; 10(9):1049. https://doi.org/10.3390/electronics10091049
Chicago/Turabian StyleJun, Sung-Bae, Chan-Ho Kim, JuKyung Cha, Jin Hwan Lee, Yong-Jae Kim, and Sang-Yong Jung. 2021. "A Novel Method for Establishing an Efficiency Map of IPMSMs for EV Propulsion Based on the Finite-Element Method and a Neural Network" Electronics 10, no. 9: 1049. https://doi.org/10.3390/electronics10091049
APA StyleJun, S.-B., Kim, C.-H., Cha, J., Lee, J. H., Kim, Y.-J., & Jung, S.-Y. (2021). A Novel Method for Establishing an Efficiency Map of IPMSMs for EV Propulsion Based on the Finite-Element Method and a Neural Network. Electronics, 10(9), 1049. https://doi.org/10.3390/electronics10091049







