Theoretical Study of the Input Impedance and Electromagnetic Field Distribution of a Dipole Antenna Printed on an Electrical/Magnetic Uniaxial Anisotropic Substrate
Abstract
1. Introduction
2. Analytical Formulation
3. Method of Solution
- 1st region:
- 2nd region:where and are the Fourier transforms of the current densities, and
4. Fields Computations
5. Numerical Results
5.1. Validation
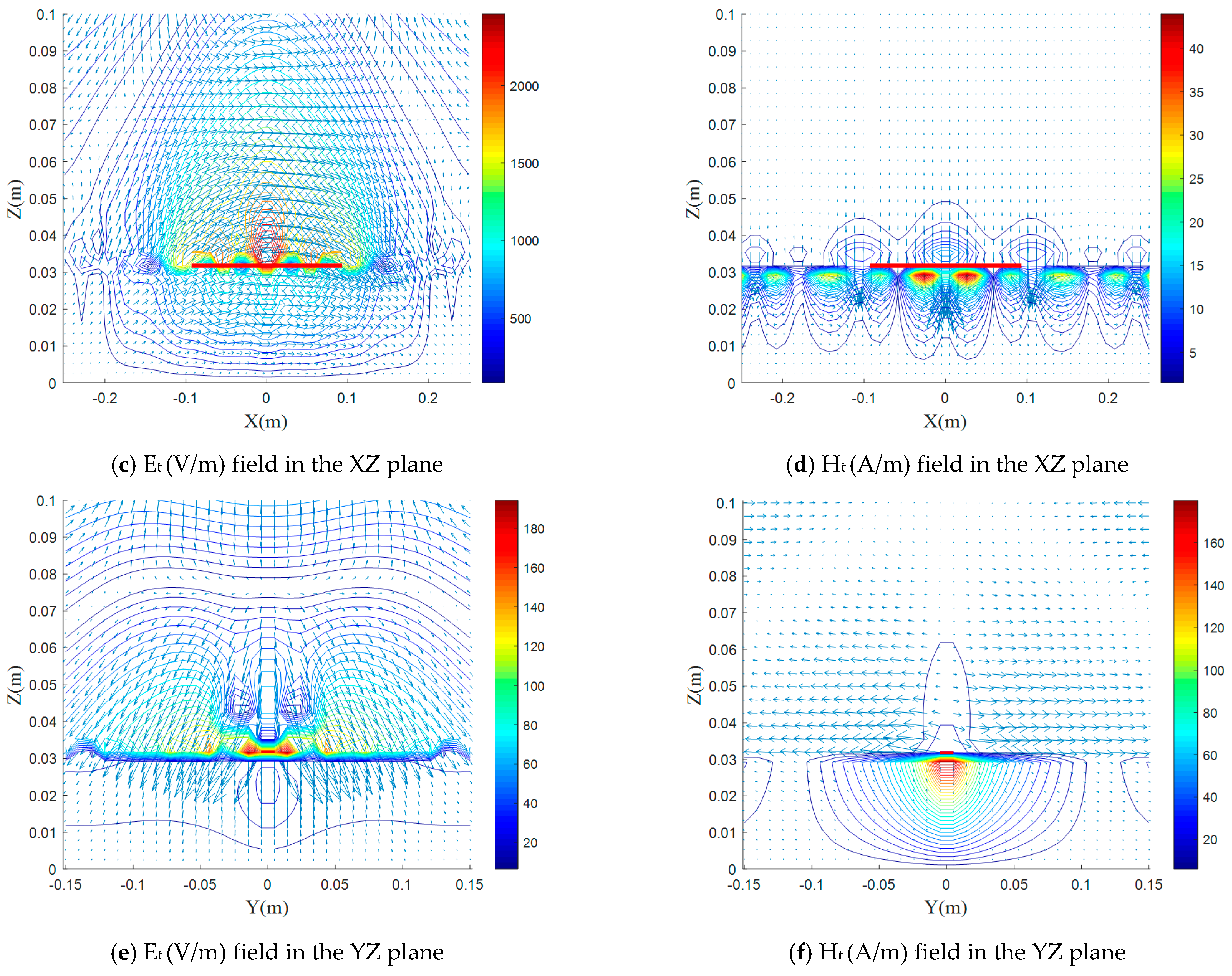
5.2. Electromagnetic-Field Distributions in Isotropic Case
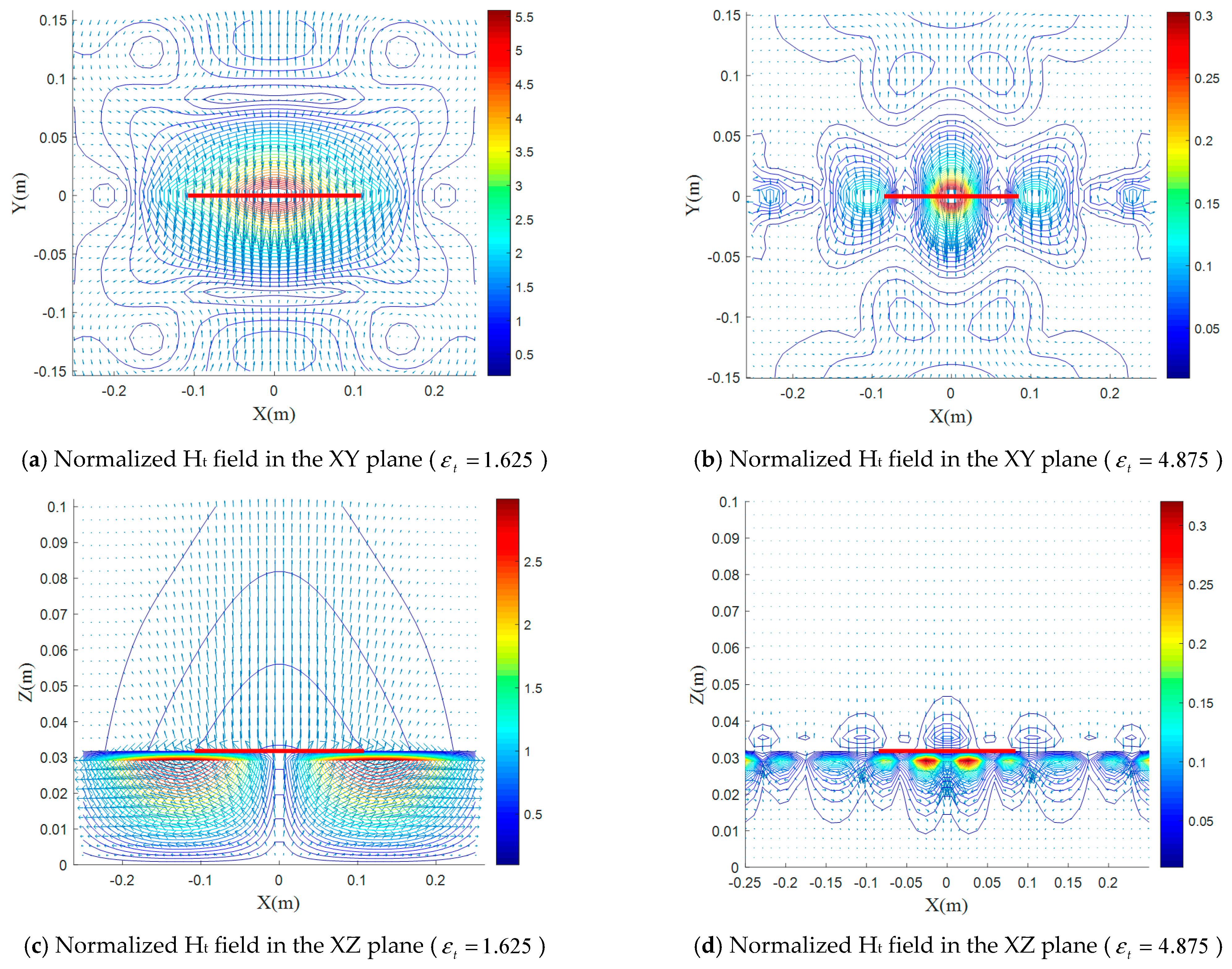
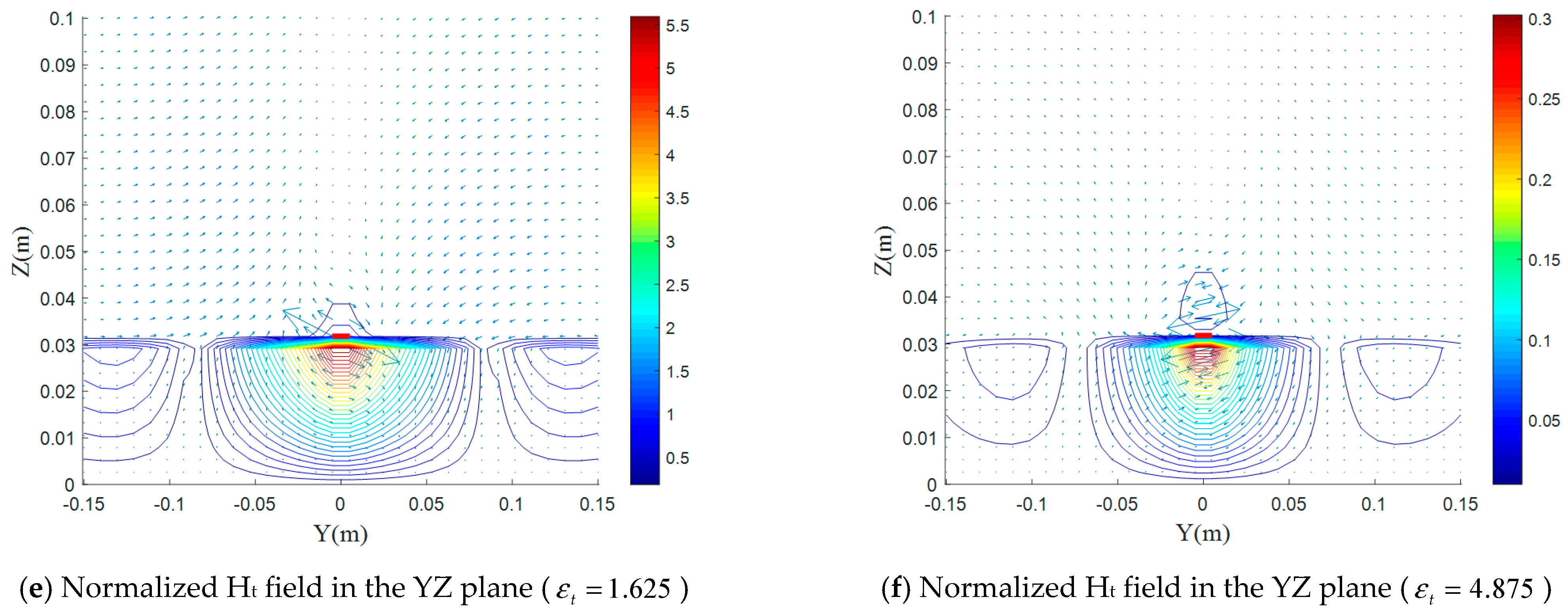
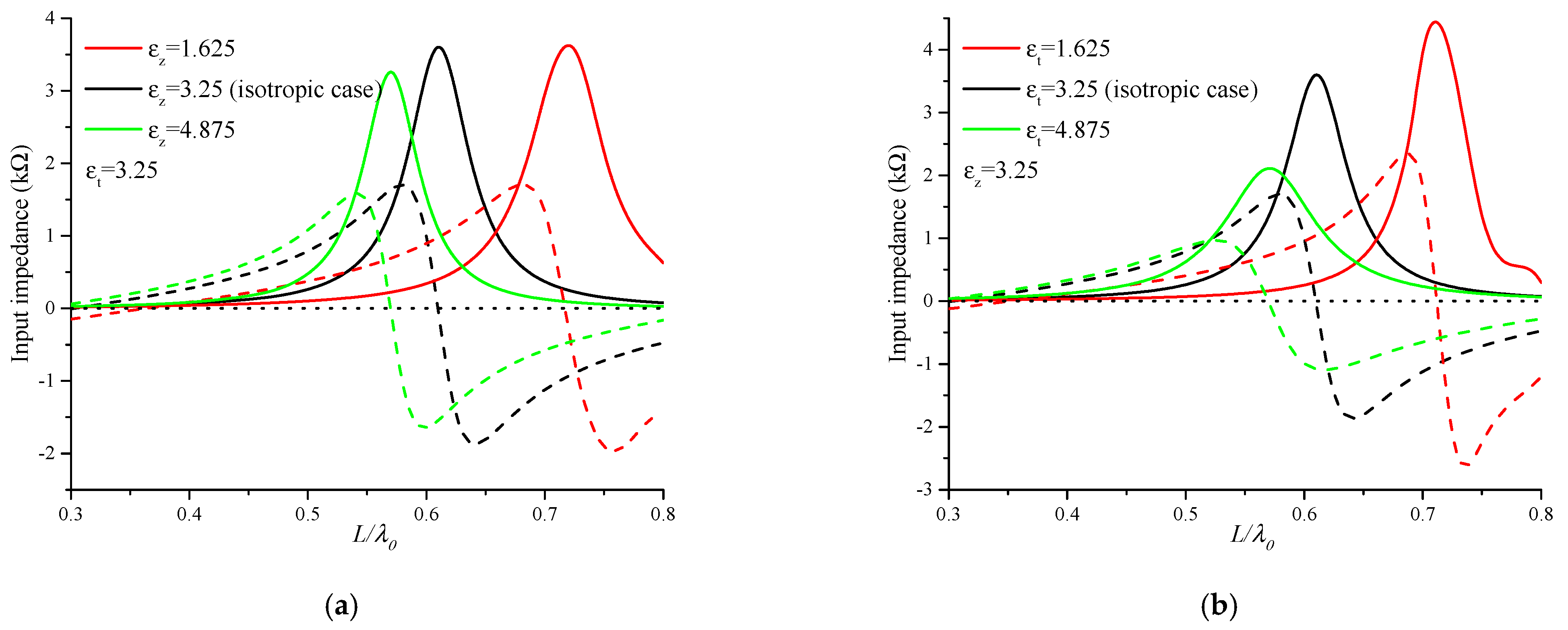
5.3. Effect of the Electrical Uniaxial Anisotropy on the Electromagnetic-Field Distributions
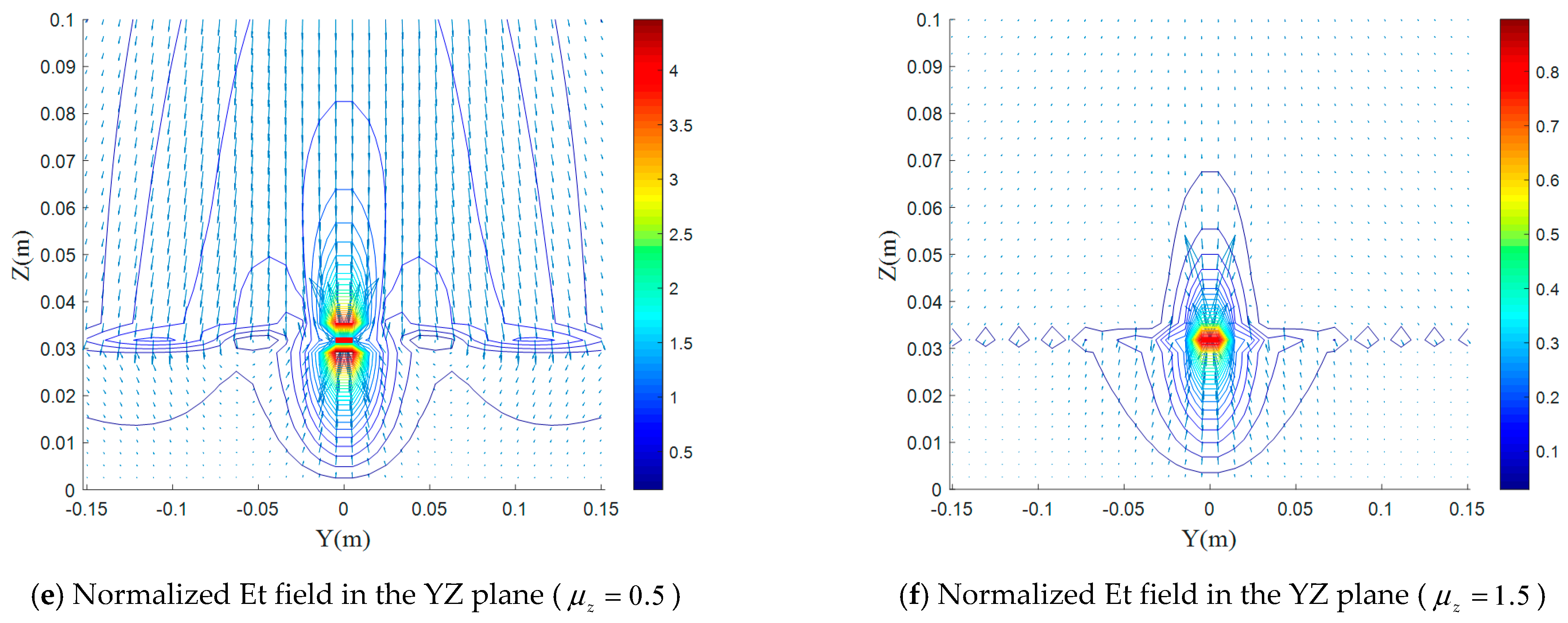
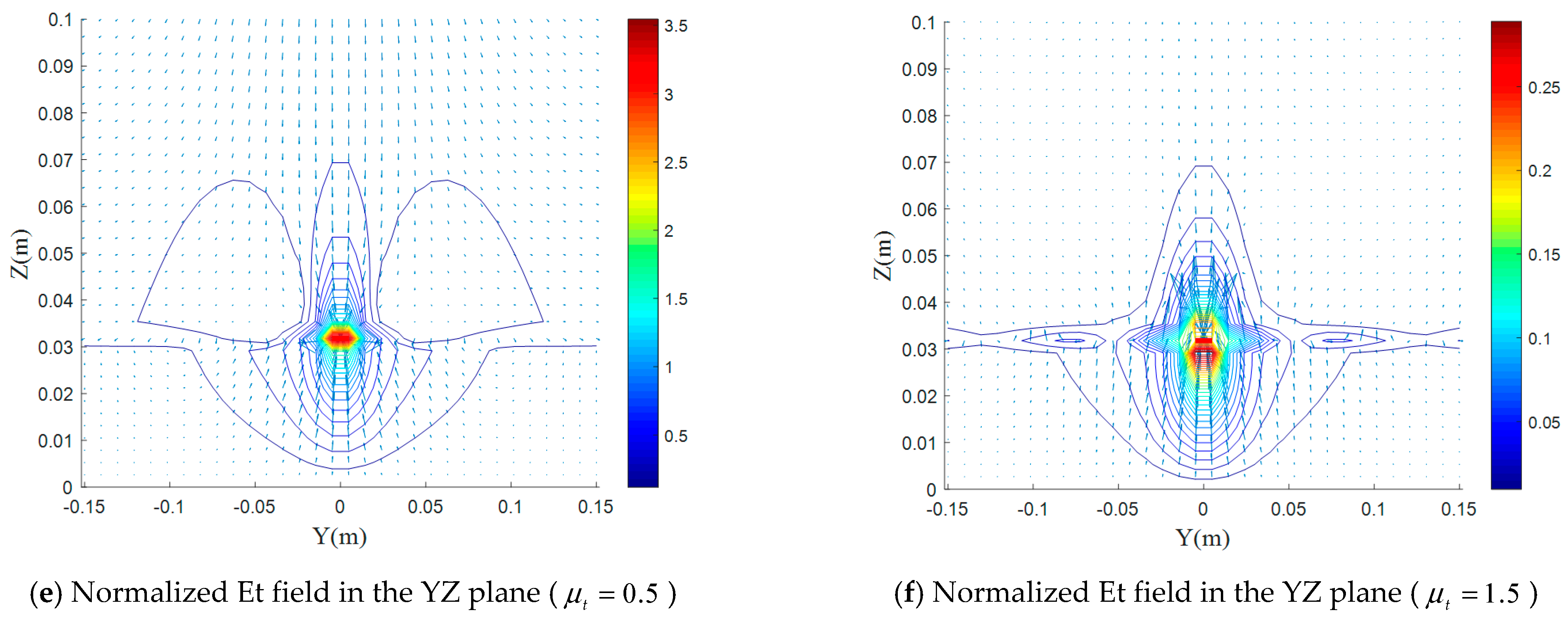
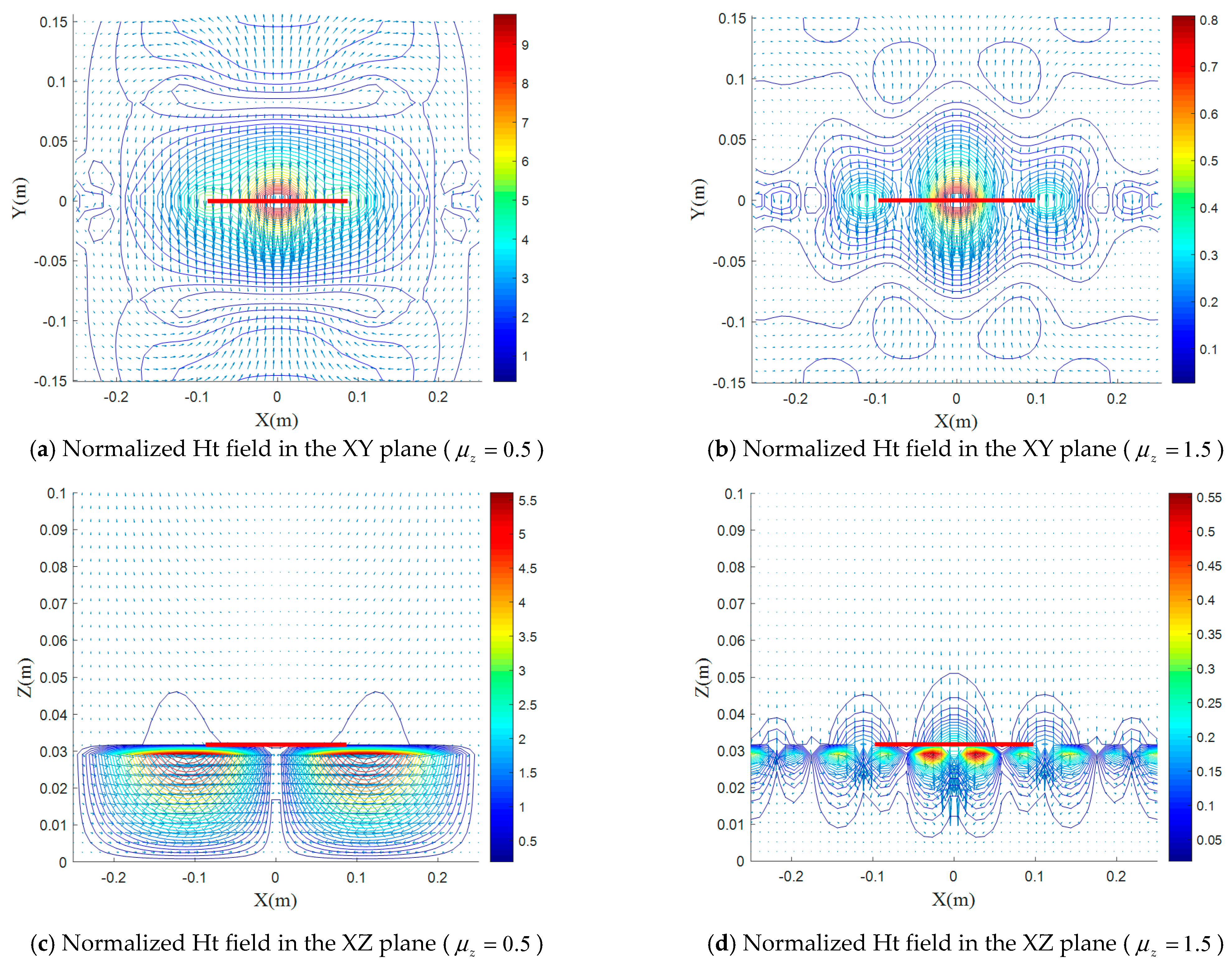
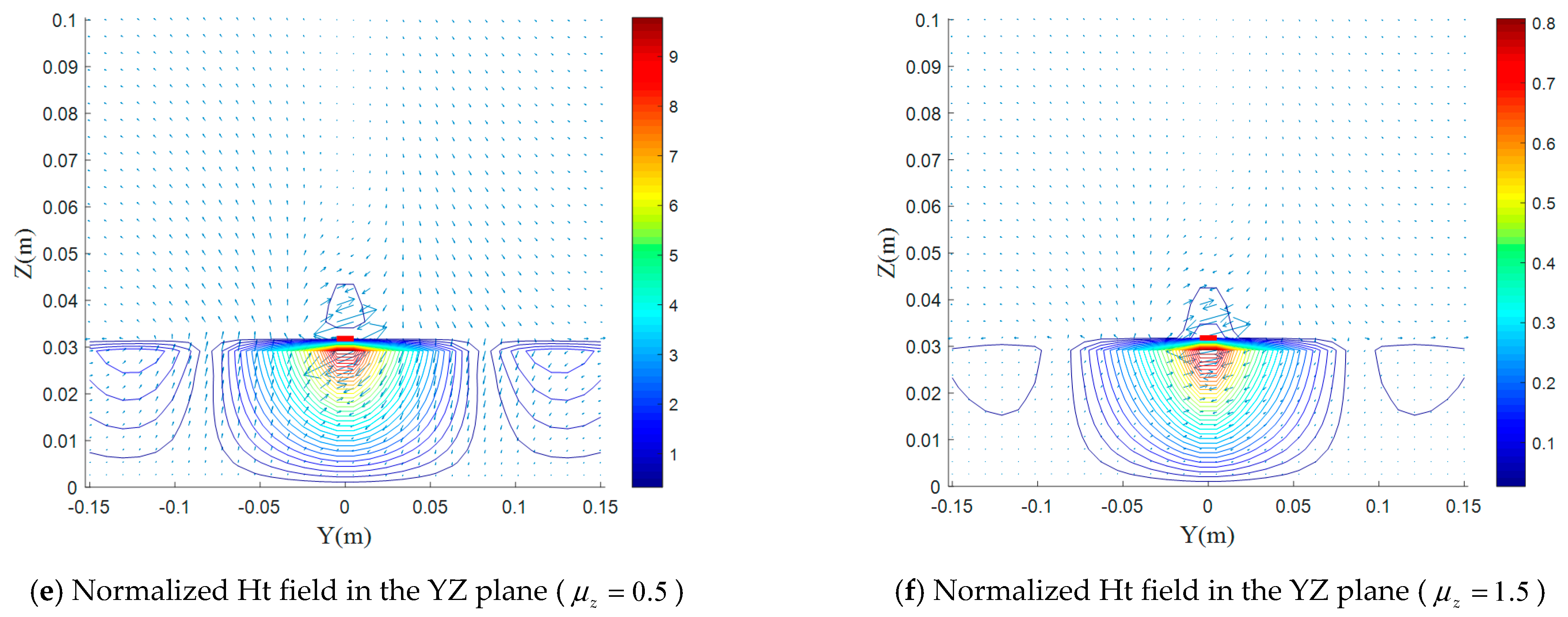
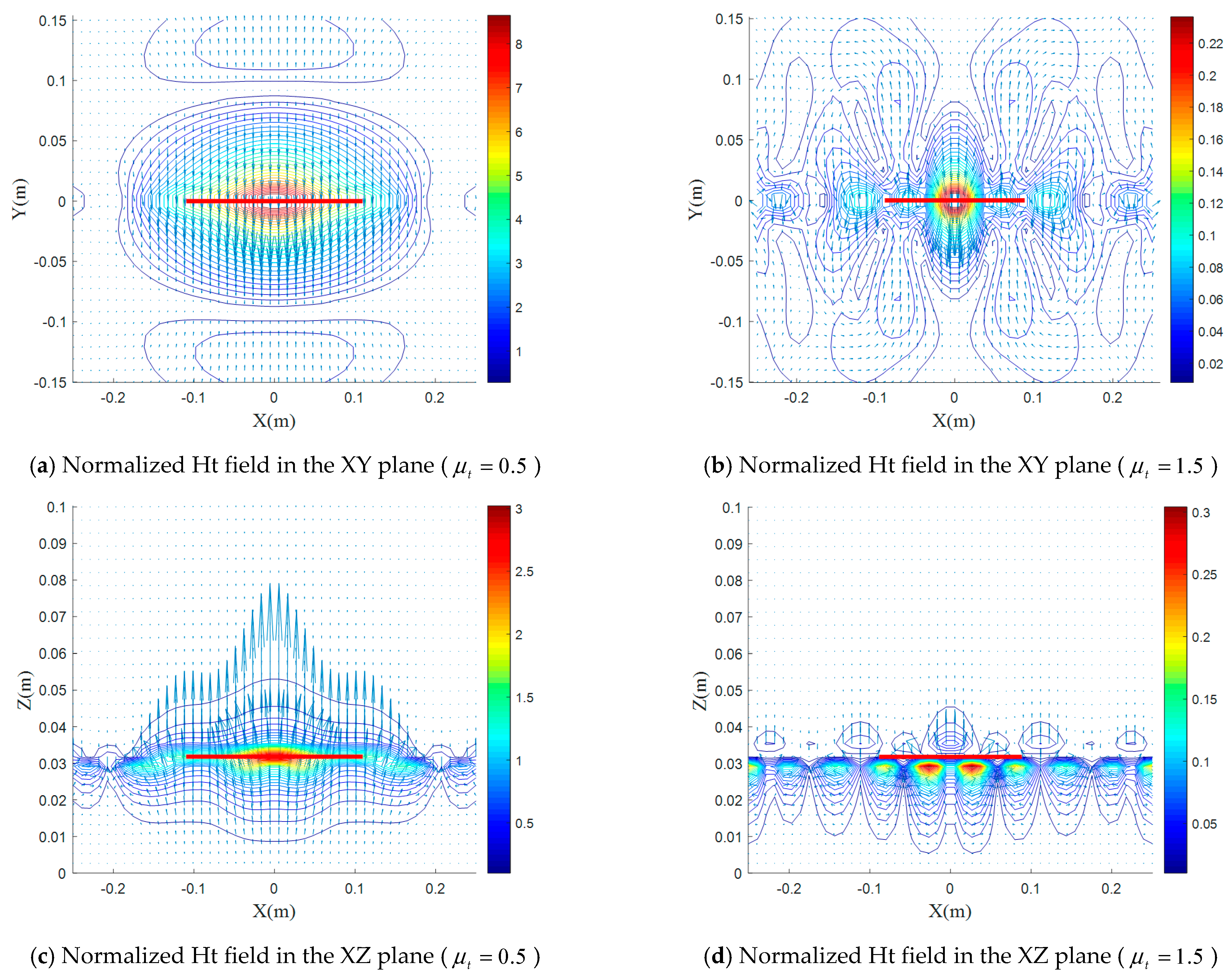
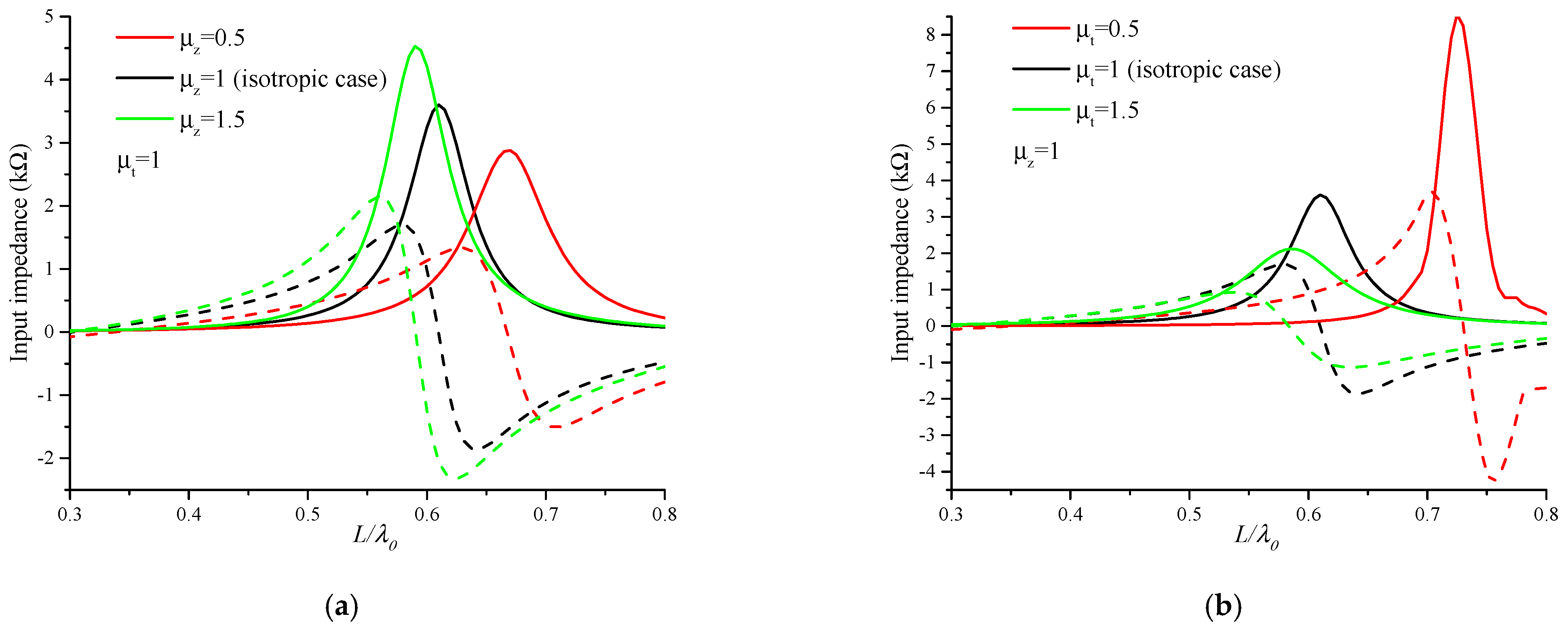
5.4. Effect of the Magnetic Uniaxial Anisotropy on Electromagnetic-Field Distributions
5.5. Effect of the Uniaxial Anisotropy on Input Impedance
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kirilenko, A.A.; Steshenko, S.O.; Derkach, V.N.; Prikolotin, S.A.; Kulik, D.Y.; Prosvirnin, S.; Mospan, L.P. Rotation of the polarization plane by double-layer planar-chiral structures. Review of the results of theoretical and experimental studies. Radioelectron. Commun. Syst. 2017, 60, 193–205. [Google Scholar] [CrossRef]
- Akdagli, A. Behaviour of Electromagnetic Waves in Different Media and Structures, 1st ed.; BoD–Books on Demand: Rijeka, Croatia, 2011. [Google Scholar]
- Guo, B. Photonic band gap structures of obliquely incident electromagnetic wave propagation in a one-dimension absorptive plasma photonic crystal. Phys. Plasmas 2009, 16, 043508. [Google Scholar] [CrossRef]
- Krowne, C.M. Left-handed material anisotropy effect on guided wave electromagnetic fields. J. Appl. Phys. 2006, 99, 044914. [Google Scholar] [CrossRef]
- Krowne, C.M.; Daniel, M. Electromagnetic field behavior in dispersive isotropic negative phase velocity/negative refractive index guided wave structures compatible with millimeter-wave monolithic integrated circuits. J. Nanomater. 2007, 2007, 054568. [Google Scholar] [CrossRef]
- Krowne, C.M. Electromagnetic-field theory and numerically generated results for propagation in left-handed guided-wave single-microstrip structures. IEEE Trans. Microw. Theory Tech. 2003, 51, 2269–2283. [Google Scholar] [CrossRef]
- Krowne, C.M. Electromagnetic distributions demonstrating asymmetry using a spectral-domain dyadic Green’s function for ferrite microstrip guided-wave structures. IEEE Trans. Microw. Theory Tech. 2005, 53, 1345–1361. [Google Scholar] [CrossRef]
- Zebiri, C.; Lashab, M.; Benabdelaziz, F. Effect of anisotropic magneto-chirality on the characteristics of a microstrip resonator. IET Microw. Antennas Propag. 2010, 4, 446–452. [Google Scholar] [CrossRef]
- Zebiri, C.; Lashab, M.; Benabdelaziz, F. Rectangular microstrip antenna with uniaxial bi-anisotropic chiral substrate–superstrate. IET Microw. Antennas Propag. 2011, 5, 17–29. [Google Scholar] [CrossRef]
- Sayad, D.; Zebiri, C.; Daoudi, S.; Benabdelaziz, F. Analysis of the effect of a gyrotropic anisotropy on the phase constant and characteristic impedance of a shielded microstrip line. Adv. Electromagn. 2019, 8, 15–22. [Google Scholar] [CrossRef]
- Heydari, M.B.; Ahmadvand, A. A novel analytical model for a circularly-polarized; ferrite-based slot antenna by solving an integral equation for the electric field on the circular slot. Waves Random Complex Media 2020, 1–20. [Google Scholar] [CrossRef]
- Lee, W.; Hong, Y.K.; Choi, M.; Won, H.; Lee, J.; Park, S.O.; Yoon, H.S. Ferrite-cored patch antenna with suppressed harmonic radiation. IEEE Trans. Antennas Propag. 2018, 66, 3154–3159. [Google Scholar] [CrossRef]
- Kamra, V.; Dreher, A. Efficient analysis of multiple microstrip transmission lines with anisotropic substrates. IEEE Microw. Wirel. Compon. Lett. 2018, 28, 636–638. [Google Scholar] [CrossRef]
- Buzov, A.L.; Buzova, M.A.; Klyuev, D.S.; Mishin, D.V.; Neshcheret, A.M. Calculating the Input Impedance of a Microstrip Antenna with a Substrate of a Chiral Metamaterial. J. Commun. Technol. Electron. 2018, 63, 1259–1264. [Google Scholar] [CrossRef]
- Klyuev, D.S.; Minkin, M.A.; Mishin, D.V.; Neshcheret, A.M.; Tabakov, D.P. Characteristics of Radiation from a Microstrip Antenna on a Substrate Made of a Chiral Metamaterial. Radiophys. Quantum Electron. 2018, 61, 445–455. [Google Scholar] [CrossRef]
- Hu, Y.; Fang, Y.; Wang, D.; Zhan, Q.; Zhang, R.; Liu, Q.H. The scattering of electromagnetic fields from anisotropic objects embedded in anisotropic multilayers. IEEE Trans. Antennas Propag. 2019, 67, 7561–7568. [Google Scholar] [CrossRef]
- Zebiri, C.; Daoudi, S.; Benabdelaziz, F.; Lashab, M.; Sayad, D.; Ali, N.T.; Abd-Alhameed, R.A. Gyro-chirality effect of bianisotropic substrate on the operational of rectangular microstrip patch antenna. Int. J. Appl. Electromagn. Mech. 2016, 51, 249–260. [Google Scholar] [CrossRef]
- Zebiri, C.; Benabdelaziz, F.; Sayad, D. Surface waves investigation of a bianisotropic chiral substrate resonator. Prog. Electromagn. Res. 2012, 40, 399–414. [Google Scholar] [CrossRef][Green Version]
- Eroglu, A.; Lee, J.K. Far field radiation from an arbitrarily oriented Hertzian dipole in the presence of a layered anisotropic medium. IEEE Trans. Antennas Propag. 2005, 53, 3963–3973. [Google Scholar] [CrossRef]
- Sayad, D.; Benabdelaziz, F.; Zebiri, C.; Daoudi, S.; Abd-Alhameed, R.A. Spectral domain analysis of gyrotropic anisotropy chiral effect on the input impedance of a printed dipole antenna. Prog. Electromagn. Res. 2016, 51, 1–8. [Google Scholar] [CrossRef][Green Version]
- Braaten, B.D.; Rogers, D.A.; Nelson, R.M. Multi-conductor spectral domain analysis of the mutual coupling between printed dipoles embedded in stratified uniaxial anisotropic dielectrics. IEEE Trans. Antennas Propag. 2012, 60, 1886–1898. [Google Scholar] [CrossRef]
- Soares, A.; Fonseca, S.B.D.A.; Giarola, A. The effect of a dielectric cover on the current distribution and input impedance of printed dipoles. IEEE Trans. Antennas Propag. 1984, 32, 1149–1153. [Google Scholar] [CrossRef]
- Nelson, R.M.; Rogers, D.A.; D’Assuncao, A.G. Resonant frequency of a rectangular microstrip patch on several uniaxial substrates. IEEE Trans. Antennas Propag. 1990, 38, 973–981. [Google Scholar] [CrossRef]
- Davidson, D.B.; Aberle, J.T. An introduction to spectral domain method-of-moments formulations. IEEE Antennas Propag. Mag. 2004, 46, 11–19. [Google Scholar] [CrossRef]
- Wait, J. Fields of a horizontal dipole over a stratified anisotropic half-space. IEEE Trans. Antennas Propag. 1966, 14, 790–792. [Google Scholar] [CrossRef]
- Kong, J.A. Electromagnetic fields due to dipole antennas over stratified anisotropic media. Geophysics 1972, 37, 985–996. [Google Scholar] [CrossRef]
- Tang, C.M. Electromagnetic fields due to dipole antennas embedded in stratified anisotropic media. IEEE Trans. Antennas Propag. 1979, 27, 665–670. [Google Scholar] [CrossRef]
- Lee, J.K.; Kong, J.A. Dyadic Green’s functions for layered anisotropic medium. Electromagnetics 1983, 3, 111–130. [Google Scholar] [CrossRef]
- Braaten, B.D.; Nelson, R.M.; Rogers, D.A. Input impedance and resonant frequency of a printed dipole with arbitrary length embedded in stratified uniaxial anisotropic dielectrics. IEEE Antennas Wirel. Propag. Lett. 2009, 8, 806–810. [Google Scholar] [CrossRef]
- Eroglu, A.; Lee, Y.H.; Lee, J.K. Dyadic Green’s functions for multi-layered uniaxially anisotropic media with arbitrarily oriented optic axes. IET Microw. Antennas Propag. 2011, 5, 1779–1788. [Google Scholar] [CrossRef]
- Wang, N.; Wang, G.P. Effective medium theory with closed-form expressions for bi-anisotropic optical metamaterials. Opt. Express 2019, 27, 23739–23750. [Google Scholar] [CrossRef]
- Erturk, V.B.; Rojas, R.G. Efficient analysis of input impedance and mutual coupling of microstrip antennas mounted on large coated cylinders. IEEE Trans. Antennas Propag. 2003, 51, 739–749. [Google Scholar] [CrossRef]
- leukenov, S.K.; Assilbekova, A.M. Surface of wave vectors of electromagnetic waves in anisotropic dielectric media with rhombic symmetry. Telecommun. Radio Eng. 2017, 76, 1231–1238. [Google Scholar] [CrossRef]
- Sayad, D.; Zebiri, C.; Elfergani, I.; Rodriguez, J.; Abobaker, H.; Ullah, A.; Benabdelaziz, F. Complex bianisotropy effect on the propagation constant of a shielded multilayered coplanar waveguide using improved full generalized exponential matrix technique. Electronics 2020, 9, 243. [Google Scholar] [CrossRef]
- Sayad, D.; Zebiri, C.; Elfergani, I.; Rodriguez, J.; Abd-Alhameed, R.A.; Benabdelaziz, F. Analysis of Chiral and Achiral Medium Based Coplanar Waveguide Using Improved Full Generalized Exponential Matrix Technique. Radioengineering 2020, 29, 591–600. [Google Scholar] [CrossRef]
- Zebiri, C.; Sayad, D. Effect of bianisotropy on the characteristic impedance of a shielded microstrip line for wideband impedance matching applications. Waves Random Complex Media 2020, 1–14. [Google Scholar] [CrossRef]
- Nakano, H.; Kerner, S.R.; Alexopoulos, N.G. The moment method solution for printed wire antennas of arbitrary configuration. IEEE Trans. Antennas Propag. 1988, 36, 1667–1674. [Google Scholar] [CrossRef]
- Lee, H.; Tripathi, V.K. Spectral domain analysis of frequency dependent propagation characteristics of planar structures on uniaxial medium. IEEE Trans. Microw. Theory Tech. 1982, 30, 1188–1193. [Google Scholar]
- Harrington, R.F. Field Computation by Moment Methods; IEEE Press, Inc.: New York, NY, USA, 1992. [Google Scholar]
- Itoh, T. Numerical Techniques for Microwave and Millimeter Wave Passive Structures, 1st ed.; John Wiley and Sons: Hoboken, NJ, USA, 1988. [Google Scholar]
- Bianconi, G.; Mittra, R. Efficient Numerical Techniques for Analyzing Microstrip Circuits and Antennas Etched on Layered Media via the Characteristic Basis Function Method. In Computational Electromagnetics; Springer: New York, NY, USA, 2014; pp. 111–148. [Google Scholar]
- Rana, I.; Alexopoulos, N. Current distribution and input impedance of printed dipoles. IEEE Trans. Antennas Propag. 1981, 29, 99–105. [Google Scholar] [CrossRef]
- Braaten, B.D.; Rogers, D.A.; Nelson, R.M. Current distribution of a printed dipole with arbitrary length embedded in layered uniaxial anisotropic dielectrics. In Proceedings of the 2009 SBMO/IEEE MTT-S International Microwave and Optoelectronics Conference (IMOC), Belem, Brazil, 3–6 November 2009; pp. 72–77. [Google Scholar]
- MATLAB, version 2018a; The MathWorks, Inc.: Natick, MA, USA, 2018.
- Codreanu, I.; Boreman, G.D. Influence of dielectric substrate on the responsivity of microstrip dipole-antenna-coupled infrared microbolometers. Appl. Opt. 2002, 41, 1835–1840. [Google Scholar] [CrossRef]








Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bouknia, M.L.; Zebiri, C.; Sayad, D.; Elfergani, I.; Rodriguez, J.; Alibakhshikenari, M.; Abd-Alhameed, R.A.; Falcone, F.; Limiti, E. Theoretical Study of the Input Impedance and Electromagnetic Field Distribution of a Dipole Antenna Printed on an Electrical/Magnetic Uniaxial Anisotropic Substrate. Electronics 2021, 10, 1050. https://doi.org/10.3390/electronics10091050
Bouknia ML, Zebiri C, Sayad D, Elfergani I, Rodriguez J, Alibakhshikenari M, Abd-Alhameed RA, Falcone F, Limiti E. Theoretical Study of the Input Impedance and Electromagnetic Field Distribution of a Dipole Antenna Printed on an Electrical/Magnetic Uniaxial Anisotropic Substrate. Electronics. 2021; 10(9):1050. https://doi.org/10.3390/electronics10091050
Chicago/Turabian StyleBouknia, Mohamed Lamine, Chemseddine Zebiri, Djamel Sayad, Issa Elfergani, Jonathan Rodriguez, Mohammad Alibakhshikenari, Raed A. Abd-Alhameed, Francisco Falcone, and Ernesto Limiti. 2021. "Theoretical Study of the Input Impedance and Electromagnetic Field Distribution of a Dipole Antenna Printed on an Electrical/Magnetic Uniaxial Anisotropic Substrate" Electronics 10, no. 9: 1050. https://doi.org/10.3390/electronics10091050
APA StyleBouknia, M. L., Zebiri, C., Sayad, D., Elfergani, I., Rodriguez, J., Alibakhshikenari, M., Abd-Alhameed, R. A., Falcone, F., & Limiti, E. (2021). Theoretical Study of the Input Impedance and Electromagnetic Field Distribution of a Dipole Antenna Printed on an Electrical/Magnetic Uniaxial Anisotropic Substrate. Electronics, 10(9), 1050. https://doi.org/10.3390/electronics10091050










