The Possibility of Enhanced Power Transfer in a Multi-Terminal Power System through Simultaneous AC–DC Power Transmission
Abstract
:1. Introduction
2. Control Strategy
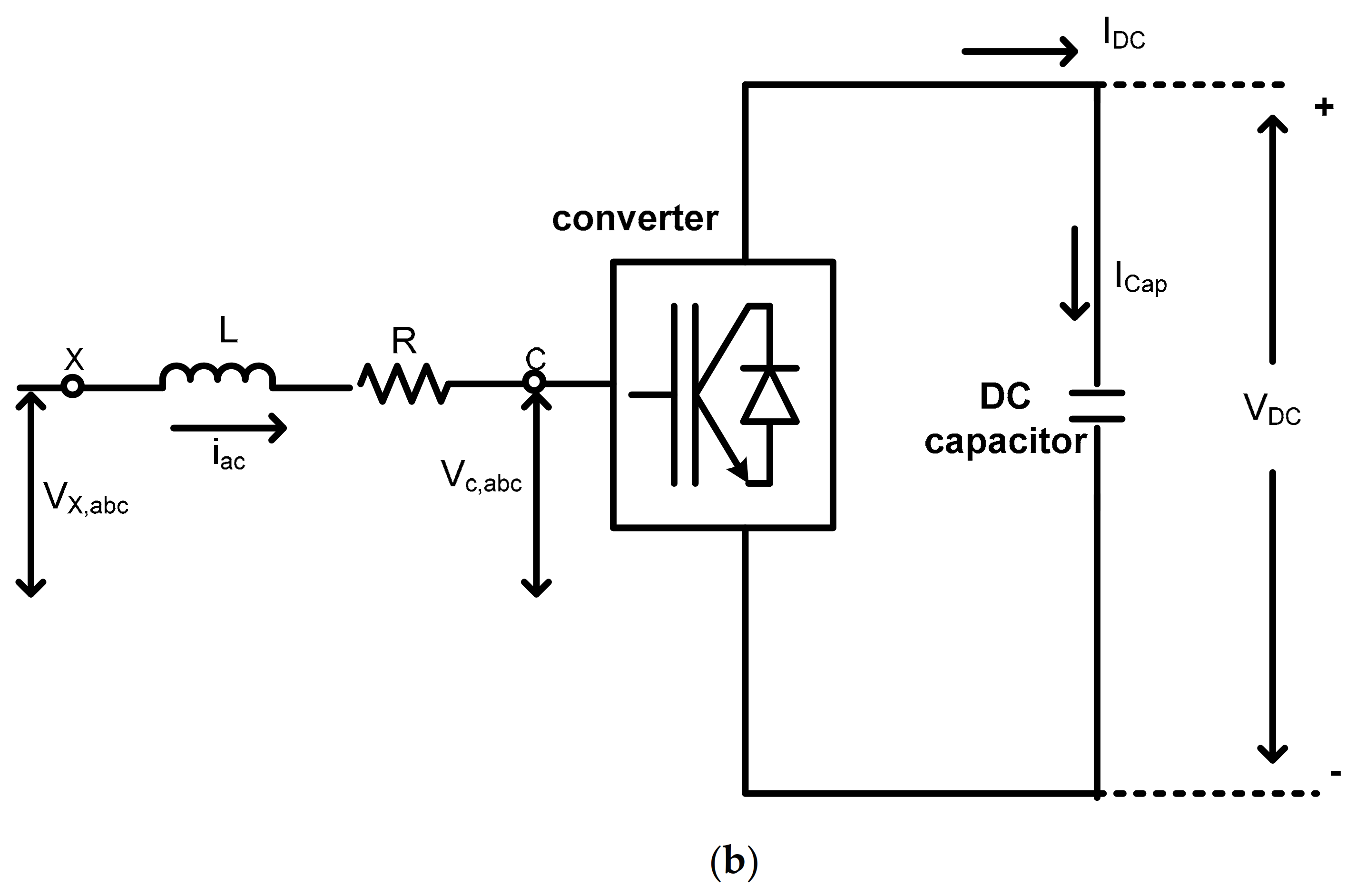
2.1. Equivalent Circuit of Voltage Source Converter
2.2. Control of VSC Connected to Passive Network
2.3. VSC Control Connected to Active AC Network
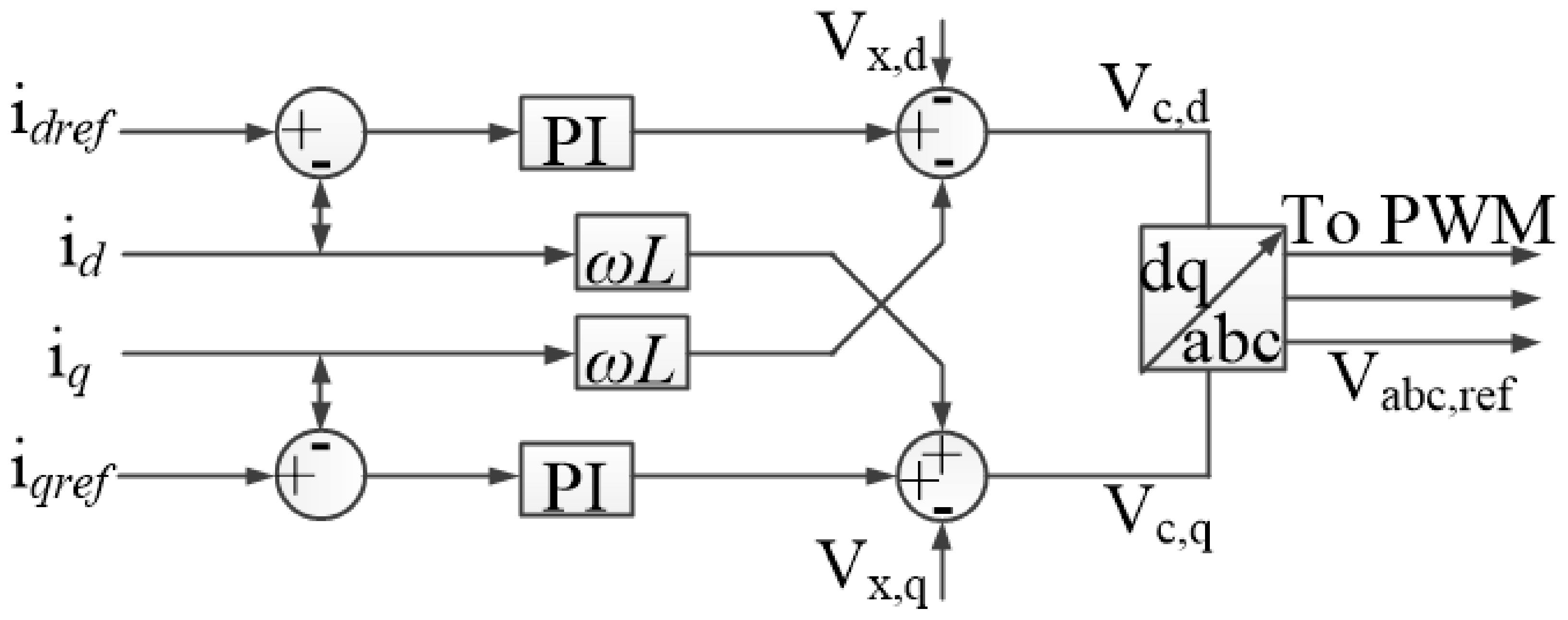
2.4. The Inner and Outer Current Controller
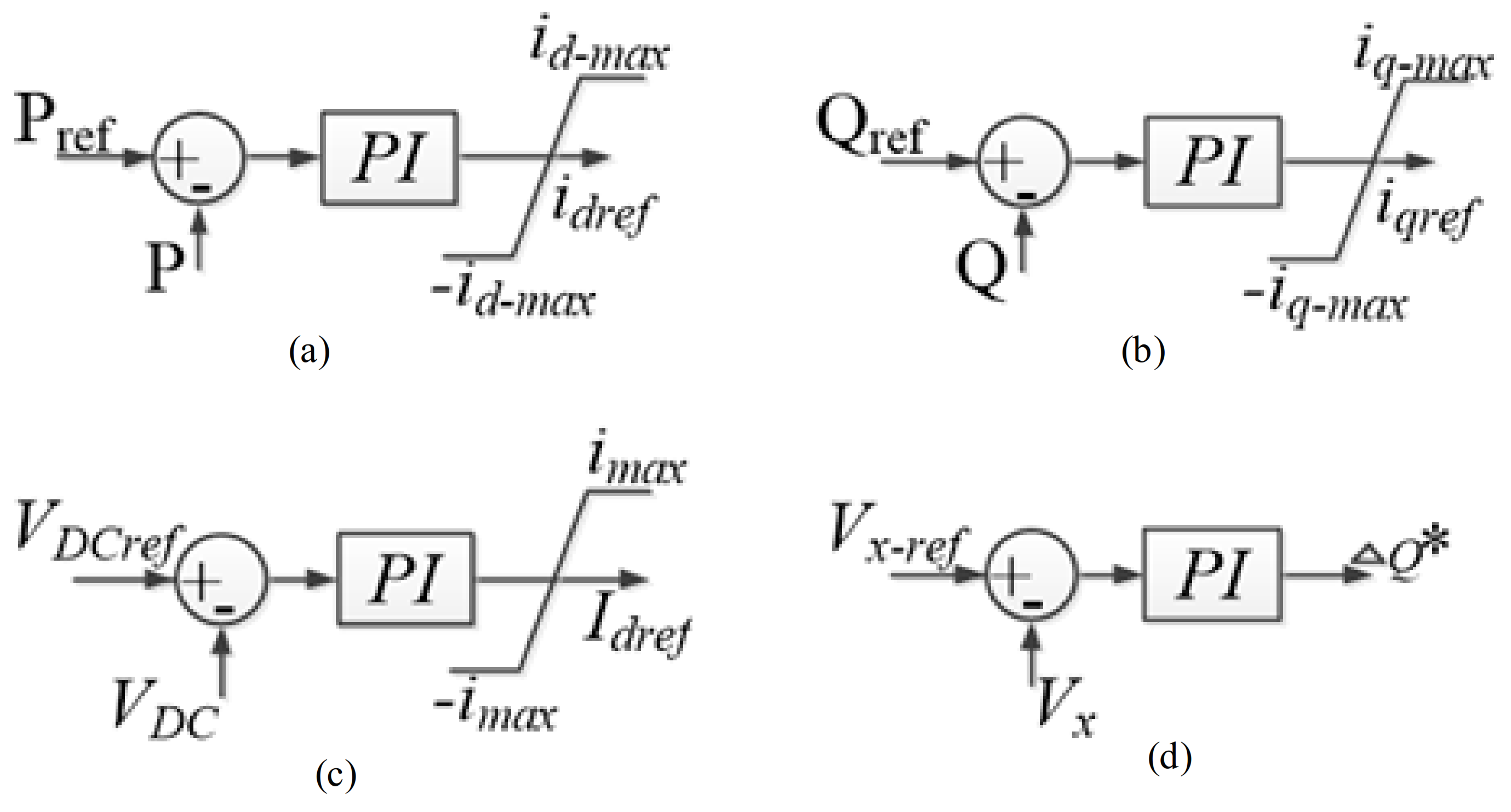
2.5. Active Power Control
2.6. DC and AC Voltage Control
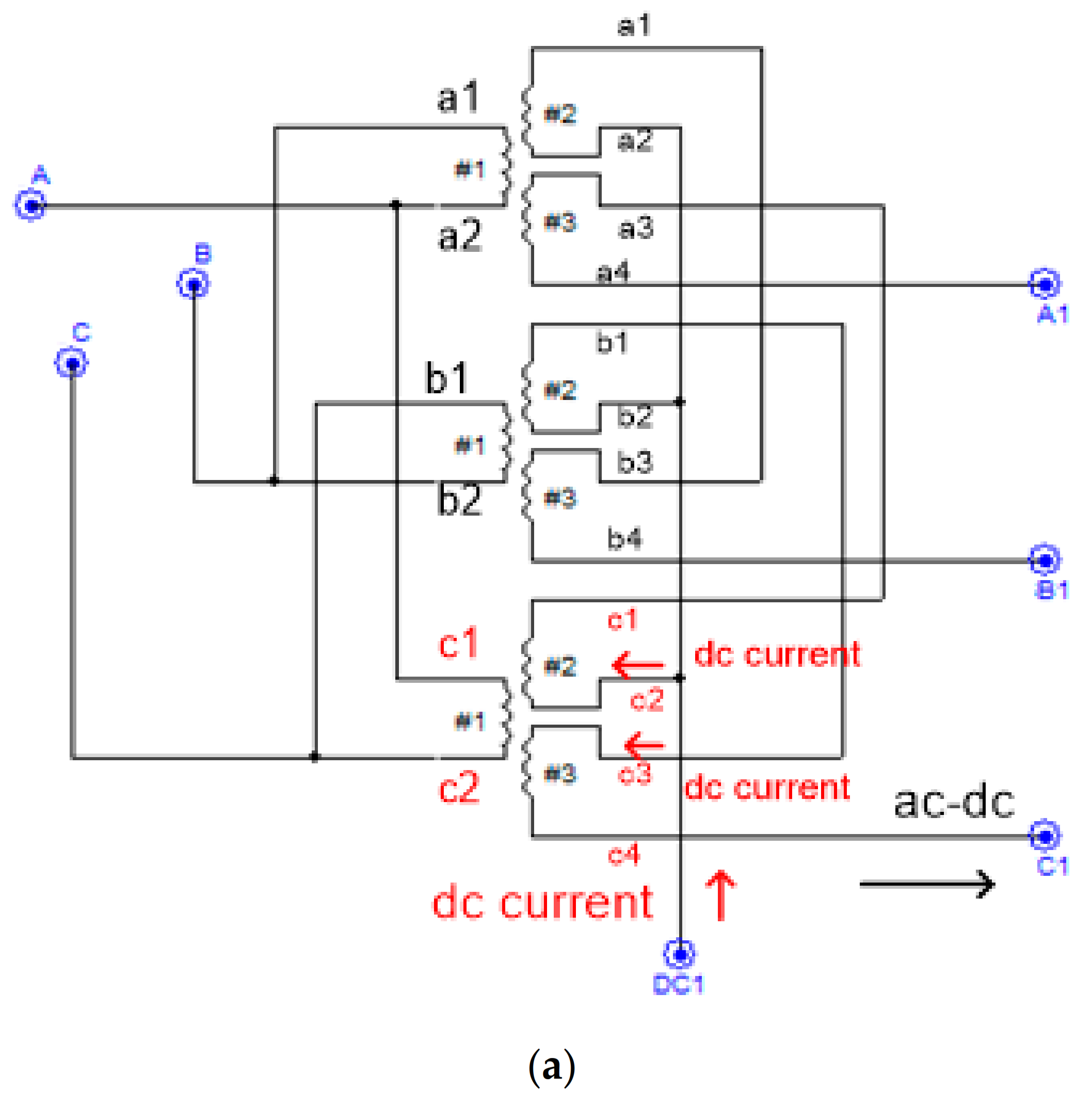
2.7. Simultaneous AC–DC System
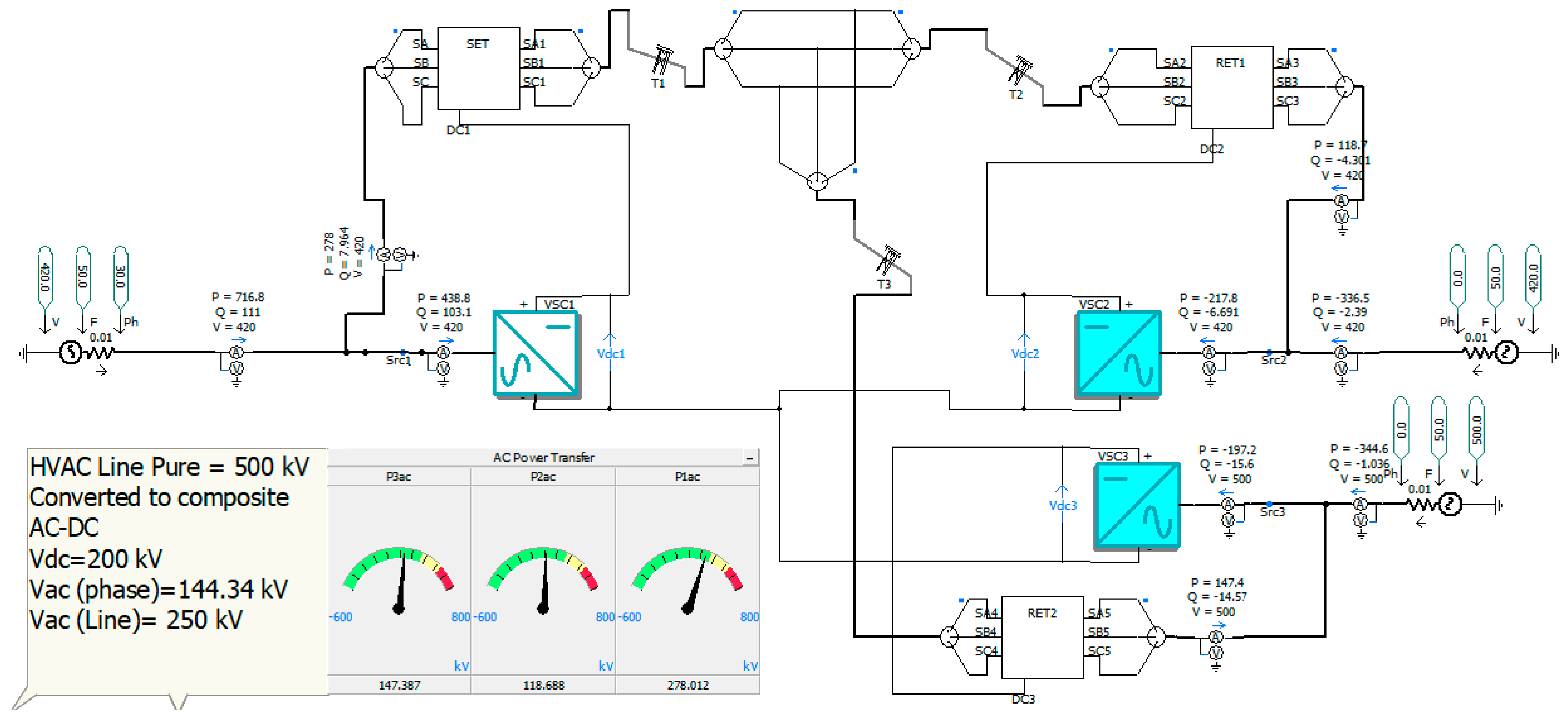
3. System under Study and Its Simulation Results
3.1. Multi-Terminal, Simultaneous AC–DC Power Transmission
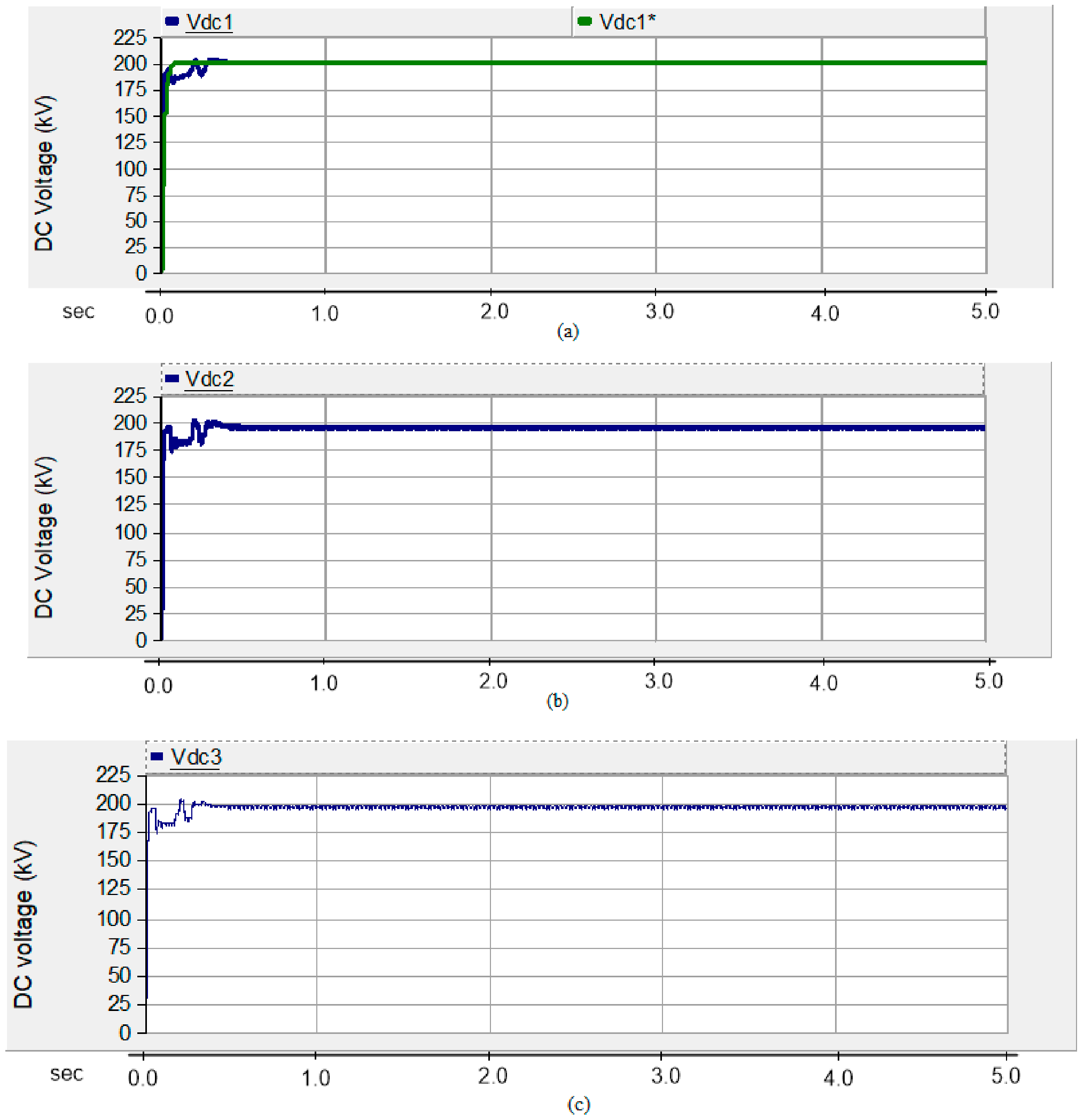
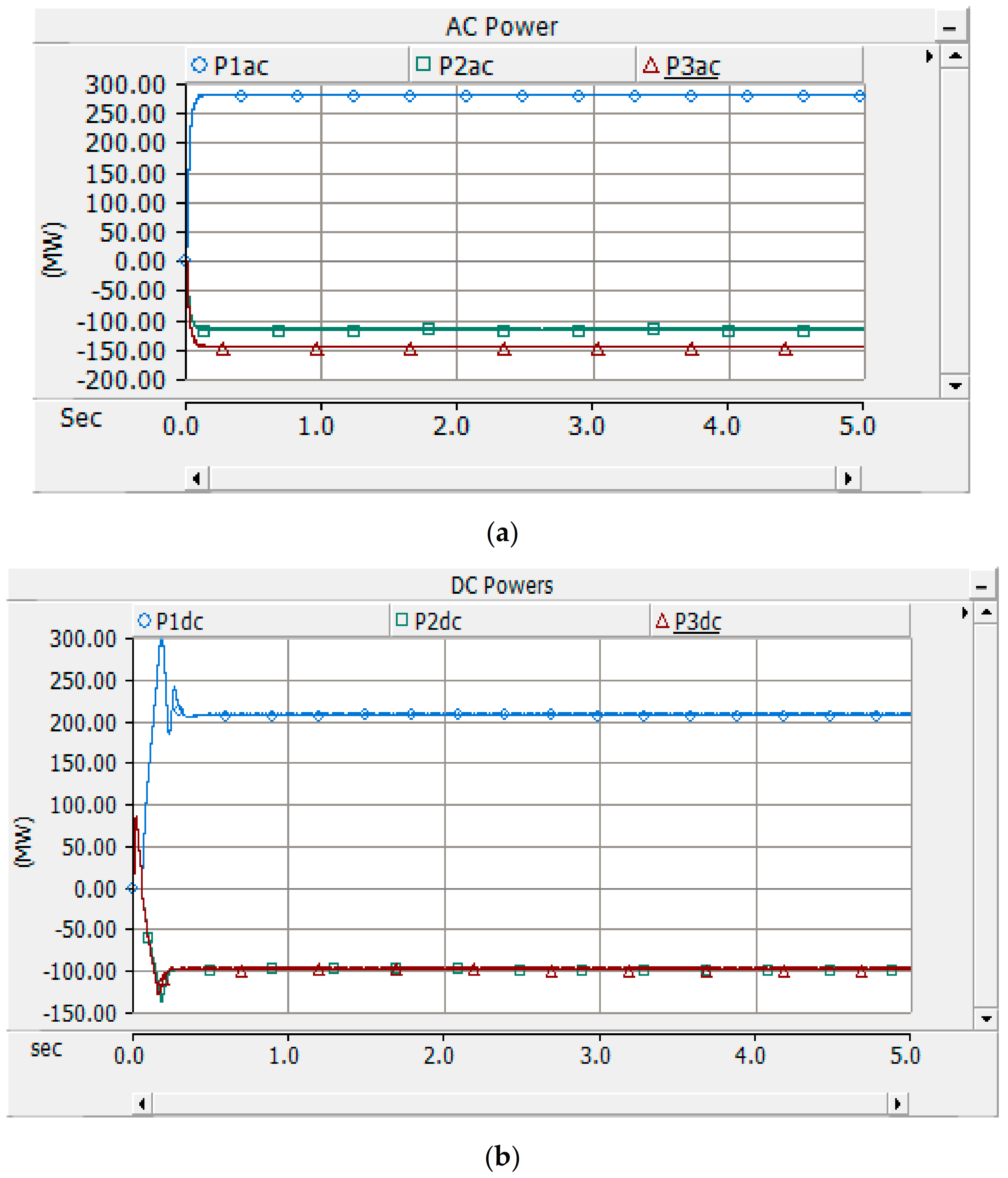
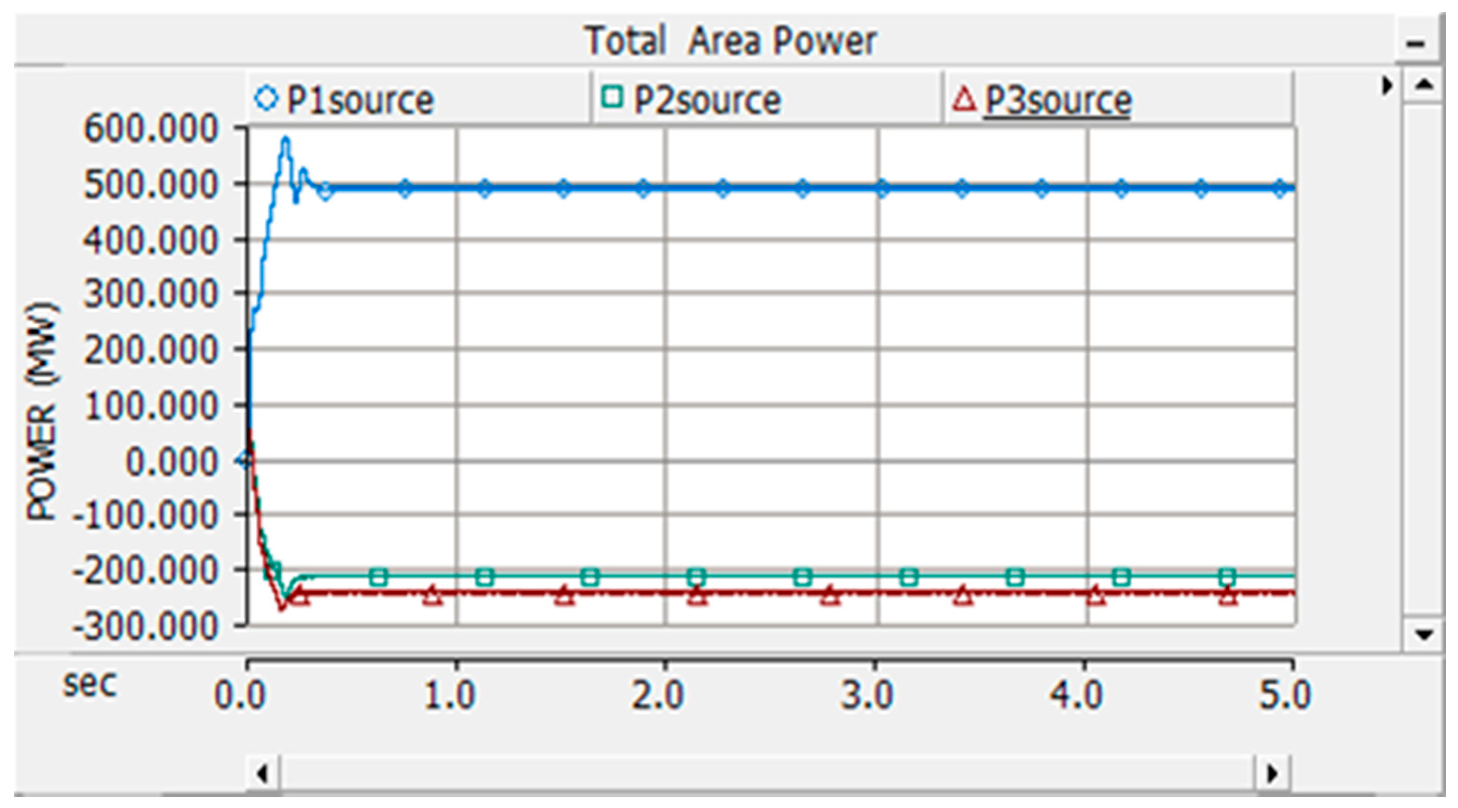
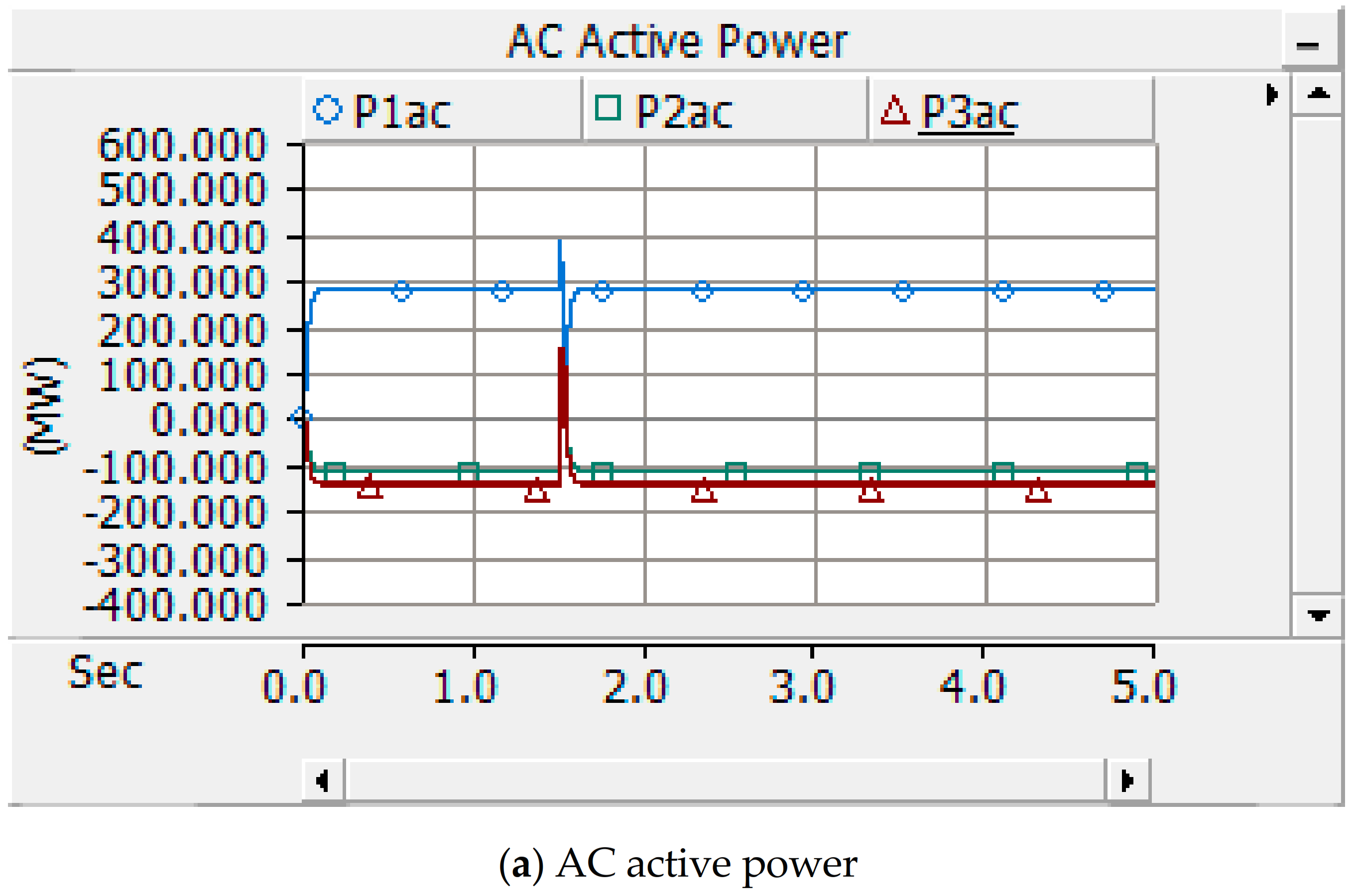
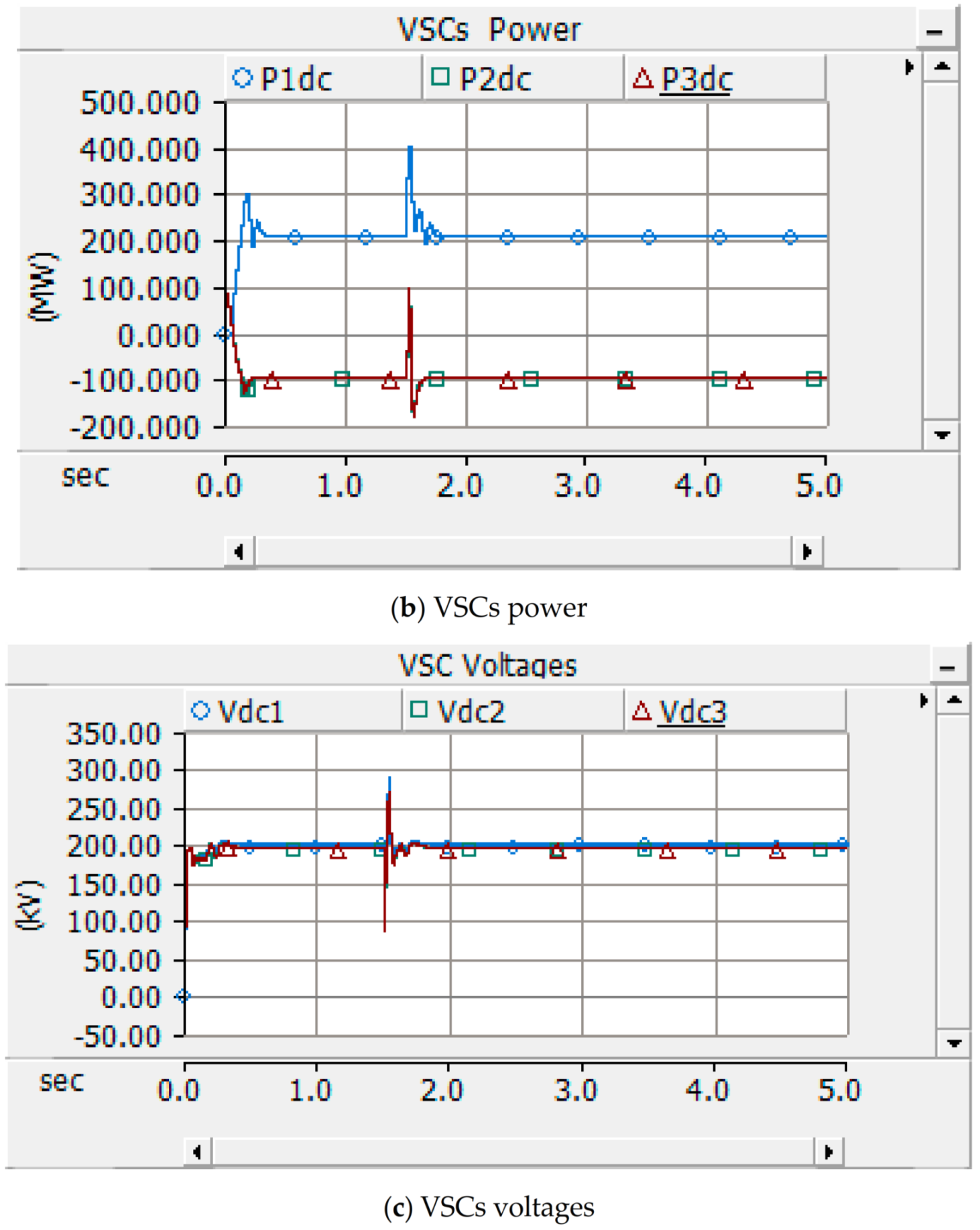
3.2. Case 1: All Three Areas Connected to the Source
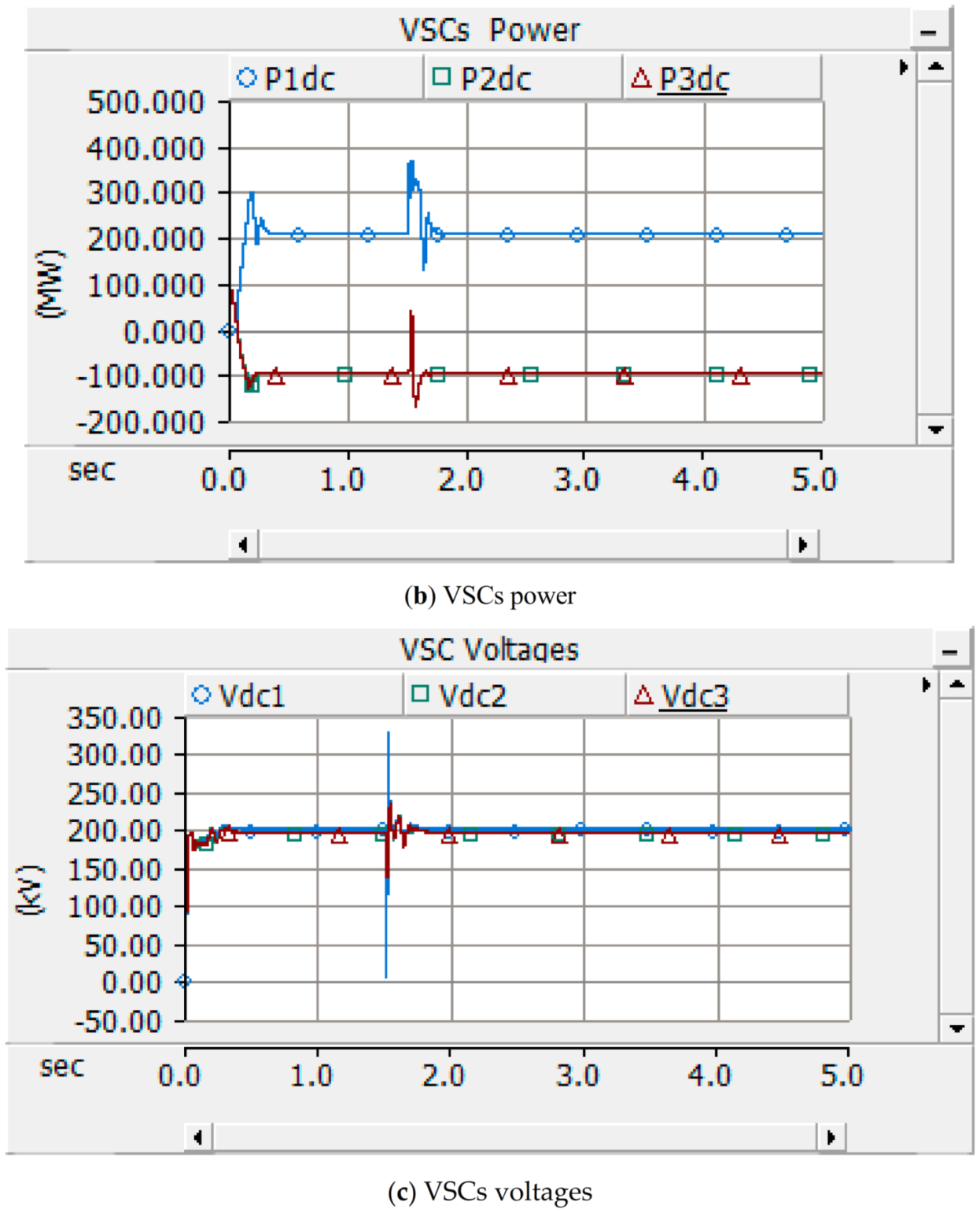
4. System under Fault
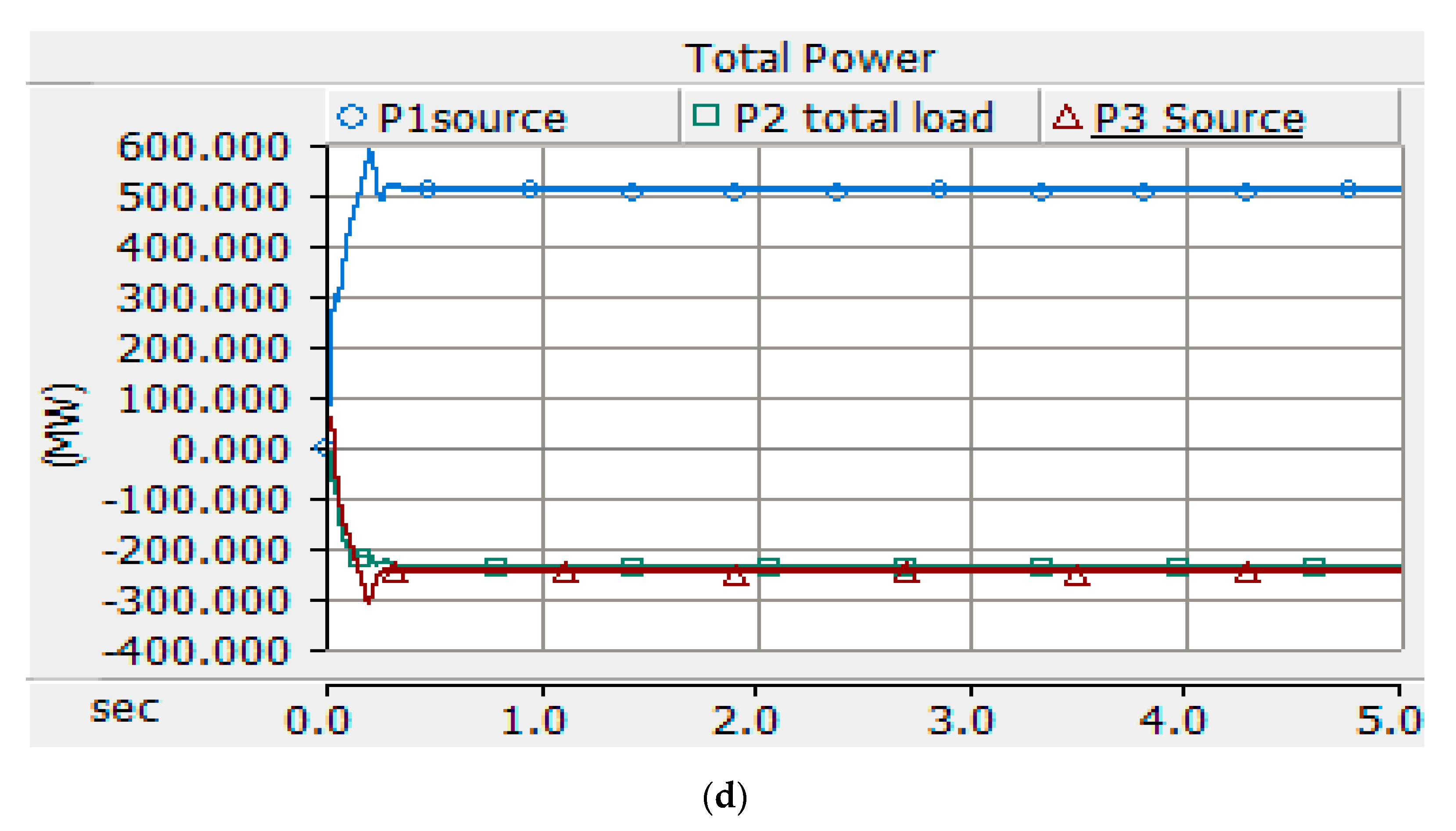
5. Case 2: Two Areas Connected to the Source and One Area Connected to Load
6. Economic Aspect
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Lachs, W.R.; Sutanto, D. Different types of voltage instability. IEEE Trans. Power Syst. 1994, 9, 1126–1134. [Google Scholar] [CrossRef]
- Rahman, H.; Khan, B.H. Power upgrading of transmission line by combining AC-DC transmission. IEEE Trans. Power Syst. 2007, 22, 459–466. [Google Scholar] [CrossRef]
- Basler, M.J.; Schaefer, R.C. Understanding Power-System Stability. IEEE Trans. Ind. Appl. 2008, 44, 463–474. [Google Scholar] [CrossRef]
- Noroozian, M.; Angquist, L.; Ghandhari, M.; Andersson, G. Improving power system dynamics by series-connected FACTS devices. IEEE Trans. Power Deliv. 1997, 12, 1635–1641. [Google Scholar] [CrossRef]
- Tan, Y.L.; Wang, Y. Effects of FACTS controller line compensation on power system stability. IEEE Power Eng. Rev. 1998, 18, 55–56. [Google Scholar] [CrossRef]
- Edris, A. FACTS technology development: An update. IEEE Power Eng. Rev. 2000, 20, 4–9. [Google Scholar] [CrossRef]
- Flourentzou, N.; Agelidis, V.G.; Demetriades, G.D. VSC-based HVDC power transmission systems: An overview. IEEE Trans. Power Electron. 2009, 24, 592–602. [Google Scholar] [CrossRef]
- Bikash, M.; Sahoo, K. Dynamic Stability Improvement of Power System with VSC-HVDC Transmission; Science Publishing Corporation: Amman, Jordan, 2014; Volume 7, pp. 500–503. [Google Scholar]
- Thams, F.; Suul, J.A.; Arco, S.D.; Molinas, M.; Fuchs, F.W. Stability of DC voltage droop controllers in VSC HVDC systems. IEEE Eindh. PowerTech. 2015, 1–7. [Google Scholar]
- Cole, S.; Beerten, J.; Belmans, R. Generalized dynamic VSC MTDC model for power system stability studies. IEEE Trans. Power Syst. 2010, 25, 1655–1662. [Google Scholar] [CrossRef] [Green Version]
- Beerten, J.; Cole, S.; Belmans, R. Generalized steady-state VSC MTDC model for sequential AC/DC power flow algorithms. IEEE Trans. Power Syst. 2012, 27, 821–829. [Google Scholar] [CrossRef] [Green Version]
- Liang, J.; Jing, T. Operation and control of multiterminal HVDC transmission for offshore wind farms. IEEE Trans. Power Deliv. 2011, 26, 2596–2604. [Google Scholar] [CrossRef]
- Zhang, L.; Zou, Y.; Yu, J.; Qin, J.; Vittal, V.; Karady, G.G.; Shi, D.; Wang, Z. Modeling, control, and protection of modular multilevel converter-based multi-terminal HVDC systems: A review. CSEE J. Power Energy Syst. 2017, 3, 340–352. [Google Scholar] [CrossRef]
- Rahman, H.; Khan, B.H. Possibility of power tapping from simultaneous AC-DC power transmission lines. IEEE Trans. Power Deliv. 2008, 23, 1464–1471. [Google Scholar] [CrossRef]
- Peterson, H.A.; Reitan, D.K.; Phadke, A.G. Parallel Operation of AC and DC Power Transmission. IEEE Trans. Power Appar. Syst. 1965, 84, 15–19. [Google Scholar] [CrossRef]
- Pedra, J.; Sainz, L.; Monjo, L. Three-Port Small Signal Admittance-Based Model of VSCs for Studies of Multi-terminal HVDC Hybrid AC/DC Transmission Grids. IEEE Trans. Power Syst. 2020, 36, 732–743. [Google Scholar] [CrossRef]
- Wang, P.; Goel, L.; Liu, X.; Choo, F.H. Harmonizing AC and DC: A Hybrid AC/DC Future Grid Solution. IEEE Power Energy Mag. 2013, 11, 76–83. [Google Scholar] [CrossRef]
- Carroll, D.P. Coordinated active and reactive power modulation of multiterminal HVDC systems. IEEE Trans. Power Appar. Syst. 1984, 6, 1480–1485. [Google Scholar]
- Wang, H.; Tang, G.; He, Z.; Yang, J. Efficient Grounding for Modular Multilevel HVDC Converters (MMC) on the AC Side. IEEE Trans. Power Deliv. 2014, 29, 1262–1272. [Google Scholar] [CrossRef]
- Abdelwahed, M.A.; El-Saadany, E.F. Power Sharing Control Strategy of Multiterminal VSC-HVDC Transmission Systems Utilizing Adaptive Voltage Droop. IEEE Trans. Sustain. Energy 2017, 8, 605–615. [Google Scholar] [CrossRef]
- Gonzalez-Longatt, F.; Roldan, J. Effects of DC Voltage control strategy on voltage response on multi-terminal HVDC following loss of a converter station. In Proceedings of the IEEE Power and Energy Society General Meeting, Vancouver, BC, Canada, 21–25 July 2013. [Google Scholar]
- Zhang, L.; Harnefors, L.; Nee, H. Modeling and Control of VSC-HVDC Links Connected to Island Systems. IEEE Trans. Power Syst. 2011, 26, 783–793. [Google Scholar] [CrossRef]
- Castro, L.M.; Acha, E. A Unified Modeling Approach of Multi-Terminal VSC-HVDC Links for Dynamic Simulations of Large-Scale Power Systems. IEEE Trans. Power Syst. 2016, 31, 5051–5060. [Google Scholar] [CrossRef]
- Li, Z.; He, Y.; Li, Y.; Gu, W.; Tang, Y.; Zhang, X. Hybrid Control Strategy for AC Voltage Stabilization in Bipolar VSC-MTDC. IEEE Trans. Power Syst. 2019, 34, 129–139. [Google Scholar] [CrossRef]
- Yazdani, A.; Iravani, R. Voltage-Sourced Converters in Power Systems: Modeling, Control, and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2010. [Google Scholar]
- Rahman, H.; Khan, B.H. Stability improvement of power system by simultaneous ac-dc power transmission. Electr. Power Syst. Res. 2007, 78, 756–764. [Google Scholar] [CrossRef]







| AC Side Data | ||||
|---|---|---|---|---|
| Area-1 | Area-2 | Area-3 | ||
| AC voltage | 420 kV | 420 kV | 500 kV | |
| Frequency Delta-Zig-Zag Transformer | 50 Hz 1000 MVA 420/250 kV | 50 Hz 1000 MVA 420/250 kV | 50 Hz 1000 MVA 500/250 kV | |
| Converter Transformer | 1000 MVA 420/115 kV | 1000 MVA 420/115 kV | 1000 MVA 500/115 kV | |
| Simultaneous AC–DC Transmission Line Parameters | ||||
| Length | R (ohms/m) | XL (ohms/m) | XC (mohms/m) | |
| VSC1 to VSC2 | 500 km | 0.3252 × 10−4 | 0.33086 × 10−3 | 295.88 |
| VSC1 to VSC3 | 500 km | 0.3252 × 10−4 | 0.33086 × 10−3 | 295.88 |
| DC side capacitor: 300 µF; DC voltage: 200 kV; Line-line AC voltage of VSC: 115 kV | ||||
| Reference Power | Area-1 Active Power | Area-2 Active Power | Area-3 Active Power | Ptotal Active Power | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Pref2 | Pref3 | P1ac | P1dc | P2ac | P2dc | P3ac | P3dc | P1source | P2source | P3source |
| −100 | −100 | 278 | 204.7 | −118.7 | −98.8 | −147.4 | −98.81 | 482.8 | −217.5 | −246.21 |
| −100 | −50 | 278 | 152.9 | −118.7 | −98.8 | −147.4 | −48.81 | 430.9 | −217.5 | −196.21 |
| −50 | −100 | 278 | 152.7 | −118.7 | −48.7 | −147.4 | −98.78 | 430.7 | −167.4 | −246.18 |
| −50 | −50 | 278 | 101.4 | −118.7 | −48.7 | −147.4 | −48.76 | 379.4 | −167.4 | −196.16 |
| 100 | 100 | −265.5 | −196.2 | 123.6 | 101.4 | 153.8 | 101.4 | −461.7 | 225.1 | 255.3 |
| Reference Power | Area-1 Active Power | Area-2 Active Power | Area-3 Active Power | Ptotal Active Power | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Pref2 | Pref3 | P1ac | P1dc | P2ac | P2dc | P3ac | P3dc | P1source | P2souce | P3source |
| −100 | −100 | 274.06 | 228.94 | −113.5 | −121.0 | −148.2 | −98.81 | 503.012 | −234.55 | −247 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Parveen, S.; Hameed, S.; Rahman, H.; Rahman, K.; Tariq, M.; Alamri, B.; Ahmad, A. The Possibility of Enhanced Power Transfer in a Multi-Terminal Power System through Simultaneous AC–DC Power Transmission. Electronics 2022, 11, 108. https://doi.org/10.3390/electronics11010108
Parveen S, Hameed S, Rahman H, Rahman K, Tariq M, Alamri B, Ahmad A. The Possibility of Enhanced Power Transfer in a Multi-Terminal Power System through Simultaneous AC–DC Power Transmission. Electronics. 2022; 11(1):108. https://doi.org/10.3390/electronics11010108
Chicago/Turabian StyleParveen, Shaista, Salman Hameed, Hafizur Rahman, Khaliqur Rahman, Mohd Tariq, Basem Alamri, and Akbar Ahmad. 2022. "The Possibility of Enhanced Power Transfer in a Multi-Terminal Power System through Simultaneous AC–DC Power Transmission" Electronics 11, no. 1: 108. https://doi.org/10.3390/electronics11010108







