Adaptive Scheduling for Time-Triggered Network-on-Chip-Based Multi-Core Architecture Using Genetic Algorithm
Abstract
:1. Introduction
- It introduces a Genetic Algorithm (GA)-based metascheduler for time-triggered NoC-based architectures.
- It presents a solution to combat the state-space explosion problem in the MSG using a reconvergence of paths algorithm.
- It implements a reconvergence horizon to maintain schedule generation within configured bounds.
- It further evaluates the reconvergence of paths algorithm using different input model sizes and configurations for the reconvergence horizon.
2. Related Work
3. System Model
3.1. Input Models
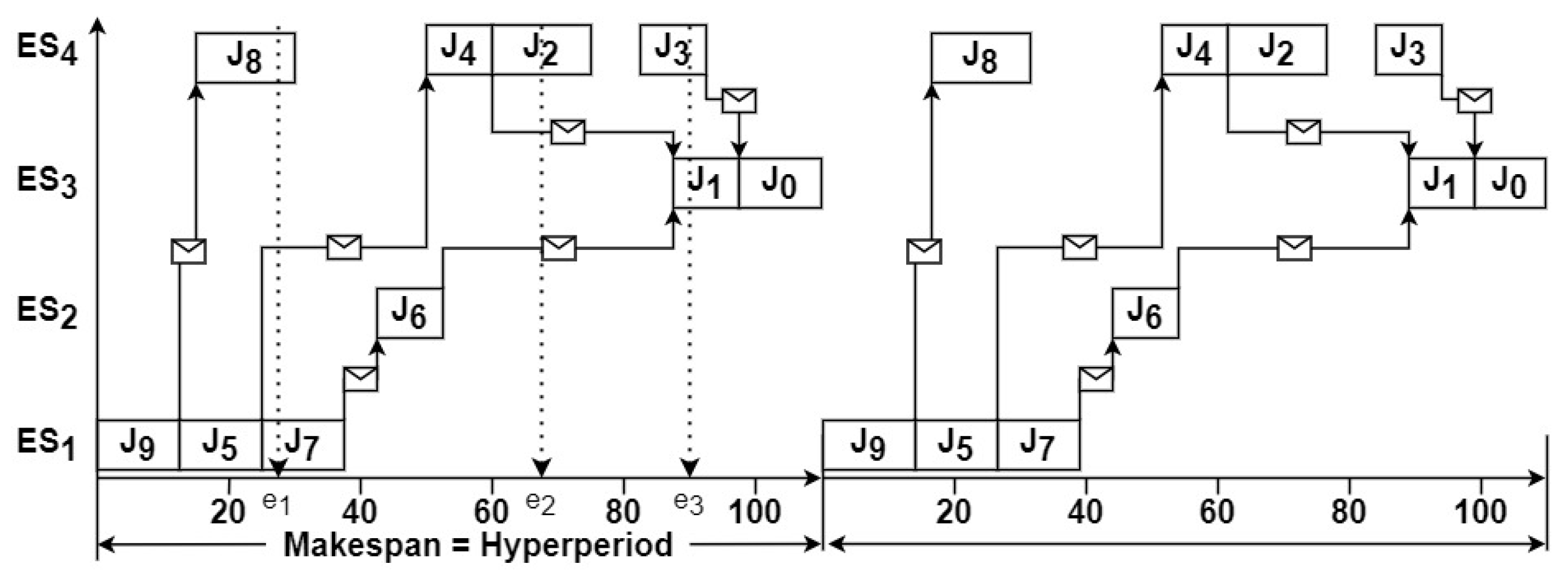
3.2. Output Model
4. Proposed Approach
4.1. Genetic Algorithm
| Algorithm 1: Genetic Algorithm Adaptation for TTNoC Architecture. |
 |
4.2. Metascheduler with Reconvergence of Paths in MSG
| Algorithm 2: GA-based Metascheduler with reconvergence of paths in MSG. |
 |
5. Results and Discussions
5.1. Architectures and Applications
5.2. Selection of Genetic Algorithm Parameters
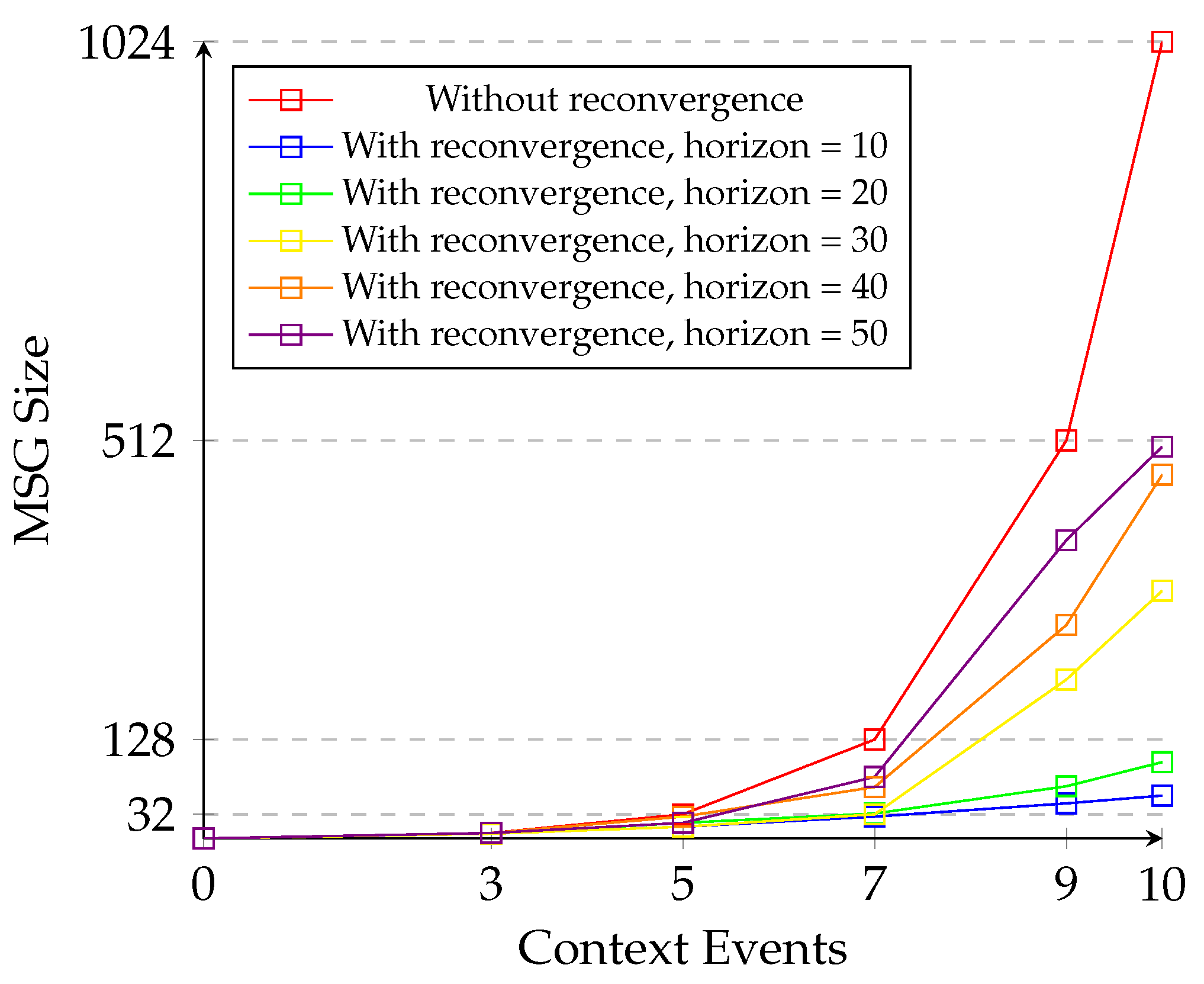
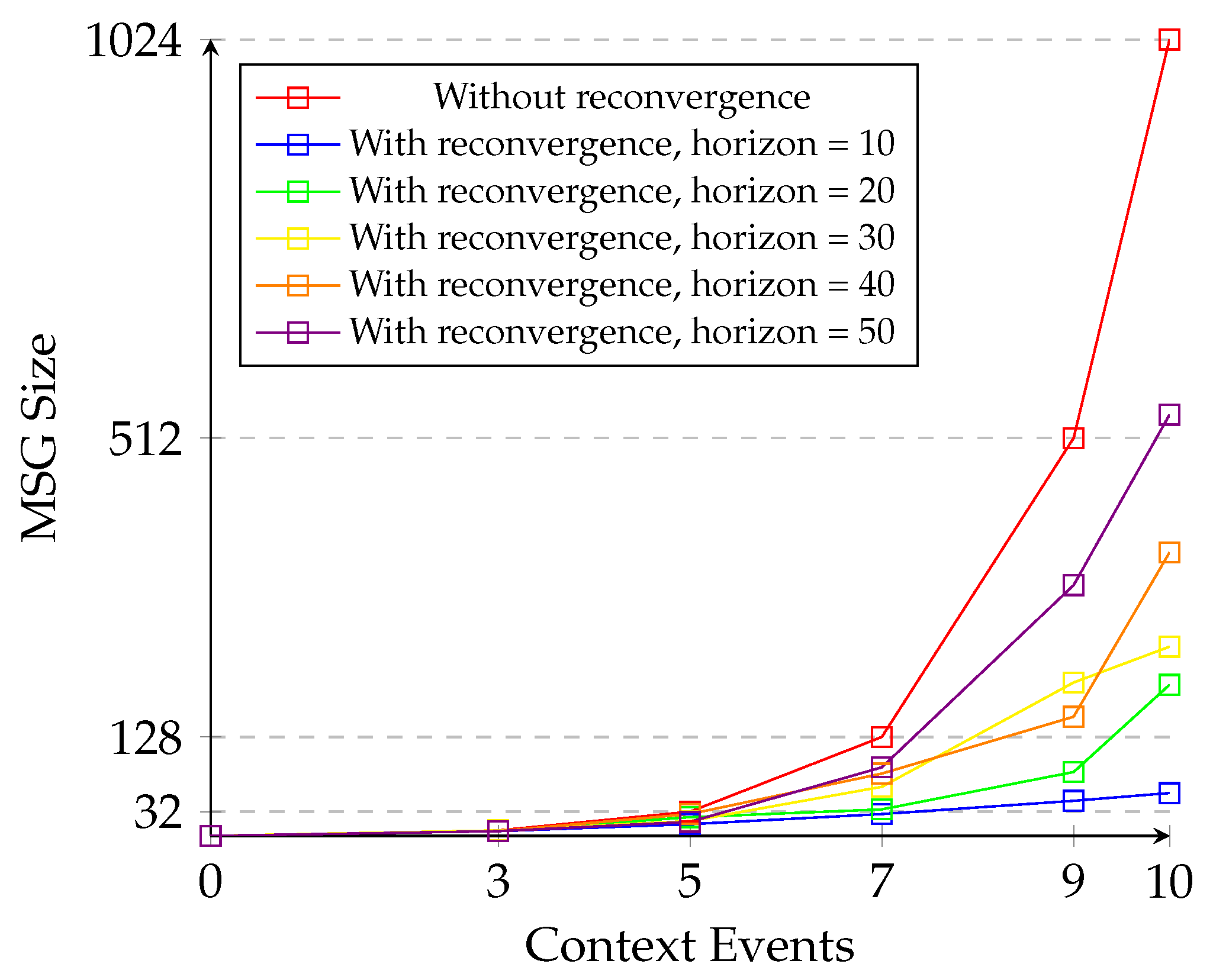
5.3. Evaluation of State Space Reduction
5.4. State-Space Exploration Time
5.5. Sleep Time for Energy Saving
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Paul, S.; Chatterjee, N.; Ghosal, P.; Diguet, J. Adaptive Task Allocation and Scheduling on NoC-based Multicore Platforms with Multitasking Processors. ACM Trans. Embed. Comput. Syst. 2021, 20, 1–26. [Google Scholar] [CrossRef]
- Obermaisser, R.; Ahmadian, H.; Maleki, A.; Bebaway, Y.; Alina, L.; Sorkhpour, B. Adaptive Time-Triggered Multi-Core Architecture. Designs 2019, 3, 7. [Google Scholar] [CrossRef] [Green Version]
- Ahmadian, H.; Obermaisser, R. Time-Triggered Extension Layer for On-Chip Network Interfaces in Mixed-Criticality Systems. In Proceedings of the Euromicro Conference on Digital System Design DSD, Madeira, Portugal, 26–28 August 2015; pp. 693–699. [Google Scholar]
- Ahmadian, H.; Nekouei, F.; Obermaisser, R. Fault recovery and adaptation in time-triggered Networks-on-Chips for mixed-criticality systems. In Proceedings of the 12th International Symposium on Reconfigurable Communication-Centric Systems-on-Chip (ReCoSoC), Madrid, Spain, 12–14 July 2017; pp. 1–8. [Google Scholar]
- Murshed, A. Scheduling Event-Triggered and Time-Triggered Applications with Optimal Reliability and Predictability on Networked Multi-Core Chips. Ph.D. Thesis, University of Siegen, Siegen, Germany, 2018. [Google Scholar]
- Sorkhpour, B.; Murshed, A.; Obermaisser, R. Meta-scheduling techniques for energy-efficient robust and adaptive time-triggered systems. In Proceedings of the IEEE 4th International Conference on Knowledge-Based Engineering and Innovation (KBEI), Tehran, Iran, 22 December 2017; pp. 0143–0150. [Google Scholar]
- Lee, C.; Kim, H.; Park, H.; Kim, S.; Oh, H.; Ha, S. A task remapping technique for reliable multi-core embedded systems. In Proceedings of the IEEE/ACM/IFIP International Conference on Hardware/Software Codesign and System Synthesis (CODES+ISSS), Scottsdale, AZ, USA, 24–29 October 2010; pp. 307–316. [Google Scholar]
- Lenz, A.; Pieper, T.; Obermaisser, R. Global Adaptation for Energy Efficiency in Multicore Architectures. In Proceedings of the 25th Euromicro International Conference on Parallel, Distributed and Network-Based Processing (PDP), St. Petersburg, Russia, 6–8 March 2017; pp. 551–558. [Google Scholar]
- Zhang, L.; Yang, J.; Xue, C.; Ma, Y.; Cao, S. A two-stage variation-aware task mapping scheme for fault-tolerant multi-core Network-on-Chips. In Proceedings of the IEEE International Symposium on Circuits and Systems (ISCAS), Baltimore, MD, USA, 28–31 May 2017; pp. 1–4. [Google Scholar]
- Zou, Y.; Pasricha, S. HEFT: A hybrid system-level framework for enabling energy-efficient fault-tolerance in NoC based MPSoCs. In Proceedings of the International Conference on Hardware/Software Codesign and System Synthesis (CODES+ISSS), New Delhi, India, 12–17 October 2014; pp. 1–10. [Google Scholar]
- Bolanos, F.; Rivera, F.; Aedo, J.E.; Bagherzadeh, N. From UML specifications to mapping and scheduling of tasks into a NoC, with reliability considerations. J. Syst. Archit. 2013, 59, 429–440. [Google Scholar] [CrossRef] [Green Version]
- Das, A.; Kumar, A. Fault-aware task re-mapping for throughput constrained multimedia applications on NoC-based MPSoCs. In Proceedings of the 23rd IEEE International Symposium on Rapid System Prototyping (RSP), Tampere, Finland, 11–12 October 2012; pp. 149–155. [Google Scholar]
- Yang, X. Nature-Inspired Optimization Algorithms, 2nd ed.; Academic Press: London, UK, 2020. [Google Scholar]
- Wall, M.; Galib, A. A C++ Library of Genetic Algorithm Components; Mechanical Engineering Department Massachusetts Institute of Technology: Boston, MA, USA, 1996. [Google Scholar]
- Leskovec, J.; Sosič, R. SNAP: A General-Purpose Network Analysis and Graph-Mining Library. ACM Trans. Intell. Syst. Technol. 2016, 8, 1–20. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hassanat, A.; Almohammadi, K.; Alkafaween, E.; Abunawas, E.; Hammouri, A.; Prasath, V.B.S. Choosing Mutation and Crossover Ratios for Genetic Algorithms—A Review with a New Dynamic Approach. Information 2019, 10, 390. [Google Scholar] [CrossRef] [Green Version]










| Generation | Population | Computational Time (s) | Makespan |
|---|---|---|---|
| 1000 | 100 | 31 | 444 |
| 1000 | 100 | 31 | 466 |
| 1000 | 100 | 32 | 457 |
| 1000 | 100 | 31 | 459 |
| 1000 | 100 | 32 | 427 |
| 1000 | 500 | 160 | 550 |
| 1000 | 500 | 162 | 508 |
| 1000 | 500 | 160 | 505 |
| 1000 | 500 | 160 | 485 |
| 1000 | 500 | 161 | 476 |
| 3000 | 100 | 96 | 508 |
| 3000 | 100 | 94 | 484 |
| 3000 | 100 | 93 | 493 |
| 3000 | 100 | 95 | 427 |
| 3000 | 100 | 93 | 436 |
| 3000 | 500 | 474 | 458 |
| 3000 | 500 | 474 | 450 |
| 3000 | 500 | 473 | 463 |
| 3000 | 500 | 476 | 544 |
| 3000 | 500 | 483 | 445 |
| 5000 | 100 | 158 | 439 |
| 5000 | 100 | 160 | 443 |
| 5000 | 100 | 158 | 478 |
| 5000 | 100 | 159 | 453 |
| 5000 | 100 | 158 | 449 |
| 5000 | 200 | 326 | 419 |
| 5000 | 200 | 322 | 385 |
| 5000 | 200 | 321 | 387 |
| 5000 | 200 | 321 | 410 |
| 5000 | 200 | 325 | 427 |
| Setup | Scenario 1 | Scenario 2 | ||
|---|---|---|---|---|
| PBIL | Proposed | PBIL | Proposed | |
| AM Size | 20 | 20 | 35 | 40 |
| NoC Architecture | 3 × 3 | 3 × 3 | 3 × 3 | 3 × 3 |
| Processors | 9 | 4 | 9 | 4 |
| Computational Time | 30 | 8 | 110 | 22 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Muoka, P.; Onwuchekwa, D.; Obermaisser, R. Adaptive Scheduling for Time-Triggered Network-on-Chip-Based Multi-Core Architecture Using Genetic Algorithm. Electronics 2022, 11, 49. https://doi.org/10.3390/electronics11010049
Muoka P, Onwuchekwa D, Obermaisser R. Adaptive Scheduling for Time-Triggered Network-on-Chip-Based Multi-Core Architecture Using Genetic Algorithm. Electronics. 2022; 11(1):49. https://doi.org/10.3390/electronics11010049
Chicago/Turabian StyleMuoka, Pascal, Daniel Onwuchekwa, and Roman Obermaisser. 2022. "Adaptive Scheduling for Time-Triggered Network-on-Chip-Based Multi-Core Architecture Using Genetic Algorithm" Electronics 11, no. 1: 49. https://doi.org/10.3390/electronics11010049
APA StyleMuoka, P., Onwuchekwa, D., & Obermaisser, R. (2022). Adaptive Scheduling for Time-Triggered Network-on-Chip-Based Multi-Core Architecture Using Genetic Algorithm. Electronics, 11(1), 49. https://doi.org/10.3390/electronics11010049






