A Precise Current Detection Method Using a Single Shunt and FET Rds(on) of a Low-Voltage Three-Phase Inverter
Abstract
:1. Introduction
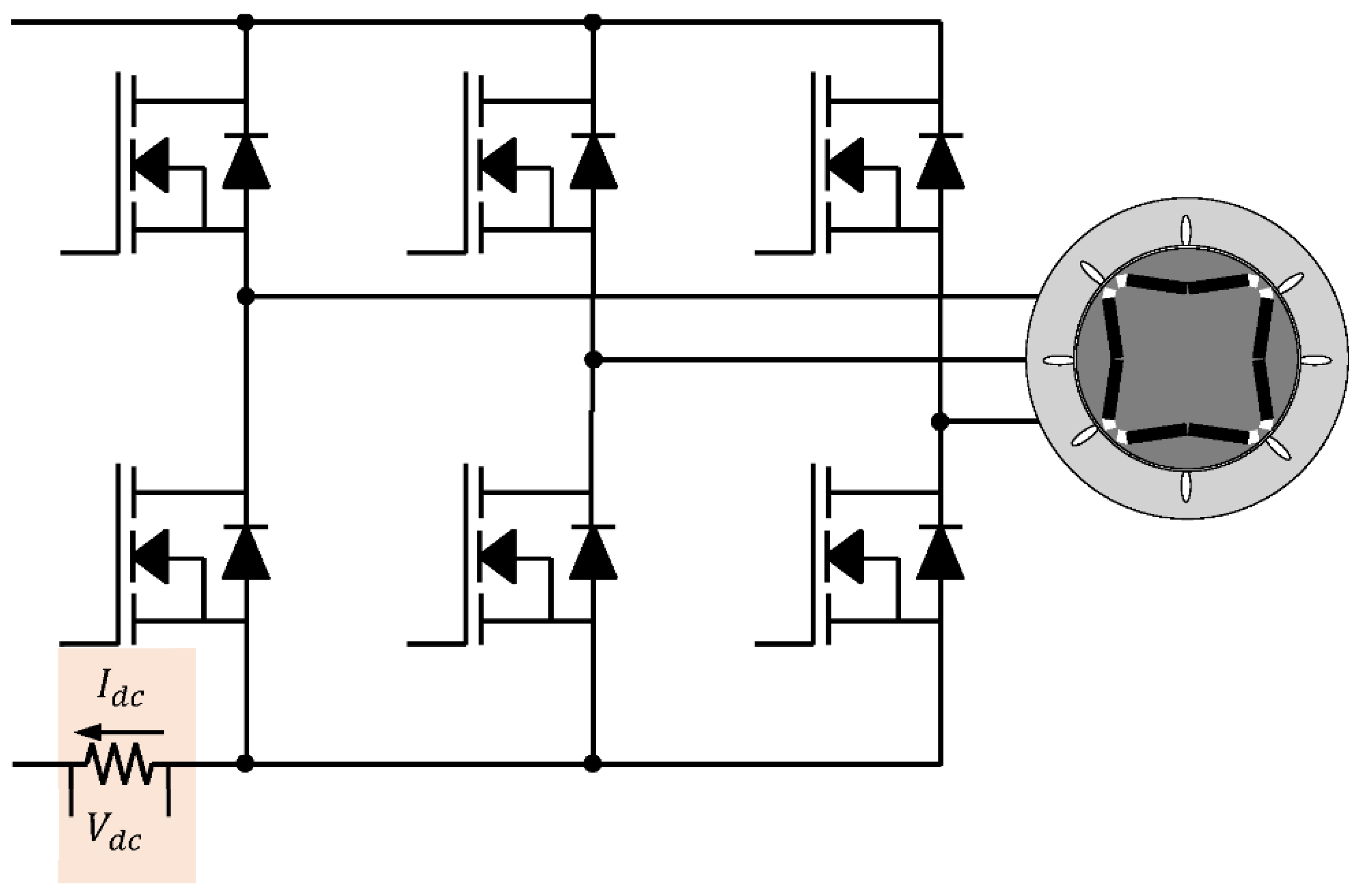
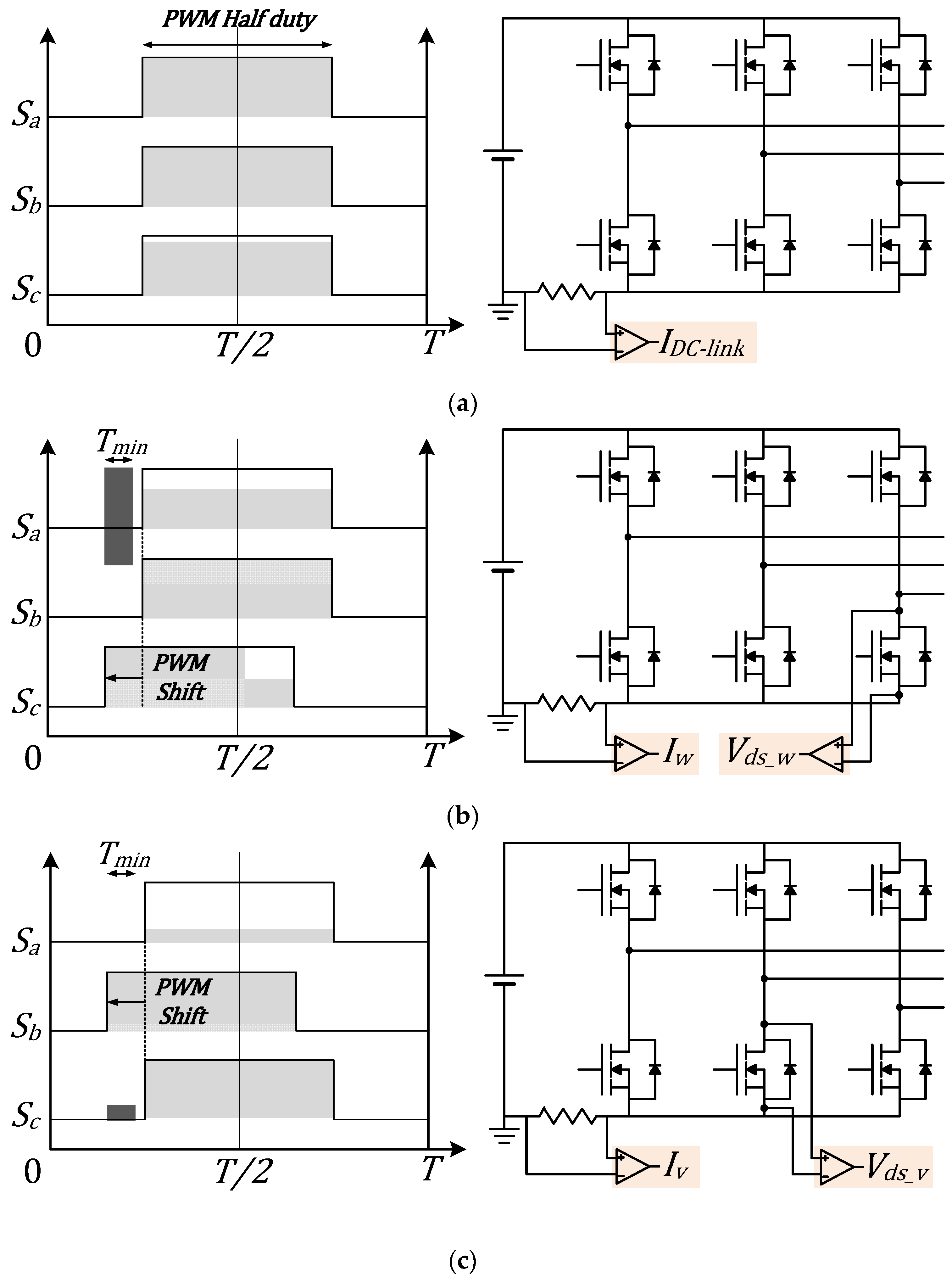
2. Current Detection Method Using Single-Shunt Resistor and MOSFET Rds(on) in Low-Voltage Three-Phase Inverter
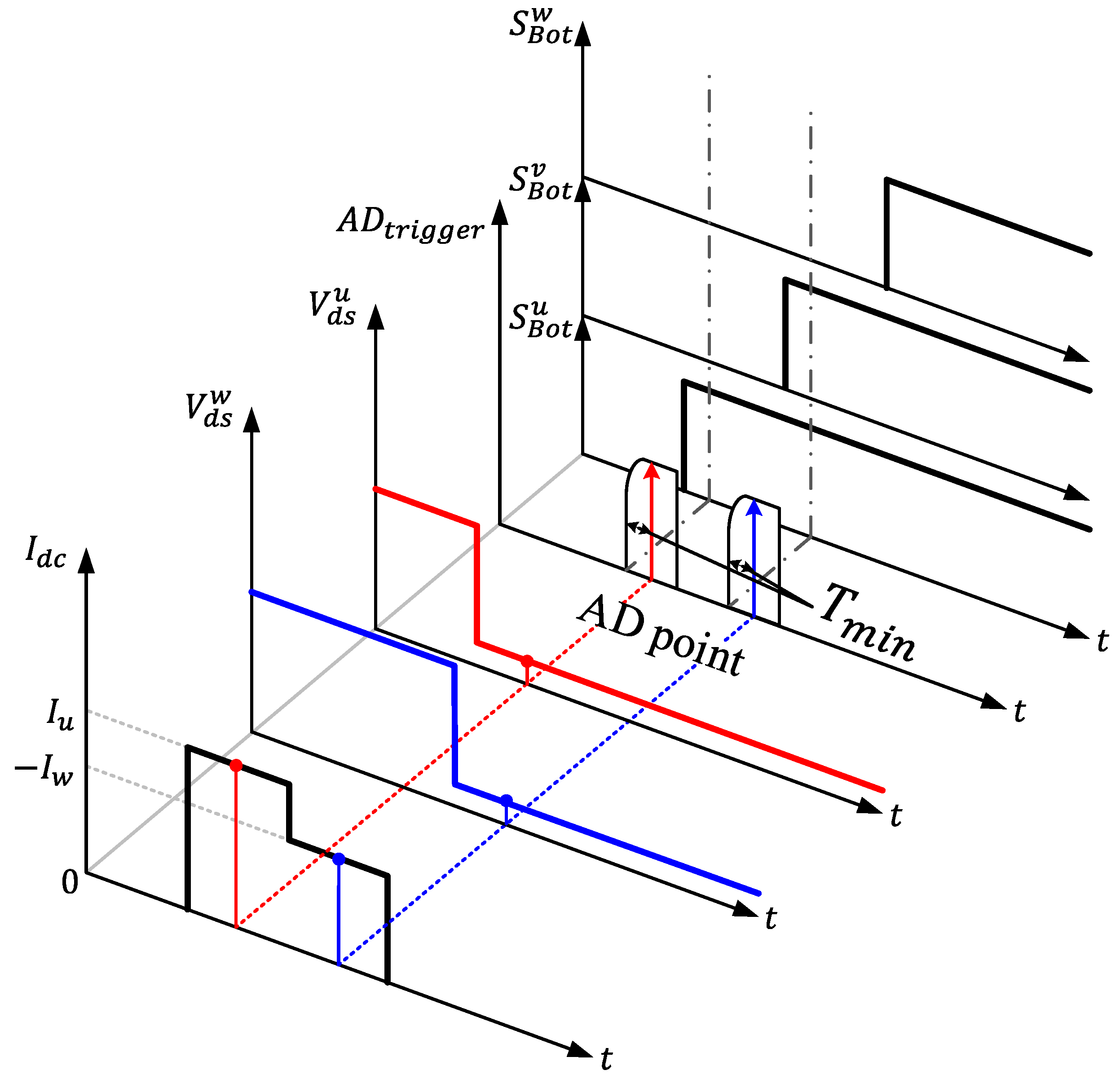
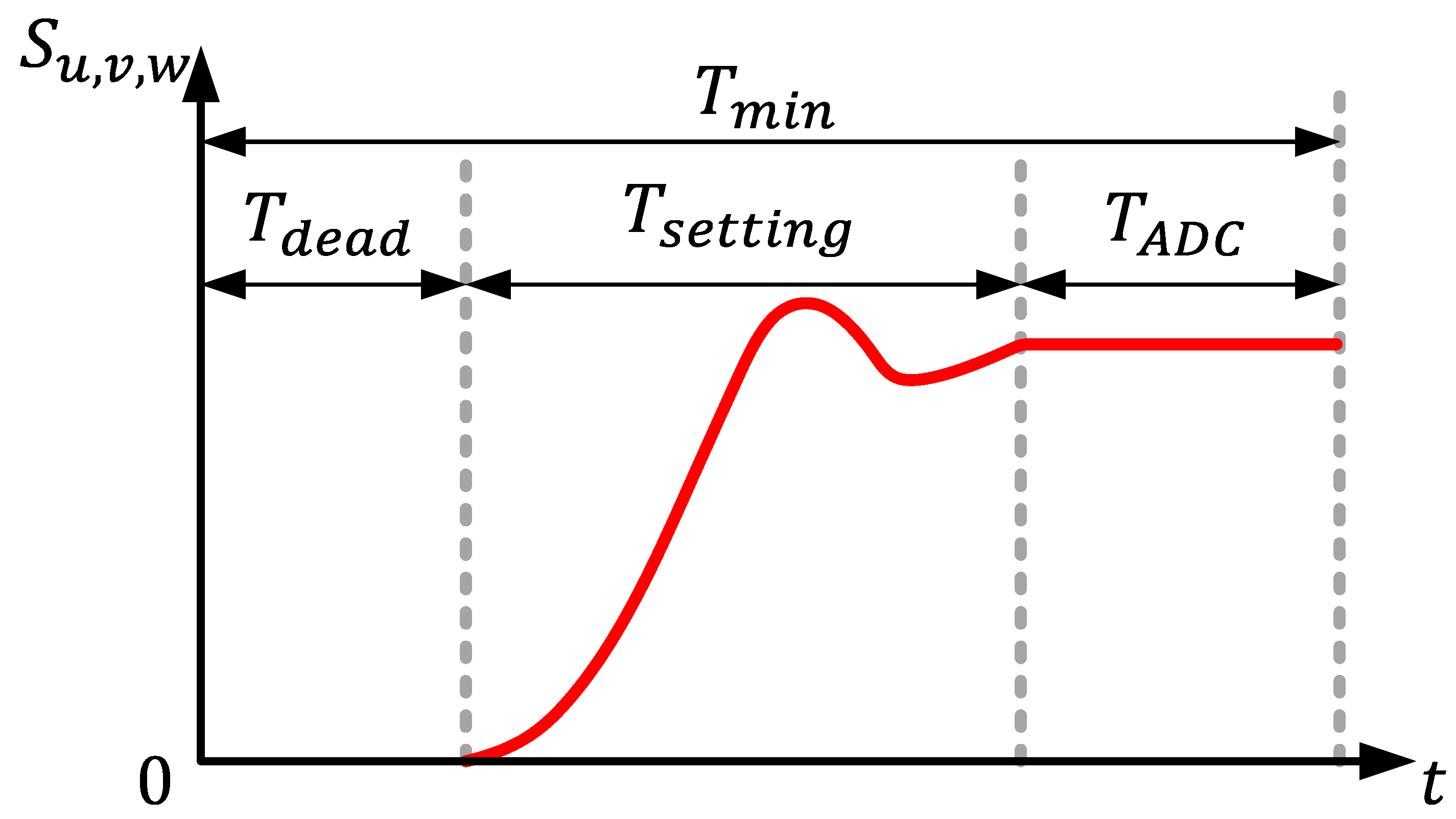
2.1. Current Detection Method Using the Existing Single Shunt Resistor
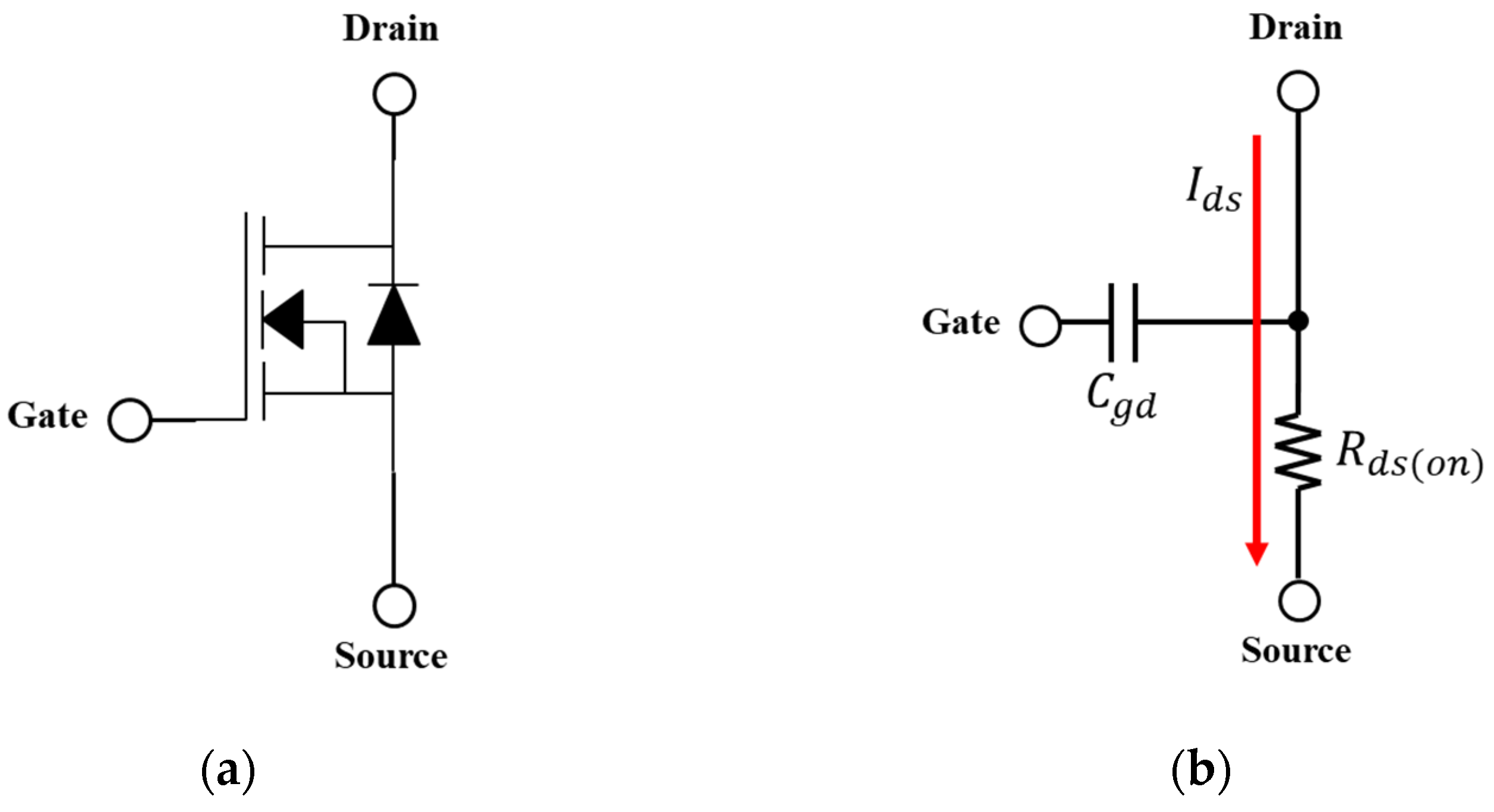
2.2. Current Measurement Method Using MOSFET Rds(on)
2.2.1. Basic Operating Characteristics of MOSFET Rds(on)
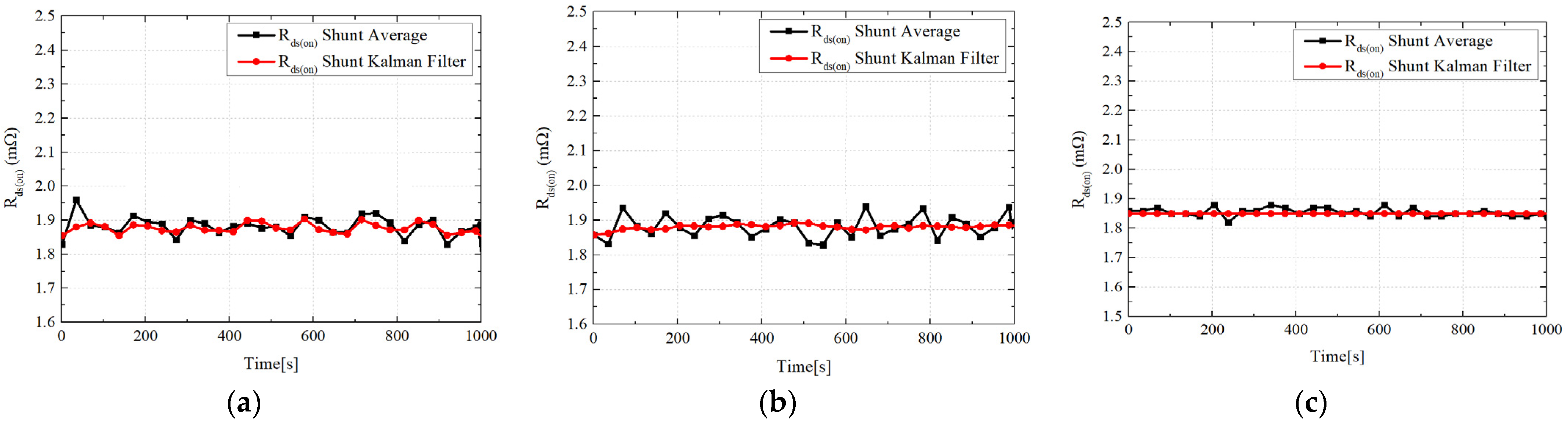
2.2.2. Correction of MOSFET Rds(on) Using Kalman Filter
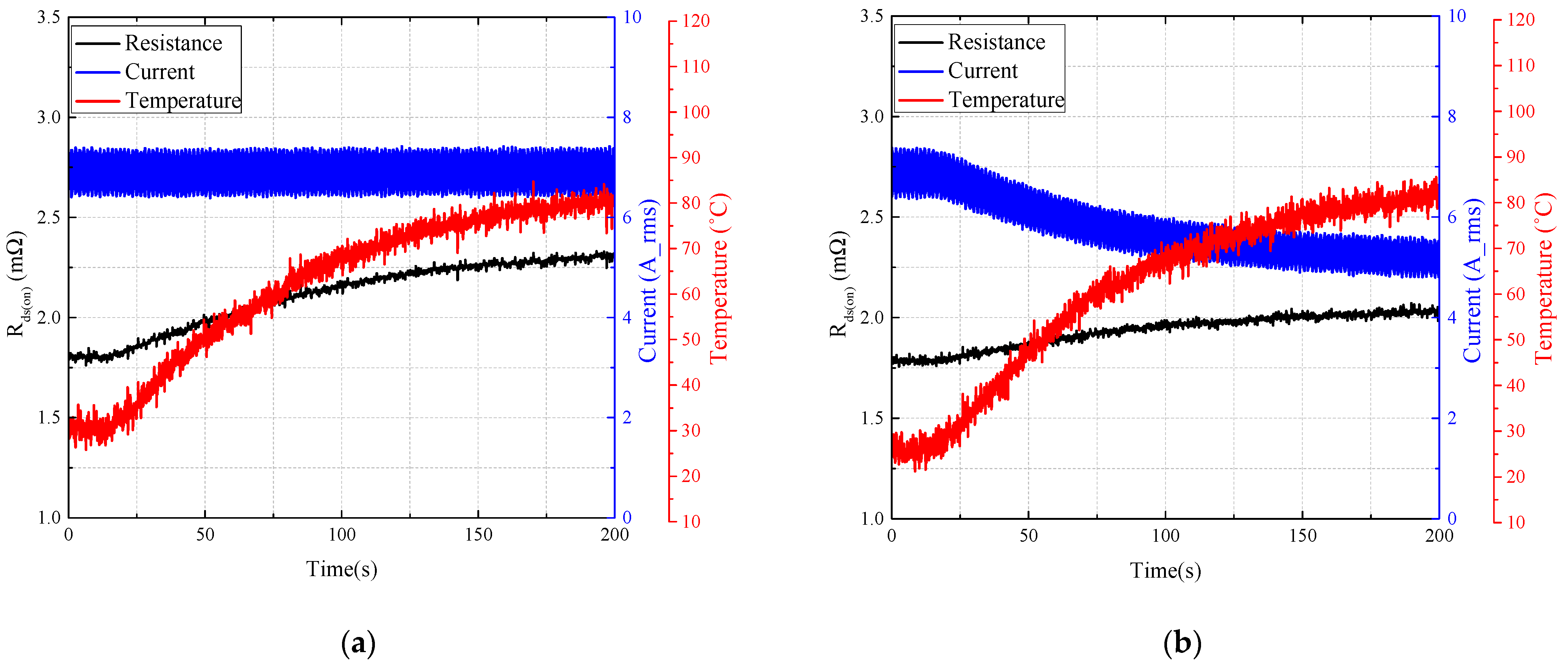
2.2.3. MOSFET Junction Temperature Estimation
3. Experiment Using Rds(on) of MOSFET in Single Shunt Inverter System
3.1. Rds(on) Initial Value of MOSFET
3.1.1. Rds(on) of MOSFET Using Kalman filter
3.1.2. Estimation of Rds(on) According to Rds(on) Temperature Change
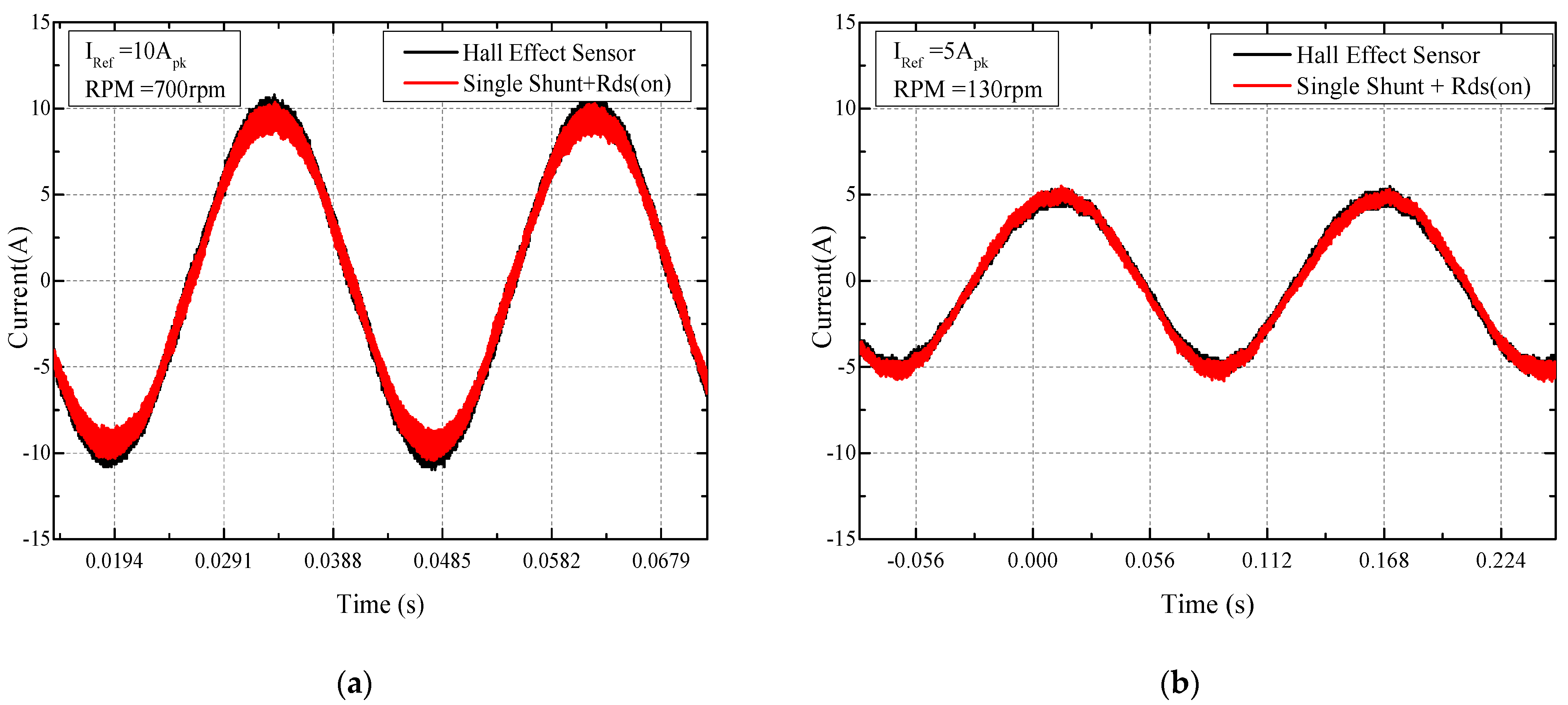
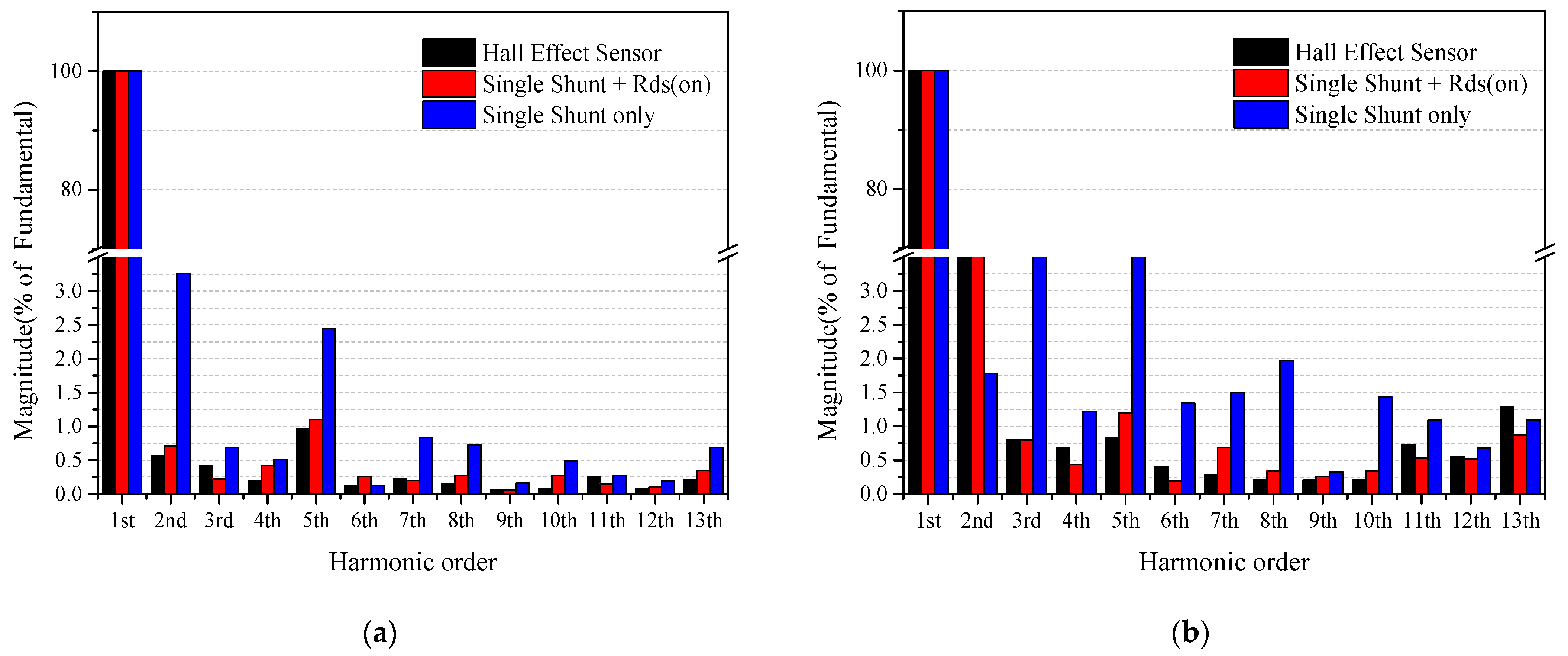
3.2. Current Measurement Using Rds(on) of MOSFET
4. Conclusions and Further Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chou, H.-H.; Chen, H.-L.; Fan, Y.-H.; Wang, S.-F. Adaptive On-Time Control Buck Converter with a Novel Virtual Inductor Current Circuit. Electronics 2021, 10, 2143. [Google Scholar] [CrossRef]
- Zhen, S.; Zeng, P.; Chen, J.; Zhou, W.; Wang, J.; Luo, P.; Zhang, B. Transient Response Improvement of DC-DC Converter by Current Mode Variable on Time Control. In Proceedings of the 2018 IEEE 61st International Midwest Symposium on Circuits and Systems (MWSCAS), Windsor, ON, Canada, 5–8 August 2018. [Google Scholar]
- Jiang, C.R.; Chai, C.C.; Han, C.X.; Yang, Y.T. A high performance adaptive on-time controlled valley-current-mode DC-DC buck converter. J. Semicond. 2020, 41, 062406. [Google Scholar] [CrossRef]
- Chen, J.J.; Hwang, Y.S.; Ku, Y.T.; Li, Y.H.; Chen, J.A. A Current-Mode-Hysteretic Buck Converter with Constant-Frequency-Controlled and New Active-Current-Sensing Techniques. IEEE Trans. Power Electron. 2021, 36, 3126–3134. [Google Scholar] [CrossRef]
- Zhao, J.; Nalakath, S.; Emadi, A. A High Frequency Injection Technique with Modified Current Reconstruction for Low-Speed Sensorless Control of IPMSMs With a Single DC-Link Current Sensor. IEEE Access 2019, 7, 136137–136147. [Google Scholar] [CrossRef]
- Li, X.; Cheng, S.; Wang, D.; Ji, Z.; Hu, Y.; Lv, Y. A Nonintrusive Current Sensor Gain Tuning Method for Interior Permanent Magnet Synchronous Motor Drives Using Controlled Short Circuit Tests. IEEE Trans. Transp. Electrif. 2021, 2021, 1. [Google Scholar] [CrossRef]
- Lu, J.; Hu, Y.; Liu, J.; Wang, Z. All Current Sensor Survivable IPMSM Drive with Reconfigurable Inverter. IEEE Trans. Ind. Electron. 2020, 67, 6331–6341. [Google Scholar] [CrossRef]
- Sun, K.; Wei, Q.; Huang, L.; Matsuse, K. An Overmodulation Method for PWM-Inverter-Fed IPMSM Drive with Single Current Sensor. IEEE Trans. Ind. Electron. 2010, 57, 3395–3404. [Google Scholar] [CrossRef]
- Lu, J.; Hu, Y.; Liu, J. Analysis and Compensation of Sampling Errors in TPFS IPMSM Drives with Single Current Sensor. IEEE Trans. Ind. Electron. 2019, 66, 3852–3855. [Google Scholar] [CrossRef]
- Lu, J.; Hu, Y.; Liu, J.; Zhang, X.; Wen, H.; Wang, Z. Position Sensor Fault Detection of IPMSM Using Single DC-Bus Current Sensor With Accuracy Uncertainty. IEEE/ASME Trans. Mechatron. 2019, 24, 753–762. [Google Scholar] [CrossRef]
- Jena, M.R.; Mohanty, K.B. Maximum efficiency controller for IPMSM using single DC link current sensor. In Proceedings of the 2020 IEEE International Symposium on Sustainable Energy, Signal Processing and Cyber Security (iSSSC), Gunupur Odisha, India, 16–17 December 2020. [Google Scholar]
- Zhang, G.; Zhou, H.; Wang, G.; Li, C.; Xu, D. Current Sensor Fault-Tolerant Control for Encoderless IPMSM Drives Based on Current Space Vector Error Reconstruction. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 3658–3668. [Google Scholar] [CrossRef]
- Aiello, O. Hall-Effect Current Sensors Susceptibility to EMI: Experimental Study. Electronics 2019, 8, 1310. [Google Scholar] [CrossRef] [Green Version]
- Andreozzi, E.; Gargiulo, G.D.; Fratini, A.; Esposito, D.; Bifulco, P. A Contactless Sensor for Pacemaker Pulse Detection: Design Hints and Performance Assessment. Sensors 2018, 18, 2715. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ali, I.; Rikhan, B.S.; Kim, D.-G.; Lee, D.-S.; Rehman, M.R.U.; Abbasizadeh, H.; Asif, M.; Lee, M.; Hwang, K.C.; Yang, Y.; et al. Design of a Low-Power, Small-Area AEC-Q100-Compliant SENT Transmitter in Signal Conditioning IC for Automotive Pressure and Temperature Complex Sensors in 180 Nm CMOS Technology. Sensors 2018, 18, 1555. [Google Scholar] [CrossRef] [Green Version]
- Aiello, O.; Fiori, F. A New Mirroring Circuit for Power MOS Current Sensing Highly Immune to EMI. Sensors 2013, 13, 1856–1871. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Khvitia, B.; Gheonjian, A.; Kutchadze, Z.; Jobava, R. A SPICE Model for IGBTs and Power MOSFETs Focusing on EMI/EMC in High-Voltage Systems. Electronics 2021, 10, 2822. [Google Scholar] [CrossRef]
- Ha, J.I. Voltage injection method for three-phase current reconstruction in PWM inverters using a single sensor. IEEE Trans. Power Electron. 2009, 24, 767–775. [Google Scholar]
- Van Wyk, J.D. Power electronics for motion control. Proc. IEEE 1994, 82, 1164–1193. [Google Scholar] [CrossRef]
- Guanqun, Q.; Qiu, G.; Liao, J.; Wu, B.; Shi, Z. Suppressing DC Current Injection in Transformerless Grid-Connected Inverter Using a Customized Current Sensor. IEEE Trans. Power Electron. 2021, 36, 11003–11008. [Google Scholar]
- Abdelhakim, A.; Mattavelli, P.; Yang, D.; Blaabjerg, F. Coupled-Inductor-Based DC Current Measurement Technique for Transformerless Grid-Tied Inverters. IEEE Trans. Power Electron. 2018, 33, 18–23. [Google Scholar] [CrossRef] [Green Version]
- Adamczyk, M.; Orlowska-Kowalska, T. Post-Fault Direct Field-Oriented Control of Induction Motor Drive using Adaptive Virtual Current Sensor. IEEE Trans. Industrial Electron. 2021, 2021, 1. [Google Scholar] [CrossRef]
- Jahns, T.M. Motion control with permanent-magnet AC machines. Proc. IEEE 1994, 82, 1241–1252. [Google Scholar] [CrossRef]
- Blaabjerg, F.; Pedersen, J.K.; Jaeger, U.; Thoegersen, P. Single current sensor technique in the DC link of three-phase PWM-VS inverters. IEEE Trans. Ind. Appl. 1997, 33, 1241–1253. [Google Scholar] [CrossRef]
- Bang, J.O. A Study on High Performance Current Detection Method Using Shunt Resistor of 3-Phase Inverter; Kookmin University: Seoul, Korea, 2019. [Google Scholar]
- Kwon, S.H. A Study on Sensorless and Over-Modulation Algorithm Based on Single Current Sensor of PMSM; Kookmin University: Seoul, Korea, 2018. [Google Scholar]
- Wang, Y.; Duan, B.; Song, H.; Yang, Y. Novel Lateral Double-Diffused MOSFET with Ultralow On-Resistance by the Variable Resistivity of Drift Region. IEEE Electron. Device Lett. 2020, 41, 1681–1684. [Google Scholar] [CrossRef]
- Lim, H.J. Current Detection Technique Using DC-Shunt and FET Voltage Drop of Three Phase Inverter; Kookmin University: Seoul, Korea, 2020. [Google Scholar]
- Lavrič, H.; Fišer, R. Lossless current sensing technique on MOSFET RDS(on) with improved accuracy. Electron. Lett. 2010, 46, 370–371. [Google Scholar] [CrossRef]
- Aiello, O.; Fiori, F. A new current sensor based on MagFET highly immune to EMI. In Proceedings of the 2009 International Conference on Electromagnetics in Advanced Applications, Turin, Italy, 14–18 September 2009; pp. 784–787. [Google Scholar] [CrossRef]
- Kim, S. Kalman Filter Is Not Difficult with MATLAB Example; HANBIT Academy: Seoul, Korea, 2013; p. 62. [Google Scholar]
- Three Phase Full Bridge MOSFET, IXYS DCB-Isolated High-Current Package MTI145WX100GD. 2017. Available online: https://kr.mouser.com/datasheet/2/240/MTI145WX100GD-1623320.pdf (accessed on 12 October 2021).
- Buttay, C.; Bergogne, D.; Herve, M.; Bruno, A.; Rene, E.; Pascal, B. Towards a Sensorless Current and Temperature Monitoring in MOS-FET-Based H-Bridge. In Proceedings of the 2003 IEEE 34th Annual Power Electronics Specialist Conference, Acapulco, Mexico, 15–19 June 2003; pp. 901–906. [Google Scholar]
- Pajer, R. MOS-FET as a Current Sensor in Power Electronics Converters. Sensors 2015, 15, 18061–18079. [Google Scholar] [CrossRef] [PubMed]





| Tj (°C) | 0 | 25 | 50 | 75 | 100 | 125 | 150 |
|---|---|---|---|---|---|---|---|
| r | 0.887 | 1 | 1.133 | 1.284 | 1.455 | 1.649 | 1.868 |
| Rds-on (Tj) (Ω) | 1.50 | 1.70 | 1.93 | 2.18 | 2.47 | 2.80 | 3.18 |
| Coefficients | K0 | K1 | K2 |
|---|---|---|---|
| 1.63 × 10−5 | 3.28 × 10−3 | 7.85 × 10−1 |
| Property | (a) | (b) | (c) |
|---|---|---|---|
| Rds(on) Avg (mΩ) | 1.706 | 1.941 | 2.192 |
| Rds(on) Data Sheet (mΩ) | 1.7 | 1.95 | 2.2 |
| Rds(on) Err (%) | 0.36 | 0.44 | 0.35 |
| Temperature Est (°C) | 25.11 | 52.42 | 76.57 |
| Temperature Act (°C) | 24.62 | 50.91 | 74.01 |
| Temperature Err (%) | 1.98 | 2.89 | 3.35 |
| Case | Operating Condition | |
|---|---|---|
| 10 Apk@700 rpm | 5 Apk@130 rpm | |
| Hall-effect sensor | 1.73% | 2.37% |
| Shingle shunt + Rds(on) | 1.75% | 2.14% |
| Single shunt only | 3.05% | 4.89% |
| Reference | 2020 3 | 2021 2 | 2021 1 | This Work |
|---|---|---|---|---|
| Results | Simulation | Measurement | Simulation | Measurement |
| Control scheme | AOT * | Hysteretic PLL | AOT * | PCS ** |
| Process (μm) | 0.18 | 0.35 | 0.35 | 0.3–0.5 |
| Input voltage (V) | 3.3–5.0 | 3.3–3.6 | 3.0–3.6 | 3.3–5.0 |
| Output voltage (V) | 1.8 | 0.9–2.5 | 1.0–2.5 | 2.5 |
| Inductor (μH) | 1.5 | 4.7 | 4.7 | 4.0 |
| Output capacitor (μF) | 20 | 10 | 10 | 10 |
| Max. load current (mA) | 2000 | 600 | 500 | 10000 |
| Load current step (mA) | 800 | 400 | 400 | 1000 |
| Undershoot/overshoot (mV) | 13/14 | 30/60 | 23/26 | 22/30 |
| Recovery time (μs) (rise/fall) | 6/2 | 2.6/2.2 | 1.98/1.6 | 2.5/2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hwang, J.-Y.; Park, J.-H.; Choi, J.-H.; Uhm, J.-I.; Lee, G.-H.; Lim, H.-S. A Precise Current Detection Method Using a Single Shunt and FET Rds(on) of a Low-Voltage Three-Phase Inverter. Electronics 2022, 11, 9. https://doi.org/10.3390/electronics11010009
Hwang J-Y, Park J-H, Choi J-H, Uhm J-I, Lee G-H, Lim H-S. A Precise Current Detection Method Using a Single Shunt and FET Rds(on) of a Low-Voltage Three-Phase Inverter. Electronics. 2022; 11(1):9. https://doi.org/10.3390/electronics11010009
Chicago/Turabian StyleHwang, Jae-Yeob, Ji-Hwan Park, Ji-Ho Choi, Jun-Ik Uhm, Geun-Ho Lee, and Hee-Sun Lim. 2022. "A Precise Current Detection Method Using a Single Shunt and FET Rds(on) of a Low-Voltage Three-Phase Inverter" Electronics 11, no. 1: 9. https://doi.org/10.3390/electronics11010009
APA StyleHwang, J.-Y., Park, J.-H., Choi, J.-H., Uhm, J.-I., Lee, G.-H., & Lim, H.-S. (2022). A Precise Current Detection Method Using a Single Shunt and FET Rds(on) of a Low-Voltage Three-Phase Inverter. Electronics, 11(1), 9. https://doi.org/10.3390/electronics11010009






