Global Sensitivity Analysis of Economic Model Predictive Longitudinal Motion Control of a Battery Electric Vehicle
Abstract
:1. Introduction
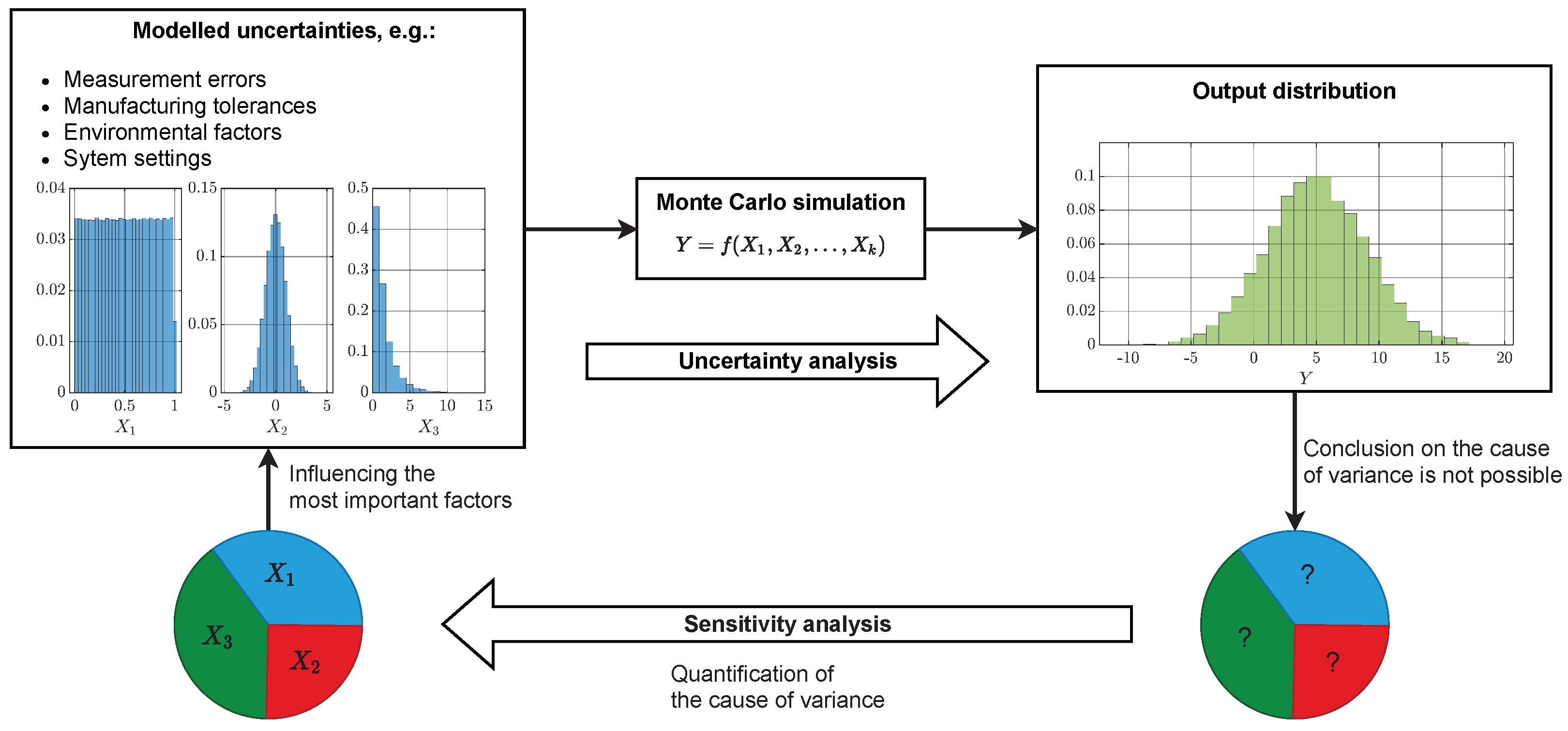
2. Sensitivity Analysis
2.1. Morris Screening
2.2. Variance-Based Sensitivity Analysis
2.3. Time and State Dependency of Technical Processes
- Point-in-time indices ignore all time correlations of the process.
- The variance of the process varies in time, which skews the relative importance across time.
3. Simulation Setup
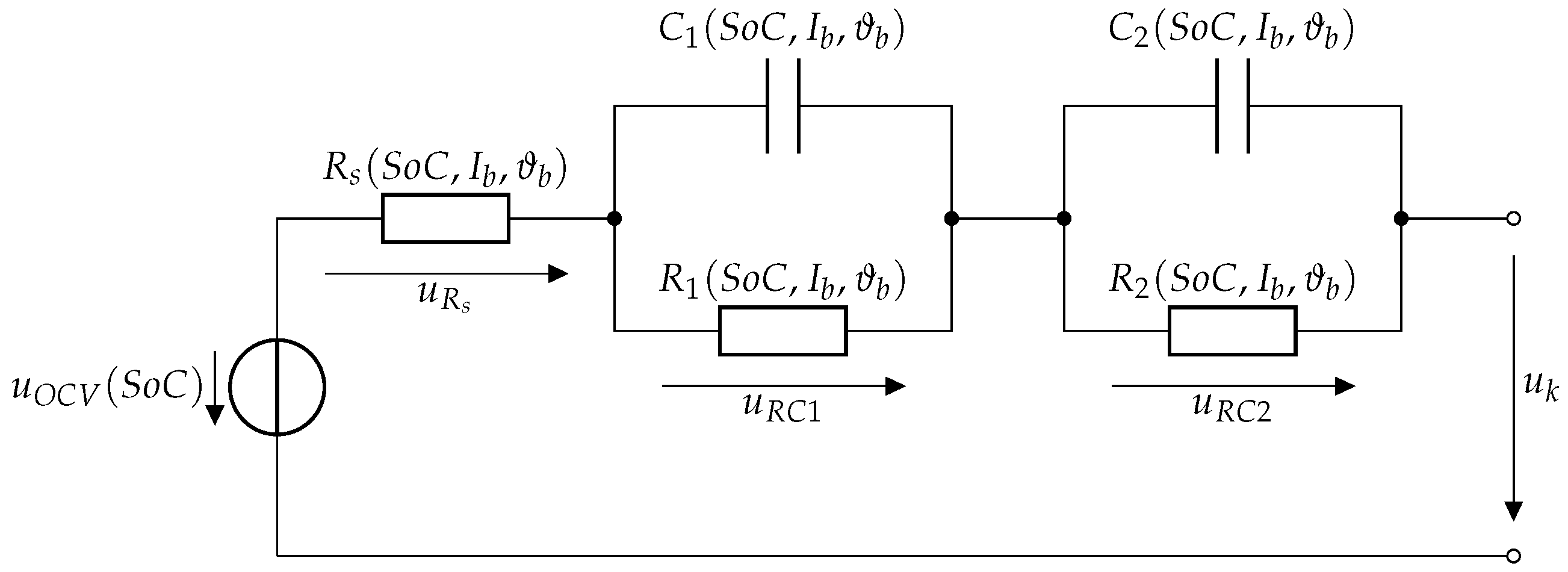
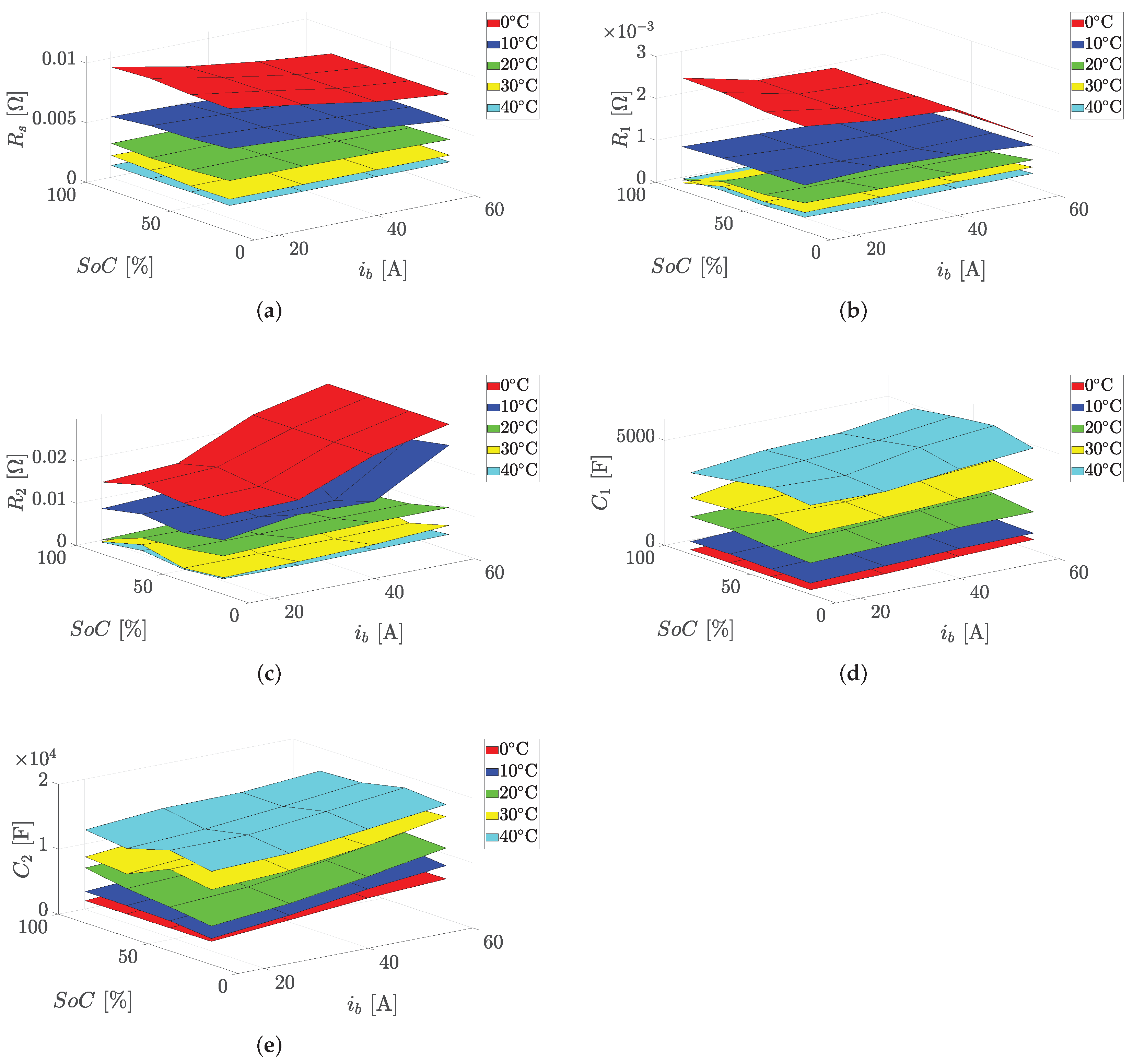
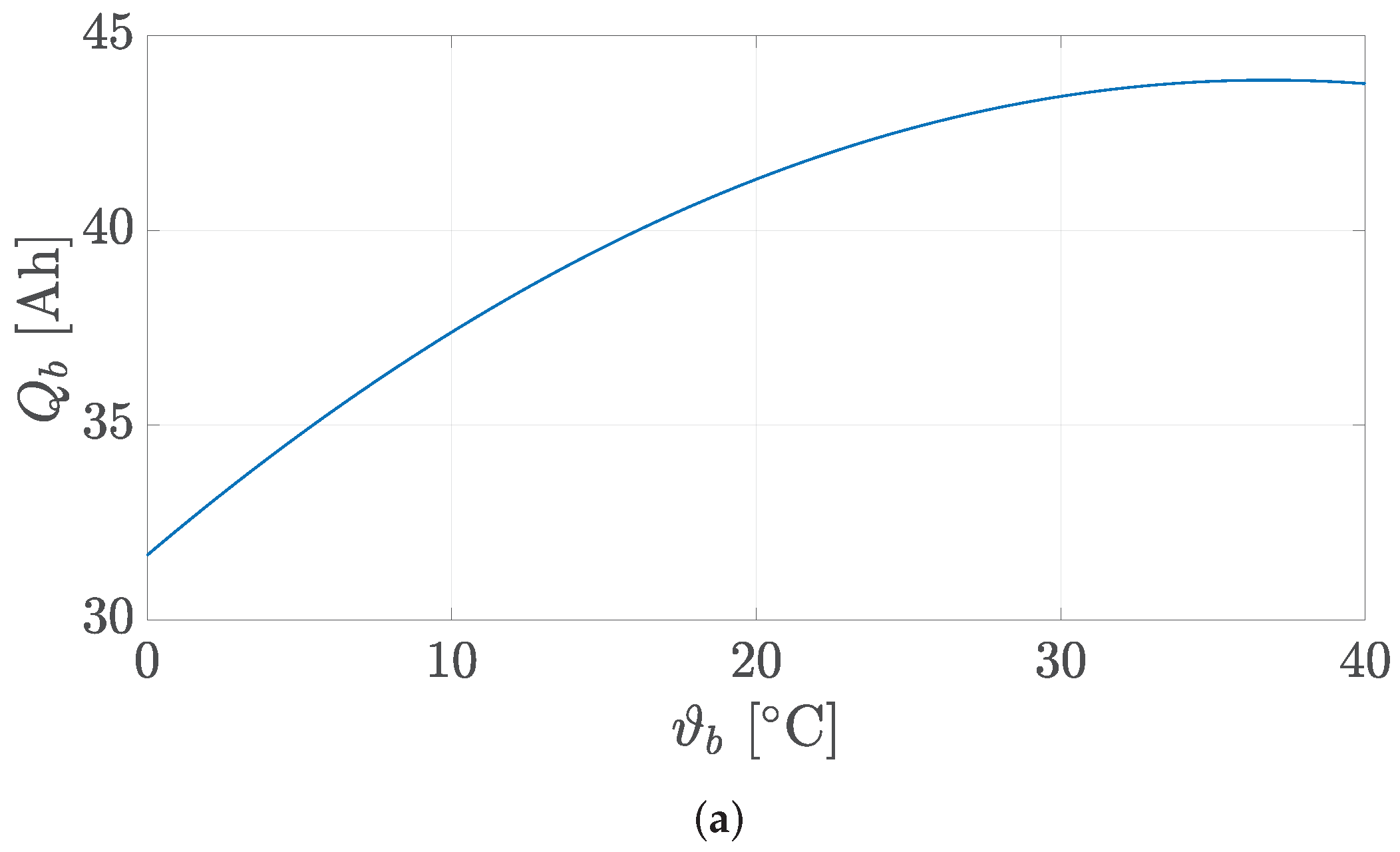
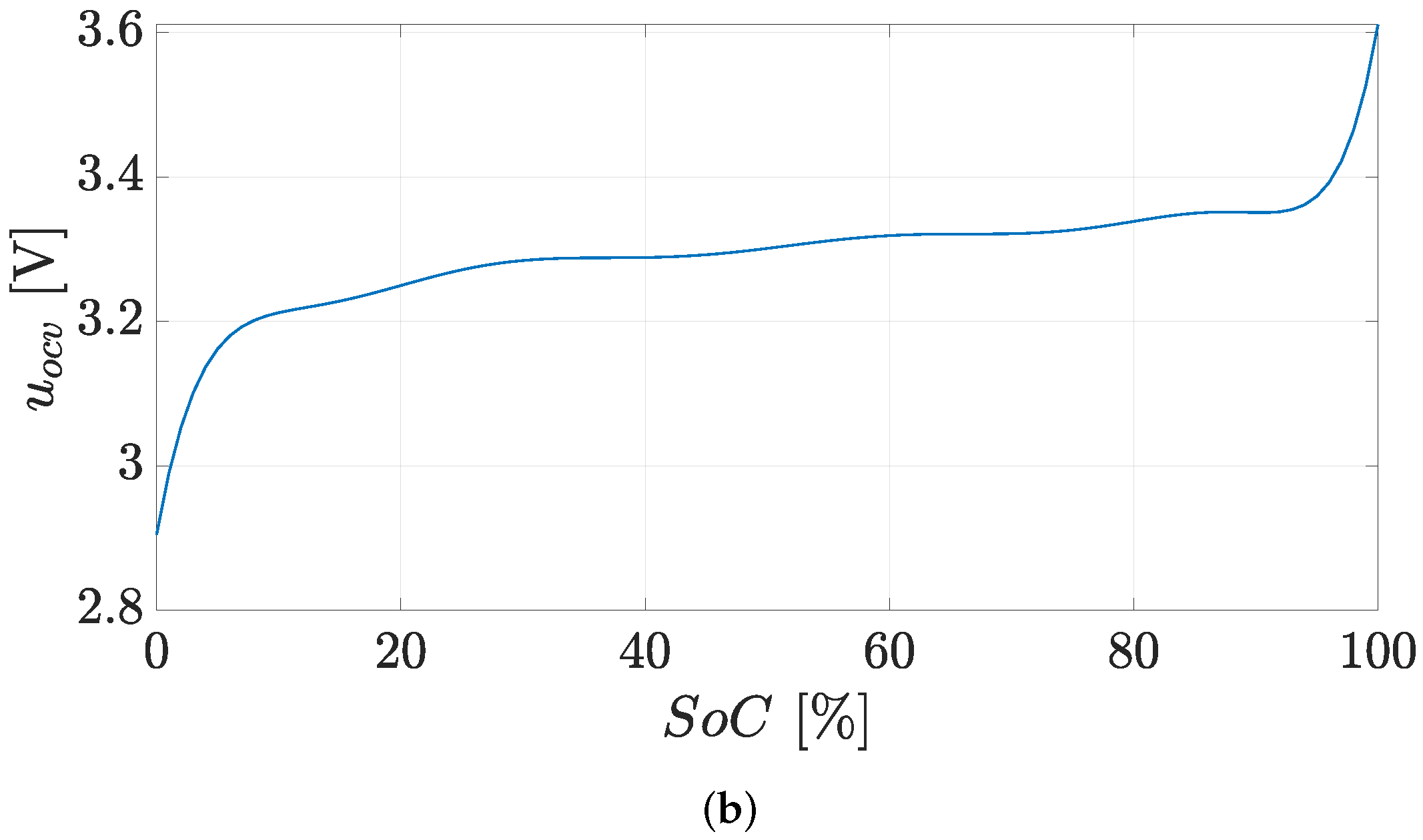
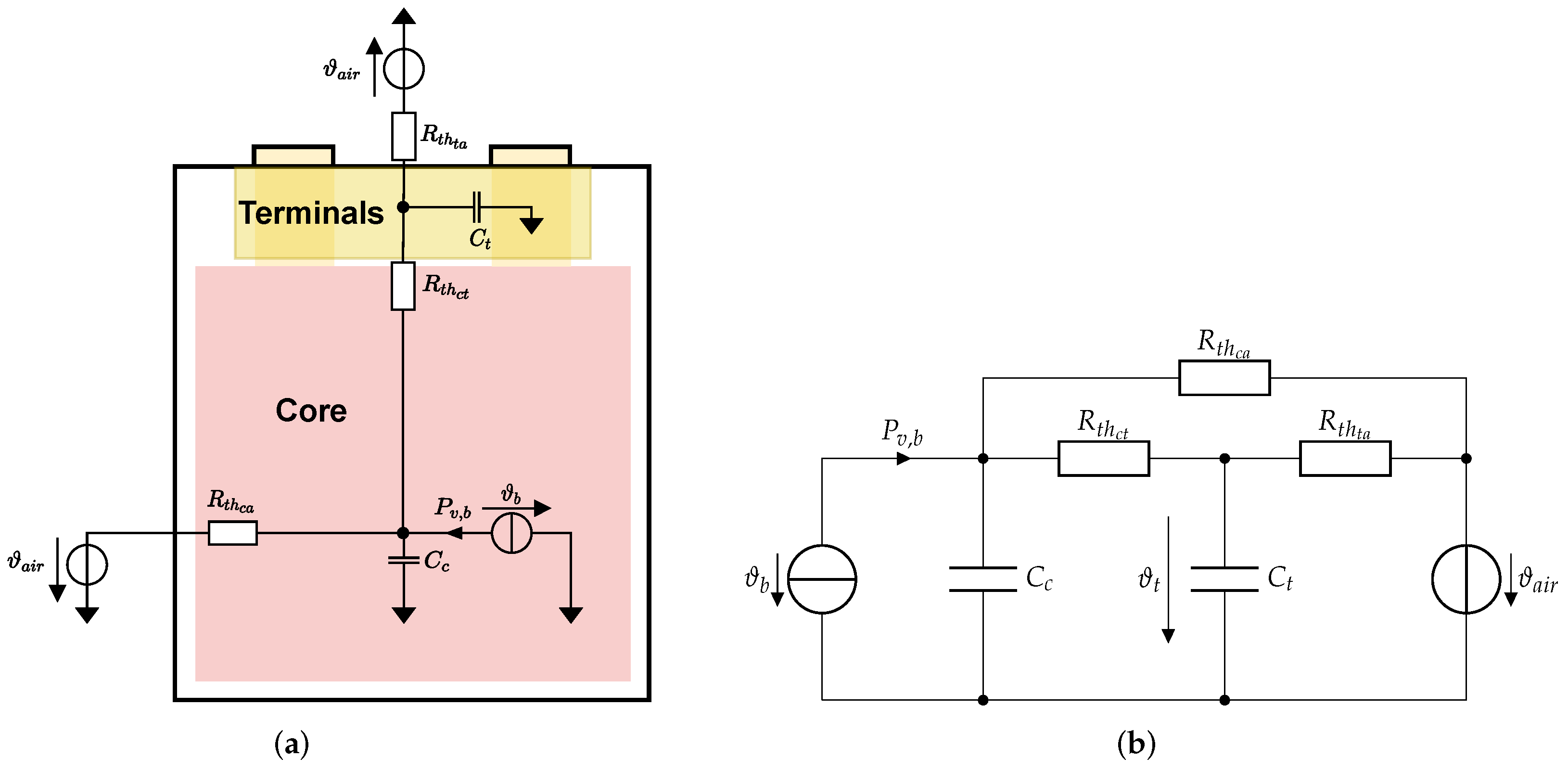
3.1. Battery Model
3.1.1. Electrical Model
3.1.2. Thermal Model
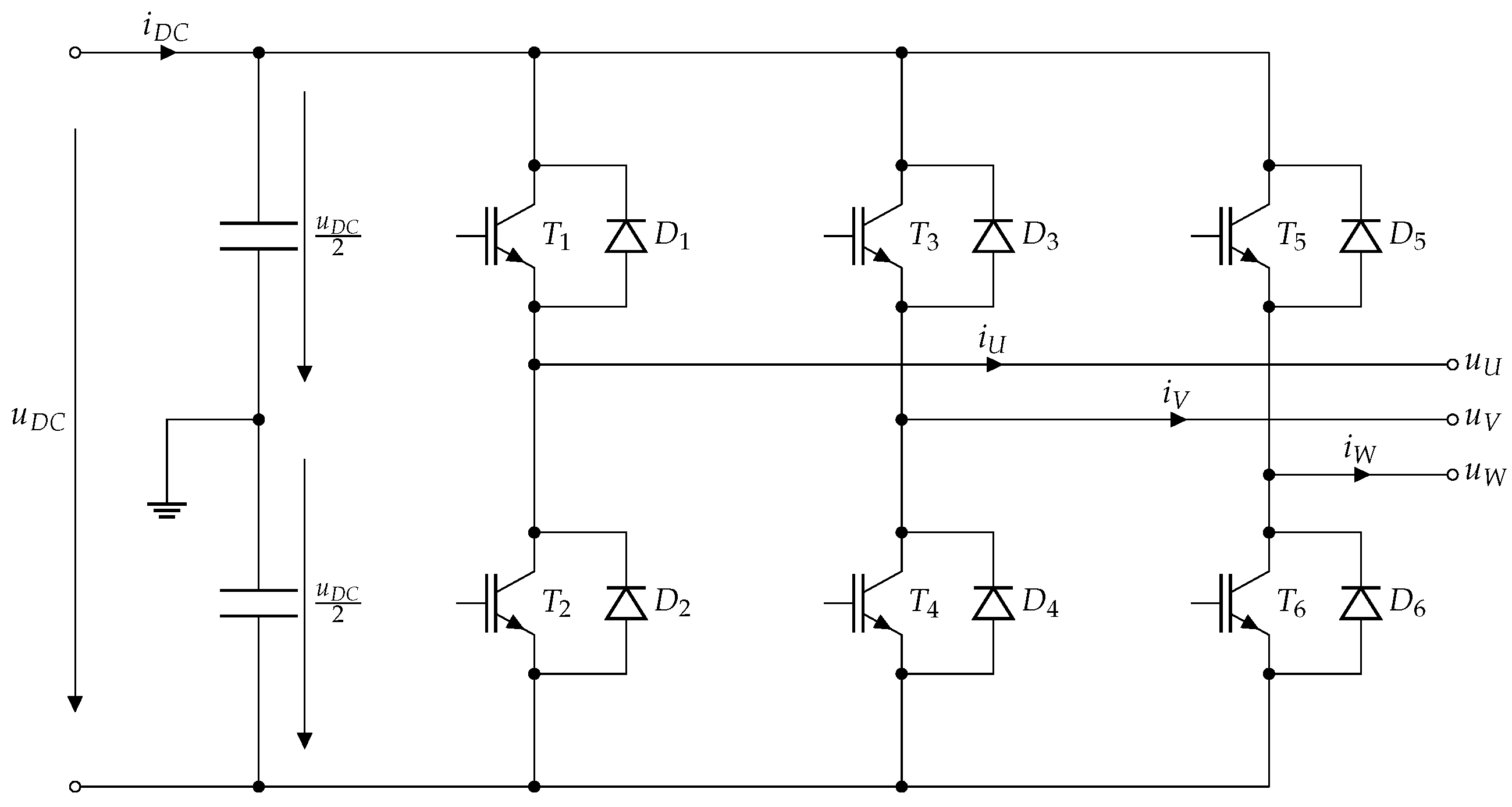
3.2. Inverter Model
3.2.1. Conduction Losses
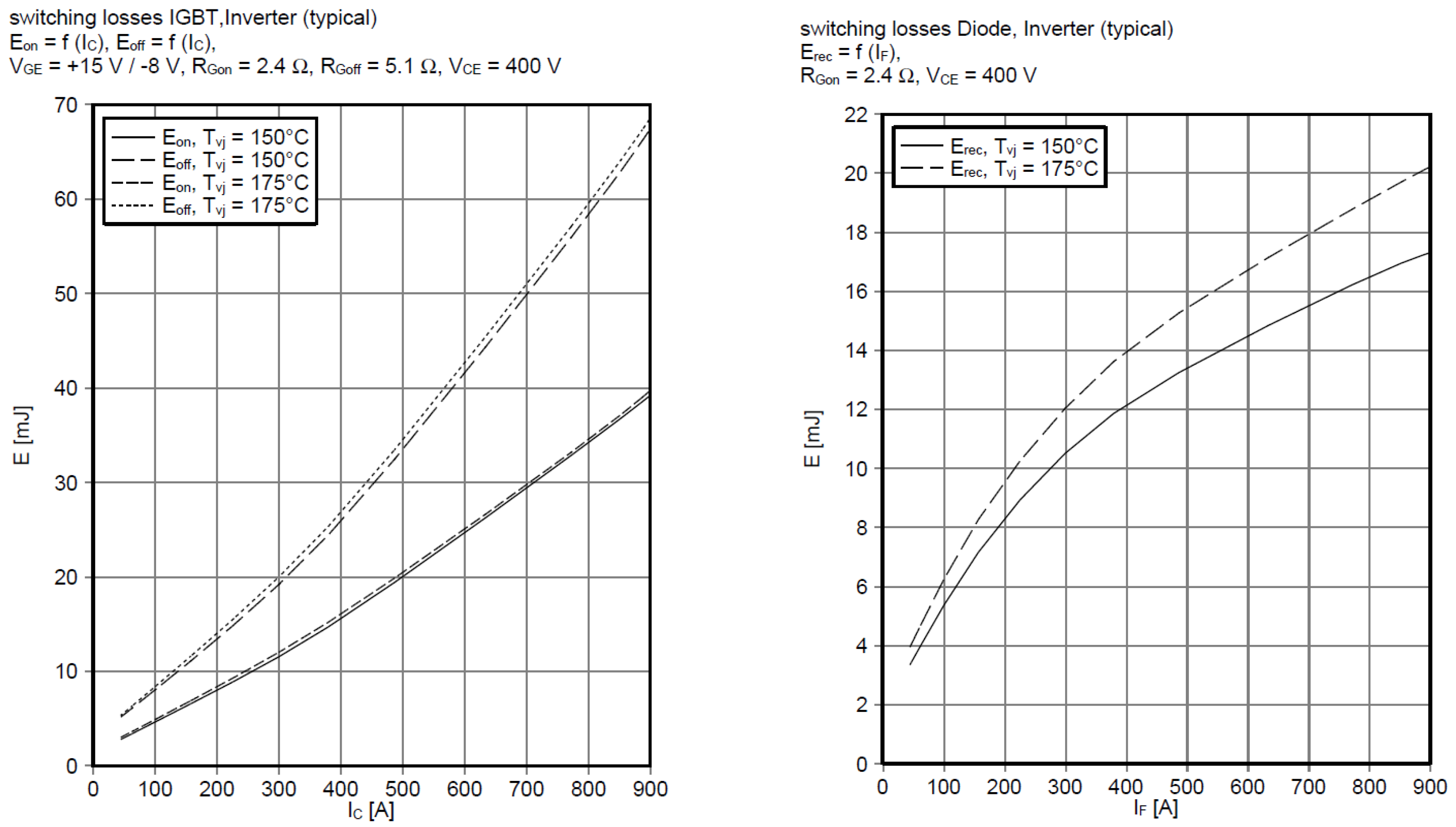
3.2.2. Switching Losses
3.2.3. Thermal Model
3.3. EM Model
3.4. Environment Model
- Legal speed limit;
- Curve radii;
- Road slope and elevation.
4. Longitudinal Economic MPC
5. Sensitivity Setup
- Which parameters are investigated;
- The injection point of each parameter;
- The distribution underlying each parameter;
- The model outputs of interest.
6. Simulation Results
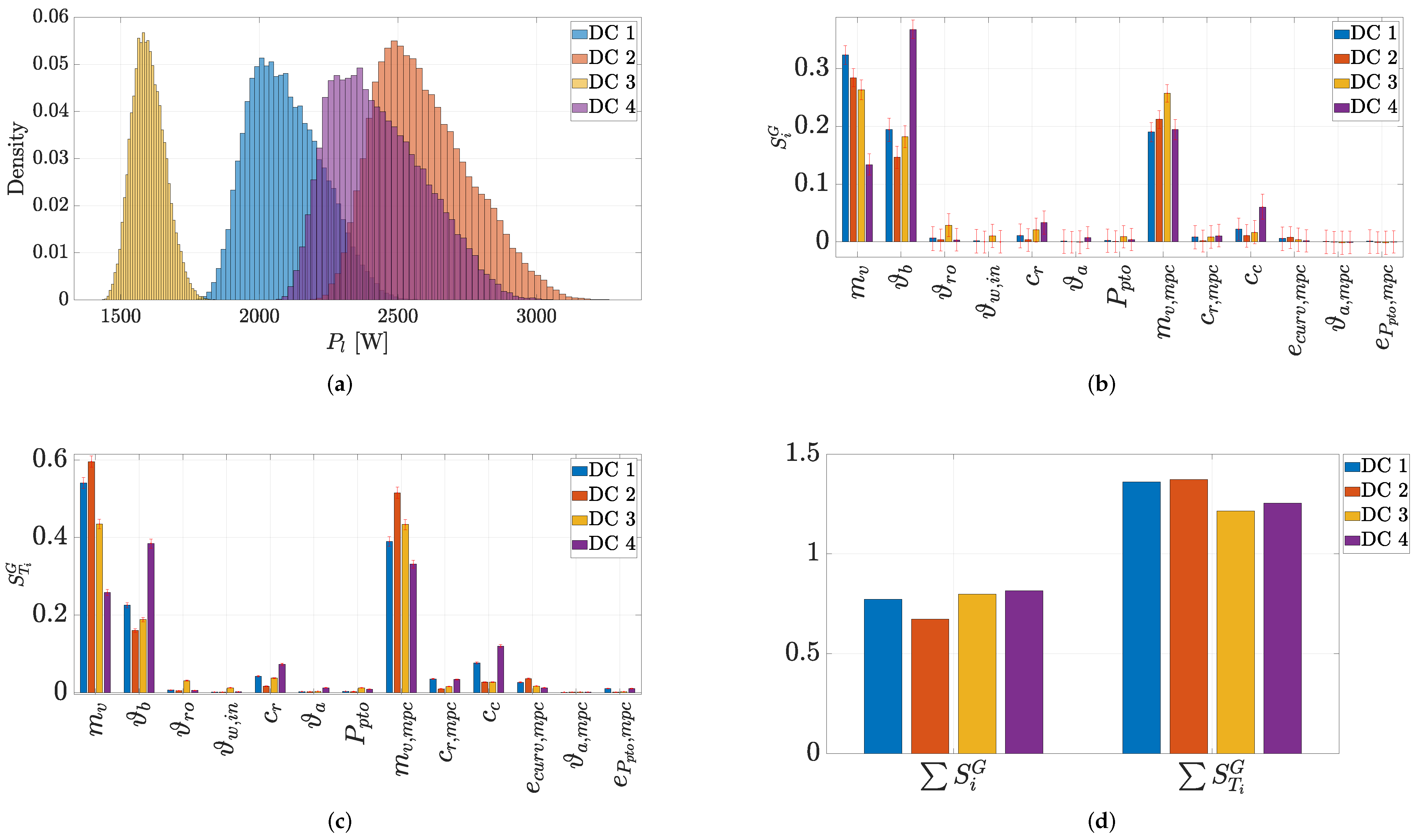
6.1. Morris Screening
6.2. Sobol Indices
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ANOVA | Analysis of variance |
| BEV | Battery electric vehicle |
| EMPC | Economic model predictive control |
| HDMR | High-dimensional model representation |
| IGBT | Insulated gate bipolar transistor |
| MPC | Model predictive control |
| NMPC | Nonlinear model predictive control |
| PMSM | Permanent magnet synchronous machine |
| PWM | Pulse width modulation |
| SoC | State of charge |
| VSI | Voltage source inverter |
Appendix A
Appendix A.1. Longitudinal Motion Model
| Parameter | Description | Value |
|---|---|---|
| Air drag coefficient | 0.262 | |
| Frontal area | 2.036 m2 | |
| Vehicle mass | 550 kg | |
| Equivalent vehicle mass (including rotational inertia) | 569 kg | |
| Wheel radius | 0.283 m | |
| Gear ratio | 5.85 |
References
- Jayakumar, A.; Chalmers, A.; Lie, T.T. Review of prospects for adoption of fuel cell electric vehicles in New Zealand. IET Electr. Syst. Transp. 2017, 7, 259–266. [Google Scholar] [CrossRef]
- Vaezipour, A.; Rakotonirainy, A.; Haworth, N. Reviewing In-vehicle Systems to Improve Fuel Efficiency and Road Safety. Procedia Manuf. 2015, 3, 3192–3199. [Google Scholar] [CrossRef]
- Barkenbus, J.N. Eco-driving: An overlooked climate change initiative. Energy Policy 2010, 38, 762–769. [Google Scholar] [CrossRef]
- Schwickart, T.; Voos, H.; Hadji-Minaglou, J.R.; Darouach, M.; Rosich, A. Design and simulation of a real-time implementable energy-efficient model-predictive cruise controller for electric vehicles. J. Frankl. Inst. 2015, 352, 603–625. [Google Scholar] [CrossRef]
- Schwickart, T.; Voos, H.; Hadji-Minaglou, J.R.; Darouach, M. A Fast Model-Predictive Speed Controller for Minimised Charge Consumption of Electric Vehicles. Asian J. Control. 2016, 18, 133–149. [Google Scholar] [CrossRef]
- Naus, G.; Ploeg, J.; van de Molengraft, M.; Heemels, W.; Steinbuch, M. Design and implementation of parameterized adaptive cruise control: An explicit model predictive control approach. Control Eng. Pract. 2010, 18, 882–892. [Google Scholar] [CrossRef]
- Jia, Y.; Jibrin, R.; Itoh, Y.; Görges, D. Energy-Optimal Adaptive Cruise Control for Electric Vehicles in Both Time and Space Domain based on Model Predictive Control. IFAC-PapersOnLine 2019, 52, 13–20. [Google Scholar] [CrossRef]
- Kamal, M.A.S.; Mukai, M.; Murata, J.; Kawabe, T. Model Predictive Control of Vehicles on Urban Roads for Improved Fuel Economy. IEEE Trans. Control Syst. Technol. 2013, 21, 831–841. [Google Scholar] [CrossRef]
- Caldas, K.A.Q.; Grassi, V. Eco-cruise NMPC Control for Autonomous Vehicles. In Proceedings of the 19th International Conference on Advanced Robotics (ICAR), Belo Horizonte, Brazil, 2–6 December 2019; IEEE: New York, NY, USA, 2019; pp. 356–361. [Google Scholar] [CrossRef]
- Chen, Y.; Li, X.; Wiet, C.; Wang, J. Energy Management and Driving Strategy for In-Wheel Motor Electric Ground Vehicles with Terrain Profile Preview. IEEE Trans. Ind. Inform. 2014, 10, 1938–1947. [Google Scholar] [CrossRef]
- Weißmann, A.; Görges, D.; Lin, X. Energy-Optimal Adaptive Cruise Control based on Model Predictive Control. IFAC-PapersOnLine 2017, 50, 12563–12568. [Google Scholar] [CrossRef]
- Sajadi-Alamdari, S.A.; Voos, H.; Darouach, M. Nonlinear model predictive extended eco-cruise control for battery electric vehicles. In Proceedings of the 24th Mediterranean Conference on Control and Automation (MED), Athens, Greece, 21–24 June 2016; IEEE: New York, NY, USA, 2016; pp. 467–472. [Google Scholar] [CrossRef] [Green Version]
- Vajedi, M.; Azad, N.L. Ecological Adaptive Cruise Controller for Plug-In Hybrid Electric Vehicles Using Nonlinear Model Predictive Control. IEEE Trans. Intell. Transp. Syst. 2016, 17, 113–122. [Google Scholar] [CrossRef]
- Frezza, G.; Evangelou, S.A. Ecological Adaptive Cruise Controller for a Parallel Hybrid Electric Vehicle. In Proceedings of the European Control Conference (ECC), St. Petersburg, Russia, 12–15 May 2020; IEEE: New York, NY, USA, 2020; pp. 491–498. [Google Scholar] [CrossRef]
- Sajadi-Alamdari, S.A.; Voos, H.; Darouach, M. Risk-averse Stochastic Nonlinear Model Predictive Control for Real-time Safety-critical Systems. IFAC-PapersOnLine 2017, 50, 5991–5997. [Google Scholar] [CrossRef]
- Sajadi-Alamdari, S.A.; Voos, H.; Darouach, M. Fast stochastic non-linear model predictive control for electric vehicle advanced driver assistance systems. In Proceedings of the IEEE International Conference on Vehicular Electronics and Safety (ICVES), Vienna, Austria, 27–28 June 2017; IEEE: New York, NY, USA, 2017; pp. 91–96. [Google Scholar] [CrossRef] [Green Version]
- Sajadi-Alamdari, S.A.; Voos, H.; Darouach, M. Nonlinear Model Predictive Control for Ecological Driver Assistance Systems in Electric Vehicles. Robot. Auton. Syst. 2019, 112, 291–303. [Google Scholar] [CrossRef] [Green Version]
- Moser, D.; Waschl, H.; Kirchsteiger, H.; Schmied, R.; del Re, L. Cooperative adaptive cruise control applying stochastic linear model predictive control strategies. In Proceedings of the European Control Conference (ECC), Linz, Austria, 15–17 July 2015; IEEE: New York, NY, USA, 2015; pp. 3383–3388. [Google Scholar] [CrossRef]
- Moser, D.; Schmied, R.; Waschl, H.; del Re, L. Flexible Spacing Adaptive Cruise Control Using Stochastic Model Predictive Control. IEEE Trans. Control Syst. Technol. 2018, 26, 114–127. [Google Scholar] [CrossRef]
- Morris, M.D. Factorial Sampling Plans for Preliminary Computational Experiments. Technometrics 1991, 33, 161–174. [Google Scholar] [CrossRef]
- Sobol, I.M. Sensitivity Analysis for Nonlinear Mathematical Models. Math. Model. Comput. Exp. 1993, 1, 407–414. [Google Scholar]
- Vepsäläinen, J.; Ritari, A.; Lajunen, A.; Kivekäs, K.; Tammi, K. Energy Uncertainty Analysis of Electric Buses. Energies 2018, 11, 3267. [Google Scholar] [CrossRef] [Green Version]
- Vepsäläinen, J.; Otto, K.; Lajunen, A.; Tammi, K. Computationally efficient model for energy demand prediction of electric city bus in varying operating conditions. Energy 2019, 169, 433–443. [Google Scholar] [CrossRef]
- Asamer, J.; Graser, A.; Heilmann, B.; Ruthmair, M. Sensitivity analysis for energy demand estimation of electric vehicles. Transp. Res. Part Transp. Environ. 2016, 46, 182–199. [Google Scholar] [CrossRef]
- Zhao, S.; Howey, D.A. Global Sensitivity Analysis of Battery Equivalent Circuit Model Parameters. In Proceedings of the IEEE Vehicle Power and Propulsion Conference (VPPC), Hangzhou, China, 17–20 October 2016; IEEE: New York, NY, USA, 2016; pp. 1–4. [Google Scholar] [CrossRef] [Green Version]
- Grandjean, T.R.B.; Li, L.; Odio, M.X.; Widanage, W.D. Global Sensitivity Analysis of the Single Particle Lithium-Ion Battery Model with Electrolyte. In Proceedings of the IEEE Vehicle Power and Propulsion Conference (VPPC), Hanoi, Vietnam, 14–17 October 2019; IEEE: New York, NY, USA, 2019; pp. 1–7. [Google Scholar] [CrossRef] [Green Version]
- Braband, M.; Adams, M.; Wilhelmi, A.; Scherer, M. Global Sensitivity Analysis on the Torque Accuracy of the Powertrain in Electric Vehicles. IFAC-PapersOnLine 2020, 53, 14067–14072. [Google Scholar] [CrossRef]
- Asef, P.; Lapthorn, A. Overview of Sensitivity Analysis Methods Capabilities for Traction AC Machines in Electrified Vehicles. IEEE Access 2021, 9, 23454–23471. [Google Scholar] [CrossRef]
- Saltelli, A.; Aleksankina, K.; Becker, W.; Fennell, P.; Ferretti, F.; Holst, N.; Li, S.; Wu, Q. Why so many published sensitivity analyses are false: A systematic review of sensitivity analysis practices. Environ. Model. Softw. 2019, 114, 29–39. [Google Scholar] [CrossRef]
- Alexanderian, A.; Gremaud, P.A.; Smith, R.C. Variance-based sensitivity analysis for time-dependent processes. Reliab. Eng. Syst. Saf. 2020, 196, 106722. [Google Scholar] [CrossRef] [Green Version]
- Campolongo, F.; Saltelli, A. Sensitivity analysis of an environmental model: An application of different analysis methods. Reliab. Eng. Syst. Saf. 1997, 57, 49–69. [Google Scholar] [CrossRef]
- Campolongo, F.; Tarantola, S.; Saltelli, A. Tackling quantitatively large dimensionality problems. Comput. Phys. Commun. 1999, 117, 75–85. [Google Scholar] [CrossRef]
- Campolongo, F.; Cariboni, J.; Saltelli, A. An effective screening design for sensitivity analysis of large models. Environ. Model. Softw. 2007, 22, 1509–1518. [Google Scholar] [CrossRef]
- Saltelli, A.; Annoni, P.; Azzini, I.; Campolongo, F.; Ratto, M.; Tarantola, S. Variance based sensitivity analysis of model output. Design and estimator for the total sensitivity index. Comput. Phys. Commun. 2010, 181, 259–270. [Google Scholar] [CrossRef]
- Homma, T.; Saltelli, A. Importance measures in global sensitivity analysis of nonlinear models. Reliab. Eng. Syst. Saf. 1996, 52, 1–17. [Google Scholar] [CrossRef]
- Gamboa, F.; Janon, A.; Klein, T.; Lagnoux, A. Sensitivity analysis for multidimensional and functional outputs. Electron. J. Stat. 2014, 8, 575–603. [Google Scholar] [CrossRef]
- Doyle, M.; Fuller, T.F.; Newman, J. Modeling of Galvanostatic Charge and Discharge of the Lithium/Polymer/Insertion Cell. J. Electrochem. Soc. 1993, 140, 1526–1533. [Google Scholar] [CrossRef]
- Fuller, T.F.; Doyle, M.; Newman, J. Simulation and Optimization of the Dual Lithium Ion Insertion Cell. J. Electrochem. Soc. 1994, 141, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Krewer, U.; Röder, F.; Harinath, E.; Braatz, R.D.; Bedürftig, B.; Findeisen, R. Review—Dynamic Models of Li-Ion Batteries for Diagnosis and Operation: A Review and Perspective. J. Electrochem. Soc. 2018, 165, A3656–A3673. [Google Scholar] [CrossRef]
- Zhao, R.; Kollmeyer, P.J.; Lorenz, R.D.; Jahns, T.M. A Compact Methodology Via a Recurrent Neural Network for Accurate Equivalent Circuit Type Modeling of Lithium-Ion Batteries. IEEE Trans. Ind. Appl. 2019, 55, 1922–1931. [Google Scholar] [CrossRef]
- Chiasserini, C.F.; Rao, R.R. Energy efficient battery management. IEEE J. Sel. Areas Commun. 2001, 19, 1235–1245. [Google Scholar] [CrossRef]
- Hageman, S.C. Simple PSpice models let you simulate common battery types. Electron. Des. News 1993, 38, 117–129. [Google Scholar]
- Hentunen, A.; Lehmuspelto, T.; Suomela, J. Time-Domain Parameter Extraction Method for Thévenin-Equivalent Circuit Battery Models. IEEE Trans. Energy Convers. 2014, 29, 558–566. [Google Scholar] [CrossRef]
- Hamm, P. Thermische Charakterisierung und Evaluierung einer LiFePO4-Batteriezelle. Master’s Thesis, University of Applied Sciences, Trier, Germany, 2021. [Google Scholar]
- Lehnertz, M. Entwicklung eines Schätzverfahrens zur Bestimmung der Inneren Zelltemperatur von LiFePO4 Batteriezellen. Master’s Thesis, University of Applied Sciences, Trier, Germany, 2021. [Google Scholar]
- Kolar, J.W.; Ertl, H.; Zach, F.C. Influence of the modulation method on the conduction and switching losses of a PWM converter system. IEEE Trans. Ind. Appl. 1991, 27, 502–512. [Google Scholar] [CrossRef]
- Schröder, D. Elektrische Antriebe—Regelung von Antriebssystemen, 4th ed.; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar] [CrossRef]
- Drofenik, U.; Kolar, J.W. A general scheme for calculating switching-and conduction-losses of power semiconductors in numerical circuit simulations of power electronic systems. Proc. IPEC 2005, 5, 4–8. [Google Scholar]
- Bierhoff, M.H.; Fuchs, F.W. Semiconductor losses in voltage source and current source IGBT converters based on analytical derivation. In Proceedings of the IEEE 35th Annual Power Electronics Specialists Conference, Aachen, Germany, 20–25 June 2004; IEEE: New York, NY, USA, 2004; pp. 2836–2842. [Google Scholar] [CrossRef]
- Infineon Technologies AG. HybridPACK Drive Module FS820R08A6P2: Final Data Sheet, V3.3; Infineon Technologies: Neubiberg, Germany, 2019. [Google Scholar]
- Windisch, T.; Hofmann, W. Energieeffiziente Regelung von Fahrzeugantrieben mit permanenterregten Synchron- und Asynchronmotoren unter Berücksichtigung von Umrichter, Eisenverlusten und Sättigung. In Elektrische Antriebstechnologie Für Hybrid-Und Elektrofahrzeuge; Schäfer, H., Ed.; Springer: Berlin/Heidelberg, Germany, 2019; pp. 218–237. [Google Scholar]
- Baehr, H.D.; Stephan, K. Wärme-Und Stoffübertragung, 8th ed.; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar] [CrossRef]
- Schröder, D. Elektrische Antriebe—Grundlagen, 5th ed.; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar] [CrossRef]
- Kellner, S.L.; Seilmeier, M.; Piepenbreier, B. Impact of iron losses on parameter identification of permanent magnet synchronous machines. In Proceedings of the 1st International Electric Drives Production Conference, Nuremberg, Germany, 28–29 September 2011; IEEE: New York, NY, USA, 2011; pp. 11–16. [Google Scholar] [CrossRef]
- Kellner, S.L. Parameteridentifikation bei Permanenterregten Synchronmaschinen. Ph.D. Thesis, University of Erlangen-Nuremberg, Erlangen, Germany, 2012. [Google Scholar]
- HERE Technologies. HERE Plattform. Available online: https://www.here.com/platform (accessed on 22 January 2022).
- Kohut, N.J.; Karl Hedrick, P.J.; Borrelli, P.F. Integrating Traffic Data and Model Predictive Control to Improve Fuel Economy. IFAC Proc. Vol. 2009, 42, 155–160. [Google Scholar] [CrossRef] [Green Version]
- Faulwasser, T.; Grüne, L.; Müller, M.A. Economic Nonlinear Model Predictive Control. Found. Trends® Syst. Control. 2018, 5, 1–98. [Google Scholar] [CrossRef]
- Verschueren, R.; Frison, G.; Kouzoupis, D.; Frey, J.; van Duijkeren, N.; Zanelli, A.; Novoselnik, B.; Albin, T.; Quirynen, R.; Diehl, M. acados—A modular open-source framework for fast embedded optimal control. Math. Program. Comput. 2022, 14, 147–183. [Google Scholar] [CrossRef]
- Schwickart, T.K. Energy-Efficient Driver Assistance System for Electric Vehicles Using Model-Predictive Control. Ph.D. Thesis, University of Luxembourg, Luxemburg, 2015. [Google Scholar]



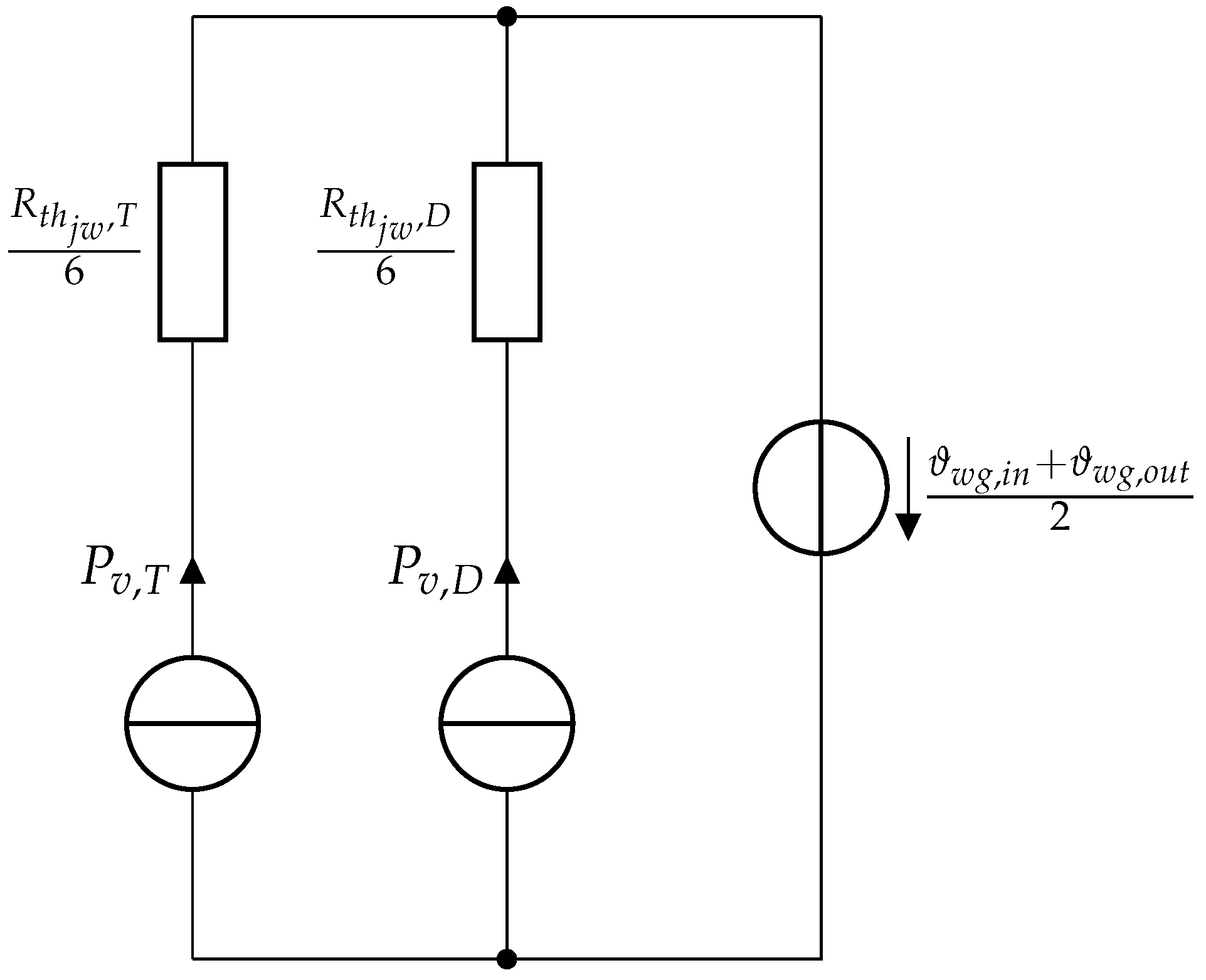
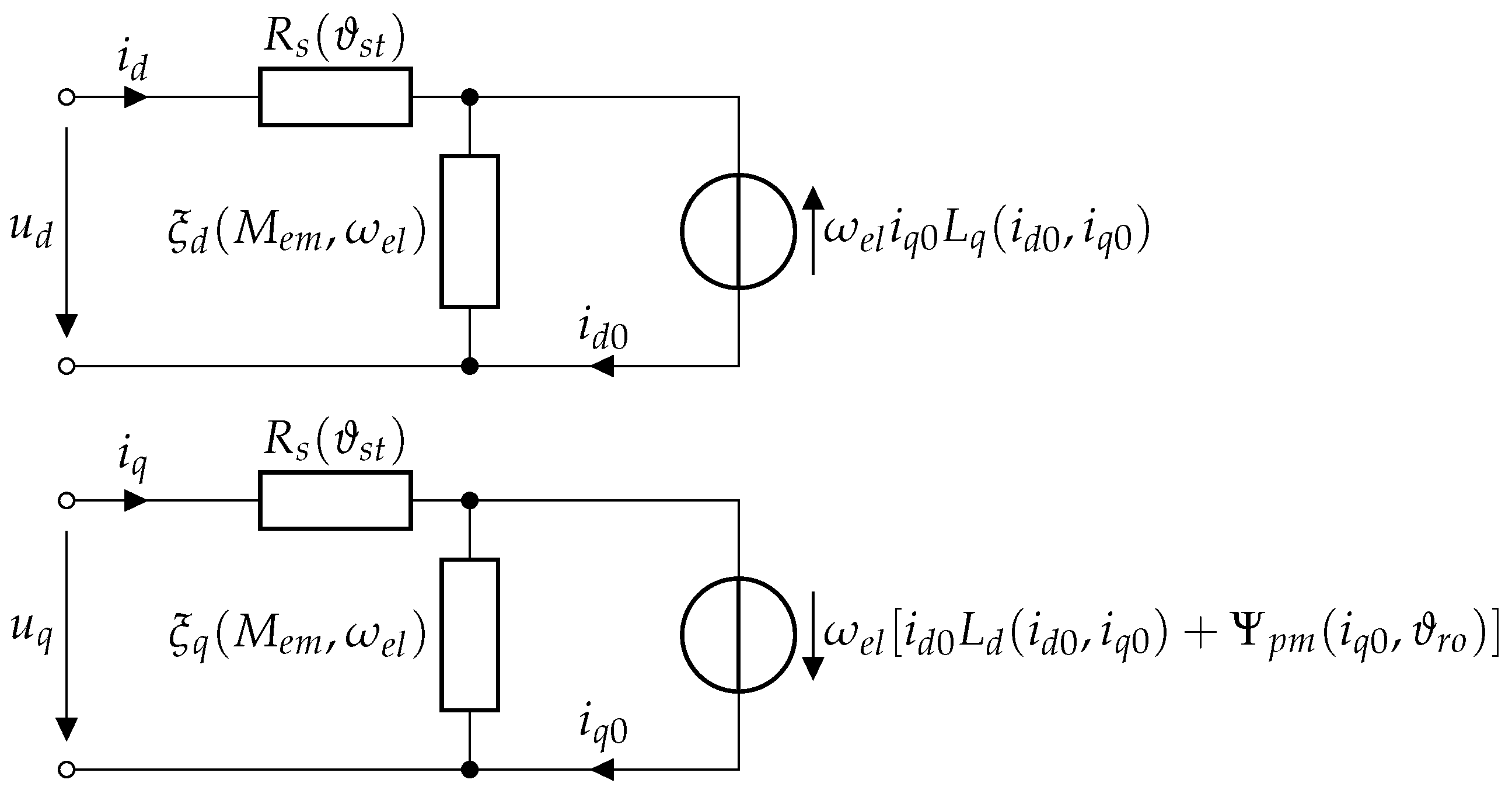

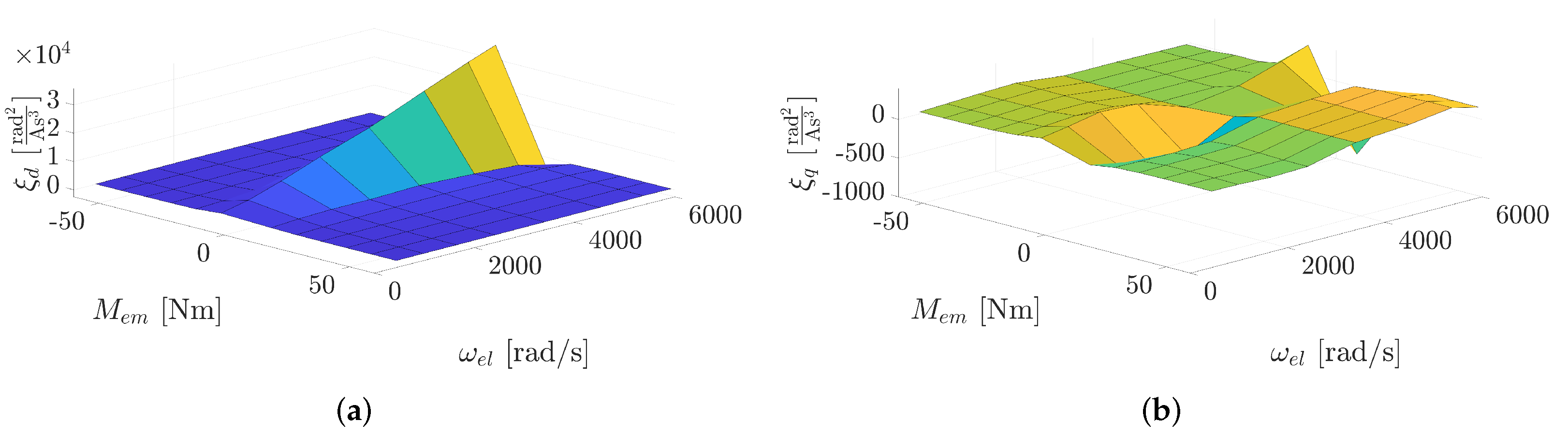

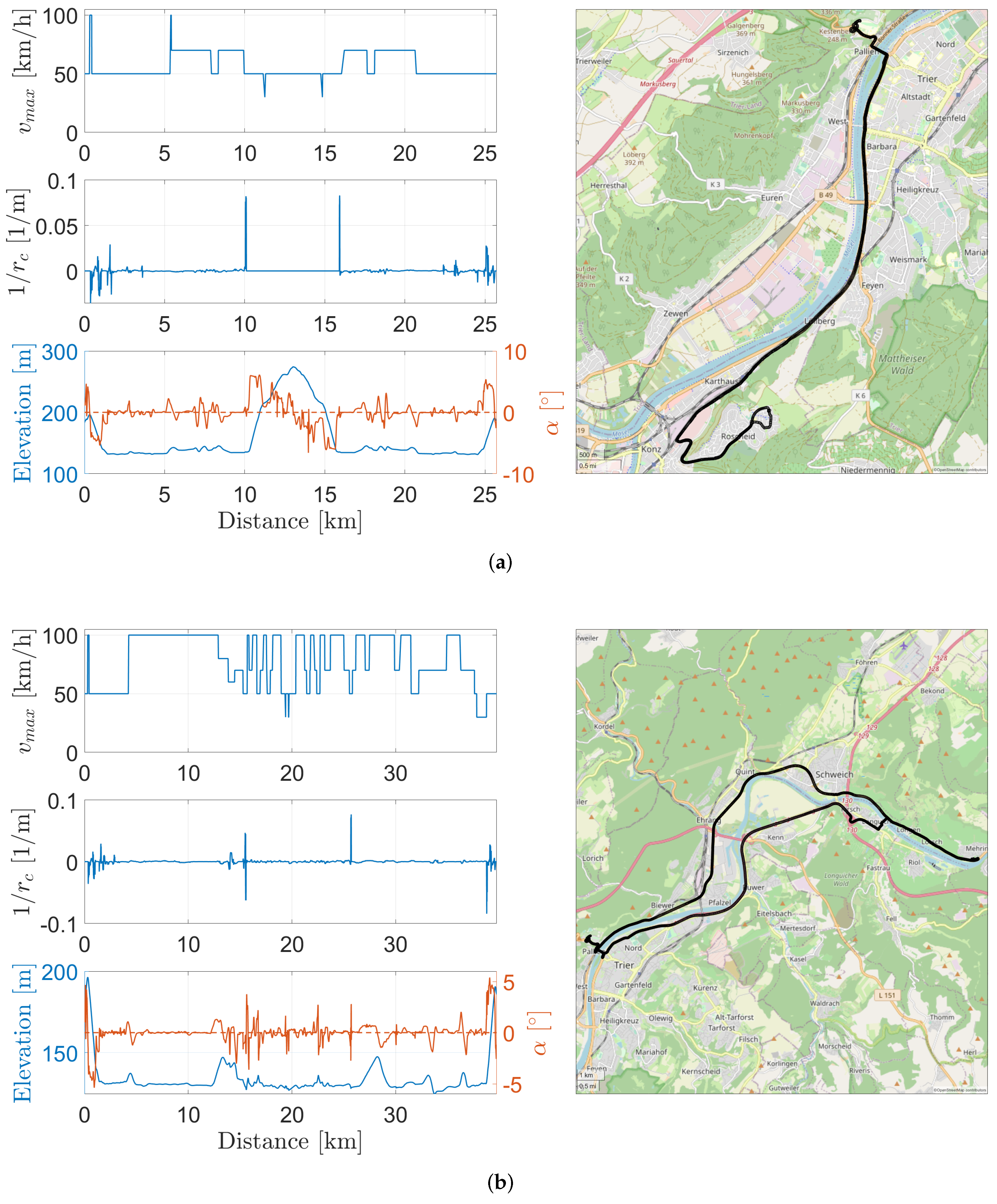


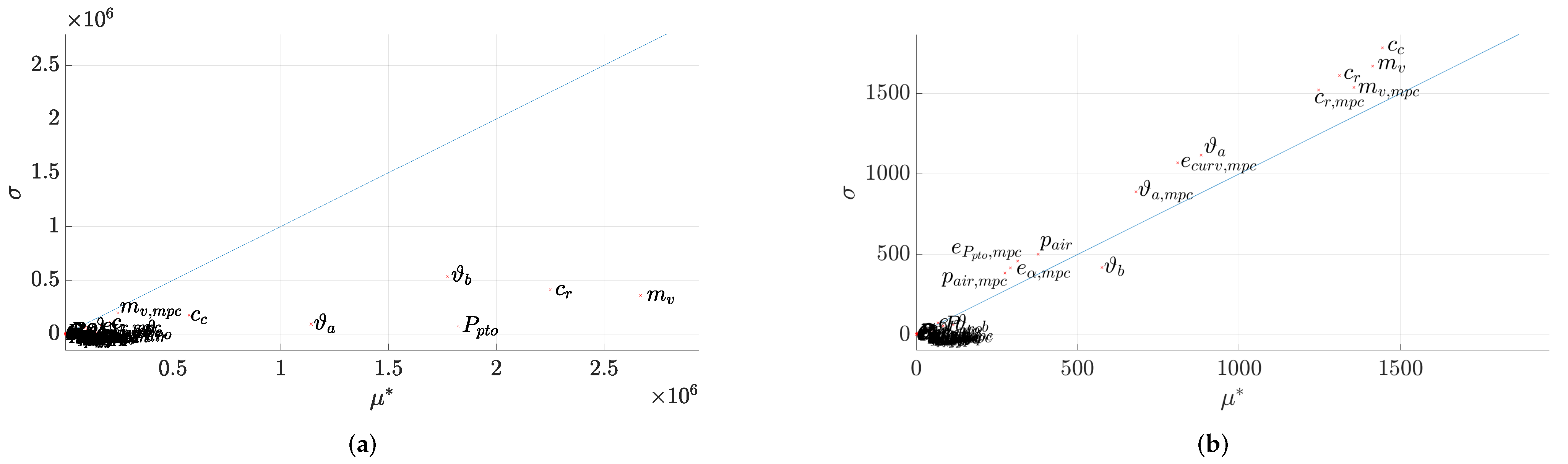
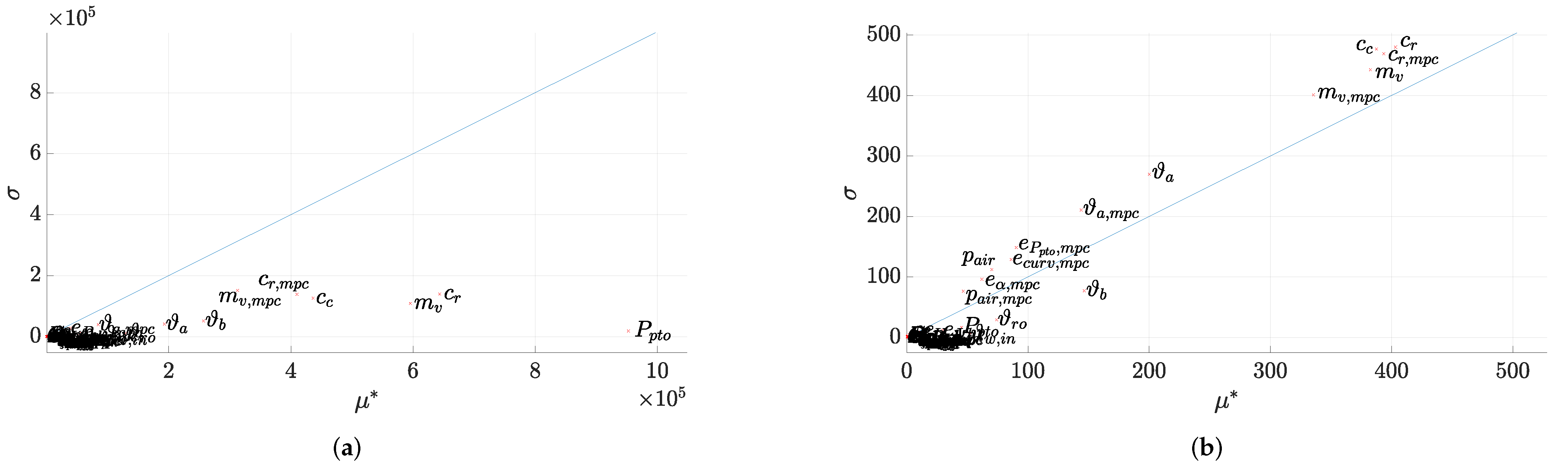
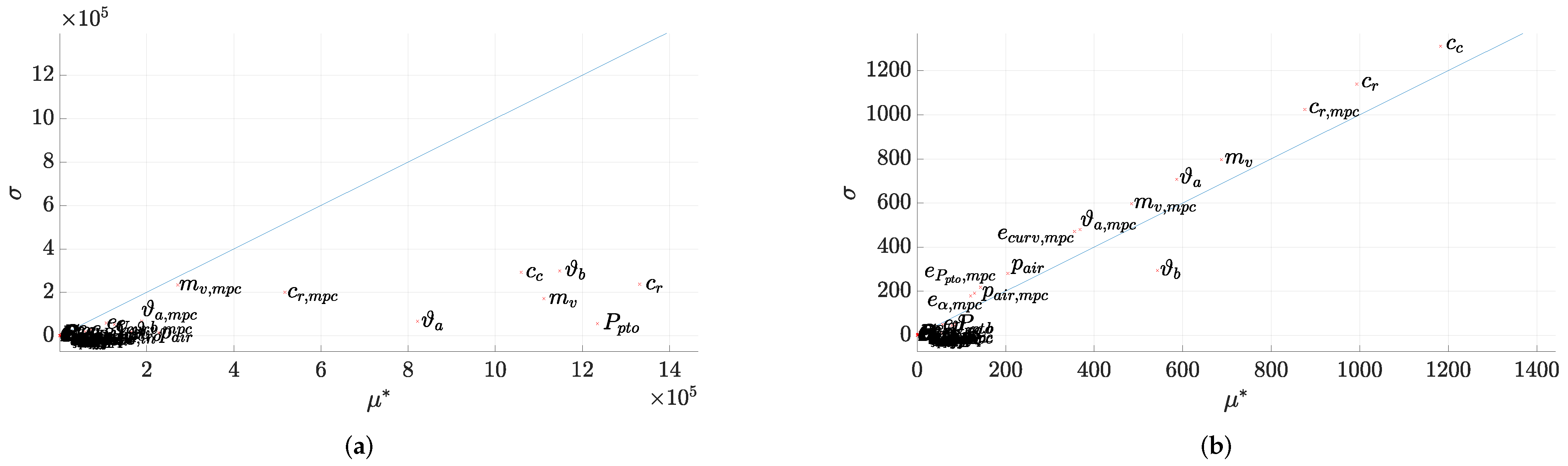
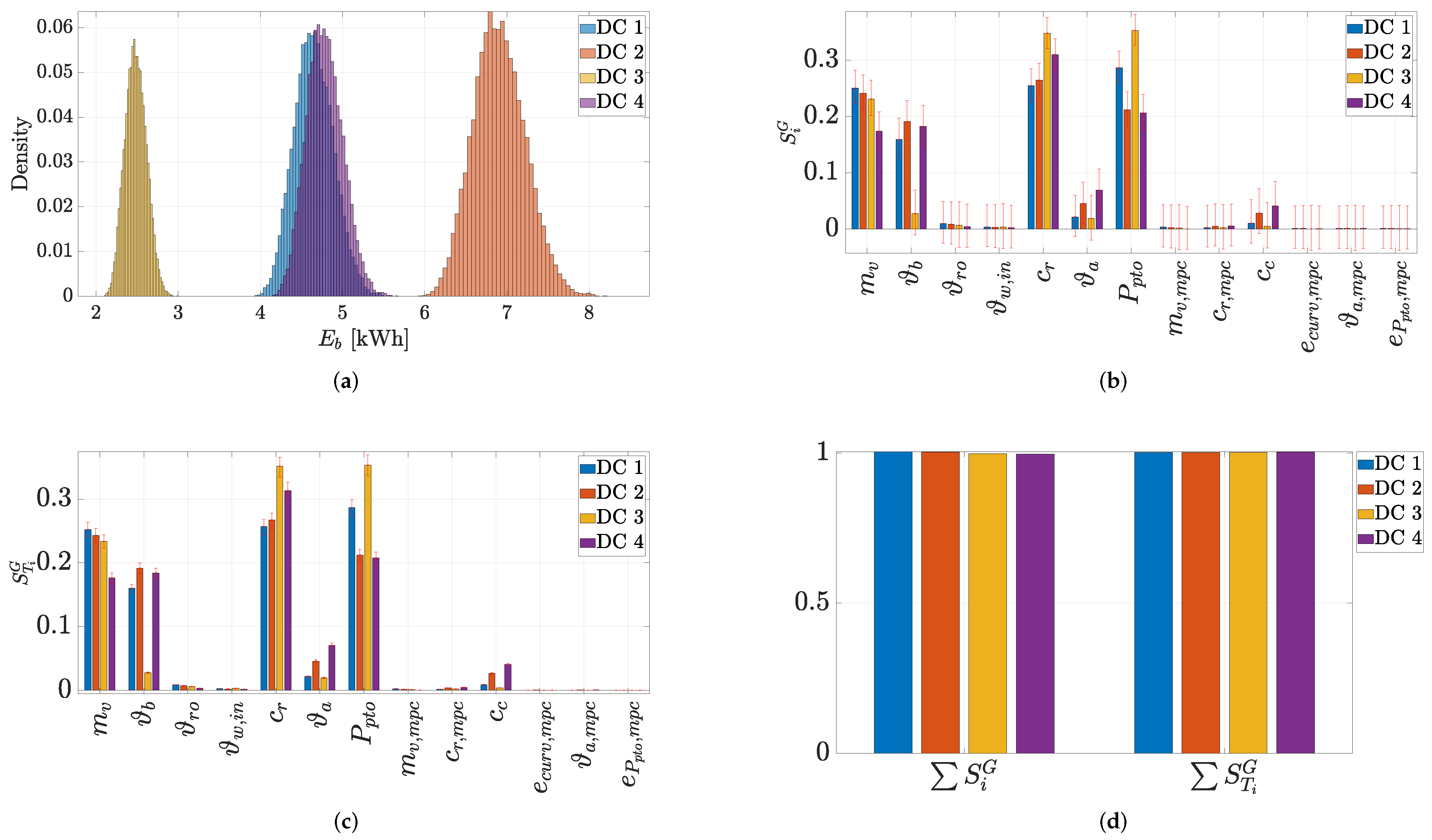

| Name | Description | Type of Error | Distribution | Parameter | Values | Units | |
|---|---|---|---|---|---|---|---|
| Battery | Deviation of series resistance | relative | Normal | , | 0, | − | |
| Deviation of capacitance | relative | Normal | , | 0, | − | ||
| Deviation of resistance | relative | Normal | , | 0, | − | ||
| Deviation of capacitance | relative | Normal | , | 0, | − | ||
| Deviation of resistance | relative | Normal | , | 0, | − | ||
| Deviation of open circuit voltage | relative | Normal | , | 0, | − | ||
| Variation of start temperature | absolute | Uniform | a, b | 20, 40 | °C | ||
| Variation of thermal resistance | absolute | Normal | , | , | |||
| Variation of thermal resistance | absolute | Normal | , | , | |||
| Variation of thermal resistance | absolute | Normal | , | , | |||
| Variation of thermal capacitance | absolute | Normal | , | , | |||
| Variation of thermal capacitance | absolute | Normal | , | , | |||
| Inverter | Deviation of forward characteristics IGBT | relative | Normal | , | 0, | − | |
| relative | Normal | , | 0, | − | |||
| Deviation of forward characteristics diode | relative | Normal | , | 0, | − | ||
| relative | Normal | , | 0, | − | |||
| Deviation of reverse recovery characteristics diode | relative | Normal | , | 0, | − | ||
| relative | Normal | , | 0, | − | |||
| relative | Normal | , | 0, | − | |||
| Deviation of turn on losses IGBT | relative | Normal | , | 0, | − | ||
| relative | Normal | , | 0, | − | |||
| relative | Normal | , | 0, | − | |||
| Deviation of turn off losses IGBT | relative | Normal | , | 0, | − | ||
| relative | Normal | , | 0, | − | |||
| relative | Normal | , | 0, | − | |||
| Variation of water inlet temperature | absolute | Uniform | a, b | 0, 50 | °C | ||
| Drive | Deviation of winding resistance | relative | Normal | , | 0, | − | |
| Deviation of direct inductance | relative | Normal | , | 0, | − | ||
| Deviation of quadrature inductance | relative | Normal | , | 0, | − | ||
| Deviation of magnetic flux | relative | Normal | , | 0, | − | ||
| Deviation of quadrature iron losses | relative | Normal | , | 0, | − | ||
| Deviation of direct iron losses | relative | Normal | , | 0, | − | ||
| Variation of rotor temperature | absolute | Uniform | a, b | 40, 80 | °C | ||
| Variation of stator temperature | absolute | Uniform | a, b | 40, 80 | °C | ||
| Vehicle | Variation of the vehicle mass | absolute | Birnbaum–Saunders | , | , | ||
| Variation of auxiliary consumers | absolute | Uniform | a, b | 250, 750 | |||
| Variation of ambient temperature | absolute | Normal | , | , | °C | ||
| Variation of ambient pressure | absolute | Normal | , | , | |||
| Variation of rolling resistance | absolute | Uniform | a, b | , | − | ||
| Controller | Energy related cost function parameter | absolute | Uniform | a, b | 0, 6 | - | |
| Error of ambient temperature measurement | absolute | Normal | , | , | °C | ||
| Error of air pressure estimation | absolute | Normal | , | , | |||
| Error of rolling resistance estimation | absolute | Uniform | a, b | , | − | ||
| Error of vehicle mass estimation | absolute | Birnbaum–Saunders | , | , | |||
| Error of open circuit voltage estimation | relative | Normal | , | 0, | − | ||
| Error of battery series resistance estimation | relative | Normal | , | 0, | − | ||
| Error of battery RC-resistance estimation | relative | Normal | , | 0, | − | ||
| Error of battery RC-capacitance estimation | relative | Normal | , | 0, | − | ||
| Error of slope measurement | relative | Normal | , | 0, | − | ||
| Error of auxiliary power estimation | absolute | Uniform | a, b | 250, 750 | |||
| Error of curvature measurement | relative | Normal | , | 0, | − | ||
| Error of SoC estimation | relative | Normal | , | 0, | − | ||
| Error of battery temperature estimation | relative | Normal | , | 0, | − | ||
| Error of battery current measurement | relative | Normal | , | 0, | − |
| Name | Description | Type of Error | Distribution | Parameter | Values | Units | |
|---|---|---|---|---|---|---|---|
| Battery | Variation of start temperature | absolute | Uniform | a, b | 20, 40 | °C | |
| Inverter | Variation of water inlet temperature | absolute | Uniform | a, b | 0, 50 | °C | |
| Drive | Variation of rotor temperature | absolute | Uniform | a, b | 40, 80 | °C | |
| Vehicle | Variation of the vehicle mass | absolute | Birnbaum–Saunders | , | , | ||
| Variation of auxiliary consumers | absolute | Uniform | a, b | 250, 750 | |||
| Variation of ambient temperature | absolute | Normal | , | , | °C | ||
| Variation of rolling resistance | absolute | Uniform | a, b | , | − | ||
| Controller | Energy related cost function parameter | absolute | Uniform | a, b | 0, 6 | - | |
| Error of ambient temperature measurement | absolute | Normal | , | , | °C | ||
| Error of rolling resistance estimation | absolute | Uniform | a, b | , | − | ||
| Error of vehicle mass estimation | absolute | Birnbaum–Saunders | , | , | |||
| Error of auxiliary power estimation | absolute | Uniform | a, b | 250, 750 | |||
| Error of curvature measurement | relative | Normal | , | 0, | − |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Braband, M.; Scherer, M.; Voos, H. Global Sensitivity Analysis of Economic Model Predictive Longitudinal Motion Control of a Battery Electric Vehicle. Electronics 2022, 11, 1574. https://doi.org/10.3390/electronics11101574
Braband M, Scherer M, Voos H. Global Sensitivity Analysis of Economic Model Predictive Longitudinal Motion Control of a Battery Electric Vehicle. Electronics. 2022; 11(10):1574. https://doi.org/10.3390/electronics11101574
Chicago/Turabian StyleBraband, Matthias, Matthias Scherer, and Holger Voos. 2022. "Global Sensitivity Analysis of Economic Model Predictive Longitudinal Motion Control of a Battery Electric Vehicle" Electronics 11, no. 10: 1574. https://doi.org/10.3390/electronics11101574
APA StyleBraband, M., Scherer, M., & Voos, H. (2022). Global Sensitivity Analysis of Economic Model Predictive Longitudinal Motion Control of a Battery Electric Vehicle. Electronics, 11(10), 1574. https://doi.org/10.3390/electronics11101574






