Reactive Voltage Control Strategy for PMSG-Based Wind Farm Considering Reactive Power Adequacy and Terminal Voltage Balance
Abstract
:1. Introduction
| research direction | 1. reactive power coordination control among various reactive power compensation devices | 2. reactive power coordinated control between wind turbines in wind farms | 3. wind turbine droop gain voltage control method |
| research method |
| ||
| advantages |
|
|
|
| defects | slow and static reactive power regulation speed is slow, while the device is high, and the application scale is limited | focus on the voltage control of the wind farm grid connection point or the voltage control of the cluster collection station. | fixed droop gain, improper gain setting will lead to unsatisfactory control effect of grid-connected point and terminal voltage |
- (1)
- Compared with the main research method 1 in Table 1, based on the mathematical model and operating characteristics of the fan, this paper deduces the expression of the maximum reactive power regulation capacity of the fan under full wind conditions, that is, the reactive power slack, so as to fully exploit the fan’s unavailability and work regulation potential.
- (2)
- Compared with the main research method 2 in Table 1, based on the equivalent model of wind farm radial topology, in this paper, the grid-connected voltage and terminal voltage of the wind farm are analytically expressed, and the key factors affecting the voltage stability of the grid-connected point and the balance of the terminal voltage are analyzed.
- (3)
- Compared with the main research method 3 in Table 1, this paper studies the adaptive adjustment of the droop gain coefficient of the wind turbine reactive power controller according to the reactive power slack of each wind turbine in the field and the electrical distance from the grid connection point. This makes it possible to maintain the balance of the terminal voltage in the field and reduce the active power loss in the field while supporting the voltage of the grid connection point with the spatiotemporal changes of the input wind speed and electrical distance.
- (1)
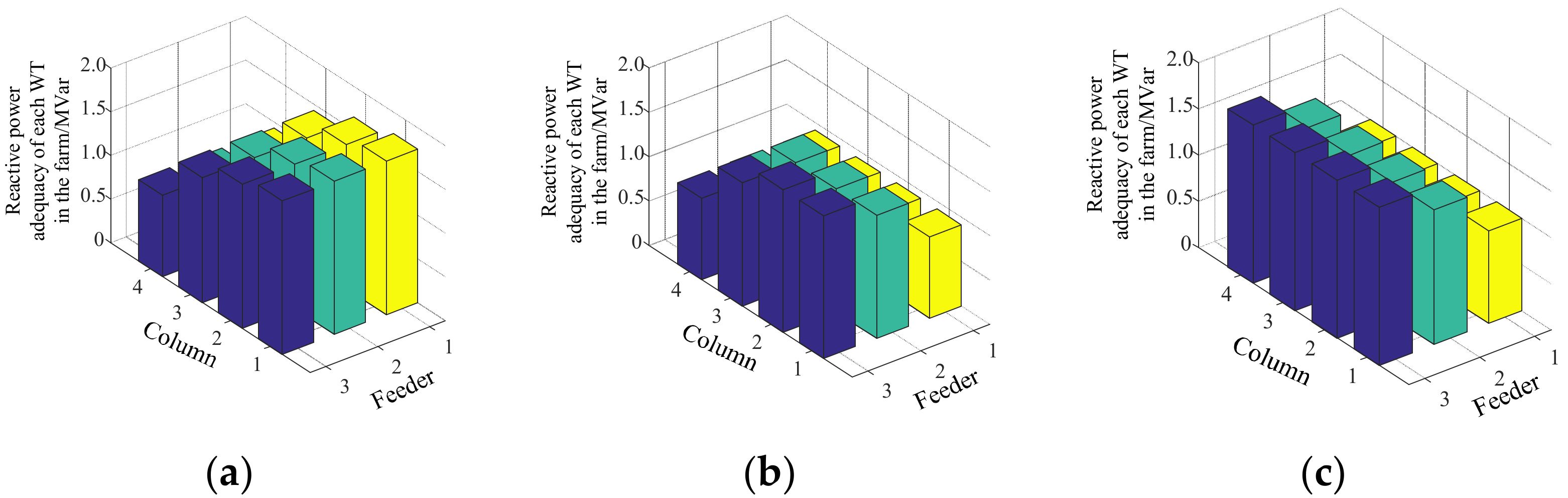
- Combined with the difference in the spatial and temporal distribution of wind energy, the reactive power sufficiency of permanent magnet direct-drive wind turbines under full wind conditions is analyzed, and the influence of wake effect on the reactive power sufficiency of wind farms is studied.
- (2)
- Combined with the difference in the spatial distribution of wind farms, the voltage distribution characteristics of permanent magnet direct drive wind farms are deduced, and the influence of electrical distance on active power loss in wind farms is studied.
- (3)
- A reactive power and voltage control strategy with adaptive gain for permanent magnet direct-drive wind farms is proposed. According to the reactive power sufficiency of each wind turbine and its electrical distance from the grid-connected point, the reactive power and voltage gain coefficient of the wind turbine is adaptively set. The coefficient makes it change with the input wind speed and electrical distance in time and space, so as to reduce the influence of wind speed fluctuation and load mutation on the wind farm terminal voltage and grid-connected point voltage. Therefore, while supporting the voltage of the grid connection point, the balance of the terminal voltage in the field is maintained, to improve the friendliness of wind power grid connection.
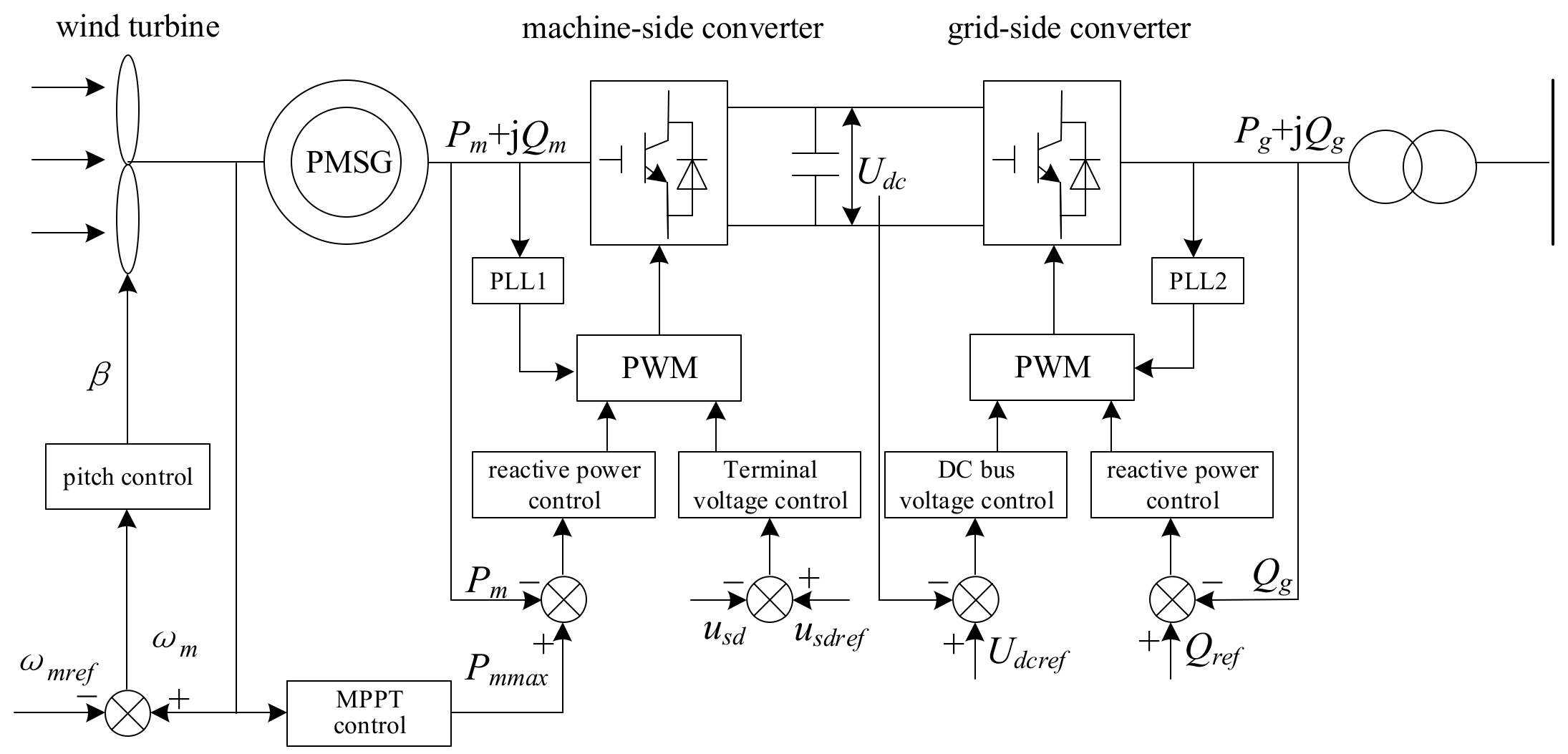
2. Distribution Characteristics of Reactive Power and Voltage for the PMSG-Based Wind Farm
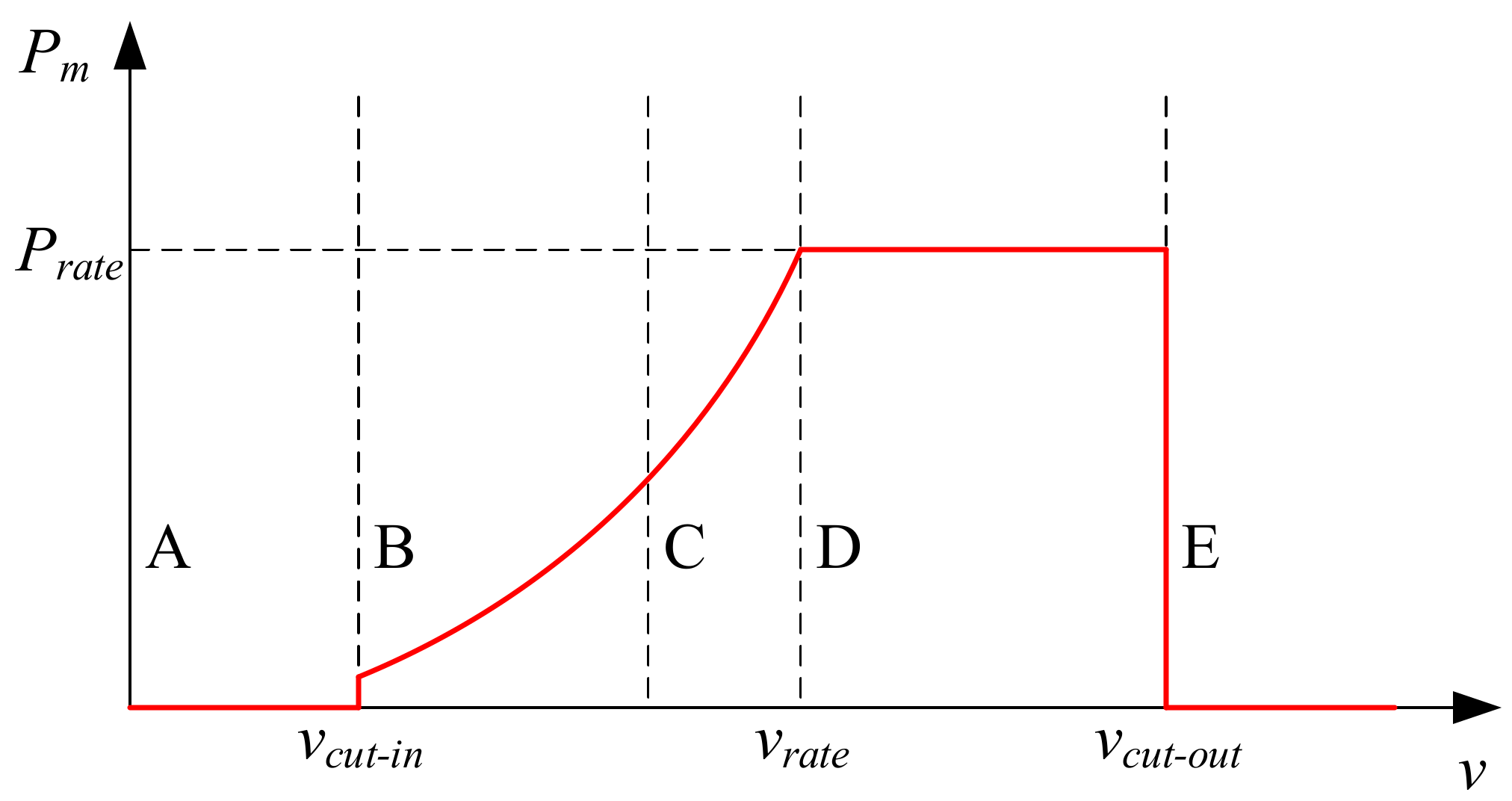
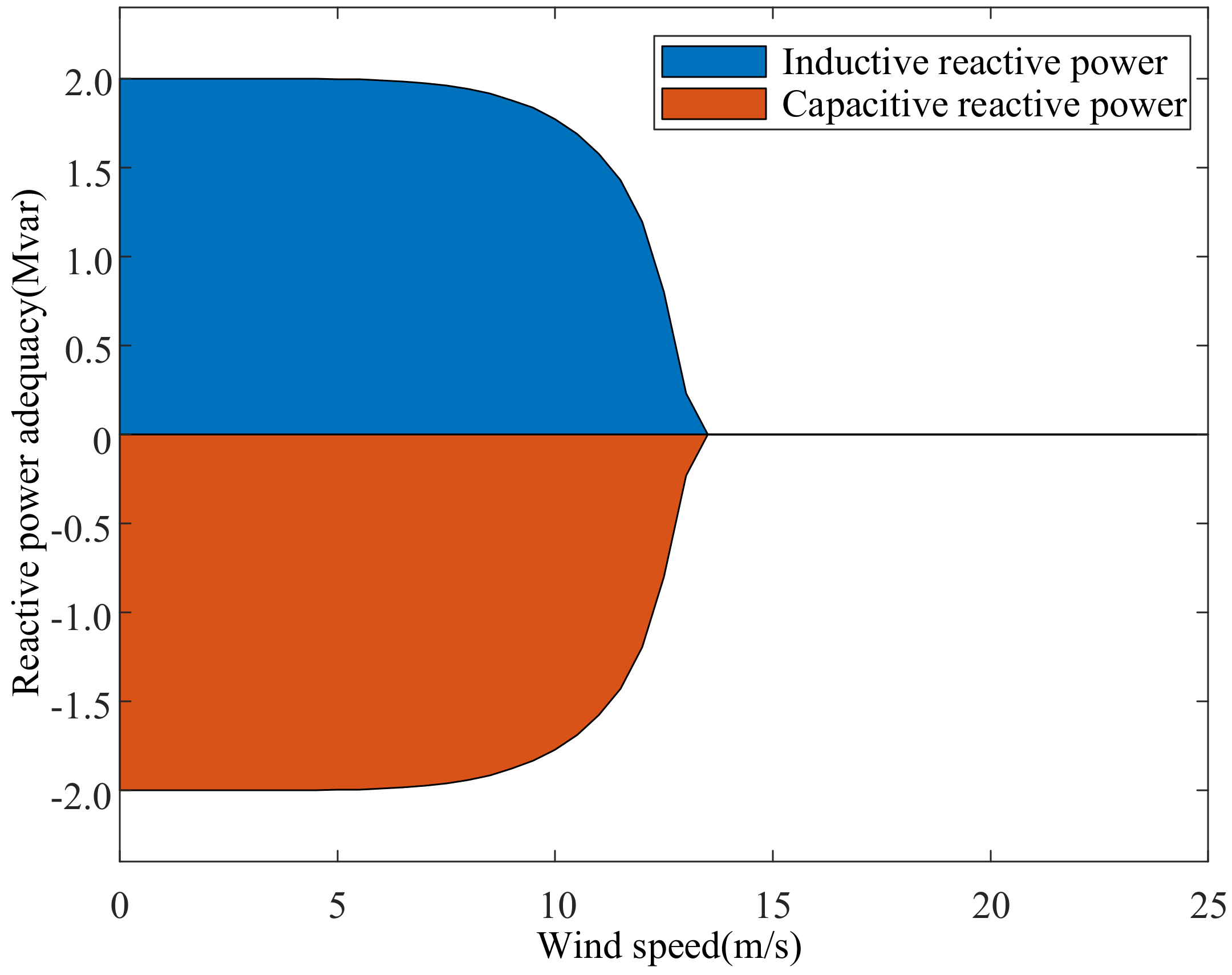
2.1. Reactive Power Adequacy of PMSG under the Complete Wind Condition
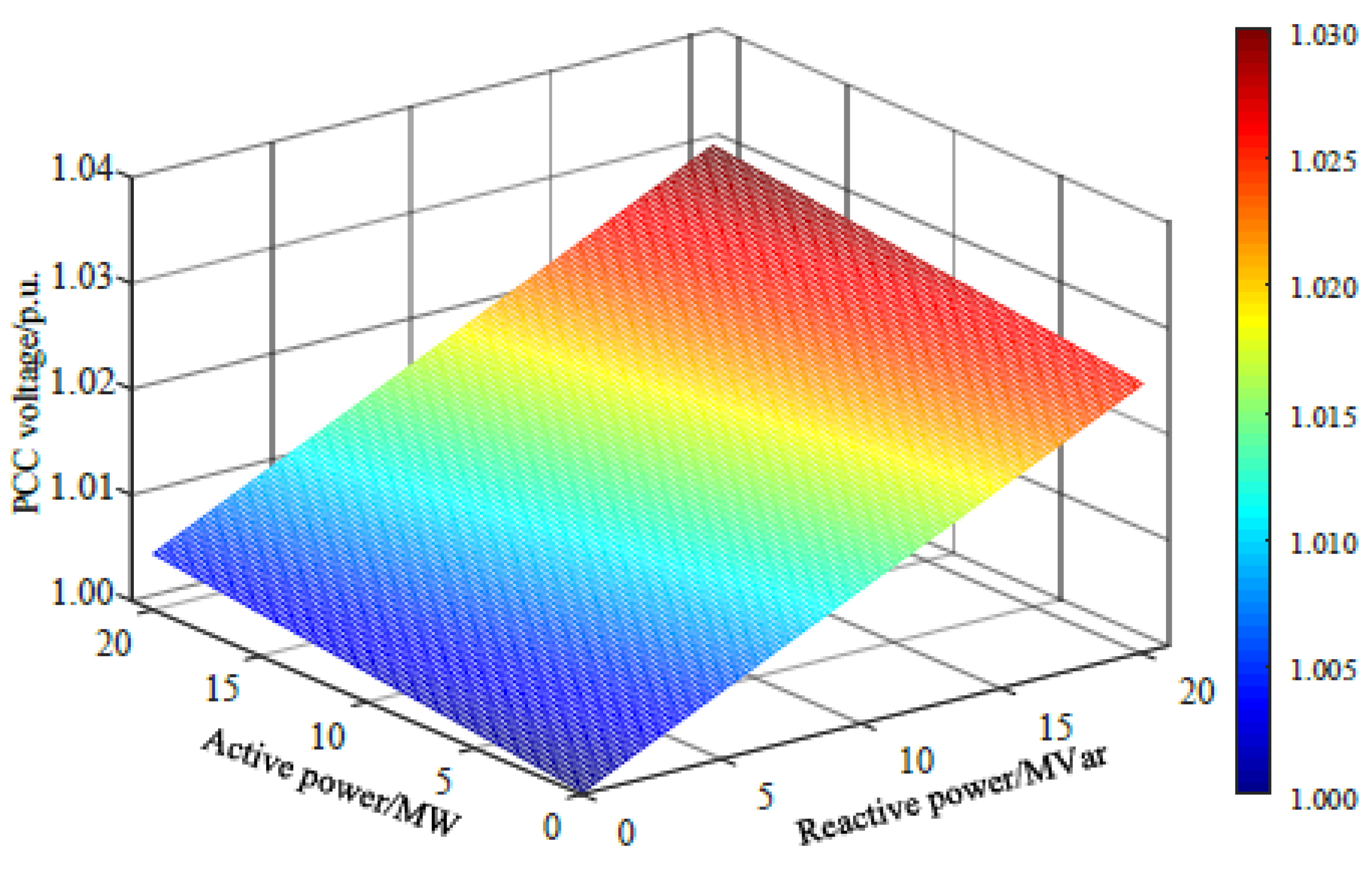
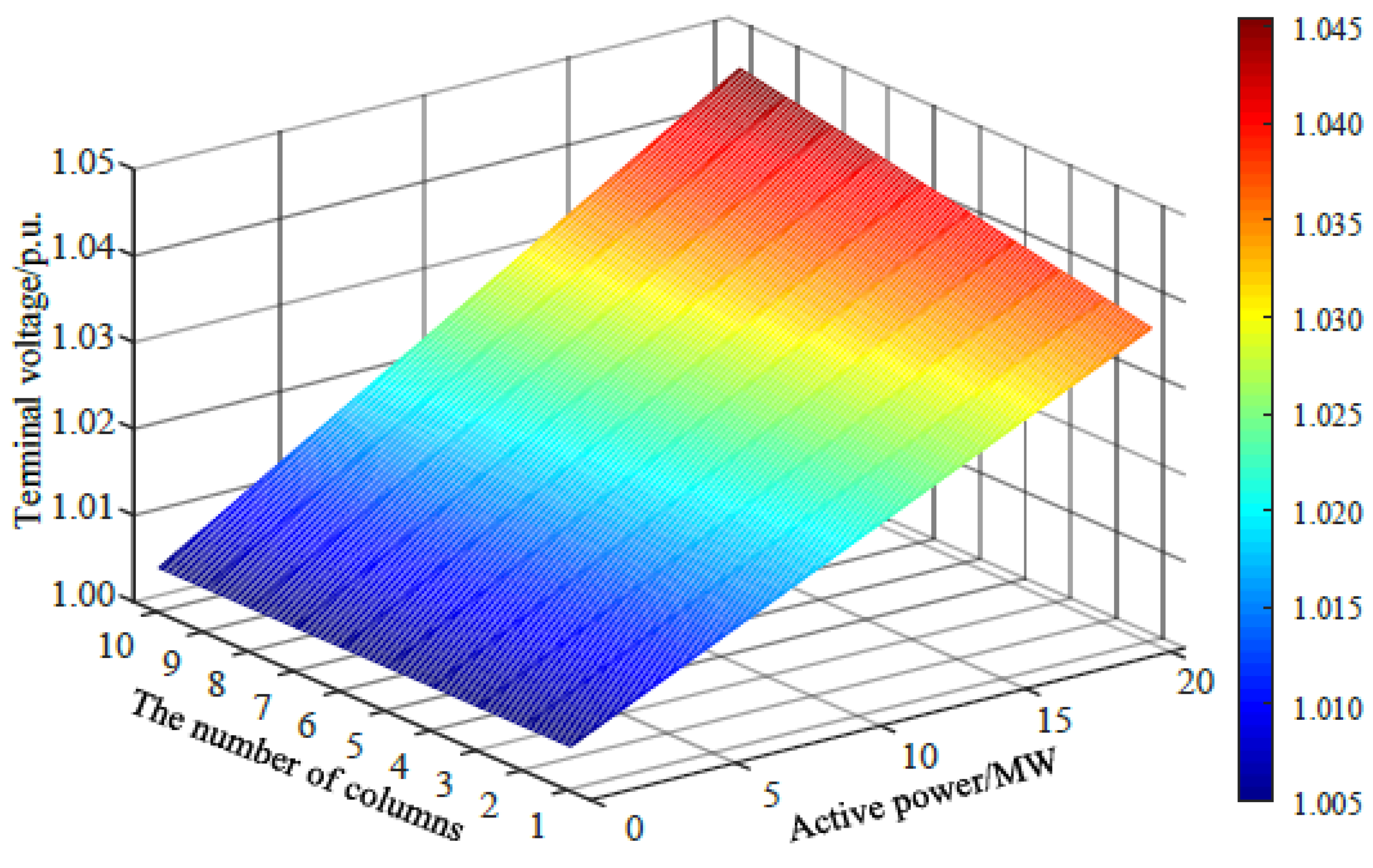
2.2. Distribution Characteristics of Voltage inside the PMSG-Based Wind Farm
3. Adaptive Gain Reactive Voltage Control Strategy for PMSG-Based Wind Farm
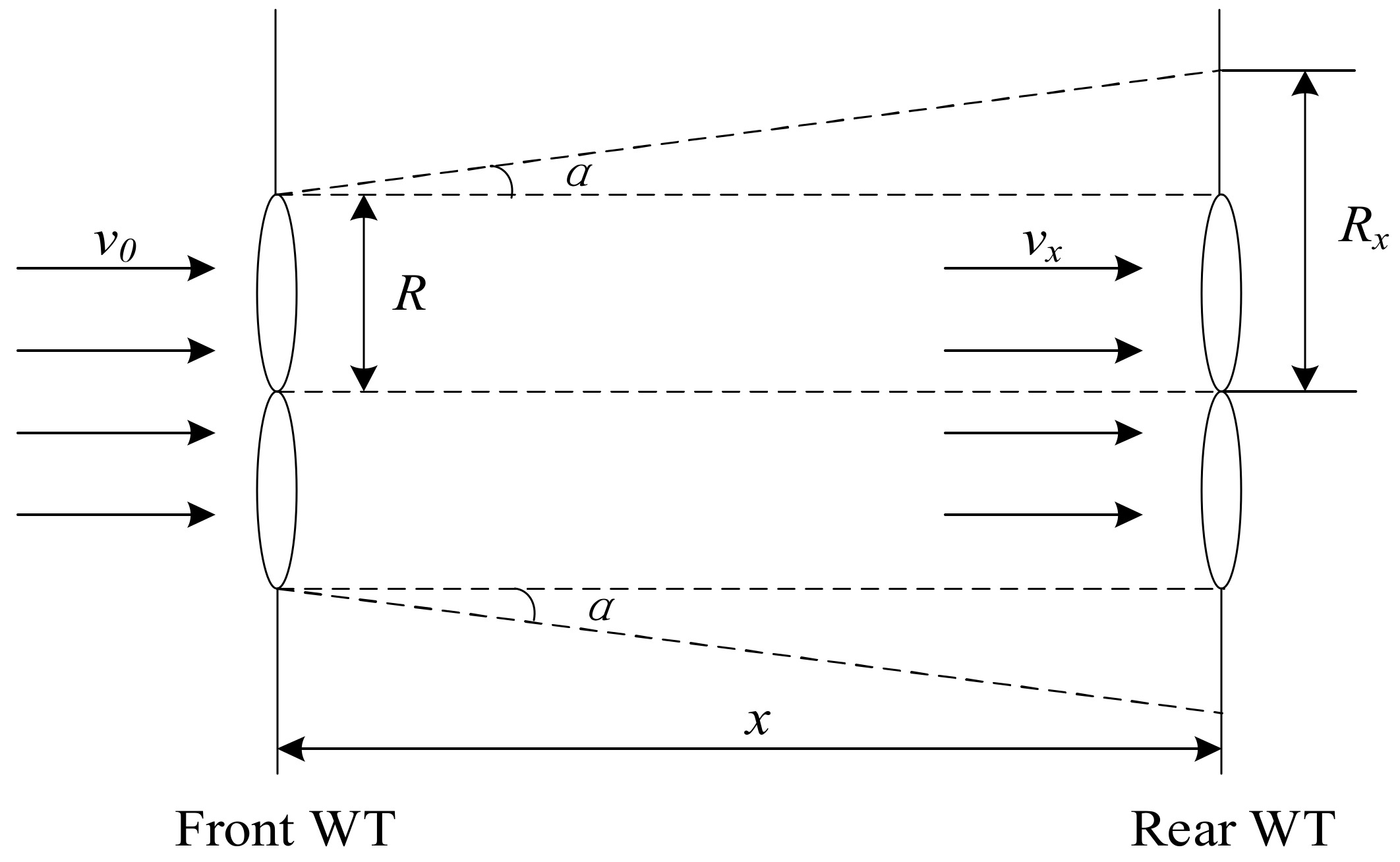
3.1. The Influence of Wake Effect on Reactive Power Adequacy of Wind Farm
3.2. The Influence of Electrical Distance on Active Power Loss of Wind Farm
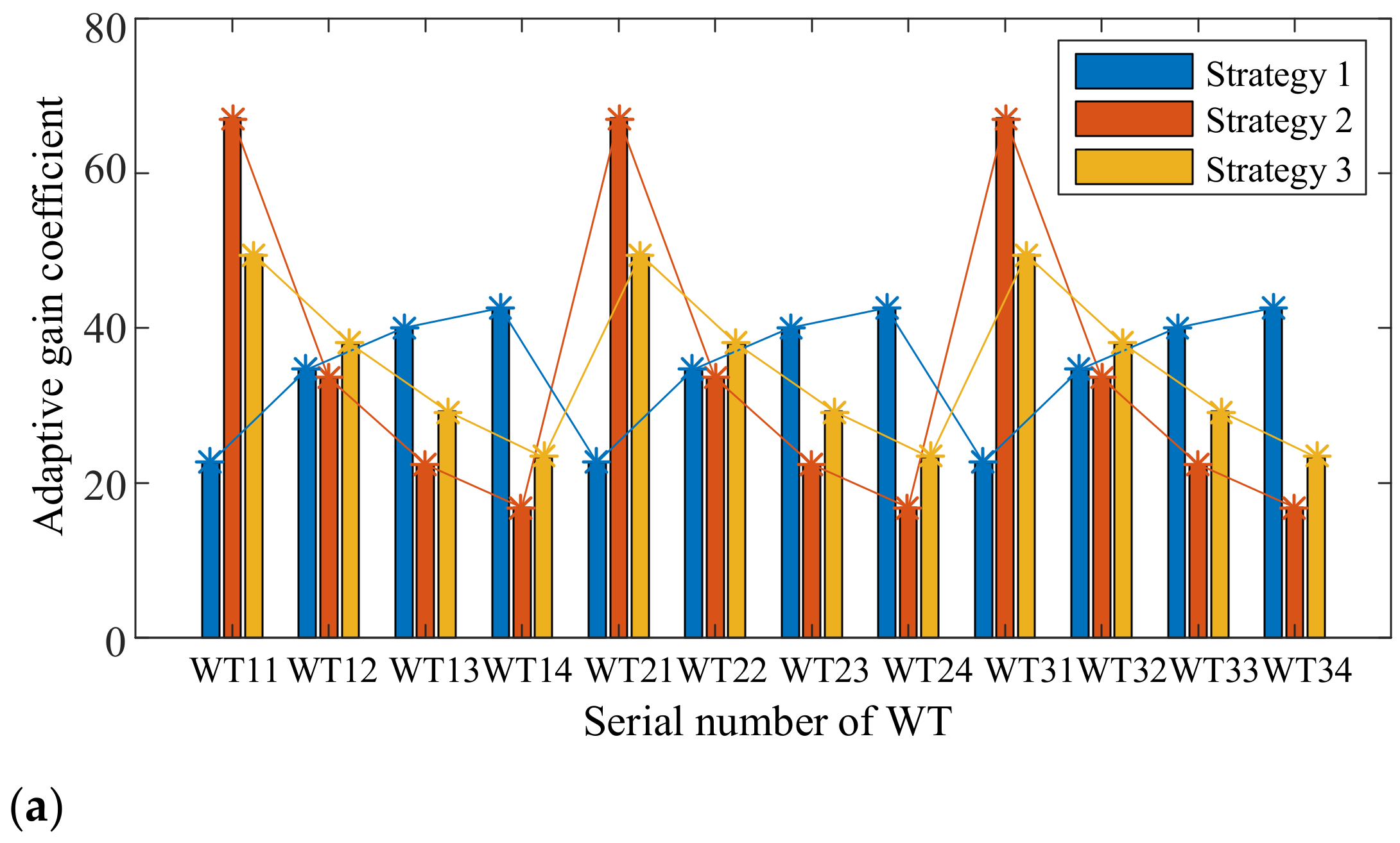
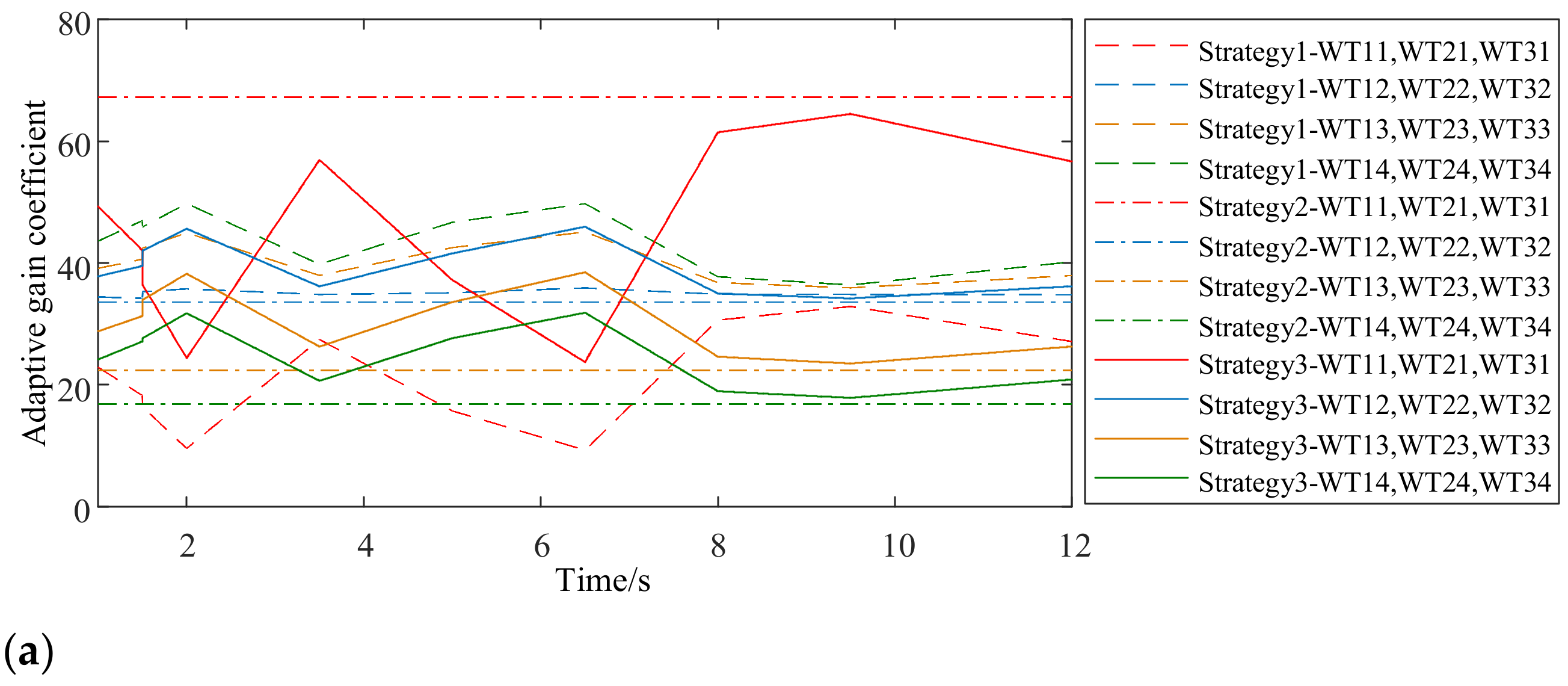
3.3. The Calculation Method of Adaptive Gain Coefficient of WT
4. Case Study
4.1. Simulation Settings
4.2. Simulation Case
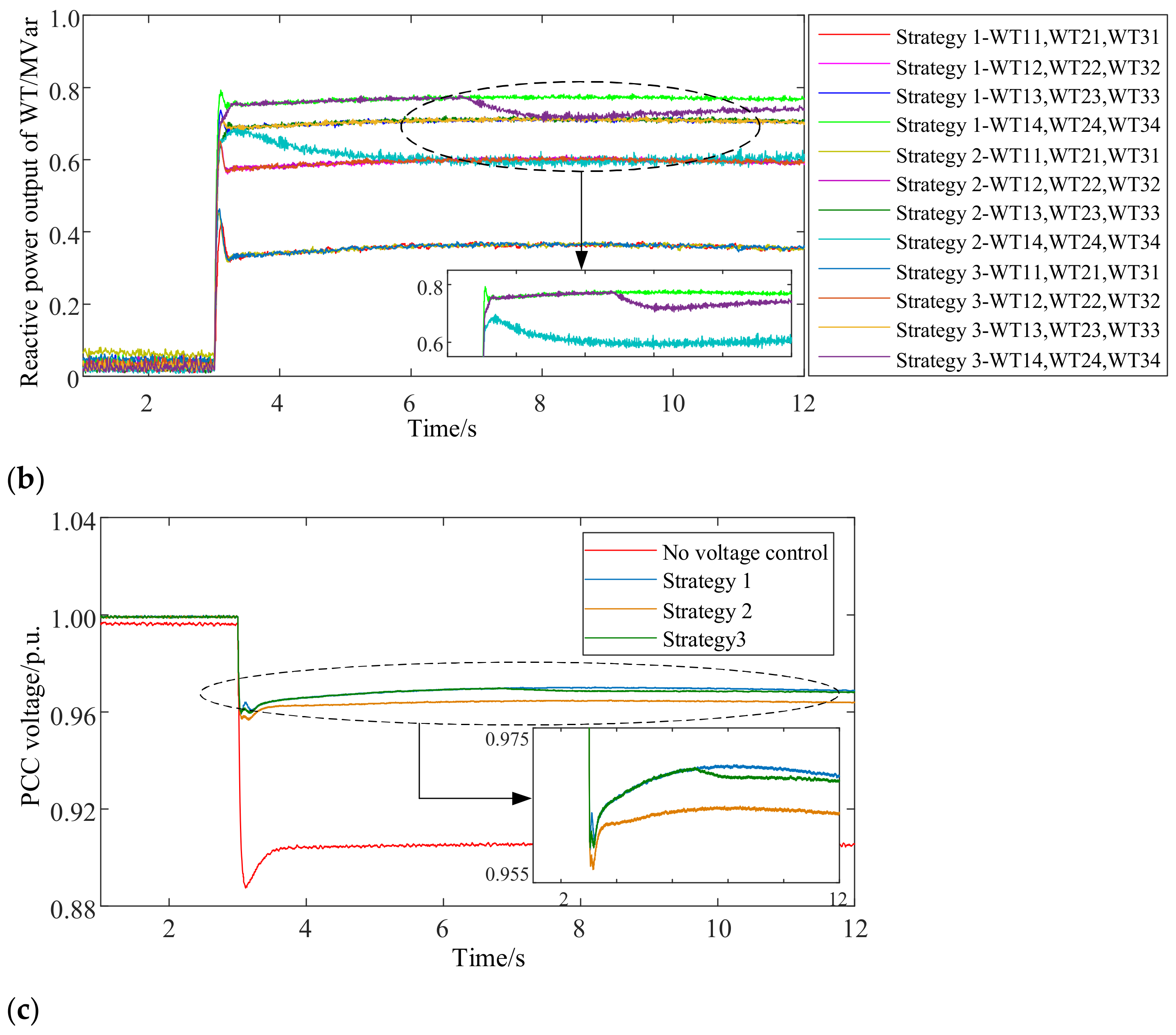
4.2.1. Scenario 1: The Wind Speed Is Constant at 13 m/s, and the Wind Direction Is 180°
4.2.2. Scenario 2: The Wind Speed Fluctuates, and the Wind Direction Is 180°
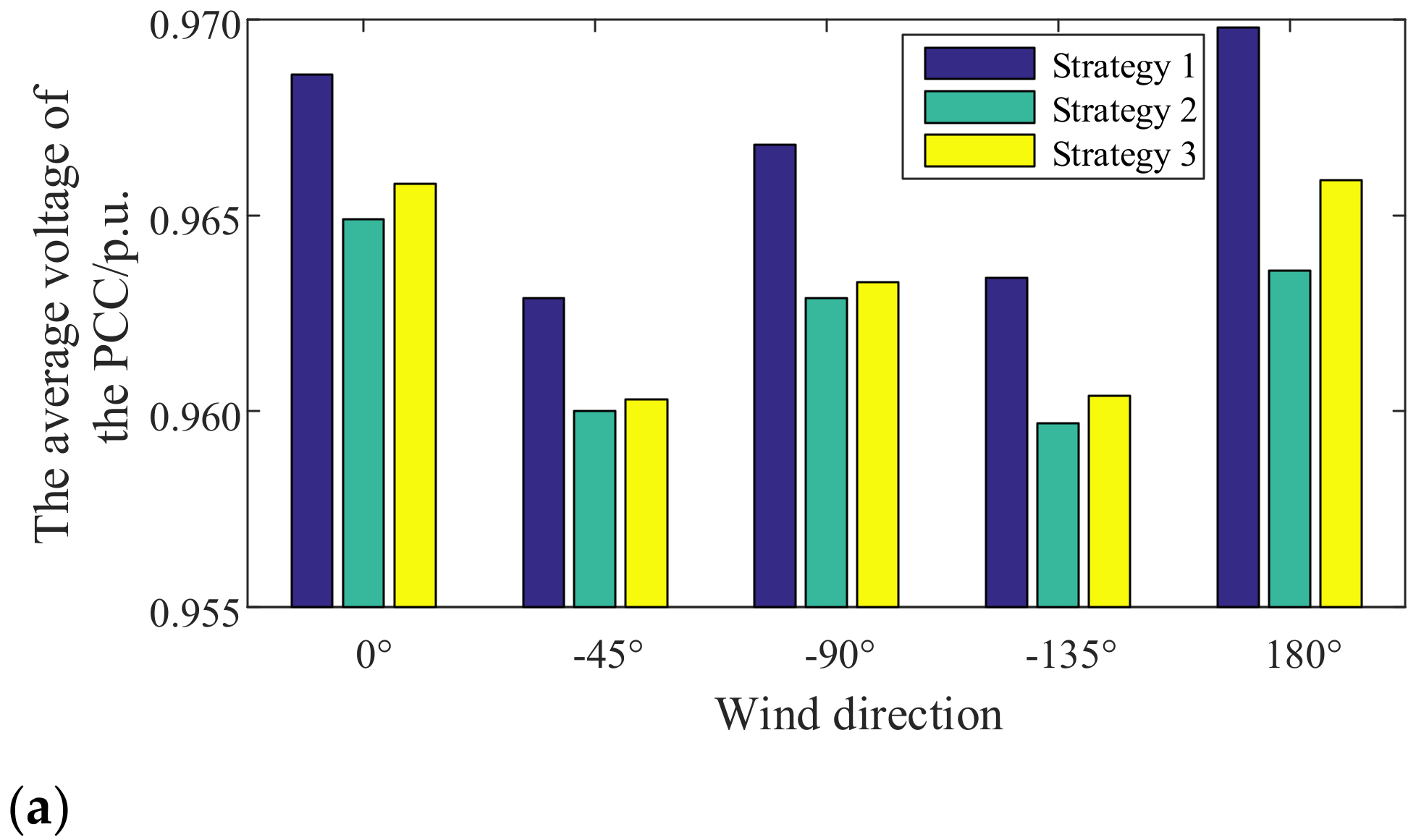
4.2.3. Scenario 3: The Wind Direction Changes with the Same Input Wind Speed
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| Acronyms | |
| PCC | point of common connection |
| PMSG | Permanent magnet synchronous generator |
| OLTC | On-load tap changer |
| SVC | Static Var compensator |
| SVG | Static Var Synchronous |
| DFIG | Doubly-Fed Induction Generators |
| MPPT | Maximum Power Point Tracking |
| Variables | |
| Pm | the output mechanical power of the WT |
| the air density | |
| R | the radius of the WT blade |
| v | the input wind speed |
| Cp | the wind energy utilization coefficient |
| the angular velocity of the WT | |
| Kopt | the equivalent coefficient to obtain the maximum wind power |
| PWT | the expression of the active power output |
| vcut-in | the cut-in wind speed |
| vrate | the rated wind speed |
| vcut-out | the cut-out wind speed |
| Prate | the rated active power of WT |
| SWT | the apparent power of the WT converter |
| QWT,ade | the reactive power adequacy of the WT |
| CT | the thrust coefficient of the WT |
| Rx | the projected cross-sectional radius of the rear WT affected by the wake of the front WT |
| UPCC | the wind farm PCC voltage |
| v0 | the input wind speed of the front WT is |
| ΔP | the minimum |
| C | the proportional constant |
| t1 | the starting time of analysis |
| tN | the end time of calculation |
| SB | the base capacity |
| WTLij | the average terminal voltage of each WT |
| UWT,ref | the reference value of terminal voltage |
| U | the power grid voltage |
References
- Mahela, O.P.; Shaik, A.G. Comprehensive overview of grid interfaced wind energy generation systems. Renew. Sustain. Energy Rev. 2016, 57, 260–281. [Google Scholar] [CrossRef]
- Asadollah, S.; Zhu, R.; Liserre, M. Analysis of voltage control strategies for wind farms. IEEE Trans. Sustain. Energy 2020, 11, 1002–1012. [Google Scholar] [CrossRef]
- Zhou, W.; Wang, Y.; Torres-Olguin, R.E.; Chen, Z. Effect of Reactive Power Characteristic of Offshore Wind Power Plant on Low-Frequency Stability. IEEE Trans. Energy Convers. 2020, 35, 837–853. [Google Scholar] [CrossRef] [Green Version]
- Kuang, H.; Zheng, L.; Li, S.; Ding, X. Voltage stability improvement of wind power grid-connected system using TCSC-STATCOM control. IET Renew. Power Gener. 2019, 13, 215–219. [Google Scholar] [CrossRef]
- Chen, X.; Yan, L.; Zhou, X.; Sun, H. A novel DVR-ESS-embedded wind-energy conversion system. IEEE Trans. Sustain. Energy 2018, 9, 1265–1274. [Google Scholar] [CrossRef]
- Ouyang, J.; Li, M.; Diao, Y.; Tang, T.; Xie, Q. Active control method of large-scale wind integrated power system with enhanced reactive power support for wind speed fluctuation. IET Gener. Transm. Distrib. 2018, 12, 5664–5671. [Google Scholar] [CrossRef]
- Mahdavi, H.; Panamtash, A.D.; Zhou, Q. Predictive Coordinated and Cooperative Voltage Control for Systems with High Penetration of PV. IEEE Trans. Ind. Appl. 2021, 57, 2212–2222. [Google Scholar] [CrossRef]
- Karbouj, H.; Rather, Z.H. Voltage control ancillary service from wind power plant. IEEE Trans. Sustain. Energy 2019, 10, 759–767. [Google Scholar] [CrossRef]
- Wang, Q.; Chen, L.; Hu, M.; Tang, X.; Li, T.; Ji, S. Voltage prevention and emergency coordinated control strategy for photovoltaic power plants considering reactive power allocation. Electr. Power Syst. Res. 2018, 163, 110–115. [Google Scholar] [CrossRef]
- Ouyang, J.; Tang, T.; Yao, J.; Li, M. Active voltage control for DFIG-based wind farm integrated power system by coordinating active and reactive powers under wind speed variations. IEEE Trans. Energy Convers. 2019, 34, 1504–1511. [Google Scholar] [CrossRef]
- Yassami, H.; Rabiee, A.; Jalilvand, A.; Bayat, F. Model predictive control scheme for coordinated voltage control of power systems at the presence of volatile wind power generation. IET Gener. Transm. Distrib. 2018, 12, 1922–1928. [Google Scholar] [CrossRef]
- Gencer, A. Analysis of fault ride through capability improvement of the permanent magnet synchronous generator based on WT using a BFCL. In Proceedings of the 2019 1st Global Power, Energy and Communication Conference (GPECOM), Nevsehir, Turkey, 12–15 June 2019; pp. 353–357. [Google Scholar]
- Tian, C.; Luo, X.; Dong, J.; Chen, B.; Yuan, J. Voltage and reactive power optimisation of offshore wind farms based on terminal voltage control mode of DFIG. J. Eng. 2017, 13, 874–879. [Google Scholar] [CrossRef]
- Ouyang, J.; Li, M.; Zhang, Z.; Tang, T. Multi-timescale active and reactive power-coordinated control of large-scale wind integrated power system for severe wind speed fluctuation. IEEE Access 2019, 7, 51201–51210. [Google Scholar] [CrossRef]
- Kim, J.; Seok, J.-K.; Muljadi, E.; Kang, Y.C. Adaptive Q–V scheme for the voltage control of a DFIG-based wind power plant. IEEE Trans. Power Electron. 2016, 31, 3586–3599. [Google Scholar] [CrossRef]
- Sun, H.; Guo, Q.; Qi, J.; Ajjarapu, V.; Bravo, R.; Chow, J.; Li, Z.; Moghe, R.; Nasr-Azadani, E.; Tamrakar, U.; et al. Review of challenges and research opportunities for voltage control in smart grids. IEEE Trans. Power Syst. 2019, 34, 2790–2801. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Xu, Z.; Zhang, J.; Meng, K. Variable droop voltage control for wind farm. IEEE Trans. Sustain. Energy 2018, 9, 491–493. [Google Scholar] [CrossRef]
- Guo, Y.; Gao, H. Data-Driven online system equivalent for self-adaptive droop voltage control of wind power plants. IEEE Trans. Energy Convers. 2020, 35, 302–305. [Google Scholar] [CrossRef]
- Xing, P.; Fu, L.; Wang, G.; Wang, Y.; Zhang, Y. A compositive control method of low-voltage ride through for PMSG-based wind turbine generator system. IET Renew. Power Gener. 2018, 12, 117–125. [Google Scholar] [CrossRef]
- Qin, N.; Bak, C.L.; Abildgaard, H.; Chen, Z. Multi-stage optimization-based automatic voltage control systems considering wind power forecasting errors. IEEE Trans. Power Syst. 2017, 32, 1073–1088. [Google Scholar] [CrossRef]
- Yin, M.; Xu, Y.; Shen, C.; Liu, J.; Dong, Z.Y.; Zou, Y. Turbine stability-constrained available wind power of variable speed wind turbines for active power control. IEEE Trans. Power Syst. 2017, 32, 2487–2488. [Google Scholar] [CrossRef]
- Dai, J.; Tang, Y.; Yi, J. Adaptive gains control scheme for PMSG-based wind power plant to provide voltage regulation service. Energies 2019, 12, 753. [Google Scholar] [CrossRef] [Green Version]
- Tian, J.; Zhou, D.; Su, C.; Chen, Z.; Blaabjerg, F. Reactive power dispatch method in wind farms to improve the lifetime of power converter considering wake effect. IEEE Trans. Sustain. Energy 2017, 8, 477–487. [Google Scholar] [CrossRef] [Green Version]
- Nath, A.P.; Paul, S.; Rather, Z.H.; Mahapatra, S. Estimation of Offshore Wind Farm Reliability Considering Wake Effect and Wind Turbine Failure. In Proceedings of the 2019 IEEE Innovative Smart Grid Technologies-Asia (ISGT Asia), Chengdu, China, 21–24 May 2019; pp. 3866–3871. [Google Scholar]








| Parameters | Values |
|---|---|
| Rated apparent power/MVA | 2 |
| Rated voltage/kV | 0.69 |
| Stator resistance/p.u. | 0.0108 |
| Stator leakage reactance/p.u. | 0.102 |
| Rotor resistance/p.u. | 0.01 |
| Rotor leakage reactance/p.u. | 0.11 |
| Inertial time constant/s | 3 |
| Parameters | Values |
|---|---|
| Zt (the equivalent impedances of all WTs’ box-type transformers)/p.u. | 0.05 + j0.2 |
| Zl (the equivalent impedance of lines between adjacent WTs)/Ω | 0.045 + j0.24 |
| ZT (the equivalent impedance of the main transformer)/p.u. | 0.05 + j0.2 |
| Zk (the equal impedance of the transmission line between the wind farm and the power grid)/Ω | 0.9 + j4.8 |
| Strategy | Strategy 1 | Strategy 2 | Strategy 3 | |
|---|---|---|---|---|
| Indicators | ||||
| PCC/p.u. | 0.9692 | 0.9641 | 0.9685 | |
| ΣΔP/MW | 1.0671 | 0.8715 | 1.0336 | |
| ΣΔU | 0.04872 | 0.04536 | 0.04837 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dai, J.; Wan, L.; Chang, P.; Liu, L.; Zhou, X. Reactive Voltage Control Strategy for PMSG-Based Wind Farm Considering Reactive Power Adequacy and Terminal Voltage Balance. Electronics 2022, 11, 1766. https://doi.org/10.3390/electronics11111766
Dai J, Wan L, Chang P, Liu L, Zhou X. Reactive Voltage Control Strategy for PMSG-Based Wind Farm Considering Reactive Power Adequacy and Terminal Voltage Balance. Electronics. 2022; 11(11):1766. https://doi.org/10.3390/electronics11111766
Chicago/Turabian StyleDai, Jianfeng, Lei Wan, Ping Chang, Lin Liu, and Xia Zhou. 2022. "Reactive Voltage Control Strategy for PMSG-Based Wind Farm Considering Reactive Power Adequacy and Terminal Voltage Balance" Electronics 11, no. 11: 1766. https://doi.org/10.3390/electronics11111766






