A Reverse Order Hierarchical Integrated Scheduling Algorithm Considering Dynamic Time Urgency Degree of the Process Sequences
Abstract
:1. Introduction
- (1)
- Flexible workshop is an IOT intelligent equipment workshop connected by a real-time sensor network [15,16], also known as an intelligent workshop. The computer numerical control (CNC) equipment in the workshop has many functions and strong adaptability. For the complex scheduling problem of a dynamic, flexible workshop, the machine-driven scheduling method based on artificial intelligence is usually used.
- (2)
- The equipment in a non-flexible workshop is single-function equipment. At present, the research on integrated scheduling is mainly based on these kinds of workshops in such Chinese enterprises.
- (1)
- Research based on processes takes the process as the scheduling unit and finds reasonable machining time points for processes on the machining equipment. The research has gone through a process from focusing on the path length (vertical) of the product process tree affecting the scheduling results to focusing on the SLP (horizontal) of the product process tree affecting the parallel scheduling results. Representative algorithms include the dynamic critical path method [17], time-selective adjustment method [18,19,20], and reverse order scheduling method [21], etc.
- (2)
- Research based on machining equipment. In this kind of research work, the end of each process is regarded as an equipment’s idle event to drive the idle equipment to find a schedulable process. Representative algorithms include a machine-driven method and a machine-driven method with a fallback pre-emption [22]. The research object of a machine-driven method can be either single-product or multi-product, and its research workshop can be either a flexible workshop or a non-flexible workshop.
- (1)
- Aiming at the integrated scheduling problem of a complex single product, the process is virtualized as the node of a tree. All processes and the constraint relationships among them are expressed as a tree structure. For this tree, the research work is carried out to find a method to minimize the machining completion time.
- (2)
- For the integrated scheduling problem of a multi-product, when the start-machining time points for a multi-product are the same, the trees of the multi-product are virtualized as a tree. In contrast, when the start-machining time points for a multi-product are different, the remaining tree of the products that are being processed and the trees of the upcoming products are virtualized as a new tree repeatedly. Each time, the existing complex single-product integrated scheduling algorithm is used to realize the machining scheduling of the single tree to simplify the solution of the problem.
2. Materials and Methods
2.1. Problem Model Description
2.1.1. Problem Statement
2.1.2. Related Definitions
2.1.3. Objective Function
2.2. Research Method
2.3. Data Structure Description
2.3.1. Process Node Structure
2.3.2. Device Structure
2.3.3. Scheme Structure
2.4. Process Sorting Strategy
2.4.1. Analysis of Process Sorting Strategy
2.4.2. Sorting Algorithm Design of Leaf Nodes in Current ROPT
| Algorithm 1 The steps of the leaf node sorting algorithm in the current ROPT. |
| Step 1. Initialize a[k], b[k], Stack1, Stack2 to null. Let j = 0. |
| Step 2. i++. |
| Step 3. Determine the CP. Take the CP as the PS with the greatest TUD in the ROPT. |
| Step 4. j++. Store the leaf node of the CP into Layeri. Assume that qj is the pointer to the first process of the PS. |
| Step 5. Judge whether the node is a fork node. If yes, go to Step 6; otherwise, go to Step 7. |
| Step 6. Push the fork node into Stack1. |
| Step 7. Move the pointer qj back to the next process. |
| Step 8. Judge whether pointer qj is null. If yes, go to Step 9; otherwise, go to Step 5. |
| Step 9. Delete the PS with the highest TUD from the ROPT. |
| Step 10. Judge whether Statck1 is empty. If yes, go to Step 16; otherwise, go to Step 11. |
| Step 11. Pop Stack1. In the ROPT forest, find a PS with the unique longest length starting from each immediate successor process of the processes that pop out of Stack1. If it is not unique, select the PS with more processes. Use a [k++] to store the pointer pointed to the PS. |
| Step 12. Calculate the TUD value of each PS and store the results in b [k++]. For the convenience of calculation, the method is to subtract the CP length of the initial ROPT from the PLoN of the leaf node on each PS, which is L-T’. |
| Step 13. Judge whether Statck1 is empty. If yes, go to Step 14; otherwise, go to Step 11. |
| Step 14. Sort the elements in a[k] according to their corresponding elements of b[k] in ascending order. If the values are equal, sort them according to the number of processes contained in the PS in ascending order. |
| Step 15. Store the elements in a[k] into Stack2 from front to back. Clear a [] and b []. |
| Step 16. Judge whether Stack2 is empty. If yes, go to Step 18; otherwise, go to Step 17. |
| Step 17. Pop Stack2. Take the PS pointed by the pointer that pops out from Stack2 as the PS with the greatest TUD in its subtree. Then go to Step 4. |
| Step 18. Return to the Layeri; Exit. |
2.4.3. Algorithm Design of Process Sorting Strategy
| Algorithm 2 The steps of the process sorting strategy. |
| Step 1. Initialize List0 and List1 to null. |
| Step 2. Establish List0. We establish nodes one by one according to the input processes’ information, partial order relationship between processes, and equipment’s information; next, we insert the nodes into List0 and input the nodes’ attribute values, where the initial values of L, Tb and Te are all 0. |
| Step 3. Calculate N and each PLoN. Update the attribute value L of each node. Determine the CP’s length T′. The root node’s PLoN is its attribute T, and the other nodes’ PLoN are equal to their attribute T plus their immediate predecessor processes’ PLoN. |
| Step 4. Initialize Layeri (1 ≤ i ≤ N) to null. |
| Step 5. i = 0. |
| Step 6. Backup List0 with List1. |
| Step 7. Judge whether the number of leaf nodes is one. If yes, go to Step 8; otherwise, go to Step 9. |
| Step 8. i++. Store the leaf node in the Layeri, and then go to Step 11. |
| Step 9. Call Algorithm 1 to sort the leaf nodes in the current ROPT and store the sorting results into Layeri in turn. |
| Step 10. List0 copy List1. Delete all leaf nodes in the current ROPT and go to Step 6. |
| Step 11. Judge whether the attribute F of node in Layeri is empty. If yes, go to Step 13; otherwise, go to Step 12. |
| Step 12. Delete all leaf nodes from the ROPT, and then go to Step 7. |
| Step 13. Reverse the order of Layeri (1 ≤ i ≤ N) and the order of elements in each Layeri. |
| Step 14. Return to Layeri (1 ≤ i ≤ N) and N; Exit. |
2.5. Reverse Order Hierarchical Scheduling Strategy
2.5.1. Analysis of Reverse Order Hierarchical Scheduling Strategy
2.5.2. Algorithm Design of Reverse Order Hierarchical Scheduling Strategy
- (1)
- When establishing the QT of process Ai, if the equipment needed by Ai is idle at the first QSTP, and if Ai’s machining at this first QSTP will not destroy the craft constraints relationship among all the processes that have been trial-scheduled, then we take the temporary SS that formed at this QSTP as Ai’s optimal temporary SS. That is, the Ai’s QT only includes the first QSTP, and the others after this QSTP are abandoned.
- (2)
- We store the established QSSSLP with PList and sort the PList’s elements in ascending order according to the attributed totaltime value of the elements. We keep the elements with the minimal totaltime value in PList and delete the others. When establishing QSSSLP, each process’s trial scheduling will form a temporary SS. If PList is not empty, we judge whether the totaltime of the newly formed temporary SS is less than or equal to that of the last element’s totaltime in PList. If yes, based on this temporary SS, we will continue to conduct trial scheduling for the remaining SLP and establish a new temporary SS. Otherwise, we abandon this temporary SS and this scheduled process’ other larger QSTPs; that is, we abandon all the temporary schemes whose attribute totaltime value is greater than this temporary SS. If the totaltime value of the QSSSLP established after all SLP have been trial-scheduled is less than or equal to the last element’s totaltime in PList, we add the newly established QSSSLP into the back of PList and delete the elements whose attributed totaltime value is greater than that of this QSSSLP from the PList.
| Algorithm 3 EstablishOptimalP.//Selecting the optimal QSSSLP |
| P EstablishOptimalP (P [] PList) |
| {Sort PList’s elements in ascending order according to the elements’ totaltime value; |
| Keep the elements with the minimal totaltime values in PList, and delete others; |
| count = The number of elements in PList; |
| if (count = 1) |
| return PList [0]; |
| return the element (QSSSLP) with the minimal sum of all processes’ start-machining time in PList; |
| } |
| Algorithm 4 EstablishQueueTime.//Establishing QT |
| QT EstablishQueueTime (P P1, Node Ai) |
| {Based on the QSSSLP P1, we find the time point at which the machining of Ai’s immediate predecessor process on its required equipment was completed and take it as the first QSTP of Ai. If the equipment needed by Ai is idle at this first QSTP, and if Ai’s machining at this first QSTP will not destroy the craft constraints relationship among all the processes that have been trial-scheduled, then the Ai’s QT only includes the first QSTP. Otherwise, we store Ai’s all QSTP into QT; |
| return QT; |
| } |
| Algorithm 5 EstablishTemporaryPlan.//Establishing temporary SS |
| P EstablishTemporaryPlan (int pt, P P1, Node n) |
| {At QSTP pt, by using the time-selective adjustment strategy of reference [18], we insert process n into P1 to establish the temporary SS PTemp; |
| return PTemp; |
| } |
| Algorithm 6 EstablishLayerSchedulingPlan.//Establishing SSSLP for the i-th layer |
| P EstablishLayerSchedulingPlan (P p, Node [] Layeri, int j = 0) |
| //parameter j means that the ROHISA will process the j-th element located in Layeri |
| {num = Number of processes in Layeri; |
| if (j >= num) exit 0; |
| QT = EstablishQueueTime (p, Layeri[j]); |
| if (j == num − 1)//The current process is the last element located in Layeri |
| {PList = null; |
| while (QT! = null) |
| {qt = Dequeue (QT); |
| p1 = EstablishTemporaryPlan (qt, p, Layeri[j]); |
| add p1 in PList; |
| } |
| pr = EstablishOptimalP (PList); |
| return pr; |
| } |
| else |
| {PList = null; |
| while (QT! = null) |
| {qt = Dequeue (QT); |
| p1 = EstablishTemporaryPlan (qt, p, Layeri[j]); |
| prt = EstablishLayerSchedulingPlan (p1, Layeri, j + 1);//recursion |
| add prt to PList; |
| } |
| pr = EstablishOptimalP (PList); |
| return pr; |
| } |
| } |
| } |
2.6. ROHISA Design and Complexity Analysis
2.6.1. ROHISA Design
| Algorithm 7 Proposed ROHISA, and its steps. |
| Step 1. Call upon Algorithm 1 to obtain N and Layeri (1 ≤ i ≤ N). |
| Step 2. Let i = 1. |
| Step 3. Call upon Algorithm 6. |
| Step 4. i++. |
| Step 5. Judge whether i ≤ N is true. If yes, go to Step 3; otherwise, go to Step 6. |
| Step 6. Generate the Gantt chart of product scheduling and output it. |
| Step 7. Exit. |
2.6.2. Complexity Analysis
- Time complexity of Algorithm 1
- (1)
- Establishing ROPT
- (2)
- Backing up ROPT
- (3)
- Circular calling Algorithm 2
- (4)
- The operation of reversing the order of LAs and the order of elements in each LA
- 2.
- Time complexity of circularly calling upon Algorithm 6
3. Comparison and Analysis
3.1. Case Comparison and Analysis
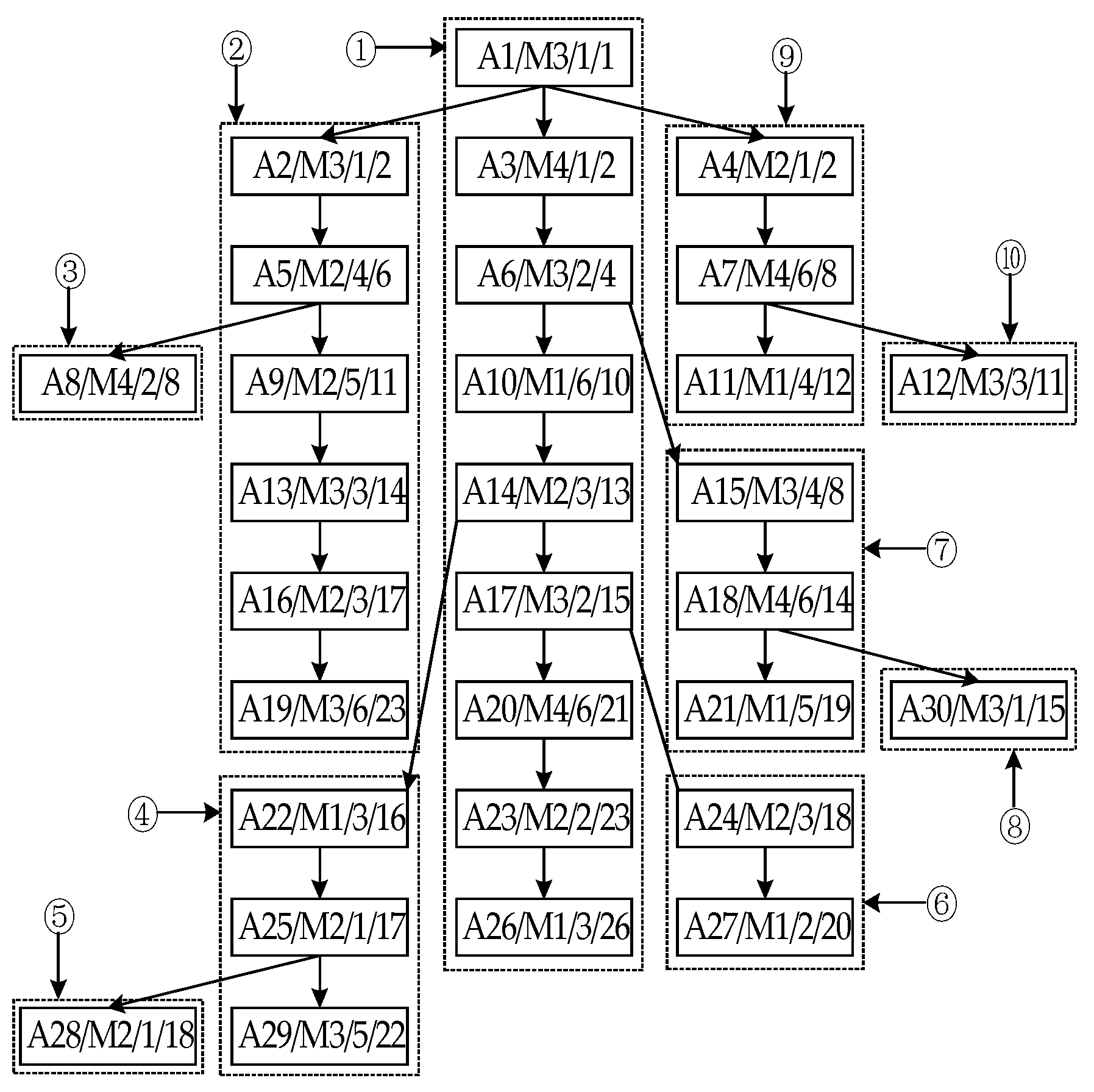
3.1.1. Case
3.1.2. Scheduling Results
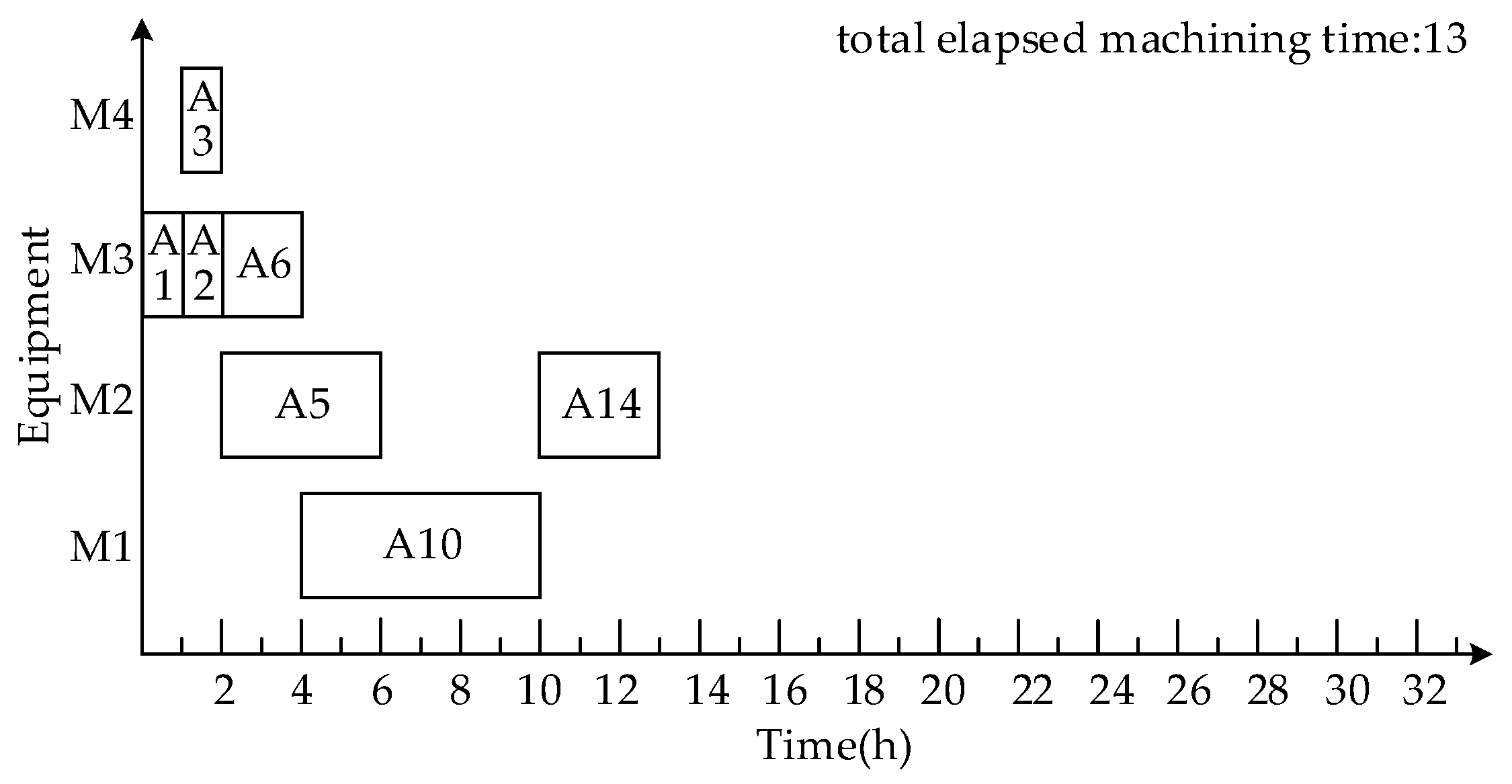
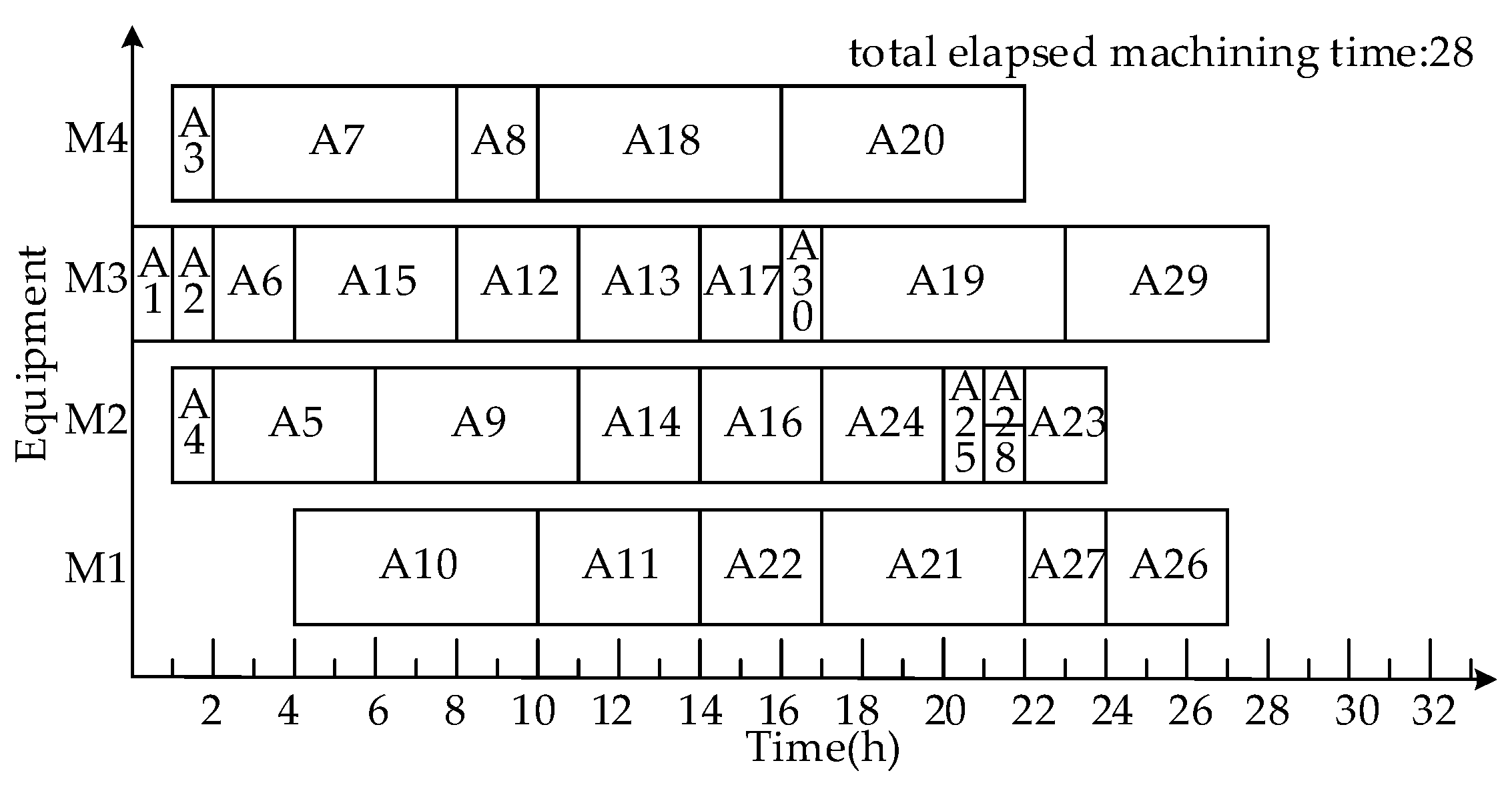
- Scheduling product A using the ROHISA
- (1)
- Process Sorting
- (1)
- The first step
- (2)
- The second step
- (3)
- The third step
- (2)
- Process Scheduling
- 2.
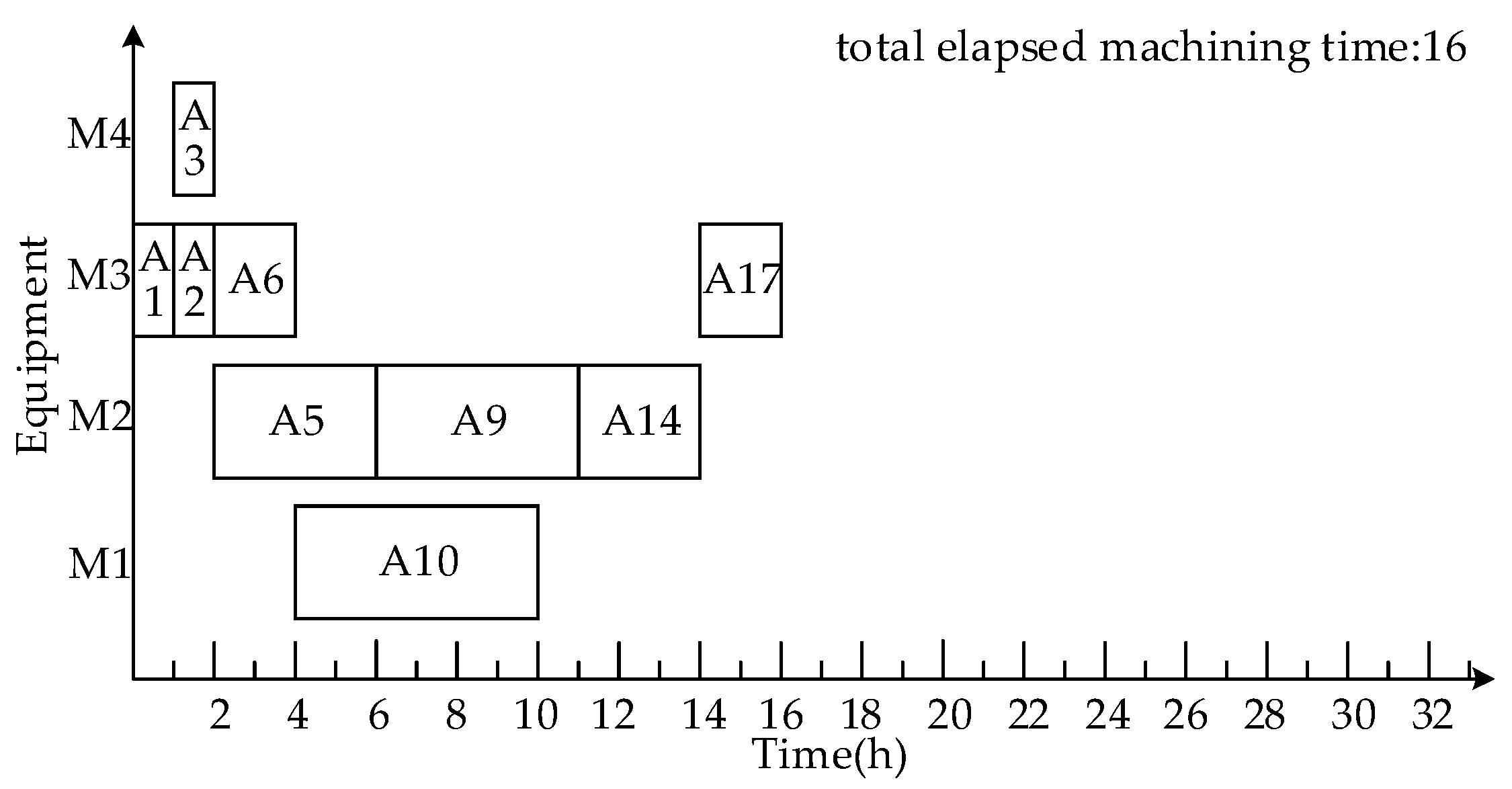
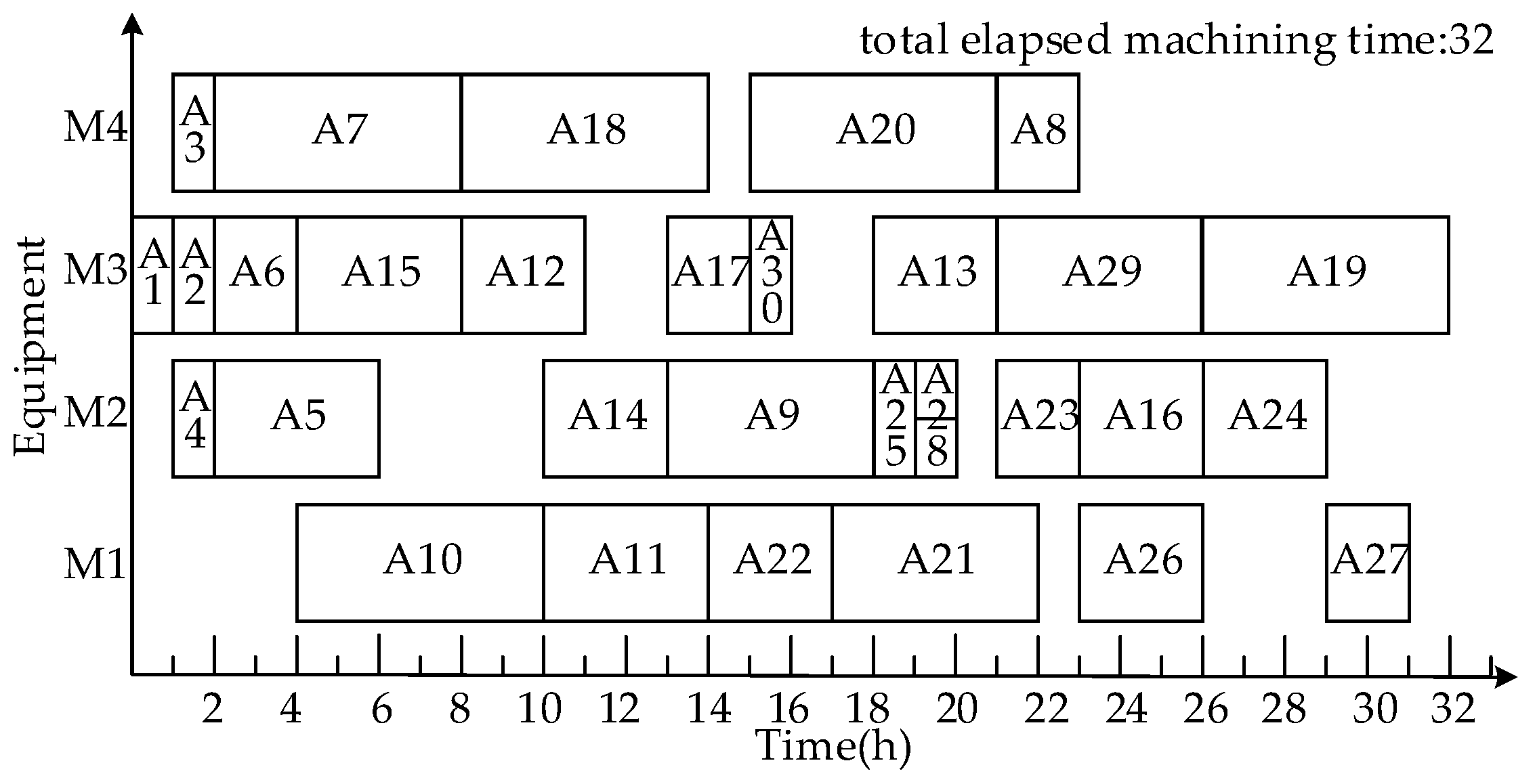
- Scheduling product A using a time-selective integrated scheduling algorithm (TISA)
- 3.
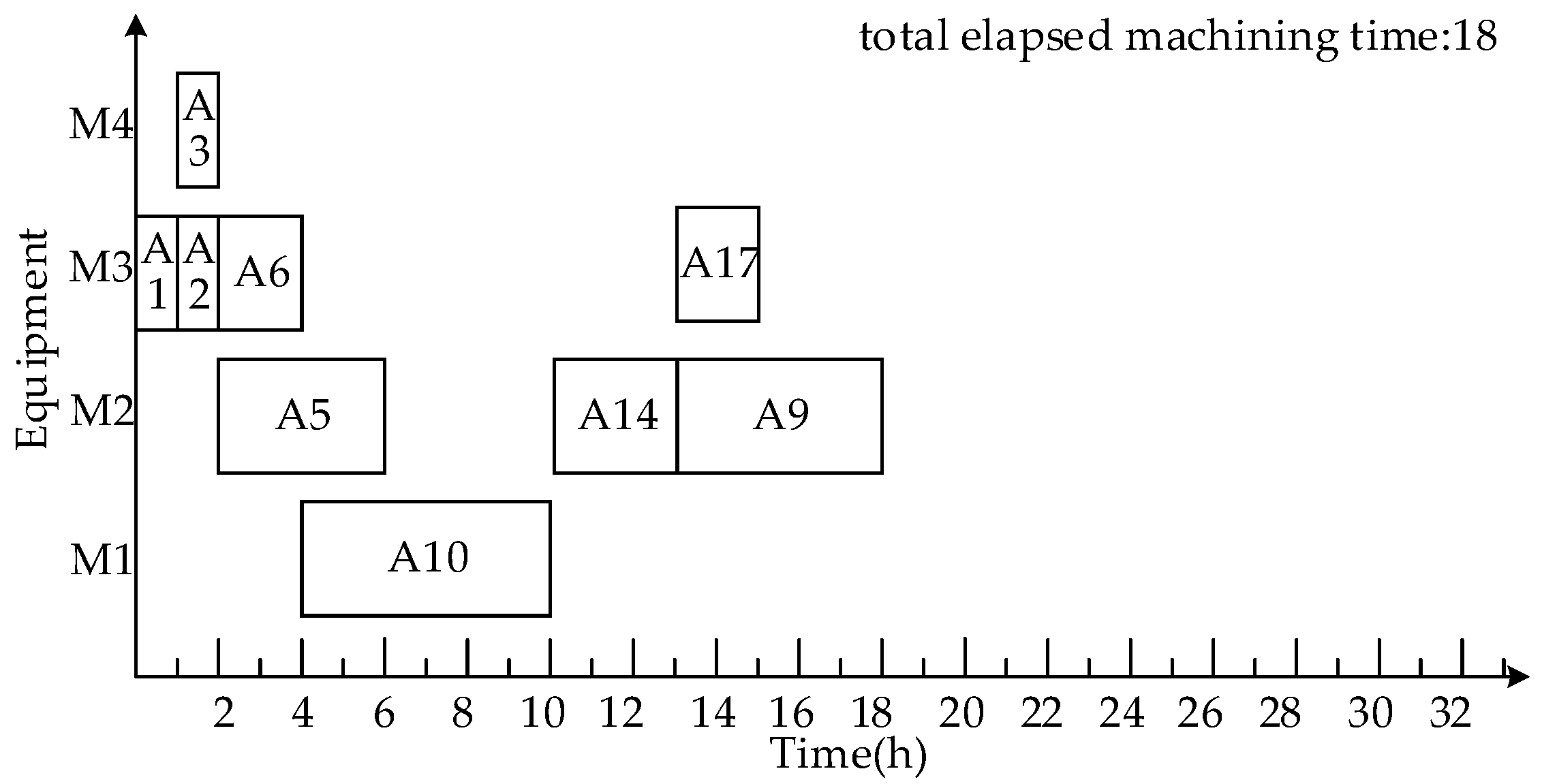
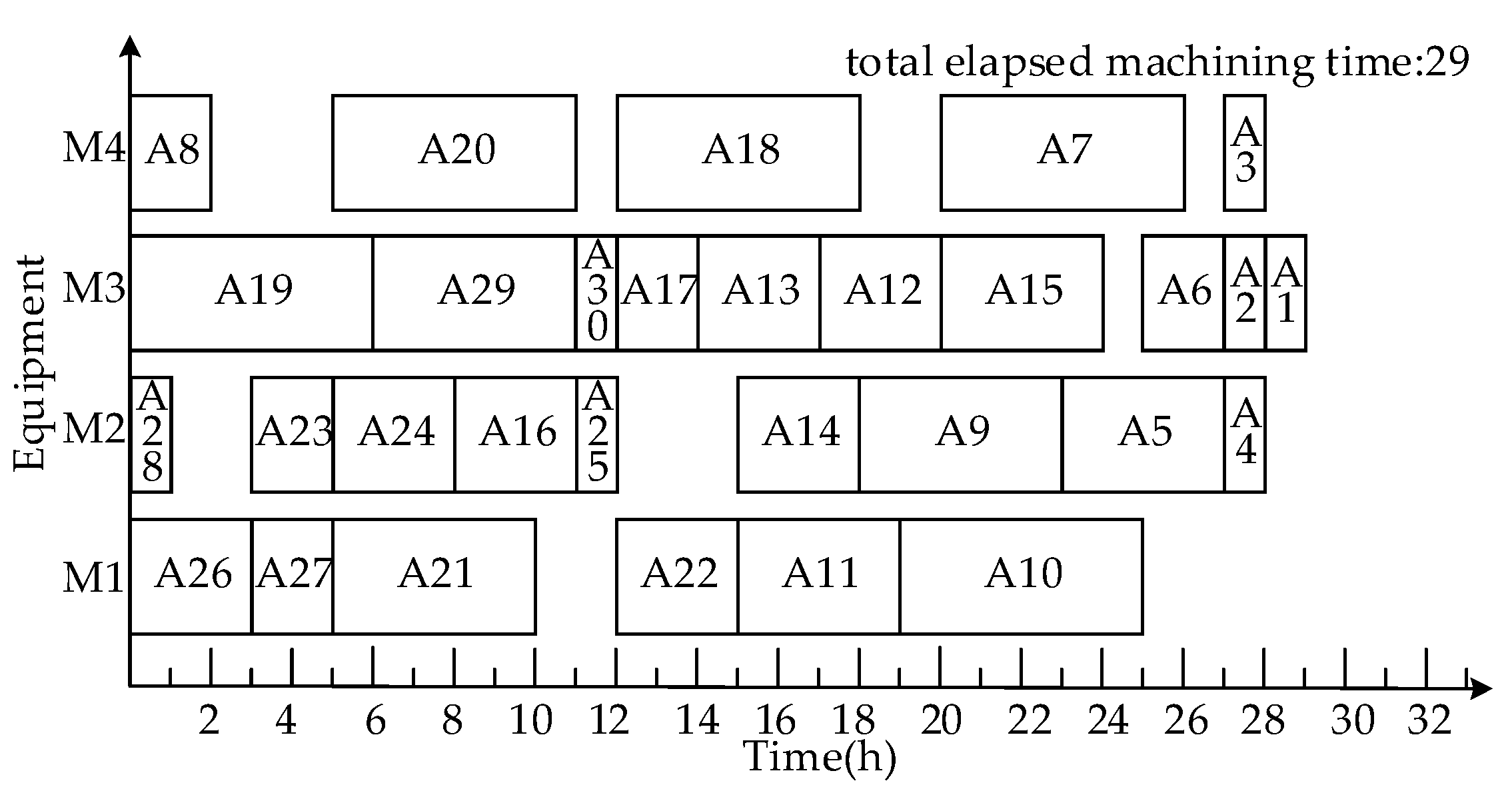
- Scheduling product A using the dynamic critical paths method (DCPM)
- 4.
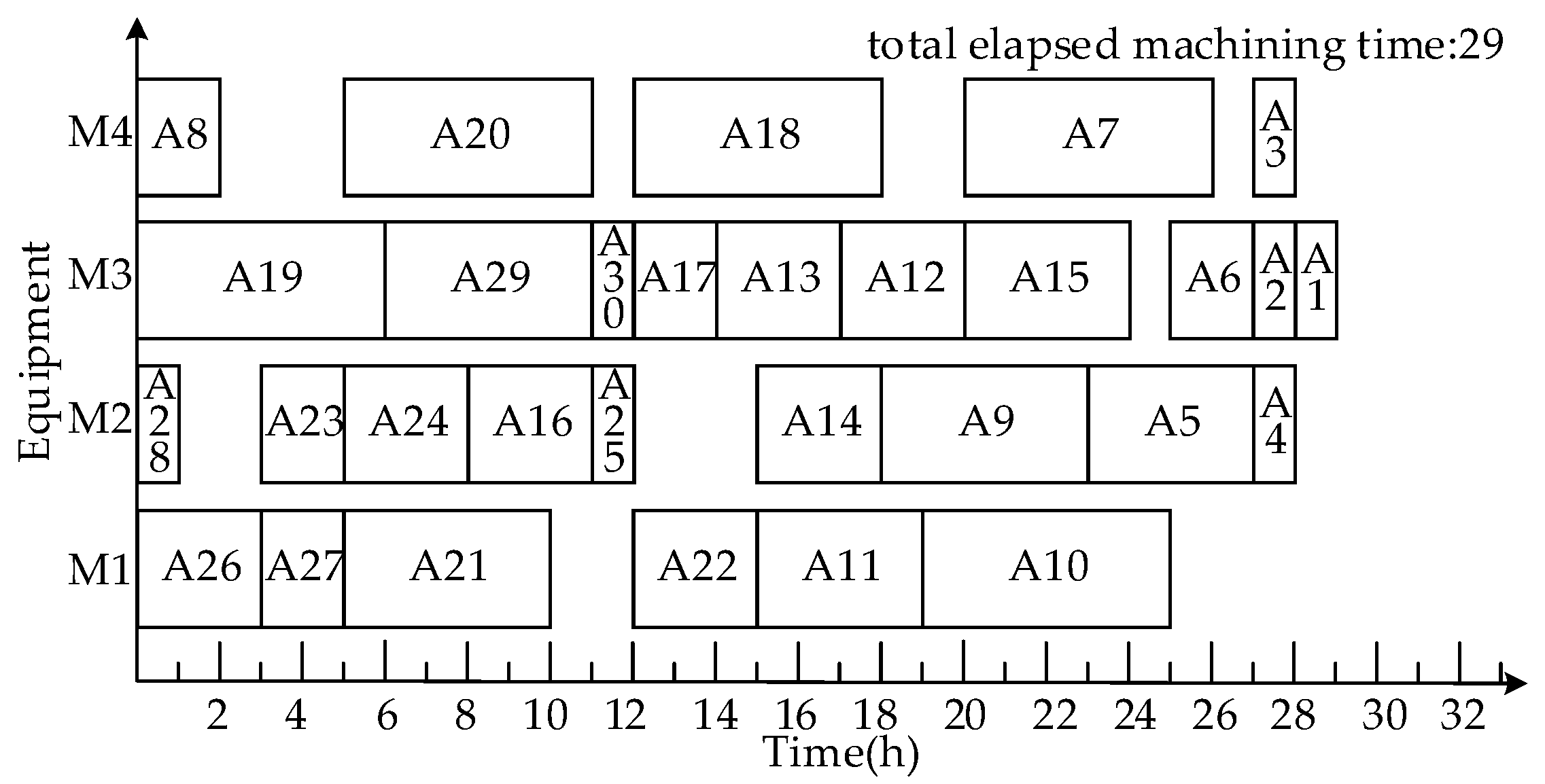
- Scheduling product A using a machine-driven integrated scheduling algorithm with rollback-preemptive (MISAR)
3.1.3. Comparison and Analysis
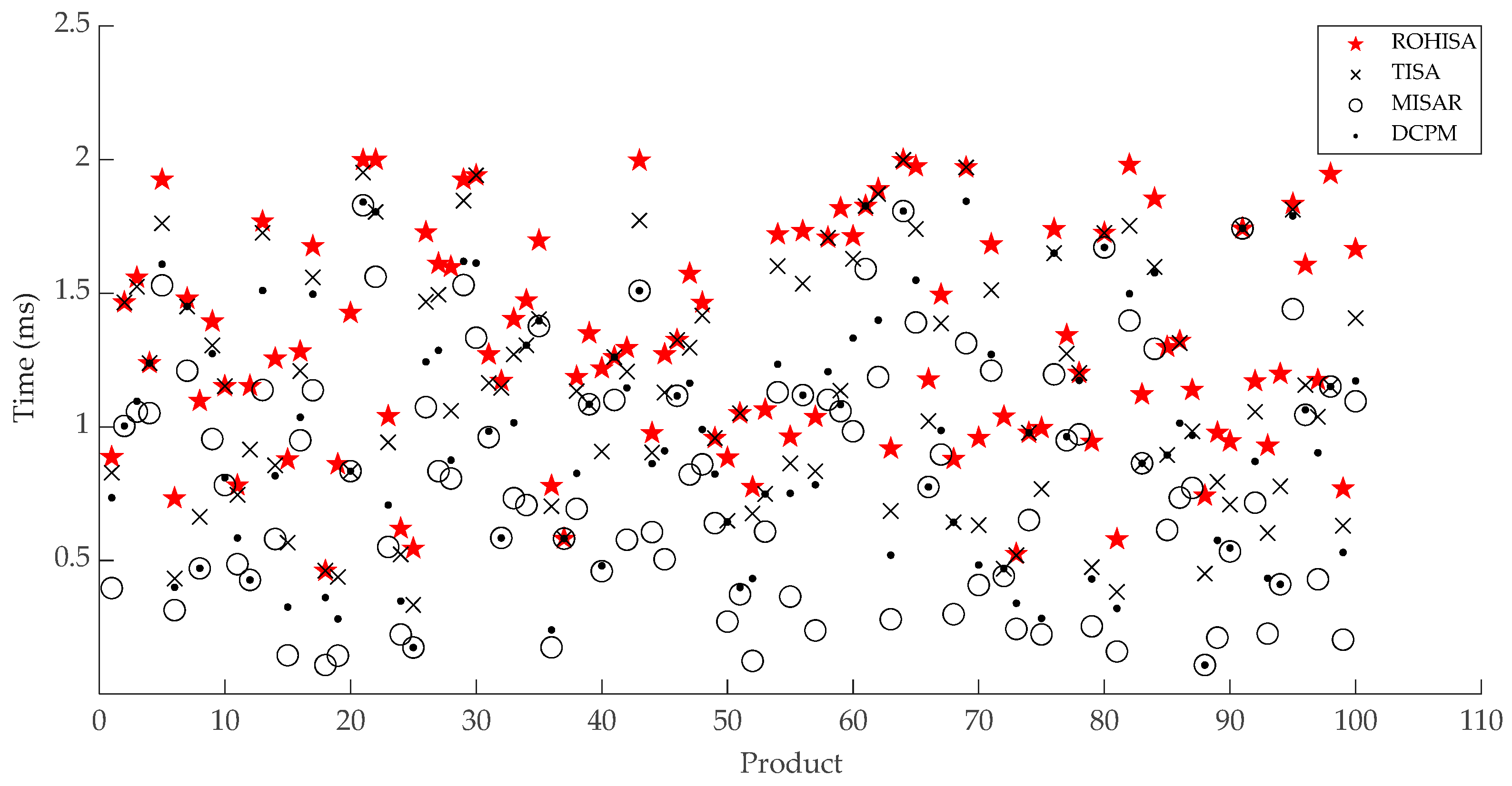
3.2. Experimental Data Comparison and Analysis
3.2.1. Experimental Data and Environment
3.2.2. Statistical Comparison of Experimental Results
3.2.3. Analysis of Experimental Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hua, H.M. Subversion of the Global Manufacturing Industrie 4.0, 1st ed.; Publishing House of Electronics Industry: Beijing, China, 2015; pp. 10–14. [Google Scholar]
- Nica, E.; Stan, C.I.; Luțan, A.G.; Oașa, R.-Ș. Internet of Things-based Real-Time Production Logistics, Sustainable Industrial Value Creation, and Artificial Intelligence-driven Big Data Analytics in Cyber-Physical Smart Manufacturing Systems. Econ. Manag. Financ. Mark. 2021, 16, 52–62. [Google Scholar] [CrossRef]
- Lăzăroiu, G.; Kliestik, T.; Novak, A. Internet of Things Smart Devices, Industrial Artificial Intelligence, and Real-Time Sensor Networks in Sustainable Cyber-Physical Production Systems. J. Self-Gov. Manag. Econ. 2021, 9, 20–30. [Google Scholar] [CrossRef]
- Yin, J. Resource Scheduling Optimization and Engineering Application, 1st ed.; Metallurgical Industry Press: Beijing, China, 2018; pp. 23–31. [Google Scholar]
- Zhang, F.F.; Mei, Y.; Nguyen, S.; Zhang, M.J. Collaborative Multifidelity-Based Surrogate Models for Genetic Programming in Dynamic Flexible Job Shop Scheduling. IEEE Trans. Cybern. 2021, 99, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Pei, Z.; Zhang, X.F.; Zheng, L.; Wan, M.Z. A column generation-based approach for proportionate flexible two-stage no-wait job shop scheduling. Int. J. Prod. Res. 2020, 58, 487–508. [Google Scholar] [CrossRef]
- Li, X.P.; Yu, W.; Ruiz, R.B.; Zhu, J. Energy-aware cloud workflow applications scheduling with geo-distributed data. IEEE Trans. Serv. Comput. 2022, 15, 891–903. [Google Scholar] [CrossRef]
- Li, X.P.; Chen, F.C.; Ruiz, R.B.; Zhu, J. MapReduce task scheduling in heterogeneous geo-distributed data centers. IEEE Trans. Serv. Comput. 2021, 99, 1. [Google Scholar] [CrossRef]
- Guo, S.P.; Dong, M. Order matching mechanism of the production intermediation internet platform between retailers and manufacturers. Int. J. Adv. Manuf. Technol. 2020, 115, 949–962. [Google Scholar] [CrossRef]
- Zou, W.Q.; Pan, Q.K.; Wang, L. An effective multi-objective evolutionary algorithm for solving the AGV scheduling problem with pickup and delivery. Knowl.-Based Syst. 2021, 218, 106881. [Google Scholar] [CrossRef]
- Chang, X.F. Challenges Posed by Multi Variety and Small Batch Production Mode and Countermeasures Acted by Chinese Small and Medium Enterprises. Adv. Mater. Res. 2013, 2393, 794–798. [Google Scholar] [CrossRef]
- Xie, Z.Q.; Yang, D.; Ma, M.R.; Yu, X. An Improved Artificial Bee Colony Algorithm for the Flexible Integrated Scheduling Problem Using Networked Devices Collaboration. Int. J. Coop. Inf. Syst. 2020, 29, 2040003. [Google Scholar] [CrossRef]
- Gao, Y.L.; Xie, Z.Q.; Yang, D.; Yu, X. Flexible integrated scheduling algorithm based on remaining work probability selection coding. Expert Syst. 2021, 38, e12683. [Google Scholar] [CrossRef]
- Xu, X.L.; Li, L.; Fan, L.X.; Zhang, J.; Yang, X.H.; Wang, W.L. Hybrid Discrete Differential Evolution Algorithm for Lot Splitting with Capacity Constraints in Flexible Job Scheduling. Math. Probl Eng. 2013, 2013, 112–128. [Google Scholar] [CrossRef]
- Novak, A.; Bennett, D.; Kliestik, T. Product Decision-Making Information Systems, Real-Time Sensor Networks, and Artificial Intelligence-driven Big Data Analytics in Sustainable Industry 4.0. Econ. Manag. Financ. Mark. 2021, 16, 62–72. [Google Scholar] [CrossRef]
- Nica, E.; Stehel, V. Internet of Things Sensing Networks, Artificial Intelligence-based Decision-Making Algorithms, and Real-Time Process Monitoring in Sustainable Industry 4.0. J. Self-Gov. Manag. Econ. 2021, 9, 35–47. [Google Scholar] [CrossRef]
- Liu, D.J.; Hu, C.M. A dynamic critical path method for project scheduling based on a generalised fuzzy similarity. J. Oper. Res. Soc. 2021, 72, 458–470. [Google Scholar] [CrossRef]
- Xie, Z.Q.; Zhang, X.H.; Gao, Y.L.; Xin, Y. Time-selective Integrated Scheduling Algorithm Considering the Compactness of Serial Processes. Chin. J. Mech. Eng. 2018, 54, 191–202. [Google Scholar] [CrossRef]
- Zhang, X.H.; Ma, C.; Wu, J. Multi-batch integrated scheduling algorithm based on time-selective. Multimed Tools Appl. 2019, 78, 29989–30010. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, X.H.; Peng, G. An Improved Integrated Scheduling Algorithm with Process Sequence Time-Selective Strategy. Complexity 2021, 2021, 5570575. [Google Scholar] [CrossRef]
- Cao, W.C.; Xie, Z.Q.; Pei, L.R. Reverse Order and Greedy Integrated Scheduling Algorithm Considering Dynamic TUD of the Process Sequences. J. Electron. Inf. Technol. 2022, 44, 1572–1580. [Google Scholar] [CrossRef]
- Xie, Z.Q.; Xin, Y.; Yang, J. Machine-driven integrated scheduling algorithm with rollback-preemptive. Acta Autom. Sin. 2011, 37, 1332–1343. [Google Scholar] [CrossRef]
- Xie, Z.Q.; Yang, J.; Zhou, Y.; Zhang, D.L.; Tan, G.Y. Dynamic critical paths multi-product manufacturing scheduling algorithm based on operation set. Chin. J. Comput. 2011, 34, 406–412. [Google Scholar] [CrossRef]


| Algorithm | Average Machining Time (h) | Average Execution Time (ms) |
|---|---|---|
| TISA | 744.3 | 1.143456 |
| DCPM | 734.77 | 0.967637 |
| MISAR | 726.43 | 0.799919 |
| ROHISA | 717.57 | 1.314644 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, W.; Xie, Z.; Yang, J.; Zhan, X.; Pei, L.; Yu, X. A Reverse Order Hierarchical Integrated Scheduling Algorithm Considering Dynamic Time Urgency Degree of the Process Sequences. Electronics 2022, 11, 1868. https://doi.org/10.3390/electronics11121868
Cao W, Xie Z, Yang J, Zhan X, Pei L, Yu X. A Reverse Order Hierarchical Integrated Scheduling Algorithm Considering Dynamic Time Urgency Degree of the Process Sequences. Electronics. 2022; 11(12):1868. https://doi.org/10.3390/electronics11121868
Chicago/Turabian StyleCao, Wangcheng, Zhiqiang Xie, Jing Yang, Xiaojuan Zhan, Lirong Pei, and Xu Yu. 2022. "A Reverse Order Hierarchical Integrated Scheduling Algorithm Considering Dynamic Time Urgency Degree of the Process Sequences" Electronics 11, no. 12: 1868. https://doi.org/10.3390/electronics11121868
APA StyleCao, W., Xie, Z., Yang, J., Zhan, X., Pei, L., & Yu, X. (2022). A Reverse Order Hierarchical Integrated Scheduling Algorithm Considering Dynamic Time Urgency Degree of the Process Sequences. Electronics, 11(12), 1868. https://doi.org/10.3390/electronics11121868






