Resource Allocation on Blockchain Enabled Mobile Edge Computing System

Abstract

Currently, the concept of Mobile Edge Computing (MEC) has been applied as a solution against the plethora of demands for high-quality computing services. It comprises several essential processes, such as resource allocation, data transmission, and task processing. Furthermore, researchers applied blockchain technology, aiming to enhance the robustness of the MEC system. At present, resource allocation in the MEC system is a very hot field, but there are still some problems in the resource allocation process under the traditional MEC architecture, such as privacy disclosure and so on. Moreover, the resource allocation problem in a blockchain-enabled MEC system will be more complicated, while the mining process may have an impact on resource allocation policy. To address this issue, this paper investigates the resource allocation problem with blockchain-based MEC system architecture. A brand new consensus mechanism: proof of learning (PoL), is applied to the system, which does not waste the computing resources of edge computing servers. Based on this, we modeled the system mathematically, focusing on server processing latency, mining latency, rewards under the new consensus, and total cost. The asynchronous advantage Actor-Critic (A3C) algorithm is used to optimize resource allocation policy. To better capture the long-time trend of the system, the temporal convolutional network (TCN) is implemented to represent the policy function and state-value function in the reinforcement learning model. The results show that the A3C algorithm based on TCN not only converges faster but also is more stable.

1. Introduction

With the development of intelligent science and technology, more and more mobile devices have access to the mobile network wirelessly. According to Cisco’s report in 2019 [1]: there will be 29.3 billion mobile devices by 2023, up from 18.4 billion in 2018. The burst of mobile devices would lead to a rapid increase in data service. Faced with the burden of growing network traffic and the requirements of high-quality service, the traditional wireless communication network is under great pressure. The European Telecommunications Standards Institute (ETSI) proposed the concept of Mobile Edge Computing (MEC) [2] to cater the demands of massive connections and low latency services, which provides computational processing and data storage capabilities for these mobile devices at the edge of the network [3,4]. MEC mitigates the end-to-end latency of service delivery by moving the cloud computing platform to the edge of the network. Furthermore, it can hold various business scenarios such as smart device applications, health monitoring, connected vehicles, 5G network data migration service [5,6,7], and even a satellite-terrestrial network [8]. Therefore, the MEC has attracted extensive attention from the industry since its birth. This new mode can not only bring changes to traditional service providers, but also affect the interaction modes of many industries and networks. However, considering that MEC is a distributed architecture, it will be very different from cloud computing in processing uploading tasks. Hence, it is necessary to comprehensively consider the delay of various tasks and whether the processing mode of tasks are economical enough. The design of a reasonable resource allocation policy in MEC system has become the focus of research in the industry.

At present, the research on resource allocation of MEC has made great progress. Allocation policies can be categorized into many different types based on different classification criteria. The policies can be classified into static and dynamic ones according to whether they are adjusted according to the current system status. According to whether the task is completely allocated to MEC system for processing, it can be divided into full allocation and partial allocation. The complexity of different allocation policies are also different. For example, partial allocation needs to consider processing the task locally, and the local processing time needs to be compared with the processing time of uploading to the MEC server (the delay of wireless transmission needs to be taken into account) when making decisions. This allocation policy is more complicated and needs more consideration and [9]. Researchers have proposed many solutions to the resource allocation problem. Some algorithms are mentioned in the survey of optimization algorithms conducted by Faiza Cul et al. [10], such as numerical methods including the Bisection method, Newton–Raphson, and bio-inspired algorithms, which are often widely used to solve resource allocation problems. Huang Dong et al. [11] applied Lyapunov Optimization for resource allocation, which is also a traditional one. Some work applies reinforcement learning, a state-of-the-art methodology. A deep Q-learning method [12] is used to optimize the real-time adaptive policy of computing resource allocation for multi-user unloading tasks. To solve the problem of joint subchannel allocation and power allocation in uplink, Wang X.M. et al. [13] proposed three frameworks based on discrete DRL, continuous DRL and joint DRL to solve the above non-convex optimization problem. Furthermore, Agostino Forestiero et al. [14] proposed NLP-based multiagent algorithm for a distributed information system, which allows the built of dynamic and organized overlay network. These policies can balance the delay of task processing and the cost of server well, and thus provide theoretical support for the application of MEC system.

Moreover, security is a problem that cannot be ignored in the MEC system [15]. The possible security risks of MEC are as follows: the distributed architecture tells that the whole system will not be controlled by one single owner, such as the network infrastructure, service infrastructure, and user devices. This can result to a situation that every aspect is under potential attack [16]. Moreover, the deployed edge computing servers often call some application programming interfaces (APIs) about physical and logical environments. If those APIs are not well-protected, there might be a loss of privacy for clients [16]. These issues are critical for the reliability of MEC system. According to the problems mentioned above, the researchers presented blockchain technology to enhance the security level of MEC systems. Blockchain technology is a general combination of distributed data storage, peer-to-peer transmission, consensus mechanism, encryption algorithms, and other computer technologies [17]. Through consensus mechanism, the cost of being malicious greatly aggrandizes, making the system more robust; through asymmetric encryption algorithm and zero-knowledge proof, the blockchain efficiently protects clients’ privacy [18]. Besides security, the blockchain implements managing and deploying edge computing nodes autonomously through the smart contract. Its programmability also enhances the scalability of MEC [19]. At present, many solutions of blockchain-enabled MEC framework have been proposed [19,20,21]. Researchers have validated some of the architectures in real-world environments [22].

Nonetheless, when blockchain and MEC are integrated, the resource allocation problem should be revised. The resource allocation policy in traditional MEC mainly focuses on the latency of communication and data processing. However, when blockchain and MEC systems are combined, the time of mining and reward from mining can affect resource allocation policy: the former can affect total time delay, which is sensitive for clients, the latter is associated with the allocated computing resource. Therefore, further research on the resource allocation policy of blockchain enabled MEC is required. Meanwhile, some researchers have carried out works related to the resource allocation problems within blockchain-based MEC systems. Alia Asheralieva et al. [23] utilized Bayesian reinforcement learning and deep learning to deal with mining tasks based on MEC. However, they did not consider the resource allocation tasks raised by mobile devices. He Y. et al. [24] proposed a comprehensive blockchain-based MEC system, using the reinforcement learning method to optimize resource allocation policy. Nonetheless, the policy did not mention the time of mining and the reward from mining. Qiu X.Y. et al. [25] took reward from mining into consideration, but all the indicators in the reward function have the same weight coefficient, which means the reward function is just added by all the indicators, and the proof of work (PoW) consensus algorithm applied in the system would lower the computation resource usage. To sum up, the previous works remain the following questions. First, the impact of blockchain on edge computing resource allocation is not fully considered. Second, the consensus mechanism in blockchain system needs to be improved to save computing resources of edge computing server. Third, the impact of these indicators on resource allocation policies is not explored. In this case, our research proposed corresponding solutions, which are also one of the main contributions of this paper. The main contributions of our work are listed below:

(1)

As the blockchain system has something to do with the resource allocation policy in MEC systems, the blockchain mining process is taken into account in resource allocation model. There into, mining delay and mining reward are considered.

(2)

To improve the utilization of edge computing resources, the new consensus algorithm: proof of learning (PoL), is applied in the system based on previous studies [26,27]. PoL replaces the meaningless hash puzzle with the task of training neural networks, which are common in MEC application scenarios. Furthermore, the mining delay and mining reward are calculated according to this consensus.

(3)

To learn the impact of these indicators on resource allocation policies, we set different combinations of weight coefficients to adjust the resource allocation policies to different tendencies. Furthermore, we explored the effect of varying task arrival rates on policies with different preferences.

(4)

To learn the long-term pattern of impending tasks, the structure of temporal convolutional network (TCN) [28] is referred to as the policy function and state-value function in asynchronous advantage Actor-Critic (A3C) algorithm. The convergence speed of TCN enabled A3C algorithm and traditional A3C algorithm, which choose action only depends on current state, is compared, and it is found that using TCN as the policy and state-value functions can converge faster and more stable.

In keeping with the purpose of our research orientation, the rest of the article is generalized as follows: In Section 2, the design of a blockchain-based MEC system is proposed, illustrating its step-by-step procedure. In Section 3, we model the resource allocation problem in the system above firstly, presenting the exact problems needed to optimize. Then the combination of TCN and A3C algorithm is introduced. In Section 4, we simulate, analyze the model, and investigate the results. In Section 5, a detailed discussion is given, which consists of four parts: research results, comparison with other studies, significance of research, and unanswered questions. In Section 6, a conclusion is presented, figuring out the deficiencies and indicating the future work.

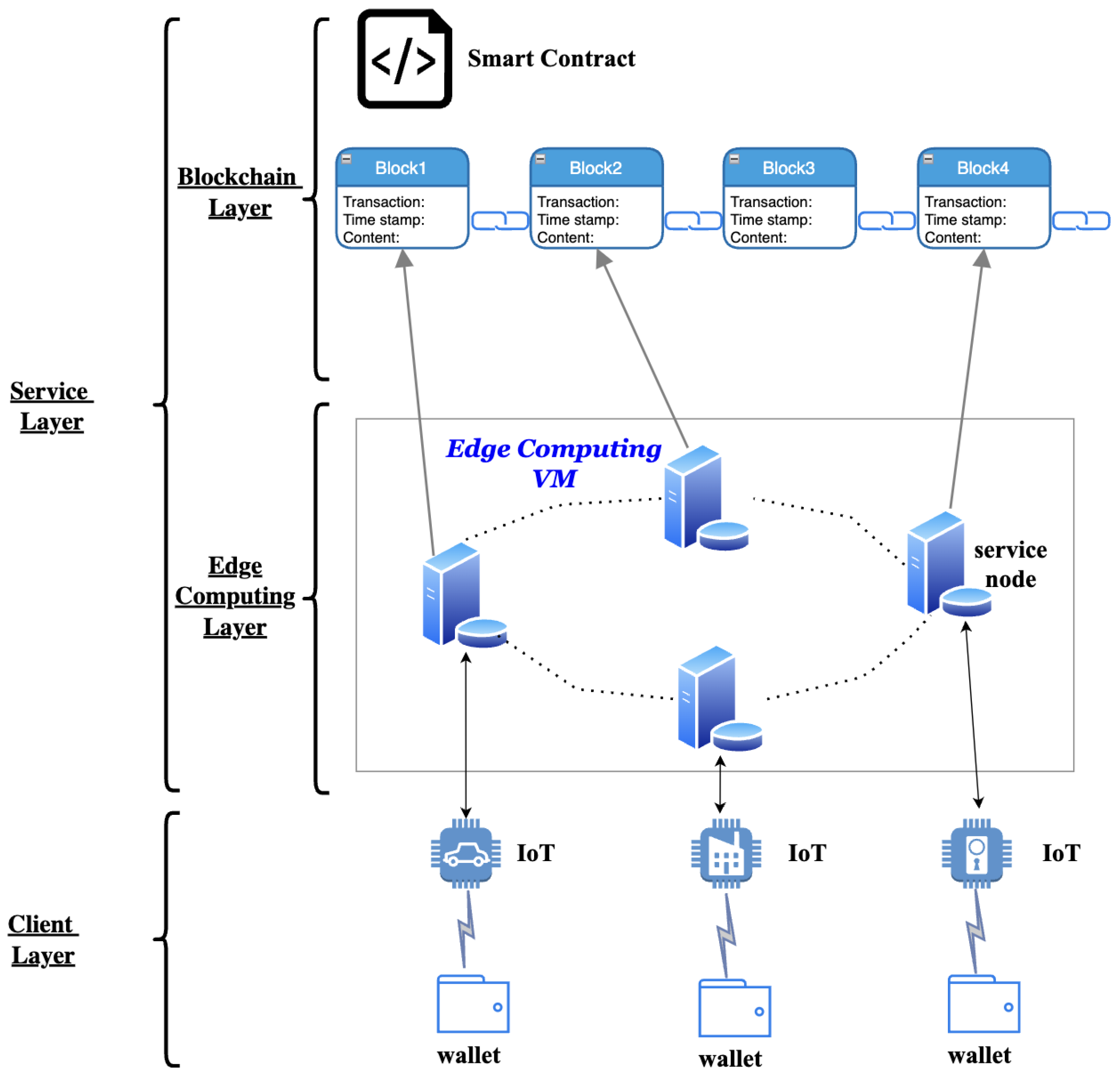
2. Overview of the System

In this part, a comprehensive MEC system based on blockchain is proposed. We will give a fundamental description of the whole system and introduce the working procedure of the system.

2.1. Framework of the System

In this part, the detailed blockchain-based MEC system architecture is proposed. As shown in Figure 1, the proposed model mainly consists of two parts: service layer and client layer, and the service layer can be further separated into blockchain layer and edge computing layer.

The client layer consists of many mobile devices, such as temperature and humidity sensors, smart watches, and monitors, which are common in normal life and industry application scenario currently. Each device connects to a blockchain wallet, as the wallet contains a certain amount of crypto token which is a basic instrument in the blockchain system. The connection between mobile devices and edge computing servers is achieved wirelessly, for both the connection between wallet and blockchain system and data uploading. The service layer consists of two parts, which are blockchain layer and edge computing layer. Many edge computing service nodes, which provide the computing resources to take charge of processing the clients’ data, make up the edge computing layer. Meanwhile, each service node also plays the role of the miner in the blockchain system to maintain the ongoing of the whole system, which means they generate blocks after finishing a neural network training task released by the PoL consensus mechanism. Service node needs to upload the results of the training task, for example: accuracy, neural network parameters, so that other service nodes (miners) can verify the correctness and make sure it will not do malicious things. To ensure that the computing resources will be allocated efficiently, the smart contract, which consists of several functions that control the working flow, needs to make optimal decisions on such limited computing resources.

The specific framework is designed for three reasons.

(1)

While using the blockchain technology, the MEC system that could previously run only on a trusted intermediary, can now operate safely without the need for a central authority [29]. Furthermore, the heavy use of cryptography brings authoritativeness and security [29]. For example, the zero-knowledge proof can protect the information with anonymity [18], the consensus algorithms can avoid malicious attacks [30], and the script validation used in transactions, namely Pay-to-Public-Key-Hash transaction (en.bitcoinwiki.org/wiki/Pay-to-Pubkey_Hash, accessed on 4 February 2020) and multi-signature transaction (en.bitcoin.it/wiki/Multi-signature, accessed on 20 July 2021), can improve the security [31].

(2)

As the MEC system is in a quite decentralized environment, using just an online platform may suffer from “a central point of failure” [32]. The decentralized trait of blockchain technology can build mutual trust among participants by implement specific consensus: PoW, proof of stake (PoS), and thus enhance the robustness of the system [31]. The model proposed by Xu J.L. et al. [31] have proved its correctness.

(3)

Smart contracts, which are scripts that reside on the blockchain that allow for the automation of multi-step processes, translate contractual clauses into code and embed them into property that can self-enforce them. They operate as autonomous actors, whose behavior is based on the embedded logic [30]. When combined with MEC system, the smart contract can provide flexible and scalable computing capability to address the tradeoff between limited computing capacity and high latency [33]. The work performed by Ye X.Y. et al. [34] has proved that the combination of blockchain and MEC can have an improvement on optimal allocation policy compared with other existing schemes.

2.2. Working Flow of the System

This section will go over the entire working flow, which is the procedure by which mobile devices in daily and industrial application situations complete transactions based on this system.

Taking air quality sensors as a vivid example, they collect air quality indicators, such as the concentrations of carbon dioxide, the concentrations of PM 2.5 [35], etc. Then they analyze the collected data above to estimate the situation of surroundings. However, the sensors, cannot process the data themselves. They need to send it to edge computing servers so that servers would help conduct it.

As shown in Figure 2, the complete procedure can be included as following:

(1)

The air quality sensor, which is a mobile device, connects to the wallet to make sure the device itself links to the blockchain-based mobile edge computing system.

(2)

The wallet is used to send a request to the service node, along with a certain amount of crypto token for the cost of edge computing services.

(3)

The smart contract will detect this transaction and allocate computing resources to the data, which is uploaded by the air quality sensor, based on the current state of the system and the size of the uploaded data, and it is called the “edge task”.

(4)

The allocated computing resources then start dealing with the “edge task”, and the processed result is finally obtained. After that, the service node, or the miner, needs to finish the training of a specific neural network under the PoL consensus, which is the “mining task”, for the preparation of block generation.

(5)

Once the “mining task” is finished, the service node is required to upload the training results, such as the accuracy of the training model and the neural network parameters. Furthermore, other miners can thus verify its correctness and make sure the service node is not doing malicious things. After everything is completed, a block is generated and stored in the blockchain system.

(6)

Finally, the result of “edge task” will be sent back to the air quality sensor.

As the purpose of this article is to deal with the resource allocation problems, the implementation of this system will not be discussed. In the next part, the inner mechanism of allocating computing resources will be discussed in detail, which is also the main focus of this study.

3. Resource Allocation Problem

Typically, the purpose of resource allocation is to allocate computing resources, which are used on data processing. A good allocation policy can optimize latency, for both transmission and processing. However, when the blockchain technology is combined, its impact on resource allocation policy can not be ignored. Based on the MEC system model mentioned in Section 2, despite the processing latency and cost of servers, which are the two main indicators in the traditional model, the mining process also needs to be considered, as the mining reward is associated with the allocation of computing resource and the mining delay is part of the latency for clients.

In this part, firstly, edge computing systems are taken into consideration, which includes two indicators: latency and cost. Then, we introduce the details of mining process. After that, the TCN enabled A3C is proposed, a state-of-the-art methodology used to solve resource allocation problems.

3.1. Edge Computing System Model

Assuming that one service node (SN) has m servers, they are in charge of n mobile devices (MD). In the model, two sets are used to present service node and mobile devices, respectively: $\mathbf{SN}=\{E_1,E_2,\dots ,E_m\}$, $\mathbf{MD}=\{I_1,I_2,\dots ,I_n\}$.

Each mobile device will send different tasks to the service node, as for the latency of a specific task, two parameters are taken into consideration:

$$t_{process}=t_q+t_p$$

(1)

where $t_{process}$ denotes the latency of data processing, $t_q$ denotes the queuing latency, and $t_p$ denotes the time for a server to process the data.

Assume that the CPU cycles required by the edge computing servers to process 1 bit of data is M, the CPU dominant frequency is f GHz, and d represents the data size of the task so Equation (1) can be changed as:

$$t_{process}=t_q+d\frac{M}{f}$$

(2)

The service model is actually a queuing model [36], based on the queuing theory [37], here $\mathcal{M}$/G/s model is chosen to simplify the service model. $\mathcal{M}$ shows that the arrival rate of tasks is subject to Poisson distribution. G shows that the processing time is subject to general distribution with certain mean and variance, s denotes that there are s servers.

When the system is in steady state, according to the time approximation formula raised by Boxma [38]:

$$\mathbb{E}\left[W_q(\mathcal{M}/G/s)\right]\simeq \frac{1+{\sigma }^2}{\frac{2J_G\left(s\right)}{\mathbb{E}\left[W_q(\mathcal{M}/\mathcal{M}/s)\right]}+\frac{1-J_G\left(s\right)}{\mathbb{E}\left[W_q(\mathcal{M}/D/s)\right]}}$$

(3)

$$J_G\left(s\right)=\left\{\begin{array}{cc}1,\hfill & s=1\hfill \\ \frac{s+1}{s-1}\left\{\frac{1+{\sigma }^2}{(s+1)\mu I_G\left(s\right)}\right\},\hfill & s\ge 2\hfill \end{array}\right.$$

(4)

$$I_G\left(s\right)={\int }_0^{+\infty }{\{1-G_e\left(t\right)\}}^s\mathrm{d}t,t\ge 0$$

(5)

$$G_e\left(s\right)=\mu {\int }_0^t\{1-G\left(u\right)\}\mathrm{d}u,s\ge 1$$

(6)

where $G_e$ is the stationary-excess cdf associated with the service-time cdf G.

Because the reward would be determined using the latency of task in the resource allocation algorithm later, the average latency of the queuing model in its steady state is not chosen when calculating the waiting time of one single task. Specifically, the service time of all the tasks in the target’s queue is mentioned, regarding it as the latency of the target task. Relying on that, Equation (2) can be improved as:

$$t_{process}=\frac{{\sum }_i{d}_i·M_i}{f}+d\frac{M}{f}=\frac{b}{f}+d\frac{M}{f}$$

(7)

where ${\sum }_i{d}_i·M_i$ denotes the total amount of tasks in the buffer. b is used to represent how much task has left in the buffer in the rest part of the paper.

Assuming the data size d obeys general distribution with certain mean and variance: $d\sim \mathcal{N}(\mu ,{\sigma }^2)$, and the arrival rate follows the Poisson distribution with parameter $\lambda$ in order to fit $\mathcal{M}$/G/s model.

In real-world scenarios, the latency should also include the delay in wireless transportation. However, considering that all the servers are deployed in a service node in one certain place, which means that the delay in each server would be the same. Thus, it is left out in the model.

Based on the kW·h concept in the electricity field, we propose a fresh new unit: GHz.h. The cost of data processing is calculated in GHz.h that the server consumes. So the cost can be presented as:

$$\begin{array}{c}\hfill cost=h·u,h=f·d\frac{M}{f}=d·M\end{array}$$

(8)

where $cost$ denotes the fee that the client needs to pay; u denotes the cost in GHz.h.

3.2. Blockchain Model

In this part, the mining process of PoL is introduced, along with the calculation of mining delay and the mining reward.

Mining is the process by which blockchain transactions are validated digitally on the blockchain network and added to the blockchain ledger. For example, the mining process in Bitcoin system is the process of solving a hash problem, which means using hashing operations to obtain a specified answer. However, the meaningless hash puzzle will waste a lot of computing resources, which is quite insupportable in edge computing systems. In order to fit the edge computing system, Qiu C. et al. [26] proposed a new consensus algorithm: PoL. By just replacing the hash puzzles with the training task of neural networks, each service node trains the model locally in a fixed time, and when a training task is finished, the service node is required to encapsulate the learning results into the transaction so that other nodes can check if the training result is correct based on neural network parameters, output sets and loss functions. In this way, PoL can deter abuse attacks and save computing resources at the same time.

However, the previous PoL consensus mentioned above is not that perfect, because by setting a fixed training time, the rate of block generation cannot adujust according to congestion level of blockchain network. To tackle this issue, we improved the PoL that the service node only needs to complete the given number of training sessions based on the given data sets, where the given number represents the training difficulty level. The system can adjust the difficulty level to change the rate of block generation.

Assume that the neural network architecture in the training task is multilayer perceptron (MLP). First, the floating point operations (FLOPs) [39] of the Forward propagation and backward propagation is given.

(1)

Forward Propagation

Let us consider the propagation process from layer i to layer j. The output matrix $S_j$ of layer j can be written in:

$$S_j=W_{ji}*Z_i$$

(9)

where $W_{ji}$ represents the weight coefficient matrix between layer j and layer i, and $Z_i$ represents the output matrix of layer i after the calculation of activation function, such as sigmoid or Relu functions. So, $Z_i$ can be given as:

$$Z_i=f\left(S_i\right)$$

(10)

where f represents the activation function mentioned above.

Thus, the floating point operations of the forward propagation is $(j\times i+j)\mathrm{FLOPs}$. Furthermore, if the MLP obtains N layers, and this process will run $N-1$ times.

(2)

Backward Propagation

The backward propagation proceeds as follows. The error matrix of layer j is first calculated. If the layer j is the output layer of MLP, then it can be written as:

$$E_j=f^{\prime }\left(S_j\right)\odot (Z_j-O_j)$$

(11)

where ⊙ represents the element-wise multiplication. If layer j is the hidden layer, and suppose layer k is the next layer of j, then Equation (11) can be transferred to:

$$E_j=f^{\prime }\left(S_j\right)\odot (W_{kj}^T*E_k)$$

(12)

To update the weight coefficient matrix between layer i and layer j, the “delta” weight matrix is calculated.

$$D_{ji}=E_j*Z_i^T$$

(13)

where $Z_i^T$ is the transpose of $Z_i$.

Finally, the weight coefficient matrix is adjusted:

$$W_{ji}=W_{ji}-D_{ji}$$

(14)

The floating point operations of backward propagation is $(j+j+j\times i+j\times i)\mathrm{FLOPs}$ for Equation (11), and $(j\times k+j+j\times i+j\times i)\mathrm{FLOPs}$ for Equation (12).

Based on all the equations mentioned above, the total FLOPs of the forward and backward propagation can be calculated by given a specific MLP model. Here, we use $\omega$ to represent the FLOPs of one training session, and if the number of training example is N, and the number of training sessions is D, which means the mining difficulty in the improved PoL consensus, the FLOPs Ω of finishing the mining task can be shown as:

$$\mathsf{\Omega }=\omega \times N\times D$$

(15)

Furthermore, the mining time is obtained:

$$t_{mining}=\frac{\mathsf{\Omega }}{f}$$

(16)

As for the mining reward (bonus), if the mining time of a service node is shorter than the average mining time of the system, it will receive corresponding reward. Furthermore, if it is longer than the average mining time, the service node will receive negative reward. The formula of mining reward can be given as:

$$bonus=\frac{t_{average}-t_{mining}}{t_{average}}$$

(17)

3.3. Reinforcement Learning Model

In real-world cases, each service node runs in a specific situation. The A3C algorithm is employed, aiming to enable the nodes adapting complex situations. The core of the distributed algorithm is to increase the convergence rate towards the best policy. To obtain that, the system manages to extend the receptive field of the global network through multiple workers renewing parameters asynchronously. In the model, each worker corresponds to one service node.

There are two important functions in the A3C algorithm, one is the policy function, which is used to select the corresponding optimal action according to the current state, and the other is the state-value function, which is used to calculate the expected reward after taking a certain action. However, if the policy is only made by the current state, the chosen action may not be the best one, since the algorithm just observed one single time point and don’t make decision upon the past varying trends. Inspired by some state-of-the-art time series forecasting model, TCN, which is the combination of causal convolution and residual blocks, is applied as the policy function and state-value function in this paper, while the causal convolution can extract features over time, and residual model can prevent A3C from falling into gradient vanishing during parameter update [28].

In the next of this part, firstly, the four aspects of reinforcement learning model will be described: state, action, the transition of state, and reward function. Secondly, the architecture of TCN enabled A3C algorithm is introduced.

3.3.1. State

The simulation includes the whole process in the system: from queuing to processing, the server’s state needs to be recorded. In the model, $\mathbf{S}$ is used to represent the state of the server:

$$\mathbf{S}=\{I_1,I_2,\dots ,I_n;b_1,b_2,\dots ,b_m;D\}$$

(18)

In Equation (18), $b_i$ indicates the remaining tasks in server i and D represent the difficulty level of mining. Furthermore, $I_j$ indicates some task-related information of device No. j, including the data size d and the required M GPU cycles per bit, thus, we can use another way to represent set $\mathbf{S}$:

$$\mathbf{S}=\{d_1,M_1;d_2,M_2;\dots ;d_n,M_n;b_1,b_2,\dots ,b_m;D\}$$

(19)

In the model, we assume that the buffer size is infinity, but that does not mean that there could be infinite devices obtaining access to one server in the meantime. Assuming the maximum number of simultaneously accessed to one server is n, in this way, both the access and exit processes can be simulated.

As for the mining difficulty, service nodes choose appropriate policies according to the difficulty level and balance the reward of mining and the consumption of computing resources.

3.3.2. Action

The action is the response of a particular state, so actions are determined by arriving tasks and buffer size in the server. Dividing the arriving data into m pieces is the first step because there are m servers in one service node. Meanwhile, several servers are chosen to deal with the mining task. Due to the limitation of simulation, only two of them are chosen to do the mining task. The action can be defined as:

$$\begin{array}{c}\hfill \mathbf{A}=\{a_1,a_2,\dots ,a_n;e_1,e_2,\dots ,e_m\},a_i=\{c_{i1},c_{i2},\dots c_{im}\},\\ \hfill \sum _{j=1}^m{c}_{ij}=d_i,\sum _{k=1}^m{e}_k=2_{\{e_k=0or1\}}\end{array}$$

(20)

where $a_i$ denotes the action of splitting the task towards device i, $e_k$ can only be 0 or 1. If $e_k=0$, it means that server k is not chosen to mine. On the contrary, if $e_k=1$, server k is chosen to mine. Specifically, data in each device is diversified by servers. For the task of device i, $c_{ij}$ denotes the part of which being distributed in sever j.

3.3.3. Transition of State

In the previous discussion, the arrival rate of each task is subject to Poisson distribution with parameter $\lambda$, and the data size obeys general distribution: $d\sim \mathcal{N}(\mu ,{\sigma }^2)$. Knowing that the Poisson stream is additive so that Poisson distribution can also fit the arrival of tasks assigned by many other devices.

We assume the arrival rate of device $I_j$ as ${\lambda }_j$ so the total arrival rate for a service node is $\lambda ={\sum }_{j=1}^n{\lambda }_j$. When the task arrives, the state S is updated. The interval between the new state and old state is $\Delta t$, and it is subject to a negative exponential distribution with parameter $\lambda$ because the arrival rate obeys Poisson distribution. The cumulative distribution function is: $F(\Delta t)=1-e^{-\lambda \Delta t}$.

Then a function that integrates the system state with time is proposed. Firstly, to simplify the transition of state, we assume that all the tasks arrives at the same time, the current system state at time t is:

$$\mathbf{S}\left(t\right)=\{d_1\left(t\right),M_1\left(t\right);\dots ;d_n\left(t\right),M_n\left(t\right);b_1\left(t\right),b_2\left(t\right),\dots ,b_m\left(t\right);D\}$$

(21)

After a time slot $\Delta t$, another group of tasks arrive, the system state changes to:

$$\begin{array}{c}\hfill \mathbf{S}(t+\Delta t)=\{d_1(t+\Delta t),M_1(t+\Delta t);\dots ;d_n(t+\Delta t),M_n(t+\Delta t);\\ \hfill b_1(t+\Delta t),\dots ,b_m(t+\Delta t);D\}\end{array}$$

(22)

$$b_i(t+\Delta t)=\left\{\begin{array}{cc}{b}_i+\sum _{j=1}^n{c}_{ji}{M}_j-f_i\Delta t,\hfill & b_i+\sum _{j=1}^n{c}_{ji}{M}_j-f_i\Delta t>0\hfill \\ 0,\hfill & b_i+\sum _{j=1}^n{c}_{ji}{M}_j-f_i\Delta t\le 0\hfill \end{array}\right.$$

(23)

In this way, system states will change through the arrival and action of the task. It is noted that the system state still belongs to Discrete Markov Model though it depends on both t and $\Delta t$.

3.3.4. Reward Function

Reinforcement learning is a type of unsupervised learning, in which the reward function is used to back-propagate to update the parameters of the policy function and the state-value function, guaranteeing its policies would converge towards expectation.

As mentioned before, action $\mathbf{A}$ is chosen according to the current system state $\mathbf{S}$. Corresponding to each $s\in \mathbf{S}$ and $a\in \mathbf{A}$, we obtain policy Π:

$$\mathsf{\Pi }=\{\pi :s\to a;s\in \mathbf{S},a\in \mathbf{A}\}$$

(24)

Then the reward is measured in four aspects: process delay of the task, mining delay, cost, and the mining reward. Generally, it is a comprehensive measurement of the reward, aiming to lower the latency, contain the cost, and guarantee the mining reward as expected.

The process delay is regarded as a combination of two components: $t_q$, $t_p$. Considering that each task has been split into several servers, parameter $t_p^{ki}$ is introduced to indicate processing delay of the task k in server i. Thus, $t_{process}$ can be described as:

$$\begin{array}{cc}\hfill t_{process}=& \underset{i}{\max }[t_q+\sum _{k=1}^n{t}_p^{ki}]\hfill \\ \hfill =& \underset{i}{\max }[\frac{b_i}{f_i}+\sum _{k=1}^n{c}_{ki}\frac{M_k}{f_i}]\hfill \end{array}$$

(25)

The formula of mining delay is given in Equation (16).

Then the cost of task k is measured:

$$cost=\sum _i{h}_i·u_i+t_{mining}·\sum _{i=1}^m\left(e_i{f}_i{u}_i\right),h_i=\sum _{k=1}^n{c}_{ki}·M_k$$

(26)

where $h_i$ denotes the resource consumed in server i, $u_i$ denotes the unit price of server i.

Lastly, the mining reward is measured according to Equation (17).

From the analysis above, if time becomes longer, the cost could decrease, the mining reward would decrease. We want to reduce latency, reduce cost, and obtain more mining rewards, but these three targets cannot be obtained at the same time. Hence the reward function is given as follows:

$$R=-\alpha t_{process}-\zeta t_{mining}-\beta cost+\gamma bonus$$

(27)

where $\alpha ,\zeta ,\beta ,\gamma$ are weight coefficients of process delay, mining delay, cost, and mining reward, respectively. We expect to find a reasonable set of those coefficients through which the better policies could be obtained after training.

3.3.5. TCN Enabled A3C Model

A3C, short for Asynchronous Advanced Actor-Critic, is an improvement on the traditional Actor-Critic algorithm. A3C algorithm converges faster, contains more stable policies [40,41]. As its name shows, the A3C algorithm consists of two parts, the Actor-Critic algorithm and asynchronous algorithm. The policy function and state-value function in Actor-Critic are crucial, as they determine the available action to obtain higher reward. As mentioned above, TCN is applied to these two functions to extract long-time trend and void gradient-vanish. In the following article, firstly, the implementation of TCN in Actor-Critic is introduced. Secondly, the asynchronous algorithm, that is how A3C updates the parameters, is described.

(1) TCN and Actor-Critic

The Actor-Critic algorithm contains two neural networks, one is the Critic, the other is called Actor. The former one, or the Critic, judges the state-value function, which is the estimation of the expectation of future rewards based on current state and the corresponding policy. The latter one, or the Actor, estimates the probability of a set of output actions according to the input state. Combining two models, Actor-Critic is obtained. Furthermore, the advantage function is introduced to the model when updating parameters, it can tell whether the output of the model is good or not.

As shown in Figure 3a, here, the combination of temporal convolutional network and fully-connected network is deployed to approximate the state-value function $V\left(s\right)$ and the policy function $\pi \left(s\right)$. Different from previous architecture that only relies on current state s, the prediction of action a depends on both current state and previous states. Furthermore, with the current and previous states and the taken action a, the neural network can thus tell the state-action value. The state-value function and the policy function are given below, the left side of Equation (28) is the initial definition of the state-value function, and the right side of Equation (28) is the state-value function based on neural network. The same as the policy function shown in Equation (29):

$$V(s,a)\approx V(s_{n-l+1},\dots ,s_{n-1},s_n|a;\mathit{w})$$

(28)

$$\pi (s,a)\approx \pi \left(a\right|s_{n-l+1},\dots ,s_{n-1},s_n;\mathbf{\theta })$$

(29)

where $\mathit{w}$ is the weight coefficient of the value network, $\mathbf{\theta }$ is the weight coefficient of the policy network, s is the state of the agent, a is the action of the agent, and l is the history size.

Let us further analyze the process and structure of the neural network. To calculate the state-value function or the policy function, a state matrix needs to be put into the network, that the column of the matrix is state vector given by Equation (21). Then, the matrix is processed by TCN. As shown in Figure 3b, the TCN has two main characteristics, one is that the output size is the same as input size, and the other is that there cannot be any backsliding from the future to the present. To obtain the first characteristic, TCN uses a one dimensional fully-convolutional network, where remain the size of hidden layer and input layer the same. Furthermore, zero padding is added to keep the front and back layers equal in length. Furthermore, to achieve the second characteristic, TCN applies causal convolutions, the calculation of an output is only with elements from previous and now. The implementation of dilated convolution enables a wider range of receptive field. As you can see, if the dilatation factor d is set as 1, 2, and 4, the output layer can obtain nine units of history size from the second hidden layer, and fifteen units of history size from the input layer. Along with the dilated causal convolution, an $1\times 1$ convolution is added to avoid gradient-vanishing when the neural network is quite deep.

After the process of TCN, we use a one-dimension convolution to reduce the length in the time dimension. This is followed by the operation of flatten and finally the selection of available action and calculation of state-action value using the fully-connected neural network.

With the state-action value, we can calculate the target value, or target reward, after n steps. Here Target V is used to represent the final reward after n steps:

$$\mathrm{Target}V=r_t+\gamma r_{t+1}+\dots +{\gamma }^{n-1}{r}_{t+n-1}+\underset{a}{\max }{\gamma }^{n}V\left(s_{t+n},a\right)$$

(30)

where $\gamma$ is the discount factor.

In this way, a certain reward can interfere with n states before that, enabling the model to imitate the experience better and improving the validity of the model.

Then we introduce the advantage function. When updating policy-gradient, discount reward $R_t$ can inform the agent what actions are good, what are bad. We subtract the reward function and state-value function to obtain the advantage function $A(s_t-a_t)$. For example, based on the same state, if $A(s_t-a_t)>0$, then the chosen action is good, and vise versa.

$$A(s_t,a_t)=R(s_t,a_t)-V\left(s_t\right)$$

(31)

To calculate the advantage function, we have:

$$A(s_t,a_t;\mathbf{\theta },\mathit{w})=\sum _{i=0}^{k-1}{\gamma }^i{r}_{t+i}+{\gamma }^{k}V(s_{t+k};\mathit{w})-V(s_t,\mathit{w})$$

(32)

To avoid the algorithm trapped into local optimum, Mnih [40] added entropy $\beta {\nabla }_{\theta }H\left(\pi (s_t;\mathbf{\theta })\right)$ in policy $\pi$. The gradient updating function is:

$$\begin{array}{cc}\hfill {\nabla }_{\theta }\mathbb{E}\left[R_t\right]=& {\nabla }_{\theta }\log \pi \left(a_t\right|s_t;\mathbf{\theta })A(s_t,a_t;\mathbf{\theta },\mathit{w})\hfill \\ \hfill & +\beta {\nabla }_{\theta }H\left(\pi (s_t;\mathbf{\theta })\right)\hfill \end{array}$$

(33)

Equation (33) means that the higher expectation of the reward, the more likely the action will be chosen. $\pi \left(a_t\right|s_t;\mathbf{\theta })$ denotes the possibility to choose action at state $s_t$.

(2) Asynchronous algorithm

How does A3C exactly work? Simply, it is a process in which many Actor-Critic workers work asynchronously and update the parameters of the one policy function, or global network. To make the Actor-Critic workers work asynchronously, the asynchronous algorithm is introduced. The asynchronous framework of the A3C algorithm is given in Figure 4, and it mainly consists of environment, worker, and global network. Each worker performs as an independent agent to interact with an independent environment, using the result of interaction to update the parameters of the global network.

With each worker interacting with a certain environment, the model can obtain through more situations, which speeds up the convergence and lessen the possibility of being trapped in the local optimum.

The asynchronous algorithm works as following:

• Global network parameter initialization.
• Workers duplicate global network.
• Workers interact with their environments.
• Workers calculate the loss of value and policy.
• Workers calculate gradient through loss function.
• Workers update the parameters of global network.

4. Simulation and Analysis

In this part, the reinforcement learning approach is simulated. Assuming a service node has four different servers, each has a computing capability $f_i$, respectively. Those servers simultaneously serve five mobile devices. Each device has an arrival rate ${\lambda }_i$, its data size obeys general distribution $d\sim \mathcal{N}(\mu ,{\sigma }^2)$. The rest parameters are given in

Table 1. Parameter values in simulation.

Parameters	Explanation	Value
$\mathsf{\mu }$	the mean of data size	7 (Mb)
${\sigma }^2$	the variance of data size	2
c	minimum data size split	1 (Mb)
$\omega$	floating point operations	${10}^6$
M	CPU cycles required for 1 bit	[2, 5, 7] (bit/Hz)
N	number of training task	${10}^4$
f	domain frequency of server	[15, 16, 17, 18] (GHz)
$\lambda$	arrival rate	[14, 16, 18, 20, 22, 24]
u	server cost	[1, 1.1, 1.2, 1.3]
D	mining difficulty	[5, 6]
$\alpha$	coefficient of process delay	[100, 25, 50, 100, 100, 5, 5, 1]
$\zeta$	coefficient of mining delay	[2, 0.5, 1, 2, 2, 0.1, 0.1, 1]
$\beta$	coefficient of cost	[1, 1, 1, 1, 1, 100, 200, 1]
$\gamma$	coefficient of bonus	[20, 5, 10, 5, 1, 1, 1, 10]

:

In Table 1, $\lambda =\sum {\lambda }_i$ is the total arrival rate of all the tasks. In order to simplify the simulation, ${\lambda }_i$ is set equally, which means ${\lambda }_i=\lambda /5$. The dominant frequencies of the servers are 15, 16, 17, 18 GHz, respectively. The fee of each server is 1, 1.1, 1.2, and 1.3.

For ease of calculation, the task size is limited in set {5, 6, 7, 8, 9} (Mb). Furthermore, we set $\mathbb{E}\left[d\right]=7$, $Var\left[d\right]=2$.

A series of parameters are tested to find better policies in simulation. After training the model, its robustness is tested by changing the arrival rate of tasks.

4.1. Impacts of Weight Coefficients

Specifically, the impact to the reinforcement learning model by changing the ratio of $\alpha$, $\zeta$, $\beta$, and $\gamma$ is measured. In the experiment, eight groups of parameters are tested to determine the exact impact of the ratio mentioned above on the convergence, latency, cost and bonus of the model. Other parameters remain the same. We set the training epoch as 2000. There are 100 steps of interaction in each epoch. We set learning rate as ${10}^{-4}$, discount factor as 0.99 and the arrival rate $14 {\mathrm{s}}^{-1}$.

Especially, data presented in Figure 5 and Figure 6 has been through the Gaussian Smoothing process to appear the trend better. Meanwhile, to compare the variation trend of rewards more precisely, the reward values are normalized.

Obviously, the drift is related with the ratio of weight coefficients. In all eight groups, two distinct trends emerged. One of the trends is group 1, 2, 3, 4, 5, and 8 and the other is group 6 and 7.

Considering that the $bonus$, $t_{process}$ and $t_{mining}$ are correlative, firstly, the coefficients of these three indicators are set in equal proportions, and we change the ratio of $\alpha$ and $\beta$. Initially there are five groups tested, that are group 1, 2, 3, 6, and 7. Two distinct convergence trends emerge as the ratio changes. The process delay of group 1, 2, and 3 eventually converge at around 0.028 s. However, the process delay of group 6 and 7 only converge at 0.11 s and 0.12 s, respectively. The convergence results of mining delay and process delay are similar. As for the cost, group 6 and 7 lower than group 1, 2, and 3. It is not hard to find that the situation is closely related to the ratio of $\alpha$ and $\beta$. When $\alpha /\beta >baseline$, the policy tends to lower the latency, when $\alpha /\beta <baseline$, it tends to lower the cost. Furthermore, from the comparison of group 6 and 7, it can tell that if $\alpha /\beta$ is becoming smaller and smaller, it can help the algorithm to converge faster. This is because when the agent is observing the environment, it gonna has a certain random magnitude, if the increase in reward brought by choosing a different policy is small compared to the change brought by random search, then the algorithm will not continue to converge.

Then some possible impacts that $\gamma$ may have toward the policy of reinforcement learning model are measured. $\gamma$ controls $bonus$, when $bonus$ increases, the $t_{mining}$ decreases. That means as long as the policy tends to lower $t_{mining}$ a bit more than $cost$, when $\gamma \times \zeta >0$, the change of $\gamma$ would not have a great impact on the policy. For example, in group 1: $[\alpha ,\zeta ,\beta ,\gamma ]=[100,2,1,20]$, the policy is more inclined to reduce $t_{mining}$. In this case, no matter how the value of $\gamma$ changes, there will be no difference to the policy. In order to testify that assumption, a comparative experiment is made: group 1, 4, and 5. In these three groups, the rewards have the same growth pattern. Moreover, relying on the $cost$ and $t_{mining}$, we can figure out that the changing of $\gamma$ has a little impact on the policy of the reinforcement learning model. Their $cost$ and $t_{mining}$ converge at the same results. That presents group 1, 4, and 5, which choose nearly the same policy. In group 1, especially, we set $\gamma$ as 20, the result remains almost unaffected.

Here a further analysis is given towards the experiment results above.

The emergence of $baseline$ is within the prediction. It is obvious that $t_{process}$, $t_{mining}$ and $cost$ is correlative, we set the correlation $f(t_{process},t_{mining},cost)=0$. It can extend to $f(t_{process}-\Delta t_1,t_{mining}-\Delta t_2,cost+\Delta cost)=0$ (Servers with lower computing capabilities are usually cheaper. Servers with higher computing capabilities can lower the latency. That is to say the cost usually increases when the latency is lower). Thus, in a minimum neighborhood, $\Delta t_1$, $\Delta t_2$ and $\Delta cost$ have a positive correlation as $\Delta cost\approx k\Delta t_1+p\Delta t_2$, k, p is positive. Hence, the change of reward can be described in this neighborhood as: $\Delta R=-\alpha ·(-\Delta t_1)-\zeta ·(-\Delta t_2)-\beta ·(\Delta cost)=(\alpha -\beta k)\Delta t_1+(\zeta -\beta p)\Delta t_2$. When $\beta$ is relatively large, $\Delta R<0$ is minus, which means the policy would lower the $cost$. When $\alpha$ is relatively larger, $\Delta R>0$ is positive, which means the policy would tend to lower the latency.

Moreover, from Figure 6a,b, we can tell that the order of magnitude of process delay and mining delay is different. As mentioned above, if the increase in reward from choosing a different policy is small in comparison to the change introduced by random search, the algorithm will not converge. To avoid this phenomenon, the ratio of $\alpha$ and $\zeta$ remain the same from group 1 to 7. However, in group 8, the order of magnitude of process delay is much smaller than that of mining delay in reward function, which means that the reduction in the process can be smoothed out by the variance of mining, thus preventing the algorithm from continuing to converge. The process delay only converges at 0.04 s in the end.

4.2. Impacts of Arrival Rate

The pattern of latency is measured by changing the arrival rate with the ratio of weight coefficients stable.

As shown in Figure 7, it can be seen that the increase of $\lambda$ affects group 6 and 7 greatly. When it reaches 24 ${\mathrm{s}}^{-1}$, the $t_{process}$ of group 6 and group 7 reaches 0.18 s and 0.26 s, respectively. However, other groups manage to resist the increase, maintaining the amplification within 70%. Furthermore, it can be concluded that the results obey the latency rule of M/G/s model raised by Boxma [38]. Within the results, we fit the equivalent removing rate of edge computing service system under this circumstance as $\mathsf{\mu }\approx$ 40 ${\mathrm{s}}^{-1}$. In the experiment, the average data size is 7 × 5 Mb. If the policy is to lower the latency, the average data size distributed to each server is 35/4 Mb. Each bit needs a CPU Cycle of $(2+5+7)/3\approx 4.7$ Hz. The average capability of each server is 16.5 $\mathrm{GHz}$. Thus, the average processing rate of each server can be worked out: $\mathsf{\mu }=\frac{16.5\times {10}^9}{8.75\times {1024}^2\times 8\times 4.7}=$ 47.83 ${\mathrm{s}}^{-1}$. The estimation result and fitting result have the same order of magnitude.

4.3. Appropriate Choice of Weight Coefficients

General conclusions about the impact of changing weight coefficients have been made before. Based on that, different policies can be applied to different circumstances.

For example, when the client has no strict requirement for the latency, and its arrival rate is stable and relatively small, a parameter set [5, 0.1, 100, 1] can be applied to lower the cost. If the arrival rate fluctuates greatly, parameter sets with a larger ratio of $\alpha$ to $\beta$ such as [100, 2, 1, 20] can be applied instead in order to guarantee the steady performance of the system steady.

4.4. Comparison between TCN Enabled A3C and Fully-Connected A3C

When using TCN to enable A3C algorithm, the policy depends on both current and previous states. In order to prove that the new architecture has a better convergence performance and stability than traditional A3C, which make decision only by current state. In the experiment, fully-connected neural network is used to approximate the policy function and state-value function.

As shown in Figure 8, the convergence of TCN enabled A3C is faster and more stable. By learning previous states, TCN is able to capture the changing trend of task arrivals and make better policy choices. TCN enabled A3C is more like a global optimization, and the A3C algorithm based on a fully-connected neural network is a manifestation of greedy decision-making.

5. Discussion

In this paper, we studied the resource allocation problem of a blockchain-based MEC system. It is considered that the mining process combined with blockchain had an impact on resource allocation policies. Meanwhile, to explore the influence of different indicators on the final decision, we set up different weight parameter combinations and conducted several experiments. This is the difference between what have conducted in this paper and previous studies, or other words, we made further on the ideas of previous studies. Because of this, we can finally obtain almost optimal results under a certain decision tendency.

As suspected, delay and cost are opposite, and the allocation policy would only favor one of them. During the simulation, we applied a new A3C algorithm which uses TCN to learn the history trend, and it is proved that the new algorithm can converge faster and more stably. We also simulated the change of packet arrival rate, and the results showed that different resource allocation policies have different abilities against data congestion. When the policy is inclined to reduce the cost, the system is very likely to be congested when the arrival rate of packets is relatively large.

Of course, this is not to say that the policy of favoritism towards lower cost is undesirable. Different policies can be applied in different daily or industrial scenarios. When the data traffic is not very high, such as for some sensors that only collect parameters, the policy can be slightly biased to reduce the cost, to reduce the cost of users, and reduce the pressure on the server.

However, there are still many shortcomings and room for improvement in our work. We only studied the feasibility of using a reinforcement learning algorithm to deal with the resource unloading problem of a blockchain-based MEC system and did not build a real system for verification. In addition, due to the limitation of simulation equipment, there is a certain gap between the simulation scale and the real scene, so the feasibility of policy transplantation to large-scale scenes cannot be verified at present. Further, the ability to adjust the allocation policy is not enough. The environment of the real world may always change, which is shown in the model as the change of arrival rate and the change of mean packet size. However, currently, our model cannot adaptively adjust the weight parameters of indicators, and its policy can only be applied to a specific application scenario.

6. Conclusions

In this article, we thoroughly analyzed the resource allocation policy in blockchain-based MEC system. A new consensus mechanism: PoL, is applied in the system to maintain the stability of blockchain and improve the efficiency of edge computing servers. The optimization target of resource allocation consists of four parts, that is the process delay and cost of servers, which are common in traditional MEC models, and the mining delay and mining reward based on aforementioned PoL consensus. Different weight coefficients are set for these indicators in the reward function to explore what the impact of each indicator on the policy. Furthermore, to better capture the long-time trend of incoming tasks, TCN enabled A3C algorithm is used to solve the resource allocation policy, which can make the policy convergence faster and more stable. However, our work also has some deficiencies. The policy can not adjust according to the arrival rate of tasks. Furthermore, due to the limitation of computing resources, the simulation environment is quite different from real-world environment, which contains more servers and clients. Furthermore, it is only a theoretical research, but the actual software system will be more complicated. In the future, we first hope to improve the algorithm so that it can adjust the allocation policy more flexibly. Secondly, we hope to extend the algorithm in large-scale application scenarios to verify its generality. Furthermore, finally, we hope to complete the implementation of blockchain-based mobile edge computing system in the laboratory and continuously optimize and adjust it.