A Nonisolated Transformerless High-Gain DC–DC Converter for Renewable Energy Applications
Abstract
:1. Introduction
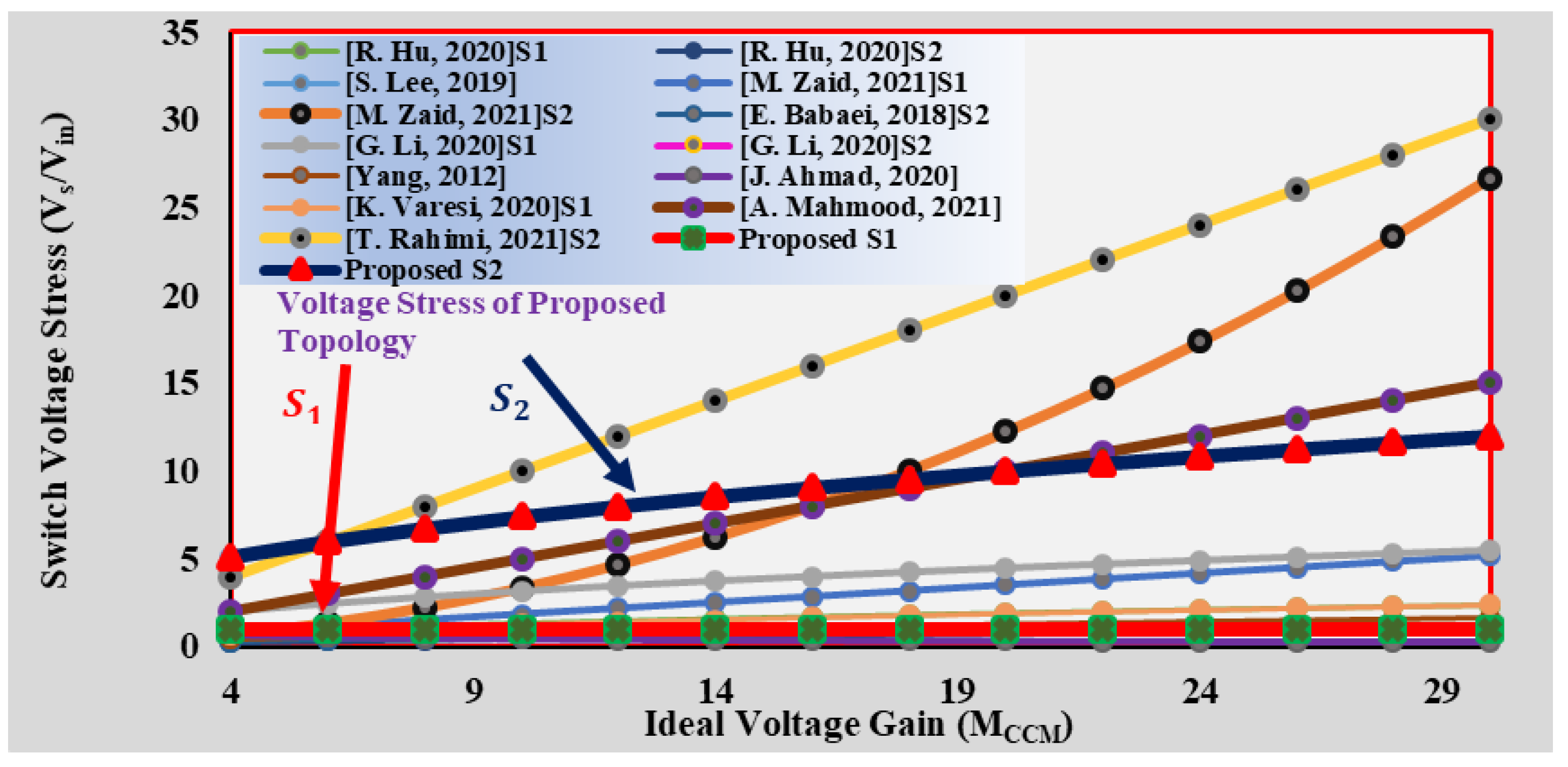
- The converter achieves a high gain of 10 times the conventional boost and 5 times that of the quadratic boost converter at a 50% duty ratio.
- The converter has low voltage stress of 5% of the output voltage across switch S1.
- The converter uses the same gate signal for both switches, which leads to its easy operation.
- The topology has a continuous input current and a common ground, making it feasible for PV applications.
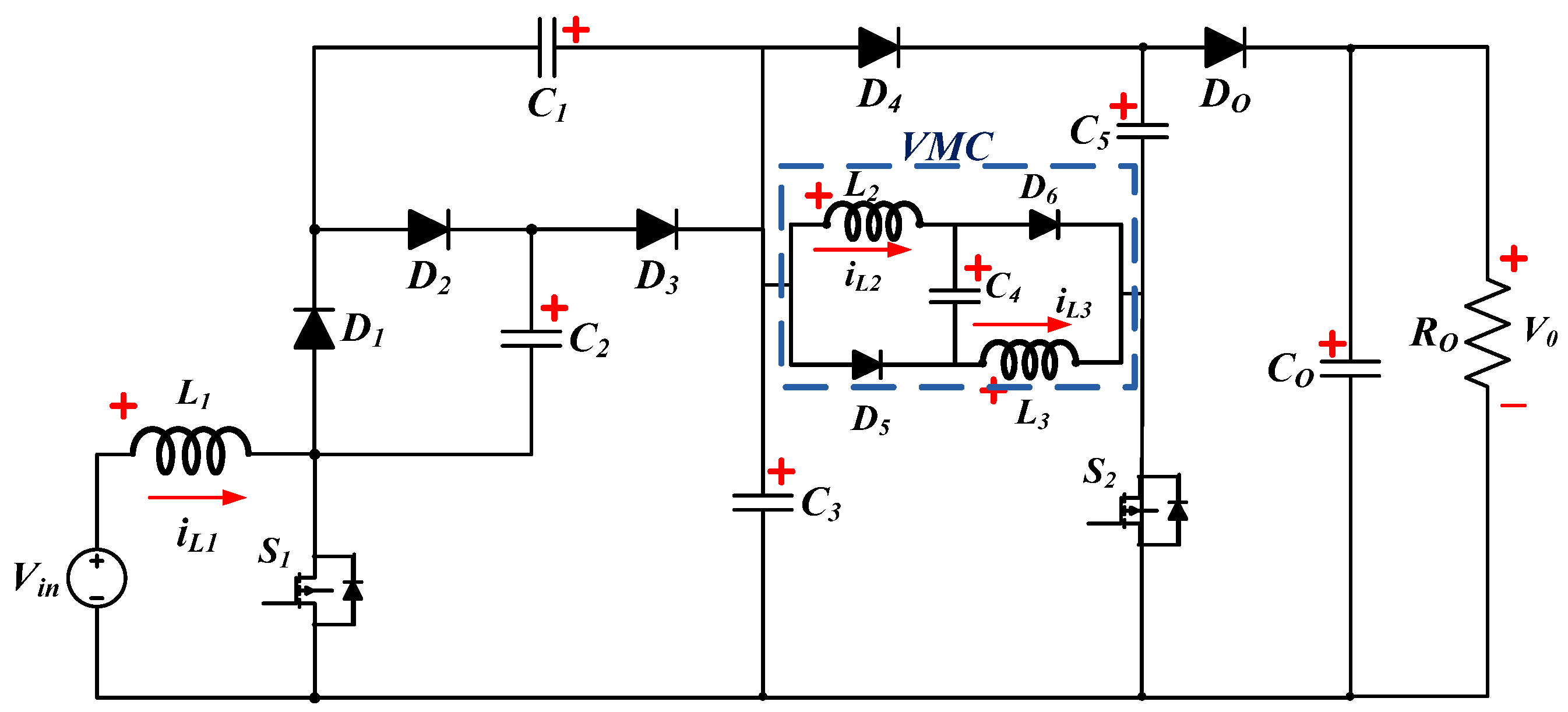
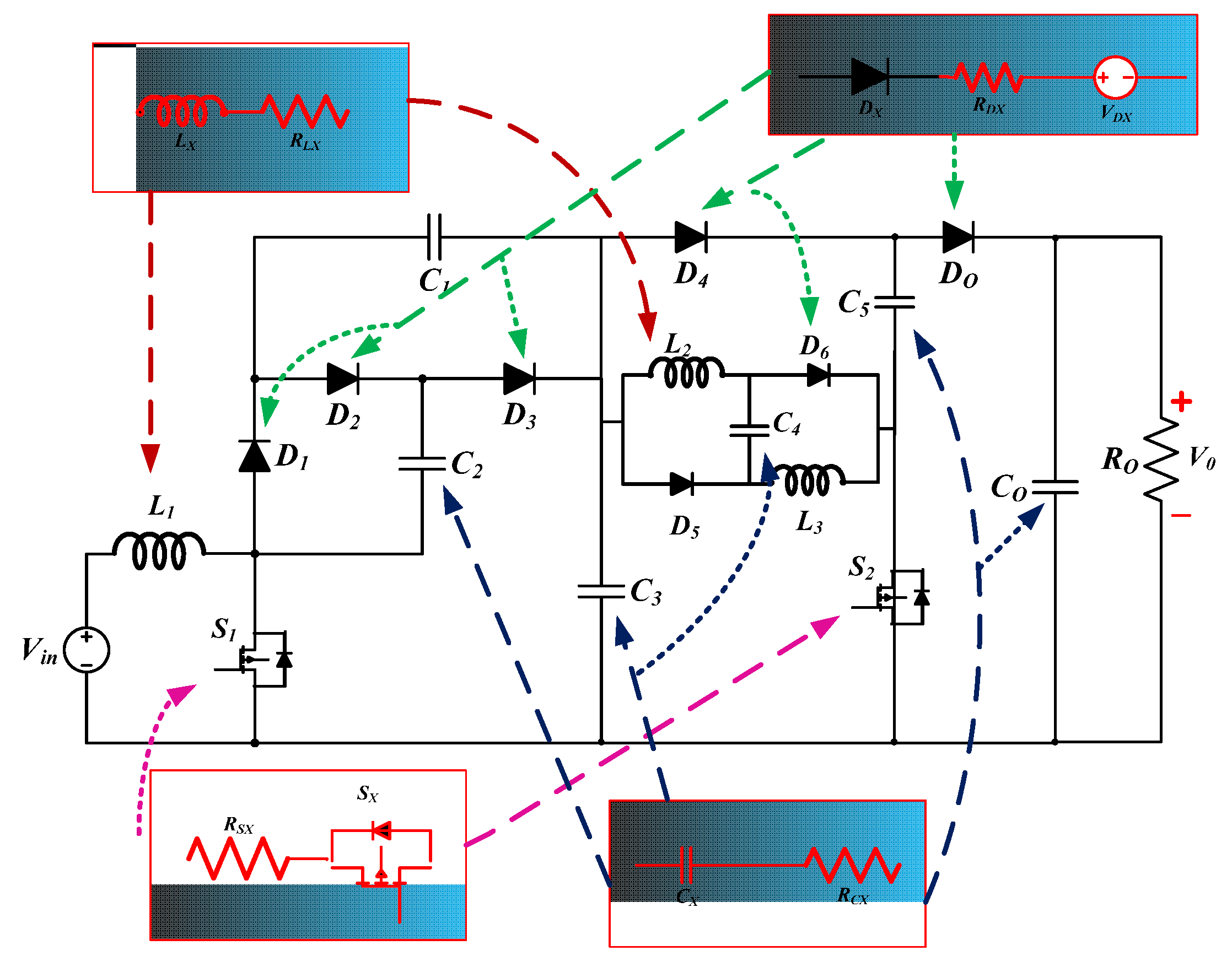
2. Structure of Proposed High-Gain DC–DC Converter Topology
2.1. Operation of the Converter in Continuous Conduction Mode (CCM)
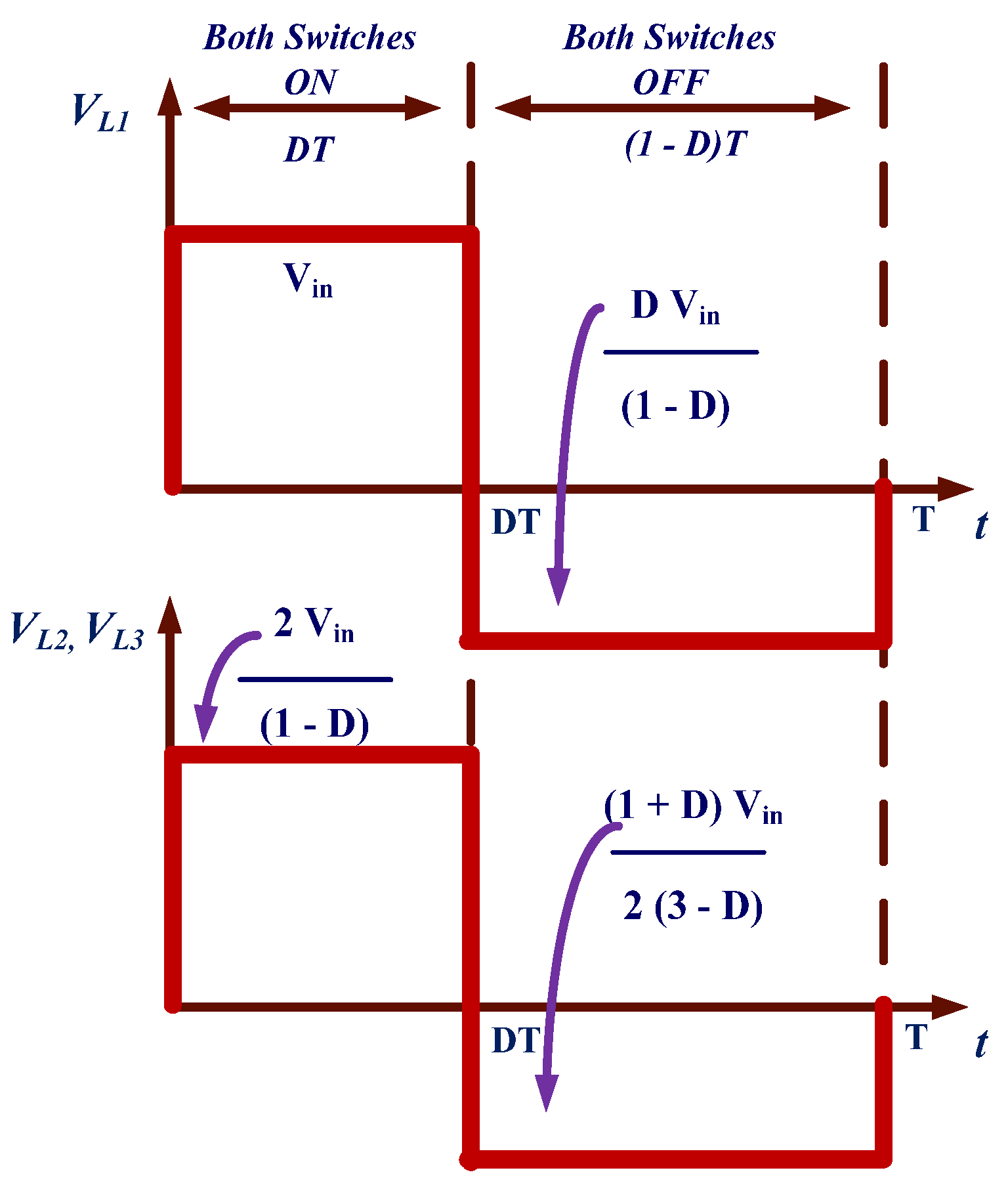
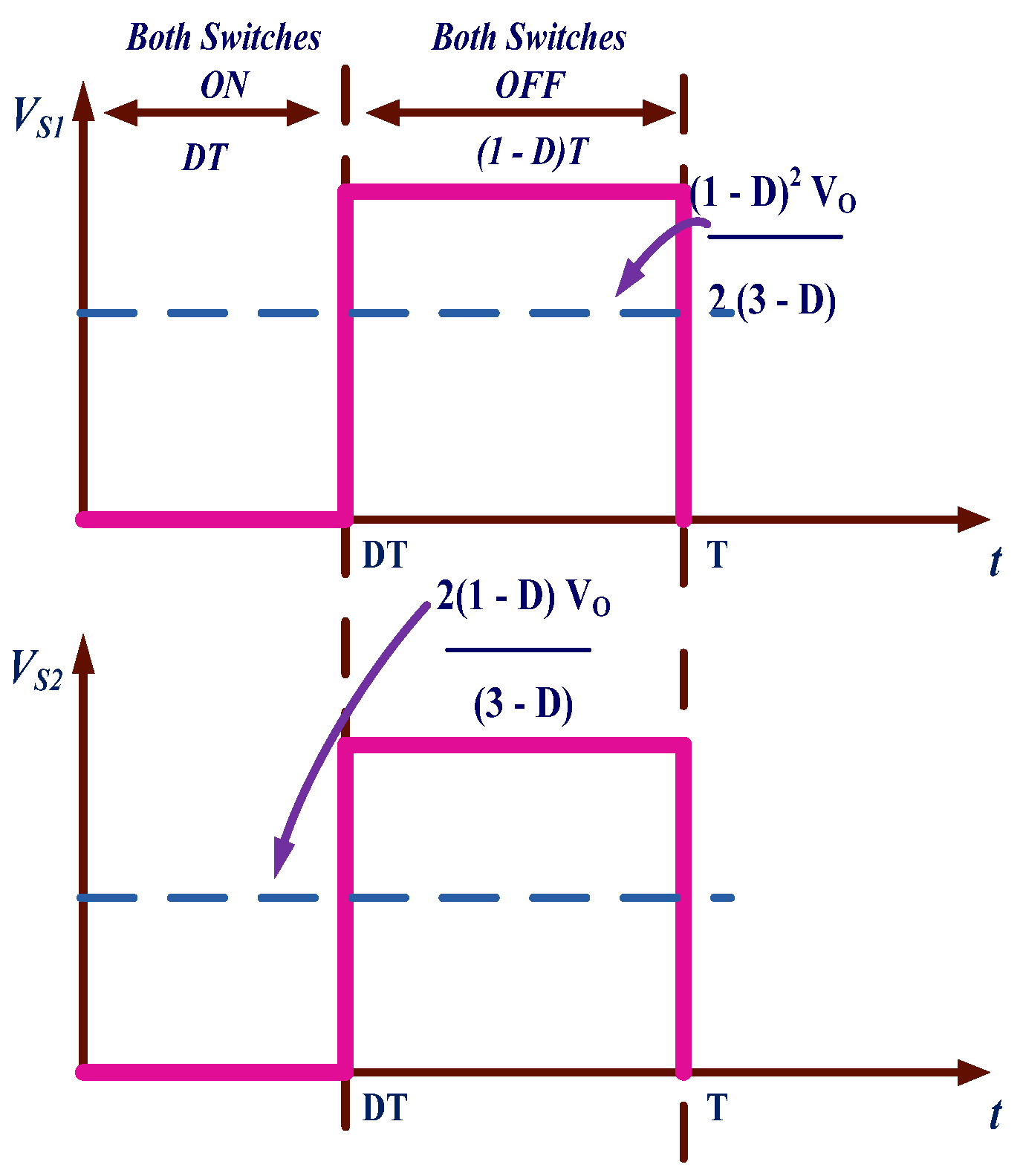
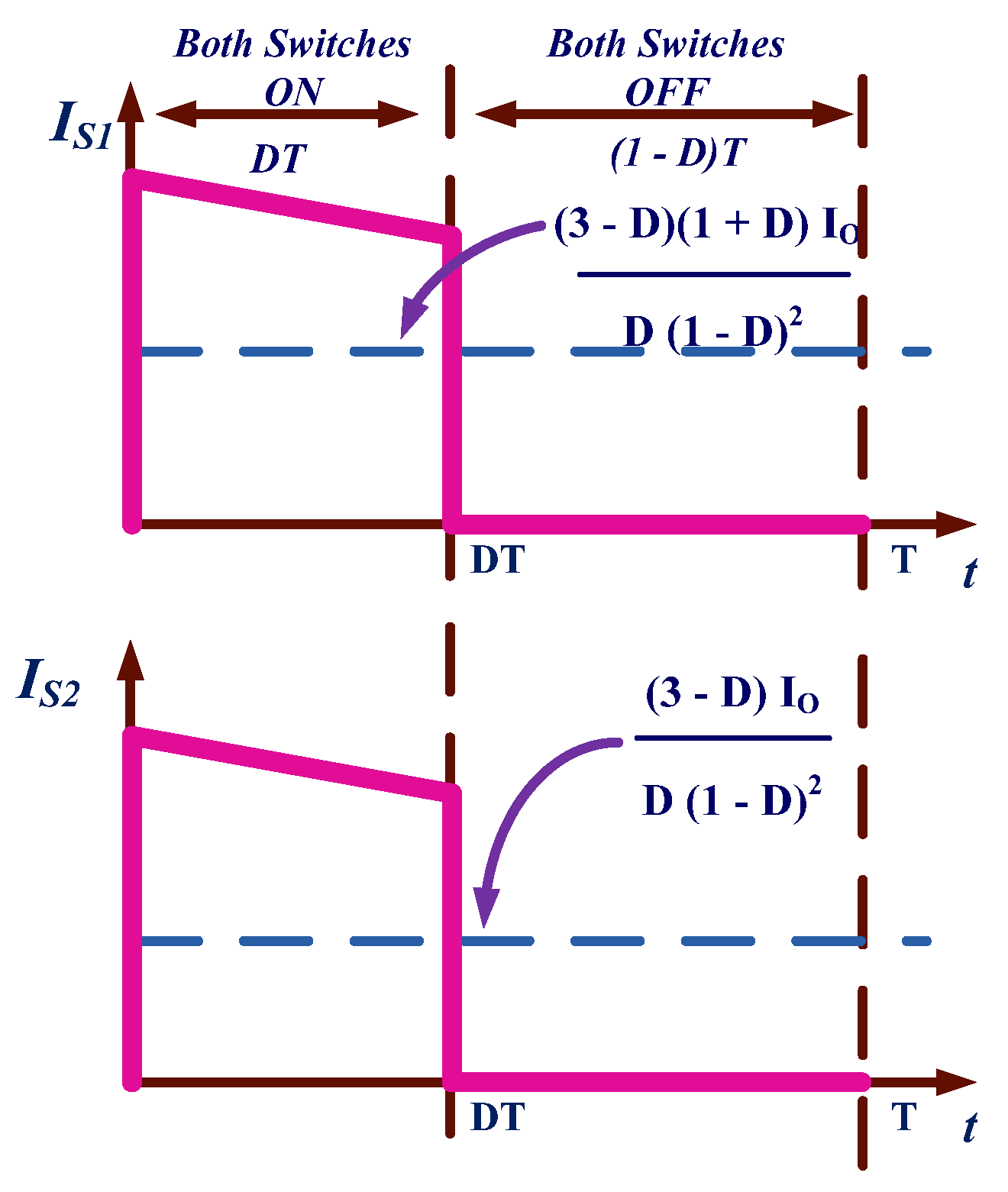
2.1.1. Calculation of Voltage Stress
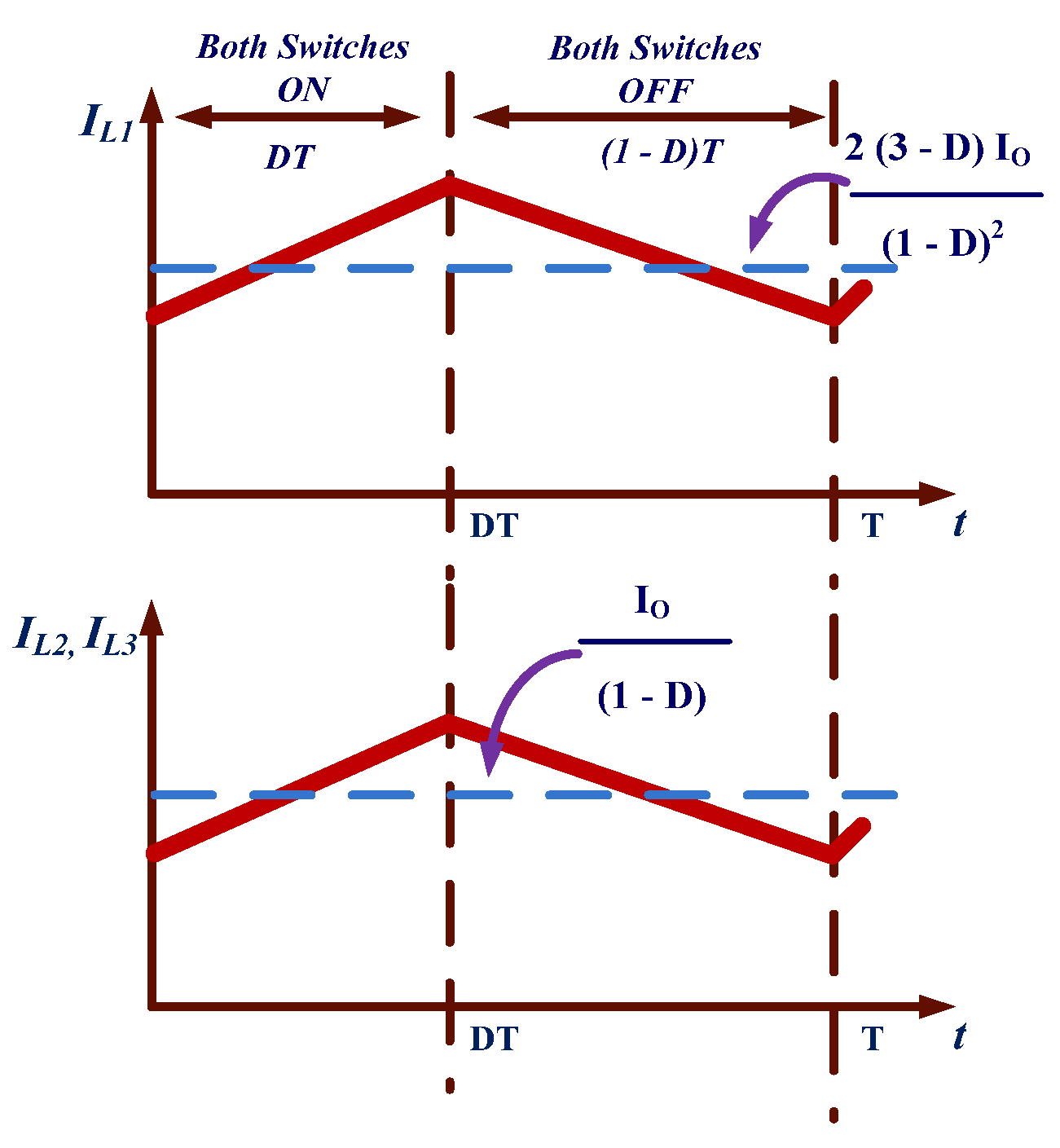
2.1.2. Calculation of Average and RMS Currents
2.1.3. Design of Inductors and Capacitors
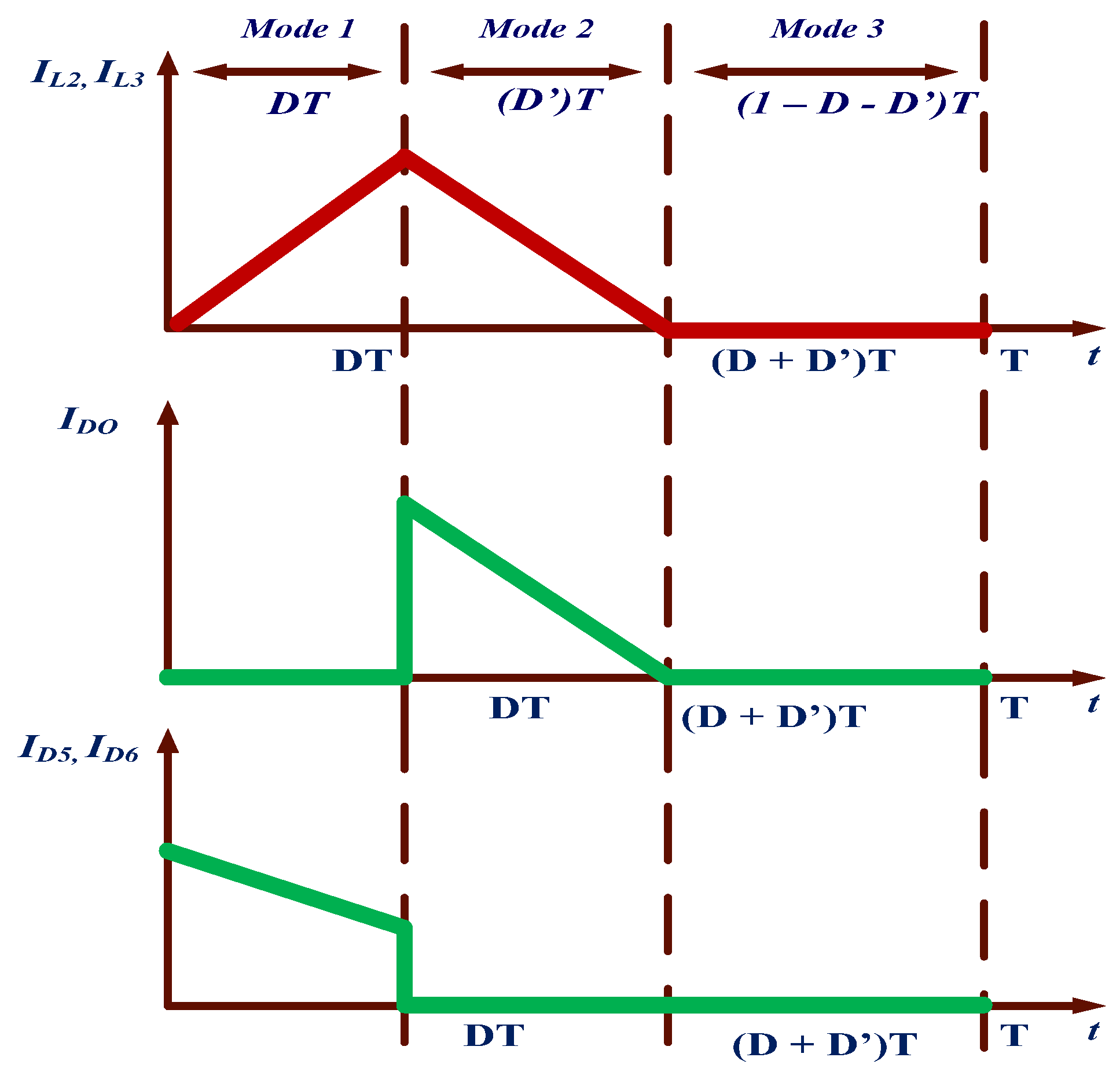
2.2. Operation of Converter in Discontinuous Conduction Mode (DCM)
- (i)
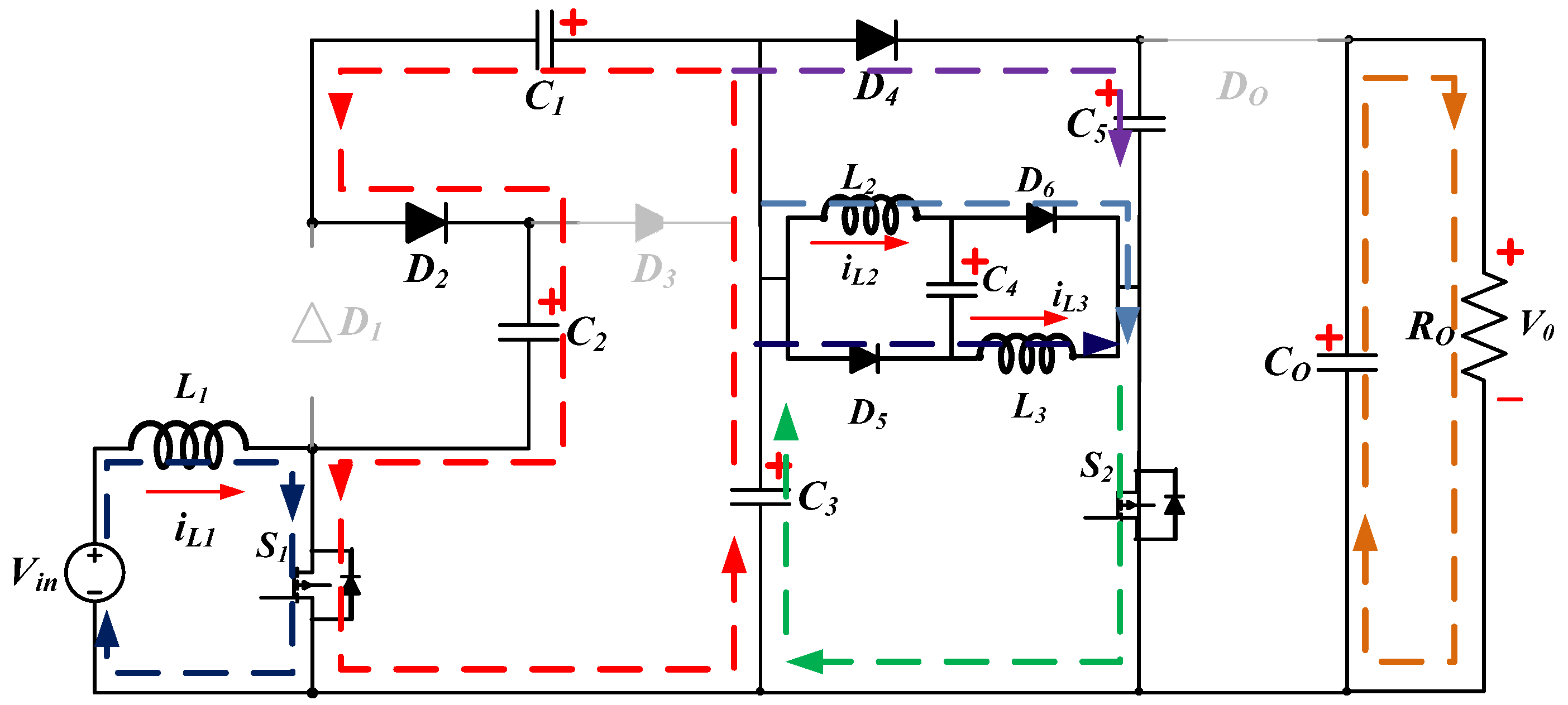
- Mode 1: In this mode, both switches are turned ON for duty cycle D as in the case of CCM.
- (ii)
- Mode 2: In this mode, both switches are turned OFF and the inductors start discharging. The inductors discharge through diodes , , and for a duty cycle D’ and the mode ends at D + D’.
- (iii)
- Mode 3: In this mode, none of the switches or diodes conduct, and the load is fed entirely through the output capacitor . The mode is operated for a duration of 1 − D − D’.
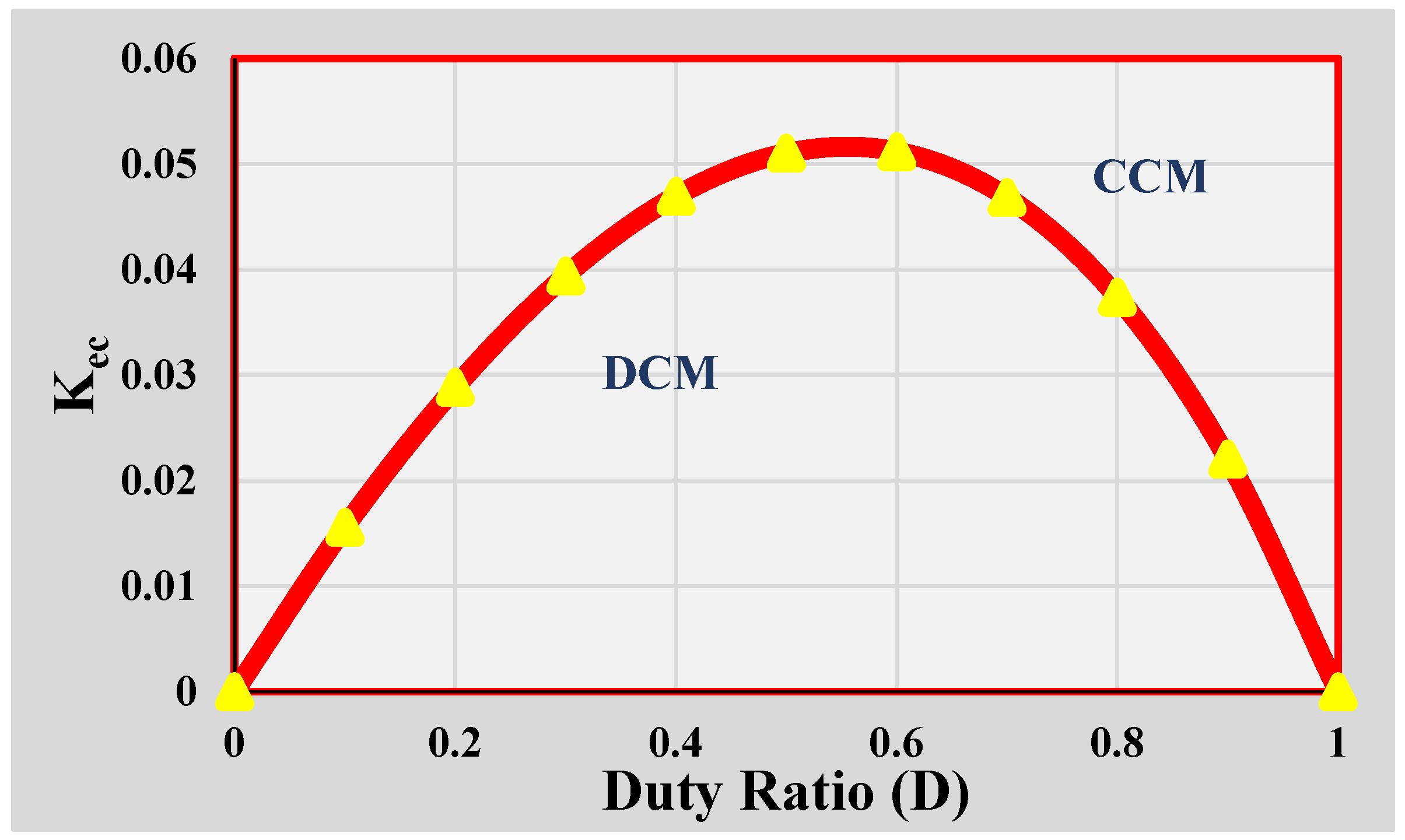
2.3. Converter Operation at Boundary Conditions
3. Nonideal Analysis
3.1. Calculation of Losses across Switches
3.2. Calculation of Losses across Diodes
3.3. Calculation of Losses across Capacitors
3.4. Calculation of Losses across Inductors
3.5. Calculation of Efficiency of the Converter in Nonideal Mode
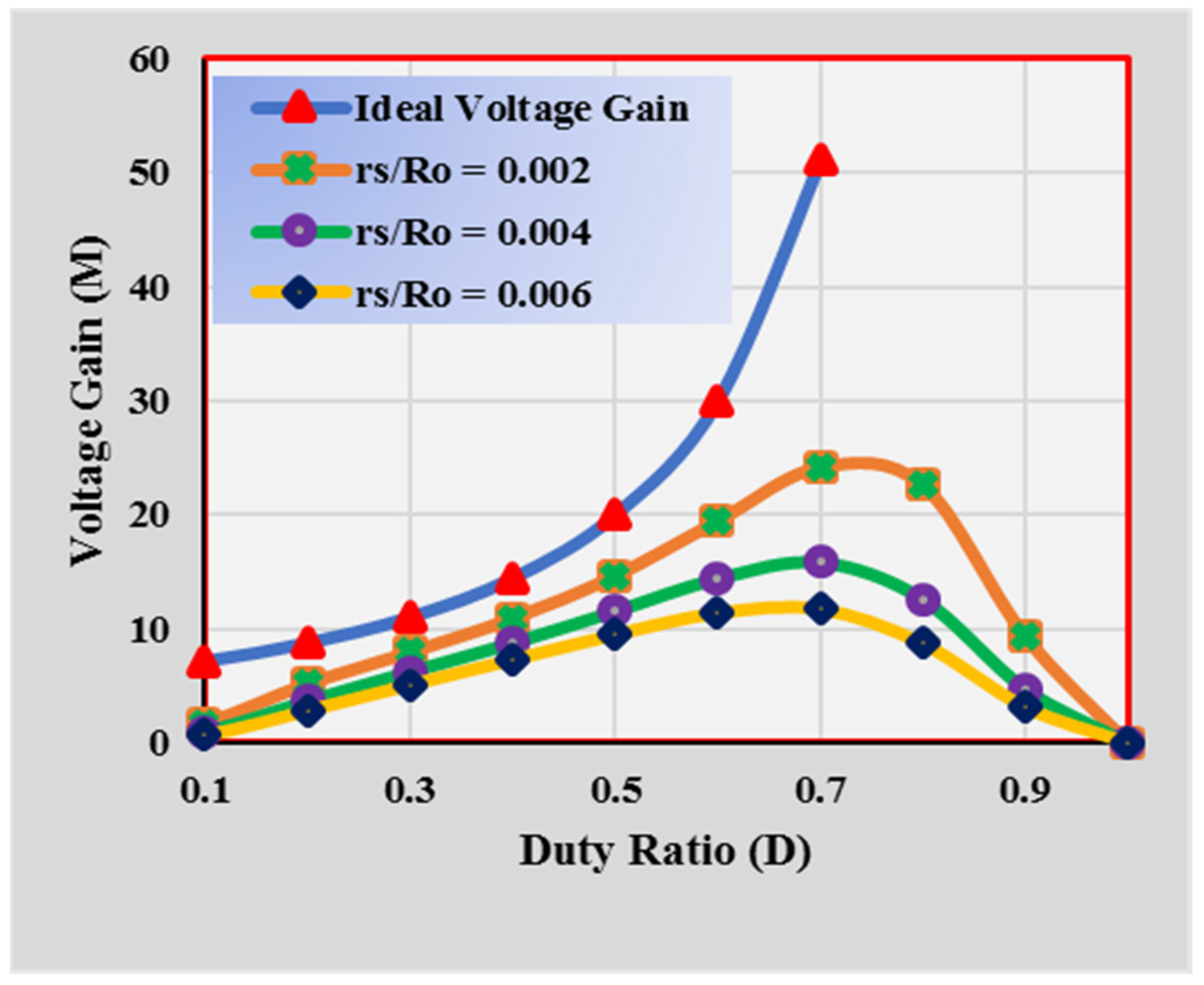
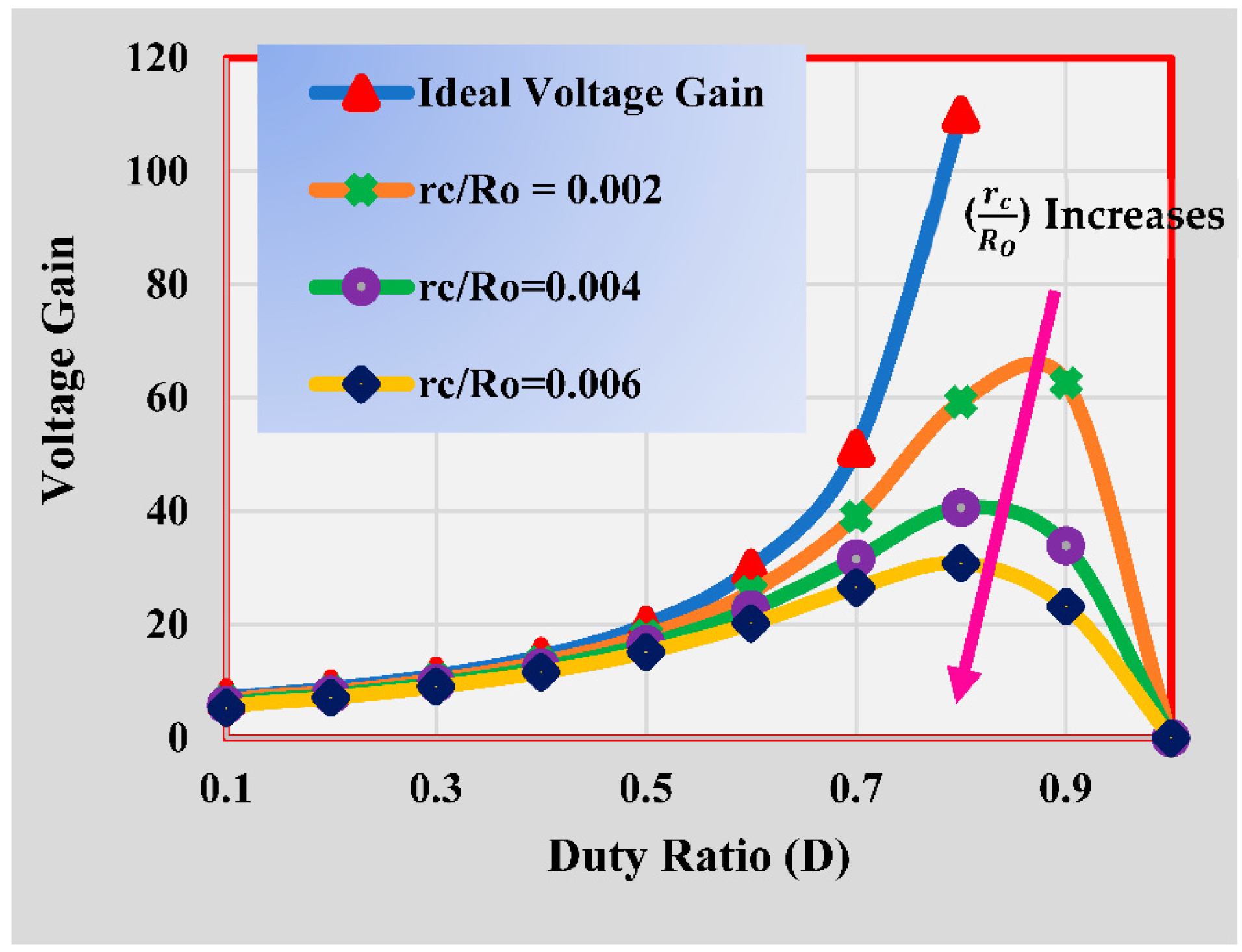
3.6. Calculation of Nonideal Voltage Gain
3.7. Variation in Nonideal Voltage Gain
4. Comparison of the Proposed Topology
5. Results
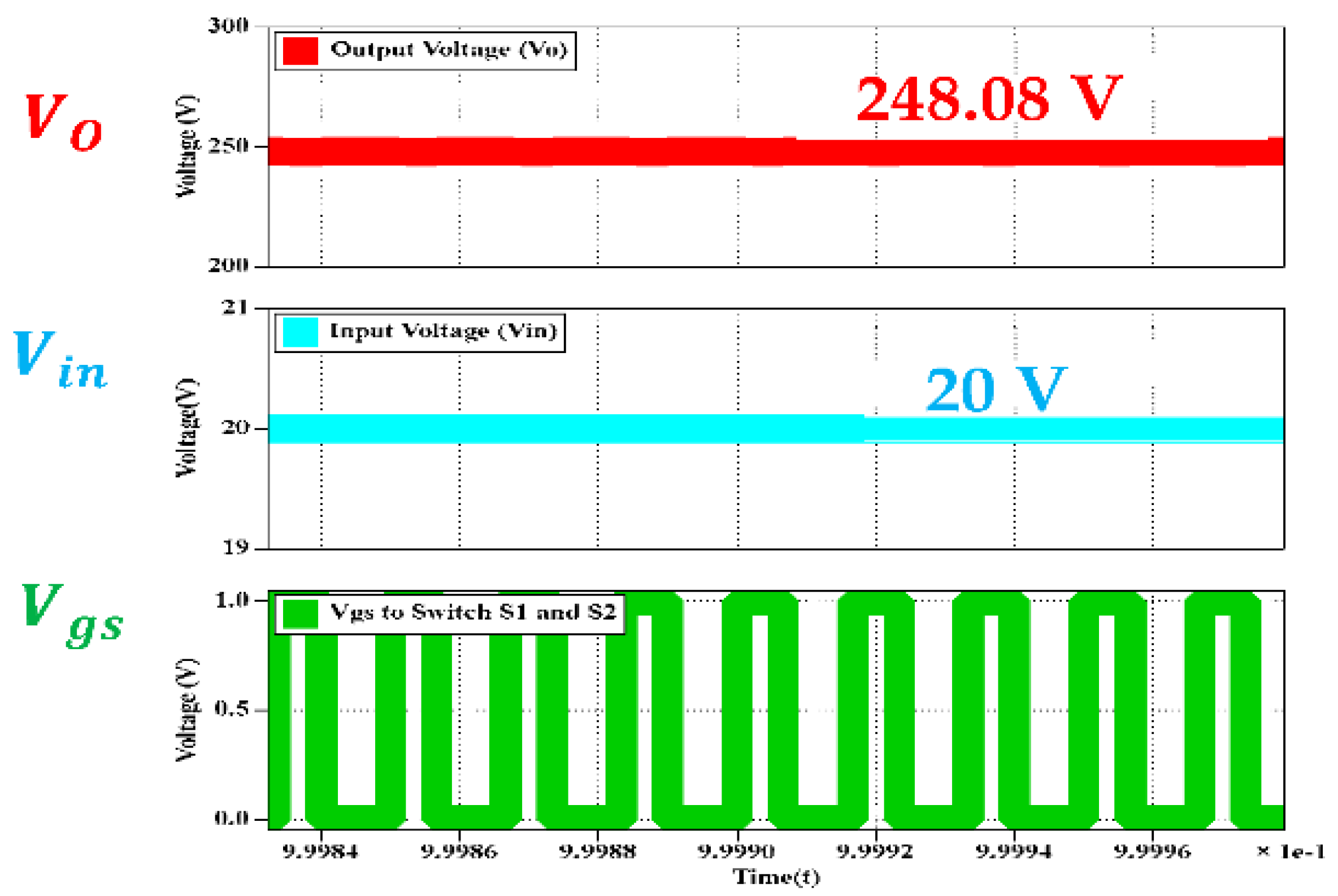
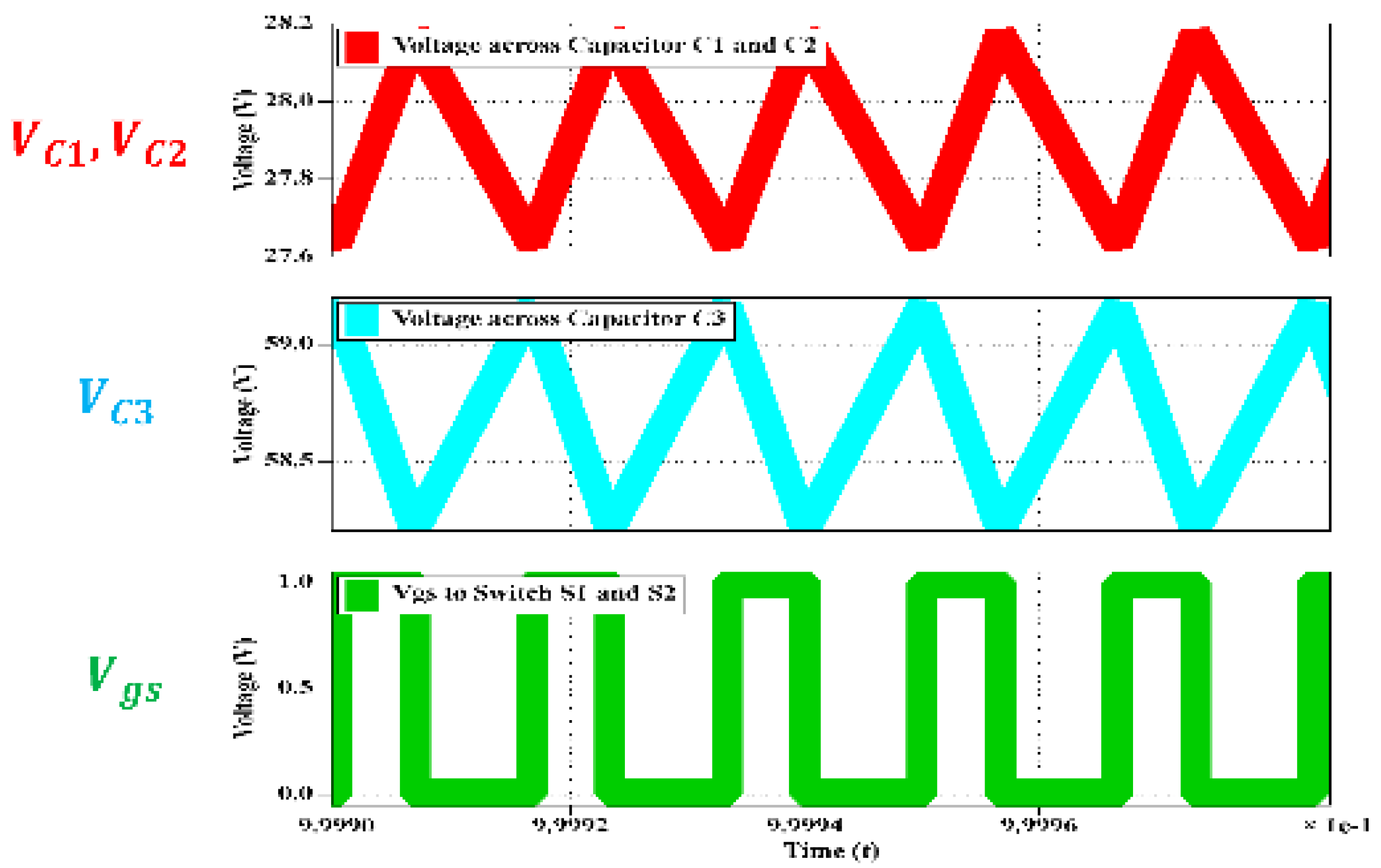
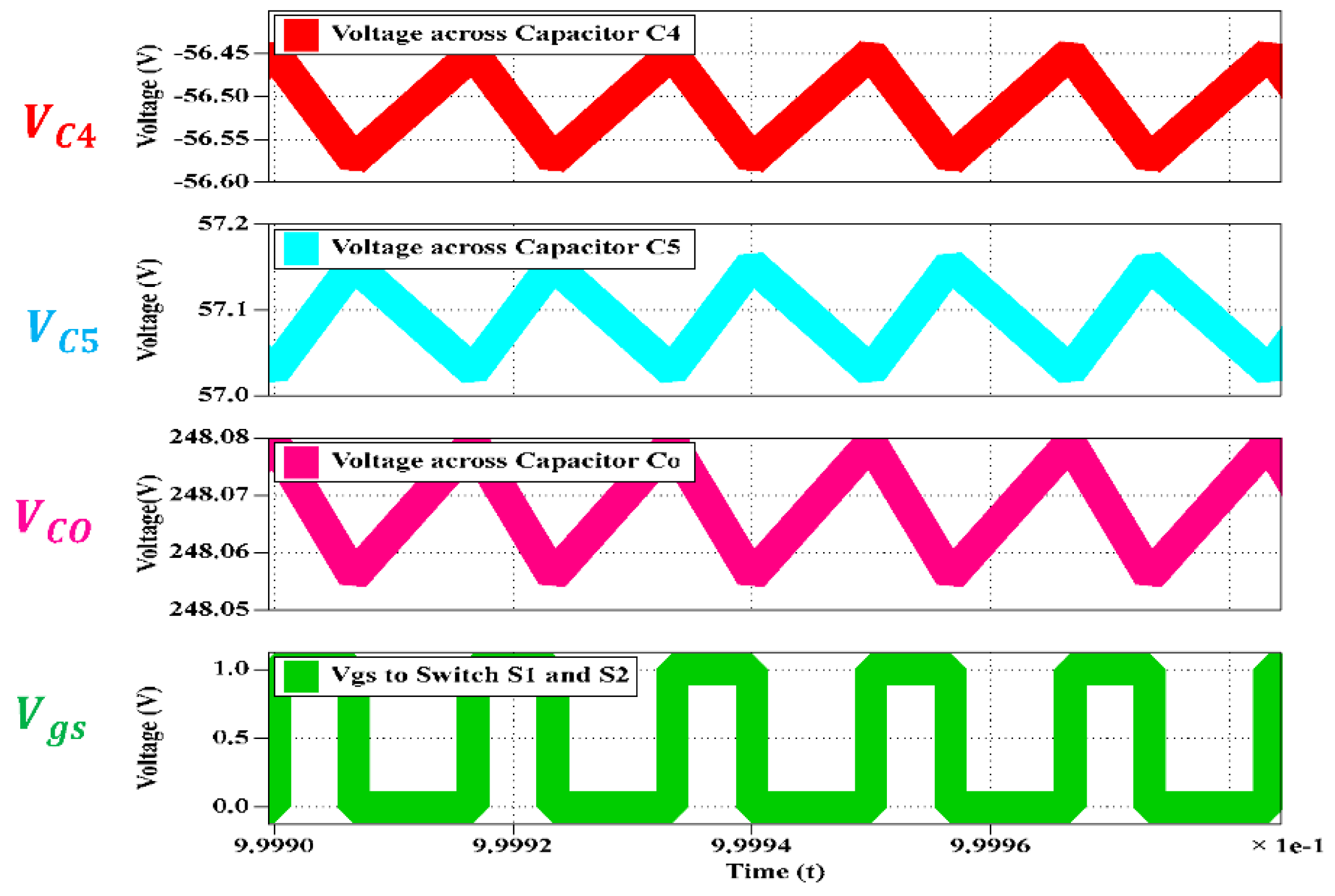
5.1. Simulation Results
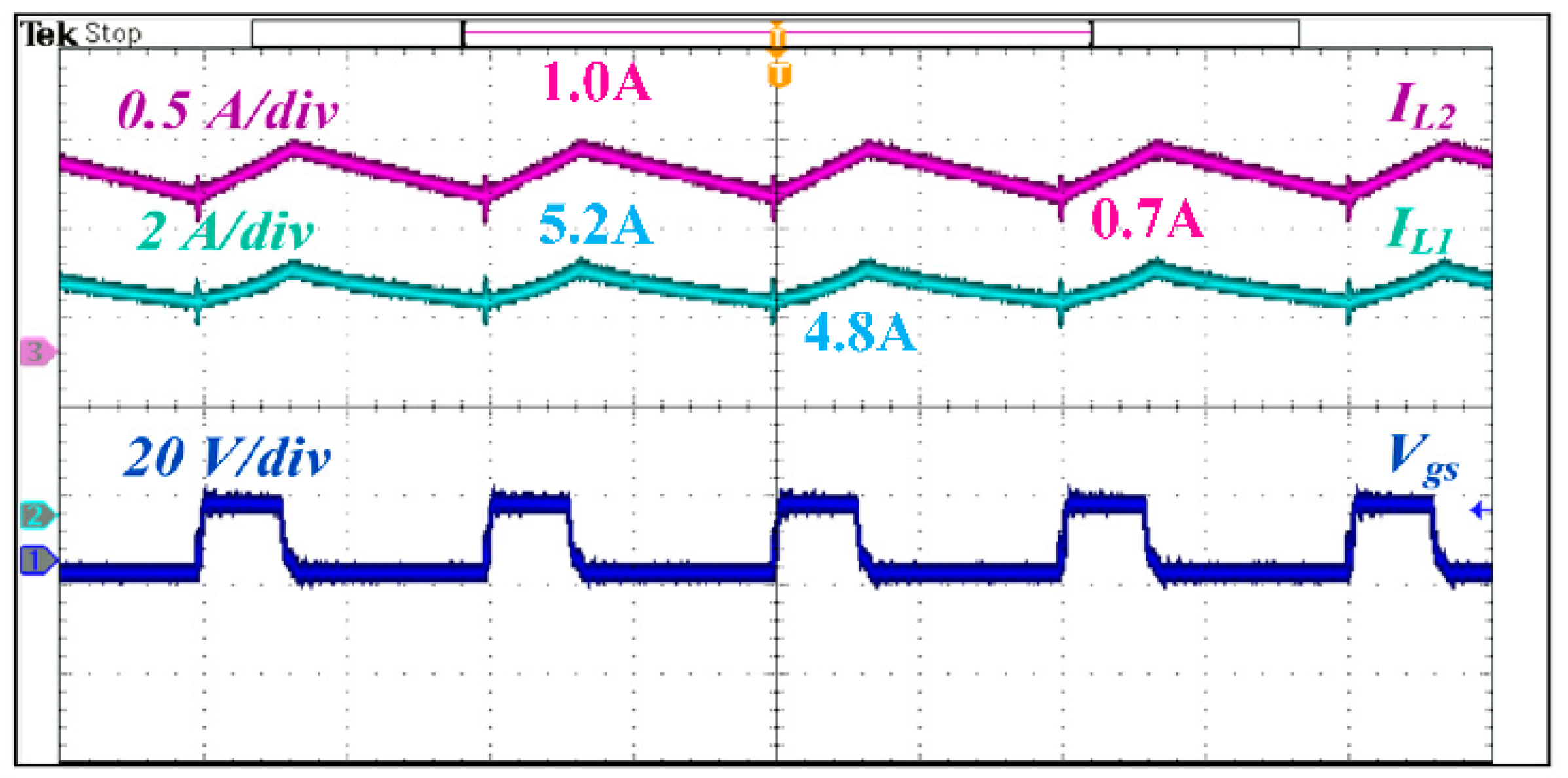
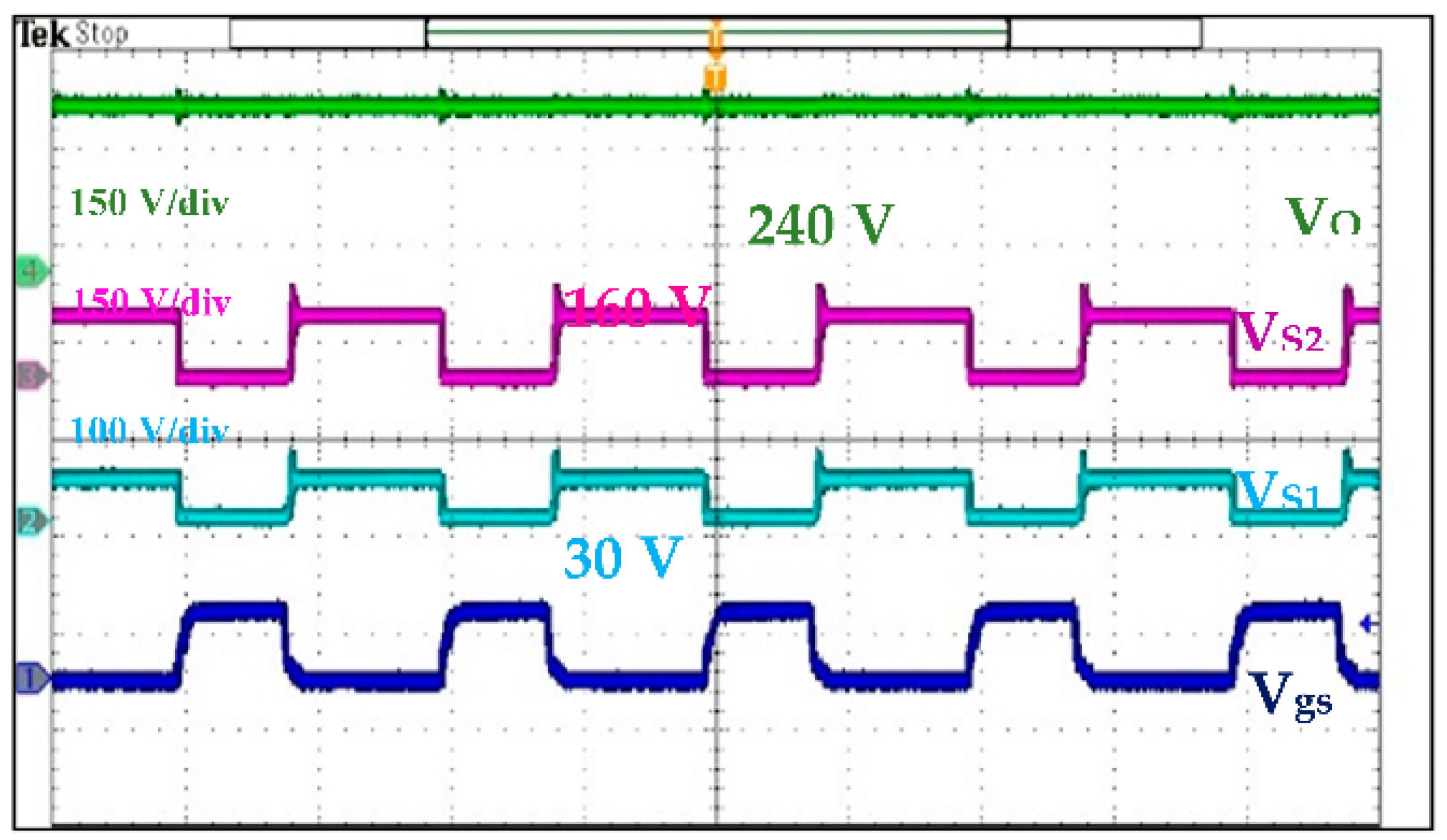
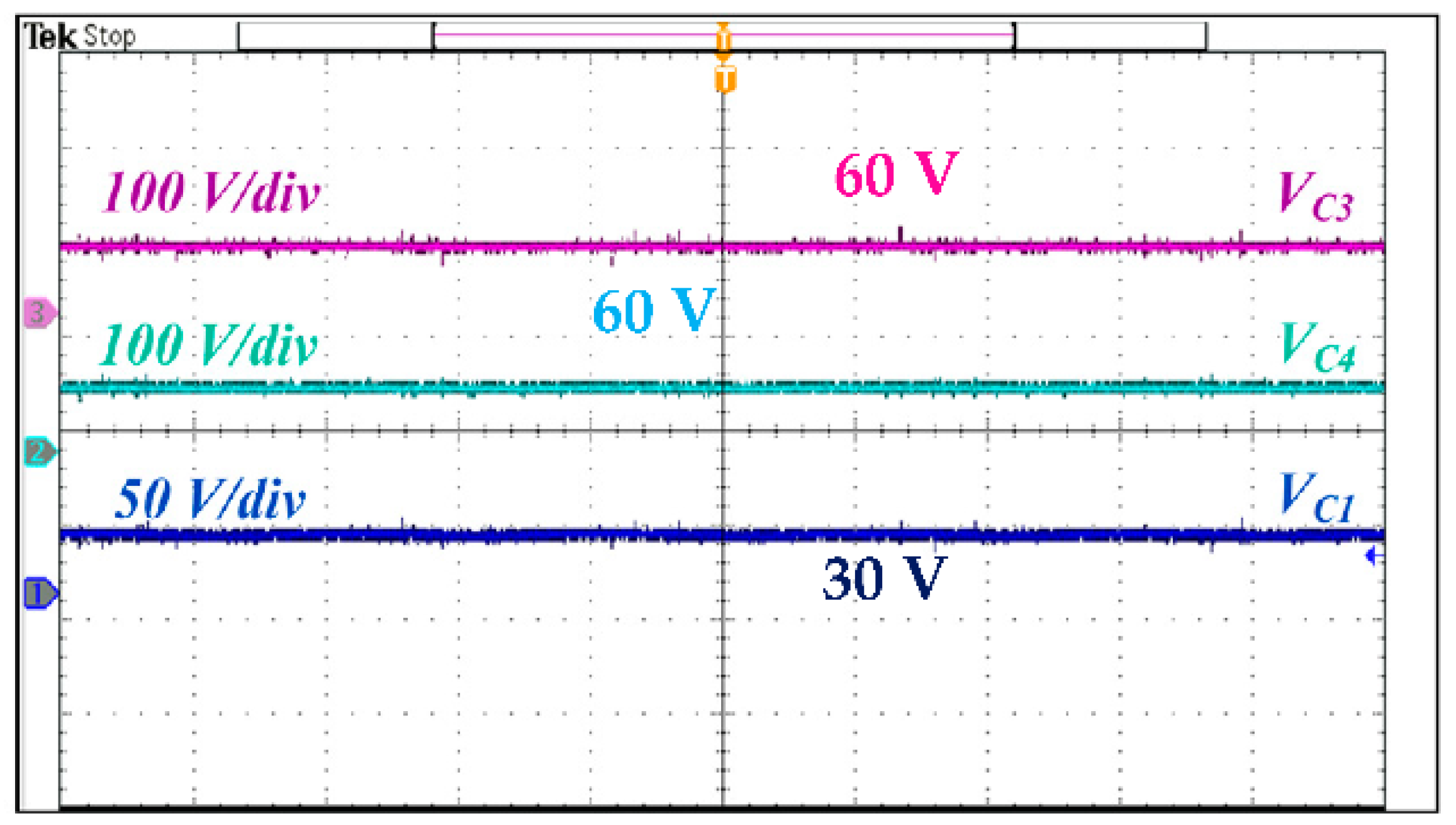
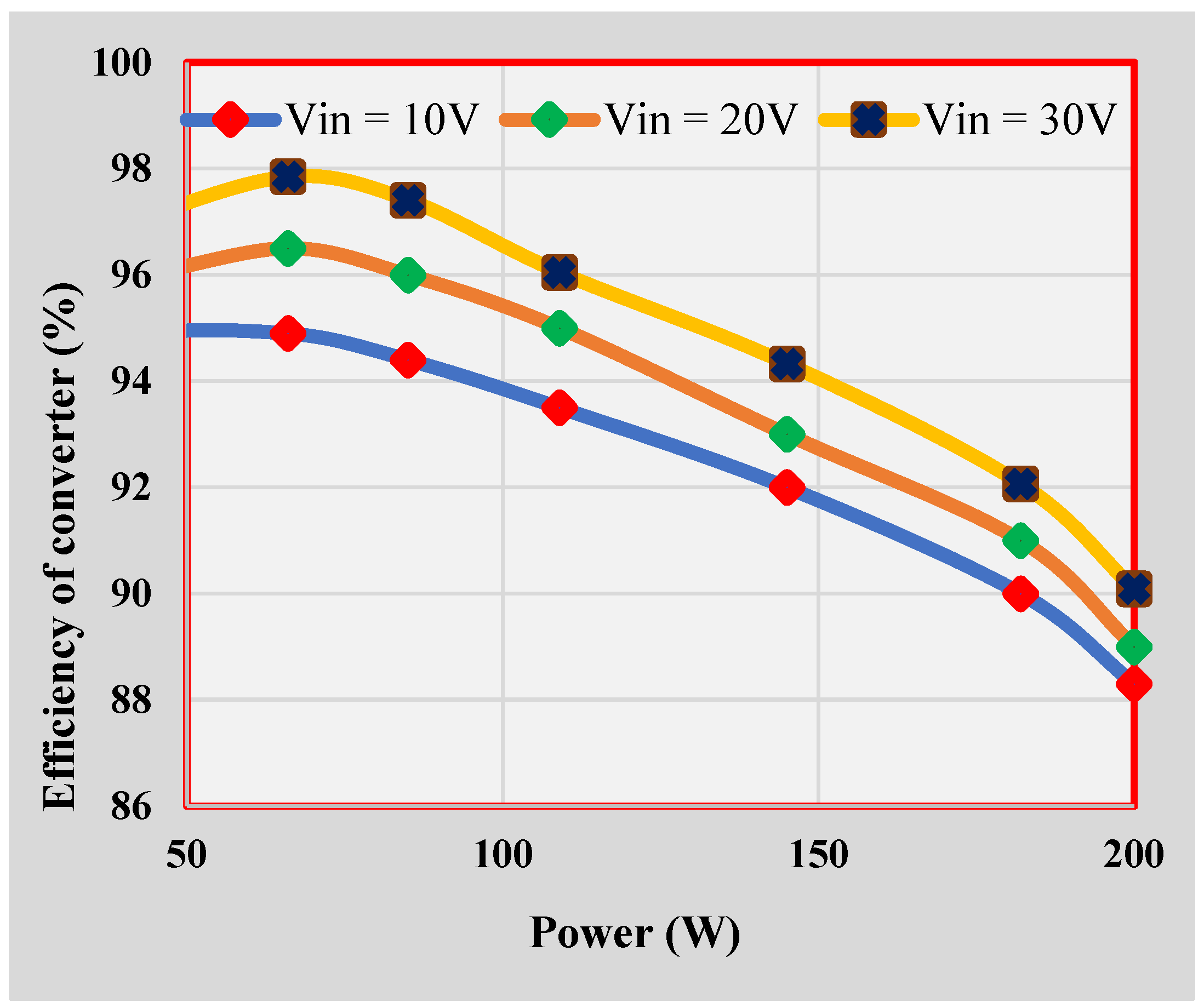
5.2. Experimental Results
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Forouzesh, M.; Siwakoti, Y.; Gorji, S.; Blaabjerg, F.; Lehman, B. Step-Up DC–DC Converters: A Comprehensive Review of Voltage-Boosting Techniques, Topologies, and Applications. IEEE Trans. Power Electron. 2017, 32, 9143–9178. [Google Scholar] [CrossRef]
- Goyal, V.K.; Shukla, A. Isolated DC–DC Boost Converter for Wide Input Voltage Range and Wide Load Range Applications. IEEE Trans. Ind. Electron. 2021, 68, 9527–9539. [Google Scholar] [CrossRef]
- Ayachit, A.; Reatti, A.; Kazimierczuk, M.K. Magnetising inductance of multiple-output flyback dc–dc convertor for discontinuous conduction mode. IET Power Electron. 2017, 10, 451–461. [Google Scholar] [CrossRef] [Green Version]
- Hu, R.; Zeng, J.; Liu, J.; Guo, Z.; Yang, N. An Ultrahigh Step-Up Quadratic Boost Converter Based on Coupled-Inductor. IEEE Trans. Power Electron. 2020, 35, 13200–13209. [Google Scholar] [CrossRef]
- Lee, S.; Do, H. Quadratic Boost DC–DC Converter with High Voltage Gain and Reduced Voltage Stresses. IEEE Trans. Power Electron. 2019, 34, 2397–2404. [Google Scholar] [CrossRef]
- Das, P.; Mousavi, S.A.; Moschopoulos, G. Analysis and Design of a Nonisolated Bidirectional ZVS-PWM DC–DC Converter with Coupled Inductors. IEEE Trans. Power Electron. 2010, 25, 2630–2641. [Google Scholar] [CrossRef]
- Da Cunha Duarte, C.; Barbi, I. A new family of ZVS-PWM active-clamping DC-to-DC boost converters: Analysis, design, and experimentation. IEEE Trans. Power Electron. 1997, 12, 824–831. [Google Scholar] [CrossRef]
- Vinnikov, D.; Roasto, I.; Strzelecki, R.; Adamowicz, M. Step-up dc/dc converter switch cascaded quasi Z-source network. IEEE Trans. Ind. Electron. 2012, 59, 3727–3736. [Google Scholar] [CrossRef]
- Liu, J.; Wu, J.; Qiu, J.; Jun, Z. Switched Z-Source/Quasi-Z-Source DC–DC Converters with Reduced Passive Components for Photovoltaic Systems. IEEE Access 2019, 7, 40893–40903. [Google Scholar] [CrossRef]
- Haji-Esmaeili, M.; Babaei, E.; Sabahi, M. High Step-Up Quasi-Z Source DC–DC Converter. IEEE Trans. Power Electron. 2018, 33, 10563–10571. [Google Scholar] [CrossRef]
- Shen, H.; Zhang, B.; Qiu, D. Hybrid Z-Source Boost DC–DC Converters. IEEE Trans. Ind. Electron. 2017, 64, 310–319. [Google Scholar] [CrossRef]
- Karthikeyan, V.; Kumaravel, S.; Gurukumar, G. High step-up gain DC–DC converter with switched capacitor and regenerative boost configuration for solar PV applications. IEEE Trans. Circuits Syst. II Express Briefs 2019, 66, 2022–2026. [Google Scholar] [CrossRef]
- Tang, Y.; Fu, D.; Wang, T.; Xu, Z. Hybrid Switched-Inductor Converters for High Step-Up Conversion. IEEE Trans. Ind. Electron. 2015, 62, 1480–1490. [Google Scholar] [CrossRef]
- Samiullah, M.; Iqbal, A.; Ashraf, I.; Maroti, P. Voltage Lift Switched Inductor Double Leg Converter with Extended Duty Ratio for DC Microgrid Application. IEEE Access 2021, 9, 85310–85325. [Google Scholar] [CrossRef]
- Bhaskar, M.S.; Meraj, M.; Iqbal, A.; Padmanaban, S.; Maroti, P.K.; Alammari, R. High gain transformer-less double-duty-triple mode DC/DC converter for DC microgrid. IEEE Access 2019, 7, 36353–36370. [Google Scholar] [CrossRef]
- Zaid, M.; Khan, S.; Siddique, M.D.; Sarwar, A.; Ahmad, J.; Sarwer, Z.; Iqbal, A. A transformerless high gain dc–dc boost converter with reduced voltage stress. Int. Trans. Electr. Energy Syst. 2021, 31, e12877. [Google Scholar] [CrossRef]
- Ahmad, J.; Siddique, M.; Sarwar, A.; Lin, C.; Iqbal, A. A high gain noninverting DC–DC converter with low voltage stress for industrial applications. Int. J. Circuit Theory Appl. 2021, 49, 4212–4230. [Google Scholar] [CrossRef]
- Saravanan, S.; Babu, N. Design and Development of Single Switch High Step-Up DC–DC Converter. IEEE J. Emerg. Sel. Top. Power Electron. 2018, 6, 855–863. [Google Scholar] [CrossRef]
- Khan, S.; Zaid, M.; Mahmood, A.; Nooruddin, A.S.; Ahmad, J.; Alghaythi, M.L.; Alamri, B.; Tariq, M.; Sarwar, A.; Lin, C.H. A New Transformerless Ultra High Gain DC–DC Converter for DC Microgrid Application. IEEE Access 2021, 9, 124560–124582. [Google Scholar] [CrossRef]
- Andrade, A.; Faistel, T.; Toebe, A.; Guisso, R. Family of Transformerless Active Switched Inductor and Switched Capacitor Ćuk DC–DC Converter for High Voltage Gain Applications. IEEE J. Emerg. Sel. Top. Ind. Electron. 2021, 2, 390–398. [Google Scholar] [CrossRef]
- Sarikhani, A.; Allahverdinejad, B.; Hamzeh, M. A Nonisolated Buck–Boost DC–DC Converter with Continuous Input Current for Photovoltaic Applications. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 804–811. [Google Scholar] [CrossRef]
- Babaei, E.; MashinchiMaheri, H.; Sabahi, M.; Hosseini, S. Extendable Nonisolated High Gain DC–DC Converter Based on Active–Passive Inductor Cells. IEEE Trans. Ind. Electron. 2018, 65, 9478–9487. [Google Scholar] [CrossRef]
- Shahir, F.M.; Babaei, E.; Farsadi, M. Extended topology for a boost DC–DC converter. IEEE Trans. Power Electron. 2019, 34, 2375–2384. [Google Scholar] [CrossRef]
- Li, G. A Novel Quadratic Boost Converter with Low Inductor Currents. CPSS Trans. Power Electron. Appl. 2020, 5, 1–10. [Google Scholar] [CrossRef]
- Yang, P.; Xu, J.; Zhou, G.; Zhang, S. A new quadratic boost converter with high voltage step-up ratio and reduced voltage stress. In Proceedings of the 7th International Power Electronics and Motion Control Conference, Harbin, China, 2–5 June 2012. [Google Scholar] [CrossRef]
- Ahmad, J.; Zaid, M.; Sarwar, A.; Tariq, M.; Sarwer, Z. A New Transformerless Quadratic Boost Converter with High Voltage Gain. Smart Sci. 2020, 8, 163–183. [Google Scholar] [CrossRef]
- Varesi, K.; Esfahlan, A.G. An Enhanced-Gain Quadratic-Boost DC–DC Configuration. In Proceedings of the 2020 28th Iranian Conference on Electrical Engineering (ICEE), Tabriz, Iran, 4–6 August 2020; pp. 1–5. [Google Scholar] [CrossRef]
- Mahmood, A.; Zaid, M.; Ahmad, J.; Khan, M.A.; Khan, S.; Sifat, Z.; Lin, C.H.; Sarwar, A.; Tariq, M.; Alamri, B. A Non-Inverting High Gain DC–DC Converter with Continuous Input Current. IEEE Access 2021, 9, 54710–54721. [Google Scholar] [CrossRef]
- Rahimi, T.; Ding, L.; Gholizadeh, H.; Shahrivar, R.S.; Faraji, R. An Ultra High Step-Up DC–DC Converter Based on the Boost, Luo, and Voltage Doubler Structure: Mathematical Expression, Simulation, and Experimental. IEEE Access 2021, 9, 132011–132024. [Google Scholar] [CrossRef]
- Varesi, K.; Hassanpour, N.; Saeidabadi, S. Novel high step-up DC–DC converter with increased voltage gain per devices and continuous input current suitable for DC microgrid applications. Int. J. Circ. Theor. Appl. 2020, 48, 1820. [Google Scholar] [CrossRef]







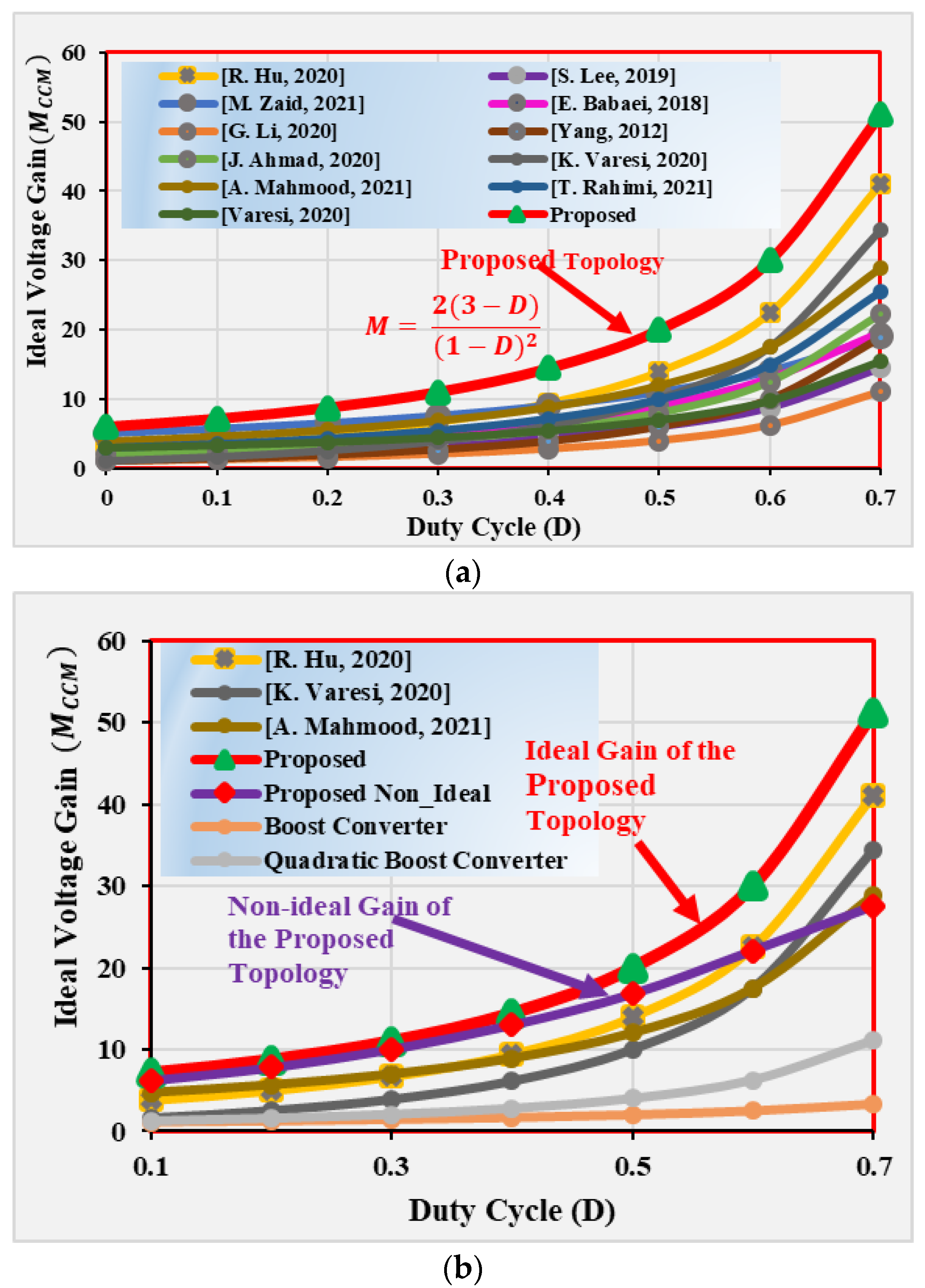





| Topology | MCCM at D = 0.5 | Common Ground | ||||||
|---|---|---|---|---|---|---|---|---|
| Boost Converter | 1 | 1 | 1 | 1 | 2 | Yes | ||
| Quadratic Boost Converter | 2 | 2 | 1 | 3 | 4 | Yes | ||
| [4] | 1 + 1 coupled inductor | 5 | 2 | 5 | 14 | Yes | ||
| [5] | 1 + 1 coupled inductor | 3 | 1 | 5 | 6 | Yes | ||
| [16] | 3 | 4 | 2 | 5 | 11 | No | ||
| [22] | 8 | 1 | 4 | 17 | 9 | No | ||
| [24] | 2 | 2 | 2 | 2 | 4 | Yes | ||
| [25] | 3 | 4 | 1 | 4 | 6 | Yes | ||
| [26] | 3 | 3 | 1 | 5 | 8 | Yes | ||
| [27] | 3 | 5 | 2 | 4 | 10 | Yes | ||
| [28] | 2 | 5 | 1 | 6 | 12 | No | ||
| [29] | 3 | 6 | 1 | 6 | 10 | Yes | . | |
| [30] | 2 | 3 | 2 | 3 | 7 | Yes | ||
| Proposed Topology | 3 | 6 | 2 | 7 | 20 | Yes |
| Parameter | Symbol | Value |
|---|---|---|
| Input Voltage | 20 V | |
| Duty Cycle | 0.4 | |
| Output Power | 67 W | |
| Load Resistance | 850 Ω | |
| Inductors | 330 μH, ESR = 0.12 Ω | |
| 0.4 mH ESR = 0.14 Ω | ||
| Capacitors | 47 μF, ESR = 0.1 Ω | |
| 100 μF, ESR = 0.22 Ω | ||
| Diodes | HER806 | |
| Power MOSFETs | SPW52N50C3 | |
| Driver | TLP250H | |
| Controller | STM32F334R8 | |
| Switching Frequency | 50 kHz |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zaid, M.; Malick, I.H.; Ashraf, I.; Tariq, M.; Alamri, B.; Rodrigues, E.M.G. A Nonisolated Transformerless High-Gain DC–DC Converter for Renewable Energy Applications. Electronics 2022, 11, 2014. https://doi.org/10.3390/electronics11132014
Zaid M, Malick IH, Ashraf I, Tariq M, Alamri B, Rodrigues EMG. A Nonisolated Transformerless High-Gain DC–DC Converter for Renewable Energy Applications. Electronics. 2022; 11(13):2014. https://doi.org/10.3390/electronics11132014
Chicago/Turabian StyleZaid, Mohammad, Ifham H. Malick, Imtiaz Ashraf, Mohd Tariq, Basem Alamri, and Eduardo M. G. Rodrigues. 2022. "A Nonisolated Transformerless High-Gain DC–DC Converter for Renewable Energy Applications" Electronics 11, no. 13: 2014. https://doi.org/10.3390/electronics11132014
APA StyleZaid, M., Malick, I. H., Ashraf, I., Tariq, M., Alamri, B., & Rodrigues, E. M. G. (2022). A Nonisolated Transformerless High-Gain DC–DC Converter for Renewable Energy Applications. Electronics, 11(13), 2014. https://doi.org/10.3390/electronics11132014








