Introduction of a Novel Image-Based and Non-Invasive Method for the Estimation of Local Elastic Properties of Great Vessels

Abstract

Background: In the context of a growing demand for the use of in silico models to meet clinical requests, image-based methods play a crucial role. In this study, we present a parametric equation able to estimate the elasticity of vessel walls, non-invasively and indirectly, from information uniquely retrievable from imaging. Methods: A custom equation was iteratively refined and tuned from the simulations of a wide range of different vessel models, leading to the definition of an indirect method able to estimate the elastic modulus E of a vessel wall. To test the effectiveness of the predictive capability to infer the E value, two models with increasing complexity were used: a U-shaped vessel and a patient-specific aorta. Results: The original formulation was demonstrated to deviate from the ground truth, with a difference of 89.6%. However, the adoption of our proposed equation was found to significantly increase the reliability of the estimated E value for a vessel wall, with a mean percentage error of 9.3% with respect to the reference values. Conclusion: This study provides a strong basis for the definition of a method able to estimate local mechanical information of vessels from data easily retrievable from imaging, thus potentially increasing the reliability of in silico cardiovascular models.

1. Introduction

Over recent decades, the use of patient-specific numerical models has continued to grow for an increasing range of applications [1,2,3]. Recent technological advances in medical imaging and computational power have enabled the increased use of numerical patient-specific modeling, providing a reliable tool for the study of cardiovascular problems in a highly accurate way.

The use of computer-based models has been strongly encouraged for in silico clinical trials, as advocated by the FDA (Food and Drug Administration) to enable the development of new devices and therapeutic applications [4]. Moreover, these models represent a powerful and promising tool for the pre-procedural assessment of cardiovascular interventions during the decision-making process [5].

However, the translation of numerical modeling into effective clinical applications is still limited, as the reliable adaption of cardiovascular models for patient-specific conditions represents a major challenge [6,7,8]. The current imaging techniques allow a high-fidelity depiction of in vivo anatomical structures of the patient, and structural 3D-imaging methods, such as computed tomography (CT) and magnetic resonance imaging (MRI) are commonly used worldwide. However, a proper numerical replica of the patient’s case requires faithful implementation of boundary conditions and material properties, with the latter currently representing the biggest source of uncertainty [9,10]. However, functional imaging methodologies, such as phase contrast MRI, 4D flow and Doppler ultrasound, can provide useful and detailed in vivo information on the patient’s hemodynamics, allowing for the implementation of accurate boundary conditions [11,12,13], when patient-specific material characteristics remain unknown.

The lack of such crucial information results in approximations in material modeling [14,15,16], thus strongly limiting the reliability of numerical tools. The mechanical response of vessels, as a result of blood flowing [17,18] or device interaction [19], depends not only on the material properties of the vessel itself, but also on the surrounding structures and tissues [20], thus, in some cases, reducing the value of ex vivo data [21]. Given the importance of non-invasively extrapolating in vivo material information relating to cardiovascular structures, several approaches have been investigated over recent years, such as inverse numerical methodologies and image-based techniques [22,23,24]. The high computational cost of iterative methods strongly limits their practical use in clinics, where prompt feedback is necessary. However, actual image-based strategies for inferring mechanical properties are limited to the use of pressure information [25,26], which is not only invasive but is also not always available for patients. Among such methodologies, elastography represents a non-invasive imaging technique for the quantitative assessment of tissue elasticity [27,28,29]. However, despite its increasing clinical relevance, especially in non-vascular areas [27], vascular elastography was demonstrated to detect statistically significant elasticity differences in patient tissues, and was thus able to distinguish different plaque types with acceptable reproducibility [30], but without providing exact absolute stiffness values for vessel structures in a way that can be implemented in numerical models.

Such strategies highlight the importance of image-based methods, which are now crucial elements of clinical workflow [31,32], to be considered for the estimation of the material characteristics of in vivo vessel walls. Enhanced material information, which includes in vivo patient-specific data, may significantly improve the accuracy of computational models, increasing their validity and applicability in clinical practice.

In this study, we develop a non-invasive image-based methodology able to infer the local elastic modulus of arterial walls at specific sections of the vessels, without using pressure invasive information. The unique requirements of the proposed method are dynamic information of area deformation and flow measurements along the cardiac cycle, which are both easily retrievable from standard functional imaging, such as phase contrast MRI, which is a routine examination in the pre-procedural assessment of the patient before scheduled cardiovascular intervention. The method described here is based on our previous results [33], where a new formulation was introduced. In this study, we generalize its application to a wide range of vessels, enabling the estimation of patient-specific material information from solely in vivo MRI data. The methodology was refined based on a series of numerical simulations, enabling the exploration of a huge number of vascular geometries and fluid dynamics scenarios in a fully controlled in silico environment. In particular, each numerical vessel was treated as a virtual patient, from which virtual phase contrast MRI information was acquired at specific cross-sections, in terms of velocity variation and area deformation along the simulated cardiac cycle, thus permitting the application of the $QA$ method and consequent $PWV$ and E value estimation. After finalizing its mathematical formulation, the presented technique was tested on two virtual datasets generated from computer simulations with increased complexity, thus demonstrating its efficacy.

2. Materials and Methods

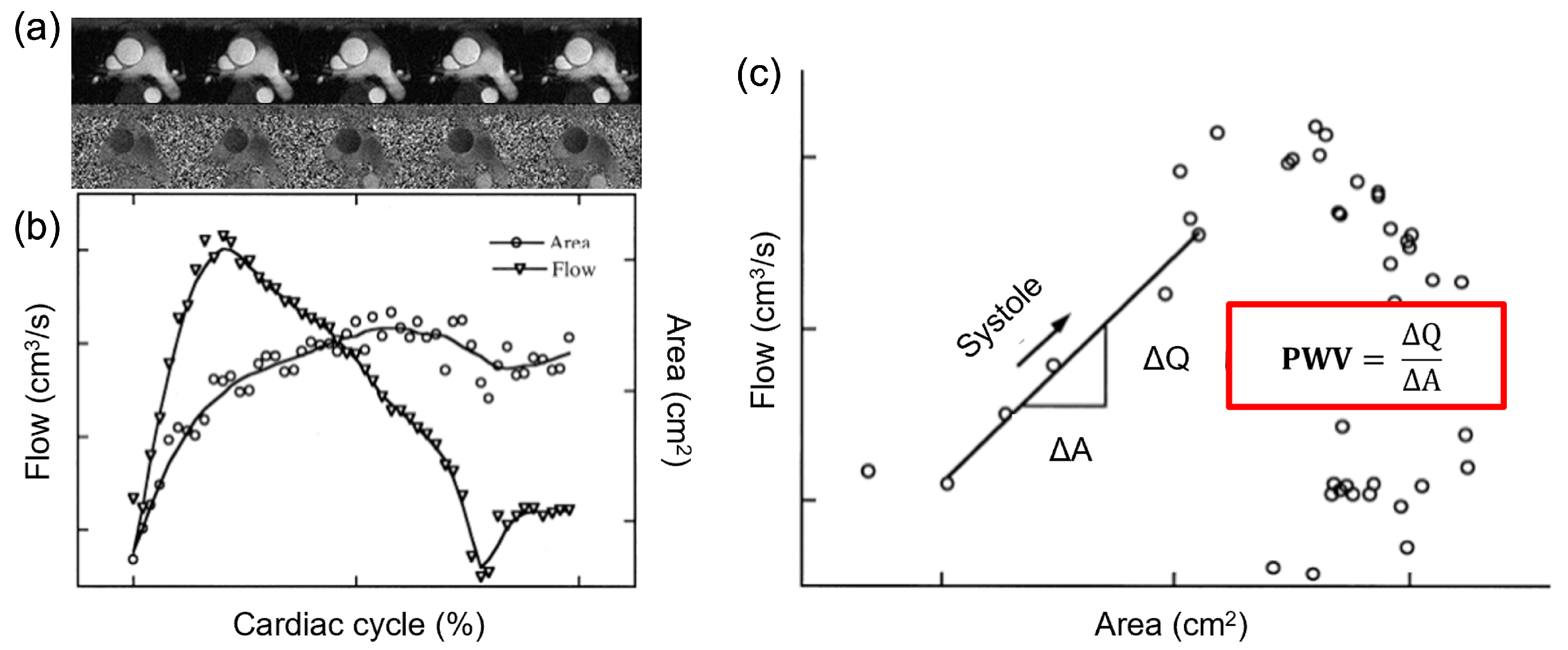
2.1. Theoretical Background

The so-called flow-area ($QA$) method is an image-based technique which enables the calculation of the local pulse wave velocity ($PWV$) [34] of a vessel from through-plane flow and cross-sectional area as extracted from imaging, such as phase contrast MRI [35] or Doppler ultrasound [36]. The $PWV$ is a widely accepted parameter for the estimation of arterial stiffness in clinics [37,38,39].

The $QA$ methodology is based on the assumption that, during the reflection-free period of the cardiac cycle, i.e., the early systolic phase, the relationship between the cross-sectional area A of the vessel and the passing flow Q can be approximated as a first-order linear equation, allowing the estimation of the $PWV$ as:

$$PWV={\left.\frac{dQ}{dA}\right|}_{\mathrm{early}\mathrm{systole}}$$

(1)

where $dA$ is the incremental variation of the cross-sectional area and $dQ$ is the incremental variation of the flow passing through the section. A representation of the steps for the computing of the $PWV$ from phase contrast MRI data is depicted in Figure 1.

The $PWV$ can be used as a starting point for the estimation of additional parameters providing further information on the mechanical response of an in vivo vessel wall.

By inverting the well-known Bramwell–Hill equation [40], the distensibility ($Dist$) of a vessel can be defined from the $PWV$:

$$Dist=\frac{1}{\rho PW{V}^2}$$

(2)

where $\rho$ is the density of the fluid passing through the cross-section of the vessel, i.e., the blood density in vascular structures.

Finally, according to [41], an estimation of the elastic modulus E of the vessel wall can be expressed as a function of the $Dist$ and some geometrical features of the vessel:

$$E_{Dist}=\frac{\left[3\left(1+\frac{A_0}{WCSA}\right)\right]}{Dist}$$

(3)

in which $A_0$ is the diastolic inner area of the vessel and $WCSA$ is the wall cross-sectional area (i.e., the area between the inner and outer diameter), also measured at diastole, expressed as:

$$WCSA=\pi {(r_0+thk)}^2-\pi r_0^2$$

(4)

where $r_0$ represents the inner diastolic radius of the vessel and $thk$ is the wall thickness.

By combining Equations (1) and (3), a $PWV$-based E value of the vessel wall can be therefore defined as:

$$E_{PWV}=3\rho PW{V}^2\left(1+\frac{A_0}{WCSA}\right)$$

(5)

where the $PWV$ can be obtained from the $QA$ method using Equation (1). Hence, Equation (5) can be used to estimate a surrogate of the E value of a vessel wall from solely image-based information.

In the following, an improved version of Equation (5) is presented, obtained from a recursive in silico method based on FSI simulations.

2.2. Definition of the Image-Based Formulation

In this section, the image-based formulation for the estimation of the E value of vessel walls is described. The starting point was represented by the Equation (5), based on $PWV$ and other parameters. First, the aforementioned formulation was tested to assess its capability to predict the E value of a vessel wall. In particular, an in silico workflow based on a series of FSI simulations of vessels models was developed. FSI results of vessel models were treated as super-resolution phase contrast MRI datasets, with the advantage of an absence of noise and artifacts with respect to real imaging. Hence, flow and area information were extracted for each simulated model from a single cross-section, as occurs in proper image data, to compute $PWV$ and then the E value from Equation (5). For each simulated vessel, the outcome from Equation (5) was compared to the E value assigned to the in silico model. Since a discrepancy was observed between E estimation and the ground truth, a correction factor was included in the formula and iteratively calibrated to reduce the error.

Following the preliminary results from [33], the correction factor ($\chi$) was defined as:

$$\chi =\gamma RAC$$

(6)

where $RAC$ is the relative area change in the cardiac cycle, expressed as:

$$RAC=\frac{A_{max}-A_0}{A_{max}}$$

(7)

in which $A_{max}$ is the maximum cross-sectional area of the vessel lumen, i.e., the area value at systolic peak, and $A_0$ is the area value at diastole. The parameter $\gamma$ was assumed as a function of some model characteristics, such as geometry, flow and pressure quantities, as detailed in the following.

The inclusion of the $\chi$ factor (Equation (6)) in the formulation was demonstrated to increase its predictive capability in the estimation of the E value of the vessel wall [33]. Briefly, the enhanced formula for the estimation of the E value is provided by multiplying the Equations (5) and (6):

$$E_{\chi }=3\chi \rho PW{V}^2\left(1+\frac{A_0}{WCSA}\right)$$

(8)

The $\chi$-method is able to estimate the local E value of a vessel wall at a selected cross-section, using the Equation (1), which considers the $PWV$ as computed from the $QA$ method, specific geometric features of the section, and a crucial corrective factor $\chi$.

The original formulation (Equation (5)) was used to indirectly compute the E value, which was compared to the E value assigned as input in the numerical model. Due to the non-linearity observed between input and output E values, the corrective factor $\chi$ (Equation (6)) was introduced to reduce such non-linearity and increase the goodness of the estimation.

While in the previous study, $\gamma$ was computed for a single configuration, here, in order to generalize its formulation, we defined the variable $\gamma$ as a function of three main parameters: the cross-sectional area of the vessel at diastole ($A^d$), the peak of the passing through-plane flow ($Q^p$) and the internal pressure range (P):

$$\gamma =\mathsf{\Gamma }(A^d,Q^p,P)$$

(9)

Solving the problem for two principal pressure configurations, the P range can be assumed to be equal to 80–120 mmHg in the case of aortic pressure ($P_{Ao}$) or 10–22 mmHg in the case of pulmonary artery pressure ($P_{PA}$). These ranges were selected to cover the cases of the two main great vessels pressure ranges. Hence, Equation (10) becomes:

$${\gamma |}_{P_{Ao}}=\mathsf{\Gamma }(A^d,Q^p,P=P_{Ao}){\mathrm{and}\gamma |}_{P_{PA}}=\mathsf{\Gamma }(A^d,Q^p,P=P_{PA})$$

(10)

To investigate the influence of $A^d$ and $Q^p$ values on $\gamma$, five pipe vessels with inner diameters (D) equal to 1, 2, 3, 4 and 5 cm were modeled, corresponding to human vessel common sizes (

Table 1. List of parameters used for the FSI simulations.

${\mathit{A}}_{\mathit{i}}^{\mathit{d}}$ (cm${}^2$)	${\mathit{Q}}_{\mathit{j}}^{\mathit{p}}$ (mL/s)	${\mathit{E}}_{\mathit{k}}^{\mathit{w}}$ (MPa)
0.78	100	0.5
3.14	200	1.0
7.07	300	2.0
12.57	400	4.0
19.64	500	8.0

). The length and wall thickness of vascular models were maintained constant, i.e., 15 cm and 0.2 cm, respectively.

For the i-th geometry characterized by a diastolic cross-sectional area A${}_i^d$, five different inflow velocity boundary conditions were adopted, so that five flow peaks $Q^p$ were considered, ranging from 100 to 500 mL/s (Table 1). The outflow pressure boundary condition was imposed according to the two main pressure ranges $P_{Ao}$ and $P_{PA}$.

Then, for each model characterized by the i-th geometry and the j-th inflow boundary condition ($A_i^d$ and $Q_j^p$, respectively), five simulations with increasing elastic modulus assigned to the vessel wall ($E^w$), in the range 0.5–8 MPa (Table 1), were run.

The value of ${\gamma }_{i,j}$ for the vessel model characterized by a diastolic area $A_i^d$ and a flow peak of $Q_j^p$ at the selected section, and an internal pressure range $P_0$ ($P_{Ao}$ or $P_{PA}$ in this study) is estimated as:

$${\gamma }_{i,j}=\mathsf{\Gamma }(A_i^d,Q_j^p,P_0)=\sum _{k=1}^n\frac{{\psi }_k}{n}$$

(11)

with ${\psi }_k$ computed as follows:

$${\psi }_k=\frac{E_k^w}{RAC\left(A_i^d\right)E_{PWV}(A_i^d,Q_j^p)}$$

(12)

where $E_k^w$ is the k-th elastic modulus assigned to the vessel wall in the simulation, $RAC$ is the relative area change of the model (Equation (7)), which is a function of the cross-sectional area $A_i^d$, and $E_{PWV}$ is the E value as obtained from standard Equation (5), dependent on both the diastolic area $A_i^d$ and the flow peak $Q_j^p$ for the calculation of $PWV$ (Equation (1)) and the geometric features. Parameters $A_i^d$, $Q_j^p$ and $E_k^w$ are listed in Table 1.

Each simulation, characterized by a diastolic area $A_i^d$, a flow peak $Q_j^p$ and an elastic modulus for the vessel wall $E_k^w$, was run twice, first with an outflow pressure condition $P_{Ao}$ and then with $P_{PA}$, while inflow boundary condition was maintained.

The two obtained datasets were interpolated using the thin-plate spline for surfaces using MATLAB (MathWorks, Inc., Natick, MA, USA), to obtain a complete estimation of ${\gamma |}_{Ao}$ and ${\gamma |}_{PA}$ domains.

Due to the huge amount of simulations required to characterize the $\gamma$ domain, a custom-made pipeline was developed in Python to automatize all the steps of the process in an optimized manner, from the set-up of the simulations to the elaboration of the results.

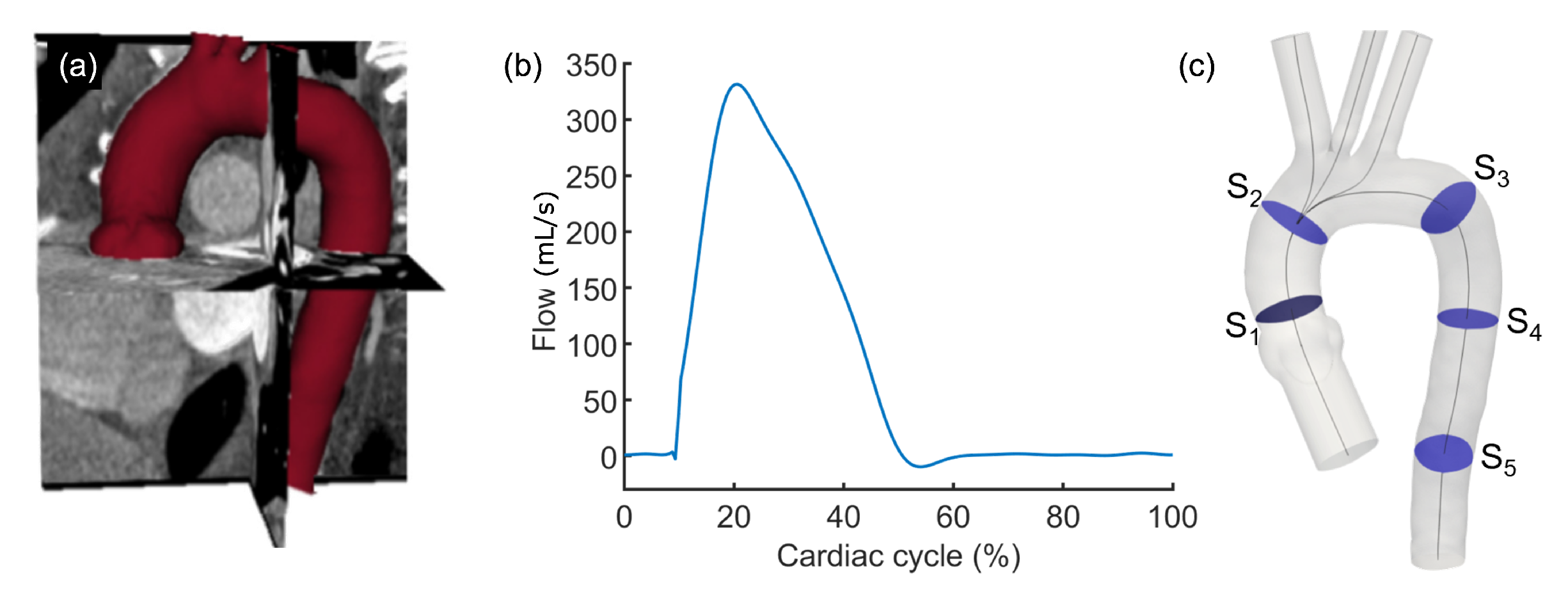
2.3. Fluid-Structure Interaction Simulation Workflow

The numerical simulations were carried out with the commercial software LS-DYNA R.11 (Ansys/LST, Ansys Inc., Canonsburg, PA, USA). In order to simulate pulsatile cardiac-like flow within the different compliant virtual vessel models, a two-way approach with a strong coupling scheme was adopted to encompass the influence of the passing flow on the deformable structure of the vessel wall and the reciprocal effect. An arbitrary Lagrangian Eulerian formulation was used for the mesh deformation. Both fluid and solid discrete systems were considered as converged when their respective residuals dropped below threshold $ϵ$ = $1\times {10}^{-6}$ at every time step. Fluid and structural domains had matching interfaces for an optimal solution exchange.

In silico models. The FSI simulations were run for a set of vessel pipe models with cylindrical shape, and used to estimate the $\gamma$ domain, as described in Section 2.2. The model sets included a total of five different cylindrical geometries, with inner diameters (D), according to Table 1.

Fluid domains. The unsteady fluid computation analysis of the FSI models was performed using the ICFD solver of LS-DYNA. The fluid behavior is governed by the Navier–Stokes equations, with the ICFD solver discretizing the governing equations using a low-order continuous finite element method. The models were meshed with tetrahedral elements using the commercial package ANSA (BETA CAE Systems International AG, Luzern, Switzerland), using an average element size of 1 mm. A preliminary mesh convergence study was performed to confirm a mesh-independent solution. The blood behaviour was simulated as an incompressible and Newtonian fluid with a density of 1060 kg m${}^3$ and a dynamic viscosity of 0.05 kg m${}^{-1}$ s${}^{-1}$. The boundary conditions were implemented to impose idealised, but physically based, waveforms of cardiac-like velocities at the inlet and pressures at the outlet. In particular, boundary conditions for the five pipe models are shown in Figure 2, with reference to the different $Q^p$ for the inlet (Figure 2a) and the two analyzed pressure conditions ($P_{Ao}$ and $P_{PA}$) for the outlet (Figure 2b).

Structural domains. Structural models consisted of the solid walls of the FSI models. In all cases a constant wall thickness of 2 mm was set. A node-to-node correspondence between the fluid and solid parts was accomplished by the ANSA meshing software. The governing equations for the structural domain are those of linear elasticity for small deformations, discretized by the solver with a continuous finite element method. Material was modeled as isotropic linear elastic, with a Poisson ratio of 0.49. A range of different E values was assigned to the models. The different values of stiffness were set according to Table 1. The structural models were bounded with fixed edges.

Post-processing of simulations. The post-processing of the run models was handled in ParaView (www.paraview.org, accessed on 28 March 2022) [42] and MATLAB. Results from the FSI simulations were exported in .vtk format to be elaborated in ParaView. Treated as virtual patients, the results from the FSI models were analyzed at a selected cross-section (S), as happens during real phase contrast MRI acquisitions. In particular, the results from pipe vessel models were analyzed at the middle cross-section of the cylindrical models, to avoid edge effects. Area deformation and through-plane flow over time were extracted for each case to define the related $QA$ loop. Finally, the procedure described in the previous Section 2.2 was applied for the definition of the $\gamma$ domain.

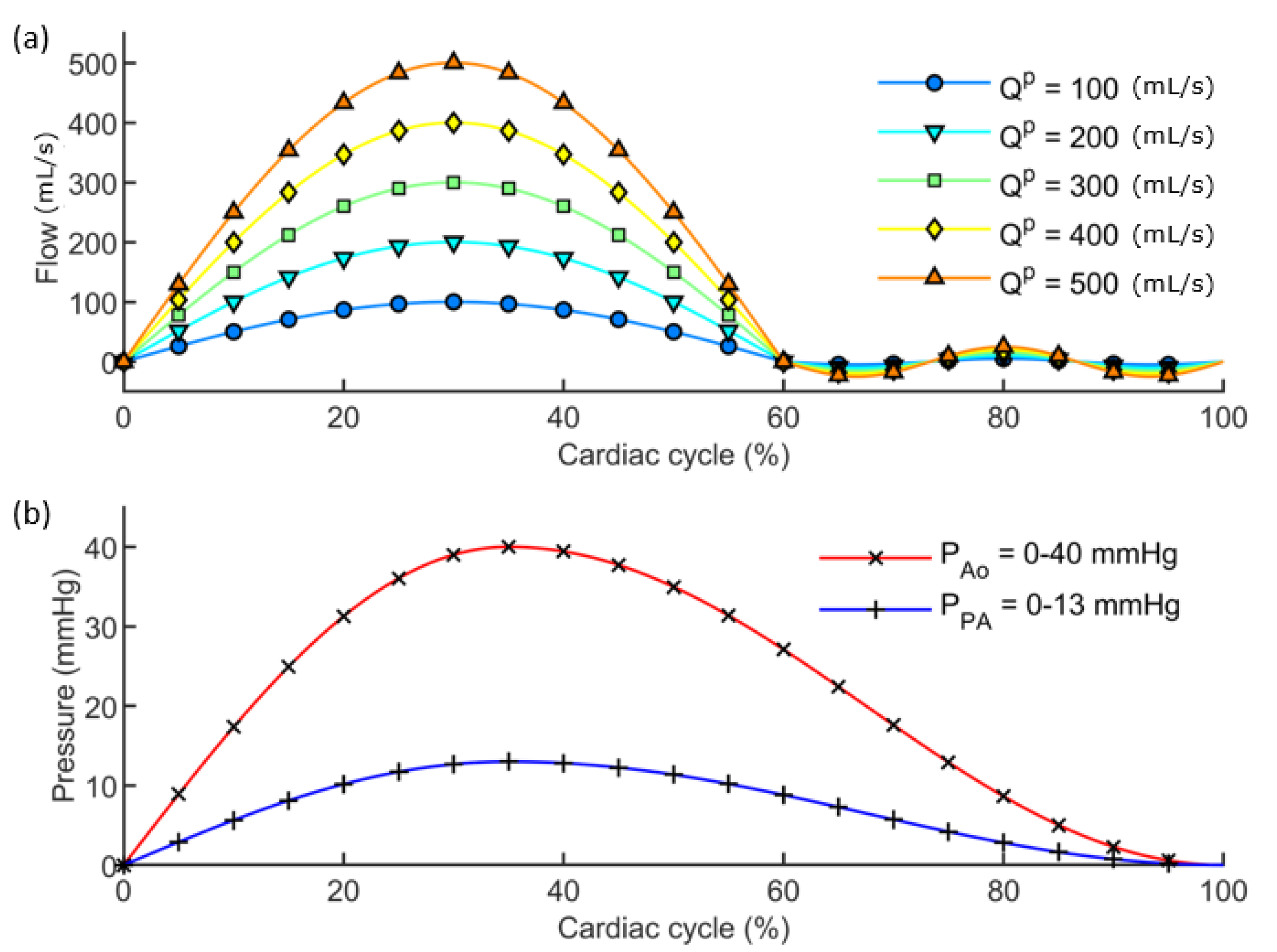
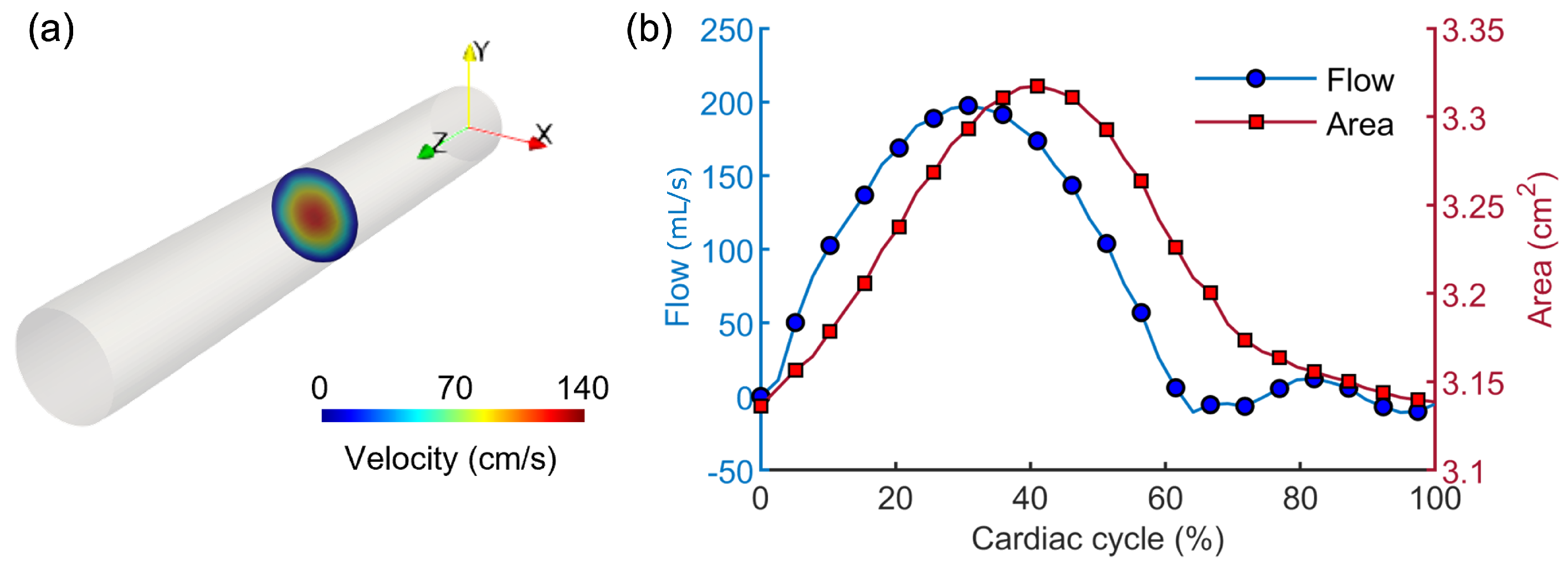
2.4. Application of the Image-Based Method to Virtual Models

The $\chi$-method described in the previous sections was applied for validation purposes on two different models $M_1$ and $M_2$ consisting of two FSI models of increasing morphological complexity.

Geometries. The first model ($M_1$) consisted of a more complex version of the pipe vessels used to define the $\gamma$ domain (Section 2.3), where the cylindrical shape was bent in a “U” configuration, thus representing an idealized model of an aortic arch (Figure 3a). The $M_2$ geometry was designed in the Fusion 360 environment (Autodesk, San Rafael, California). A U-shape presented a circular section characterized by a diameter of 2 cm. The straight tracts measured 10 cm, with a curvature radius of 3 cm in the bent region.

The second model ($M_2$) was of an actual patient-specific aorta, including ascending and descending tracts and supra-aortic vessels. The geometry of $M_2$ was extracted from the segmentation of patient CT imaging (Figure 4a) using the open source package 3D Slicer (Slicer, USA). A 2 mm thickness wall was set for both $M_1$ and $M_2$ models.

Materials. Material of the structural wall was modeled as isotropic linear elastic, with a Poisson ratio of 0.49. FSI simulations of $M_1$ and $M_2$ models were run with different E values for the vessel wall, from softer to harder values. In this testing phase, the a priori knowledge of the E values of $M_1$ and $M_2$ models permitted the availability of a reliable ground truth for the comparison with the $E_{\chi }$ values, as computed from Equation (8) including the corrective factor $\chi$. However, the assigned stiffness values were different from the E values used to populate the $\gamma$ domain (Section 2.2), to quantify the goodness of the obtained surface in regions out of the interpolation points. In particular, four E values were assigned, i.e., 1.5, 2.3, 2.7 and 3.0 MPa. The blood behaviour was simulated as an incompressible and non-Newtonian fluid with a density of 1060 kg m${}^3$ and a dynamic viscosity of 0.05 kg m${}^{-1}$ s${}^{-1}$.

Meshes. All fluid parts were meshed with tetrahedral elements using the commercial package ANSA The $M_1$ model was meshed with 82,803 elements. $M_2$ was meshed with 835,156 elements including four inflation layers with a growth rate of 1.5. Additional extrusions were added at the inlet of the model, and at the supra-aortic and descendent tracts, to allow the flow to fully develop. Structural meshes were defined with two layers among the thickness wall, imposing a node-to-node correspondence between domains. A preliminary mesh convergence study was performed to confirm a mesh-independent solution for the two models.

Boundary conditions. All the structural models were bounded with fixed edges. Concerning fluid domains, the boundary conditions were implemented to impose cardiac-like velocities at the inlet and pressures at the outlet.

$M_2$ was treated as a simplified aorta, thus modeled with the $P_{Ao}$ outflow pressure condition and the flow curve equivalent to $Q_p=200$ mL/s for the inlet condition (Figure 3b), with reference to Figure 2. Regarding $M_2$, a complete patient-specific model was implemented. The inlet condition was set according to flow measurements from phase contrast MRI of the patient at the aortic valve level (Figure 4b), while outlet conditions for the descending aorta and supra-aortic vessels were based on the Windkessel model [43], with RCR parameters set according to a previous study [1] in order to guarantee the pressure range of the patient (40 mmHg peak-to-peak) and a physiological waveform.

Solutions. A total of eight FSI simulations were run, considering the two models $M_1$ and $M_2$ and the four values of stiffness implemented for the walls ($E_1$ = 1.5 MPa, $E_2$ = 2.3 MPa, $E_3$ = 2.7 MPa, $E_4$ = 3.0 MPa). The solving was carried out in LS-DYNA and using the same solution parameters set in Section 2.3. Three cardiac cycles were simulated for $M_1$, and only the last cycle was considered for analysis. Instead, a total of ten cardiac cycles were simulated for $M_2$, allowing the $RCR$ models to reach the regime state.

Post processing. Being treated as virtual patients, the results from the two FSI models were analyzed at selected cross-sections (S), as happens during phase MRI acquisitions.

Seven cross-sections were extracted from the FSI results of $M_1$, to capture the effect of straight and bent tracts on the analysis (Figure 3b). In particular, $S_1$ and $S_7$ originated from a cut-plane at 5 cm height from base. Similarly, a cut-plane at 10 cm height was used to select $S_2$ and $S_6$. Instead, $S_3$ and $S_5$ were derived from the cut-planes defined in the regions of maximum warp, for ascending and descending tracts, respectively, while $S_4$ was extracted from the plane of symmetry.

For the patient-specific case, $M_2$, the cut planes for the extraction of the slices were defined as perpendicular to the center line of the model. The open source library VMTK (Orobix srl, Bergamo, Italy) was used to compute the center line. Five slices were analyzed for $M_2$: on the aortic root ($S_1$), on the ascending tract ($S_2$), on the descending bend after the supra-aortic vessels ($S_3$), and on the descending tract at proximal ($S_4$) and distal positions ($S_5$), as depicted in Figure 4c.

For each slice S of each model, area deformation and through-plane flow along time were extracted. The $QA$ method was applied to compute the $PWV$ according to Equation (1). Then, $E_{\chi }$ at section S was calculated according to Equation (8), with $\gamma$ value equal to:

$${\gamma }_S=\mathsf{\Gamma }(A_S^d,Q_S^p,P_0=P_{Ao}),$$

(13)

where $A_S^d$ and $Q_S^p$ are the diastolic area and the flow peak measured at section S, and $P_0$ the known pressure range ($P_{Ao}$ in these cases). The estimated $E_{\chi }$ value was compared with respect to the E value assigned as input to the numerical simulation to verify the efficacy of the $\chi$-method. $E_{PWV}$ was computed as well using Equation (5), to compare the standard methodology and the novel $\chi$-method in terms of inferring the capability of the E value.

3. Results

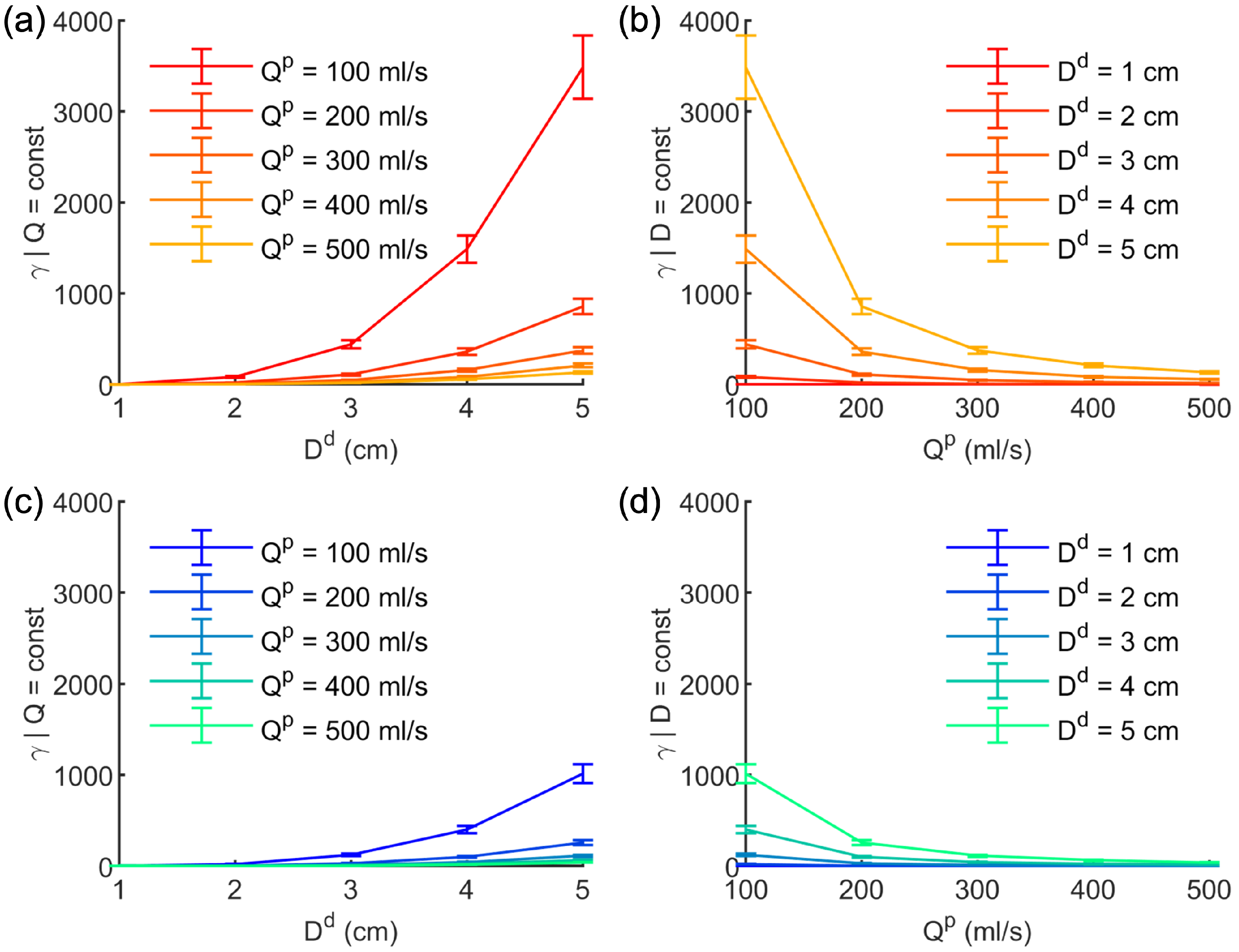
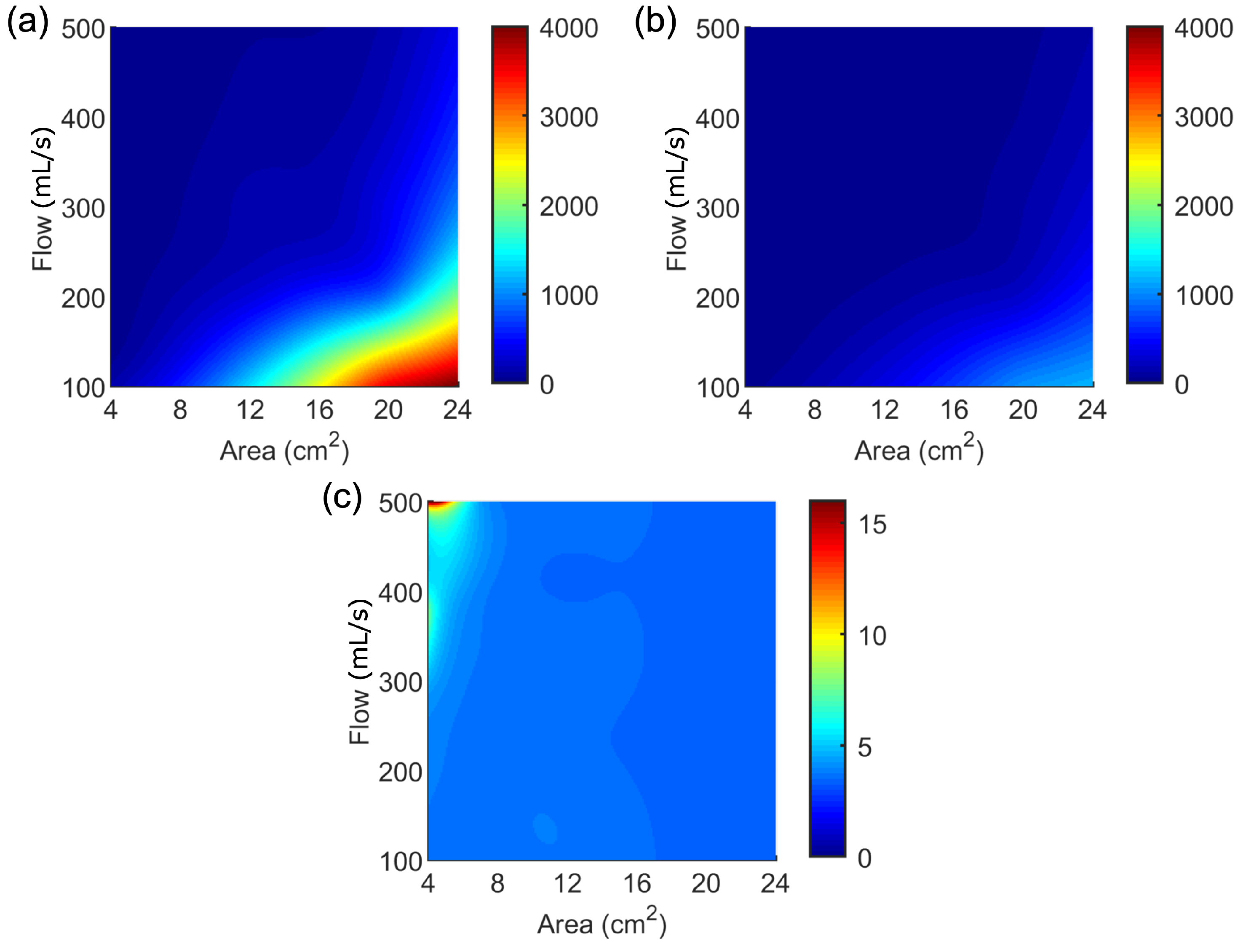
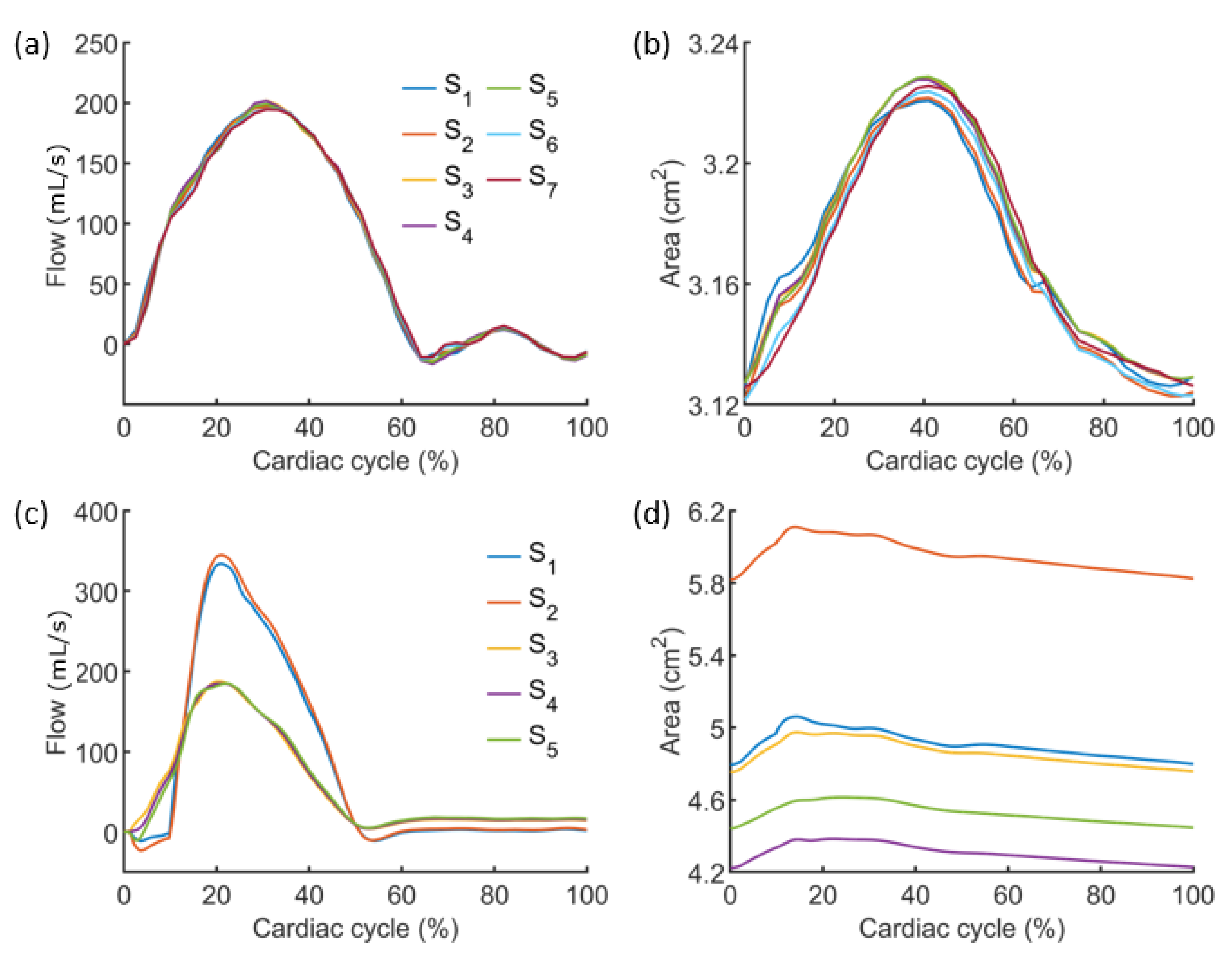
3.1. Results from the Simulations Workflow

The definition of the $\gamma$ function through the massive in silico campaign was achieved successfully. Figure 5 depicts the post-processing of an example case of an FSI simulation, from the selection of the middle cross-section of the model results to the computation of area and flow quantities along the cardiac cycle for the building of the $QA$ loop.

The execution of the same procedure for all the run models allowed the population of the $\gamma$ domain at selected $(A,Q)$ points, based on the value listed in Table 1.

Figure 6 shows the trend of $\gamma$ values (mean ± standard deviation) with respect to the diastolic inner diameter $D^d$ (hence, inner diastolic area $A^d$) at constant flow (Figure 6a–c) and vice versa (Figure 6b–d), for the two analyzed pressure scenarios (i.e., $P_{Ao}$ and $P_{PA}$). In particular, $\gamma$ was found to increase with larger vessels and decrease with greater passing flow. Moreover, $\gamma$ appeared to be specifically sensible to pressure variations, presenting higher values with higher pressures, as demonstrated by the difference between the graphs related to $P_{Ao}$ and $P_{PA}$, respectively, reported in Figure 6a,b and Figure 6c,d.

In order to determine the effect of the mutual contribution of A and Q on the $\gamma$ response, a 3D interpolation using a thin-plate spline for surfaces was performed. Figure 7 shows the results of the interpolation for ${\gamma |}_{Ao}$ and ${\gamma |}_{PA}$, respectively, depicted in Figure 7a and Figure 7b.

As can be seen in Figure 7a,b, a difference in the $\gamma$ range between the two pressure scenarios was found. As expected, ${\gamma |}_{Ao}$ exhibited higher values with respect to the ${\gamma |}_{PA}$. However, their ratio ${\gamma |}_{Ao}$:${\gamma |}_{PA}$ was relatively constant among the flow-area plane (Figure 7c), except for the regions representing non-realistic conditions, as for vessels with significantly reduced lumen and high flows.

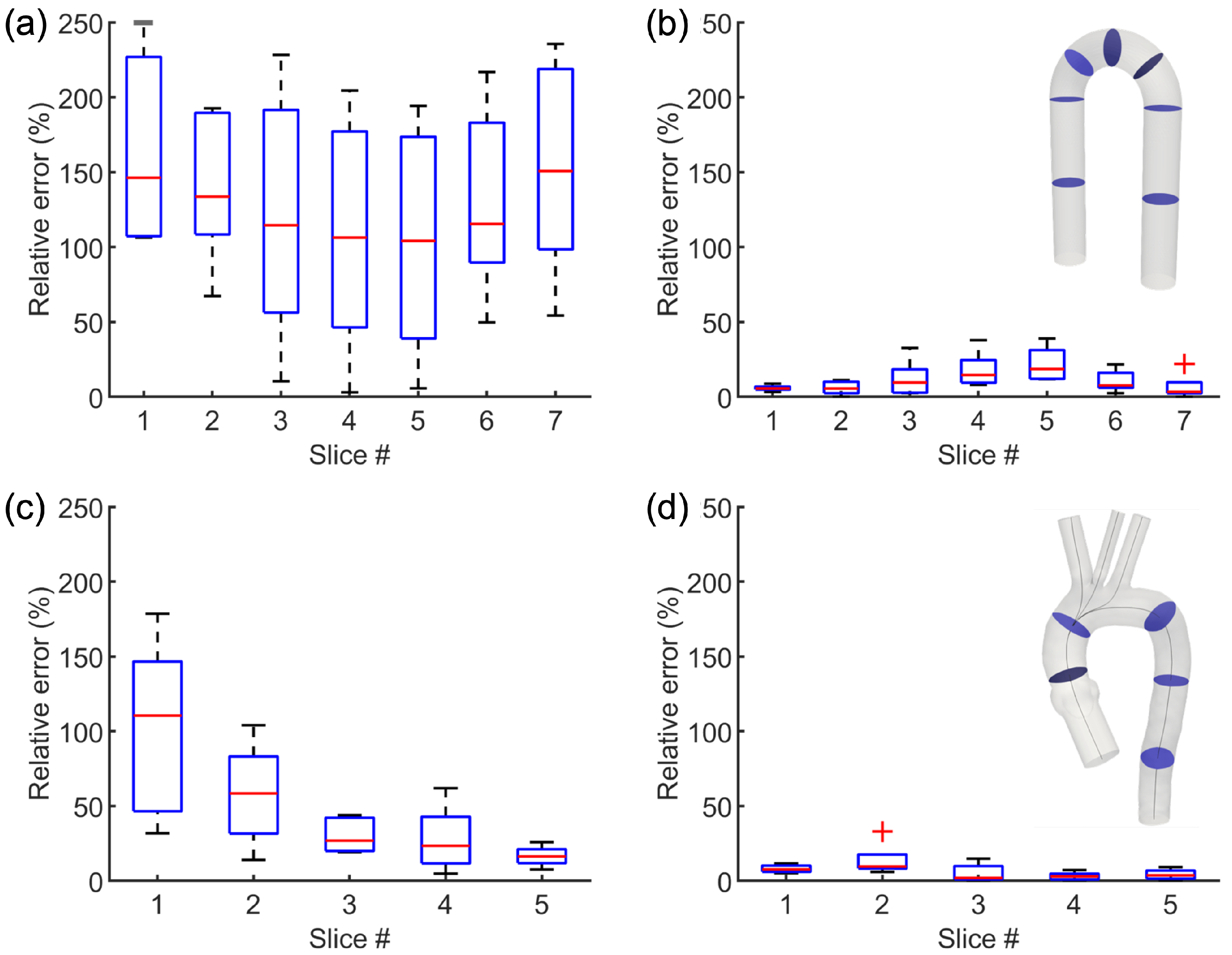
3.2. Results from the Application of the Image-Based Method

The results related to the application of the $\chi$-method on the in silico models are reported here.

The FSI simulations of both models $M_1$ and $M_2$ for all the different stiffnesses assigned to the vessel wall achieved solution convergence. An example of flow and area variations (for E = 1.7 MPa), as extracted from the slices S perpendicular to the model’s center lines, are reported in Figure 8.

Negligible variations among sections were found for the $M_1$ case, for both flow and area waveforms, according to the regular shape of the model, assuring the conservation of the investigated quantities (Figure 8a,b). However, the flow and area trends at the sections from $M_2$ showed significant differences, due to either flow partition through supra-aortic branches (Figure 8c) or lumen reduction in the center line of the vessel (Figure 8d).

Generally, the flow was found to preserve the same trend among the different tested E values, while the area changed accordingly, i.e., increasing for softer walls and reducing for higher stiffnesses. Figure 9 shows the coupling of flow and area information, namely the $QA$ loop, together with the points considered for linear interpolation for the $PWV$ estimation. The reported example plots are referred to the $S_3$ of both models, for E = 1.7 MPa. $QA$ loops changed according to the area variations due to the E of the vessel wall.

Given one of the eight FSI simulations run, the $PWV$ was computed for each slice S from the related $QA$ loop, together with $A_S^d$ and $Q_S^p$. Therefore, $\gamma$ was obtained according to the ${\gamma |}_{Ao}$ function, using Equation (13). $E_{PWV}$ and $E_{\chi }$ values were calculated and compared to the ground truth represented by the E values assigned to the vessel wall of the two models.

The comparative results are summarized in Figure 10, showing the percentage differences between the estimated ($E_{PWV}$ and $E_{\chi }$) and the assigned E value for $M_1$ and $M_2$ models, at each specific slice.

The overall trend was maintained for both models, with $E_{\chi }$ crucially reducing the gap between the stiffness wall estimation from virtual image data and the ground truth (Figure 10c,d), with an average difference of less than 10%. However, the standard $E_{PWV}$ prediction resulted in mean percentage errors even greater than 150%, as in the case of the $S_7$ section of model $M_1$ (Figure 10a,b).

Despite these remarkable results, a residual error was still found in the outcomes of the $\chi$-method, with a maximum difference of 22%, for the slice $S_5$ of $M_1$ case.

4. Discussion

In this paper, we described a non-invasive methodology to extract local information of a surrogate of the Young’s modulus E of the vessel wall, potentially ready-to-use in numerical simulations of vascular interventions, from solely MRI-based data, commonly acquired in routine clinical assessment of patients undergoing minimally invasive cardiovascular procedures.

The presented method is based on the $PWV$, which is a clinically relevant marker of arterial stiffness, strongly correlated with vascular status in aging and disease [44]. The $PWV$ represents the portion of vessel traveled by the systolic wave in the time unit, and is commonly computed in clinical practice with the direct transit-time method [45]. Aside from invasive pressure measurements, the velocity encoded MRI modality is the only technique able to provide an estimation of $PWV$ non-invasively, with the same accuracy as catheter-based recordings [46].

However, although several MRI-based approaches have been proposed to establish in vivo vascular material properties from $PWV$ [25,26,47], the effective mechanical estimation is still bounded to the coupling of image-based information with invasive pressure data, thus limiting their practical usage.

Among MRI-based methods, an indirect measurement technique of local $PWV$, namely the $QA$ method, was proposed by Vulliémoz et al. [35], based on the acquisition of a single-slice bi-dimensional phase contrast MRI. The main advantage of the $QA$ method is the estimation of $PWV$ without requiring any invasive pressure measurements. Hence, Equation (1) can provide reliable local information on vessel stiffness by considering variation in the flow with respect to the lumen deformation, measured from phase contrast image data.

However, $PWV$ is a measure of velocity, describing the speed at which the systolic pulse propagates along a specific segment of the vessel. This makes the $PWV$ unsuitable to describe a proper material parameter such as the Young’s modulus in an isotropic linear elastic model.

For this reason, an alternative strategy was initially attempted exploiting the available formulation using the $PWV$ and other geometric parameters to infer the module E (Equation (5)). However, this expression was found to be related to the stiffness wall but was still not fully descriptive of its proper Young’s modulus, as demonstrated in the preliminary work available at [33].

In particular, the inclusion of a specific corrective factor, namely $\chi$, is crucial to enhance the formula capability of estimating a reliable local E value of a vessel wall, referred to a specific vessel cross-section.

The $\chi$ factor was assumed to be a function of the relative area change $RAC$ and a parameter, $\gamma$. First, the $RAC$ value included in the formula additional information about the dynamic variation of the area along the cardiac cycle, which is otherwise not present in the standard Equation (5). Second, the $\gamma$ parameter was the unknown variable, whose preliminary definition was given by assuming a dependence on the dimensions of the vessel lumen in diastole ($A^d$), the peak of the flow passing trough the section ($Q^p$) and the inner pressure range (P).

The problem was solved in two main scenarios, considering the pressure ranges of the two main large vessels, i.e., the aorta and the pulmonary artery. The $\gamma$ function was then defined according to these two pressure conditions (Equation (10)).

Following the initial hypotheses, a massive in silico campaign was carried out by varying in simplified FSI vessel models the caliber ($A^d$) and the maximum of the inflow boundary condition ($Q^p$), at each pressure condition ($P_{Ao}$ and $P_{PA}$), according to Figure 2. Moreover, for each model characterized by a cross-sectional area $A^d$, an inlet flow condition with a maximum at $Q^p$ and a specific outflow pressure ($P_{Ao}$ or $P_{PA}$), five different stiffness values were assigned to the vessel wall ($E^w$), as listed in Table 1.

The huge amount of simulations were managed using a custom Python pipeline, programmed to automatically handle the entire workflow, composed of simple but time-consuming steps.

The first of the main results was the definition of the two $\gamma$ functions, one for the $P_{Ao}$ condition and the other for the $P_{PA}$ condition. Generally, this two-variable function was found to increase with vessel dimensions and to decrease with flow rate (Figure 7). Although ${\gamma |}_{Ao}$ and ${\gamma |}_{PA}$ resulted in different ranges, as expected, their ratio was quite constant, with some significant peaks in regions related to unrealistic vascular conditions. Hence, the complete Equation (8), inclusive of the corrective factor including the $\gamma$ function, was tested on “virtual” image data extracted by specific FSI models.

In the computational cases, the increased effectiveness of the Equation (8), with respect to the standard Equation (5), in the prediction of the E value was amply demonstrated. The application of the $\chi$-method on the simulated image data resulted in an average divergence from the reference E values of 9.3%. However, an error of 89.6% was found from the adoption of the original formulation with no correction factor (Equation (5)). These first tests provided strong evidence of the necessity of modifying the standard $PWV$-based method to obtain a reliable estimate of the E value of the vessel wall, remarkably achieved by Equation (8).

A proper transition from the $PWV$ information to a completely reliable E estimation of the vessel wall is still some way away, requiring further investigation. Additional simulations could be conducted to either increment the amount of $\gamma$ points for the interpolation or increase the number of variables. Second, numerical models can be further exploited to produce knowledge and to highlight strategies to increase the value of the method outcomes.

In addition, the effect of uncertainties plays an important role in this context, and the implementation of stochastic analyses is crucial to assess the limitations present in the methodology. Among the image-related uncertainties, the wall thickness value, which is required to determine the $WCSA$ (Equation (4)) as part of the $\chi$-method, is challenging to detect from imaging, due to low image resolution and a partial volume effect. In this regard, uncertainty quantification techniques [12,16] represent a valuable strategy to quantify the effect of the thickness error on the final outcome.

To provide a reliable image-based technique, in vitro models will be developed for validation purposes, using 3D-printing techniques for the fabrication of different vascular models with different deformable materials, whose mechanical properties, assessed via tensile tests, represent the ground truth. These experiments would allow the testing of the $\chi$-method workflow in several conditions, using different phantom shapes and materials, under reliable and reproducible physiological and/or pathological conditions during the MRI acquisition phase. Doppler ultrasound represents another valuable image technique which is worth investigating, providing information on flow and vessel deformation along the cardiac cycle [48].

Such studies in the future would enhance the confidence of the predictive results provided by the proposed image-based methodology, thus favoring its application for the acquisition of in vivo patient-specific imaging data, as routinely acquired in clinics.

With respect to limitations of the study, the method presented in this study was calibrated to provide an estimation of the Young’s modulus, modeling the vessel wall as an isotropic linear elastic material, thus neglecting the established hyperelastic and anisotropic properties of vascular tissues [18,49,50]. The E value computed from the $\chi$-method is referred not only to a specific section of the vessel, providing local information on the wall stiffness, but also to the environment surrounding the vessel of interest, i.e., other vascular structures and anatomical constraints. Hence, despite considering the simplest mechanical model, the extracted E value is comprehensive of the particular and overall context in which the patient-specific vessel occurs. The possibility of estimating, in a non-invasive and direct way, the elastic properties of a vessel in its in vivo environment would represent crucial information for patient-specific numerical modeling. The results from simulations of cardiovascular interventions would benefit from the implementation of a more reliable mechanical interaction between the implanted device and the patient-specific implantation site, which would correspond to the overall in vivo scenario of the patient’s vessel of interest.

The long-term objectives of the research will include evolution from the isotropic linear elastic material to more complex models, since the workflow presented here was based on an iterative definition of unknown parameters from a series of numerical simulations. These can be applied for the extrapolation of additional mechanical parameters, taking into account the viscoelastic, hyperelastic and anisotropic features typical of vessels, in order, in the future, to provide as accurate as possible a depiction of the in vivo patient-specific mechanical properties of vascular structures in their biological environment.

Succeeding in developing a fully reliable image-based framework able to characterize the mechanical behaviour of a patient-specific vessel, directly and non-invasively, will help enhance both device design and clinical decisions towards personalised care solutions using new modelling environments for predictive, individualised healthcare to guarantee better patient safety and enhanced efficacy.