Artificial Intelligence-Based Multimodal Medical Image Fusion Using Hybrid S2 Optimal CNN
Abstract
:1. Introduction
2. Review of Biomedical Imaging Process
3. Proposed Methodology
3.1. Shearlet Transform
3.2. Modified Discrete Wavelet Transform
- Obtain the original source image as well as the secret image and then obtain the red (R) plane distinctly and establish the single level 2-DDaubechies DWT decomposition on the input source image and the secret image.
- Let us assume the embedding coefficient is represented as , then the embedding coefficient value is extended from 0 to 1, the coefficient of , and there is a huge rise in robustness and a small rise in transparency.
- The approximation coefficient is established by utilizing the expression of the horizontal coefficient, diagonal coefficient, and vertical coefficient. The approximation coefficient of the inserted image approximation coefficient of the input image approximation coefficient of the secret image. In addition, asimilar expression is utilized to compute the diagonal coefficient, horizontal coefficient, and vertical coefficient of the inserted image.
- Establish the single level 2-D Daubechies inverse DWT decomposition on the computed horizontal, diagonal, approximation, and vertical coefficients to obtain the horizontal, diagonal, approximation, and vertical coefficients of the R plane of the integrated image.
- The above declared scheme is completed for the blue (B) plane and green (G) plane disjointedly and integrates the blue (B), green (G) and red (R) plane to achieve the integrated image.
3.3. CNN-HOD-Based Image Fusion Process
3.3.1. Convolutional Neural Network (CNN)
Convolutional Layer
Pooling Layer
SoftMax Layer
3.4. Hybrid Optimization Dynamic (HOD) Algorithm
3.4.1. Sailfish Optimizer Algorithm
Initialization
Migration
Collision Avoidance
Moving towards the Direction of the Optimum Seagull
Sustaining Close to the Shortest Distance to the Optimal Search Agent
Attack-Interchange Scheme
Hunting as Well as Catching Prey
4. Results and Discussions
4.1. Performance Measures
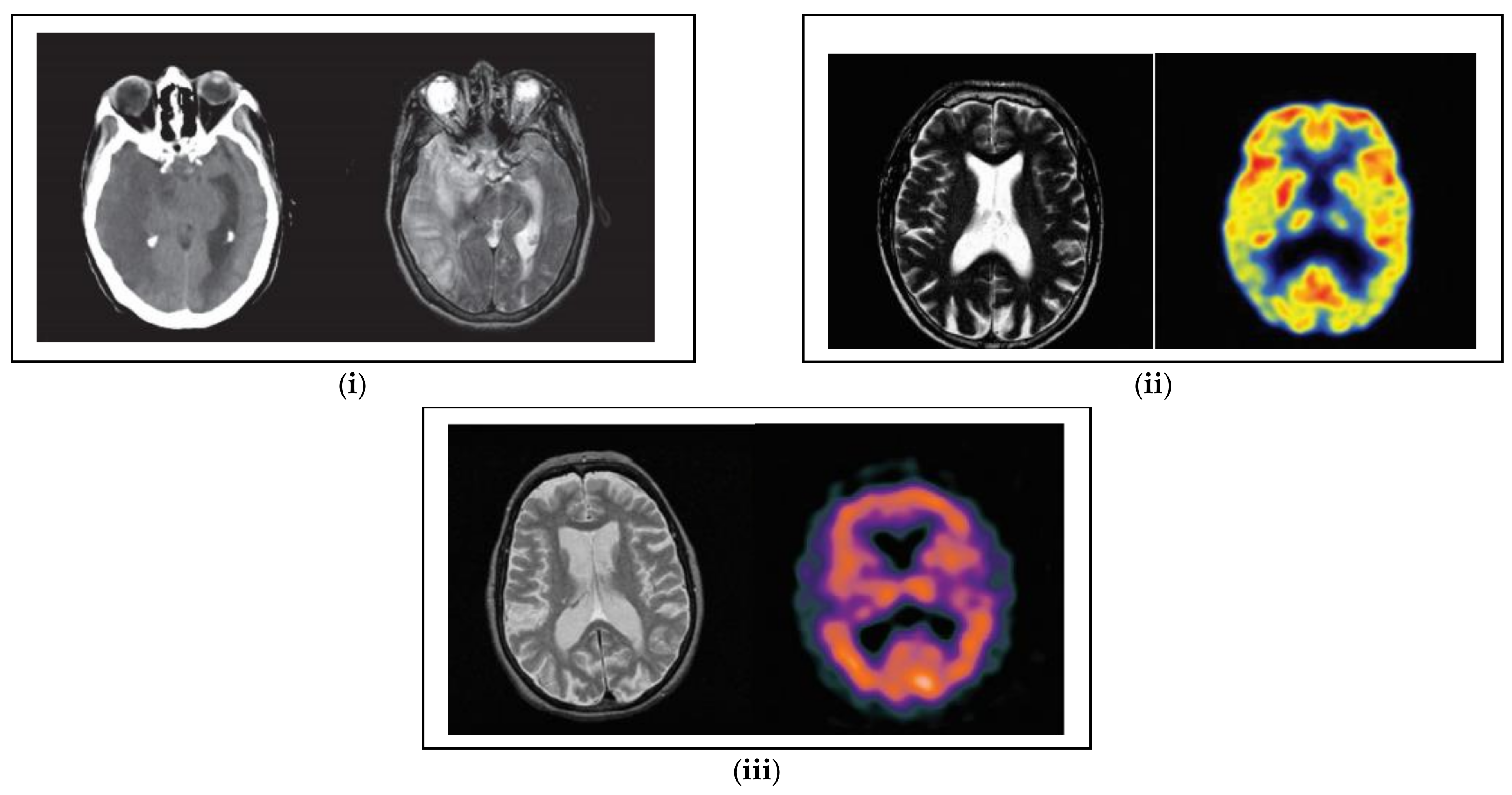
4.2. Quantitative Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Tawfik, N.; Elnemr, H.A.; Fakhr, M.; Dessouky, M.I.; Abd El-Samie, F.E. Survey study of multimodality medical image fusion methods. Multimed. Tools Appl. 2021, 80, 6369–6396. [Google Scholar] [CrossRef]
- Kumar, P.; Diwakar, M. A novel approach for multimodality medical image fusion over secure environment. Trans. Emerg. Telecommun. Technol. 2021, 32, e3985. [Google Scholar] [CrossRef]
- Tang, L.; Tian, C.; Li, L.; Hu, B.; Yu, W.; Xu, K. Perceptual quality assessment for multimodal medical image fusion. Signal Process. Image Commun. 2020, 85, 115852. [Google Scholar] [CrossRef]
- Li, W.; Lin, Q.; Wang, K.; Cai, K. Improving medical image fusion method using fuzzy entropy and non-subsampling contourlet transform. Int. J. Imaging Syst. Technol. 2021, 31, 204–214. [Google Scholar] [CrossRef]
- Ullah, H.; Ullah, B.; Wu, L.; Abdalla, F.Y.; Ren, G.; Zhao, Y. Multimodality medical images fusion based on local-features fuzzy sets and novel sum-modified-Laplacian in non-subsampled shearlet transform domain. Biomed. Signal Process. Control 2020, 57, 101724. [Google Scholar] [CrossRef]
- Fu, J.; Li, W.; Du, J.; Xiao, B. Multimodal medical image fusion via laplacian pyramid and convolutional neural network reconstruction with local gradient energy strategy. Comput. Biol. Med. 2020, 126, 104048. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Zhao, J. A novel multi-modal medical image fusion algorithm. J. Ambient Intell. Humaniz. Comput. 2021, 12, 1995–2002. [Google Scholar] [CrossRef]
- Singh, S.; Gupta, D. Multistage multimodal medical image fusion model using feature-adaptive pulse coupled neural network. Int. J. Imaging Syst. Technol. 2020, 31, 981–1001. [Google Scholar] [CrossRef]
- Huang, B.; Yang, F.; Yin, M.; Mo, X.; Zhong, C. A review of multimodal medical image fusion techniques. Comput. Math. Methods Med. 2020, 2020, 8279342. [Google Scholar] [CrossRef] [Green Version]
- Tirupal, T.; Mohan, B.C.; Kumar, S.S. Multimodal medical image fusion techniques—A review. Curr. Signal Transduct. Ther. 2020, 15, 142–163. [Google Scholar] [CrossRef]
- Yadav, S.P.; Yadav, S. Image fusion using hybrid methods in multimodality medical images. Med. Biol. Eng. Comput. 2020, 58, 669–687. [Google Scholar] [CrossRef]
- Subbiah Parvathy, V.; Pothiraj, S.; Sampson, J. A novel approach in multimodality medical image fusion using optimal shearlet and deep learning. Int. J. Imaging Syst. Technol. 2020, 30, 847–859. [Google Scholar] [CrossRef]
- Wang, K.; Zheng, M.; Wei, H.; Qi, G.; Li, Y. Multi-modality medical image fusion using convolutional neural network and contrast pyramid. Sensors 2020, 20, 2169. [Google Scholar] [CrossRef] [Green Version]
- Parvathy, V.S.; Pothiraj, S.; Sampson, J. Optimal Deep Neural Network model-based multimodality fused medical image classification. Phys. Commun. 2020, 41, 101119. [Google Scholar] [CrossRef]
- Tan, W.; Tiwari, P.; Pandey, H.M.; Moreira, C.; Jaiswal, A.K. Multimodal medical image fusion algorithm in the era of big data. Neural Comput. Appl. 2020, 1–21. [Google Scholar] [CrossRef]
- Li, X.; Guo, X.; Han, P.; Wang, X.; Li, H.; Luo, T. Laplacian redecomposition for multimodal medical image fusion. IEEE Trans. Instrum. Meas. 2020, 69, 6880–6890. [Google Scholar] [CrossRef]
- Arif, M.; Wang, G. Fast curvelet transform through genetic algorithm for multimodal medical image fusion. Soft Comput. 2020, 24, 1815–1836. [Google Scholar] [CrossRef]
- Kaur, M.; Singh, D. Multi-modality medical image fusion technique using multi-objective differential evolution based deep neural networks. J. Ambient. Intell. Humaniz. Comput. 2021, 12, 2483–2493. [Google Scholar] [CrossRef]
- Hu, Q.; Hu, S.; Zhang, F. Multi-modality medical image fusion based on separable dictionary learning and Gabor filtering. Signal Process. Image Commun. 2020, 83, 115758. [Google Scholar] [CrossRef]
- Xia, J.; Lu, Y.; Tan, L. Research of multimodal medical image fusion based on parameter-adaptive pulse-coupled neural network and convolutional sparse representation. Comput. Math. Methods Med. 2020, 2020, 3290136. [Google Scholar] [CrossRef]
- Shehanaz, S.; Daniel, E.; Guntur, S.R.; Satrasupalli, S. Optimum weighted multimodal medical image fusion using particle swarm optimization. Optik 2021, 231, 166413. [Google Scholar] [CrossRef]
- Dinh, P.H. Multi-modal medical image fusion based on equilibrium optimizer algorithm and local energy functions. Appl. Intell. 2021, 51, 8416–8431. [Google Scholar] [CrossRef]
- Dinh, P.H. A novel approach based on three-scale image decomposition and marine predators algorithm for multi-modal medical image fusion. Biomed. Signal Process. Control 2021, 67, 102536. [Google Scholar] [CrossRef]
- Lu, Y.; Yi, S.; Zeng, N.; Liu, Y.; Zhang, Y. Identification of rice diseases using deep convolutional neural networks. Neurocomputing 2017, 267, 378–384. [Google Scholar] [CrossRef]
- Dhiman, G.; Kumar, V. Seagull optimization algorithm: Theory and its applications for large-scale industrial engineering problems. Knowl.-Based Syst. 2019, 165, 169–196. [Google Scholar] [CrossRef]






| Authors | Fusion Schemes | Modality | Datasets | Metrics | Cons |
|---|---|---|---|---|---|
| Yadav et al. [11] | Hybrid DWT-PCA | MRI, PET, SPECT, CT | Online repository datasets | EN, SD, RMSE, and PSNR | Low image quality, performance was not consistent so low efficiency |
| Subbiah et al. [12] | EMBO-DST with RBM model | MRI, PET, SPECT, CT | Four sets of database images (represented as D1, D2, D3, and D4) | SD, EQ, MI, FF, EN, CF and SF | Implementation was complex |
| Wang et al. [13] | CNN | MRI, CT, MRI, T1, T2, PET, and SPECT | Online eight fused images | TE, AB/F, MI, and VIF | Difficult to fuse infrared-visible and multi-focus image fusion. |
| Parvathy et al. [14] | DNN with DGSA | CT, SPECT, and MRI | Four datasets (I, II, III and IV) | Fusion factor and spatial frequency | Failed to execute in real-time applications |
| Tan et al. [15] | PCNN-NSST | MRI, PET, and SPECT | 100 pairs of multimodal medical images from the Whole Brain Atlas dataset | Entropy (EN), standard deviation (SD), normalized mutual information (NMI), Piella’s structure similarity (SS), and visual information fidelity (VIF) | Fused image quality was poor |
| Li et al. [16] | Laplacian re-decomposition method (LRD) | MRI, PET, and SPECT | 20 pairs of multimodal medical images collected from Harvard University medical library | Standard deviation (STD), mutual information (MI), universal quality index (UQI), and tone-mapped image quality index (TMQI) | Difficult to propose more rapid and active methods of medical image enhancement and fusion |
| Kaur et al. [18] | NSCT | MRI, CT | Multi-modality biomedical images dataset is obtained from Ullah et al. (2020) [5] | Fusion factor, fusion symmetry, mutual information, edge strength | Difficult to fuse the remote sensing images |
| Hu et al. [19] | Analytic separable dictionary learning (ASeDiL) method in NSCT domain | CT and MRI | 127 groups of brain anatomical images from the Whole Brain Atlas medical image database | Piella–Heijmans’ similarity based metric QE, spatial frequency (SF), universal image quality index (UIQI), and mutual information | Time consumption was more |
| Xia et al. [20] | Parameter-adaptive pulse-coupled neural network (PAPCNN) method | CT, MRI, T1, T2, PET, and SPECT | Database from the Whole Brain Atlas of Harvard Medical School [13] and the Cancer Imaging Archive (TCIA) | Entropy (EN), edge information retention (QAB/F), mutual information (MI), average gradient (AG), space frequency (SF), and standard deviation (SD) | Implementation was complex |
| Shehanaz et al. [21] | Optimum weighted average fusion (OWAF) with particle swarm algorithm (PSO) | MR-CT, MR-SPECT, and MR-PET | Brain images (http://www.med.harvard.edu/AANLIB/) accessed on 18 January 2022 | Standard deviation (STD), mutual information (MI), universal quality index (UQI), | Required more computational time to perform the task |
| Dinh et al. [22] | SLE-PCO with EOA | MRI-PET medical images | http://www.med.harvard.edu/AANLIB/ accessed on 18 January 2022 | SD, EQ, MI, FF, EN, CF, and SF | Computational complexity was high |
| Dinh et al. [23] | FRKCO and MPA | MRI-PET medical images | http://www.med.harvard.edu/AANLIB/ accessed on 18 January 2022 | Standard deviation (STD), mutual information (MI), universal quality index (UQI), and tone-mapped image quality index (TMQI) | Information entropy was low |
| Techniques | Parameters | Ranges |
|---|---|---|
| Convolutional neural network | Kernel size | |
| Learning rate | 0.001 | |
| Batch size | 32 | |
| Optimizer | Adam | |
| Dropout rate | 0.5 | |
| Sailfish optimization algorithm | Initial population | 30 |
| Total iteration | 100 | |
| Fluctuation range | −1 and 1 | |
| Random number | 0 and 1 | |
| Seagull optimization algorithm | Population size | 100 |
| Maximum iterations | 200 | |
| Control parameter | [2, 0] | |
| Frequency control parameter | 2 |
| Measures | PCNN-NSST | DNN-DGSA | EMBO-DST | NSST-PAPCNN | Proposed |
|---|---|---|---|---|---|
| QAB/F | 0.2082 | 0.2284 | 0.2653 | 0.3645 | 0.4672 |
| AG | 6.3128 | 6.6754 | 6.9816 | 7.6542 | 7.8914 |
| SD | 47.2761 | 48.1692 | 50.7616 | 51.6723 | 54.6870 |
| MI | 2.6892 | 2.7654 | 2.8974 | 3.1678 | 3.4152 |
| EN | 4.4264 | 4.5298 | 4.6784 | 4.8532 | 4.9952 |
| SF | 19.9757 | 20.7865 | 21.6738 | 23.8761 | 24.7622 |
| FF | 5.9824 | 6.0935 | 6.1382 | 6.5665 | 8.3281 |
| Measures | PCNN-NSST | DNN-DGSA | EMBO-DST | NSST-PAPCNN | Proposed |
|---|---|---|---|---|---|
| QAB/F | 0.3186 | 0.3484 | 0.3941 | 0.4457 | 0.5392 |
| AG | 6.1326 | 6.8331 | 7.9814 | 8.0642 | 8.4631 |
| SD | 46.1488 | 49.9126 | 51.8674 | 53.5648 | 55.4872 |
| MI | 2.9827 | 3.2673 | 3.8915 | 4.2186 | 4.6524 |
| EN | 4.5148 | 4.7528 | 4.9921 | 5.0885 | 5.1872 |
| SF | 22.8907 | 25.8733 | 28.9154 | 30.7372 | 32.8245 |
| FF | 6.1429 | 6.4634 | 6.8736 | 7.1984 | 7.3562 |
| Measures | PCNN-NSST | DNN-DGSA | EMBO-DST | NSST-PAPCNN | Proposed |
|---|---|---|---|---|---|
| QAB/F | 0.4177 | 0.4575 | 0.5884 | 0.6429 | 0.7362 |
| AG | 7.7648 | 7.9731 | 8.1583 | 8.6758 | 8.8763 |
| SD | 50.8734 | 52.7615 | 54.8324 | 56.7522 | 58.6421 |
| MI | 4.2541 | 4.4659 | 4.9826 | 5.0942 | 5.1644 |
| EN | 4.4328 | 4.6715 | 4.8259 | 5.2781 | 5.4638 |
| SF | 27.5714 | 29.8765 | 30.9816 | 32.7625 | 34.8712 |
| FF | 6.9876 | 7.6978 | 7.8573 | 8.2538 | 8.7642 |
| Methods | Average Gradient | Fusion Factor | Standard Deviation |
|---|---|---|---|
| DWT | 6.5342 | 7.0346 | 50.4563 |
| Shearlet | 7.6859 | 7.2785 | 53.098 |
| Contourlet | 7.8219 | 7.8654 | 55.5231 |
| MDWT | 8.2731 | 8.0457 | 57.4563 |
| Hybrid MDWT-Shearlet | 8.9142 | 8.8012 | 59.7314 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Almasri, M.M.; Alajlan, A.M. Artificial Intelligence-Based Multimodal Medical Image Fusion Using Hybrid S2 Optimal CNN. Electronics 2022, 11, 2124. https://doi.org/10.3390/electronics11142124
Almasri MM, Alajlan AM. Artificial Intelligence-Based Multimodal Medical Image Fusion Using Hybrid S2 Optimal CNN. Electronics. 2022; 11(14):2124. https://doi.org/10.3390/electronics11142124
Chicago/Turabian StyleAlmasri, Marwah Mohammad, and Abrar Mohammed Alajlan. 2022. "Artificial Intelligence-Based Multimodal Medical Image Fusion Using Hybrid S2 Optimal CNN" Electronics 11, no. 14: 2124. https://doi.org/10.3390/electronics11142124
APA StyleAlmasri, M. M., & Alajlan, A. M. (2022). Artificial Intelligence-Based Multimodal Medical Image Fusion Using Hybrid S2 Optimal CNN. Electronics, 11(14), 2124. https://doi.org/10.3390/electronics11142124





