Implementation of an Electronically Based Active Power Filter Associated with a Digital Controller for Harmonics Elimination and Power Factor Correction
Abstract
:1. Introduction
- -
- The development of an effective method to enhance power factor and reduce %THD;
- -
- The simulation for single-phase SAPF is achieved utilizing a MATLAB/Simulink environment;
- -
- The pre-test of the proposed design is achieved using Proteus VMS. The prototype is implemented using PCB boards;
- -
- Significant improvement in power factor is reported;
- -
- The results emphasize the importance of SAPF in eliminating harmonics and enhance power factor.
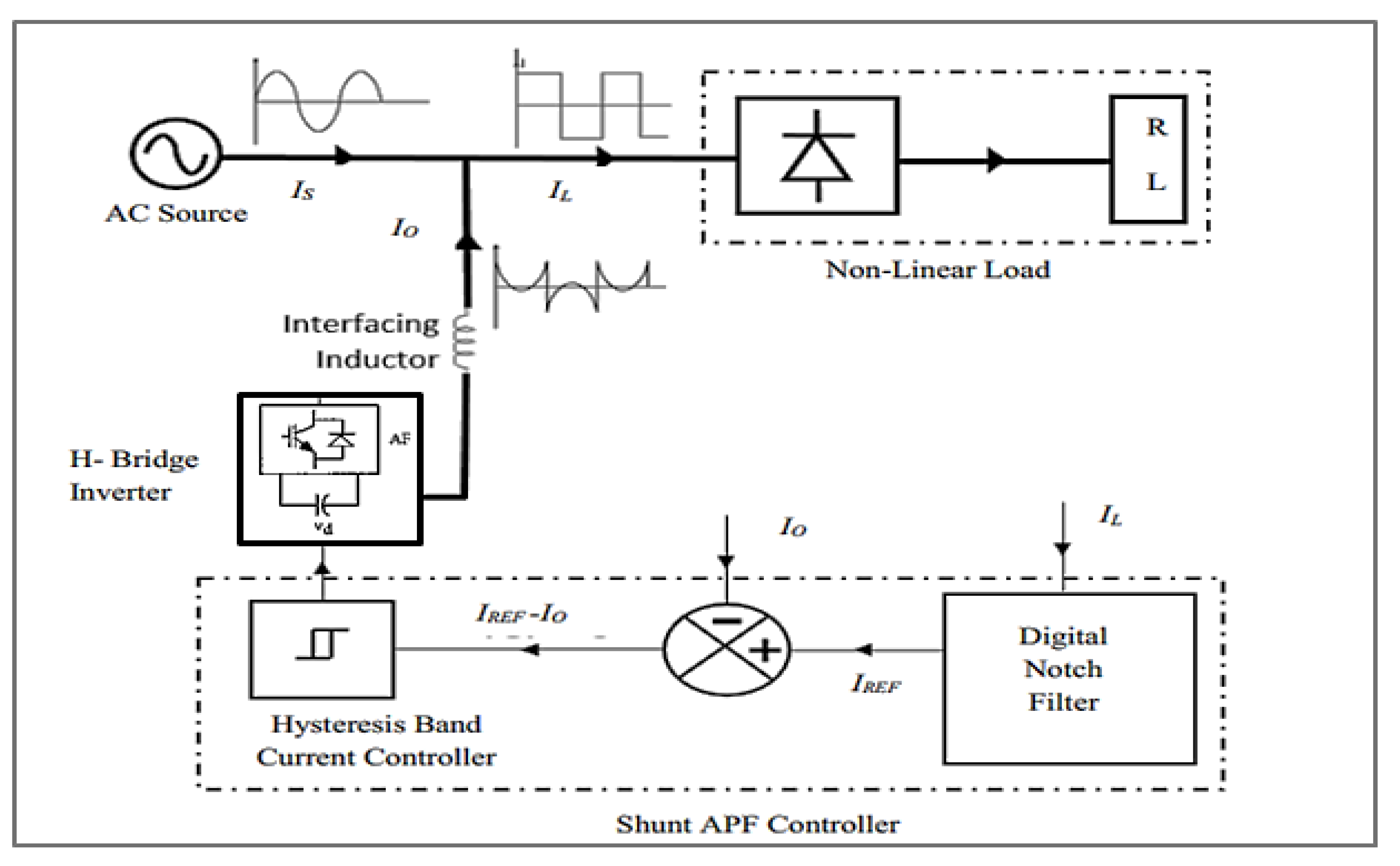
2. Description of Shunt Active Power Filter and Its Controller
2.1. Shunt Active Power Filter (SAPF)
2.2. Control Strategy for SAPF
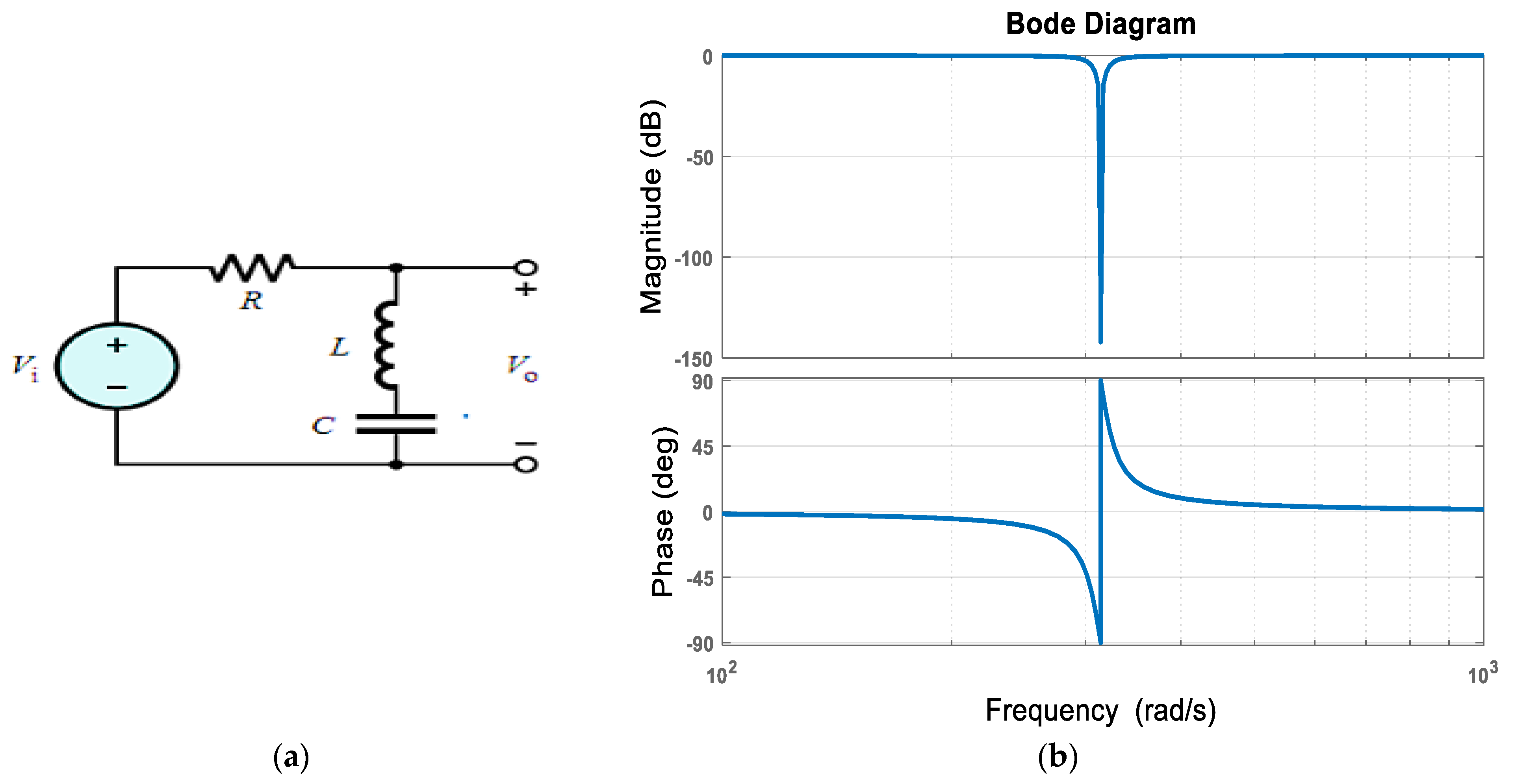
2.2.1. Extraction of Reference Current Signal Using Digital Notch Filter
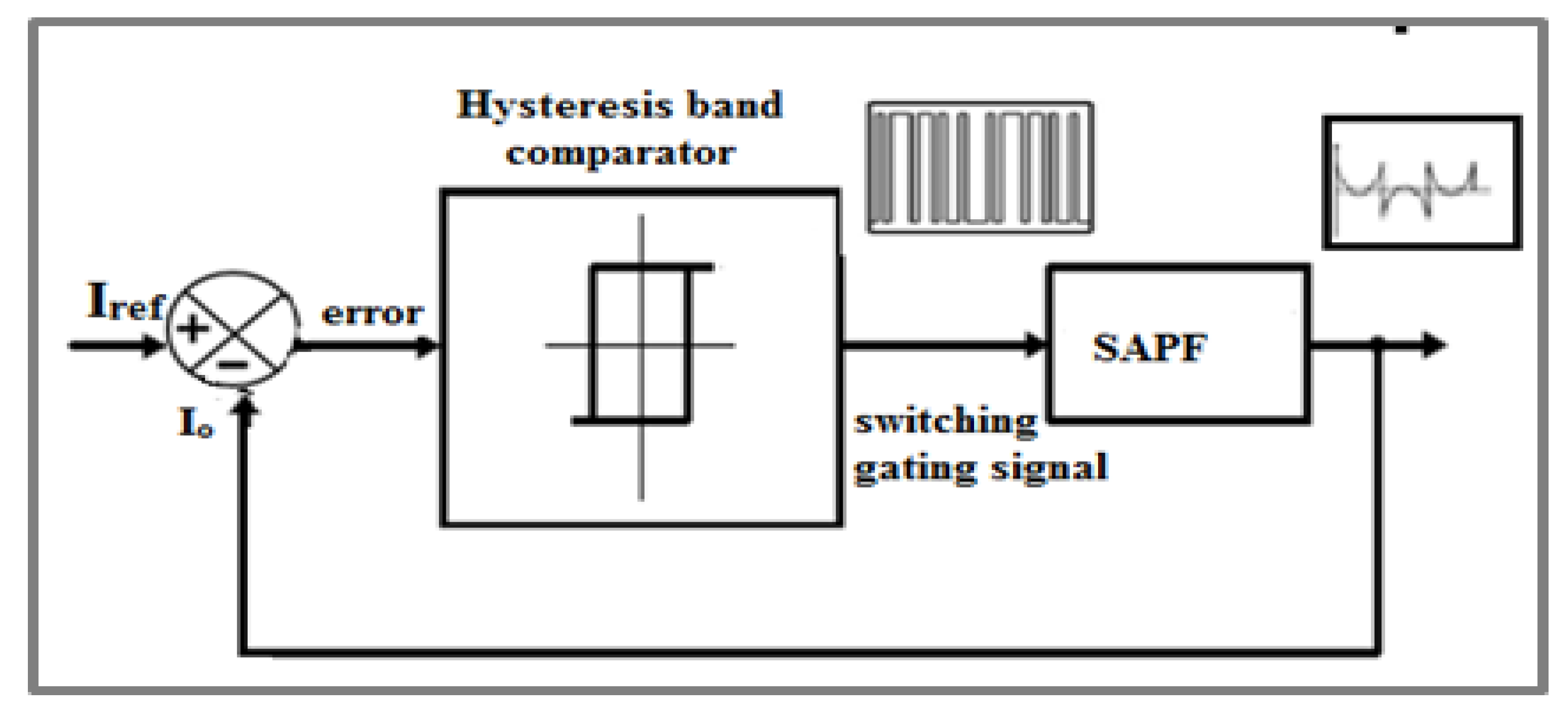
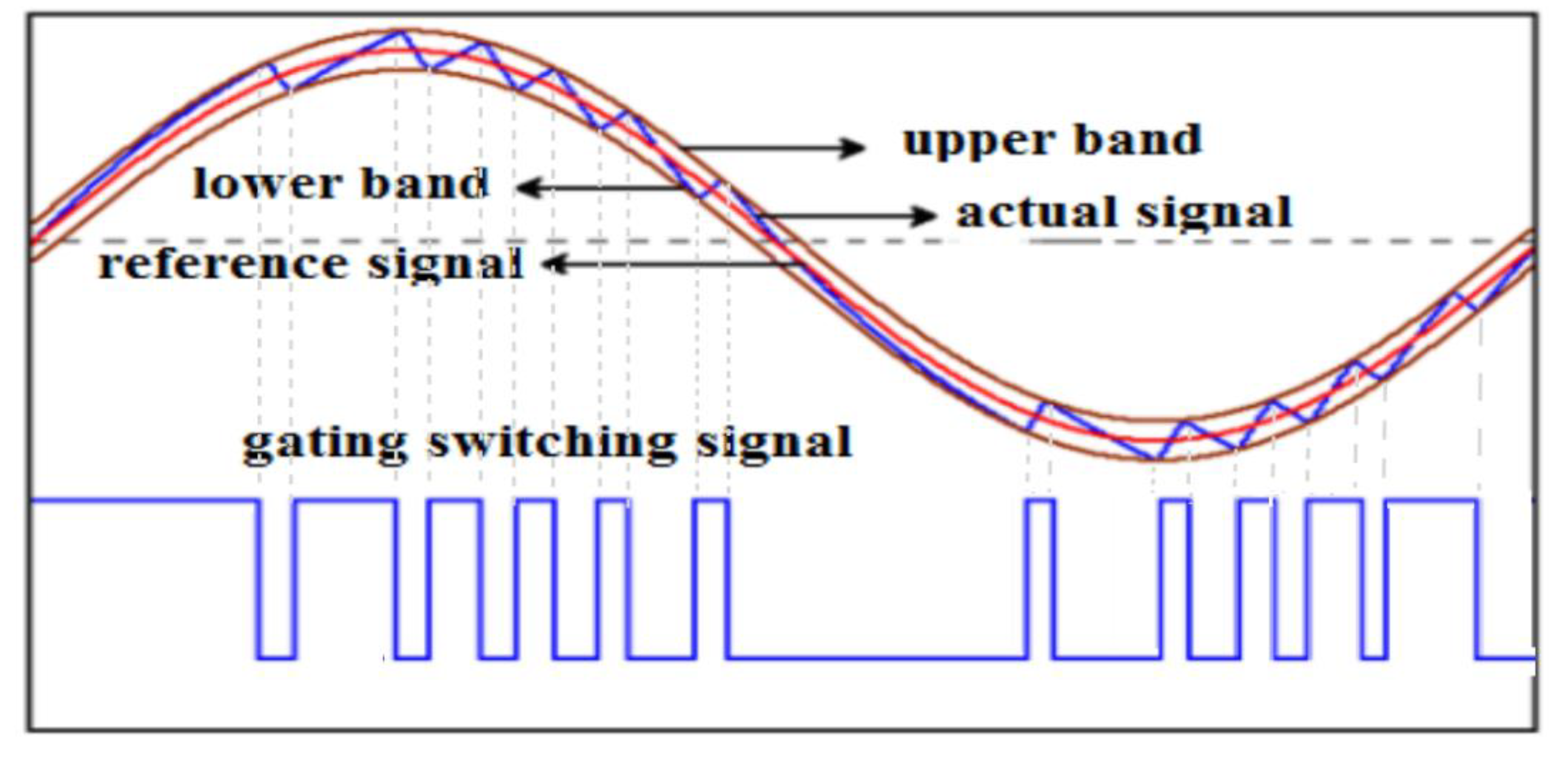
2.2.2. Hysteresis Band Current Controller
2.2.3. Voltage Source Inverter
3. Simulation and Hardware Implementation for Single-Phase SAPF
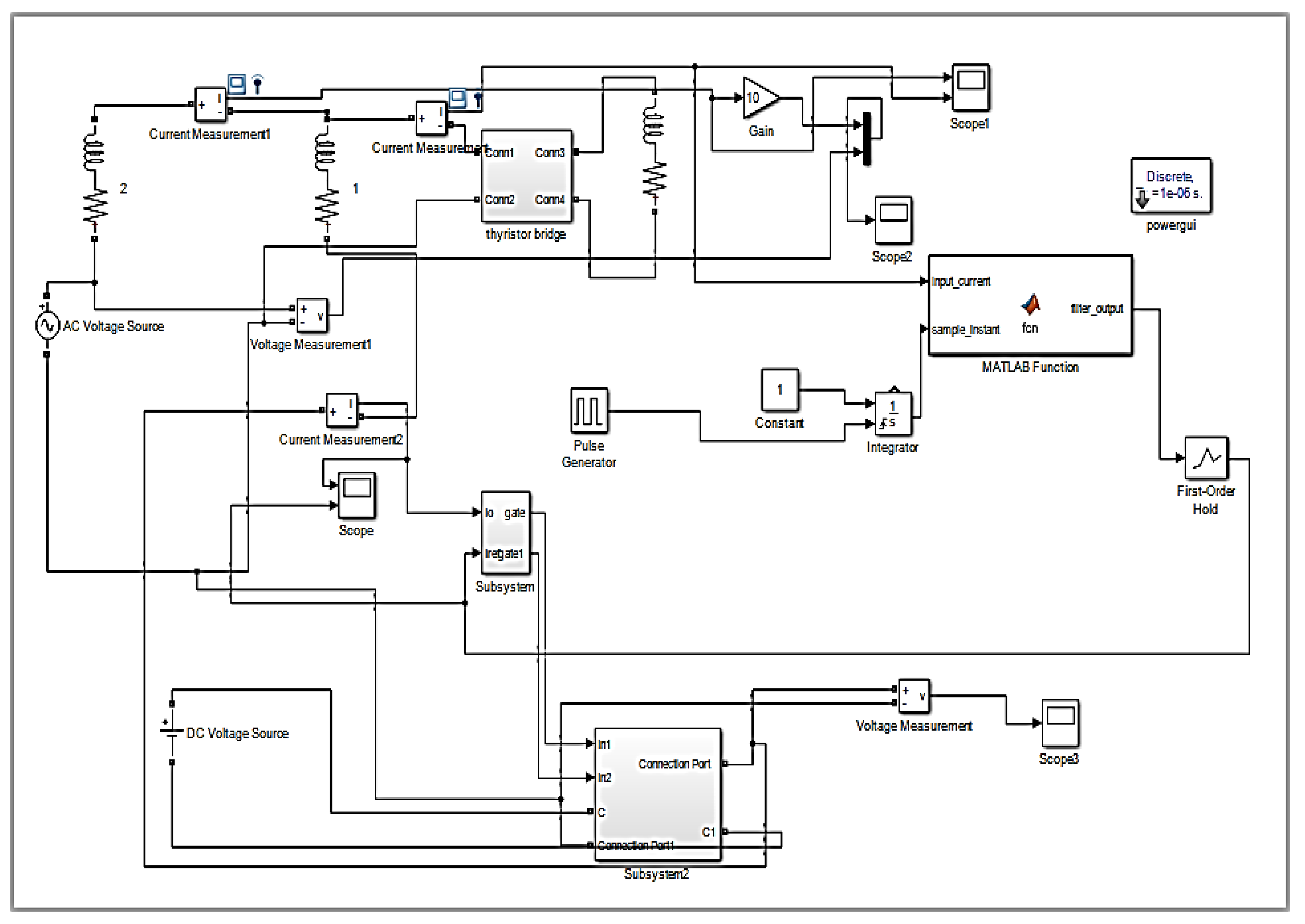
3.1. Simulation of SAPF Utilizing MATLAB/Simulink
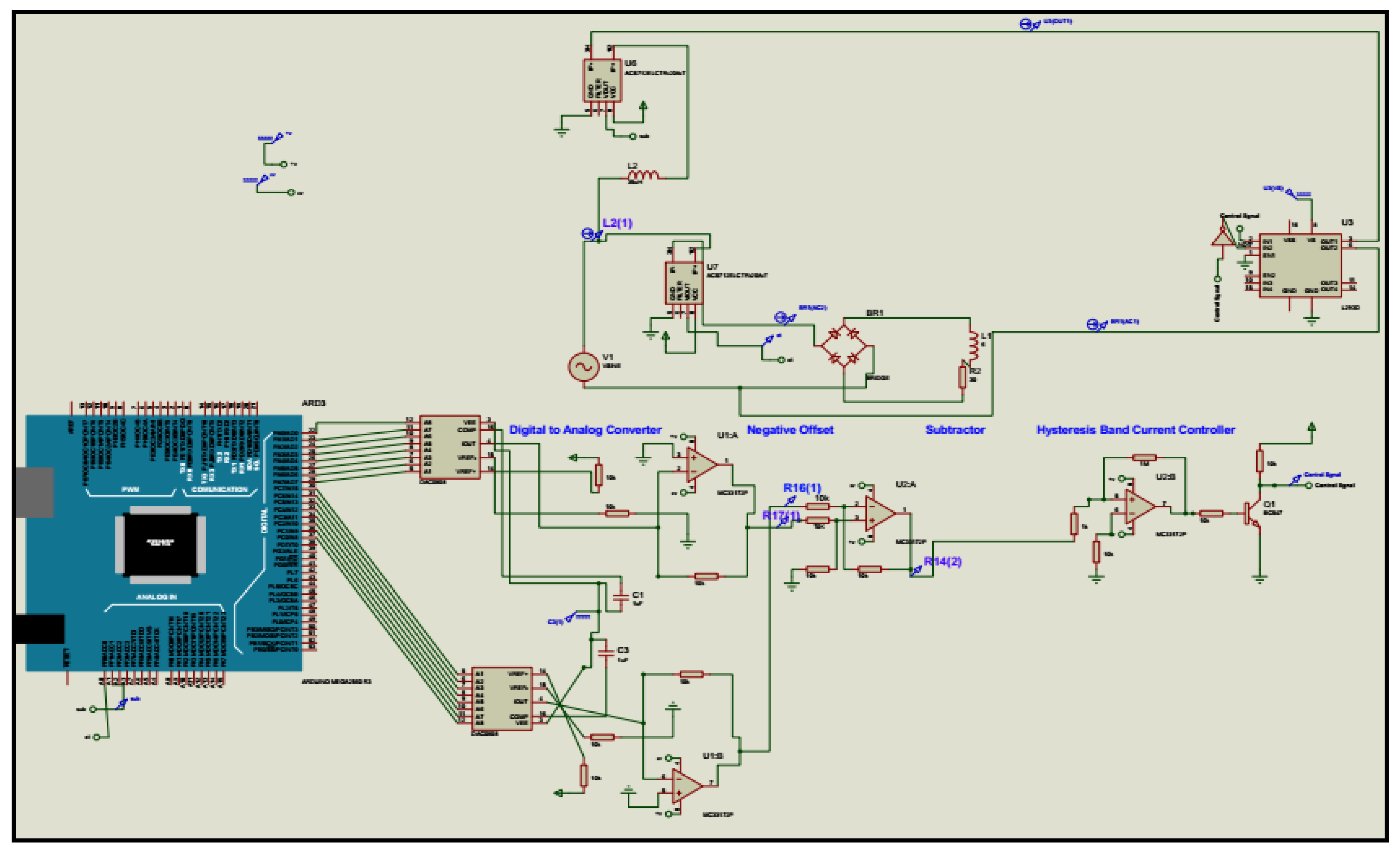
3.2. Simulation of SAPF Prototype Using Proteus Simulator
3.2.1. Nonlinear Load
3.2.2. Digital Notch Filter
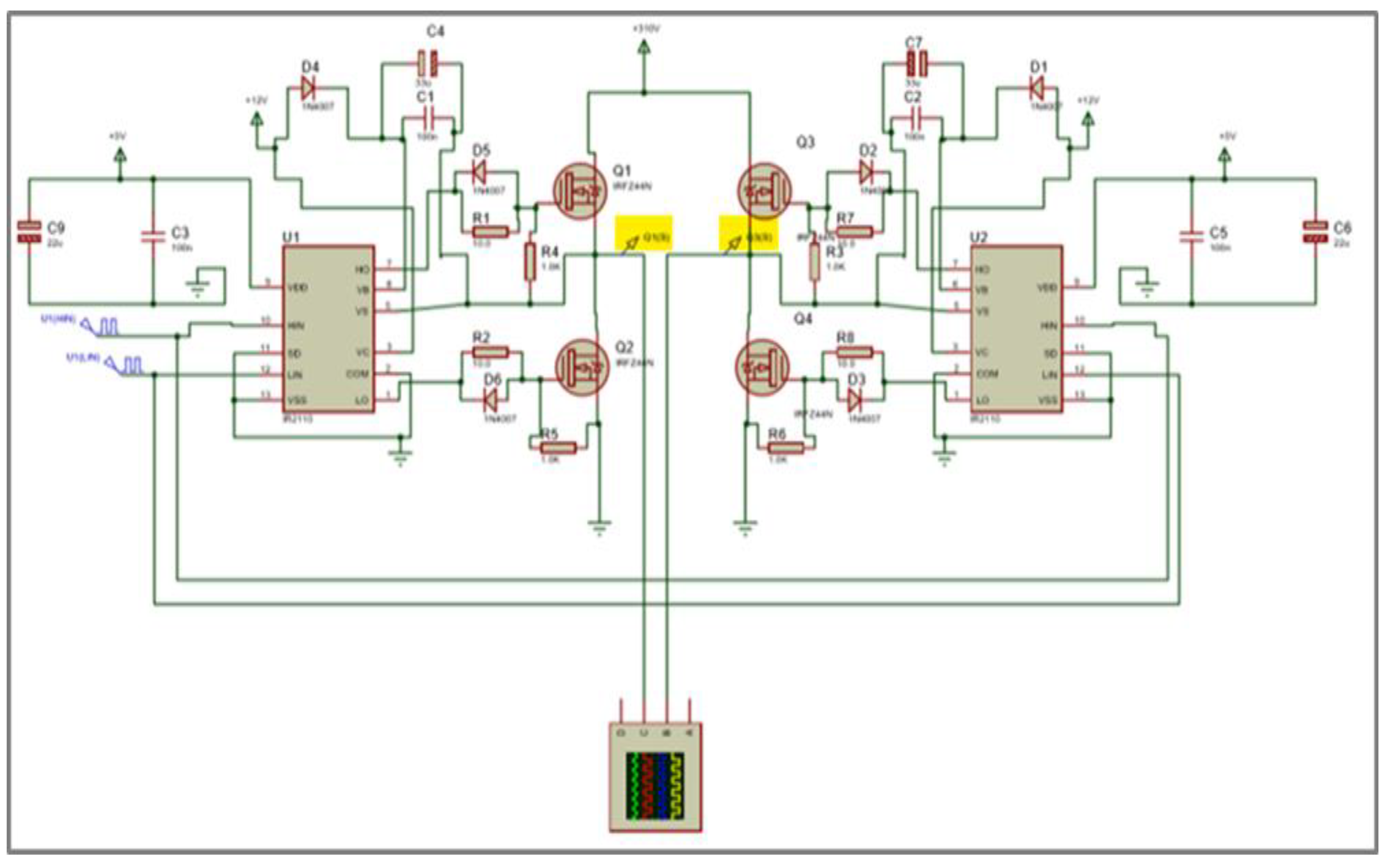
3.2.3. H-Bridge Voltage Source Inverter
3.2.4. Hysteresis Band Current Controller (Schmitt Trigger) and Overall Simulation
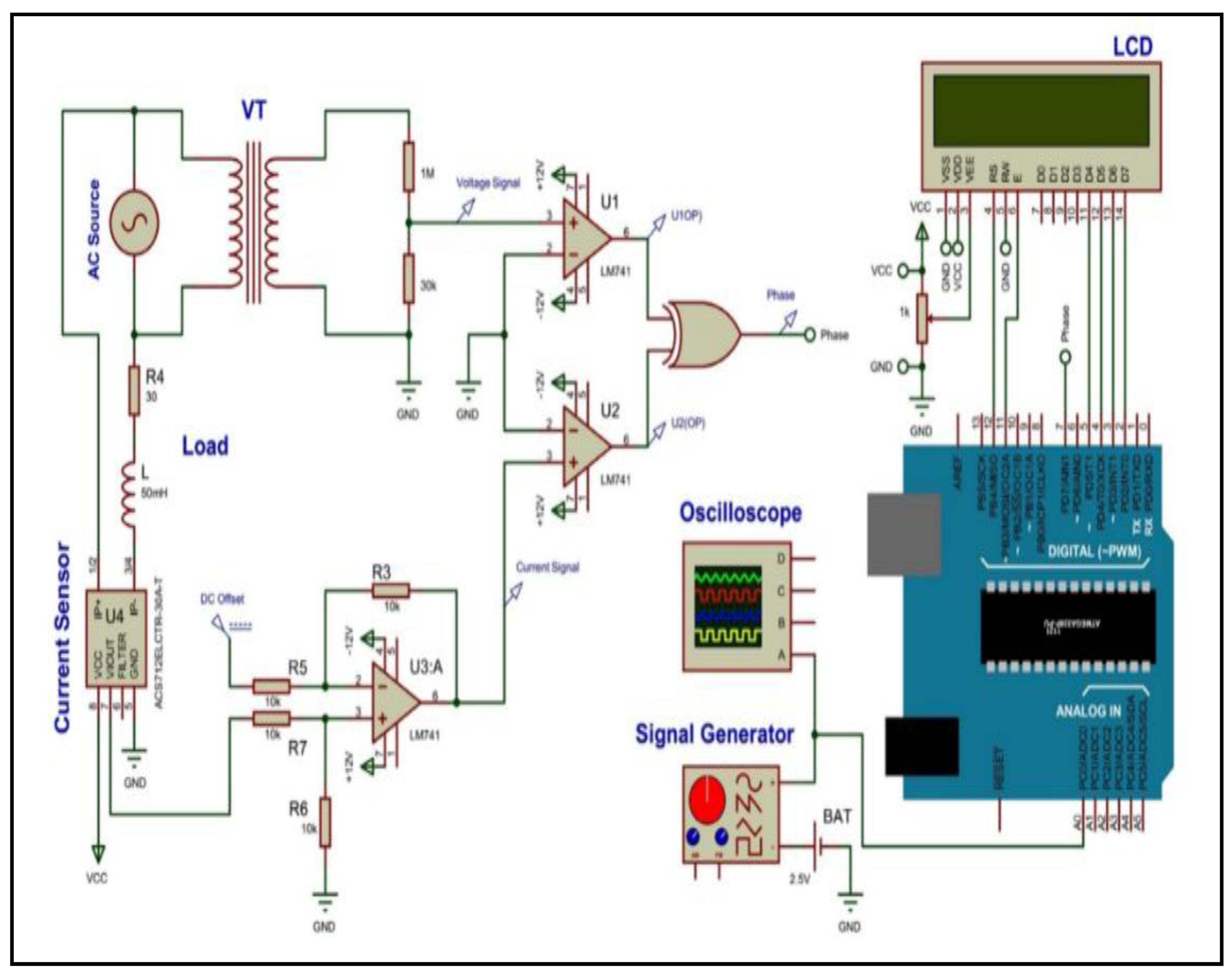
3.3. Hardware Implementation of SAPF
4. Results and Discussion
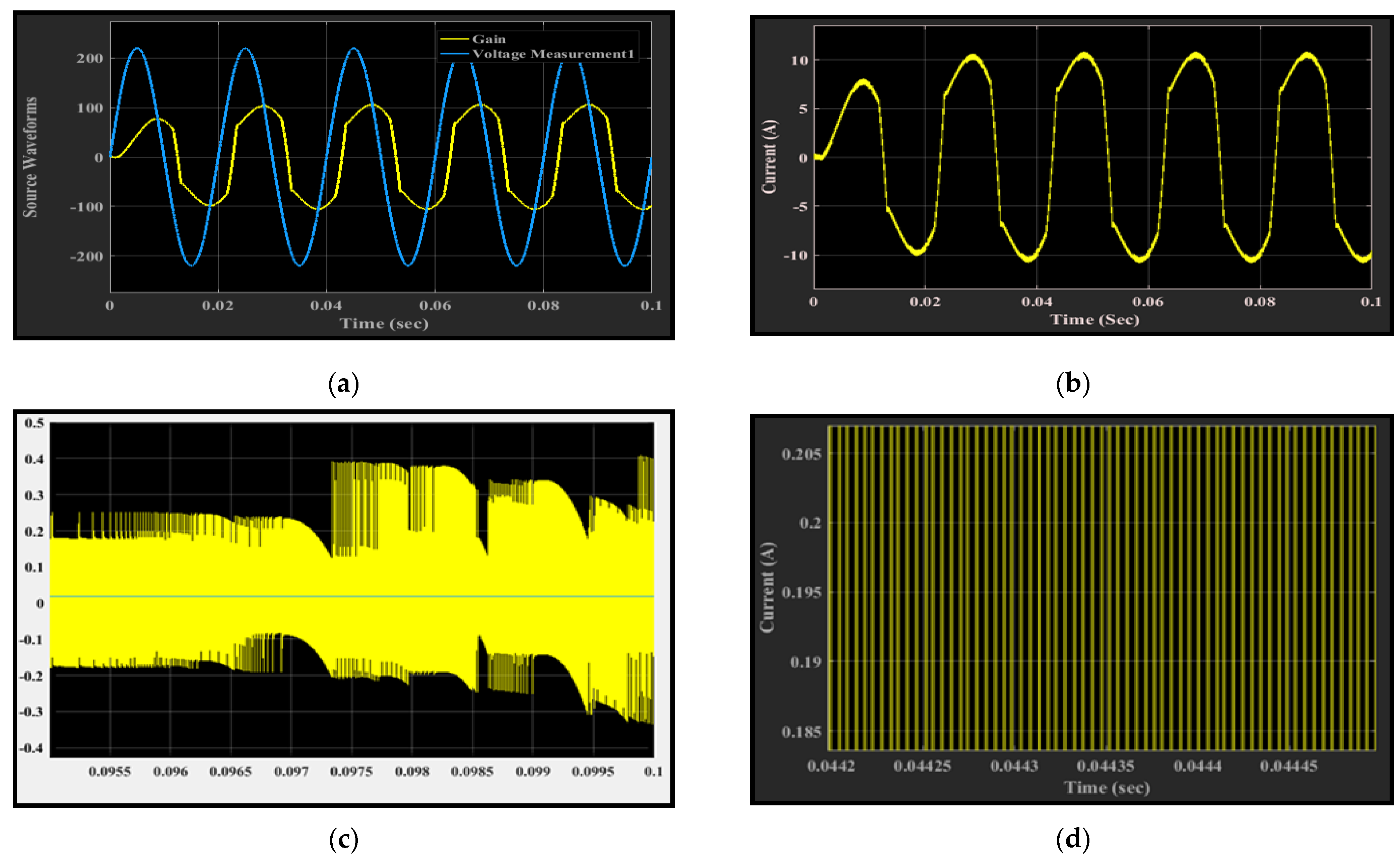
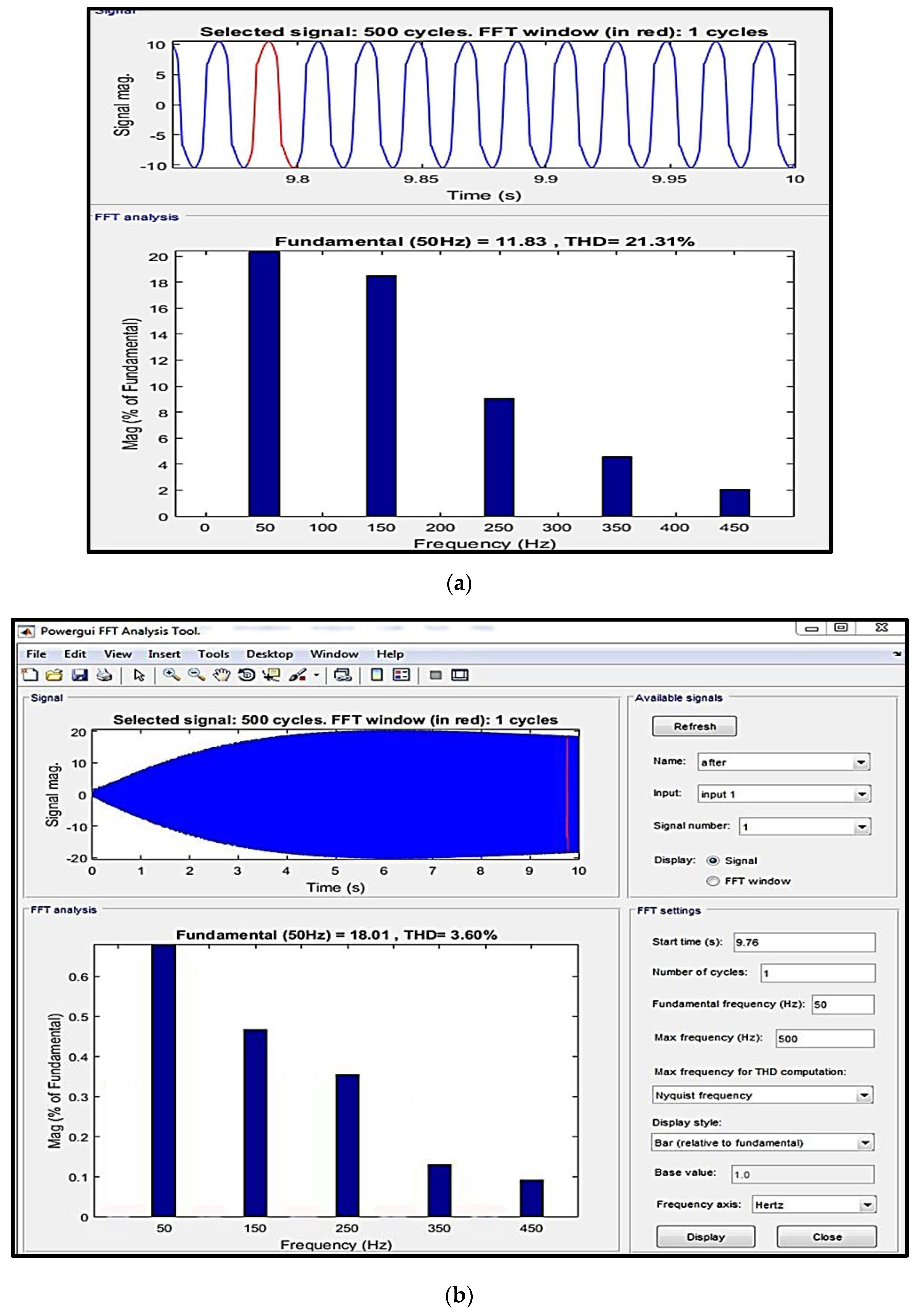
4.1. Simulation Results of SAPF Using MATLAB/Simulink
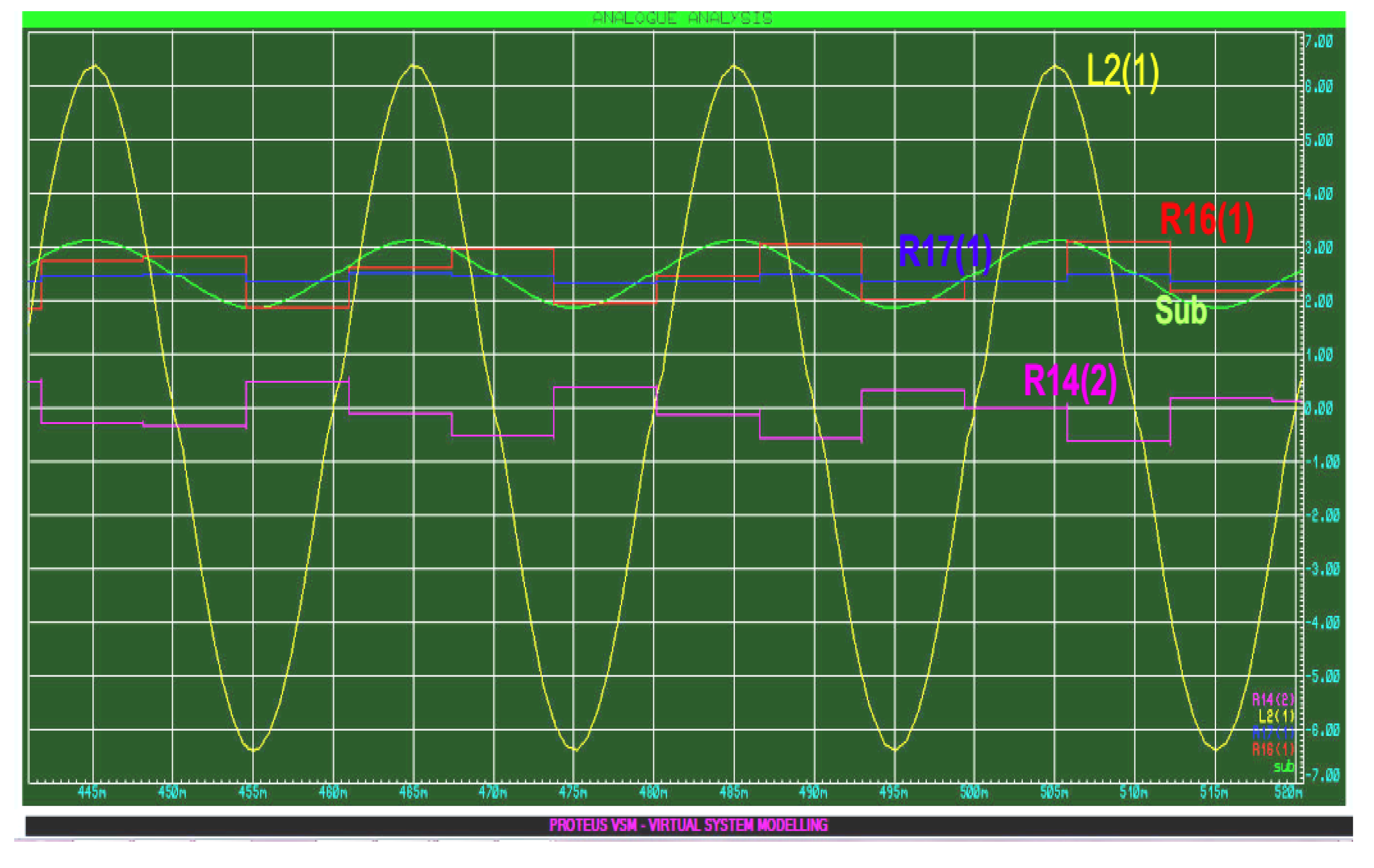
4.2. Simulation Results of SAPF Using Proteus Simulator
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Martins, A.P. The use of an active power filter for harmonic elimination and power quality improvement in a nonlinear loaded electrical installation. In Proceedings of the International Conference on Renewable Energies and Power Quality, ICREPQ, Vigo, Spain, 9–12 April 2003; Volume 3. [Google Scholar]
- Boukezata, B.; Chaoui, A.; Gaubert, J.-P.; Hachemi, M. Power Quality Improvement by an Active Power Filter in Grid-connected Photovoltaic Systems with Optimized Direct Power Control Strategy. Electr. Power Compon. Syst. 2016, 44, 2036–2047. [Google Scholar] [CrossRef]
- Rameshkumar, K.; Indragandhi, V.; Palanisamy, K.; Arunkumari, T. Model Predictive Current Control of Single Phase Shunt Active Power Filter. Energy Procedia 2017, 117, 658–665. [Google Scholar] [CrossRef]
- Das, S.; Ray, P.; Sahoo, A.; Ramasubbareddy, S.; Babu, T.; Kumar, N.; Elavarasan, R.; Mihet-Popa, L. A Comprehensive Survey on Different Control Strategies and Applications of Active Power Filters for Power Quality Improvement. Energies 2021, 14, 4589. [Google Scholar] [CrossRef]
- Rani, R.S.; Rao, C.S.; Kumar, M.V. PSPWM based Five-Level Shunt Active Filter for Power Quality Improvement in Power System Network. Energy Procedia 2017, 117, 794–801. [Google Scholar] [CrossRef]
- Agrawal, S.; Vaishnav, S.K.; Somani, R.K. Active Power Filter for Harmonic Mitigation of Power Quality Issues in Grid Integrated Photovoltaic Generation System. In Proceedings of the 2020 7th International Conference on Signal Processing and Integrated Networks (SPIN), Noida, India, 27–28 February 2020; IEEE: Piscataway, NJ, USA, 2020. [Google Scholar]
- Martins, A.; Ferreira, J.; Azevedo, H. Active power filters for harmonic elimination and power quality improvement. In Power Quality; InTech: London, UK, 2011. [Google Scholar]
- De Araujo Ribeiro, R.L.; de Azevedo, C.C.; de Sousa, R.M. A robust adaptive control strategy of active power filters for power-factor correction, harmonic compensation, and balancing of nonlinear loads. IEEE Trans. Power Electron. 2011, 27, 718–730. [Google Scholar] [CrossRef]
- Jain, S.; Agrawal, P.; Gupta, H. Fuzzy logic controlled shunt active power filter for power quality improvement. IEE Proc.-Electr. Power Appl. 2002, 149, 317–328. [Google Scholar] [CrossRef]
- Tang, Y.; Loh, P.C.; Wang, P.; Choo, F.H.; Gao, F.; Blaabjerg, F. Generalized Design of High Performance Shunt Active Power Filter With Output LCL Filter. IEEE Trans. Ind. Electron. 2011, 59, 1443–1452. [Google Scholar] [CrossRef]
- Asirninoaei, L.; Blaabjerg, F.; Hansen, S. Evaluation of harmonic detection methods for active power filter applications. In Proceedings of the Twentieth Annual IEEE Applied Power Electronics Conference and Exposition, 2005, APEC 2005, Austin, TX, USA, 6–10 March 2005; IEEE: Piscataway, NJ, USA, 2005; Volume 1. [Google Scholar]
- Izhar, M.; Hadzer, C.; Syafrudin, M.; Taib, S.; Idris, S. Performance for passive and active power filter in reducing harmonics in the distribution system. In Proceedings of the PECon 2004. Proceedings. National Power and Energy Conference, 2004, Kuala Lumpur, Malaysia, 29–30 November 2004; IEEE: Piscataway, NJ, USA, 2004. [Google Scholar]
- Ullah, A.; Sheikh, I.U.H.; Arshad, S.; Saleem, F. Digital active power filter controller design for current harmonics in power system. In Proceedings of the 2019 16th International Bhurban Conference on Applied Sciences and Technology (IBCAST), Islamabad, Pakistan, 8–12 January 2019; IEEE: Piscataway, NJ, USA, 2019. [Google Scholar]
- Shyu, K.-K.; Yang, M.-J.; Chen, Y.-M.; Lin, Y.-F. Model Reference Adaptive Control Design for a Shunt Active-Power-Filter System. IEEE Trans. Ind. Electron. 2008, 55, 97–106. [Google Scholar] [CrossRef]
- Akagi, H.; Watanabe, E.H.; Aredes, M. Instantaneous Power Theory and Applications to Power Conditioning; IEEE Press: Piscataway, NJ, USA, 2007. [Google Scholar]
- Magdum, P.S.; Patil, U.T. Development of single-phase shunt active power filter. In Proceedings of the 2017 International Conference on Inventive Communication and Computational Technologies (ICICCT), Coimbatore, India, 27–28 February 2020; IEEE: Piscataway, NJ, USA, 2017. [Google Scholar]
- Khadkikar, V.; Chandra, A.; Singh, B.N. Generalized single-phase p-q theory for active power filtering: Simulation and DSP-based experimental investigation. IET Power Electron. 2009, 2, 67–78. [Google Scholar] [CrossRef] [Green Version]
- Mattavelli, P. A closed-loop selective harmonic compensation for active filters. IEEE Trans. Ind. Appl. 2001, 37, 81–89. [Google Scholar] [CrossRef] [Green Version]
- Chilipi, R.S.R.; Sayari, N.A.; Hosani, K.H.A.; Beig, A.R. Adaptive Notch Filter-Based Multipurpose Control Scheme for Grid- Interfaced Three-Phase Four-Wire DG Inverter. IEEE Trans. Ind. Appl. 2017, 53, 4015–4027. [Google Scholar] [CrossRef]
- Kusljevic, M. Simultaneous Frequency and Harmonic Magnitude Estimation Using Decoupled Modules and Multirate Sampling. IEEE Trans. Instrum. Meas. 2009, 59, 954–962. [Google Scholar] [CrossRef]
- Kumar, P.; Mahajan, A. Soft Computing Techniques for the Control of an Active Power Filter. IEEE Trans. Power Deliv. 2008, 24, 452–461. [Google Scholar] [CrossRef]
- Abbas, A.S.; El-Sehiemy, R.A.; Abou El-Ela, A.; Ali, E.S.; Mahmoud, K.; Lehtonen, M.; Darwish, M.M. Optimal harmonic mitigation in distribution systems with inverter based distributed generation. Appl. Sci. 2021, 11, 774. [Google Scholar] [CrossRef]
- Hou, S.; Fei, J.; Chen, C.; Chu, Y. Finite-Time Adaptive Fuzzy-Neural-Network Control of Active Power Filter. IEEE Trans. Power Electron. 2019, 34, 10298–10313. [Google Scholar] [CrossRef]
- George, M.; Basu, K.P. Modeling and Control of Three-Phase Shunt Active Power Filter 1. 2008. Available online: https://thescipub.com/pdf/ajassp.2008.1064.1070.pdf (accessed on 1 January 2022).
- Cirrincione, M.; Pucci, M.; Vitale, G.; Miraoui, A. Current Harmonic Compensation by a Single-Phase Shunt Active Power Filter Controlled by Adaptive Neural Filtering. IEEE Trans. Ind. Electron. 2009, 56, 3128–3143. [Google Scholar] [CrossRef]
- Kale, M.; Ozdemir, E. A novel adaptive hysteresis band current controller for shunt active power filter. In Proceedings of the 2003 IEEE Conference on Control Applications, 2003, CCA 2003, Istanbul, Turkey, 25 June 2003; IEEE: Piscataway, NJ, USA, 2003; Volume 2. [Google Scholar]
- Vazquez, J.; Salmeron, P. Active power filter control using neural network technologies. IEE Proc.-Electr. Power Appl. 2003, 150, 139–145. [Google Scholar] [CrossRef]
- Milasi, R.M.; Lynch, A.F.; Li, Y. Adaptive control of an active power filter for harmonic suppression and power factor correction. Int. J. Dyn. Control 2021, 10, 473–482. [Google Scholar] [CrossRef]
- Khan, A.; Jaffery, M.H.; Javed, Y.; Arshad, J.; Rehman, A.U.; Khan, R.; Bajaj, M.; Kaabar, M.K.A. Hardware-in-the-Loop Implementation and Performance Evaluation of Three-Phase Hybrid Shunt Active Power Filter for Power Quality Improvement. Math. Probl. Eng. 2021, 2021, 8032793. [Google Scholar] [CrossRef]
- De Souza, L.L.; Rocha, N.; Fernandes, D.A.; De Sousa, R.P.; Jacobina, C.B. Grid Harmonic Current Correction Based on Parallel Three-Phase Shunt Active Power Filter. IEEE Trans. Power Electron. 2021, 37, 1422–1434. [Google Scholar]
- Echalih, S.; Abouloifa, A.; Lachkar, I.; Guerrero, J.M.; Hekss, Z.; Giri, F. Hybrid automaton-fuzzy control of single phase dual buck half bridge shunt active power filter for shoot through elimination and power quality improvement. Int. J. Electr. Power Energy Syst. 2021, 131, 106986. [Google Scholar] [CrossRef]
- Thananukul, P.; Kamsuwan, Y. Active Power Filter in Linear Systems for Power Factor Correction. In Proceedings of the 2021 3rd International Conference on Smart Power & Internet Energy Systems (SPIES), Shanghai, China, 25–28 September 2021; IEEE: Piscataway, NJ, USA, 2021. [Google Scholar]
- Singh, V.; Gupta, S.; Yadav, A.; Rajashekar, J. Harmonic Reduction and Reactive Power Improvement using Shunt Active Power Filter And Thyristor-Controlled Reactor. In Proceedings of the 2022 Second International Conference on Power, Control and Computing Technologies (ICPC2T), Raipur, India, 1–3 March 2022; IEEE: Piscataway, NJ, USA, 2022. [Google Scholar]
- Espinosa, T.B.P.; Magwili, G.V. Synchronous Reference Frame Method with PLL and Hysteresis Current Controller for Three Phase Shunt Active Power Filter to Mitigate Harmonics Caused by Nonlinear Loads. In Proceedings of the 2022 14th International Conference on Computer and Automation Engineering (ICCAE), Brisbane, Australia, 25–27 March 2022; IEEE: Piscataway, NJ, USA, 2022. [Google Scholar]
- Pinto, J.G.; Neves, P.; Pregitzer, R.G.; Monteiro, L.F.; Afonso, J.L. Single-phase shunt active filter with digital control. In Proceedings of the ICREPQ’07—International Conference on Renewable Energies and Power Quality, Seville, Spain, 28–30 March 2007; ISBN 978-84-611-4707-6. [Google Scholar]
- Srinath, S.; Prabakaran, S.; Mohan, K.; Selvan, M.P. Implementation of Single Phase Shunt Active Filter for Low Voltage Distribution System. In Proceedings of the 16th National Power Systems Conference, Hyderabad, India, 15–17 December 2010. [Google Scholar]
- Babu, N.; Guerrero, J.M.; Siano, P.; Peesapati, R.; Panda, G. An improved adaptive control strategy in grid-tied PV system with active power filter for power quality enhancement. IEEE Syst. J. 2021, 15, 2859–2870. [Google Scholar] [CrossRef]
- The PCB Library. Available online: https://www.componentsearchengine.com/pcb_library/proteus (accessed on 1 January 2022).
- Abdul-Hamied, D.T.; Shaheen, A.M.; Salem, W.A.; Gabr, W.I.; El-Sehiemy, R.A. Equilibrium optimizer based multi dimensions operation of hybrid AC/DC grids. Alex. Eng. J. 2020, 59, 4787–4803. [Google Scholar] [CrossRef]
- Shaheen, A.M.; El-Sehiemy, R.A. Optimal allocation of capacitor devices on MV distribution networks using crow search algorithm. CIRED-Open Access Proc. J. 2017, 2017, 2453–2457. [Google Scholar] [CrossRef] [Green Version]
- Rizk-Allah, R.M.; Mageed, H.M.A.; El-Sehiemy, R.; Aleem, S.A.; El Shahat, A. A New Sine Cosine Optimization Algorithm for Solving Combined Non-Convex Economic and Emission Power Dispatch Problems. Int. J. Energy Convers. 2017, 5, 180–192. [Google Scholar] [CrossRef]





| Parameter | Value |
|---|---|
| AC source: voltage | 220 |
| AC source: impedance | Resistance: 0.002 Ω, inductor of 20 mH |
| AC source: frequency | 50 Hz |
| Nonlinear load impedance | Resistance: 10 Ω, inductor of 100 mH |
| Filter interface impedance | Resistance: 0.5 Ω, inductor of 1 mH |
| Firing angle of the converter | 30° |
| DC-bus capacitor: voltage | 330 V |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abaza, A.; El-Sehiemy, R.A.; Said, M.; Ghoniem, R.M.; Barakat, A.F. Implementation of an Electronically Based Active Power Filter Associated with a Digital Controller for Harmonics Elimination and Power Factor Correction. Electronics 2022, 11, 2205. https://doi.org/10.3390/electronics11142205
Abaza A, El-Sehiemy RA, Said M, Ghoniem RM, Barakat AF. Implementation of an Electronically Based Active Power Filter Associated with a Digital Controller for Harmonics Elimination and Power Factor Correction. Electronics. 2022; 11(14):2205. https://doi.org/10.3390/electronics11142205
Chicago/Turabian StyleAbaza, Amlak, Ragab A. El-Sehiemy, Mokhtar Said, Rania M. Ghoniem, and Asmaa F. Barakat. 2022. "Implementation of an Electronically Based Active Power Filter Associated with a Digital Controller for Harmonics Elimination and Power Factor Correction" Electronics 11, no. 14: 2205. https://doi.org/10.3390/electronics11142205







