Hybrid CNN-SVM Inference Accelerator on FPGA Using HLS
Abstract
:1. Introduction
- A novel computing architecture based on hardware reuse is designed for compatibility with hybrid CNN-SVM. We apply a resource-efficient general operator to implement typical calculation modes, such as convolution in CNN and decision functions in SVM.
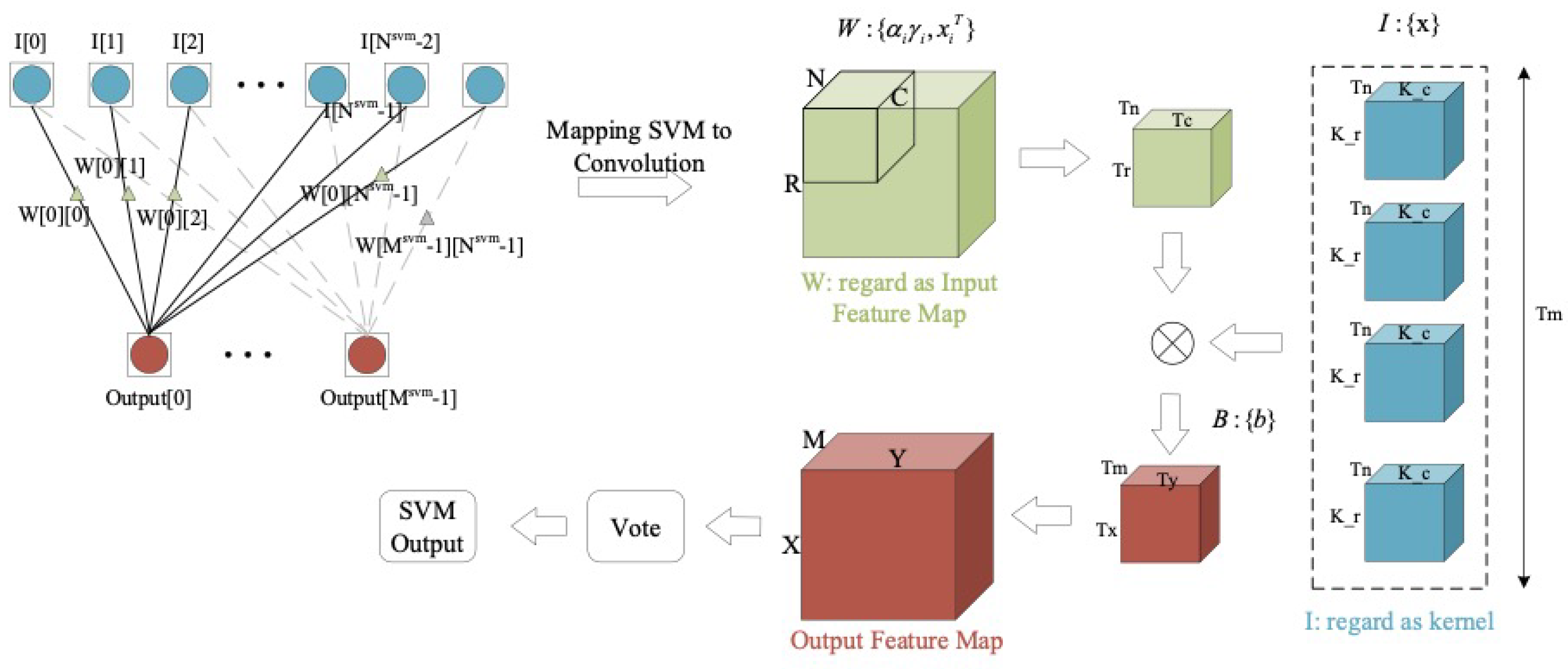
- A computation mapping strategy is adapted for transforming SVM to spatial convolution. In this way, the accelerator can efficiently reuse the computing logic resource to complete the inference calculations of CNN-SVM.
- A universal deployment methodology is provided that combines the uniformed representation of CNN and SVM with the computing architecture of our accelerator. According to the target platform and algorithm, it supports searching the optimal implementation parameters for CNN, SVM or CNN-SVM through design space exploration.
- A typical CNN-SVM hybrid network is implemented with the proposed computing architecture and computation mapping strategy. It can achieve a high performance with 13.33 GOPs and 0.066 NTP with very few resources, which outperforms other state-of-the-art methods.
2. Architecture and Realization
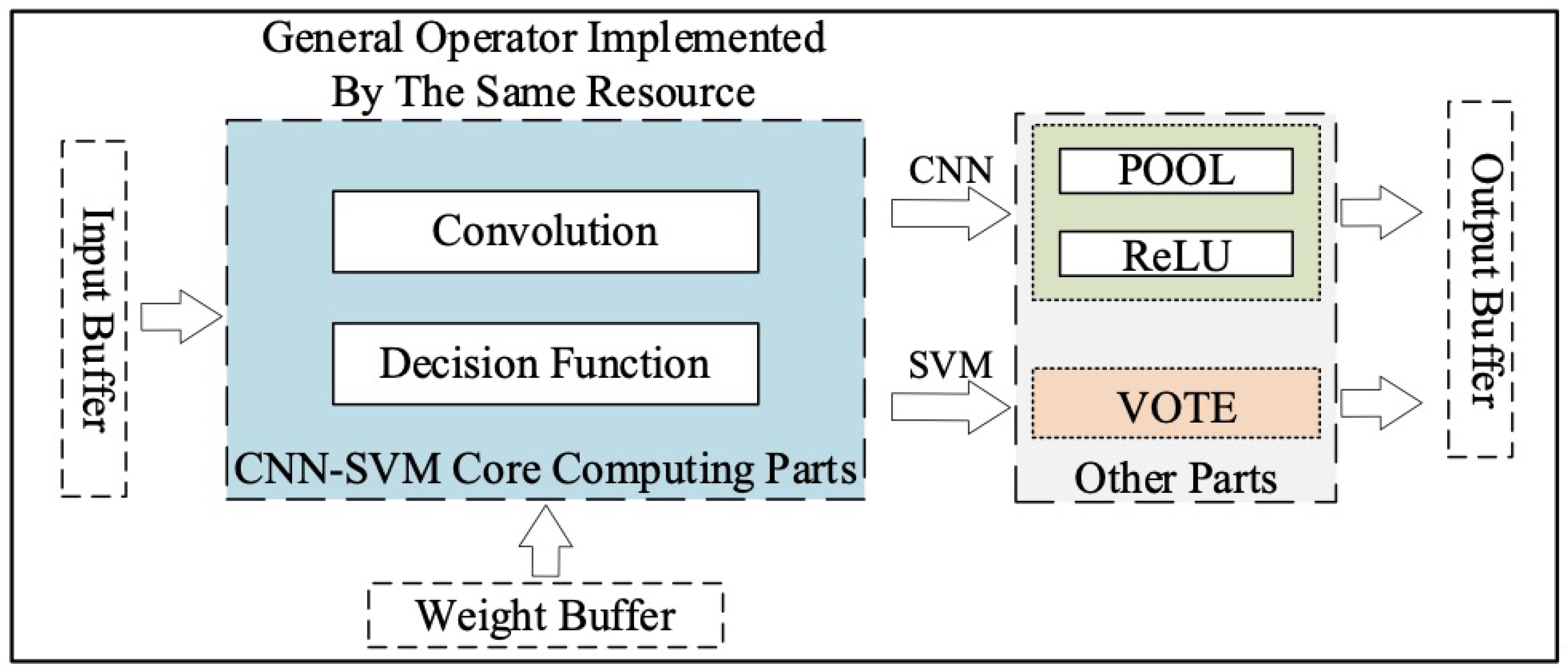
2.1. Hybrid CNN-SVM Accelerator Architecture
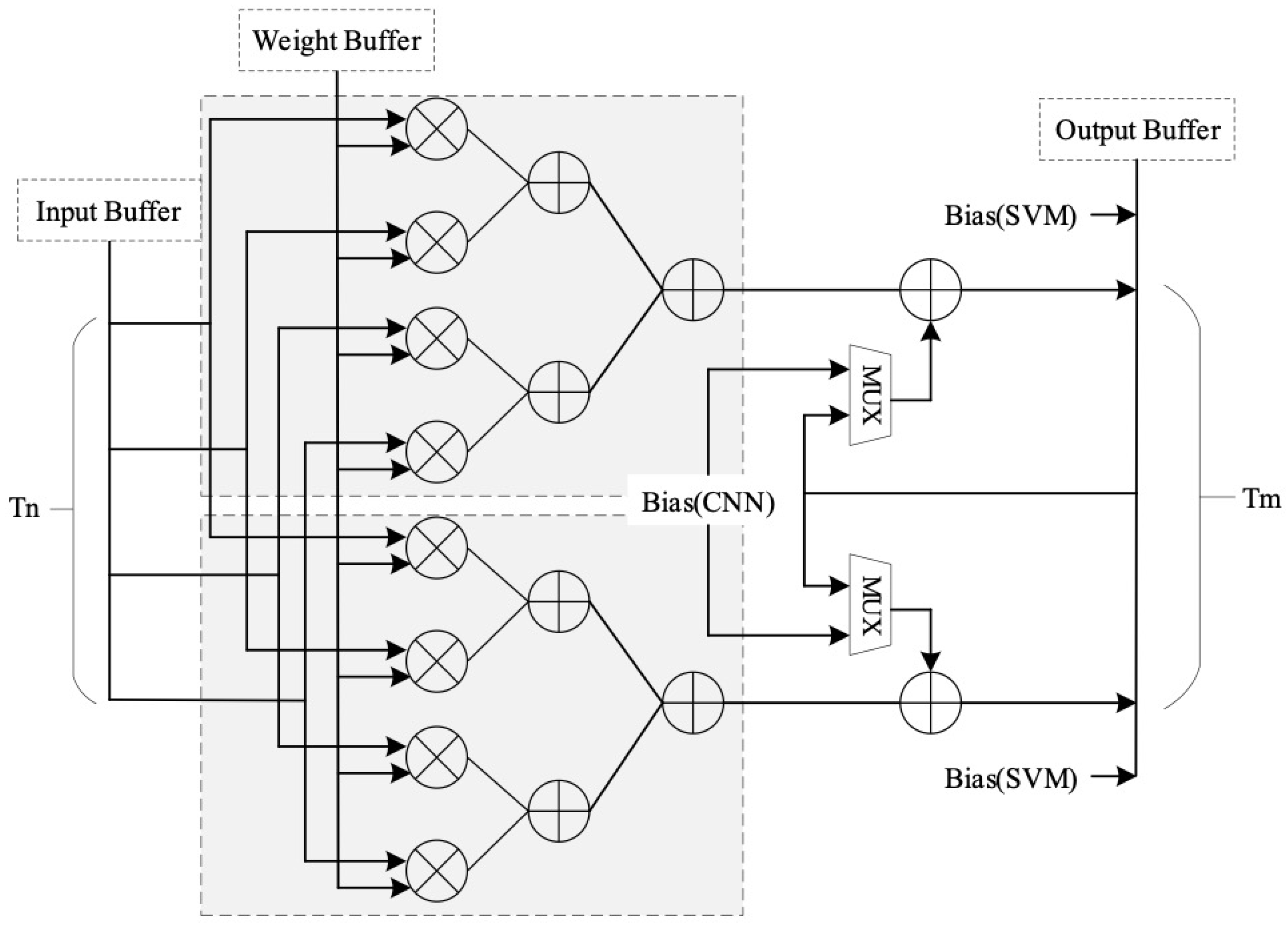
2.2. Resource-Efficient General Operator
2.3. General Implementation of CNN-SVM
3. Universal Deployment Methodology
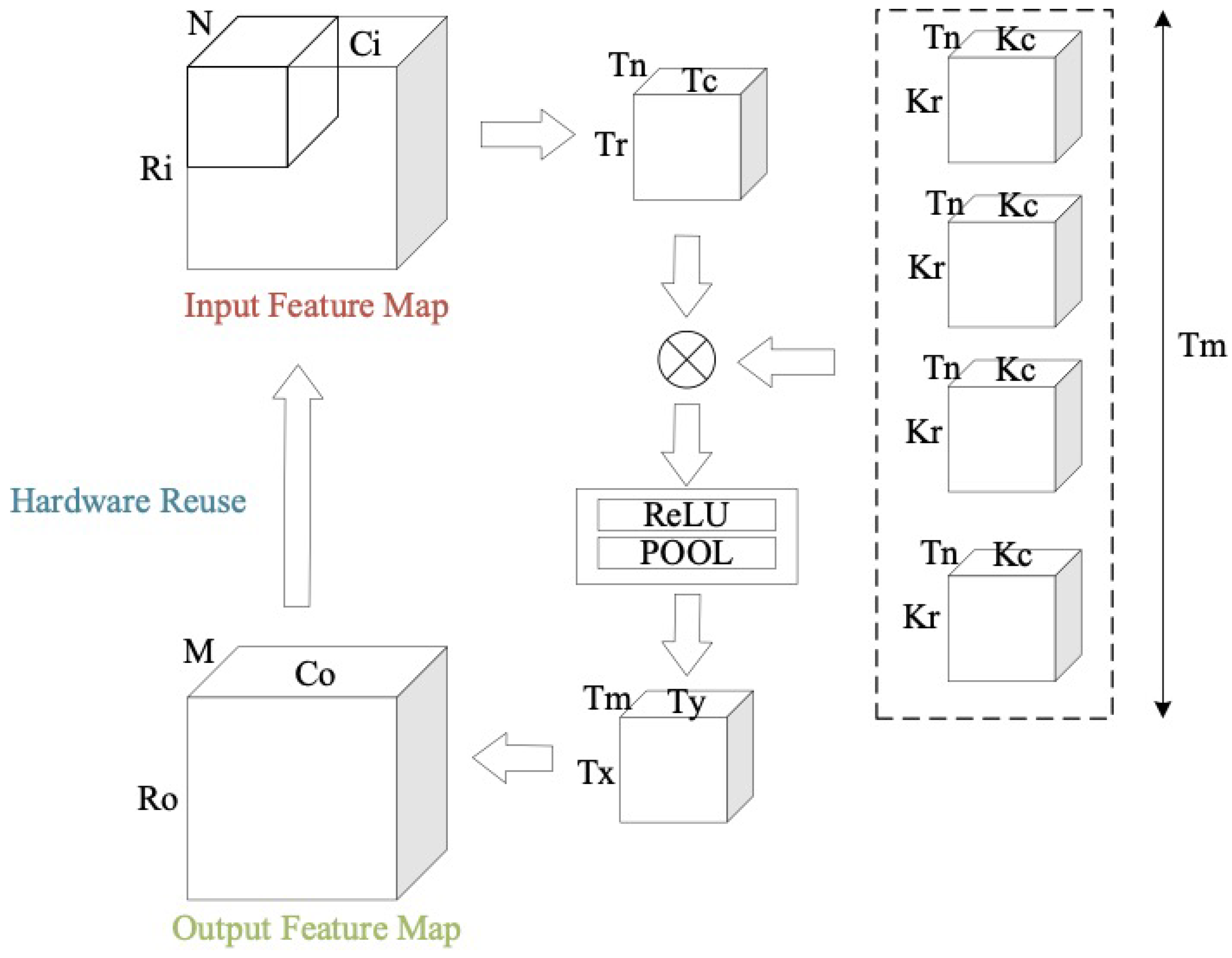
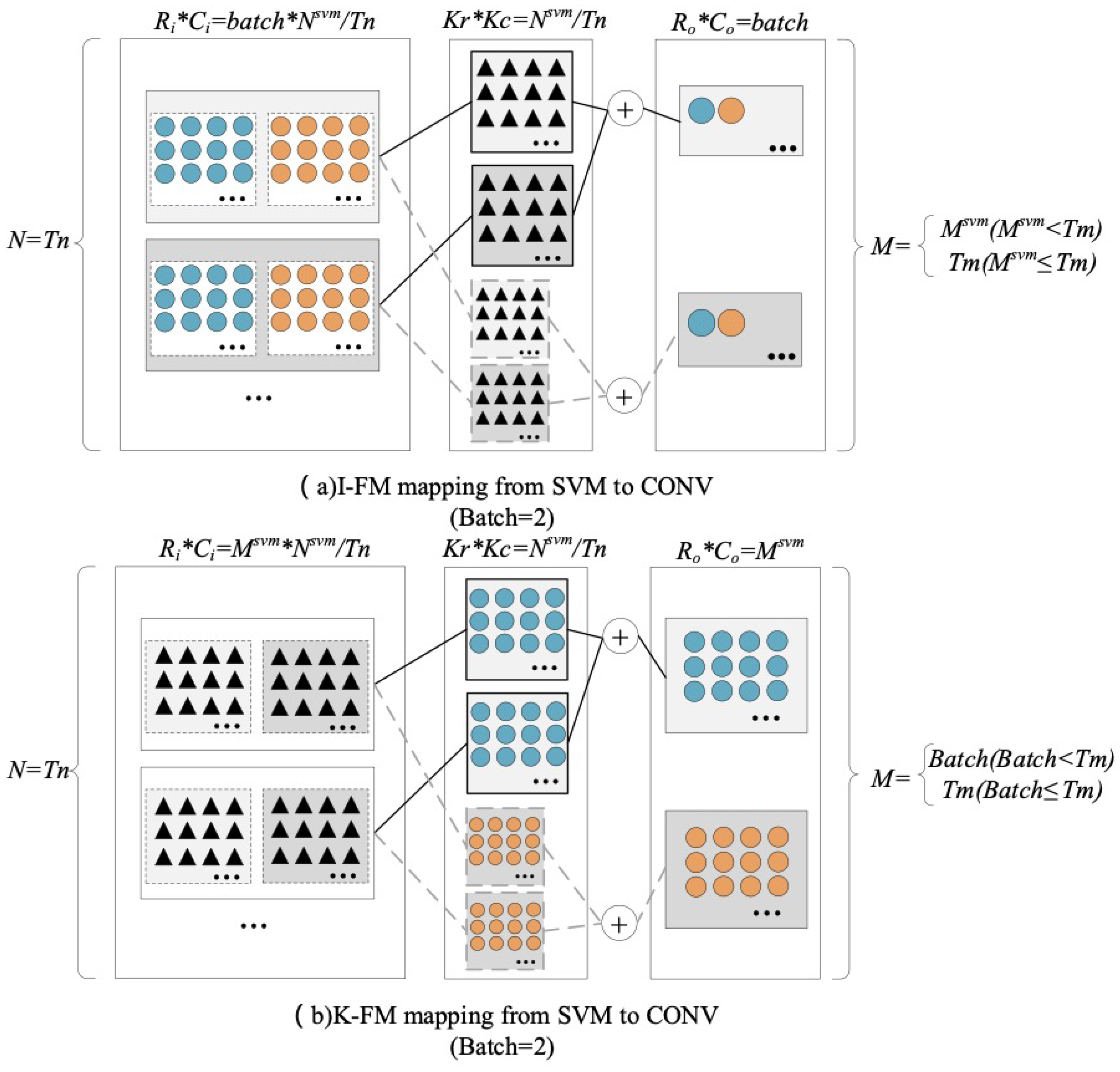
3.1. Uniformed Representation
3.2. Resource Evaluation Model
3.3. Design Space Exploration
4. Evaluation
4.1. Environment Setup
4.2. Design Space Exploration
4.3. Results and Comparison
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Convolution neural network | |
| Support vector machine | |
| Mapping strategies of SVM | |
| Row, column and input channel of input feature map | |
| Row, column and channels of output feature map | |
| Size of convolution kernel | |
| Size of kernel moving stride in row and column | |
| Tiling width and height of input feature map | |
| Parallelisms of input channel and output channel | |
| Size of sub-block in output feature map |
References
- Xue, D.X.; Zhang, R.; Feng, H.; Wang, Y.L. CNN-SVM for microvascular morphological type recognition with data augmentation. J. Med. Biol. Eng. 2016, 36, 755–764. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kang, J.; Park, Y.J.; Lee, J.; Wang, S.H.; Eom, D.S. Novel leakage detection by ensemble CNN-SVM and graph-based localization in water distribution systems. IEEE Trans. Ind. Electron. 2018, 65, 4279–4289. [Google Scholar] [CrossRef]
- Guo, K.; Sui, L.; Qiu, J.; Yu, J.; Wang, J.; Yao, S.; Han, S.; Wang, Y.; Yang, H. Angel-Eye: A complete design flow for mapping CNN onto embedded FPGA. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 2017, 37, 35–47. [Google Scholar] [CrossRef]
- Zhang, C.; Li, P.; Sun, G.; Guan, Y.; Xiao, B.; Cong, J. Optimizing fpga-based accelerator design for deep convolutional neural networks. In Proceedings of the 2015 ACM/SIGDA International Symposium on Field-Programmable Gate Arrays, Monterey, CA, USA, 22–24 February 2015. [Google Scholar]
- Dass, J.; Narawane, Y.; Mahapatra, R.N.; Sarin, V. Distributed Training of Support Vector Machine on a Multiple-FPGA System. IEEE Trans. Comput. 2020, 69, 1015–1026. [Google Scholar] [CrossRef]
- Zeng, S.; Guo, K.; Fang, S.; Kang, J.; Xie, D.; Shan, Y.; Wang, Y.; Yang, H. An Efficient Reconfigurable Framework for General Purpose CNN-RNN Models on FPGAs. In Proceedings of the 2018 IEEE 23rd International Conference on Digital Signal Processing (DSP), Shanghai, China, 19–21 November 2018; pp. 1–5. [Google Scholar]
- Suda, N.; Chra, V.; Dasika, G.; Mohanty, A.; Ma, Y.; Vrudhula, S.; Seo, J.S.; Cao, Y. Throughput-optimized openCL-based FPGA accelerator for large-scale convolutional neural networks. In Proceedings of the 2016 ACM/SIGDA International Symposium on Field-Programmable Gate Arrays, Monterey, CA, USA, 21–23 February 2016; pp. 16–25. [Google Scholar]
- Sun, Y.; Liu, B.; Xu, X. An OpenCL-Based Hybrid CNN-RNN Inference Accelerator On FPGA. In Proceedings of the 2019 International Conference on Field-Programmable Technology (ICFPT), Tianjin, China, 9–13 December 2019; pp. 283–286. [Google Scholar]
- Li, H.; Fan, X.; Jiao, L.; Cao, W.; Zhou, X.; Wang, L. A high performance FPGA-based accelerator for large-scale convolutional neural networks. In Proceedings of the Field Programmable Logic and Applications (FPL), 2016 26th International Conference on IEEE, Lausanne, Switzerland, 29 August–2 September 2016. [Google Scholar]
- Wu, D.; Zhang, Y.; Jia, X.; Tian, L.; Li, T.; Sui, L.; Xie, D.; Shan, Y. A high-performance CNN processor based on FPGA for MobileNets. In Proceedings of the 2019 29th International Conference on Field Programmable Logic and Applications (FPL), Barcelona, Spain, 9–13 September 2019. [Google Scholar]
- Afifi, S.; GholamHosseini, H.; Sinha, R. FPGA implementations of SVM classifiers: A review. SN Comput. Sci. 2020, 1, 1–17. [Google Scholar] [CrossRef] [Green Version]
- Ons, B.; Bahoura, M. Efficient FPGA-based architecture of an automatic wheeze detector using a combination of MFCC and SVM algorithms. J. Syst. Archit. 2018, 88, 54–64. [Google Scholar]
- Yin, S.; Tang, S.; Lin, X.; Ouyang, P.; Tu, F.; Liu, L.; Wei, S. A high throughput acceleration for hybrid neural networks with efficient resource management on FPGA. IEEE Trans. Comput. Aided Design Integr. Circuits Syst. 2019, 38, 678–691. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, X.; Ramachran, A.; Zhuge, C.; Tang, S.; Ouyang, P.; Cheng, Z.; Rupnow, K.; Chen, D. High-performance video content recognition with long-term recurrent convolutional network for FPGA. In Proceedings of the 2017 27th International Conference on Field Programmable Logic and Applications (FPL), Ghent, Belgium, 4–8 September 2017. [Google Scholar]
- Ma, Y.; Cao, Y.; Vrudhula, S.; Seo, J.S. Automatic compilation of diverse CNNs onto high-performance FPGA accelerators. IEEE Trans. Comput. Aided Design Integr. Circuits Syst. 2020, 39, 424–437. [Google Scholar] [CrossRef]

| Network Parameters | Uniformed Representation | CNN | SVM | |
|---|---|---|---|---|
| I-FM | K-FM | |||
| Input FM | ||||
| Output FM | ||||
| Input Channel | N | |||
| Output Channel | M | |||
| Kernel | ||||
| Stride | ||||
| Layer1 | Layer2 | Layer3 | Layer4 | |
|---|---|---|---|---|
| Type | CNN | CNN | CNN | SVM |
| 28/28 | 14/14 | 7/7 | 1/1 | |
| N | 1 | 4 | 8 | 256 |
| M | 4 | 8 | 16 | 45 |
| Strategy | Resource | |||
|---|---|---|---|---|
| BRAM | DSP | FF | LUT | |
| I-FM | 40 | 201 | 28,728 | 38,307 |
| K-FM | 64 | 203 | 28,396 | 38,071 |
| Strategy | Batch Size | |||
|---|---|---|---|---|
| 1 | 8 | 16 | 32 | |
| I-FM | 7703 | 8567 | 17,130 | 34,256 |
| K-FM | 7512 | 7953 | 8541 | 17,074 |
| [4] | [13] | [14] | Ours | |
|---|---|---|---|---|
| Device | VX485T | VX690T | VC709 | ZYNQ7020 |
| Frequency | 100 MHz | 250 MHz | 100 MHz | 200 MHz |
| Precision | 32 bit | 8 bit | 12 bit | 16 bit |
| Total DSP | 2800 | 3600 | 3600 | 220 |
| Used DSP | 2240 | 3104 | 3130 | 203 |
| Utilization | 80% | 86% | 87% | 92% |
| Power(W) | 18.61 | ∖ | 23.6 | 2.03 |
| GOPs | 61.62 | 13.74 | 36.25 | 13.33 |
| NTP | 0.027 | 0.004 | 0.012 | 0.066 |
| Normalize | 1.0 | 0.15 | 0.44 | 2.44 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, B.; Zhou, Y.; Feng, L.; Fu, H.; Fu, P. Hybrid CNN-SVM Inference Accelerator on FPGA Using HLS. Electronics 2022, 11, 2208. https://doi.org/10.3390/electronics11142208
Liu B, Zhou Y, Feng L, Fu H, Fu P. Hybrid CNN-SVM Inference Accelerator on FPGA Using HLS. Electronics. 2022; 11(14):2208. https://doi.org/10.3390/electronics11142208
Chicago/Turabian StyleLiu, Bing, Yanzhen Zhou, Lei Feng, Hongshuo Fu, and Ping Fu. 2022. "Hybrid CNN-SVM Inference Accelerator on FPGA Using HLS" Electronics 11, no. 14: 2208. https://doi.org/10.3390/electronics11142208
APA StyleLiu, B., Zhou, Y., Feng, L., Fu, H., & Fu, P. (2022). Hybrid CNN-SVM Inference Accelerator on FPGA Using HLS. Electronics, 11(14), 2208. https://doi.org/10.3390/electronics11142208






