Application of Generative Adversarial Network and Diverse Feature Extraction Methods to Enhance Classification Accuracy of Tool-Wear Status
Abstract
:1. Introduction
2. Related Work
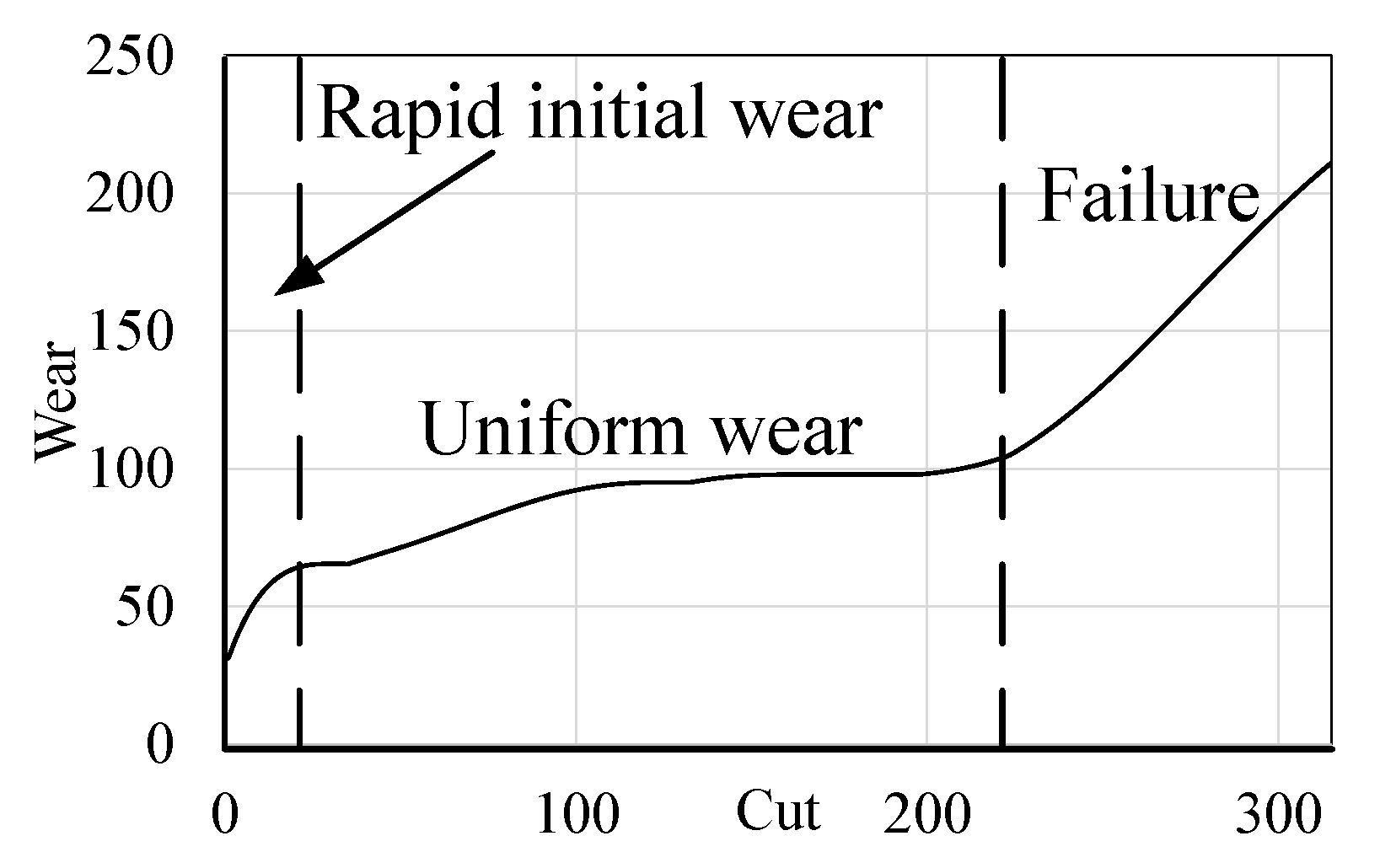
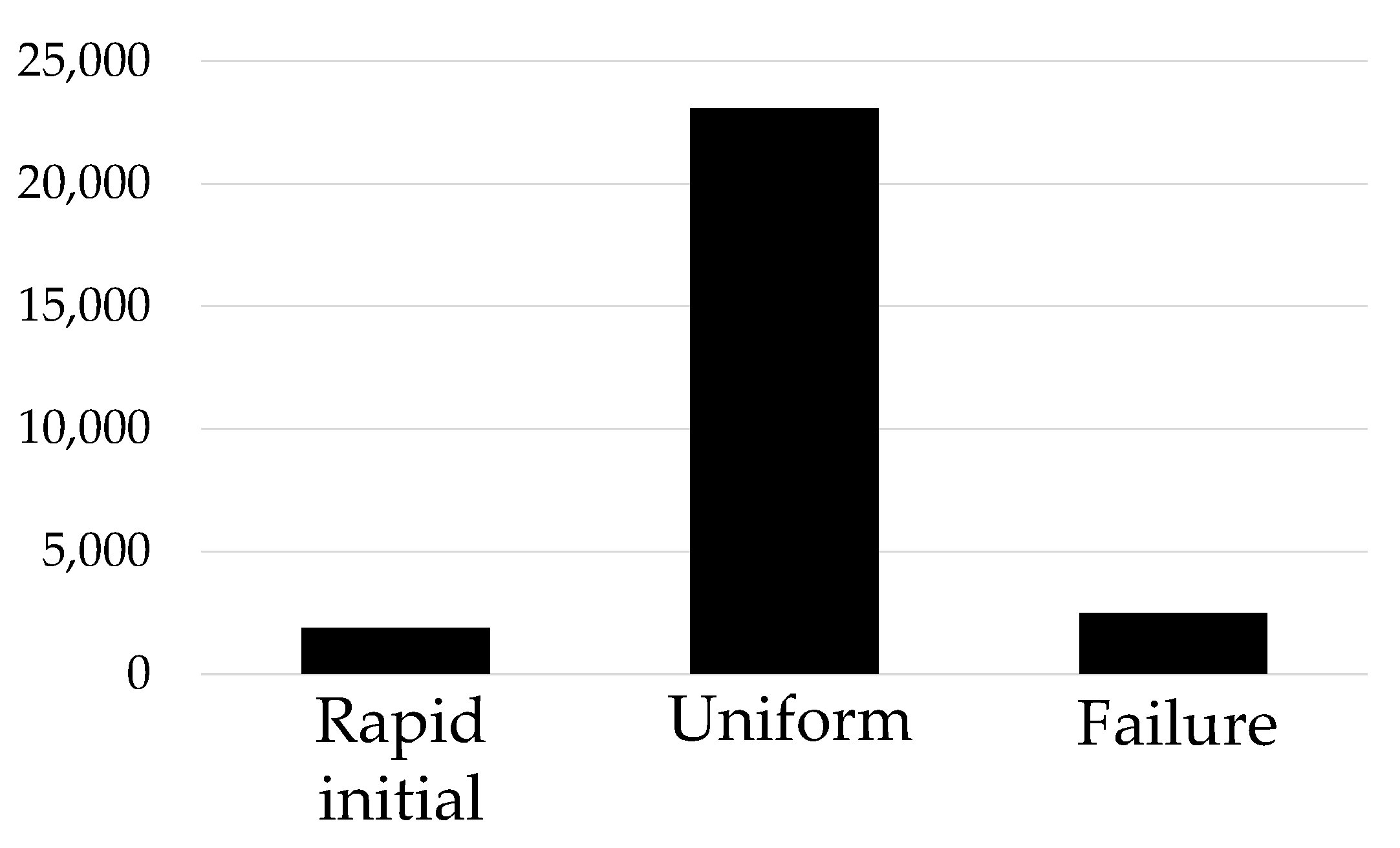
2.1. Tool-Wear Statuses
2.2. Data Fields Suitable for Tool Wear Predictions
2.3. Existing Tool Wear Prediction Methods
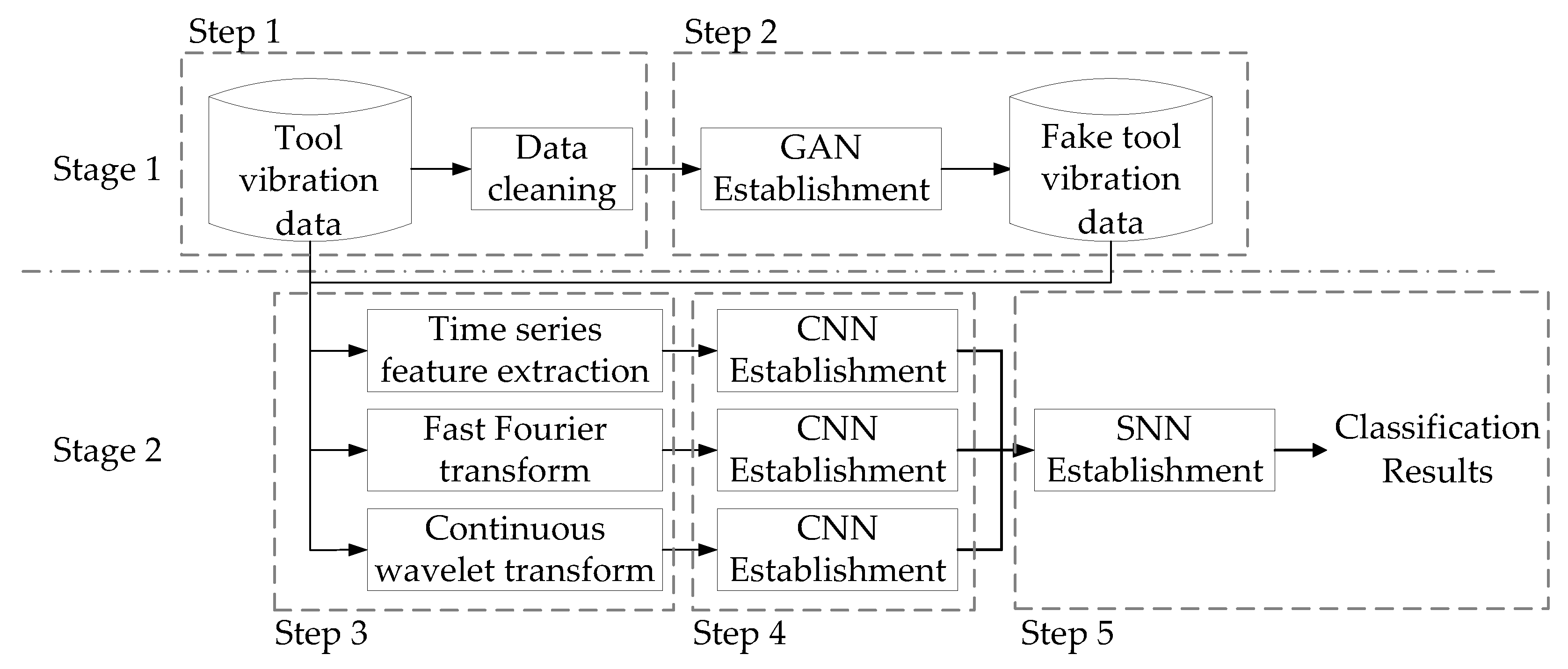
3. Frameworks
3.1. Introduction to the Dataset and the Methods for Data Cleaning
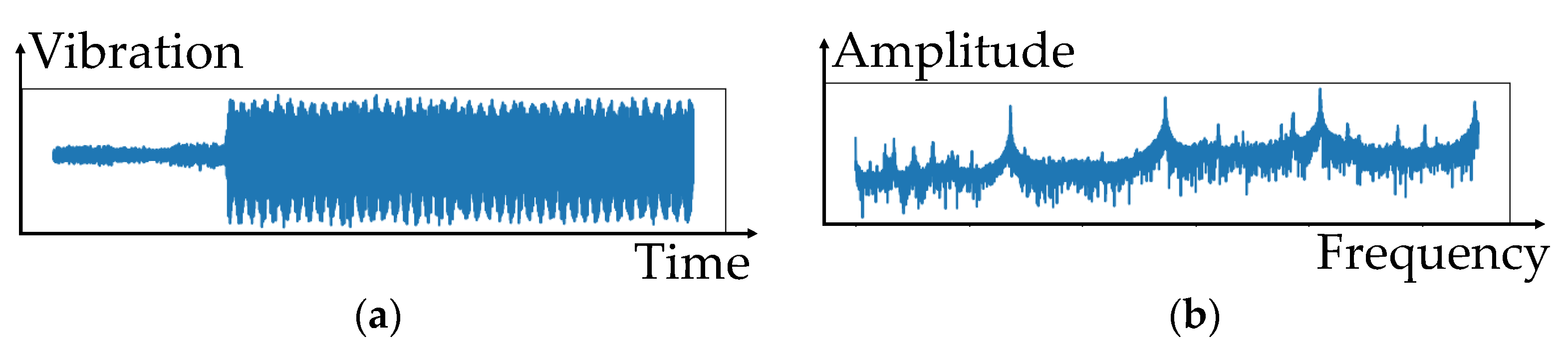
3.2. Use of GAN to Generate Realistic Vibration Data to Overcome Data Imbalance
3.3. Feature Selection
3.3.1. Time Series Feature Extraction
- is the maximum value in ;
- is the minimum value in ;
- is the mean of all values in ;
- is the sum of all values in ;
- is the degree of dispersion among all values in :
- is the root mean square error of all values in X(t):
- is the standard deviation of all of the values in X(t):
3.3.2. Fast Fourier Transform (FFT)
3.3.3. Continuous Wavelet Transform
3.4. CNN
3.5. Use of SNN to Achieve Ensemble Learning
4. Experiments
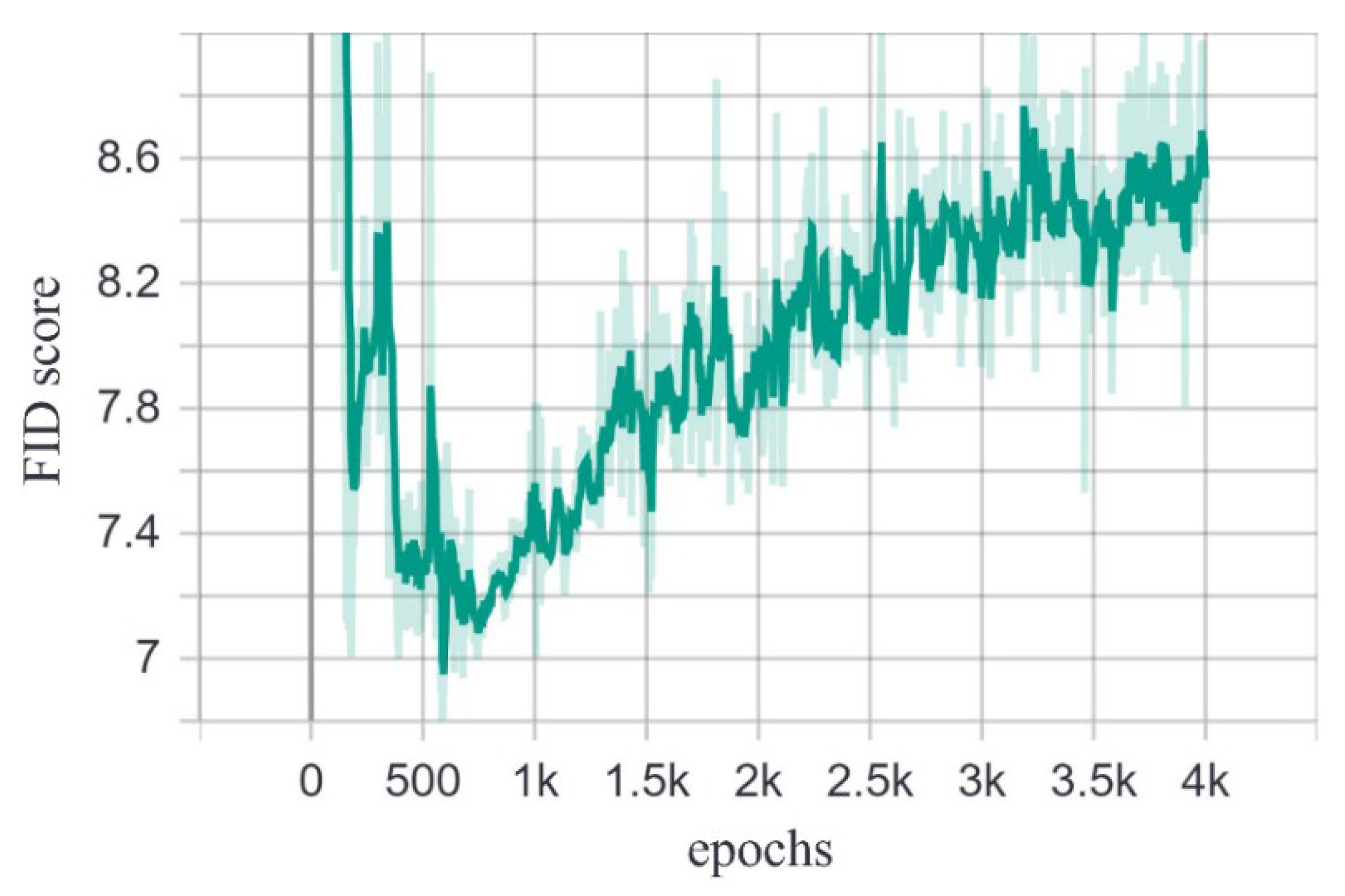
4.1. Results of Using GAN to Generate Data
4.2. Validity of Using GAN-Generated Data to Overcome Imbalance in Tool-Wear Data
4.3. Verification of Necessity of Multiple Feature Extraction Methods for Tool Wear
5. Conclusions and Directions for Future Research
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hu, Y.; Miao, X.; Si, Y.; Pan, E.; Zio, E. Prognostics and health management: A review from the perspectives of design, development and decision. Reliab. Eng. Syst. Saf. 2022, 217, 108063. [Google Scholar] [CrossRef]
- Zio, E. Prognostics and Health Management (PHM): Where are we and where do we (need to) go in theory and practice. Reliab. Eng. Syst. Saf. 2022, 218, 108119. [Google Scholar] [CrossRef]
- Vrignat, P.; Kratz, F.; Avila, M. Sustainable manufacturing, maintenance policies, prognostics and health management: A literature review. Reliab. Eng. Syst. Saf. 2022, 218, 108140. [Google Scholar] [CrossRef]
- Sun, C.; Wang, P.; Yan, R.Q.; Gao, R.X.; Chen, X.F. Machine health monitoring based on locally linear embedding with kernel sparse representation for neighborhood optimization. Mech. Syst. Signal Processing 2019, 114, 25–34. [Google Scholar] [CrossRef]
- Sun, C.; Ma, M.; Zhao, Z.; Tian, S.; Yan, R.; Chen, X. Deep transfer learning based on sparse auto-encoder for remaining useful life prediction on tool in manufacturing. IEEE Trans. Ind. Inform. 2018, 15, 2416–2425. [Google Scholar] [CrossRef]
- Chen, B.; Chen, X.; Li, B.; He, Z.; Cao, H.; Cai, G. Reliability estimation for cutting tools based on logistic regression model using vibration signals. Mech. Syst. Signal Processing 2011, 25, 2526–2537. [Google Scholar] [CrossRef]
- Kong, D.; Chen, Y.; Li, N. Gaussian process regression for tool wear prediction. Mech. Syst. Signal Processing 2018, 104, 556–574. [Google Scholar] [CrossRef]
- Benkedjouh, T.; Medjaher, K.; Zerhouni, N.; Rechak, S. Health assessment and life prediction of cutting tools based on support vector regression. J. Intell. Manuf. 2015, 26, 213–223. [Google Scholar] [CrossRef] [Green Version]
- Cai, G.; Chen, X.; Chen, B.L.B.; He, Z. Operation reliability assessment for cutting tools by applying a proportional covariate model to condition monitoring information. Sensors 2012, 12, 12964–12987. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhu, K.; Liu, T. Online Tool Wear Monitoring via Hidden Semi-Markov Model with Dependent Durations. IEEE Trans. Ind. Inform. 2018, 14, 69–78. [Google Scholar] [CrossRef]
- Yu, J.; Liang, S.; Tang, D.; Liu, H. A weighted hidden Markov model approach for continuous-state tool wear monitoring and tool life prediction. Int. J. Adv. Manuf. Technol. 2017, 91, 201–211. [Google Scholar] [CrossRef]
- Kurek, J.; Wieczorek, G.; Kruk, B.S.M.; Jegorowa, A.; Osowski, S. Transfer learning in recognition of drill wear using convolutional neural network. In Proceedings of the 2017 18th International Conference on Computational Problems of Electrical Engineering (CPEE), Kutna Hora, Czech Republic, 11–13 September 2017. [Google Scholar]
- Rohan, A. A Holistic Fault Detection and Diagnosis System in Imbalanced, Scarce, Multi-Domain (ISMD) Data Setting for Component-Level Prognostics and Health Management (PHM). arXiv 2022, arXiv:2204.02969. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, P.; Yan, R.; Gao, R. Deep Learning for Improved System Remaining Life Prediction. Procedia CIRP 2018, 72, 1033–1038. [Google Scholar] [CrossRef]
- Cao, P.; Zhang, S.; Tan, J. Preprocessing-Free Gear Fault Diagnosis Using Small Datasets with Deep Convolutional Neural Network-Based Transfer Learning. IEEE Access 2018, 6, 26241–26253. [Google Scholar] [CrossRef]
- Chiu, S.M.; Chen, Y.C.; Kuo, C.J.; Hung, L.C.; Hung, M.H.; Chen, C.C.; Lee, C. Development of Lightweight RBF-DRNN and Automated Framework for CNC Tool-Wear Prediction. IEEE Trans. Instrum. Meas. 2022, 71, 2506711. [Google Scholar] [CrossRef]
- Carino, J.A.; Delgado-Prieto, M.; Iglesias, J.A.; Sanchis, A.; Zurita, D.; Millan, M.; Redondo, J.A.O.; Romero-Troncoso, R. Fault Detection and Identification Methodology under an Incremental Learning Framework Applied to Industrial Machinery. IEEE Access 2018, 6, 49755–49766. [Google Scholar] [CrossRef]
- Brito, L.C.; da Silva, M.B.; Duarte, M.A.V. Identification of cutting tool wear condition in turning using self-organizing map trained with imbalanced data. J. Intell. Manuf. 2021, 32, 127–140. [Google Scholar] [CrossRef]
- Miao, H.; Zhao, Z.; Sun, C.; Li, B.; Yan, R. A U-Net-Based Approach for Tool Wear Area Detection and Identification. IEEE Trans. Instrum. Meas. 2021, 70, 5004110. [Google Scholar] [CrossRef]
- Rohan, A.; Raouf, I.; Kim, H.S. Rotate Vector (RV) Reducer Fault Detection and Diagnosis System: Towards Component Level Prognostics and Health Management (PHM). Sensors 2020, 20, 6845. [Google Scholar] [CrossRef]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Aaron, C.; Bengio, Y. Generative adversarial nets. Adv. Neural Inf. Processing Syst. 2014, 27, 2672–2680. [Google Scholar]
- Karras, T.; Aila, T.; Laine, S.; Lehtinen, J. Progressive Growing of GANs for Improved Quality, Stability, and Variation. arXiv 2017, arXiv:1710.10196. [Google Scholar]
- Yadav, N.K.; Singh, S.K.; Dubey, S.R. CSA-GAN: Cyclic synthesized attention guided generative adversarial network for face synthesis. Appl. Intell. 2022. [Google Scholar] [CrossRef]
- Shi, Y.; Aggarwal, D.; Jain, A.K. Lifting 2D StyleGAN for 3D-Aware Face Generation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021; pp. 6258–6266. [Google Scholar]
- Fang, Z.; Liu, Z.; Liu, T.; Hung, C.C.; Xiao, J.; Feng, G. Facial expression GAN for voice-driven face generation. Vis. Comput. 2022, 38, 1151–1164. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, H.; Liu, L.; Chen, X.; Zhang, Q.; Yang, K.; Xia, R.; Xie, J. Research on image Inpainting algorithm of improved GAN based on two-discriminations networks. Appl. Intell. 2021, 51, 3460–3474. [Google Scholar] [CrossRef]
- Wei, D.; Huang, K.; Ma, L.; Hua, J.; Lai, B.; Shen, H. OAW-GAN: Occlusion-aware warping GAN for unified human video synthesis. Appl. Intell. 2022, 1–18. [Google Scholar] [CrossRef]
- Tagawa, Y.; Maskeliūnas, R.; Damaševičius, R. Acoustic Anomaly Detection of Mechanical Failures in Noisy Real-Life Factory Environments. Electronics 2021, 10, 2329. [Google Scholar] [CrossRef]
- Zhang, F.; Ma, Y.; Yuan, G.; Zhang, H.; Ren, J. Multiview image generation for vehicle reidentification. Appl. Intell. 2021, 51, 5665–5682. [Google Scholar] [CrossRef]
- Gan, Y.S.; Liong, S.-T.; Wang, S.-Y.; Cheng, C.T. An improved automatic defect identification system on natural leather via generative adversarial network. Int. J. Comput. Integr. Manuf. 2022, 1–17. [Google Scholar] [CrossRef]
- Gu, J.; Qi, Y.; Zhao, Z.; Su, W.; Su, L.; Li, K.; Pecht, M. Fault diagnosis of rolling bearings based on generative adversarial network and convolutional denoising auto-encoder. J. Adv. Manuf. Sci. Technol. 2022, 2, 2022009. [Google Scholar] [CrossRef]
- Wang, M.; Zhou, J.; Gao, J.; Li, Z.; Li, E. Milling Tool Wear Prediction Method Based on Deep Learning under Variable Working Conditions. IEEE Access 2020, 8, 140726–140735. [Google Scholar] [CrossRef]
- ISO 3685:1993; Tool-Life Testing with Single-point Turning Tools. International Organization for Standardization: Geneva, Switzerland, 1993.
- Ertürk, Ş.; Kayabaşi, O. Investigation of the Cutting Performance of Cutting Tools Coated with the Thermo-Reactive Diffusion (TRD) Technique. IEEE Access 2019, 7, 106824–106838. [Google Scholar] [CrossRef]
- Bhuiyan, M.S.H.; Choudhury, I.A.; Dahari, M.; Nukman, Y. Application of acoustic emission sensor to investigate the frequency of tool wear and plastic deformation in tool condition monitoring. Measurement 2016, 92, 208–217. [Google Scholar] [CrossRef]
- Dolinšek, S.; Kopač, J. Acoustic emission signals for tool wear identification. Wear 1999, 225, 295–303. [Google Scholar] [CrossRef]
- Bhuiyan, M.S.H.; Choudhury, I.A.; Nukma, Y.n. An innovative approach to monitor the chip formation effect on tool state using acoustic emission in turning. Int. J. Mach. Tools Manuf. 2012, 58, 19–28. [Google Scholar]
- Li, Z.; Liu, R.; Wu, D. Data-driven smart manufacturing: Tool wear monitoring with audio signals and machine learning. J. Manuf. Processes 2019, 48, 66–76. [Google Scholar] [CrossRef]
- Gomes, M.C.; Brito, L.C.; da Silva, M.B.; Duarte, M.A.V. Tool wear monitoring in micromilling using Support Vector Machine with vibration and sound sensors. Precis. Eng. 2021, 67, 137–151. [Google Scholar] [CrossRef]
- Mohanraj, T.; Yerchuru, J.; Krishnan, H.; Aravind, R.S.N.; Yameni, R. Development of tool condition monitoring system in end milling process using wavelet features and Hoelder’s exponent with machine learning algorithms. Measurement 2021, 173, 108671. [Google Scholar] [CrossRef]
- Jalali, S.K.; Ghandi, H.; Motamedi, M. Intelligent condition monitoring of ball bearings faults by combination of genetic algorithm and support vector machines. J. Nondestruct. Eval. 2020, 39, 25. [Google Scholar] [CrossRef]
- Corne, R.; Nath, C.; el Mansori, M.; Kurfess, T. Study of spindle power data with neural network for predicting real-time tool wear/breakage during inconel drilling. J. Manuf. Syst. 2017, 43, 287–295. [Google Scholar] [CrossRef]
- Hesser, D.F.; Markert, B. Tool wear monitoring of a retrofitted CNC milling machine using artificial neural networks. Manuf. Lett. 2019, 19, 1–4. [Google Scholar] [CrossRef]
- Zhao, R.; Yan, R.; Wang, J.; Mao, K. Learning to monitor machine health with convolutional bi-directional LSTM networks. Sensors 2017, 17, 273. [Google Scholar] [CrossRef] [PubMed]
- Cheng, C.; Li, J.; Liu, Y.; Nie, M.; Wang, W. Deep convolutional neural network-based in-process tool condition monitoring in abrasive belt grinding. Comput. Ind. 2019, 106, 1–13. [Google Scholar] [CrossRef]
- Zhao, R.; Wang, D.; Yan, R.; Mao, K.; Shen, F.; Wang, J. Machine health monitoring using local feature-based gated recurrent unit networks. IEEE Trans. Ind. Electron. 2017, 65, 1539–1548. [Google Scholar] [CrossRef]
- 2010 PHM Society Conference Data Challenge. Available online: https://www.phmsociety.org/competition/phm/10 (accessed on 1 June 2022).
- Chen, Y.C.; Li, D.C. Selection of key features for PM2.5 prediction using a wavelet model and RBF-LSTM. Appl. Intell. 2021, 51, 2534–2555. [Google Scholar] [CrossRef]
- Kuo, C.J.; Ting, K.C.; Chen, Y.C.; Yang, D.L.; Chen, H.M. Automatic machine status prediction in the era of industry 4.0: Case study of machines in a spring factory. J. Syst. Archit. 2017, 81, 44–53. [Google Scholar] [CrossRef]
- Duerden, A.; Marshall, F.E.; Moon, N.; Swanson, C.; Donnell, K.; Grubbs, G.S., II. A chirped pulse Fourier transform microwave spectrometer with multi-antenna detection. J. Mol. Spectrosc. 2021, 376, 111396. [Google Scholar] [CrossRef]
- Xu, W.; Xu, K.J.; Yu, X.L.; Huang, Y.; Wu, W.K. Signal processing method of bubble detection in sodium flow based on inverse Fourier transform to calculate energy ratio. Nucl. Eng. Technol. 2021, 53, 3122–3125. [Google Scholar] [CrossRef]
- Jalayer, M.; Orsenigo, C.; Vercellis, C. Fault detection and diagnosis for rotating machinery: A model based on convolutional LSTM, Fast Fourier and continuous wavelet transforms. Comput. Ind. 2021, 125, 103378. [Google Scholar] [CrossRef]
- Koga, K. Signal processing approach to mesh refinement in simulations of axisymmetric droplet dynamics. J. Comput. Appl. Math. 2021, 383, 113131. [Google Scholar] [CrossRef]
- Grossmann, A.; Kronland-Martinet, R.; Morlet, J. Reading and Understanding Continuous Wavelet Transforms. In Wavelets. Inverse Problems and Theoretical Imaging; Combes, J.M., Grossmann, A., Tchamitchian, P., Eds.; Springer: Berlin/Heidelberg, Germany, 1989. [Google Scholar]
- Heusel, M.; Ramsauer, H.; Unterthiner, T.; Nessler, B.; Hochreiter, S. GANs trained by a two time-scale update rule converge to a local nash equilibrium. In Proceedings of the International Conference on Neural Information Processing Systems (NIPS’17), Long Beach, CA, USA, 4–9 December 2017; pp. 6629–6640. [Google Scholar]
- Shorten, C.; Khoshgoftaar, T.M. A survey on image data augmentation for deep learning. J. Big Data 2019, 6, 1–48. [Google Scholar] [CrossRef]
- Koziarski, M.; Kwolek, B.; Cyganek, B. Convolutional neural network-based classification of histopathological images affected by data imbalance. In Proceedings of the Video Analytics. Face and Facial Expression Recognition, 3rd International Workshop, FFER 2018, and 2nd International Workshop, DLPR 2018, Beijing, China, 20 August 2018; pp. 1–11. [Google Scholar]
- Bustillo, A.; Rodríguez, J.J. Online breakage detection of multitooth tools using classifier ensembles for imbalanced data. Int. J. Syst. Sci. 2014, 45, 2590–2602. [Google Scholar] [CrossRef]
- Mathew, J.; Pang, C.K.; Luo, M.; Leong, W.H. Classification of imbalanced data by oversampling in kernel space of support vector machines. IEEE Trans. Neural Netw. Learn. Syst. 2017, 29, 4065–4076. [Google Scholar] [CrossRef] [PubMed]
- Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic minority over-sampling technique. J. Artif. Intell. Res. 2002, 16, 321–357. [Google Scholar] [CrossRef]
- Hassan, A.R.; Bhuiyan, M.I.H. Automated identification of sleep states from EEG signals by means of ensemble empirical mode decomposition and random under sampling boosting. Comput. Methods Programs Biomed. 2017, 140, 201–210. [Google Scholar] [CrossRef] [PubMed]
- Krawczyk, B.; Galar, M.; Jeleń, Ł.; Herrera, F. Evolutionary undersampling boosting for imbalanced classification of breast cancer malignancy. Appl. Soft Comput. 2016, 38, 714–726. [Google Scholar] [CrossRef]

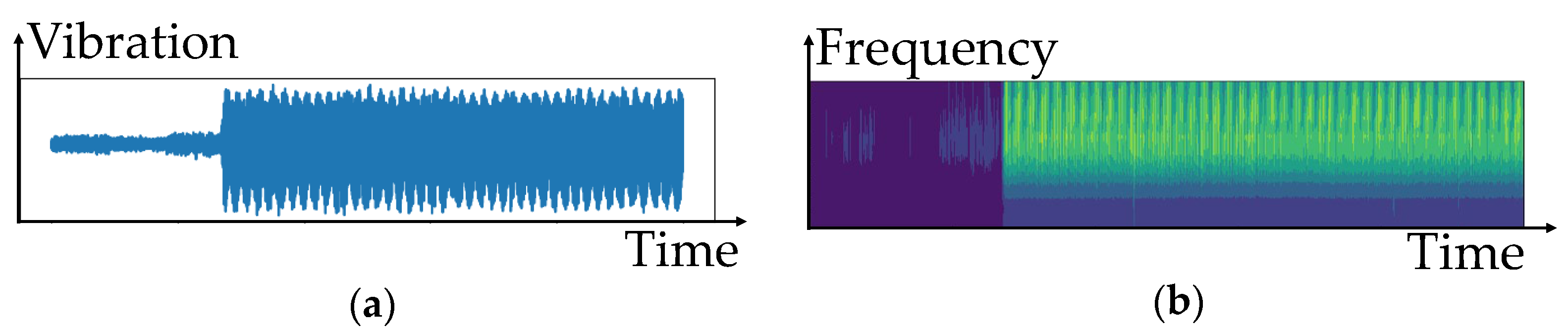



| Acceleration in x Axis | Acceleration in y Axis | Acceleration in z Axis | x Vibrations | y Vibrations | z Vibrations | Acoustic Emission | |
|---|---|---|---|---|---|---|---|
| 1 | 0.704 | −0.387 | −1.084 | 0.018 | 0.031 | 0.027 | −0.004 |
| 2 | 0.772 | −0.573 | −1.153 | −0.056 | −0.057 | −0.058 | −0.004 |
| 3 | 0.828 | −0.673 | −1.242 | 0.037 | 0.019 | 0.031 | −0.004 |
| … | … | … | … | … | … | … | … |
| 127,399 | 0.207 | 0.483 | 0.292 | 0.111 | 0.114 | 0.125 | −0.004 |
| Layer | Type | Output Size | Kernel Size | Stride | Activation Function |
|---|---|---|---|---|---|
| Input | Input | - | - | - | |
| U1 | Upsampling | - | - | - | |
| C2 | Convolutional | 3 | 2 | LeakyReLU | |
| U3 | Upsampling | - | - | - | |
| C4 | Convolutional | 3 | 2 | LeakyReLU | |
| U5 | Upsampling | - | - | - | |
| C6 | Convolutional | 3 | 2 | LeakyReLU | |
| U7 | Upsampling | - | - | - | |
| Output | Convolutional | - | - | tanh |
| Layer | Type | Output Size | Kernel Size | Stride | Activation Function |
|---|---|---|---|---|---|
| Input | Input | - | - | - | |
| C1 | Convolutional | 3 | 2 | LeakyReLU | |
| C2 | Convolutional | 3 | 2 | LeakyReLU | |
| BN3 | Batch normalization | - | - | - | |
| C4 | Convolutional | 3 | 2 | LeakyReLU | |
| BN5 | Batch normalization | - | - | - | |
| C6 | Convolutional | 3 | 1 | LeakyReLU | |
| BN7 | Batch normalization | - | - | - | |
| Output | Fully connected | 1 | - | - | - |
| Layer | Type | Output Size | Kernel Size | Stride | Activation Function |
|---|---|---|---|---|---|
| Input | Input | - | - | - | |
| C1 | Convolutional | 3 | 1 | Relu | |
| P2 | Max pooling | - | - | - | |
| C3 | Convolutional | 3 | 1 | Relu | |
| P4 | Max pooling | - | - | - | |
| C5 | Convolutional | 3 | 1 | Relu | |
| P6 | Max pooling | - | - | - | |
| C7 | Convolutional | 3 | 1 | Relu | |
| P8 | Max pooling | - | - | - | |
| F9 | Fully connected | 512 | - | - | Relu |
| Output | Fully connected | 3 | - | - | softmax |
| Time Series Feature Extraction | FFT | Continuous Wavelet Transform | |
|---|---|---|---|
| Original data | 90.08% | 88.13% | 94.41% |
| Augmentation | 83.40% | 84.01% | 93.51% |
| SMOTE | 83.45% | 82.88% | 92.67% |
| Downsampling | 86.09% | 86.22% | 95.05% |
| GAN | 88.17% | 85.85% | 96.50% |
| Time Series Feature Extraction | FFT | Continuous Wavelet Transform | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Rapid Initial | Uniform | Failure | Rapid Initial | Uniform | Failure | Rapid Initial | Uniform | Failure | |
| Number of data | 124 | 9919 | 3543 | 124 | 9919 | 3543 | 124 | 9919 | 3543 |
| Original data | 98.39% | 96.22% | 72.88% | 100.00% | 84.50% | 98.11% | 0.00% | 97.43% | 89.53% |
| Augmentation | 100.00% | 86.95% | 73.13% | 100.00% | 93.30% | 57.69% | 84.68% | 93.93% | 92.89% |
| SMOTE | 100.00% | 88.03% | 70.31% | 100.00% | 85.35% | 75.61% | 83.87% | 92.48% | 93.76% |
| Downsampling | 100.00% | 87.68% | 81.40% | 100.00% | 88.05% | 80.86% | 45.16% | 96.85% | 92.01% |
| GAN | 97.58% | 98.75% | 58.51% | 100.00% | 98.40% | 50.52% | 64.52% | 98.93% | 91.08% |
| Rapid Initial Wear (Recall) | Uniform Wear (Recall) | Failure Wear (Recall) | |
|---|---|---|---|
| Time series feature extraction | 97.58% | 98.75% | 58.51% |
| FFT | 100.00% | 98.40% | 50.52% |
| Continuous wavelet transform | 64.52% | 98.93% | 91.08% |
| Ensemble | 98% | 99% | 88% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, B.-X.; Chen, Y.-C.; Loh, C.-H.; Chou, Y.-C.; Wang, F.-C.; Su, C.-T. Application of Generative Adversarial Network and Diverse Feature Extraction Methods to Enhance Classification Accuracy of Tool-Wear Status. Electronics 2022, 11, 2364. https://doi.org/10.3390/electronics11152364
Chen B-X, Chen Y-C, Loh C-H, Chou Y-C, Wang F-C, Su C-T. Application of Generative Adversarial Network and Diverse Feature Extraction Methods to Enhance Classification Accuracy of Tool-Wear Status. Electronics. 2022; 11(15):2364. https://doi.org/10.3390/electronics11152364
Chicago/Turabian StyleChen, Bo-Xiang, Yi-Chung Chen, Chee-Hoe Loh, Ying-Chun Chou, Fu-Cheng Wang, and Chwen-Tzeng Su. 2022. "Application of Generative Adversarial Network and Diverse Feature Extraction Methods to Enhance Classification Accuracy of Tool-Wear Status" Electronics 11, no. 15: 2364. https://doi.org/10.3390/electronics11152364
APA StyleChen, B.-X., Chen, Y.-C., Loh, C.-H., Chou, Y.-C., Wang, F.-C., & Su, C.-T. (2022). Application of Generative Adversarial Network and Diverse Feature Extraction Methods to Enhance Classification Accuracy of Tool-Wear Status. Electronics, 11(15), 2364. https://doi.org/10.3390/electronics11152364







