A Novel MPPT Algorithm for Photovoltaic Systems Based on Improved Sliding Mode Control
Abstract
:1. Introduction
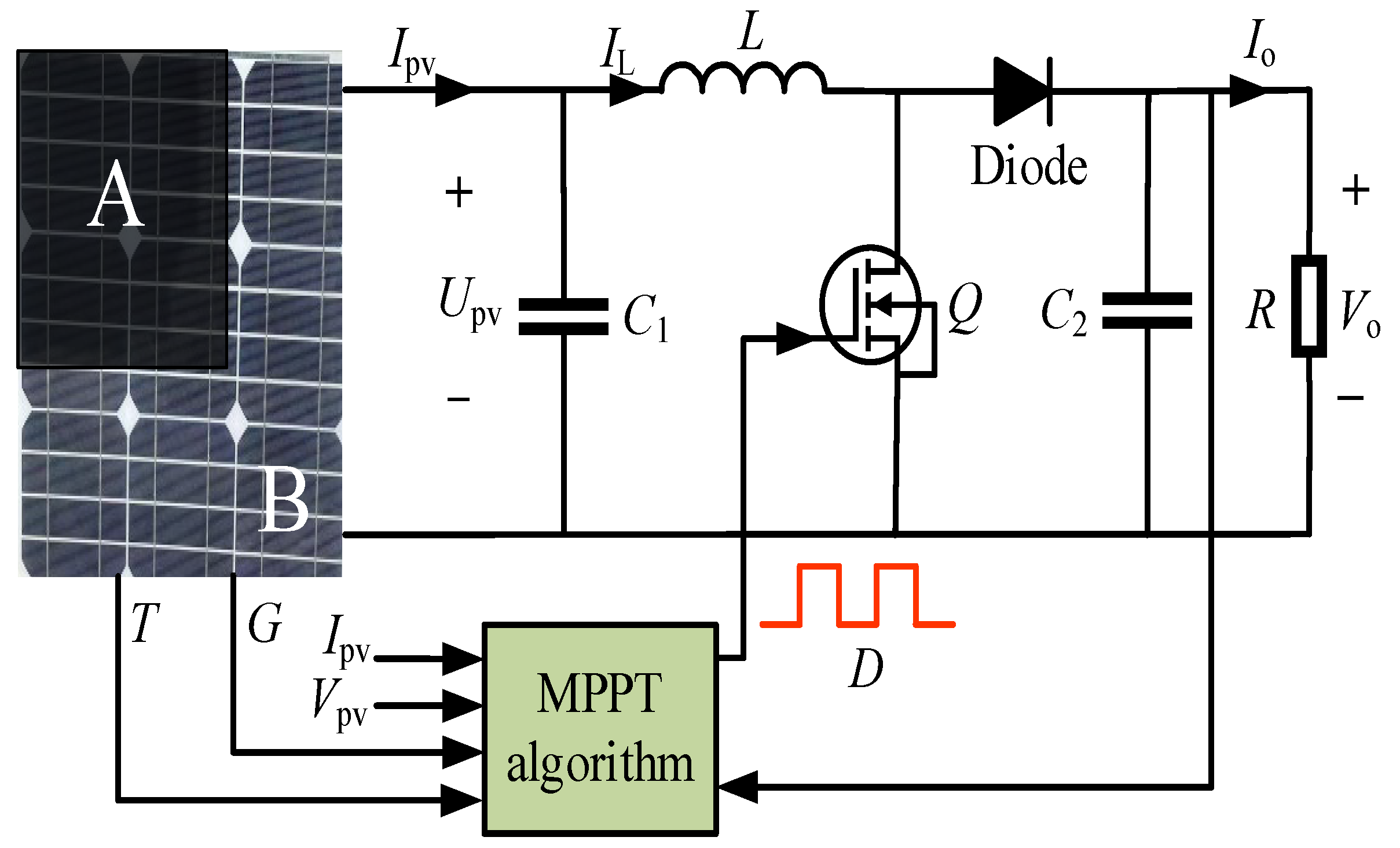
2. Control Principle of PV System
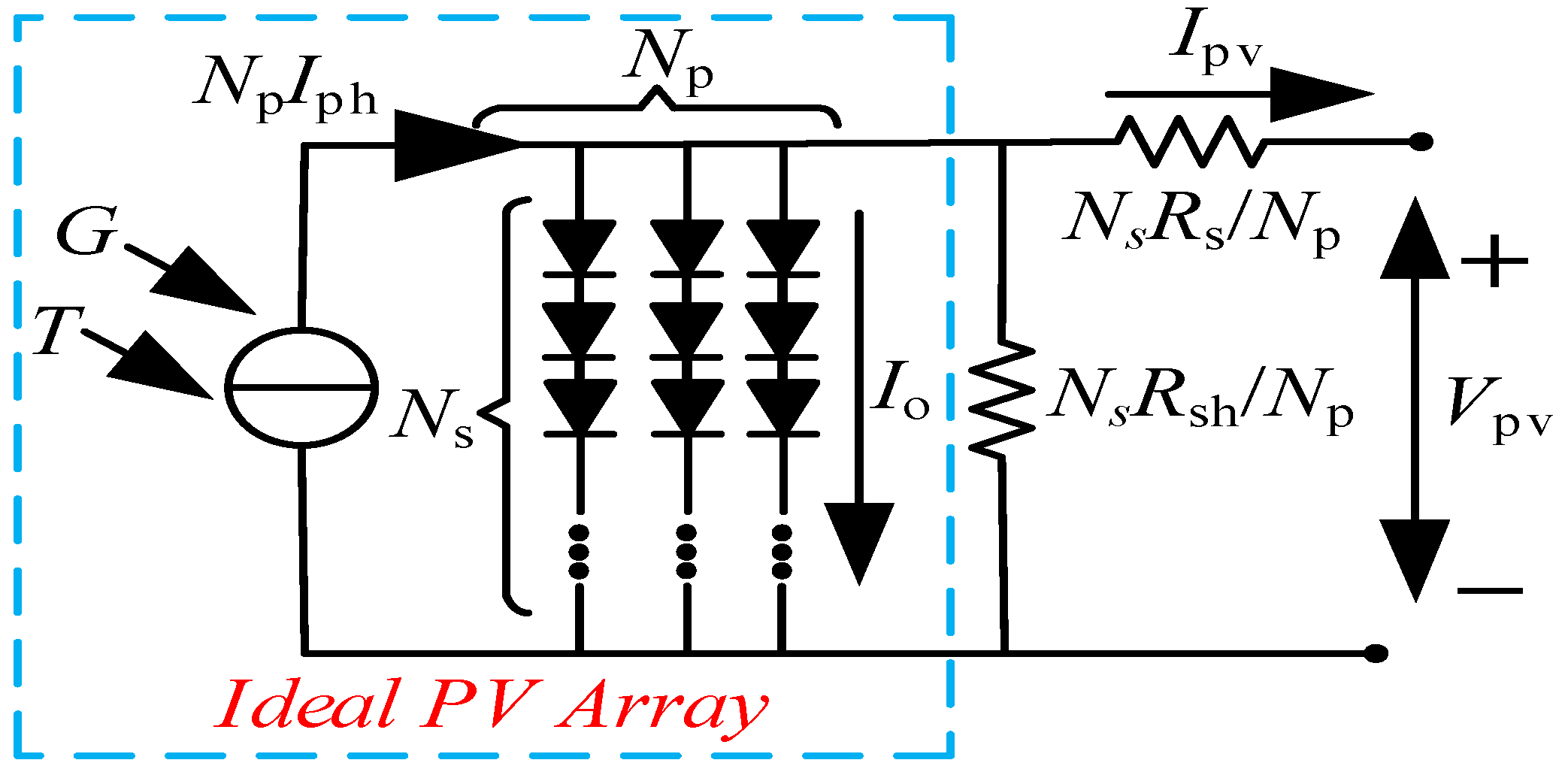
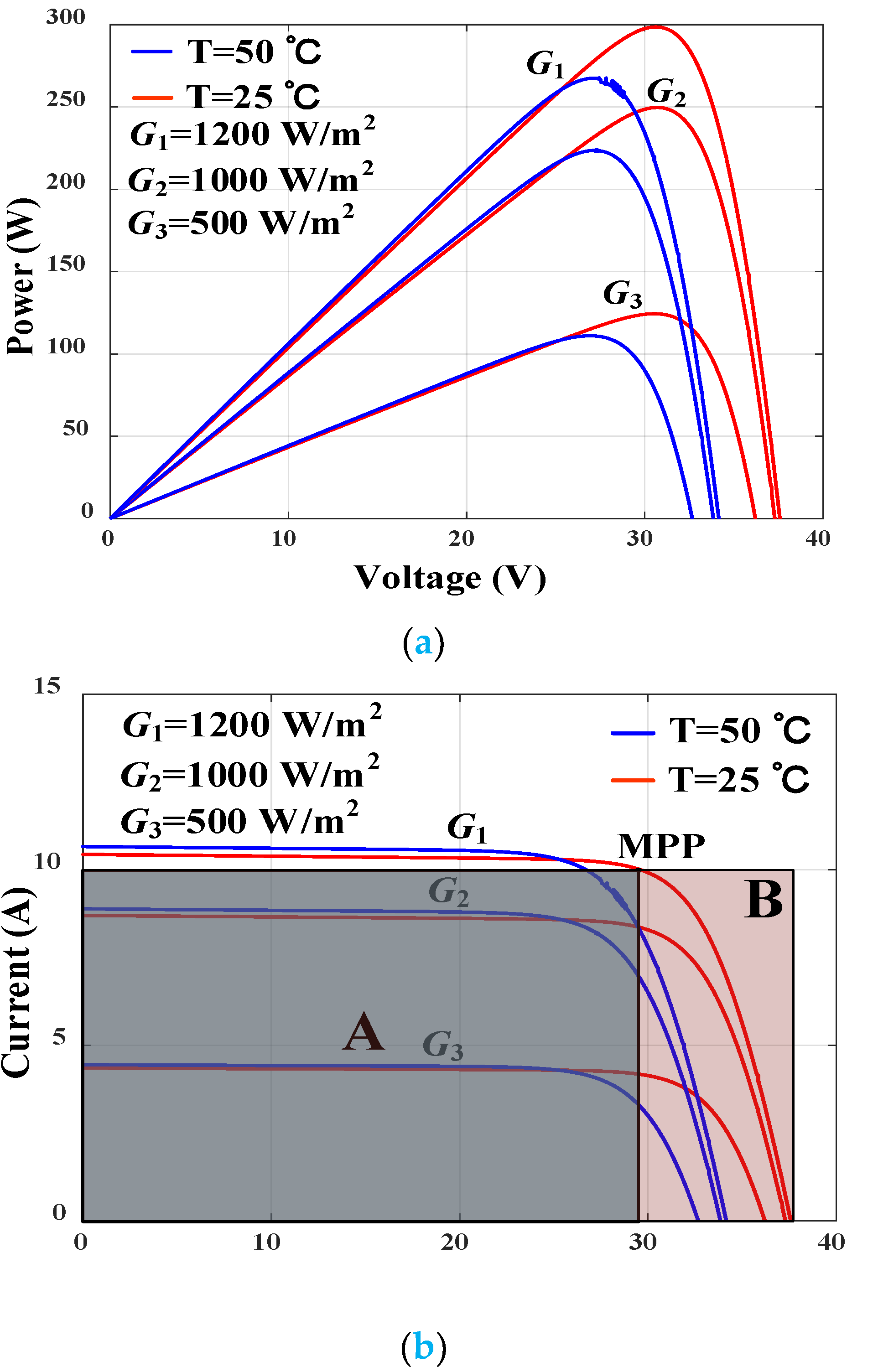
2.1. Mathematical Model of PV Array
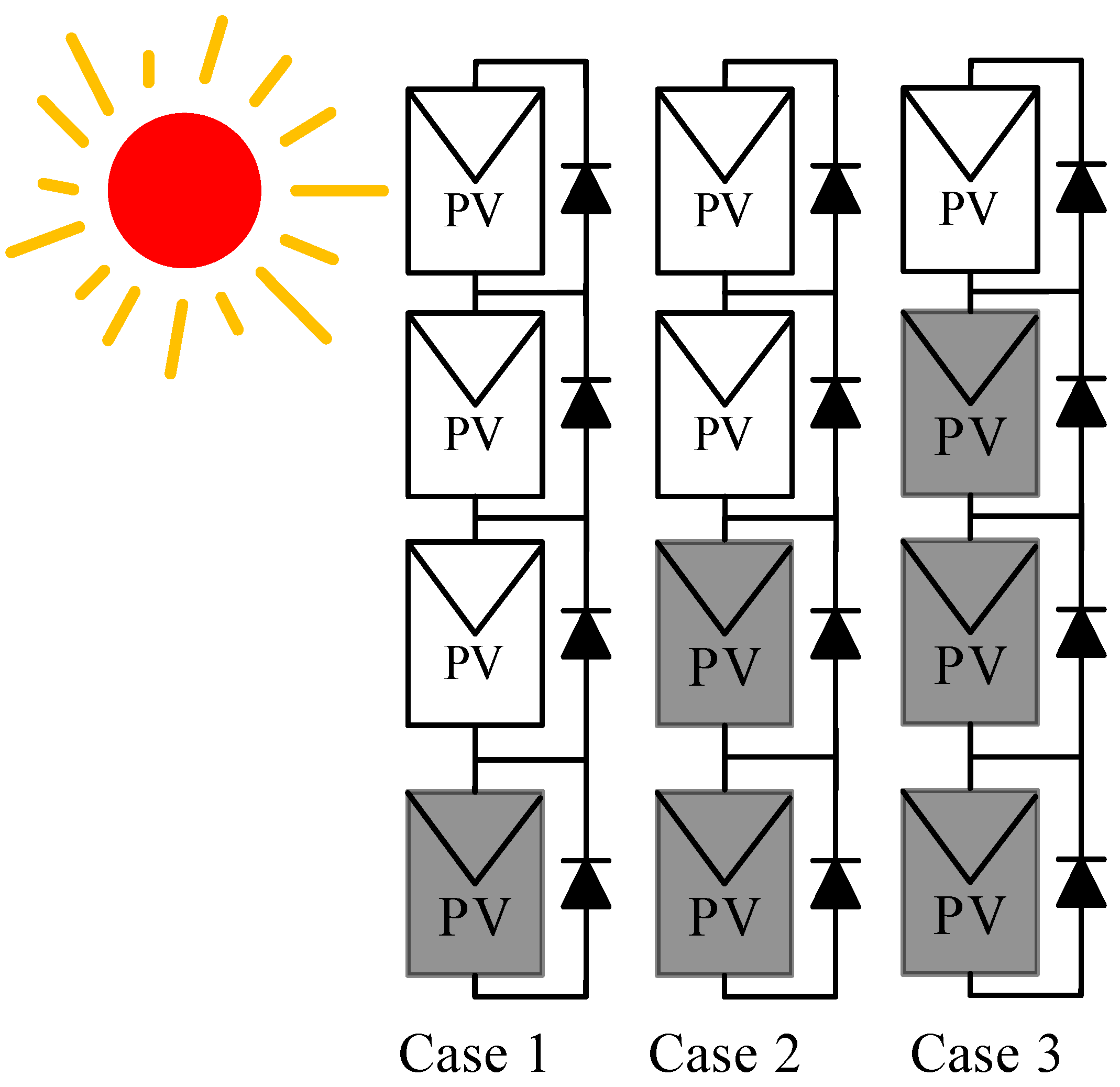
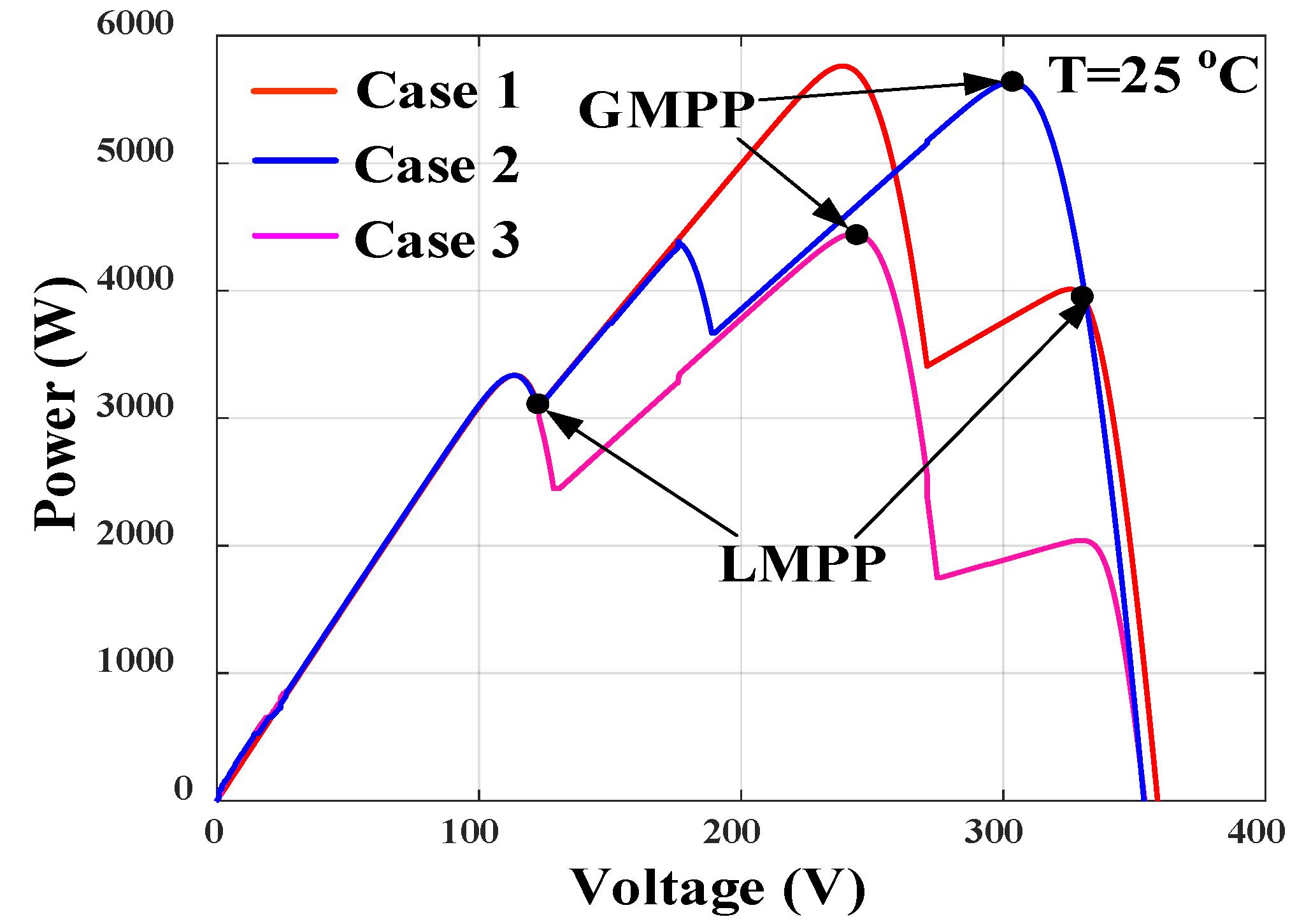
2.2. Modeling of PV Array at Partial Shading Conditions
2.3. Mathematical Model of Boost Converter
3. Improved SMC Strategy
3.1. Improvement of Sliding Surface
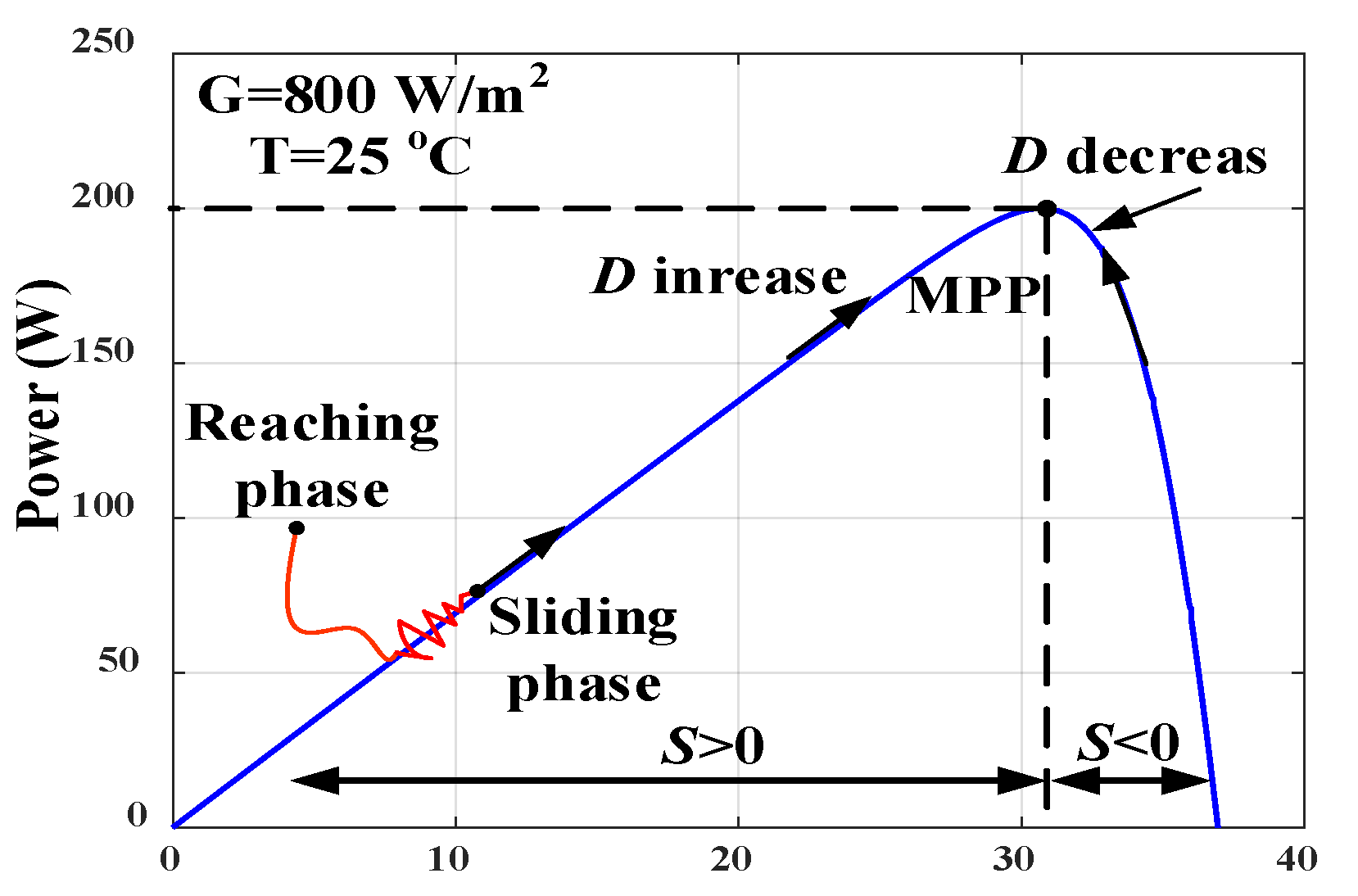
3.2. Selection of Control Law
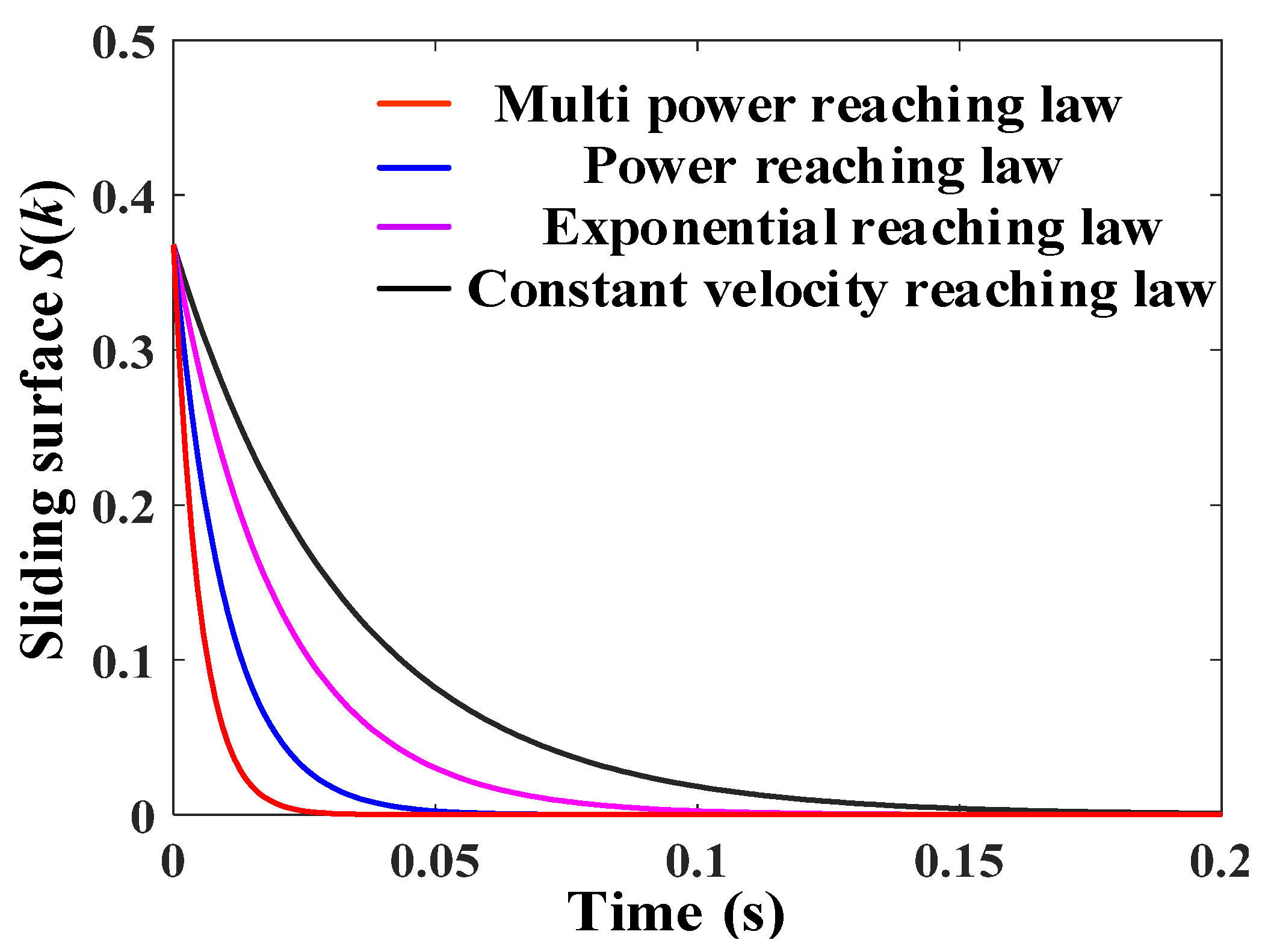
3.3. Multi-Power Reaching Law
- Constant velocity reaching law:where ε represents the reaching rate. The constant velocity reaching law has characteristics of simplicity and expansion. However, the reaching rate is a fixed value and the convergence is incompatible with system buffeting in SMC structures [25].
- Exponential reaching law:where −kS represents the exponential reaching term, and the numerical solution is S = S(0)e−kt. The exponential reaching law reduces the reaching time and system inertia of SMC by using the exponential reaching term. However, reaching the sliding surface is an asymptotic process with finite convergence [26].
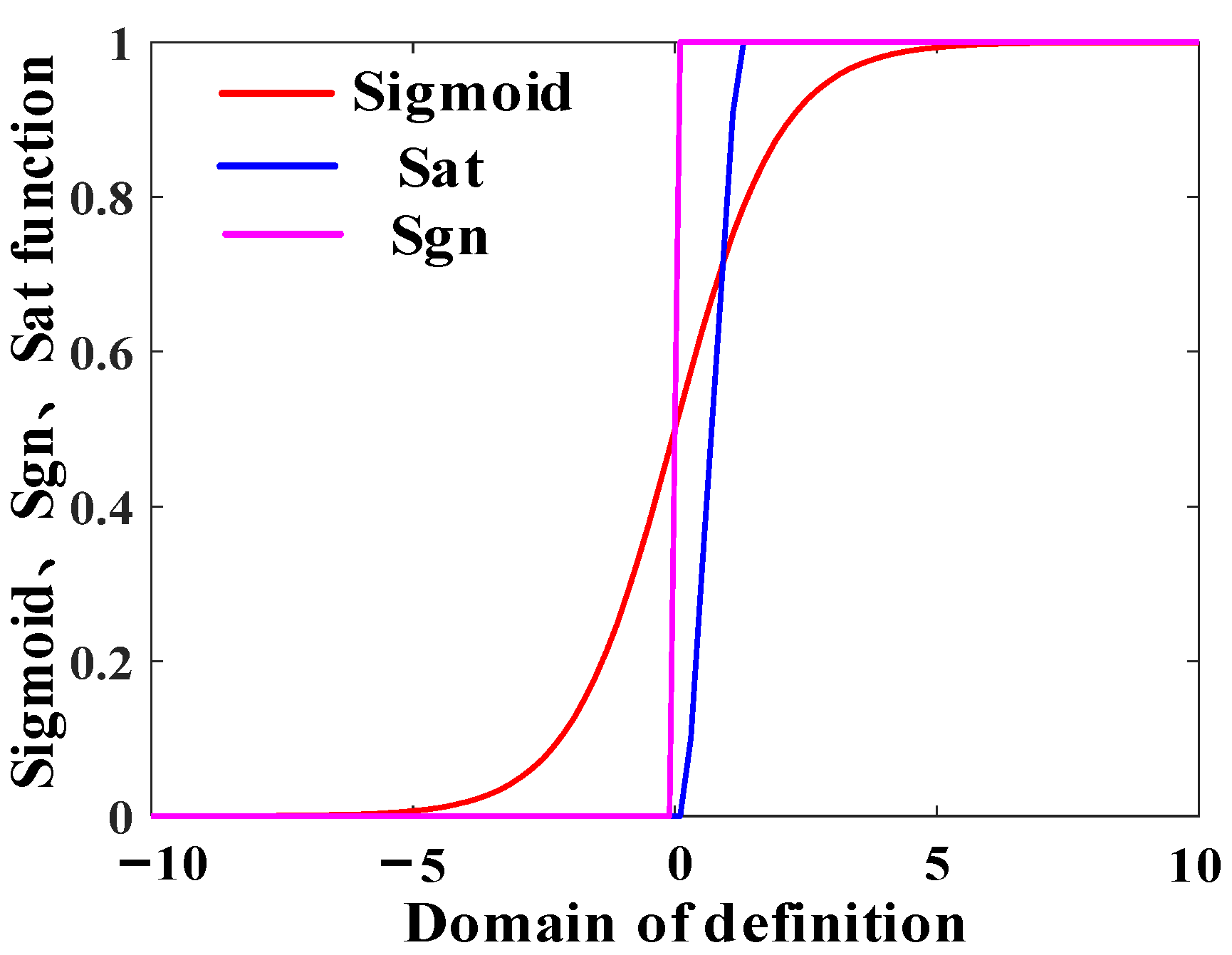
- Power reaching law:where −k|S|a is the power term. The power reaching law reaches to the sliding surface S with a great velocity by adjusting the power exponent a, yet the system state trajectory is stabilized in the neighborhood of origin. In addition, in the power reaching law exists a quantitative feedback gain, which deteriorates the buffeting of PV systems. In addition, there are trailing currents and parasitic diodes in the switching tube Q, and the symbolic function (sgn) is an ideal switching characteristic and the switching action has hysteresis and trailing phenomenon, which further exacerbates the dead zone range of the state quantity and the switching discontinuity [27]. To solve the problems mentioned above, a multi-power sliding reaching law is proposed, in which the sigmod function is used to replace the sgn function to improve the dynamic control quality of PV systems. Figure 10 shows the sigmoid, sat and sgn functions. A multi-power reaching law is defined in Equation (19).
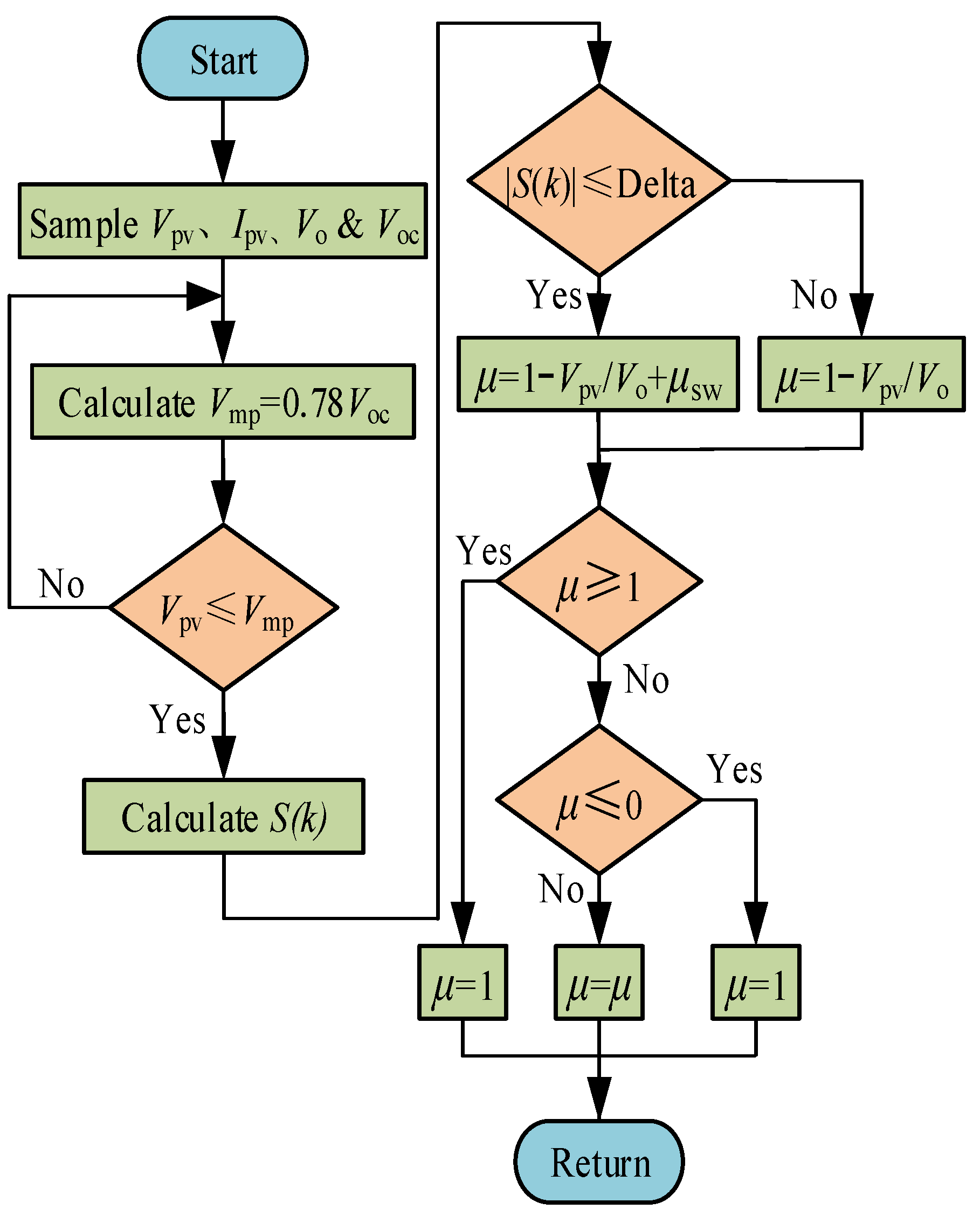
3.4. The Flowchart of Improved SMC Strategy
4. Simulation Results and Discussions
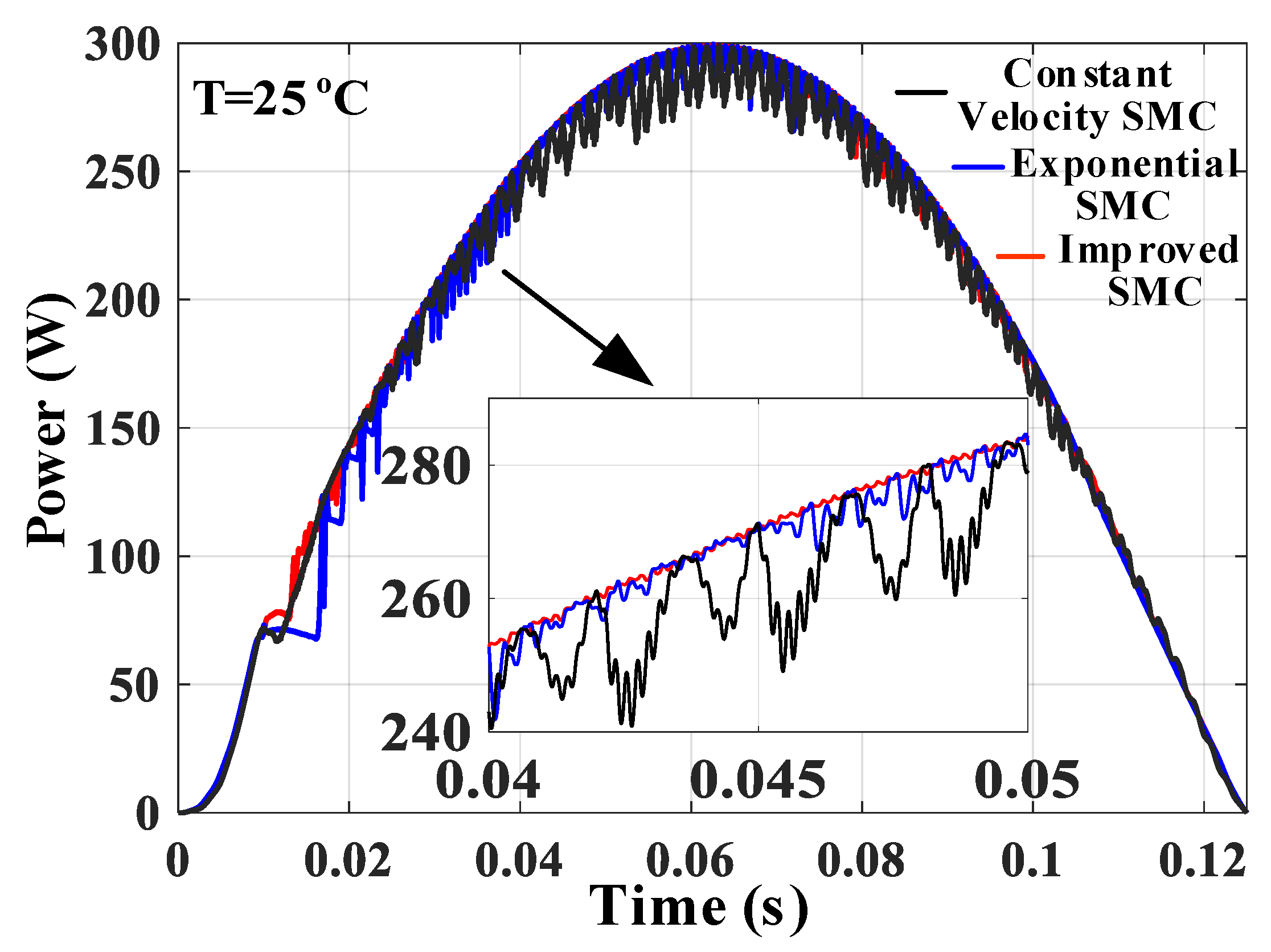
4.1. MPPT Tracking Performance at Dynamic Condition
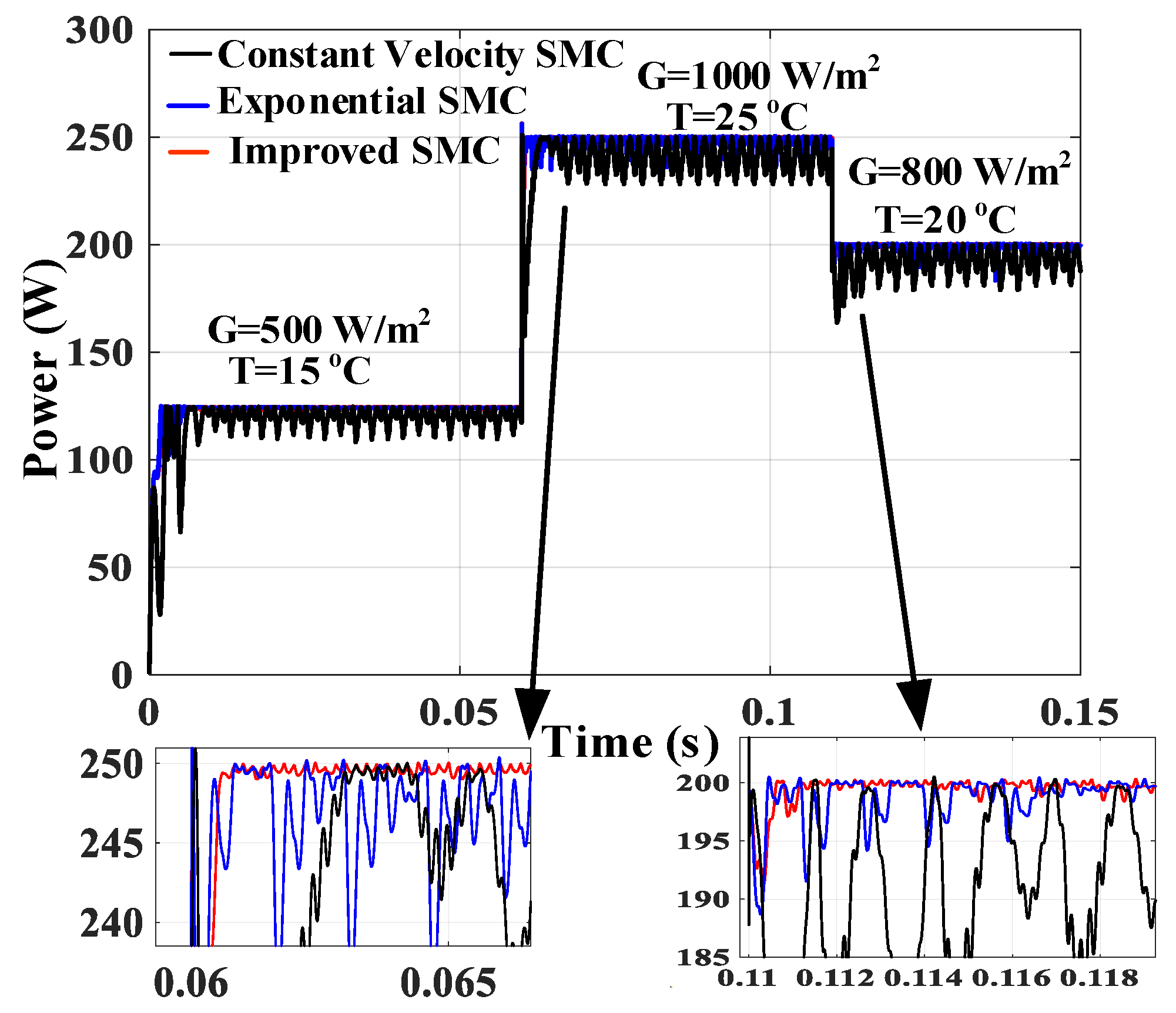
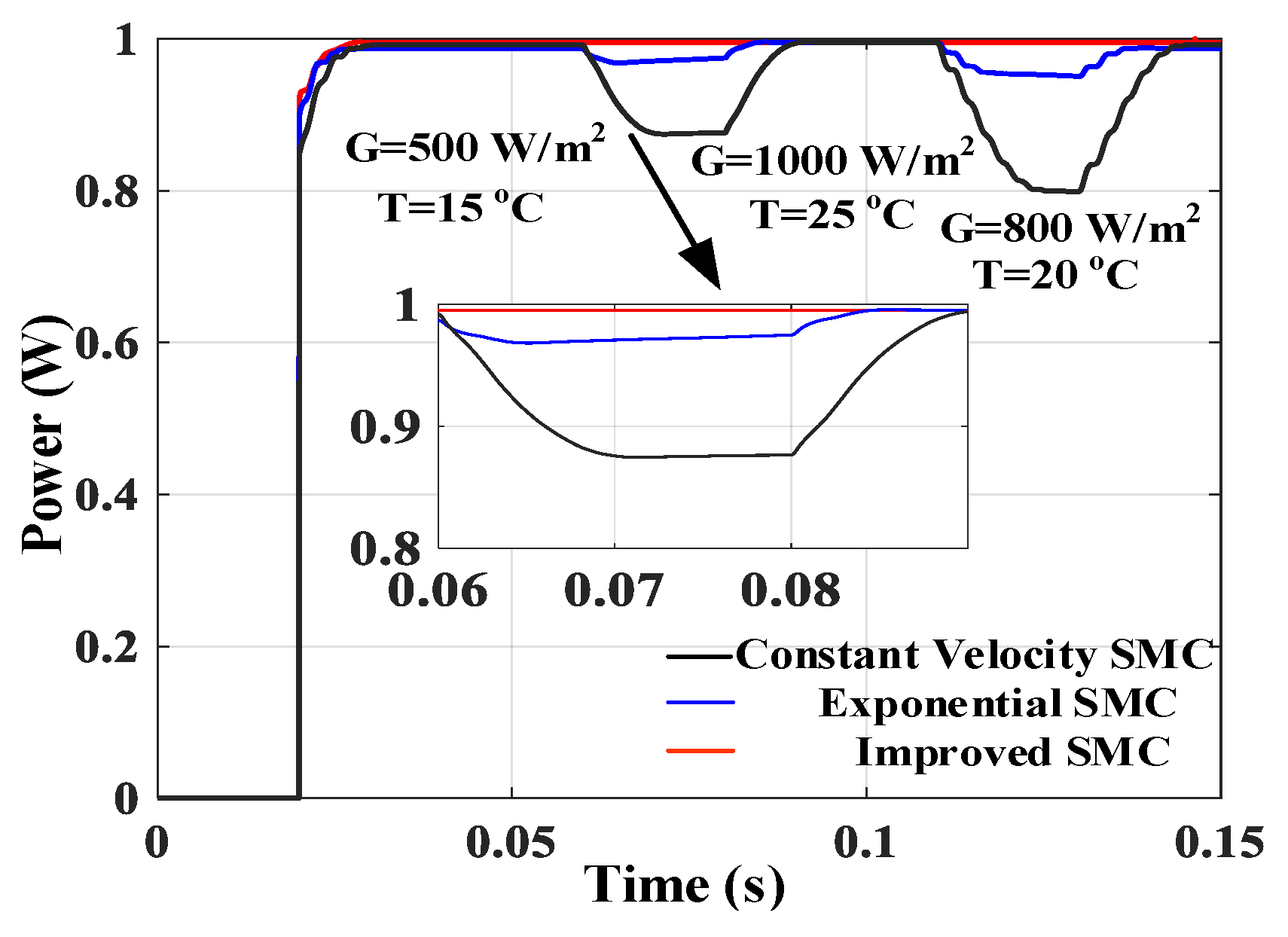
4.2. MPPT Tracking Performance at PSC
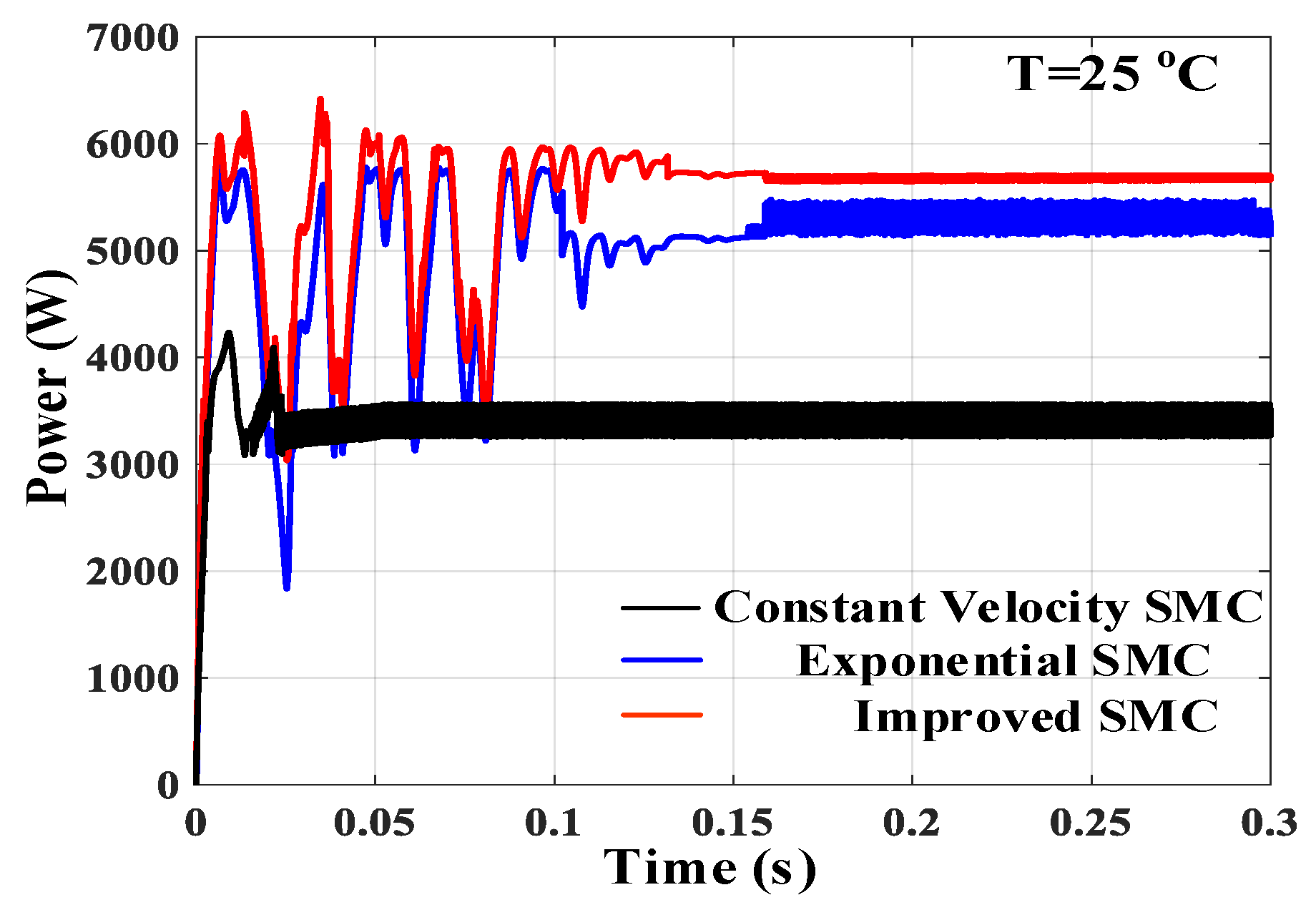
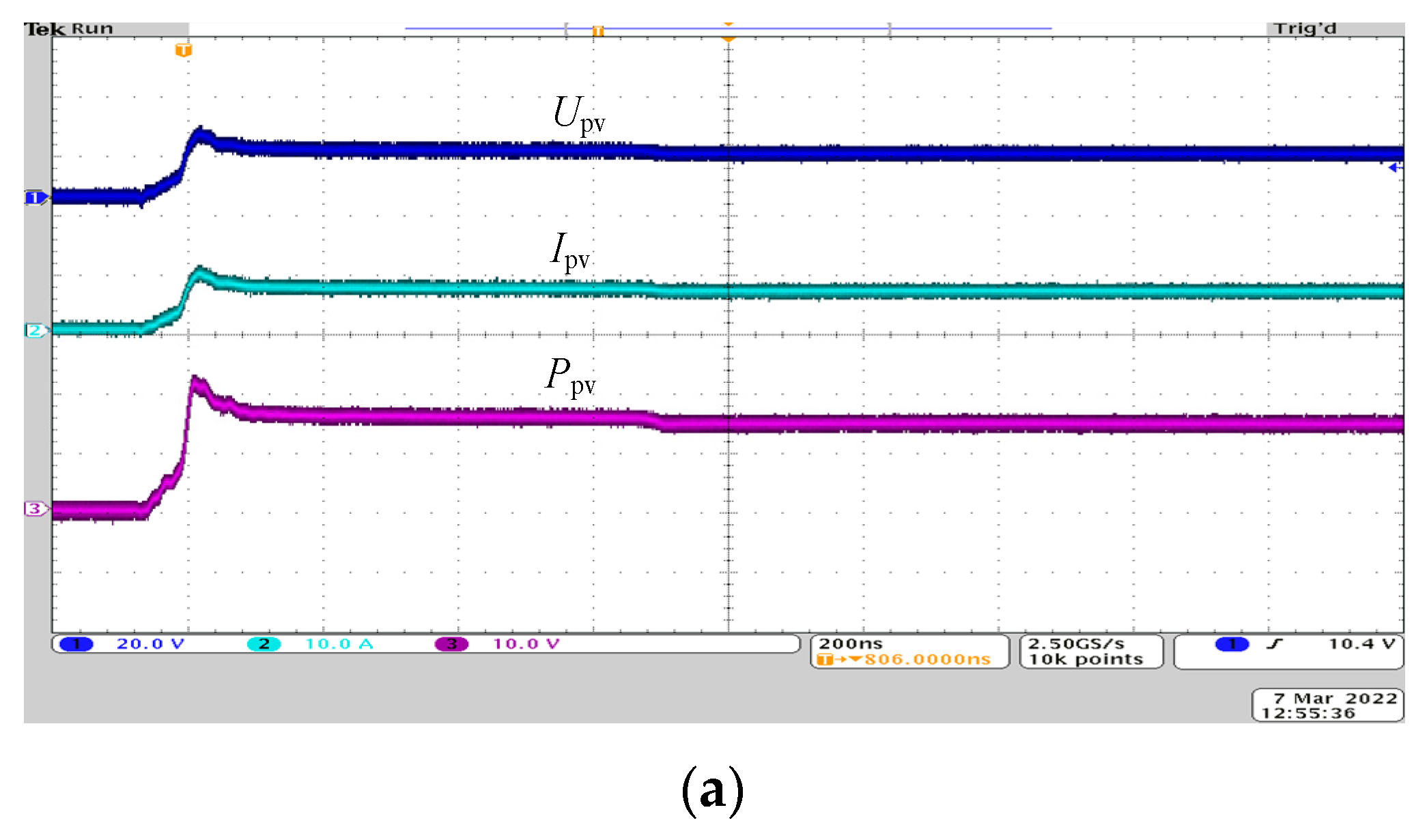
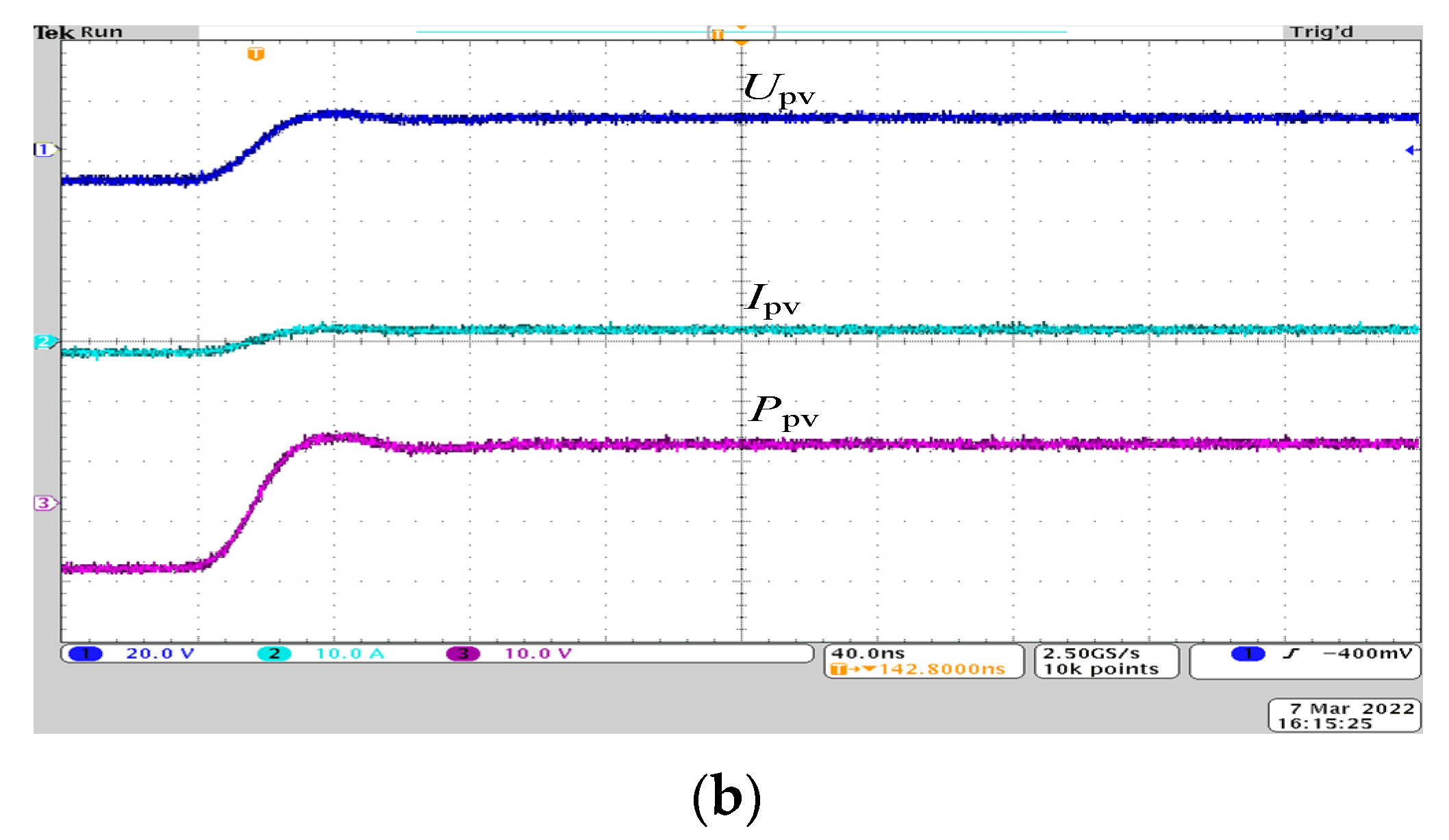
5. Experimental Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| PV | photovoltaic |
| MPP | maximum power point |
| MPPT | maximum power point tracking |
| P&O | perturbation and observation |
| INC | incremental conductance |
| G | irradiance |
| T | temperature |
| STC | standard test conditions (G = 1000 W/m2, T = 25 °C) |
| ANN | artificial neural network |
| SMC | sliding model control |
| Sat | saturation function |
| PSC | partial shading condition |
| D | duty cycle |
| KVL | Kirchhoff Voltage Law |
| Isc | short-circuit current |
| Voc | open-circuit voltage |
| Impp | maximum power point current |
| Vmpp | maximum power point voltage |
| FF | fill factor |
| GMPP | global maximum power point |
| LMPP | local maximum power point |
| CCM | continuous conduction mode |
| BCM | boundary conduction mode |
| DCM | discontinuous conduction mode |
| s | sliding mode surface |
| S(k) | proposed sliding mode surface |
| Sgn | symbolic function |
References
- Bollipo, R.B.; Mikkili, S.; Bonthagorla, P.K. Hybrid, optimal, intelligent and classical PV MPPT techniques: A review. CSEE J. Power Energy 2020, 7, 9–33. [Google Scholar]
- Eltamaly, A.M. A novel musical chairs algorithm applied for MPPT of PV systems. Renew. Sust. Energ. Rev. 2021, 146, 111135–111148. [Google Scholar] [CrossRef]
- Priyadarshi, N.; Padmanaban, S.; Holm-Nielsen, J.B.; Blaabjerg, F.; Bhaskar, M.S. An experimental estimation of hybrid ANFIS–PSO-based MPPT for PV grid integration under fluctuating sun irradiance. IEEE Syst. J. 2019, 14, 1218–1229. [Google Scholar] [CrossRef]
- Podder, A.K.; Roy, N.K.; Pota, H.R. MPPT methods for solar PV systems: A critical review based on tracking nature. IET Renew. Power Gen. 2019, 13, 1615–1632. [Google Scholar] [CrossRef]
- Mansoor, M.; Mirza, A.F.; Ling, Q. Harris hawk optimization-based MPPT control for PV systems under partial shading conditions. J. Clean. Prod. 2020, 274, 122857–122871. [Google Scholar] [CrossRef]
- Valenciaga, F.; Inthamoussou, F.A. A novel PV-MPPT method based on a second order sliding mode gradient observer. Energy Convers. Manag. 2018, 176, 422–430. [Google Scholar] [CrossRef]
- Mirz, A.F.; Mansoor, M.; Ling, Q.; Yin, B.; Javed, M.Y. A Salp-Swarm Optimization based MPPT technique for harvesting maximum energy from PV systems under partial shading conditions. Energy Convers. Manag. 2020, 209, 112625–112637. [Google Scholar] [CrossRef]
- Shao, W.Q.; Wang, M.; Wu, C.Q.; Cheng, Y.; Liu, Y.L. MPPT control strategy based on improved sliding mode control for photovoltaic power system. Acta Energy Sol. Sin. 2021, 42, 87–93. [Google Scholar]
- Li, Z.M.; Shan, X.C.; Xu, P.K. Super-twisting sliding mode controller used in photovoltaic system MPPT. Power Syst. Prot. Control. 2018, 46, 32–37. [Google Scholar]
- Luo, D.; Zheng, J.D. MPPT technology based on improved sliding mode control. Electr. Drive 2017, 47, 63–66. [Google Scholar]
- Nadeem, A.; Sher, H.A.; Murtaza, A.F.; Ahmed, N. An online fractional open-circuit voltage maximum power point tracking (MPPT) algorithm based on sliding mode control. In Proceedings of the 2020 International Symposium on Recent Advances in Electrical Engineering & Computer Sciences (RAEE & CS), Islamabad, Pakistan, 20–22 October 2020; Volume 5, pp. 1–6. [Google Scholar]
- Latifi, M.; Abbassi, R.; Jerbi, H.; Ohshima, K. Improved krill herd algorithm based sliding mode MPPT controller for variable step size P&O method in PV system under simultaneous change of irradiance and temperature. J. Franklin. Ist. 2021, 358, 3491–3511. [Google Scholar]
- Khan, Z.A.; Khan, L.; Ahmad, S.; Mumtaz, S.; Jafar, M.; Khan, Q. RBF neural network based backstepping terminal sliding mode MPPT control technique for PV system. PLoS ONE 2021, 16, e0249705. [Google Scholar] [CrossRef]
- Rafika, E.L.; Abbou, A.; Mokhlis, M.; Bouzakri, H. Real-Time implementation of a PV system maximum power point tracking based on the ANN-Backstepping sliding mode control. Int. J. Renew. Energy Res. 2021, 11, 1959–1967. [Google Scholar]
- Nkambule, M.S.; Hasan, A.N.; Ali, A.; Hong, J.; Geem, Z.W. Comprehensive evaluation of machine learning MPPT algorithms for a PV system under different weather conditions. J. Electr. Eng. Technol. 2021, 16, 411–427. [Google Scholar] [CrossRef]
- Ali, A.I.M.; Mohamed, H.R.A. Improved P&O MPPT algorithm with efficient open-circuit voltage estimation for two-stage grid-integrated PV system under realistic solar radiation. Int. J. Elec. Power 2022, 137, 107805–107827. [Google Scholar]
- Mansoor, M.; Mirza, A.F.; Ling, Q.; Javed, M.Y. Novel Grass Hopper optimization based MPPT of PV systems for complex partial shading conditions. Sol. Energy 2020, 198, 499–518. [Google Scholar] [CrossRef]
- Abdel-Salam, M.; El-Mohandes, M.T.; Goda, M. An improved perturb-and-observe based MPPT method for PV systems under varying irradiation levels. Sol. Energy 2018, 171, 547–561. [Google Scholar] [CrossRef]
- Chai, L.G.K.; Gopal, L.; Juwono, F.H.; Chiong, C.W.; Ling, H.C.; Basuki, T.A. A novel global MPPT technique using improved PS-FW algorithm for PV system under partial shading conditions. Energy Convers. Manag. 2021, 246, 114639–114653. [Google Scholar] [CrossRef]
- Zhou, Y.; Ho, C.N.M.; Siu, K.K.M. A fast PV MPPT scheme using boundary control with second-order switching surface. IEEE J. Photovolt. 2019, 9, 849–857. [Google Scholar] [CrossRef]
- Bjaoui, M.; Khiari, B.; Benadli, R.; Memni, M.; Sellami, A. Practical implementation of the backstepping sliding mode controller MPPT for a PV-storage application. Energies 2019, 12, 3539. [Google Scholar] [CrossRef] [Green Version]
- Nasir, A.; Rasool, I.; Sibtain, D.; Kamran, R. Adaptive Fractional Order PID Controller Based MPPT for PV Connected Grid System Under Changing Weather Conditions. J. Electr. Eng. Technol. 2021, 16, 2599–2610. [Google Scholar] [CrossRef]
- Pati, N.; Panda, B. Control and regulation of the conversion phase of a double-stage grid connected PV system: H∞ and voltage sliding mode control. J. Electr. Eng. Technol. 2021, 16, 2731–2742. [Google Scholar] [CrossRef]
- Chinnappan, R.; Logamani, P.; Ramasubbu, R. Fixed frequency integral sliding mode current controlled MPPT boost converter for two-stage PV generation system. IET Circ. Device. Syst. 2019, 13, 793–805. [Google Scholar] [CrossRef]
- Bag, A.; Subudhi, B.; Ray, P.K. A combined reinforcement learning and sliding mode control scheme for grid integration of a PV system. CSEE J. Power Energy 2019, 5, 498–506. [Google Scholar]
- Pahari, O.P.; Subudhi, B. Integral sliding mode improved adaptive MPPT control scheme for suppressing grid current harmonics for PV system. IET Renew. Power Gen. 2018, 12, 1904–1914. [Google Scholar] [CrossRef]
- Salimi, M. Practical implementation of the Lyapunov based nonlinear controller in DC-DC boost converter for MPPT of the PV systems. Sol. Energy 2018, 173, 246–255. [Google Scholar] [CrossRef]






| 1Soltecg 1STH-215-P | Value |
|---|---|
| Open-circuit voltage Voc/V | 37.3 |
| Short-circuit current Isc/A | 8.66 |
| MPP voltage Vmp/V | 30.7 |
| MPP current Imp/A | 8.15 |
| Voc temperature coefficient (%/deg.c) | −0.36099 |
| Isc temperature coefficient (%/deg.c) | 0.102 |
| MPP power Pmp/W | 250.205 |
| Parameters | Improved SMC | Exponential SMC | Constant Velocity SMC |
|---|---|---|---|
| Multiple correlation coefficient | 0.9887 | 0.9543 | 0.9321 |
| Complex measurement coefficient | 0.9855 | 0.9521 | 0.9313 |
| Retest coefficient | 0.9855 | 0.9521 | 0.9313 |
| Standard deviation | 2.7653 | 5.6452 | 7.0021 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Wang, Y.-J.; Yu, J.-Q. A Novel MPPT Algorithm for Photovoltaic Systems Based on Improved Sliding Mode Control. Electronics 2022, 11, 2421. https://doi.org/10.3390/electronics11152421
Zhang Y, Wang Y-J, Yu J-Q. A Novel MPPT Algorithm for Photovoltaic Systems Based on Improved Sliding Mode Control. Electronics. 2022; 11(15):2421. https://doi.org/10.3390/electronics11152421
Chicago/Turabian StyleZhang, Yan, Ya-Jun Wang, and Jia-Qi Yu. 2022. "A Novel MPPT Algorithm for Photovoltaic Systems Based on Improved Sliding Mode Control" Electronics 11, no. 15: 2421. https://doi.org/10.3390/electronics11152421
APA StyleZhang, Y., Wang, Y.-J., & Yu, J.-Q. (2022). A Novel MPPT Algorithm for Photovoltaic Systems Based on Improved Sliding Mode Control. Electronics, 11(15), 2421. https://doi.org/10.3390/electronics11152421





