Understanding and Controlling Band Alignment at the Metal/Germanium Interface for Future Electric Devices
Abstract
:1. Introduction
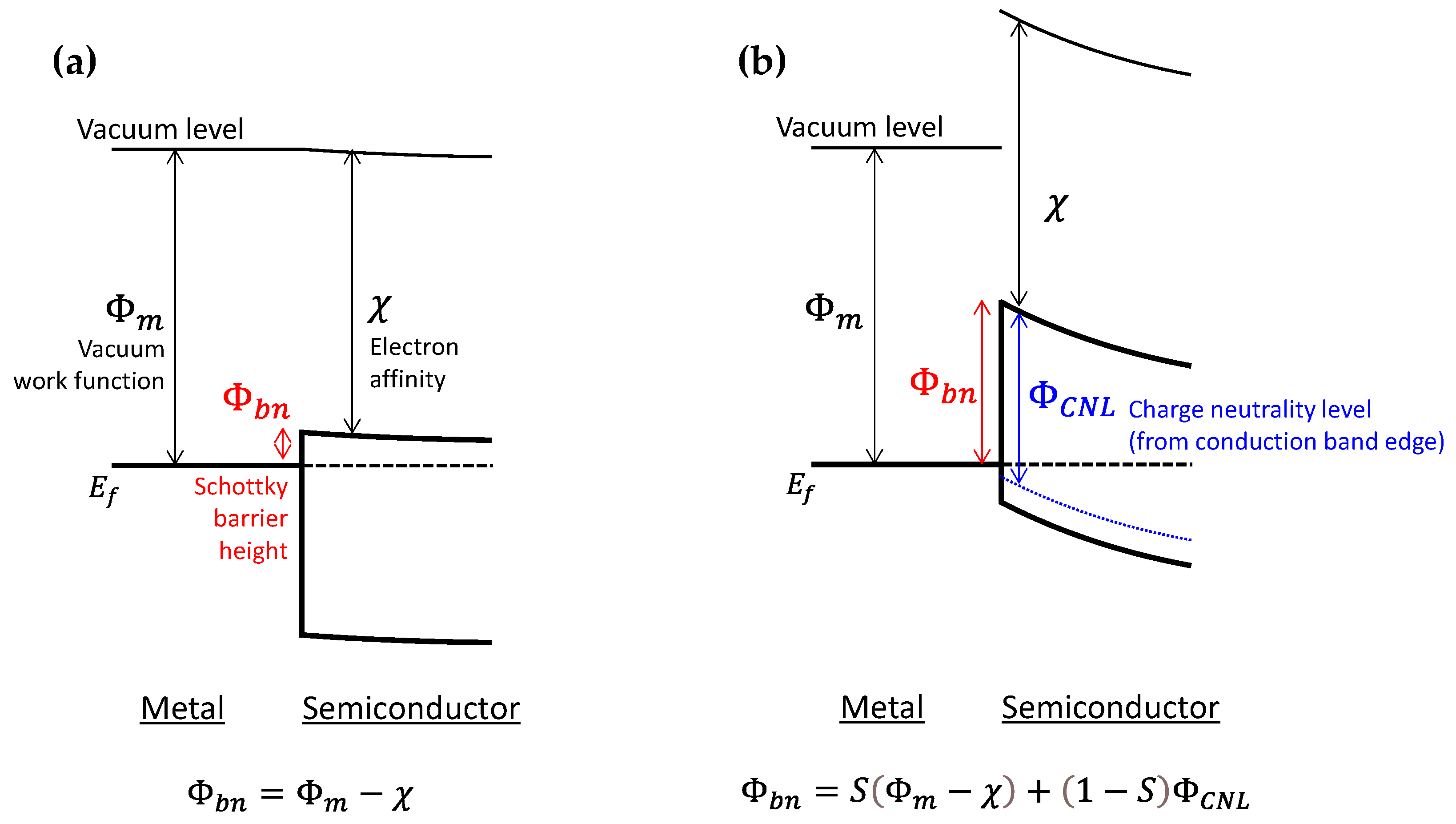
2. Fermi Level Pinning at the Metal/Ge Interface
3. Dominant FLP Mechanism at the Metal/Ge Interface
4. FLP Alleviation by Ultrathin Interface Layer
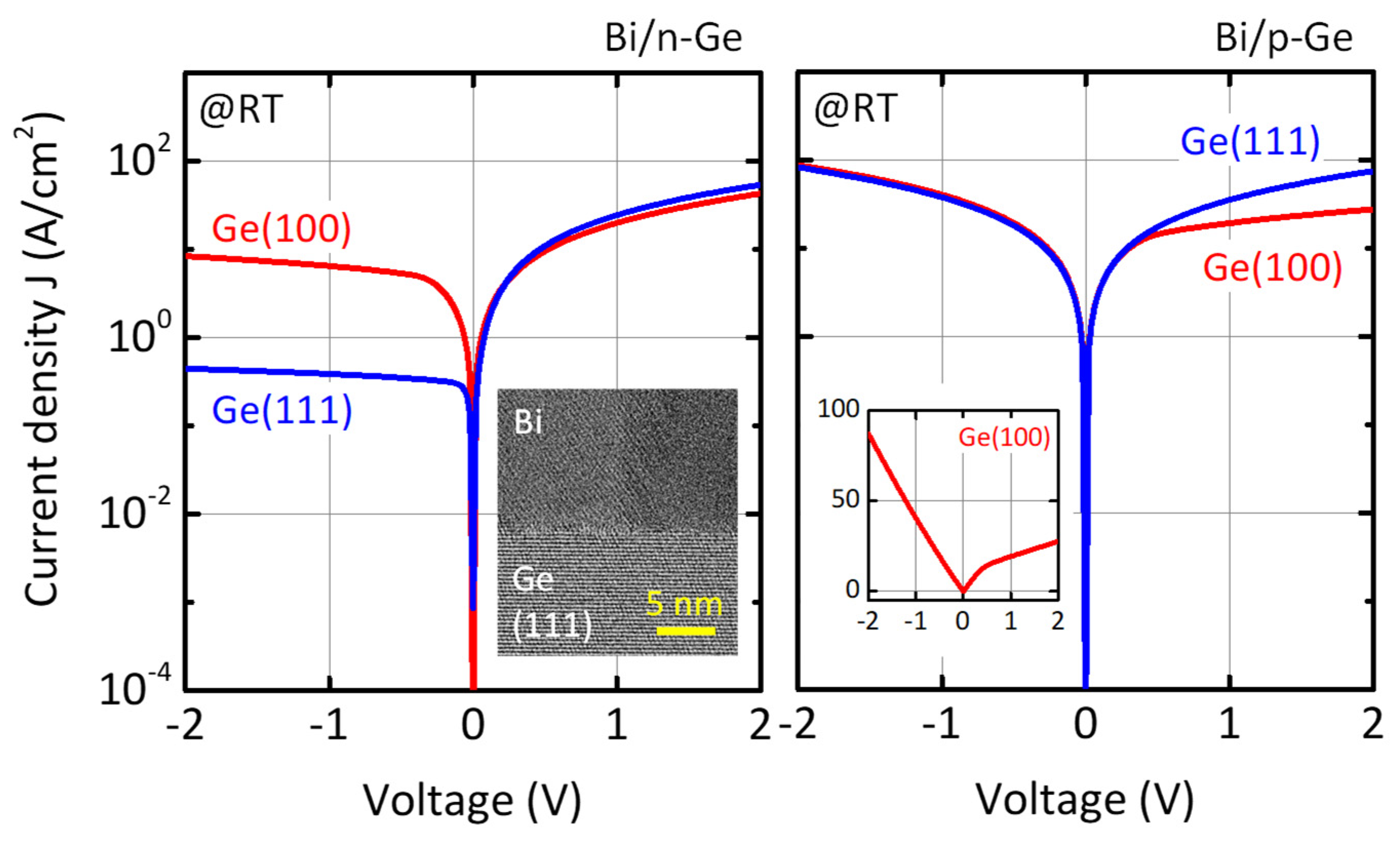
5. FLP Alleviation by Low Free-Electron-Density Metal
6. Reduction of Contact Resistivity
7. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Yeap, G.; Lin, S.S.; Chen, Y.M.; Shang, H.L.; Wang, P.W.; Lin, H.C.; Peng, Y.C.; Sheu, J.Y.; Wang, M.; Chen, X.; et al. 5nm CMOS Production Technology Platform Featuring Full-Fledged EUV, and High Mobility Channel FinFETs with Densest 0.021µm2 SRAM Cells for Mobile SoC and High Performance Computing Applications. In Proceedings of the 2019 IEEE International Electron Devices Meeting (IEDM), San Francisco, CA, USA, 7–11 December 2019; pp. 36.7.1–36.7.4. [Google Scholar]
- Fischetti, M.V.; Laux, S.E. Band Structure, Deformation Potentials, and Carrier Mobility in Strained Si, Ge, and SiGe Alloys. J. Appl. Phys. 1996, 80, 2234–2252. [Google Scholar] [CrossRef]
- Nagashio, K.; Lee, C.H.; Nishimura, T.; Toriumi, A. Thermodynamics and Kinetics for Suppression of GeO Desorption by High Pressure Oxidation of Ge. MRS Proc. 2009, 1155, C06-02. [Google Scholar] [CrossRef]
- Kita, K.; Suzuki, S.; Nomura, H.; Takahashi, T.; Nishimura, T.; Toriumi, A. Direct Evidence of GeO Volatilization from GeO2/Ge and Impact of Its Suppression on GeO2/Ge Metal–Insulator–Semiconductor Characteristics. Jpn. J. Appl. Phys. 2008, 47, 2349–2353. [Google Scholar] [CrossRef]
- Wang, S.K.; Kita, K.; Lee, C.H.; Tabata, T.; Nishimura, T.; Nagashio, K.; Toriumi, A. Desorption Kinetics of GeO from GeO2/Ge Structure. J. Appl. Phys. 2010, 108, 054104. [Google Scholar] [CrossRef]
- Wang, S.K.; Kita, K.; Nishimura, T.; Nagashio, K.; Toriumi, A. Kinetic Effects of O-Vacancy Generated by GeO2/Ge Interfacial Reaction. Jpn. J. Appl. Phys. 2011, 50, 10PE04. [Google Scholar] [CrossRef]
- Murthy, M.K.; Hill, H. Studies in Germanium Oxide Systems: III, Solubility of Germania in Water. J. App. Ceram. Soc. 1965, 48, 109–110. [Google Scholar] [CrossRef]
- Chui, C.O.; Kim, H.; Chi, D.; Triplett, B.B.; McIntyre, P.C.; Saraswat, K.C. A Sub-400C Germanium MOSFET Technology with High-k Dielectric and Metal Gate. In Proceedings of the Digest. International Electron Devices Meeting, San Francisco, CA, USA, 8–11 December 2002; pp. 437–440. [Google Scholar]
- Shang, H.; Okorn-Schmidt, H.; Chan, K.K.; Copel, M.; Ott, J.A.; Kozlowski, P.M.; Steen, S.E.; Cordes, S.A.; Wong, H.-S.P.; Jones, E.C.; et al. High Mobility P-Channel Germanium MOSFETs with a Thin Ge Oxynitride Gate Dielectric. In Proceedings of the Digest. International Electron Devices Meeting, San Francisco, CA, USA, 8–11 December 2002; pp. 441–444. [Google Scholar]
- Whang, S.J.; Lee, S.J.; Gao, F.; Wu, N.; Zhu, C.X.; Pan, J.S.; Tang, L.J.; Kwong, D.L. Germanium p- & n-MOSFETs Fabricated with Novel Surface Passivation (Plasma-PH3/ and Thin AlN) and TaN/HfO2/ Gate Stack. In Proceedings of the IEDM Technical Digest. IEEE International Electron Devices Meeting, San Francisco, CA, USA, 13–15 December 2004; pp. 307–310. [Google Scholar]
- Kamata, Y.; Kamimuta, Y.; Ino, T.; Iijima, R.; Koyama, M.; Nishiyama, A. Dramatic Improvement of Ge P-MOSFET Characteristics Realized by Amorphous Zr-Silicate/Ge Gate Stack with Excellent Structural Stability through Process Temperatures. In Proceedings of the IEEE International Electron Devices Meeting, IEDM Technical Digest, Washington, DC, USA, 5–7 December 2005; pp. 429–432. [Google Scholar]
- Zimmerman, P.; Nicholas, G.; De Jaeger, B.; Kaczer, B.; Stesmans, A.; Ragnarsson, L.-A.; Brunco, D.P.; Leys, F.E.; Caymax, M.; Winderickx, G.; et al. High Performance Ge PMOS Devices Using a Si-Compatible Process Flow. In Proceedings of the 2006 International Electron Devices Meeting, San Francisco, CA, USA, 11–13 December 2006; pp. 26.1.1–26.1.4. [Google Scholar]
- Ritenour, A.; Hennessy, J.; Antoniadis, D.A. Investigation of Carrier Transport in Germanium MOSFETs with WN/Al2O3/AlN Gate Stacks. IEEE Electron Device Lett. 2007, 28, 746–749. [Google Scholar] [CrossRef]
- Yamamoto, T.; Yamashita, Y.; Harada, M.; Taoka, N.; Ikeda, K.; Suzuki, K.; Kiso, O.; Sugiyama, N.; Takagi, S. High Performance 60 Nm Gate Length Germanium P-MOSFETs with Ni Germanide Metal Source/Drain. In Proceedings of the 2007 IEEE International Electron Devices Meeting, Washington, DC, USA, 10–12 December 2007; pp. 1041–1043. [Google Scholar]
- Xu, J.P.; Zhang, X.F.; Li, C.X.; Lai, P.T.; Chan, C.L. Improved Electrical Properties of Ge P-MOSFET with HfO2 Gate Dielectric by Using TaOxNy Interlayer. IEEE Electron Device Lett. 2008, 29, 1155–1158. [Google Scholar] [CrossRef]
- Xie, R.; Phung, T.H.; He, W.; Sun, Z.; Yu, M.; Cheng, Z.; Zhu, C. High Mobility High-k/Ge PMOSFETs with 1 Nm EOT—New Concept on Interface Engineering and Interface Characterization. In Proceedings of the 2008 IEEE International Electron Devices Meeting, San Francisco, CA, USA, 15–17 December 2008; pp. 16.2.1–16.2.4. [Google Scholar]
- Hashemi, P.; Chern, W.; Lee, H.-S.; Teherani, J.T.; Zhu, Y.; Gonsalvez, J.; Shahidi, G.G.; Hoyt, J.L. Ultrathin Strained-Ge Channel P-MOSFETs with High-K /Metal Gate and Sub-1-Nm Equivalent Oxide Thickness. IEEE Electron Device Lett. 2012, 33, 943–945. [Google Scholar] [CrossRef]
- Zhang, R.; Chern, W.; Yu, X.; Takenaka, M.; Hoyt, J.L.; Takagi, S. High Mobility Strained-Ge PMOSFETs with 0.7-Nm Ultrathin EOT Using Plasma Post Oxidation HfO2/Al2O3/GeOx Gate Stacks and Strain Modulation. In Proceedings of the 2013 IEEE International Electron Devices Meeting, Washington, DC, USA, 9–11 December 2013; pp. 26.1.1–26.1.4. [Google Scholar]
- Witters, L.; Arimura, H.; Sebaai, F.; Hikavyy, A.; Milenin, A.P.; Loo, R.; De Keersgieter, A.; Eneman, G.; Schram, T.; Wostyn, K.; et al. Strained Germanium Gate-All-Around PMOS Device Demonstration Using Selective Wire Release Etch Prior to Replacement Metal Gate Deposition. IEEE Trans. Electron Devices 2017, 64, 4587–4593. [Google Scholar] [CrossRef]
- Kuzum, D.; Pethe, A.J.; Krishnamohan, T.; Saraswat, K.C. Ge (100) and (111) N- and P-FETs with High Mobility and Low-T Mobility Characterization. IEEE Trans. Electron Devices 2009, 56, 648–655. [Google Scholar] [CrossRef]
- Zhang, R.; Huang, P.-C.; Lin, J.-C.; Taoka, N.; Takenaka, M.; Takagi, S. High-Mobility Ge p- and n-MOSFETs with 0.7-Nm EOT Using HfO2/Al2O3/GeOx/Ge Gate Stacks Fabricated by Plasma Postoxidation. IEEE Trans. Electron Devices 2013, 60, 927–934. [Google Scholar] [CrossRef]
- Lee, C.H.; Nishimura, T.; Tabata, T.; Lu, C.; Zhang, W.F.; Nagashio, K.; Toriumi, A. Reconsideration of Electron Mobility in Ge N-MOSFETs from Ge Substrate Side—Atomically Flat Surface Formation, Layer-by-Layer Oxidation, and Dissolved Oxygen Extraction. In Proceedings of the 2013 IEEE International Electron Devices Meeting, Washington, DC, USA, 9–11 December 2013; pp. 2.3.1–2.3.4. [Google Scholar]
- van Dal, M.J.H.; Duriez, B.; Vellianitis, G.; Doornbos, G.; Oxland, R.; Holland, M.; Afzalian, A.; See, Y.C.; Passlack, M.; Diaz, C.H. Ge N-Channel FinFET with Optimized Gate Stack and Contacts. In Proceedings of the 2014 IEEE International Electron Devices Meeting, San Francisco, CA, USA, 15–17 December 2014; pp. 9.5.1–9.5.4. [Google Scholar]
- Lu, C.; Lee, C.H.; Nishimura, T.; Toriumi, A. Yttrium Scandate Thin Film as Alternative High-Permittivity Dielectric for Germanium Gate Stack Formation. Appl. Phys. Lett. 2015, 107, 072904. [Google Scholar] [CrossRef]
- Lin, C.-M.; Chang, H.-C.; Wong, I.-H.; Luo, S.-J.; Liu, C.W.; Hu, C. Interfacial Layer Reduction and High Permittivity Tetragonal ZrO2 on Germanium Reaching Ultrathin 0.39 Nm Equivalent Oxide Thickness. Appl. Phys. Lett. 2013, 102, 232906. [Google Scholar] [CrossRef]
- Rachmady, W.; Agrawal, A.; Sung, S.H.; Dewey, G.; Chouksey, S.; Chu-Kung, B.; Elbaz, G.; Fischer, P.; Huang, C.Y.; Jun, K.; et al. 300 mm Heterogeneous 3D Integration of Record Performance Layer Transfer Germanium PMOS with Silicon NMOS for Low Power High Performance Logic Applications. In Proceedings of the 2019 IEEE International Electron Devices Meeting (IEDM), San Francisco, CA, USA, 7–11 December 2019; pp. 29.7.1–29.7.4. [Google Scholar]
- Lin, Y.-W.; Chang, H.-H.; Huang, Y.-H.; Sun, C.-J.; Yan, S.-C.; Lin, S.-W.; Luo, G.-L.; Wu, C.-T.; Wu, Y.-C.; Hou, F.-J. Tightly Stacked 3D Diamond-Shaped Ge Nanowire Gate-All-Around FETs with Superior NFET and PFET Performance. IEEE Electron Device Lett. 2021, 42, 1727–1730. [Google Scholar] [CrossRef]
- Nishimura, T.; Kabuyanagi, S.; Zhang, W.; Lee, C.H.; Yajima, T.; Nagashio, K.; Toriumi, A. Atomically Flat Planarization of Ge(100), (110), and (111) Surfaces in H2 Annealing. Appl. Phys. Express 2014, 7, 051301. [Google Scholar] [CrossRef]
- Morita, Y.; Ota, H.; Masahara, M.; Maeda, T. Impact of H2, O2, and N2 Anneals on Atomic-Scale Surface Flattening for 3-D Ge Channel Architecture. In Proceedings of the 2015 Silicon Nanoelectronics Workshop (SNW), Kyoto, Japan, 14–15 June 2015; pp. 1–2. [Google Scholar]
- Nishimura, T.; Takemura, S.; Wang, X.; Shibayama, S.; Yajima, T.; Toriumi, A. Atomically Flat Interface Formation on Ge (111) in Oxidation Process. In Proceedings of the 2018 International Conference on Solid State Devices and Materials, Kyoto, Japan, 9–13 September 2018; pp. 349–350. [Google Scholar]
- Datta, S.; Pandey, R.; Agrawal, A.; Gupta, S.K.; Arghavani, R. Impact of Contact and Local Interconnect Scaling on Logic Performance. In Proceedings of the 2014 Symposium on VLSI Technology (VLSI-Technology): Digest of Technical Papers, Honolulu, HI, USA, 9–12 June 2014; p. 16.1. [Google Scholar]
- Arghavani, R.; Yang, P.; Ashtiani, K.; Singh, H.; Hemker, D. Low Resistance Contacts to Enable 5 Nm Node Technology: Patterning, Etch, Clean, Metallization and Device Performance. In Proceedings of the 2016 IEEE International Electron Devices Meeting Short Course, San Francisco, CA, USA, 3–7 December 2016. [Google Scholar]
- Schroder, D.K. Semiconductor Material and Device Characterization, 3rd ed.; Wiley-IEEE Press: Hoboken, NJ, USA, 2015; ISBN 978-0-471-73906-7. [Google Scholar]
- Cowley, A.M.; Sze, S.M. Surface States and Barrier Height of Metal-Semiconductor Systems. J. Appl. Phys. 1965, 36, 3212–3220. [Google Scholar] [CrossRef]
- Thanailakis, A.; Northrop, D.C. Metal-Germanium Schottky Barriers. Solid-State Electron. 1973, 16, 1383–1389. [Google Scholar] [CrossRef]
- Marshall, E.D.; Wu, C.S.; Pai, C.S.; Scott, D.M.; Lau, S.S. Metal-Germanium Contacts and Germanide Formation. MRS Proc. 1985, 47, 161–166. [Google Scholar] [CrossRef]
- Dimoulas, A.; Tsipas, P.; Sotiropoulos, A.; Evangelou, E.K. Fermi-Level Pinning and Charge Neutrality Level in Germanium. Appl. Phys. Lett. 2006, 89, 252110. [Google Scholar] [CrossRef]
- Nishimura, T.; Kita, K.; Toriumi, A. Strong Fermi-Level Pinning of Wide Range of Work-Function Metals at Valence Band Edge of Germanium. In Proceedings of the International Conference on Solid State Devices and Materials, Yokohama, Japan, 12–15 September 2006; p. J-6-3. [Google Scholar]
- Nishimura, T.; Kita, K.; Toriumi, A. Evidence for Strong Fermi-Level Pinning Due to Metal-Induced Gap States at Metal/Germanium Interface. Appl. Phys. Lett. 2007, 91, 123123. [Google Scholar] [CrossRef]
- Michaelson, H.B. The Work Function of the Elements and Its Periodicity. J. Appl. Phys. 1977, 48, 4729–4733. [Google Scholar] [CrossRef] [Green Version]
- Malov, Y.I.; Onichchenko, A.V.; Mironkova, L.I. Work Function of Rare-Earth Metals. Phys. Met. Metall. 1980, 47, 195–197. [Google Scholar]
- Heine, V. Theory of Surface States. Phys. Rev. 1965, 138, A1689–A1696. [Google Scholar] [CrossRef]
- Louie, S.G.; Cohen, M.L. Electronic Structure of a Metal-Semiconductor Interface. Phys. Rev. B 1976, 13, 2461–2469. [Google Scholar] [CrossRef]
- Tersoff, J. Schottky Barrier Heights and the Continuum of Gap States. Phys. Rev. Lett. 1984, 52, 465–468. [Google Scholar] [CrossRef]
- Mönch, W. Role of Virtual Gap States and Defects in Metal-Semiconductor Contacts. Phys. Rev. Lett. 1987, 58, 1260–1263. [Google Scholar] [CrossRef]
- Mönch, W. Barrier Heights of Real Schottky Contacts Explained by Metal-Induced Gap States and Lateral Inhomogeneities. J. Vac. Sci. Technol. B 1999, 17, 1867–1876. [Google Scholar] [CrossRef]
- Tung, R.T. Chemical Bonding and Fermi Level Pinning at Metal-Semiconductor Interfaces. Phys. Rev. Lett. 2000, 84, 6078–6081. [Google Scholar] [CrossRef]
- Tung, R.T. Formation of an Electric Dipole at Metal-Semiconductor Interfaces. Phys. Rev. B 2001, 64, 205310. [Google Scholar] [CrossRef]
- Spicer, W.E.; Lindau, I.; Skeath, P.; Su, C.Y.; Chye, P. Unified Mechanism for Schottky-Barrier Formation and III-V Oxide Interface States. Phys. Rev. Lett. 1980, 44, 420–423. [Google Scholar] [CrossRef]
- Spicer, W.E.; Liliental-Weber, Z.; Weber, E.; Newman, N.; Kendelewicz, T.; Cao, R.; McCants, C.; Mahowald, P.; Miyano, K.; Lindau, I. The Advanced Unified Defect Model for Schottky Barrier Formation. J. Vac. Sci. Technol. B 1988, 6, 1245–1251. [Google Scholar] [CrossRef]
- Hasegawa, H.; Ohno, H. Unified Disorder Induced Gap State Model for Insulator–Semiconductor and Metal–Semiconductor Interfaces. J. Vac. Sci. Technol. B 1986, 4, 1130–1138. [Google Scholar] [CrossRef]
- Hasegawa, H.; Ishii, H.; Koyanagi, K. Formation Mechanism of Schottky Barriers on MBE-Grown GaAs Surfaces Subjected to Various Treatments. Appl. Surf. Sci. 1992, 56–58, 317–324. [Google Scholar] [CrossRef]
- Kurtin, S.; McGill, T.C.; Mead, C.A. Fundamental Transition in the Electronic Nature of Solids. Phys. Rev. Lett. 1969, 22, 1433–1436. [Google Scholar] [CrossRef] [Green Version]
- Hara, S. The Schottky Limit and a Charge Neutrality Level Found on Metal/6H-SiC Interfaces. Surf. Sci. 2001, 494, L805–L810. [Google Scholar] [CrossRef]
- Wang, H.-T.; Jang, S.; Anderson, T.; Chen, J.J.; Kang, B.S.; Ren, F.; Herrero, A.; Gerger, A.M.; Gila, B.P.; Pearton, S.J.; et al. Improved Au Schottky Contacts on GaAs Using Cryogenic Metal Deposition. J. Vac. Sci. Technol. B 2006, 24, 1799–1802. [Google Scholar] [CrossRef]
- Cardona, M.; Christensen, N.E. Acoustic Deformation Potentials and Heterostructure Band Offsets in Semiconductors. Phys. Rev. B 1987, 35, 6182–6194. [Google Scholar] [CrossRef]
- Haesslein, H.; Sielemann, R.; Zistl, C. Vacancies and Self-Interstitials in Germanium Observed by Perturbed Angular Correlation Spectroscopy. Phys. Rev. Lett. 1998, 80, 2626–2629. [Google Scholar] [CrossRef]
- Satoh, M.; Arimoto, K.; Nakagawa, K.; Koh, S.; Sawano, K.; Shiraki, Y.; Usami, N.; Nakajima, K. Acceptorlike Behavior of Defects in SiGe Alloys Grown by Molecular Beam Epitaxy. Jpn. J. Appl. Phys. 2008, 47, 4630–4633. [Google Scholar] [CrossRef]
- Sawano, K.; Hoshi, Y.; Kubo, S.; Arimoto, K.; Yamanaka, J.; Nakagawa, K.; Hamaya, K.; Miyao, M.; Shiraki, Y. Structural and Electrical Properties of Ge(111) Films Grown on Si(111) Substrates and Application to Ge(111)-on-Insulator. Thin Solid Films 2016, 613, 24–28. [Google Scholar] [CrossRef]
- Luo, X.; Nishimura, T.; Yajima, T.; Toriumi, A. Understanding of Fermi Level Pinning at Metal/Germanium Interface Based on Semiconductor Structure. Appl. Phys. Express 2020, 13, 031003. [Google Scholar] [CrossRef]
- Archer, R.J.; Atalla, M.M. Metals Contacts on Cleaved Silicon Surfaces. Anu. NY Acad. Sci. 1963, 101, 697–708. [Google Scholar] [CrossRef]
- Nishimura, T.; Kita, K.; Toriumi, A. Effect of Ultra-Thin Al2O3 Insertion on Fermi-Level Pinning at Metal/Ge Interface. In Proceedings of the International Conference on Solid State Devices and Materials, Tsukuba, Japan, 18–21 September 2007; p. A-7-3. [Google Scholar]
- Lee, C.H.; Nishimura, T.; Nagashio, K.; Kita, K.; Toriumi, A. High-Electron-Mobility Ge/GeO2 n-MOSFETs with Two-Step Oxidation. IEEE Trans. Electron Devices 2011, 58, 1295–1301. [Google Scholar] [CrossRef]
- Toriumi, A.; Nishimura, T. Germanium CMOS Potential from Material and Process Perspectives: Be More Positive about Germanium. Jpn. J. Appl. Phys. 2017, 57, 010101. [Google Scholar] [CrossRef] [Green Version]
- Nishimura, T.; Kita, K.; Toriumi, A. A Significant Shift of Schottky Barrier Heights at Strongly Pinned Metal/Germanium Interface by Inserting an Ultra-Thin Insulating Film. Appl. Phys. Express 2008, 1, 051406. [Google Scholar] [CrossRef]
- Zhou, Y.; Ogawa, M.; Han, X.; Wang, K.L. Alleviation of Fermi-Level Pinning Effect on Metal/Germanium Interface by Insertion of an Ultrathin Aluminum Oxide. Appl. Phys. Lett. 2008, 93, 202105. [Google Scholar] [CrossRef]
- Gajula, D.R.; Baine, P.; Modreanu, M.; Hurley, P.K.; Armstrong, B.M.; McNeill, D.W. Fermi Level De-Pinning of Aluminium Contacts to n-Type Germanium Using Thin Atomic Layer Deposited Layers. Appl. Phys. Lett. 2014, 104, 012102. [Google Scholar] [CrossRef] [Green Version]
- Nishimura, T.; Kita, K.; Nagashio, K.; Toriumi, A. Long Range Pinning Interaction in Ultra-Thin Insulator-Inserted Metal/Germanium Junctions. In Proceedings of the 2010 Silicon Nanoelectronics Workshop, Honolulu, HI, USA, 13–14 June 2010; p. 2.3. [Google Scholar]
- Lin, J.-Y.J.; Roy, A.M.; Nainani, A.; Sun, Y.; Saraswat, K.C. Increase in Current Density for Metal Contacts to N-Germanium by Inserting TiO2 Interfacial Layer to Reduce Schottky Barrier Height. Appl. Phys. Lett. 2011, 98, 092113. [Google Scholar] [CrossRef]
- Tsui, B.-Y.; Kao, M.-H. Mechanism of Schottky Barrier Height Modulation by Thin Dielectric Insertion on N-Type Germanium. Appl. Phys. Lett. 2013, 103, 032104. [Google Scholar] [CrossRef] [Green Version]
- Lee, D.; Raghunathan, S.; Wilson, R.J.; Nikonov, D.E.; Saraswat, K.; Wang, S.X. The Influence of Fermi Level Pinning/Depinning on the Schottky Barrier Height and Contact Resistance in Ge/CoFeB and Ge/MgO/CoFeB Structures. Appl. Phys. Lett. 2010, 96, 052514. [Google Scholar] [CrossRef]
- Zhou, Y.; Han, W.; Wang, Y.; Xiu, F.; Zou, J.; Kawakami, R.K.; Wang, K.L. Investigating the Origin of Fermi Level Pinning in Ge Schottky Junctions Using Epitaxially Grown Ultrathin MgO Films. Appl. Phys. Lett. 2010, 96, 102103. [Google Scholar] [CrossRef] [Green Version]
- Jung, H.-W.; Jung, W.-S.; Park, J.-H. Hydrazine-Based Fermi-Level Depinning Process on Metal/Germanium Schottky Junction. IEEE Electron Device Lett. 2013, 34, 599–601. [Google Scholar] [CrossRef]
- Biswas, D.; Biswas, J.; Ghosh, S.; Wood, B.; Lodha, S. Enhanced Thermal Stability of Ti/TiO2/n-Ge Contacts through Plasma Nitridation of TiO2 Interfacial Layer. Appl. Phys. Lett. 2017, 110, 052104. [Google Scholar] [CrossRef]
- Lieten, R.R.; Degroote, S.; Kuijk, M.; Borghs, G. Ohmic Contact Formation on N-Type Ge. Appl. Phys. Lett. 2008, 92, 022106. [Google Scholar] [CrossRef] [Green Version]
- Kobayashi, M.; Kinoshita, A.; Saraswat, K.; Wong, H.-S.P.; Nishi, Y. Fermi Level Depinning in Metal/Ge Schottky Junction for Metal Source/Drain Ge Metal-Oxide-Semiconductor Field-Effect-Transistor Application. J. Appl. Phys. 2009, 105, 023702. [Google Scholar] [CrossRef]
- Connelly, D.; Faulkner, C.; Clifton, P.A.; Grupp, D.E. Fermi-Level Depinning for Low-Barrier Schottky Source/Drain Transistors. Appl. Phys. Lett. 2006, 88, 012105. [Google Scholar] [CrossRef]
- Sasaki, S.; Nakayama, T. Defect Distribution and Schottky Barrier at Metal/Ge Interfaces: Role of Metal-Induced Gap States. Jpn. J. Appl. Phys. 2016, 55, 111302. [Google Scholar] [CrossRef]
- Hiraki, A.; Lugujjo, E.; Mayer, J.W. Formation of Silicon Oxide over Gold Layers on Silicon Substrates. J. Appl. Phys. 1972, 43, 3643–3649. [Google Scholar] [CrossRef]
- Lang, N.D.; Kohn, W. Theory of Metal Surfaces: Charge Density and Surface Energy. Phys. Rev. B 1970, 1, 4555–4568. [Google Scholar] [CrossRef]
- Lang, N.D.; Kohn, W. Theory of Metal Surfaces: Work Function. Phys. Rev. B 1971, 3, 1215–1223. [Google Scholar] [CrossRef]
- Kittel, C. Introduction to Solid State Physics, 6th ed.; John Wiley & Sons: New York, NY, USA, 1986; ISBN 978-0-471-87474-4. [Google Scholar]
- Nava, F.; Tu, K.N.; Thomas, O.; Senateur, J.P.; Madar, R.; Borghesi, A.; Guizzetti, G.; Gottlieb, U.; Laborde, O.; Bisi, O. Electrical and Optical Properties of Silicide Single Crystals and Thin Films. Mater. Sci. Rep. 1993, 9, 141–200. [Google Scholar] [CrossRef]
- Sanderson, R.T. Electronegativity and Bond Energy. J. Am. Chem. Soc. 1983, 105, 2259–2261. [Google Scholar] [CrossRef]
- Gordy, W.; Thomas, W.J.O. Electronegativities of the Elements. J. Chem. Phys. 1956, 24, 439–444. [Google Scholar] [CrossRef]
- Zheng, Z.-W.; Ku, T.-C.; Liu, M.; Chin, A. Ohmic Contact on N-Type Ge Using Yb-Germanide. Appl. Phys. Lett. 2012, 101, 223501. [Google Scholar] [CrossRef] [Green Version]
- Nishimura, T.; Nakatsuka, O.; Akimoto, S.; Takeuchi, W.; Zaima, S. Crystalline Orientation Dependence of Electrical Properties of Mn Germanide/Ge(111) and (001) Schottky Contacts. Microelectron. Eng. 2011, 88, 605–609. [Google Scholar] [CrossRef]
- Senga, K.; Shibayama, S.; Sakashita, M.; Zaima, S.; Nakatsuka, O. Further Reduction of Schottky Barrier Height of Hf-Germanide/n-Ge(001) Contacts by Forming Epitaxial HfGe2. In Proceedings of the 2019 19th International Workshop on Junction Technology (IWJT), Kyoto, Japan, 6–7 June 2019; pp. 1–2. [Google Scholar]
- Yamane, K.; Hamaya, K.; Ando, Y.; Enomoto, Y.; Yamamoto, K.; Sadoh, T.; Miyao, M. Effect of Atomically Controlled Interfaces on Fermi-Level Pinning at Metal/Ge Interfaces. Appl. Phys. Lett. 2010, 96, 162104. [Google Scholar] [CrossRef]
- Tu, K.N.; Thompson, R.D.; Tsaur, B.Y. Low Schottky Barrier of Rare-earth Silicide on N-Si. Appl. Phys. Lett. 1981, 38, 626–628. [Google Scholar] [CrossRef]
- Freeouf, J.L.; Woodall, J.M. Schottky Barriers: An Effective Work Function Model. Appl. Phys. Lett. 1981, 39, 727–729. [Google Scholar] [CrossRef]
- Nishimura, T.; Yajima, T.; Toriumi, A. Reexamination of Fermi Level Pinning for Controlling Schottky Barrier Height at Metal/Ge Interface. Appl. Phys. Express 2016, 9, 081201. [Google Scholar] [CrossRef] [Green Version]
- Lin, L.; Guo, Y.; Robertson, J. Metal Silicide Schottky Barriers on Si and Ge Show Weaker Fermi Level Pinning. Appl. Phys. Lett. 2012, 101, 052110. [Google Scholar] [CrossRef]
- Tung, R.T. Schottky-Barrier Formation at Single-Crystal Metal-Semiconductor Interfaces. Phys. Rev. Lett. 1984, 52, 461–464. [Google Scholar] [CrossRef]
- Williams, G.A. Alfven-Wave Propagation in Solid-State Plasmas. I. Bismuth. Phys. Rev. 1965, 139, A771–A778. [Google Scholar] [CrossRef]
- Massalski, T.B.; Murray, J.L.; Bennett, L.H.; Baker, H. Binary Alloy Phase Diagrams, 1st ed.; American Society for Metals: Novelty, OH, USA, 1986; ISBN 978-0-87170-261-6. [Google Scholar]
- Nishimura, T.; Luo, X.; Matsumoto, S.; Yajima, T.; Toriumi, A. Almost Pinning-Free Bismuth/Ge and /Si Interfaces. AIP Adv. 2019, 9, 095013. [Google Scholar] [CrossRef]
- Shen, P.-C.; Su, C.; Lin, Y.; Chou, A.-S.; Cheng, C.-C.; Park, J.-H.; Chiu, M.-H.; Lu, A.-Y.; Tang, H.-L.; Tavakoli, M.M.; et al. Ultralow Contact Resistance between Semimetal and Monolayer Semiconductors. Nature 2021, 593, 211–217. [Google Scholar] [CrossRef]
- Okada, N.; Uchida, N.; Kanayama, T. Fermi-Level Depinning and Contact Resistance Reduction in Metal/n-Ge Junctions by Insertion of W-Encapsulating Si Cluster Films. Appl. Phys. Lett. 2014, 104, 062105. [Google Scholar] [CrossRef]
- Iyota, M.; Yamamoto, K.; Wang, D.; Yang, H.; Nakashima, H. Ohmic Contact Formation on N-Type Ge by Direct Deposition of TiN. Appl. Phys. Lett. 2011, 98, 192108. [Google Scholar] [CrossRef]
- Wu, Z.; Wang, C.; Huang, W.; Li, C.; Lai, H.; Chen, S. Ohmic Contact Formation of Sputtered TaN on N-Type Ge with Lower Specific Contact Resistivity. ECS J. Solid State Sci. Technol. 2012, 1, P30–P33. [Google Scholar] [CrossRef]
- Seo, Y.; Lee, S.; Baek, S.C.; Hwang, W.S.; Yu, H.-Y.; Lee, S.-H.; Cho, B.J. The Mechanism of Schottky Barrier Modulation of Tantalum Nitride/Ge Contacts. IEEE Electron Device Lett. 2015, 36, 997–1000. [Google Scholar] [CrossRef]
- Suzuki, A.; Asaba, S.; Yokoi, J.; Kato, K.; Kurosawa, M.; Sakashita, M.; Taoka, N.; Nakatsuka, O.; Zaima, S. Reduction of Schottky Barrier Height for N-Type Ge Contact by Using Sn Electrode. Jpn. J. Appl. Phys. 2014, 53, 04EA06. [Google Scholar] [CrossRef]
- Baek, S.C.; Seo, Y.-J.; Oh, J.G.; Albert Park, M.G.; Bong, J.H.; Yoon, S.J.; Seo, M.; Park, S.; Park, B.-G.; Lee, S.-H. Alleviation of Fermi-Level Pinning Effect at Metal/Germanium Interface by the Insertion of Graphene Layers. Appl. Phys. Lett. 2014, 105, 073508. [Google Scholar] [CrossRef]
- Wei, Y.-N.; Hu, X.-G.; Zhang, J.-W.; Tong, B.; Du, J.-H.; Liu, C.; Sun, D.-M.; Liu, C. Fermi-Level Depinning in Metal/Ge Junctions by Inserting a Carbon Nanotube Layer. Small 2022, 18, 2201840. [Google Scholar] [CrossRef]
- Schroder, D.K.; Meier, D.L. Solar Cell Contact Resistance—A Review. IEEE Trans. Electron Devices 1984, 31, 637–647. [Google Scholar] [CrossRef]
- Peng, S.; Jin, Z.; Yao, Y.; Li, L.; Zhang, D.; Shi, J.; Huang, X.; Niu, J.; Zhang, Y.; Yu, G. Metal-Contact-Induced Transition of Electrical Transport in Monolayer MoS2: From Thermally Activated to Variable-Range Hopping. Adv. Electron. Mater. 2019, 5, 1900042. [Google Scholar] [CrossRef]
- Paramahans Manik, P.; Kesh Mishra, R.; Pavan Kishore, V.; Ray, P.; Nainani, A.; Huang, Y.-C.; Abraham, M.C.; Ganguly, U.; Lodha, S. Fermi-Level Unpinning and Low Resistivity in Contacts to n-Type Ge with a Thin ZnO Interfacial Layer. Appl. Phys. Lett. 2012, 101, 182105. [Google Scholar] [CrossRef]
- Yu, H.; Schaekers, M.; Demuynck, S.; Barla, K.; Mocuta, A.; Horiguchi, N.; Collaert, N.; Thean, A.V.-Y.; De Meyer, K. MIS or MS? Source/Drain Contact Scheme Evaluation for 7nm Si CMOS Technology and Beyond. In Proceedings of the 2016 16th International Workshop on Junction Technology (IWJT), Shanghai, China, 9–10 May 2016; pp. 19–24. [Google Scholar]
- Manik, P.P.; Lodha, S. Contacts on N-Type Germanium Using Variably Doped Zinc Oxide and Highly Doped Indium Tin Oxide Interfacial Layers. Appl. Phys. Express 2015, 8, 051302. [Google Scholar] [CrossRef]
- Kim, J.-K.; Kim, G.-S.; Nam, H.; Shin, C.; Park, J.-H.; Kim, J.-K.; Cho, B.J.; Saraswat, K.C.; Yu, H.-Y. The Efficacy of Metal-Interfacial Layer-Semiconductor Source/Drain Structure on Sub-10-Nm n-Type Ge FinFET Performances. IEEE Electron Device Lett. 2014, 35, 1185–1187. [Google Scholar] [CrossRef]
- Shayesteh, M.; Huet, K.; Toqué-Tresonne, I.; Negru, R.; Daunt, C.L.M.; Kelly, N.; O’Connell, D.; Yu, R.; Djara, V.; Carolan, P.B.; et al. Atomically Flat Low-Resistive Germanide Contacts Formed by Laser Thermal Anneal. IEEE Trans. Electron Devices 2013, 60, 2178–2185. [Google Scholar] [CrossRef]
- Miyoshi, H.; Ueno, T.; Hirota, Y.; Yamanaka, J.; Arimoto, K.; Nakagawa, K.; Kaitsuka, T. Low Nickel Germanide Contact Resistances by Carrier Activation Enhancement Techniques for Germanium CMOS Application. Jpn. J. Appl. Phys. 2014, 53, 04EA05. [Google Scholar] [CrossRef]
- Nishimura, T.; Toriumi, A. Nishimura, T. (The Univ. of Tokyo, Tokyo, Japan); Toriumi, A. (The Univ. of Tokyo, Tokyo, Japan) Unpublished work, 2016.
- Hutin, L.; Royer, C.L.; Tabone, C.; Delaye, V.; Nemouchi, F.; Aussenac, F.; Clavelier, L.; Vinet, M. Schottky Barrier Height Extraction in Ohmic Regime: Contacts on Fully Processed GeOI Substrates. J. Electrochem. Soc. 2009, 156, H522. [Google Scholar] [CrossRef]
- Martens, K.; Rooyackers, R.; Firrincieli, A.; Vincent, B.; Loo, R.; De Jaeger, B.; Meuris, M.; Favia, P.; Bender, H.; Douhard, B.; et al. Contact Resistivity and Fermi-Level Pinning in n-Type Ge Contacts with Epitaxial Si-Passivation. Appl. Phys. Lett. 2011, 98, 013504. [Google Scholar] [CrossRef]
- Kim, G.-S.; Kim, J.-K.; Kim, S.-H.; Jo, J.; Shin, C.; Park, J.-H.; Saraswat, K.C.; Yu, H.-Y. Specific Contact Resistivity Reduction Through Ar Plasma-Treated TiO2-x Interfacial Layer to Metal/Ge Contact. IEEE Electron Device Lett. 2014, 35, 1076–1078. [Google Scholar] [CrossRef]











Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nishimura, T. Understanding and Controlling Band Alignment at the Metal/Germanium Interface for Future Electric Devices. Electronics 2022, 11, 2419. https://doi.org/10.3390/electronics11152419
Nishimura T. Understanding and Controlling Band Alignment at the Metal/Germanium Interface for Future Electric Devices. Electronics. 2022; 11(15):2419. https://doi.org/10.3390/electronics11152419
Chicago/Turabian StyleNishimura, Tomonori. 2022. "Understanding and Controlling Band Alignment at the Metal/Germanium Interface for Future Electric Devices" Electronics 11, no. 15: 2419. https://doi.org/10.3390/electronics11152419
APA StyleNishimura, T. (2022). Understanding and Controlling Band Alignment at the Metal/Germanium Interface for Future Electric Devices. Electronics, 11(15), 2419. https://doi.org/10.3390/electronics11152419





