Dual-Anchor Metric Learning for Blind Image Quality Assessment of Screen Content Images
Abstract
:1. Introduction
1.1. Related Work
1.2. Contributions
- Metric learning is used to characterize the statistical features of SCIs, providing new thoughts and direction for the establishment of statistical feature models of complex scenes. Considering the variable composition of SCIs, statistical features cannot be accurately represented with a single statistical model but can be more reliably characterized by the measured distance with some available statistical models inspired by metric learning. In this paper, the dual-anchor and variance differences can contribute to the multi-aspect analysis of complex mixtures of SCI distortions, avoiding the dependence on some specific distortion types, and experimental results with three public SCI databases confirm the effectiveness of the proposed method.
- The performance of metric learning is directly determined by the anchor point and metrics function. Most existing studies focused on generating a single statistical model with only one dataset, based on the assumption that each distortion follows a uniform distribution. However, this strategy fails to describe the statistical characteristics of SCIs due to the intricate content, variable composition, and composite mixtures of multiple distortions. Thus, we resort to a dual-anchor statistical model as the anchor point for SCIs in this study. First, two Gaussian mixed models (GMMs) with different characteristics are generated by representative datasets with unrelated images, and then both are used as the positive and negative anchor points. Specifically, the GMM is used as the statistical model of the anchor points for more informative scene representation, because the GMM is a linear combination of multiple Gaussian distribution functions and fully incorporates prior knowledge, which is theoretically suitable for the description of complex scene distributions. Meanwhile, the measured distances of high-order statistics are used as a metric function for efficient distance calculation, and only the variance differences are used as the quality-aware features in this study to balance complexity and effectiveness via empirical analysis and experimental verification.
- Both color and brightness information are combined via tensor decomposition to avoid information loss and optimize the structure of feature extraction. As mentioned above, existing methods primarily focus on feature generation in the grayscale domain and generally ignore color information. For tensor decomposition, the brightness and color information are fused perfectly in the principal component without missing the primary texture details. With that in mind, this component is employed as the carrier to train models and extract features in this paper, as well as acquire certain positive effects.
2. Materials and Methods
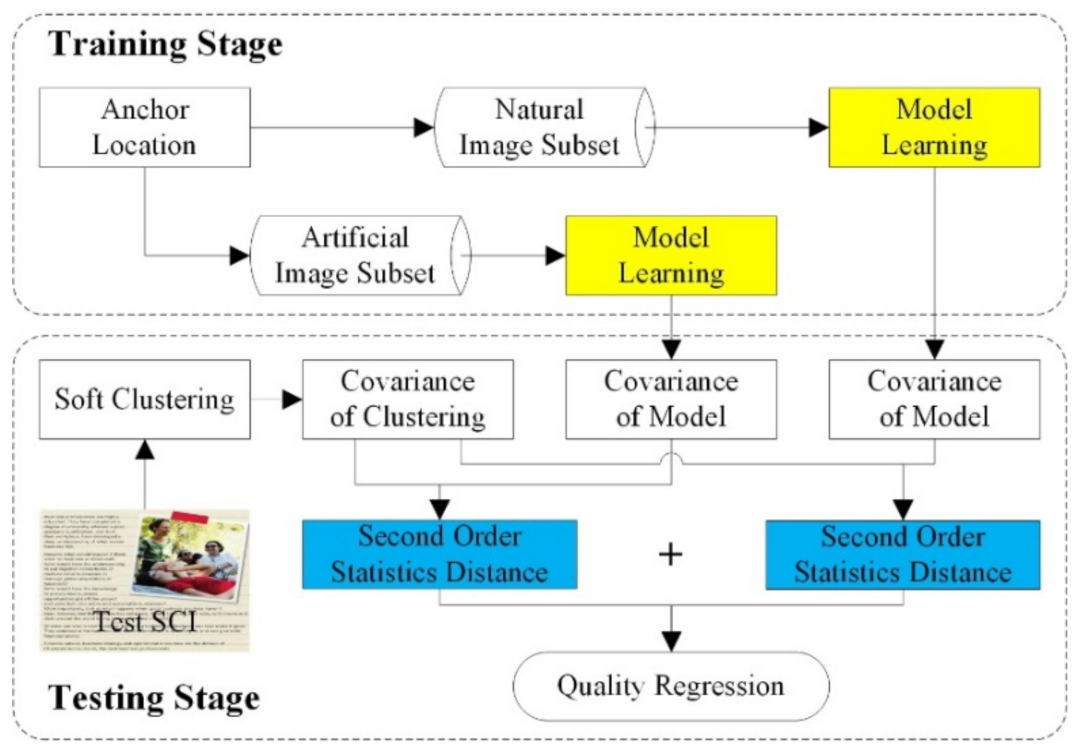
2.1. Offline Model Training
2.1.1. Anchor Location
2.1.2. Model Learning
2.2. Online Quality Prediction
2.2.1. Feature Generation
2.2.2. Quality Regression
2.3. Experimental Protocol
3. Results
3.1. Performance Comparison on the Overall Database
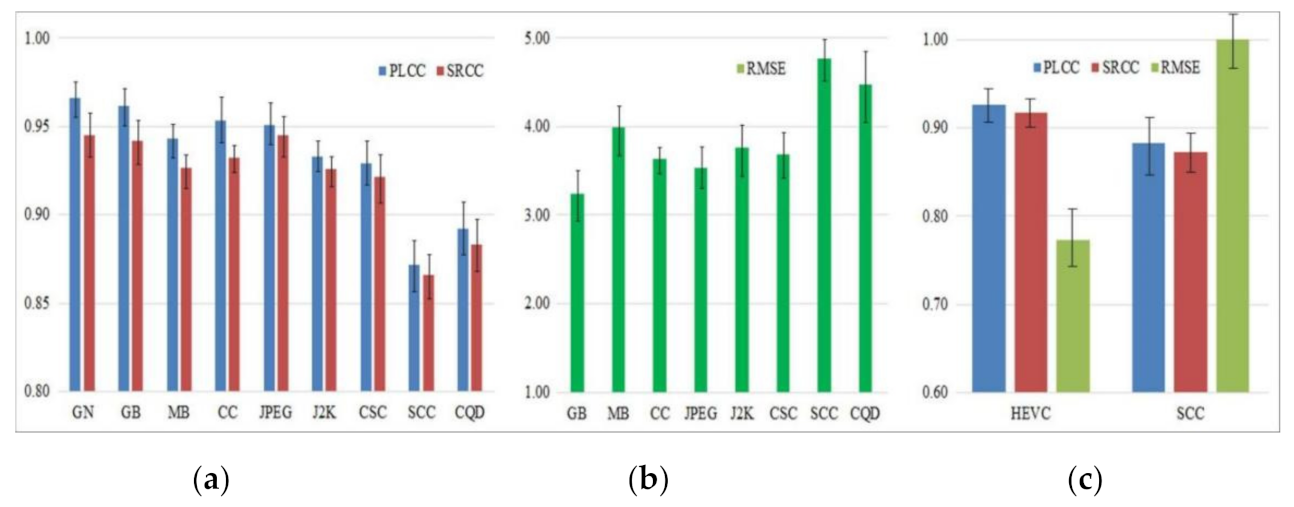
3.2. Performance Comparison of the Individual Distortion Type
3.3. Cross-Database Validation
3.4. Ablation Study
4. Conclusions
Author Contributions
Funding
Informed Consent Statement
Conflicts of Interest
References
- Kuang, W.; Chan, Y.; Tsang, S.; Siu, W. Machine learning-based fast intra mode decision for HEVC screen content coding via decision trees. IEEE Trans. Circuits Syst. Video Technol. 2020, 30, 1481–1496. [Google Scholar] [CrossRef]
- Strutz, T.; Möller, P. Screen content compression based on enhanced soft context formation. IEEE Trans. Multimed. 2020, 22, 1126–1138. [Google Scholar] [CrossRef]
- Tsang, S.; Chan, Y.; Kuang, W. Mode skipping for HEVC screen content coding via random forest. IEEE Trans. Multimed. 2019, 21, 2433–2446. [Google Scholar] [CrossRef]
- Chen, J.; Ou, J.; Zeng, H.; Cai, C. A fast algorithm based on gray level co-occurrence matrix and Gabor feature for HEVC screen content coding. J. Vis. Commun. Image Represent. 2021, 78, 103–128. [Google Scholar] [CrossRef]
- Cheng, S.; Zeng, H.; Chen, J.; Hou, J.; Zhu, J.; Ma, K. Screen content video quality assessment: Subjective and objective study. IEEE Trans. Image Process. 2020, 29, 8636–8651. [Google Scholar] [CrossRef]
- Zhang, L.; Li, M.; Zhang, H. Fast intra bit rate transcoding for HEVC screen content coding. IET Image Process. 2018, 12, 738–744. [Google Scholar] [CrossRef]
- Kuang, W.; Chan, Y.; Tsang, S.; Siu, W. Online-learning-based Bayesian decision rule for fast intra mode and cu partitioning algorithm in HEVC screen content coding. IEEE Trans. Image Process. 2020, 29, 170–185. [Google Scholar] [CrossRef]
- Yang, H.; Fang, Y.; Lin, W. Perceptual quality assessment of screen content images. IEEE Trans. Image Process. 2015, 24, 4408–4421. [Google Scholar] [CrossRef]
- Bai, Y.; Yu, M.; Jiang, Q.; Jiang, G.; Zhu, Z. Learning content-specific codebooks for blind quality assessment of screen content images. Signal Process. 2019, 161, 248–258. [Google Scholar] [CrossRef]
- Gu, K.; Zhai, G.; Lin, W.; Yang, X.; Zhang, W. Learning a blind quality evaluation engine of screen content images. Neurocomputing 2016, 196, 140–149. [Google Scholar] [CrossRef]
- Gu, K.; Zhou, J.; Qiao, J.; Zhai, G. No-reference quality assessment of screen content pictures. IEEE Trans. Image Process. 2017, 26, 4005–4018. [Google Scholar] [CrossRef]
- Min, X.; Ma, K.; Gu, K.; Zhai, G.; Wang, Z.; Lin, W. Unified blind quality assessment of compressed natural, graphic, and screen content images. IEEE Trans. Image Process. 2017, 26, 5462–5474. [Google Scholar] [CrossRef] [PubMed]
- Lu, N.; Li, G. Blind quality assessment for screen content images by orientation selectivity mechanism. Signal Process. 2018, 145, 225–232. [Google Scholar] [CrossRef]
- Fang, Y.; Yan, J.; Li, L.; Wu, J.; Lin, W. No reference quality assessment for screen content images with both local and global feature representation. IEEE Trans. Image Process. 2018, 27, 1600–1610. [Google Scholar] [CrossRef]
- Zheng, L.; Shen, L.; Chen, J.; An, P.; Luo, J. No reference quality assessment for screen content images based on hybrid region features fusion. IEEE Trans. Multimed. 2019, 21, 2057–2070. [Google Scholar] [CrossRef]
- Fang, Y.; Du, R.; Zuo, Y.; Wen, W.; Li, L. Perceptual quality assessment for screen content images by spatial continuity. IEEE Trans. Circuits Syst. Video Technol. 2020, 30, 4050–4063. [Google Scholar] [CrossRef]
- Yang, J.; Liu, J.; Jiang, B.; Lu, W. No reference quality evaluation for screen content images considering texture feature based on sparse representation. Signal Process. 2018, 153, 336–347. [Google Scholar] [CrossRef]
- Zhou, W.; Yu, L.; Zhou, Y.; Qiu, W.; Wu, M.; Luo, T. Local and global feature learning for blind quality evaluation of screen content and natural scene images. IEEE Trans. Image Process. 2018, 27, 2086–2095. [Google Scholar] [CrossRef]
- Shao, F.; Gao, Y.; Li, F.; Jiang, G. Toward a blind quality predictor for screen content images. IEEE Trans. Syst. Man Cybern. Syst. 2018, 48, 1521–1530. [Google Scholar] [CrossRef]
- Wu, J.; Xia, Z.; Zhang, H.; Li, H. Blind quality assessment for screen content images by combining local and global features. Digit. Signal Process. 2019, 91, 31–40. [Google Scholar] [CrossRef]
- Bai, Y.; Zhu, Z.; Jiang, G.; Sun, H. Blind quality assessment of screen content images via macro-micro modeling of tensor domain dictionary. IEEE Trans. Multimed. 2020, 23, 4259–4271. [Google Scholar] [CrossRef]
- Chen, J.; Shen, L.; Zheng, L.; Jiang, X. Naturalization module in neural networks for screen content image quality assessment. IEEE Signal Process. Lett. 2018, 25, 1685–1689. [Google Scholar] [CrossRef]
- Jiang, X.; Shen, L.; Feng, G.; Yu, L.; An, P. An optimized CNN-based quality assessment model for screen content image. Signal Process. Image Commun. 2021, 94, 116181. [Google Scholar] [CrossRef]
- Yue, G.; Hou, C.; Yan, W.; Choi, L.; Zhou, T.; Hou, Y. Blind quality assessment for screen content images via convolutional neural network. Digit. Signal Process. 2019, 91, 21–30. [Google Scholar] [CrossRef]
- Jiang, X.; Shen, L.; Ding, Q.; Zheng, L.; An, P. Screen content image quality assessment based on convolutional neural networks. J. Vis. Commun. Image Represent. 2020, 67, 102–745. [Google Scholar] [CrossRef]
- Yang, J.; Bian, Z.; Zhao, Y.; Lu, W.; Gao, X. Staged-learning: Assessing the quality of screen content images from distortion information. IEEE Signal Process. Lett. 2021, 28, 1480–1484. [Google Scholar] [CrossRef]
- Yang, J.; Bian, Z.; Liu, J.; Jiang, B.; Lu, W.; Gao, X.; Song, H. No-reference quality assessment for screen content images using visual edge model and adaboosting neural network. IEEE Trans. Image Process. 2021, 30, 6801–6814. [Google Scholar] [CrossRef]
- Gu, K.; Wang, S.; Yang, H.; Lin, W.; Zhai, G.; Yang, X.; Zhang, W. Saliency-guided quality assessment of screen content images. IEEE Trans. Multimed. 2016, 18, 1098–1110. [Google Scholar] [CrossRef]
- Saad, M.A.; Bovik, A.C.; Charrier, C. Blind image quality assessment: A natural scene statistics approach in the DCT domain. IEEE Trans. Image Process. 2012, 21, 3339–3352. [Google Scholar] [CrossRef]
- Jiang, Q.; Shao, F.; Jiang, G.; Yu, M.; Peng, Z. Supervised dictionary learning for blind image quality assessment using quality-constraint sparse coding. J. Visual Commun. Image Represent. 2015, 33, 123–133. [Google Scholar] [CrossRef]
- Chen, B.; Li, H.; Fan, H.; Wang, S. No-Reference Screen Content Image Quality Assessment with Unsupervised Domain Adaptation. IEEE Trans. Image Process. 2021, 30, 5463–5476. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; Zhao, Y.; Liu, J.; Jiang, B.; Meng, Q.; Lu, W.; Gao, X. No Reference Quality Assessment for Screen Content Images Using Stacked Autoencoders in Pictorial and Textual Regions. IEEE Trans. Cybern. 2022, 52, 2798–2810. [Google Scholar] [CrossRef] [PubMed]
- Kulis, B. Metric learning: A survey. Found. Trends Mach. Learn. 2012, 5, 287–364. [Google Scholar] [CrossRef]
- Ponomarenko, N.; Ieremeiev, O.; Lukin, V.; Egiazarian, K.; Jin, L.; Astola, J.; Vozel, B.; Chehdi, K.; Carli, M.; Battisti, F.; et al. Color Image Database TID2013: Peculiarities and Preliminary Results. In Proceedings of the Europian Workshop on Visual Information Process. EUVIP, Paris, France, 10–12 June 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 106–111. [Google Scholar]
- Kang, L.; Ye, P.; Li, Y.; Doermann, D. Convolutional Neural Networks for No-Reference Image Quality Assessment. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 1733–1740. [Google Scholar]
- Kolda, T.G.; Bader, B.W. Tensor decompositions and applications. SIAM Review. 2009, 51, 455–500. [Google Scholar] [CrossRef]
- Lyu, S.; Simoncelli, E.P. Nonlinear image representation using divisive normalization. In Proceedings of the 2008 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Anchorage, AK, USA, 23–28 June 2008; IEEE: Piscataway, NJ, USA, 2014; pp. 1–8. [Google Scholar]
- Mittal, A.; Moorthy, A.K.; Bovik, A.C. No-reference image quality assessment in the spatial domain. IEEE Trans. Image Process. 2012, 21, 4695–4708. [Google Scholar] [CrossRef]
- Hyvärinen, A.; Oja, E. Independent component analysis: Algorithms and applications. Neural Netw. 2000, 13, 411–430. [Google Scholar] [CrossRef]
- Xu, J.; Ye, P.; Li, Q.; Du, H.; Liu, Y.; Doermann, D. Blind Image Quality Assessment Based on High Order Statistics Aggregation. IEEE Trans. Image Process. 2016, 25, 4444–4457. [Google Scholar] [CrossRef]
- Lin, H.; Chuang, J.; Liu, T. Regularized background adaptation: A novel learning rate control scheme for Gaussian mixture modeling. IEEE Trans. Image Process. 2011, 20, 822–836. [Google Scholar]
- Akkaynak, D.; Treibitz, T. A revised underwater image formation model. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 6723–6732. [Google Scholar]
- VLFeat Open Source Library. Available online: http://www.vlfeat.org/ (accessed on 8 August 2022).
- Perronnin, F.; Sánchez, J.; Mensink, T. Improving the Fisher kernel for large-scale image classification. In Proceedings of the European Conference on Computer Vision (ECCV), Crete, Greece, 5–11 September 2010; pp. 143–156. [Google Scholar]
- Chang, C.; Lin, C. LIBSVM: A library for support vector machines. ACM Trans. Intell. Syst. Technol. 2011, 2, 1–27. [Google Scholar] [CrossRef]
- Zhou, C.; Yu, W.; Huang, K.; Zhu, H.; Li, Y.; Yang, C.; Sun, B. A New Model Transfer Strategy Among Spectrometers Based on SVR Parameter Calibrating. IEEE Trans. Instrum. Meas. 2021, 70, 1–13. [Google Scholar] [CrossRef]
- Wang, S.; Gu, K.; Zhang, X.; Lin, W.; Zhang, L.; Ma, S.; Gao, W. Subjective and objective quality assessment of compressed screen content images. IEEE J. Emerg. Sel. Topics Circuits Syst. 2016, 6, 532–543. [Google Scholar] [CrossRef]
- Ni, Z.; Ma, L.; Zeng, H.; Lin, W.; Zhang, L.; Ma, S.; Gao, W. SCID: A database for screen content images quality assessment. In Proceedings of the 2017 International Symposium on Intelligent Signal Processing and Communication Systems (ISPACS), Xiamen, China, 6–9 November 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 774–779. [Google Scholar]
- Gottschalk, P.G.; Dunn, J.R. The five-parameter logistic: A characterization and comparison with the four-parameter logistic. Anal. Biochem. 2005, 343, 54–65. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Bovik, A.; Sheikh, H.; Simoncelli, E. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Zhang, L.; Mou, X.; Zhang, D. FSIM: A feature similarity index for image quality assessment. IEEE Trans. Image Process.. 2011, 20, 2378–2386. [Google Scholar] [CrossRef]
- Zhang, L.; Shen, Y.; Li, H. VSI: A visual saliency-induced index for perceptual image quality assessment. IEEE Trans. Image Process. 2014, 23, 4270–4281. [Google Scholar] [CrossRef]
- Sheikh, H.R.; Bovik, A.C. Image information and visual quality. IEEE Trans. Image Process. 2006, 15, 430–444. [Google Scholar] [CrossRef]
- Gu, K.; Qiao, J.; Min, X.; Yue, G.; Lin, W.; Thalmann, D. Evaluating quality of screen content images via structural variation analysis. IEEE Trans. Vis. Comput. Graph. 2018, 24, 2689–2701. [Google Scholar] [CrossRef]
- Zhang, Y.; Chandler, D.M.; Mou, X. Quality assessment of screen content images via convolutional neural network-based synthetic/natural segmentation. IEEE Trans. Image Process. 2018, 27, 5113–5128. [Google Scholar]
- Wang, R.; Yang, H.; Pan, Z.; Huang, B.; Hou, G. Screen content image quality assessment with edge features in gradient domain. IEEE Access. 2019, 7, 5285–5295. [Google Scholar] [CrossRef]
- Chen, C.; Zhao, H.; Yang, H.; Peng, C.; Yu, T. Full reference screen content image quality assessment by fusing multi-level structure similarity. ACM Trans. Multimed. Comput. Commun. Appl. 2020, 17, 1–21. [Google Scholar]
- Ye, P.; Kumar, J.; Doermann, D. Beyond human opinion scores: Blind image quality assessment based on synthetic scores. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Columbus, OH, USA, 23–28 June 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 4241–4248. [Google Scholar]


| Database | Image Number | Distortion | |||
|---|---|---|---|---|---|
| Reference | Distorted | Type | Level | Notes | |
| SIQAD | 20 | 980 | 7 | 7 | Gaussian noise (GN), Gaussian blur (GB), motion blur (MB), contrast change (CC), JPEG, JPEG 2000 (J2K) and layer segmentation-based coding (LSC) |
| SCD | 24 | 492 | 2 | / | Screen content compression (SCC) and High-Efficiency Video Coding (HEVC) |
| SCID | 40 | 1800 | 9 | 5 | GN, GB, MB, CC, JPEG, J2K, color saturation change (CSC), SCC, and color quantization with dithering (CQD) |
| Method | SIQAD | SCD | SCID | ||||||
|---|---|---|---|---|---|---|---|---|---|
| PLCC | SRCC | RMSE | PLCC | SRCC | RMSE | PLCC | SRCC | RMSE | |
| PSNR | 0.5869 | 0.5608 | 11.5859 | 0.861 | 0.8589 | 1.1273 | 0.7622 | 0.7512 | 9.1682 |
| SSIM | 0.5912 | 0.5836 | 11.5450 | 0.8696 | 0.8683 | 1.0953 | 0.7343 | 0.7146 | 9.6133 |
| FSIM | 0.5746 | 0.5652 | 11.6120 | 0.9019 | 0.9039 | 0.9585 | 0.7719 | 0.7550 | 9.0040 |
| VSI | 0.5403 | 0.5199 | 11.9380 | 0.8715 | 0.8719 | 1.0879 | 0.7550 | 0.7530 | 9.3470 |
| VIF | 0.8198 | 0.8065 | 8.1969 | 0.9028 | 0.9043 | 0.9542 | 0.8200 | 0.7969 | 8.1069 |
| SVQI | 0.8911 | 0.8836 | 6.4965 | 0.9158 | 0.9194 | 0.8909 | 0.8604 | 0.8386 | 7.2178 |
| SQE | 0.9040 | 0.8940 | 6.1150 | 0.9290 | 0.9310 | 0.8210 | 0.9150 | 0.9140 | 5.7610 |
| EFGD | 0.8993 | 0.8901 | 6.2595 | / | / | / | 0.8846 | 0.8774 | 6.6044 |
| SR-CNN | 0.9160 | 0.9080 | 5.6830 | / | / | / | 0.9390 | 0.9400 | 4.8300 |
| QODCNN | 0.9142 | 0.9066 | 5.8015 | / | / | / | 0.8820 | 0.8760 | / |
| Proposed | 0.9135 | 0.9023 | 5.8088 | 0.9316 | 0.9265 | 0.7993 | 0.8737 | 0.8576 | 6.8673 |
| Method | SIQAD | SCD | SCID | ||||||
|---|---|---|---|---|---|---|---|---|---|
| PLCC | SRCC | RMSE | PLCC | SRCC | RMSE | PLCC | SRCC | RMSE | |
| SIQE | 0.7906 | 0.7625 | 8.7650 | 0.7168 | 0.7012 | 1.547 | 0.6343 | 0.6009 | 10.9483 |
| OSM | 0.8306 | 0.8007 | 7.9331 | 0.7068 | 0.6804 | 1.5301 | / | / | / |
| NRLT | 0.8442 | 0.8202 | 7.5957 | 0.9227 | 0.9156 | 0.8091 | 0.8377 | 0.8178 | 7.7265 |
| HRFF | 0.8520 | 0.8320 | 7.4150 | / | / | / | / | / | / |
| PQSC | 0.9164 | 0.9069 | 5.708 | 0.9362 | 0.9299 | 0.7746 | 0.9179 | 0.9147 | 5.4793 |
| TFSR | 0.8618 | 0.8354 | 7.4910 | / | / | / | 0.8017 | 0.7840 | 8.8041 |
| LGFL | 0.8280 | 0.7880 | / | / | / | / | / | / | / |
| CLGF | 0.8331 | 0.8107 | 7.9172 | / | / | / | 0.6978 | 0.6870 | 10.1439 |
| CSC | 0.9109 | 0.8976 | 5.8930 | 0.9182 | 0.9080 | 0.8721 | 0.8531 | 0.8377 | 7.3930 |
| MTD | 0.9162 | 0.9090 | 5.7111 | 0.9196 | 0.9123 | 0.8654 | 0.8811 | 0.8730 | 6.7031 |
| PICNN | 0.8960 | 0.8970 | 6.7900 | / | / | / | 0.8270 | 0.822 | 8.0130 |
| IGMCNN | 0.8834 | 0.8634 | 6.3971 | / | / | / | 0.8710 | 0.8663 | 6.4123 |
| SIQA-DF | 0.9000 | 0.8880 | 6.2422 | / | / | / | 0.8514 | 0.8507 | 7.0687 |
| MtDl | 0.9281 | 0.9214 | 5.611 | / | / | / | 0.9248 | 0.9233 | 5.4200 |
| ABPNN | 0.8529 | 0.8336 | 7.2817 | / | / | / | 0.7147 | 0.6920 | 10.3988 |
| Proposed | 0.9135 | 0.9023 | 5.8088 | 0.9316 | 0.9265 | 0.7993 | 0.8737 | 0.8576 | 6.8673 |
| PLCC | GN | GB | MB | CC | JPEG | J2K | LSC | Variance |
|---|---|---|---|---|---|---|---|---|
| SIQE | 0.8779 | 0.9138 | 0.7836 | 0.6856 | 0.7244 | 0.7339 | 0.7332 | 7.30 × 10−3 |
| OSM | / | / | / | / | / | / | / | |
| NRLT | 0.9131 | 0.8949 | 0.8993 | 0.8131 | 0.7932 | 0.6848 | 0.7228 | 8.17 × 10−3 |
| HRFF | 0.9020 | 0.8900 | 0.8740 | 0.8260 | 0.7630 | 0.7540 | 0.7700 | 4.08 × 10−3 |
| PQSC | 0.9200 | 0.9300 | 0.9100 | 0.8200 | 0.8500 | 0.8900 | 0.8500 | 1.75 × 10−3 |
| TFSR | 0.9291 | 0.9367 | 0.9243 | 0.6563 | 0.8334 | 0.8347 | 0.8069 | 9.84 × 10−3 |
| LGFL | 0.9030 | 0.9110 | 0.8370 | 0.6600 | 0.7620 | 0.6680 | 0.6830 | 1.20 × 10−2 |
| CLGF | 0.8577 | 0.9082 | 0.8609 | 0.7440 | 0.6598 | 0.7463 | 0.5575 | 1.55 × 10−2 |
| CSC | 0.9317 | 0.9148 | 0.8846 | 0.9229 | 0.9036 | 0.9143 | 0.9294 | 2.67 × 10−4 |
| MTD | 0.9390 | 0.9156 | 0.8844 | 0.9231 | 0.914 | 0.8949 | 0.9192 | 3.28 × 10−4 |
| PICNN | 0.9100 | 0.9190 | 0.8890 | 0.8260 | 0.8290 | 0.8520 | 0.8360 | 1.56 × 10−3 |
| IGMCNN | / | / | / | / | / | / | / | / |
| SIQA-DF | 0.9120 | 0.9240 | 0.8900 | 0.8440 | 0.8290 | 0.8280 | 0.8580 | 1.56 × 10−3 |
| MtDl | / | / | / | / | / | / | / | / |
| ABPNN | 0.9139 | 0.9225 | 0.8948 | 0.7772 | 0.8014 | 0.7984 | 0.7907 | 4.14 × 10−3 |
| Proposed | 0.9400 | 0.9131 | 0.8946 | 0.9219 | 0.9176 | 0.9119 | 0.9328 | 2.21 × 10−4 |
| SRCC | GN | GB | MB | CC | JPEG | J2K | LSC | Variance |
|---|---|---|---|---|---|---|---|---|
| SIQE | 0.8517 | 0.9174 | 0.8347 | 0.6874 | 0.7438 | 0.7241 | 0.7337 | 7.00 × 10−3 |
| OSM | / | / | / | / | / | / | / | / |
| NRLT | 0.8966 | 0.8812 | 0.8919 | 0.7072 | 0.7698 | 0.6761 | 0.6978 | 9.80 × 10−3 |
| HRFF | 0.8720 | 0.8630 | 0.8500 | 0.687 | 0.7180 | 0.7440 | 0.7400 | 5.94 × 10−3 |
| PQSC | 0.9000 | 0.9200 | 0.8900 | 0.7 | 0.8300 | 0.8800 | 0.8300 | 5.53 × 10−3 |
| TFSR | 0.9144 | 0.9311 | 0.9148 | 0.6498 | 0.8377 | 0.8354 | 0.7948 | 9.61 × 10−3 |
| LGFL | 0.8790 | 0.8940 | 0.8320 | 0.487 | 0.7440 | 0.6450 | 0.6660 | 2.16 × 10−2 |
| CLGF | 0.8478 | 0.9152 | 0.8694 | 0.5716 | 0.6778 | 0.7681 | 0.5842 | 1.93 × 10−2 |
| CSC | 0.9143 | 0.8971 | 0.8708 | 0.9075 | 0.8848 | 0.8911 | 0.9064 | 2.27 × 10−4 |
| MTD | 0.9201 | 0.8993 | 0.8703 | 0.9102 | 0.8966 | 0.8593 | 0.8867 | 4.61 × 10−4 |
| PICNN | 0.9020 | 0.9160 | 0.8800 | 0.6990 | 0.8230 | 0.8340 | 0.8720 | 5.36 × 10−3 |
| IGMCNN | / | / | / | / | / | / | / | / |
| SIQA-DF | 0.9010 | 0.9100 | 0.8800 | 0.7280 | 0.8120 | 0.8160 | 0.8580 | 4.06 × 10−3 |
| MtDl | / | / | / | / | / | / | / | / |
| ABPNN | 0.9102 | 0.9223 | 0.8867 | 0.7471 | 0.7768 | 0.7783 | 0.7585 | 5.92 × 10−3 |
| Proposed | 0.9212 | 0.8944 | 0.8834 | 0.9102 | 0.8993 | 0.8851 | 0.9061 | 1.87 × 10−4 |
| RMSE | GN | GB | MB | CC | JPEG | J2K | LSC | Variance |
|---|---|---|---|---|---|---|---|---|
| SIQE | 8.1416 | 6.4239 | 8.0783 | 9.1565 | 6.4778 | 7.6727 | 6.3160 | 1.1861 |
| OSM | / | / | / | / | / | / | / | / |
| NRLT | 6.3113 | 6.9171 | 6.4524 | 7.8433 | 5.872 | 6.5441 | 5.7864 | 0.4858 |
| HRFF | 6.2670 | 6.7380 | 6.4660 | 6.8740 | 5.8620 | 6.5010 | 5.4730 | 0.2442 |
| PQSC | / | / | / | / | / | / | / | |
| TFSR | 5.3105 | 5.2141 | 5.5266 | 10.5005 | 5.2541 | 5.6377 | 5.6217 | 3.7067 |
| LGFL | / | / | / | / | / | / | / | / |
| CLGF | / | / | / | / | / | / | / | / |
| CSC | 5.3292 | 5.3767 | 6.0794 | 5.0375 | 5.5912 | 5.4480 | 5.2539 | 0.1074 |
| MTD | 5.0506 | 5.2992 | 6.1017 | 5.0238 | 5.3266 | 5.9826 | 5.5994 | 0.1837 |
| PICNN | 6.2010 | 5.8700 | 5.7720 | 7.0120 | 5.4700 | 5.9920 | 4.6730 | 0.5049 |
| IGMCNN | / | / | / | / | / | / | / | / |
| SIQA-DF | 6.1150 | 5.7680 | 5.7910 | 6.7470 | 5.3840 | 5.8120 | 4.4620 | 0.4870 |
| MtDl | / | / | / | / | / | / | / | / |
| ABPNN | 5.9745 | 5.7319 | 6.7144 | 8.0684 | 6.8006 | 6.5538 | 5.4556 | 0.7584 |
| Proposed | 4.9987 | 5.3785 | 5.8043 | 4.9994 | 5.1861 | 5.4307 | 5.1030 | 0.0841 |
| Distortion | (a) Training with SIQAD | (b) Training with SCID | ||||
|---|---|---|---|---|---|---|
| PLCC | SRCC | RMSE | PLCC | SRCC | RMSE | |
| GN | 0.9300 | 0.9109 | 4.6213 | 0.8921 | 0.8843 | 6.7399 |
| GB | 0.9277 | 0.9088 | 4.4339 | 0.8551 | 0.8544 | 6.9978 |
| MB | 0.9059 | 0.8886 | 5.1253 | 0.8232 | 0.8317 | 7.6019 |
| CC | 0.8794 | 0.8605 | 5.8277 | 0.8236 | 0.8377 | 7.5378 |
| JPEG | 0.8359 | 0.8226 | 6.3599 | 0.8405 | 0.8365 | 7.2293 |
| J2K | 0.7148 | 0.6977 | 7.4051 | 0.7631 | 0.7546 | 7.2196 |
| Overall | 0.8541 | 0.8583 | 6.1862 | 0.8395 | 0.8438 | 7.4497 |
| Anchor Type | SIQAD | SCD | SCID | ||||||
|---|---|---|---|---|---|---|---|---|---|
| PLCC | SRCC | RMSE | PLCC | SRCC | RMSE | PLCC | SRCC | RMSE | |
| Reference + Distortion | 0.9023 | 0.8901 | 6.1512 | 0.9287 | 0.9223 | 0.8193 | 0.8647 | 0.8503 | 7.1126 |
| Natural + Artificial | 0.9135 | 0.9023 | 5.8088 | 0.9316 | 0.9265 | 0.7993 | 0.8737 | 0.8576 | 6.8673 |
| K | SIQAD | SCD | SCID | ||||||
|---|---|---|---|---|---|---|---|---|---|
| PLCC | SRCC | RMSE | PLCC | SRCC | RMSE | PLCC | SRCC | RMSE | |
| 50 | 0.9108 | 0.8979 | 5.8894 | 0.9282 | 0.922 | 0.8186 | 0.8657 | 0.8496 | 7.0651 |
| 100 | 0.9135 | 0.9023 | 5.8088 | 0.9316 | 0.9265 | 0.7993 | 0.8737 | 0.8576 | 6.8673 |
| 150 | 0.9103 | 0.8995 | 5.9006 | 0.934 | 0.9309 | 0.7868 | 0.8733 | 0.8572 | 6.8921 |
| Feature Type | SIQAD | SCD | SCID | ||||||
|---|---|---|---|---|---|---|---|---|---|
| PLCC | SRCC | RMSE | PLCC | SRCC | RMSE | PLCC | SRCC | RMSE | |
| Mean | 0.8961 | 0.8814 | 6.3428 | 0.9262 | 0.9220 | 0.8309 | 0.8586 | 0.8419 | 7.2503 |
| Variance | 0.9135 | 0.9023 | 5.8088 | 0.9316 | 0.9265 | 0.7993 | 0.8737 | 0.8576 | 6.8673 |
| Skewness | 0.8901 | 0.8774 | 6.5002 | 0.9048 | 0.9012 | 0.9385 | 0.8368 | 0.8189 | 7.7403 |
| Kurtosis | 0.8689 | 0.8529 | 7.0789 | 0.9227 | 0.9168 | 0.8544 | 0.7943 | 0.7746 | 8.5951 |
| M. + V. | 0.8978 | 0.8864 | 6.2922 | 0.9241 | 0.9209 | 0.8429 | 0.8526 | 0.8384 | 7.3896 |
| M. + V. + S. | 0.8783 | 0.8657 | 6.8292 | 0.9040 | 0.9111 | 0.9396 | 0.8175 | 0.8046 | 8.1537 |
| M. + V. + S. + K. | 0.8774 | 0.8655 | 6.8522 | 0.9030 | 0.9116 | 0.9485 | 0.8150 | 0.7995 | 8.1756 |
| Feature Type | HOSA | Proposed | ||||
|---|---|---|---|---|---|---|
| PLCC | SRCC | RMSE | PLCC | SRCC | RMSE | |
| Mean | / | 0.8137 | / | 0.8961 | 0.8814 | 6.3428 |
| Variance | / | 0.8340 | / | 0.9135 | 0.9023 | 5.8088 |
| Skewness | / | 0.8159 | / | 0.8901 | 0.8774 | 6.5002 |
| M. + V. | / | 0.8343 | / | 0.8978 | 0.8864 | 6.2922 |
| M. + V. + S. | 0.8636 | 0.8484 | 6.9594 | 0.8783 | 0.8657 | 6.8292 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jing, W.; Bai, Y.; Zhu, Z.; Zhang, R.; Jin, Y. Dual-Anchor Metric Learning for Blind Image Quality Assessment of Screen Content Images. Electronics 2022, 11, 2510. https://doi.org/10.3390/electronics11162510
Jing W, Bai Y, Zhu Z, Zhang R, Jin Y. Dual-Anchor Metric Learning for Blind Image Quality Assessment of Screen Content Images. Electronics. 2022; 11(16):2510. https://doi.org/10.3390/electronics11162510
Chicago/Turabian StyleJing, Weiyi, Yongqiang Bai, Zhongjie Zhu, Rong Zhang, and Yiwen Jin. 2022. "Dual-Anchor Metric Learning for Blind Image Quality Assessment of Screen Content Images" Electronics 11, no. 16: 2510. https://doi.org/10.3390/electronics11162510
APA StyleJing, W., Bai, Y., Zhu, Z., Zhang, R., & Jin, Y. (2022). Dual-Anchor Metric Learning for Blind Image Quality Assessment of Screen Content Images. Electronics, 11(16), 2510. https://doi.org/10.3390/electronics11162510





