Comparison and Optimization of a Magnetic Lead Screw Applied in Wave Energy Conversions
Abstract
:1. Introduction
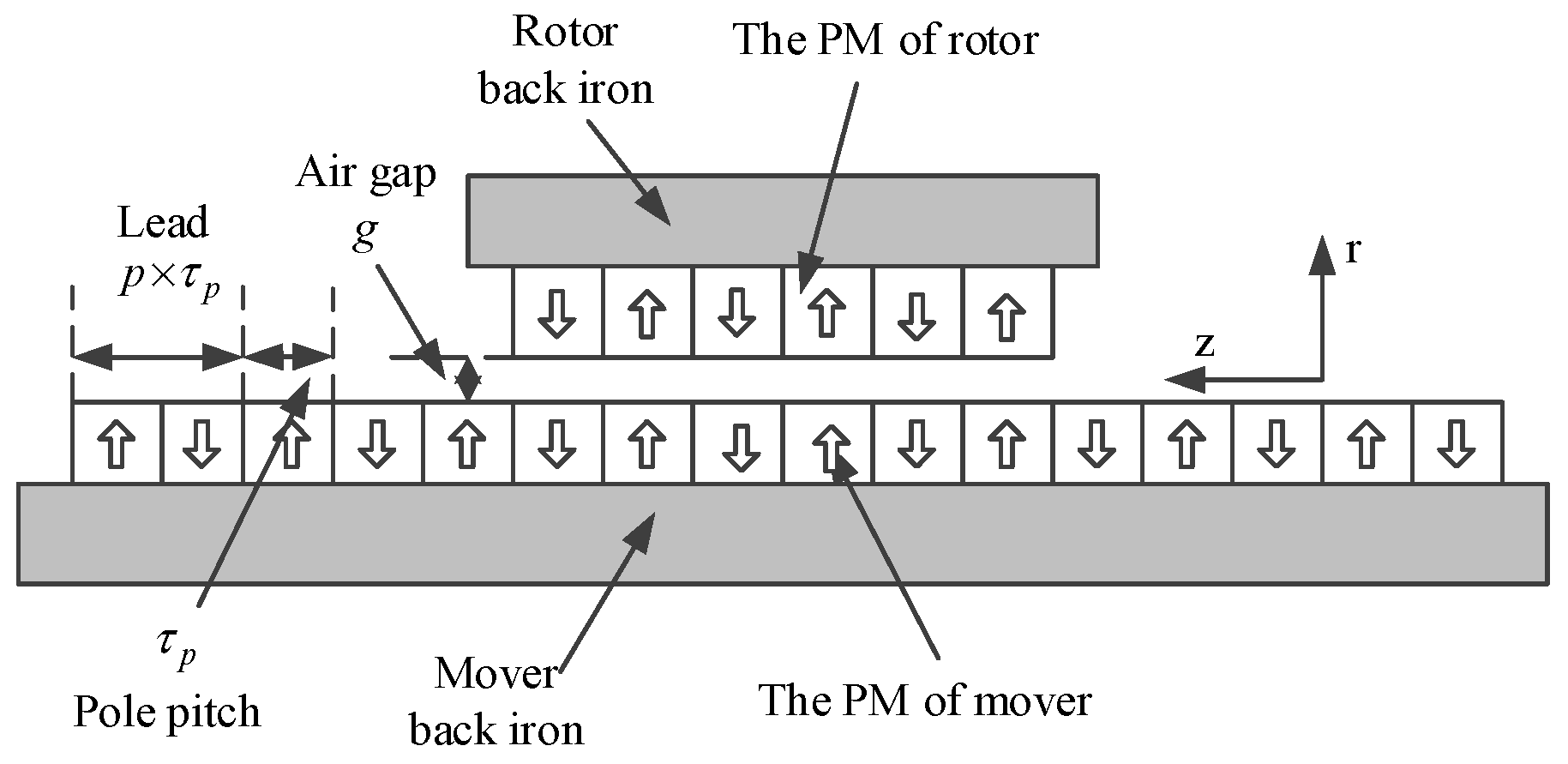
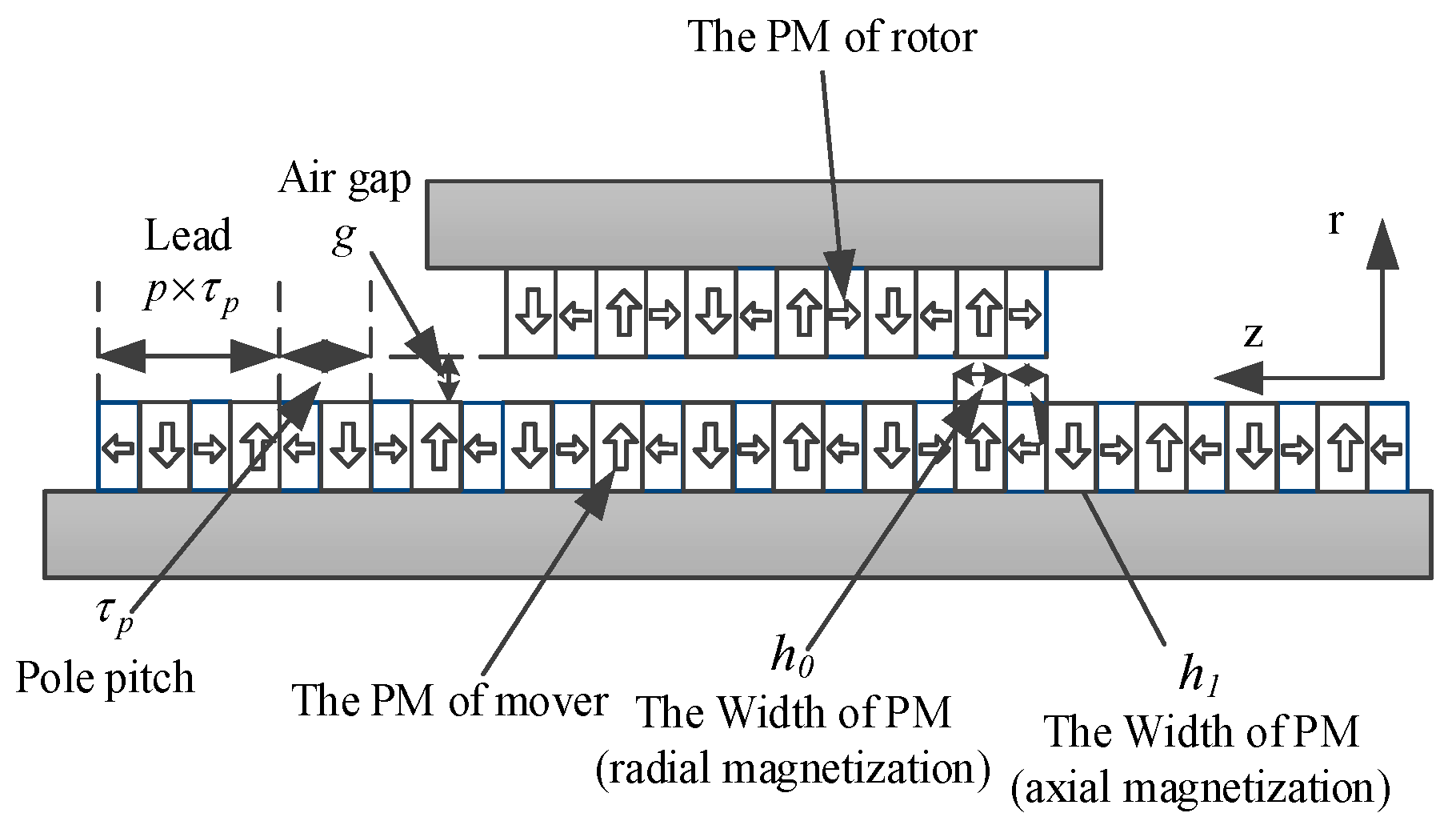
2. Principles of the MLS
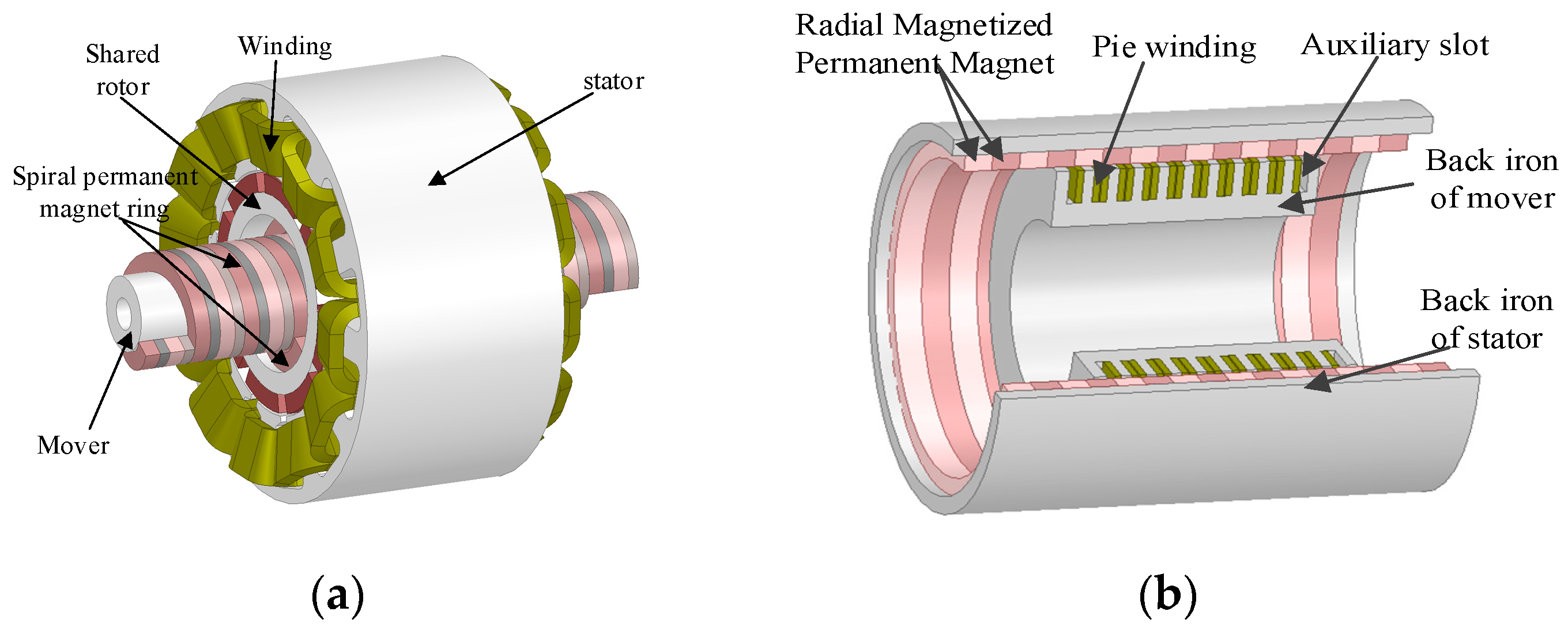
3. Magnetic Lead Screw Topology
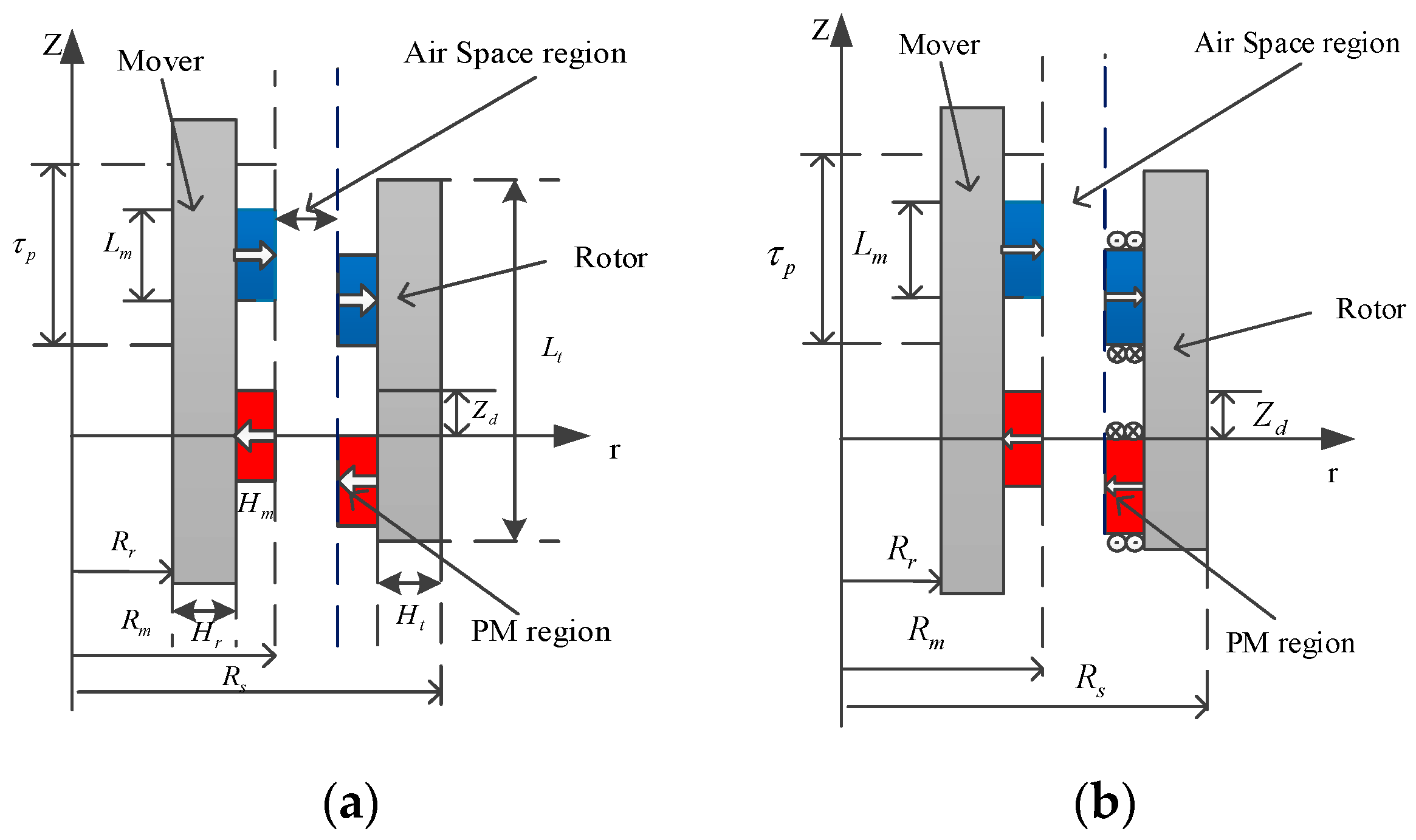
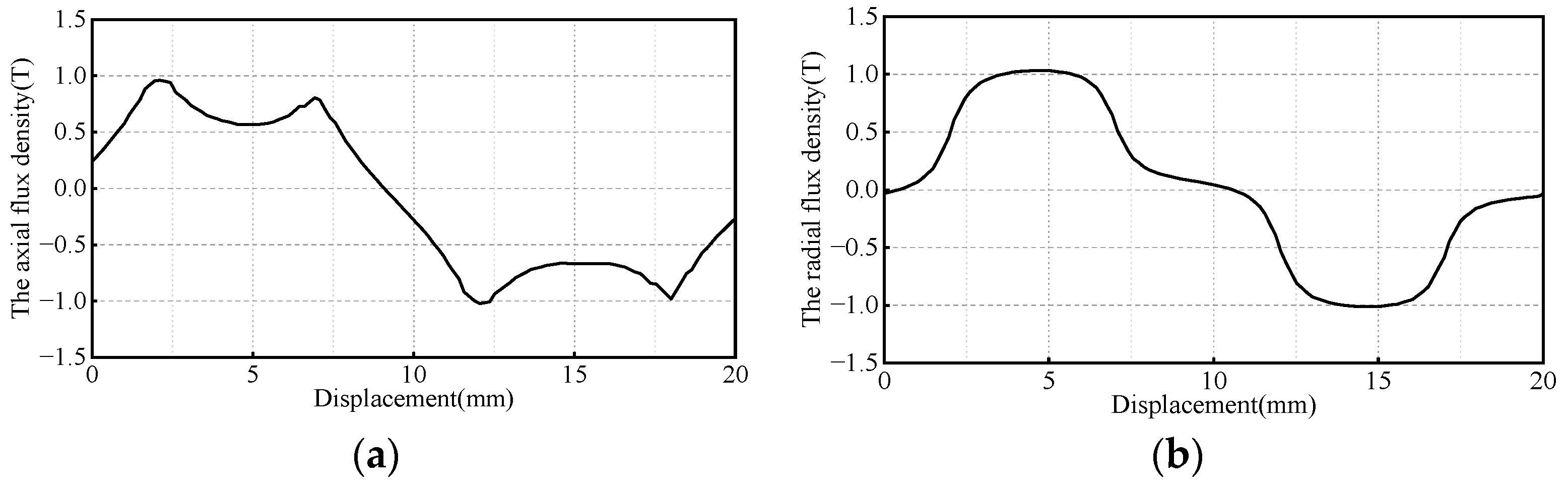
3.1. Surface-Mount Magnetic Lead Screw
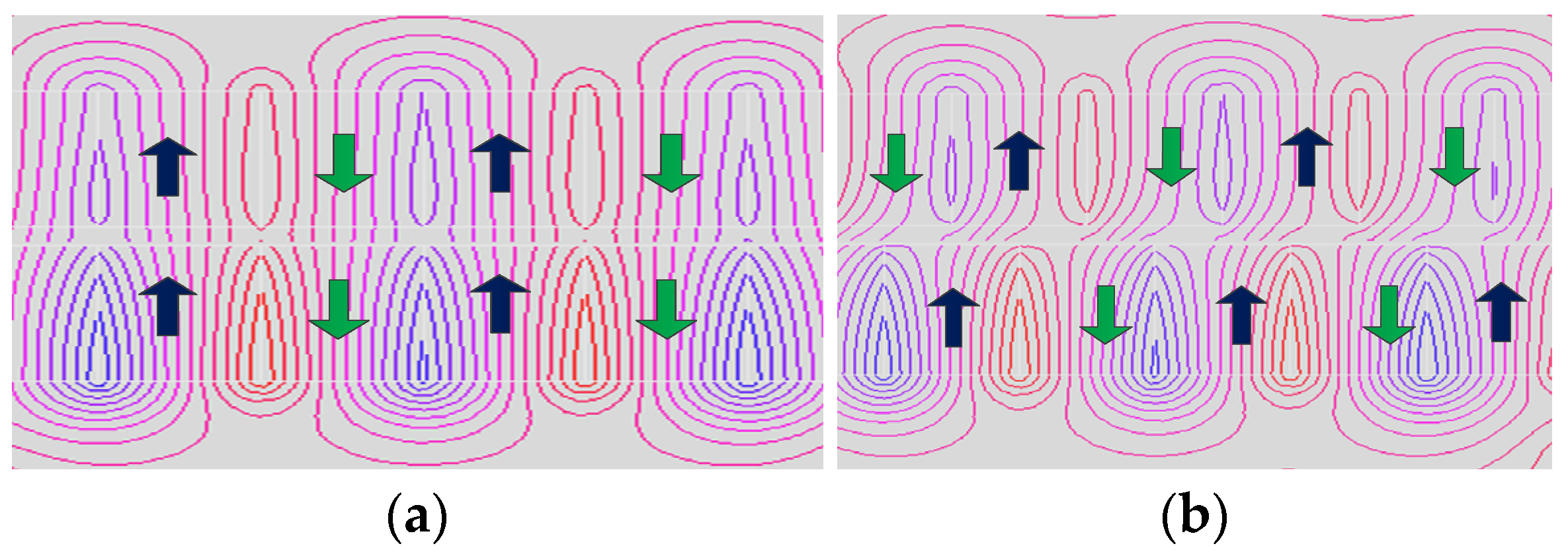
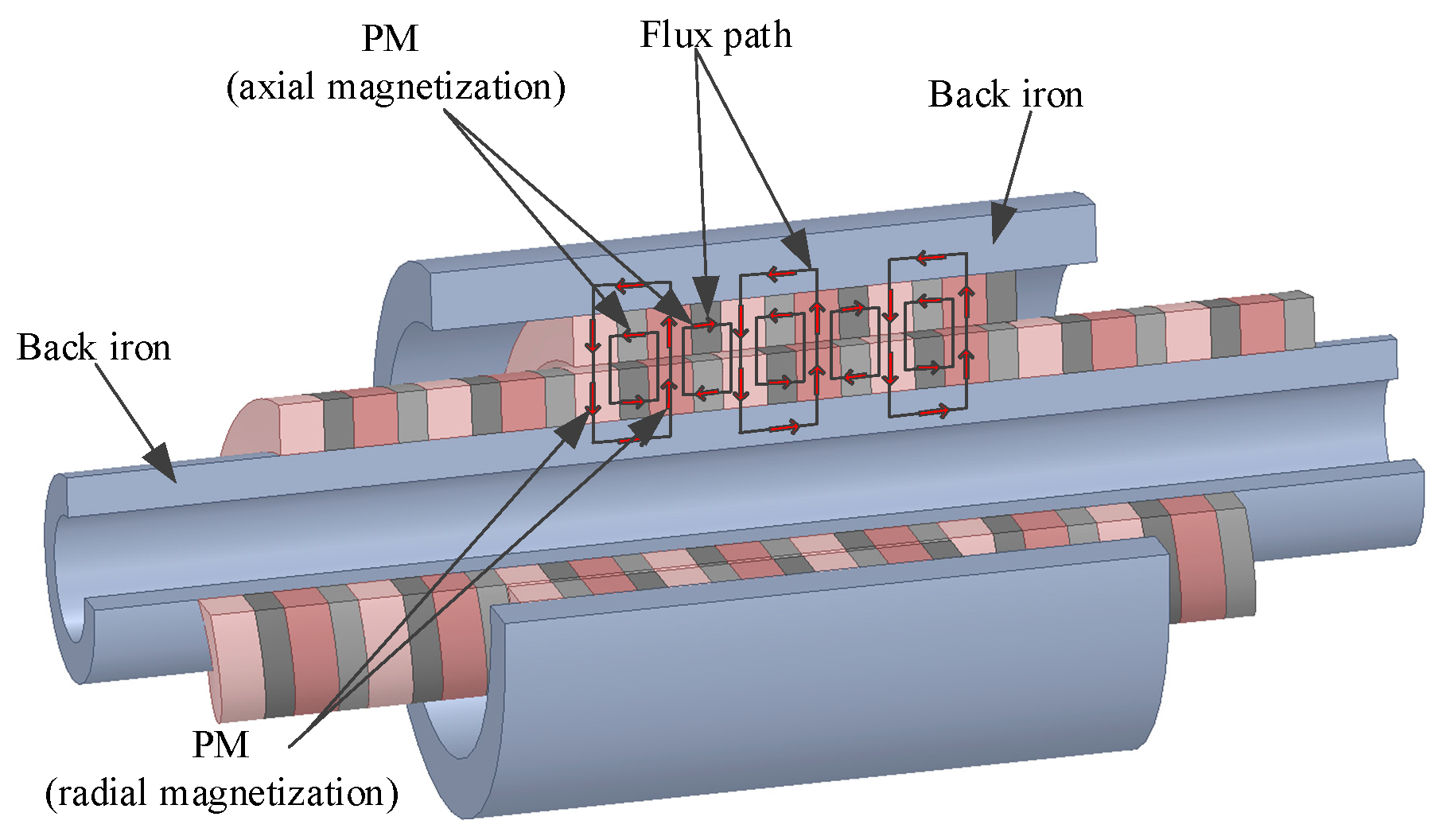
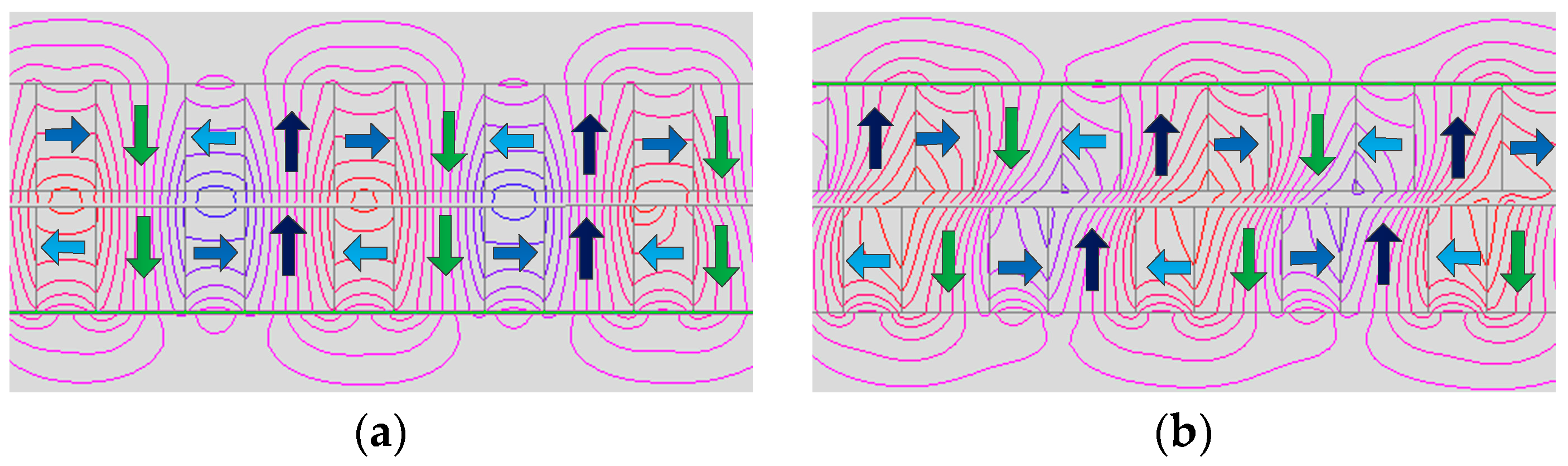
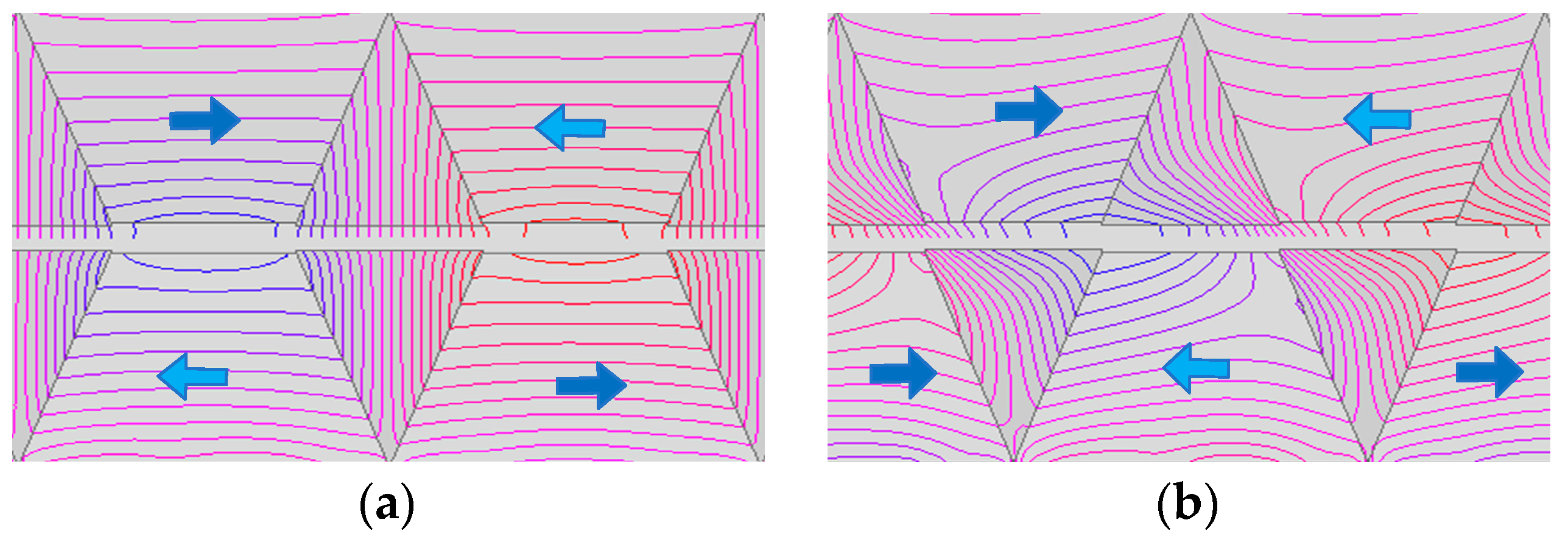
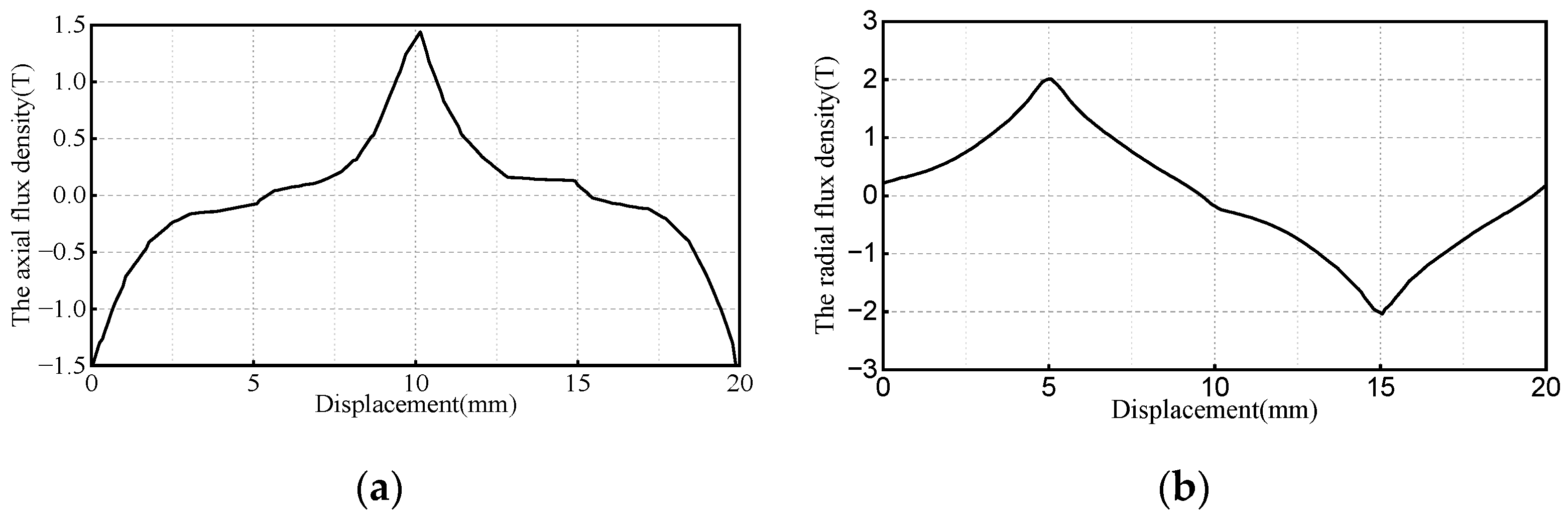
3.2. Quasi-Halbach Array Magnetic Lead Screw
3.3. Triangular Tooth Magnetic Lead Screw
4. Optimization of Different Topologies
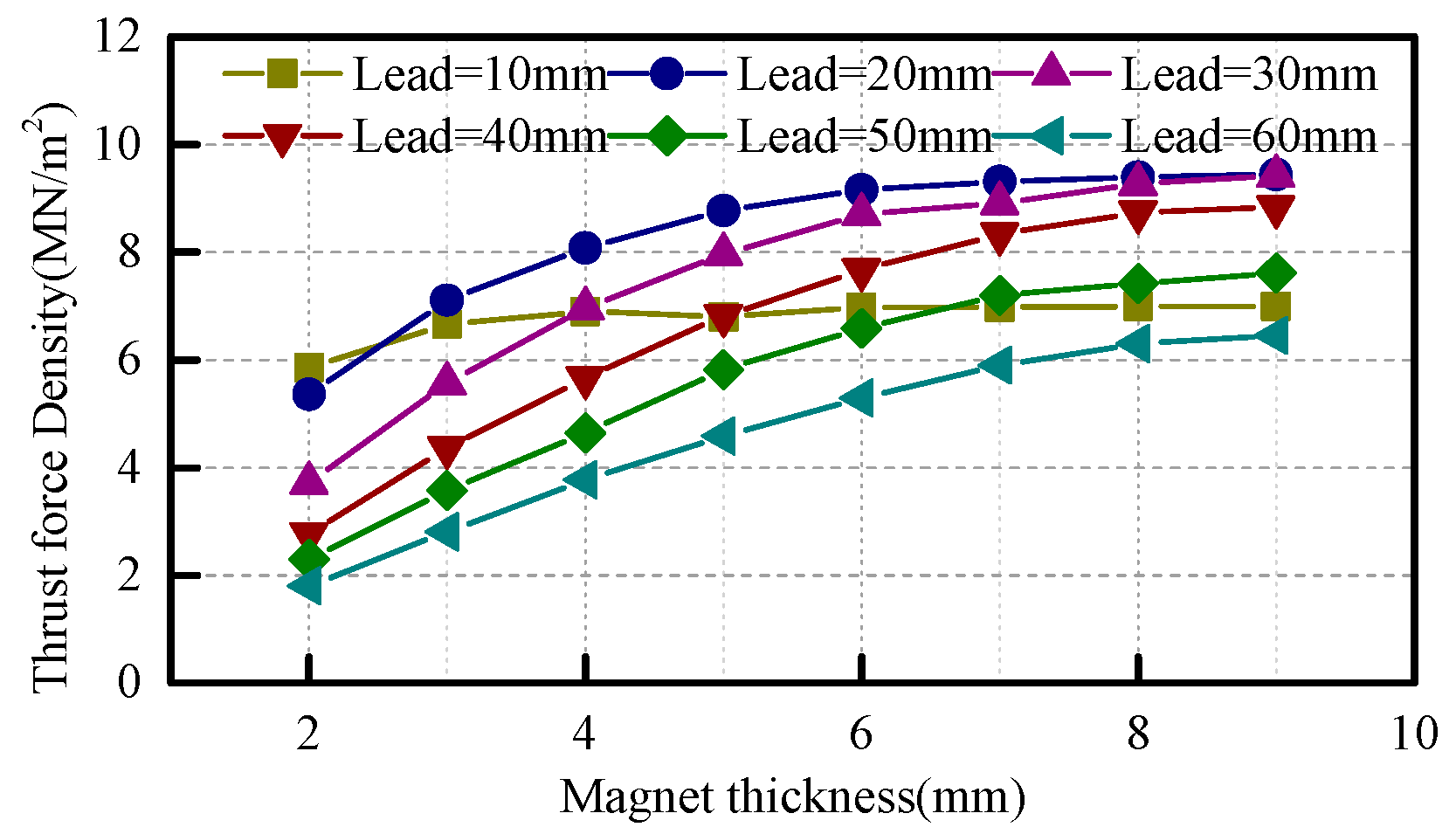
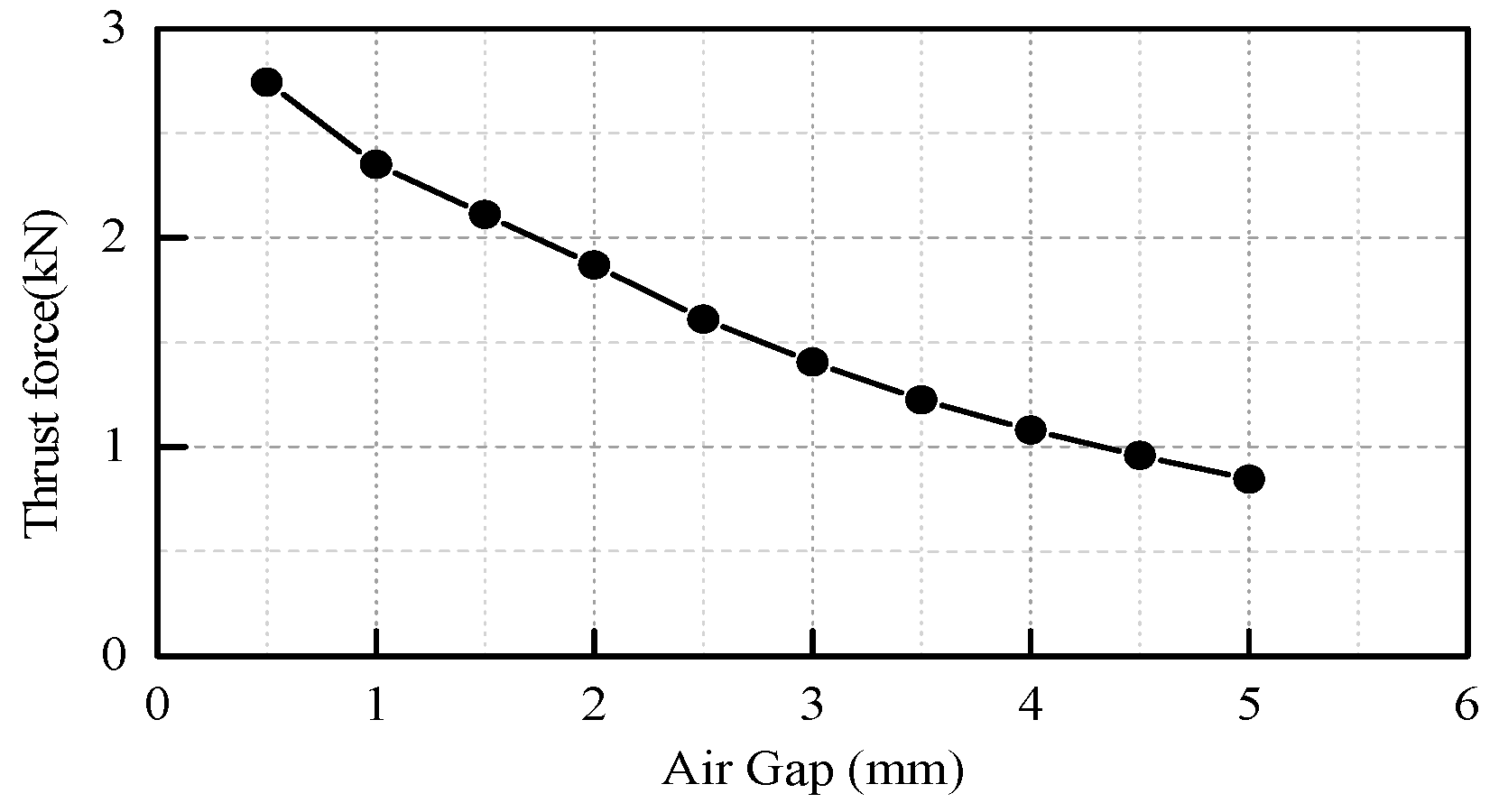
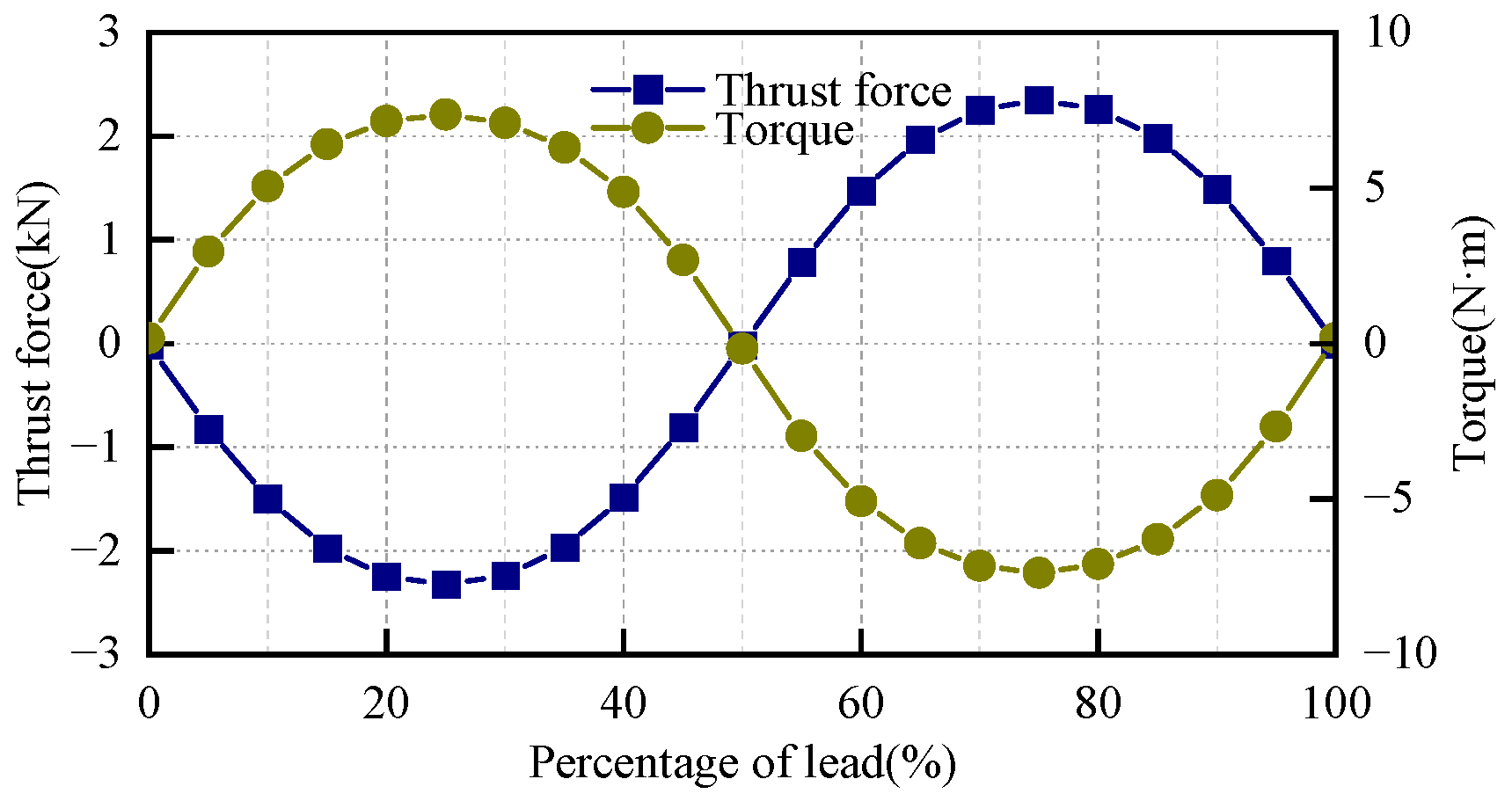
4.1. Optimization of the SMMLS
4.2. Optimization of the QHAMLS
4.3. Optimization of the TTMLS
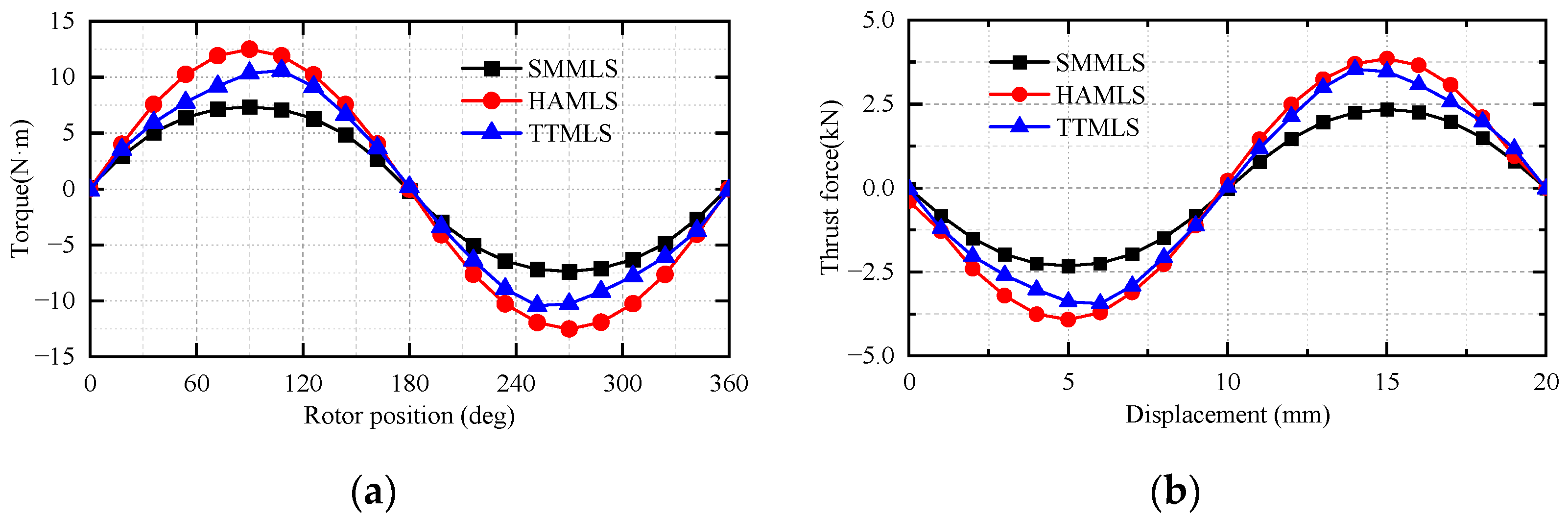
4.4. Comparison and Evaluation
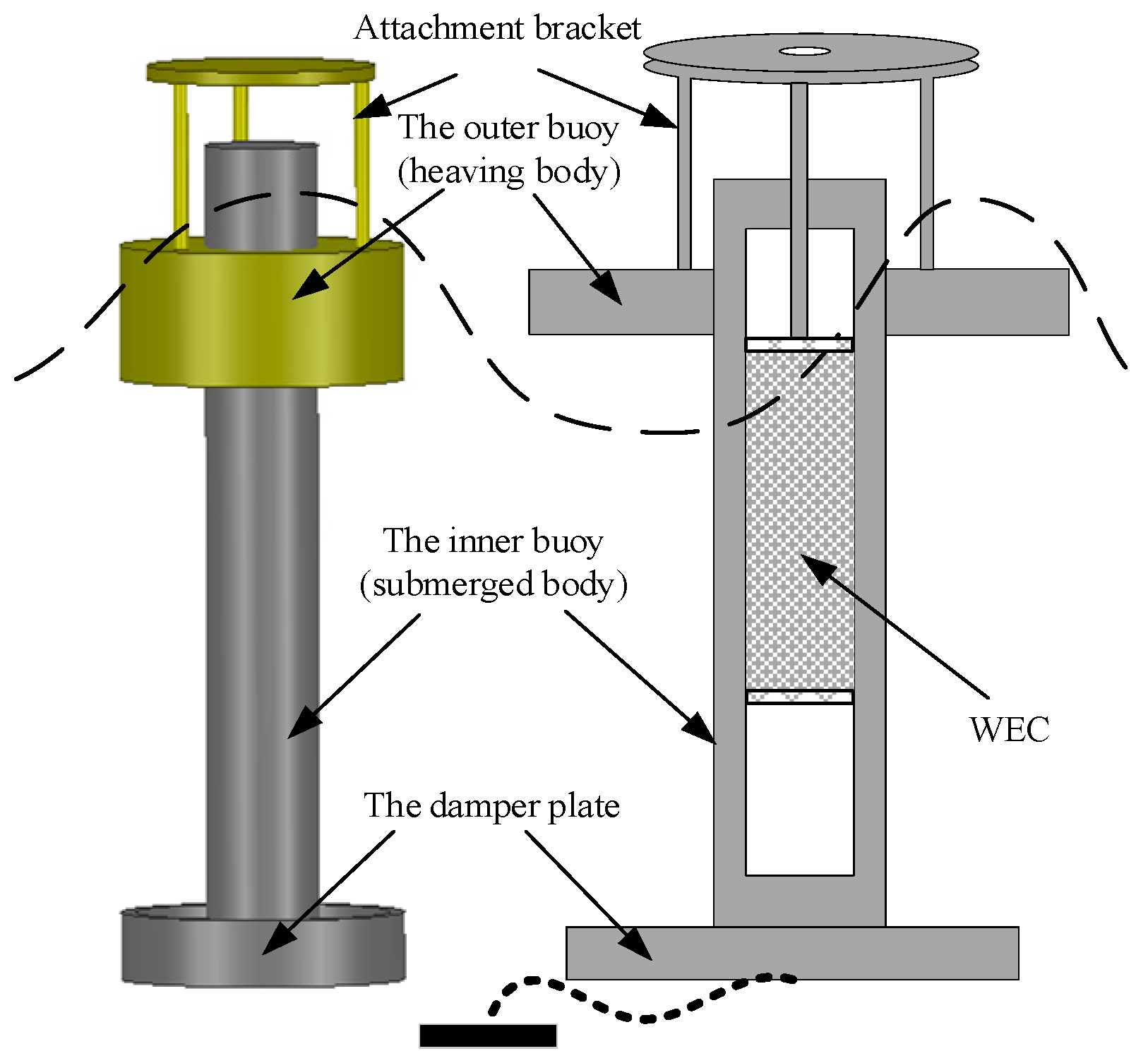
5. Application of the MLS in Wave Energy
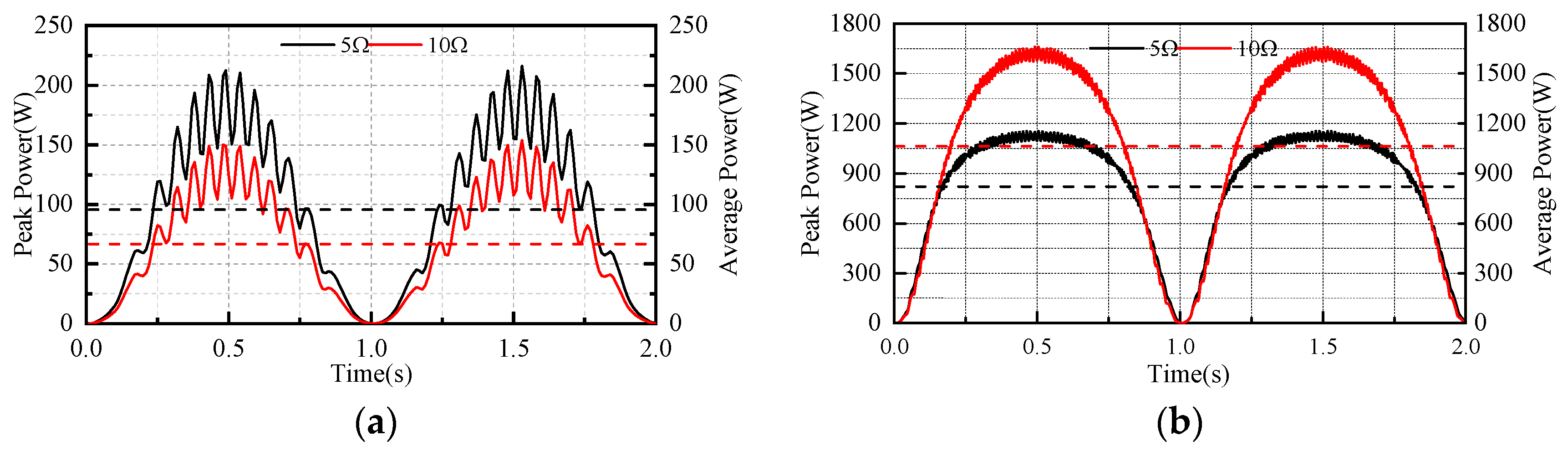
5.1. Comparison under Constant Speed Conditions
5.2. Comparison under Wave Speed Conditions
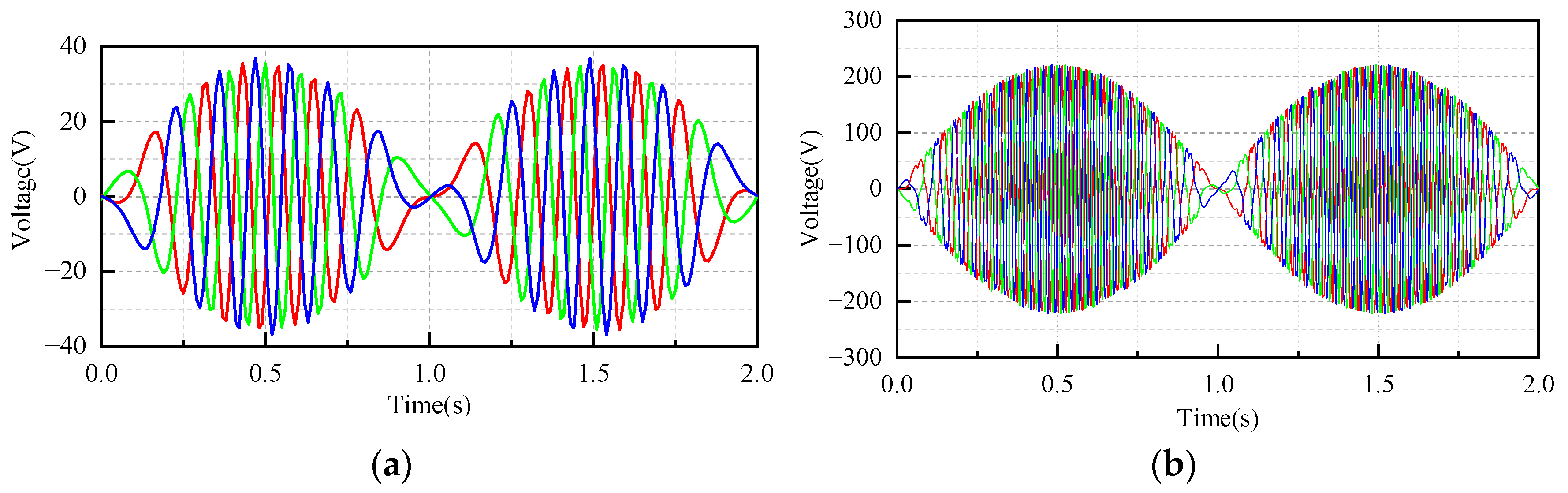
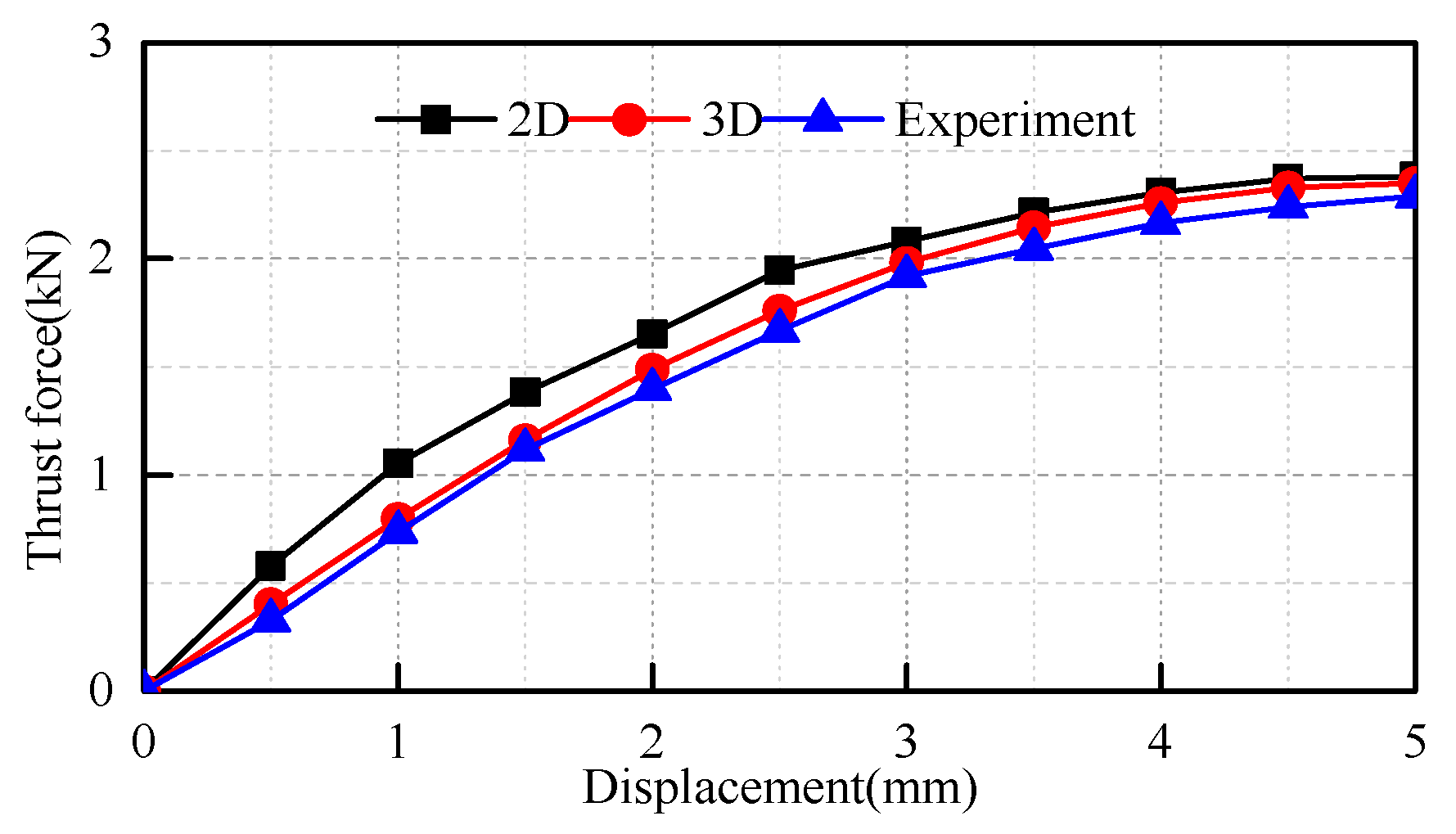
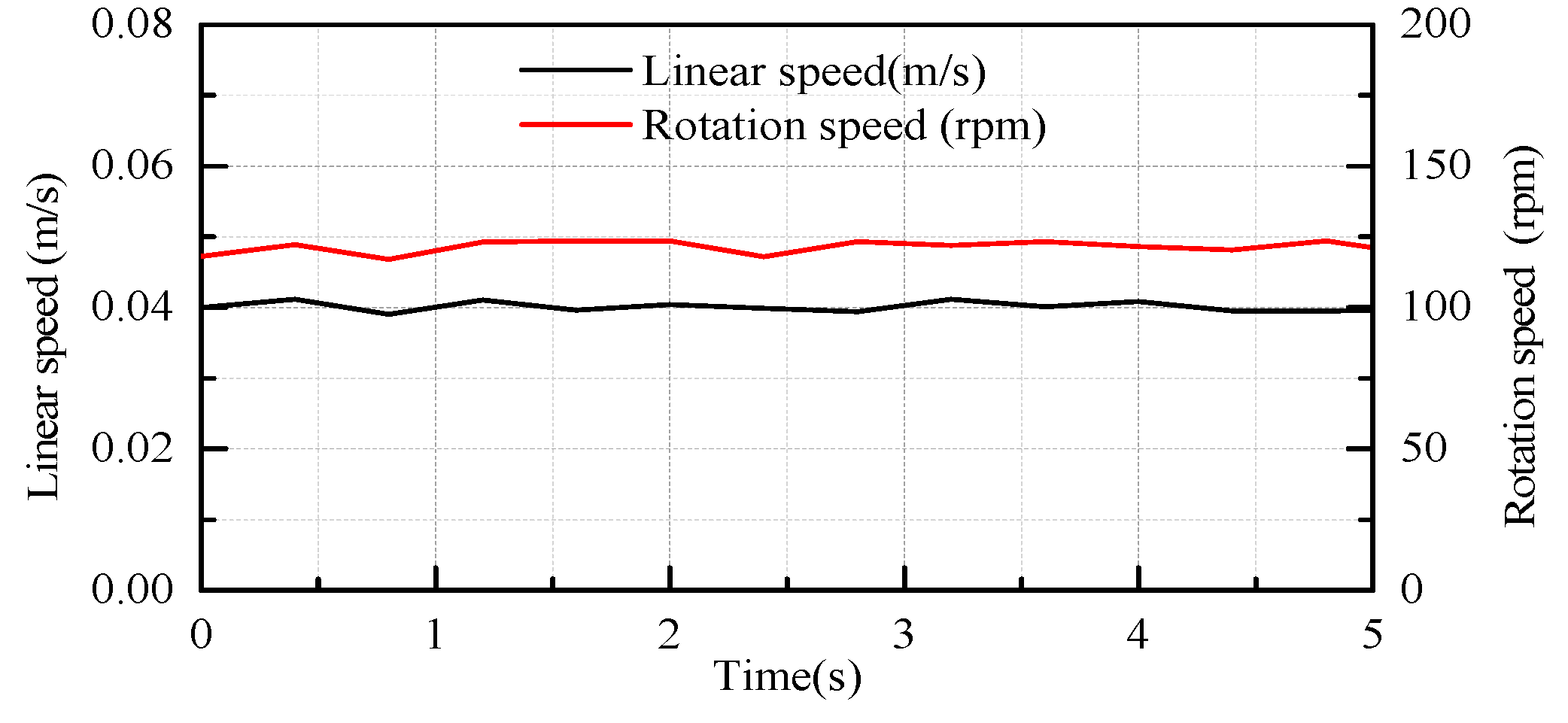
6. Experiment and Discussion
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Engin, C.D.; Yeşildirek, A. Designing and modeling of a point absorber wave energy converter with hydraulic power take-off unit. In Proceedings of the 2015 4th International Conference on Electric Power and Energy Conversion Systems (EPECS), Sharjah, United Arab Emirates, 24–26 November 2015; pp. 1–6. [Google Scholar]
- Mendonca, H.; Martinez, S. A resistance emulation approach to optimize the wave energy harvesting for a direct drive point absorber. IEEE Trans. Sustain. Energy 2016, 7, 3–11. [Google Scholar] [CrossRef]
- Ramirez, D.; Bartolome, J.P.; Martinez, S.; Herrero, L.C.; Blanco, M. Emulation of an OWC Ocean Energy Plant with PMSG and Irregular Wave Model. IEEE Trans. Sustain. Energy 2015, 6, 1515–1523. [Google Scholar] [CrossRef]
- Liu, C.; Yu, H.; Hu, M.; Liu, Q.; Zhou, S. Detent Force Reduction in Permanent Magnet Tubular Linear Generator for Direct-Driver Wave Energy Conversion. IEEE Trans. Magn. 2013, 49, 1913–1916. [Google Scholar] [CrossRef]
- Tedeschi, E.; Carraro, M.; Molinas, M.; Mattavelli, P. Effect of Control Strategies and Power Take-Off Efficiency on the Power Capture from Sea Waves. IEEE Trans. Energy Convers. 2011, 26, 1088–1098. [Google Scholar] [CrossRef]
- Farrok, O.; Islam, M.R.; Sheikh, M.R.I.; Guo, Y.; Zhu, J.G. A Split Translator Secondary Stator Permanent Magnet Linear Generator for Oceanic Wave Energy Conversion. IEEE Trans. Ind. Electron. 2018, 65, 7600–7608. [Google Scholar] [CrossRef]
- Bianchi, N.; Bolognani, S.; Corte, D.D.; Tonel, F. Tubular linear permanent magnet motors: An overall comparison. IEEE Trans. Ind. Appl. 2003, 39, 466–475. [Google Scholar] [CrossRef]
- Henry, A.; Doherty, K.; Cameron, L. Advances in the Design of the Oyster Wave Energy Converter. In Proceedings of the Marine Renewables & Offshore Wind Conference, RINA HQ, London, UK, 21–23 April 2010. [Google Scholar]
- Whittaker, T.; Collier, D.; Folley, M.; Osterried, M.; Henry, A. The development of Oyster—A shallow water surging wave energy converter. In Proceedings of the 7th European Wave Tidal Energy Conference, Porto, Portugal, 11–13 September 2007. [Google Scholar]
- Lye, J.; Brown, D.; Johnson, F. An Investigation into the non-linear effects resulting from air cushions in the Orecon oscillating water column device. In Proceedings of the 28th International Conference on Ocean Offshore Artic Engineering, Honolulu, HI, USA, 31 May–5 June 2009; p. 79115. [Google Scholar]
- Korde, U.A. Phase control of floating bodoes fron an on board reference. Appl. Ocean Res. 2001, 23, 251–262. [Google Scholar] [CrossRef]
- Rhinefrank, K.; Prudell, J.; Schacher, A. Development and characterization of a novel direct drive rotary wave energy point absorber MTS-IEEE oceans conference proceedings. In Proceedings of the Oceans 2009, Biloxi, MS, USA, 26–29 October 2009. [Google Scholar]
- Kofoed, J.; Frigaard, P. Prototype testing of the wave energy converter Wave Dragon. Renewable Energy. Renew. Energy 2006, 31, 181–189. [Google Scholar] [CrossRef]
- Polinder, H.; Damen, M.E.C.; Gardner, F. Linear PM Generator system for wave energy conversion in the AWS. IEEE Trans. Energy Convers. 2004, 19, 583–589. [Google Scholar] [CrossRef]
- Clifton, P.C.J.; McMahon, R.A.; Kelly, H.-P. Design and commissioning of a 30 kW direct drive wave generator. In Proceedings of the 5th IET International Conference on Power Electronics, Machines and Drives (PEMD 2010), Brighton, UK, 19–21 April 2010. [Google Scholar]
- Huang, L.; Yu, H.; Hu, M.; Liu, C.; Yuan, B. Research on a Tubular Primary Permanent-Magnet Linear Generator for Wave Energy Conversions. IEEE Trans. Magn. 2013, 49, 1917–1920. [Google Scholar] [CrossRef]
- Huang, L.; Hu, M.; Chen, Z.; Yu, H.; Liu, C. Research on a Direct-Drive Wave Energy Converter Using an Outer-PM Linear Tubular Generator. IEEE Trans. Magn. 2017, 53, 1–4. [Google Scholar] [CrossRef]
- Lu, K.; Wu, W. Electromagnetic Lead Screw for Potential Wave Energy Application. IEEE Trans. Magn. 2014, 50, 1–4. [Google Scholar] [CrossRef]
- Holm, R.K.; Berg, N.I.; Walkusch, M.; Rasmussen, P.O.; Hansen, R.H. Design of a magnetic lead screw for wave energy conversion. IEEE Trans. Ind. Appl. 2013, 49, 2699–2708. [Google Scholar] [CrossRef]
- Zhao, A.; Wu, W.; Zhu, L.; Chen, H.; Lu, K.; Blaabjerg, F. Design and Experiment of an Indirect Wave Power Generation Device using Magnetic Lead Screw. In Proceedings of the IECON 2019—45th Annual Conference of the IEEE Industrial Electronics Society, Lisbon, Portugal, 14–17 October 2019; pp. 6987–6991. [Google Scholar]
- Ling, Z.; Ji, J.; Wang, J.; Zhao, W. Design Optimization and Test of a Radially Magnetized Magnetic Screw with Discretized PMs. IEEE Trans. Ind. Electron. 2018, 65, 7536–7547. [Google Scholar] [CrossRef]
- Jenney, K.; Pakdelian, S. Magnetic design aspects of the trans-rotary magnetic gear using Quasi-Halbach arrays. IEEE Trans. Ind. Electron. 2020, 67, 9582–9592. [Google Scholar] [CrossRef]
- Ji, J.; Ling, Z.; Wang, J.; Zhao, W.; Liu, G.; Zeng, T. Design and Analysis of a Halbach Magnetized Magnetic Screw for Artificial Heart. IEEE Trans. Magn. 2015, 51, 1–4. [Google Scholar] [CrossRef]
- Wang, Q.; Gao, F.; Zhang, J.; Li, Y. Analysis and Reduction of Detent Effect in Magnetic Lead Screws with Parallel Magnetized Permanent Magnet Segments. IEEE Access 2020, 8, 84177–84187. [Google Scholar] [CrossRef]
- Cirolini, M.; Filho, A.F.F.; Wu, Y.C.; Dorrell, D.G. Design Aspects of a Reluctance-Based Magnetic Lead Screw. IEEE Trans. Magn. 2019, 55, 1–6. [Google Scholar] [CrossRef]
- Lu, K.; Xia, Y.; Wu, W.; Zhang, L. New Helical-Shape Magnetic Pole Design for Magnetic Lead Screw Enabling Structure Simplification. IEEE Trans. Magn. 2015, 51, 1–4. [Google Scholar]
- Ling, Z.; Ji, J.; Zeng, T.; Zhao, W. Design optimization and comparison of linear magnetic actuators under different topologies. Chin. J. Electr. Eng. 2020, 6, 41–51. [Google Scholar] [CrossRef]
- Pakdelian, S.; Frank, N.W.; Toliyat, H.A. Magnetic Design Aspects of the Trans-Rotary Magnetic Gear. IEEE Trans. Energy Convers. 2015, 30, 41–50. [Google Scholar] [CrossRef]









| Type | Device | Description |
|---|---|---|
| Hydraulic | Oyster [8] Waveroller [9] | Hydraulic WEC uses wave energy to drive the hydraulic device to act on the hydraulic turbine, which in turn drives the traditional motor to generate electricity. |
| Pneumatic | Limpet [10] Spar buoy [11] | Pneumatic WEC use air as a medium for conversion. Under the action of the wave heave, the wave energy is converted into the pressure energy and kinetic energy of the air. |
| Gearbox | Columbia Power WEC [12] Wave Dragon [13] | Gearbox WEC uses a sealed drive shaft to convert the energy of wave ups and downs into mechanical energy in a rotating motor through a gearbox, thereby generating electrical energy. |
| Direct-drive | AWS [14] TE 5 [15] | Direct-drive WEC generally use linear generators to directly convert the mechanical energy of waves into electrical energy. |
| Symbol | Parameter | Value |
|---|---|---|
| Outer radius of the rotor (mm) | 37 | |
| Outer radius of the mover (mm) | 21 | |
| Inner radius of the mover (mm) | 6 | |
| Rotor length (mm) | 60 |
| Symbol | Parameter | Value |
|---|---|---|
| Magnetic lead (mm) | 30 | |
| τp | Pole pitch (mm) | 15 |
| Rs | Outer radius of the rotor (mm) | 37 |
| Rm | Outer radius of the mover (mm) | 21 |
| Rr | Inner radius of the mover (mm) | 6 |
| Lm | Width of the PM (mm) | 15 |
| Hm | Thickness of the PM (mm) | 5 |
| Hr | Back iron thickness (mm) | 10 |
| Lt | Rotor length (mm) | 60 |
| g | Length of the air gap (mm) | 1 |
| Residual magnetic field strength | 1.23 |
| Symbol | Parameter | SMMLS | QHAMLS | TTMLS |
|---|---|---|---|---|
| Magnetic lead (mm) | 20 | 20 | 20 | |
| τp | Pole pitch (mm) | 10 | 10 | 10 |
| Rs | Outer radius of the rotor (mm) | 37 | 37 | 37 |
| Rm | Outer radius of the mover (mm) | 21 | 21 | 21 |
| Rs | Inner radius of the mover (mm) | 6 | 6 | 6 |
| Lm | Width of the PM (mm) | 10 | 10 | 10 |
| h0 | Width of the radial magnetized PM (mm) | — | 4 | — |
| hl | Width of the axial magnetized PM (mm) | — | 6 | — |
| l0 | Permanent magnet tooth width (mm) | — | — | 5 |
| l1 | Triangle tooth width (mm) | — | — | 5 |
| l2 | Triangle tooth height (mm) | — | — | 0.1 |
| a | Triangle tooth angle (deg) | — | — | 39.3 |
| Hm | Thickness of the PM (mm) | 7 | 7 | 7 |
| Hr | Back iron thickness (mm) | 8 | 8 | 8 |
| Lt | Rotor length (mm) | 60 | 60 | 60 |
| g | Length of the air gap (mm) | 1 | 1 | 1 |
| Residual magnetic field strength (T) | 1.23 | 1.23 | 1.23 |
| Symbol | Parameter | Linear Generator | MLS Hybrid Generator |
|---|---|---|---|
| Rr | Inner radius of the mover (mm) | — | 6 |
| Rm | Outer radius of the mover (mm) | — | 21 |
| Rs | Outer radius of the rotor (mm) | — | 37 |
| h0 | Width of the radial magnetized PM (mm) | — | 4 |
| hl | Width of the axial Magnetized PM (mm) | — | 6 |
| Din | Inner diameter (mm) | 37 | 37 |
| Dout | Outer diameter (mm) | 77 | 77 |
| Lt | Axial length (mm) | 100 | 100 |
| Nr | Number of rotor poles | 9 | 8 |
| Ns | Number of stator slots | 10 | 12 |
| Np | Number of motor phases | 3 | 3 |
| Hm | Thickness of the PM (mm) | 7 | 7 |
| Hr | Back iron thickness (mm) | 8 | 8 |
| τp | Pole pitch (mm) | 9.5 | 10 |
| g | Length of the air gap (mm) | 1 | 1 |
| v | Speed | 0.2 m/s | 0.2 m/s |
| Speed (m/s) | Load (ohm) | MLS Hybrid Generator | Linear Generator | ||
|---|---|---|---|---|---|
| Input Power (W) | Output Power (W) | Input Power (W) | Output Power (W) | ||
| 0.1 | 5 | 1225 | 811 | 52 | 39 |
| 10 | 1477 | 1158 | 31 | 26 | |
| 0.15 | 5 | 1367 | 923 | 118 | 87 |
| 10 | 1932 | 1534 | 68 | 58 | |
| 0.2 | 5 | 1445 | 967 | 205 | 153 |
| 10 | 2136 | 1722 | 124 | 104 | |
| 025 | 5 | 1492 | 991 | 314 | 234 |
| 10 | 2278 | 1826 | 189 | 161 | |
| 0.3 | 5 | 1508 | 1003 | 440 | 330 |
| 10 | 2356 | 1889 | 268 | 230 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xia, T.; Li, J.; Zhang, Y.; Yu, H.; Lu, K. Comparison and Optimization of a Magnetic Lead Screw Applied in Wave Energy Conversions. Electronics 2022, 11, 2825. https://doi.org/10.3390/electronics11182825
Xia T, Li J, Zhang Y, Yu H, Lu K. Comparison and Optimization of a Magnetic Lead Screw Applied in Wave Energy Conversions. Electronics. 2022; 11(18):2825. https://doi.org/10.3390/electronics11182825
Chicago/Turabian StyleXia, Tao, Junhui Li, Yangfei Zhang, Haitao Yu, and Kaiyuan Lu. 2022. "Comparison and Optimization of a Magnetic Lead Screw Applied in Wave Energy Conversions" Electronics 11, no. 18: 2825. https://doi.org/10.3390/electronics11182825
APA StyleXia, T., Li, J., Zhang, Y., Yu, H., & Lu, K. (2022). Comparison and Optimization of a Magnetic Lead Screw Applied in Wave Energy Conversions. Electronics, 11(18), 2825. https://doi.org/10.3390/electronics11182825






