A Threshold Voltage Model for AOS TFTs Considering a Wide Range of Tail-State Density and Degeneration
Abstract
:1. Introduction
2. Model Derivation
2.1. Threshold Voltage Model
2.2. Surface Potential Calculations
2.3. Drain Current for Parameter Extraction
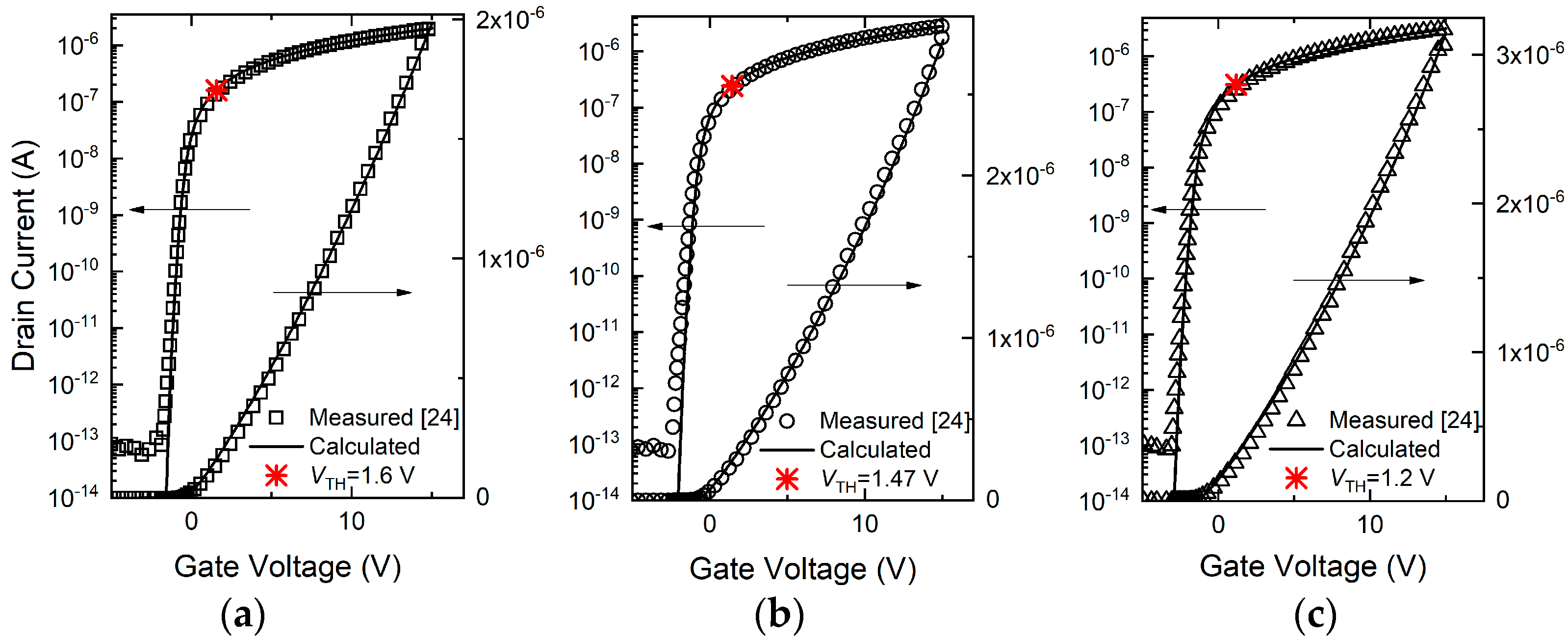
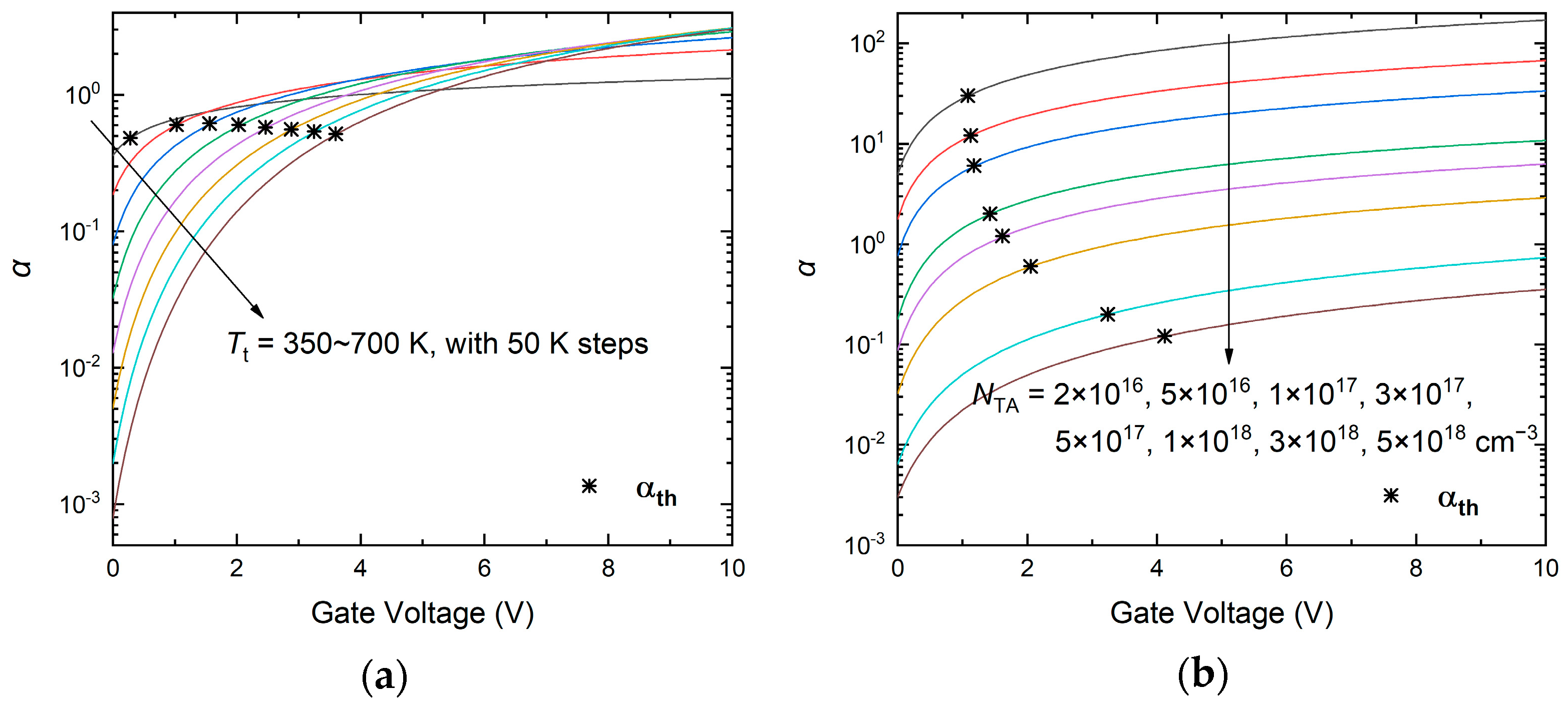
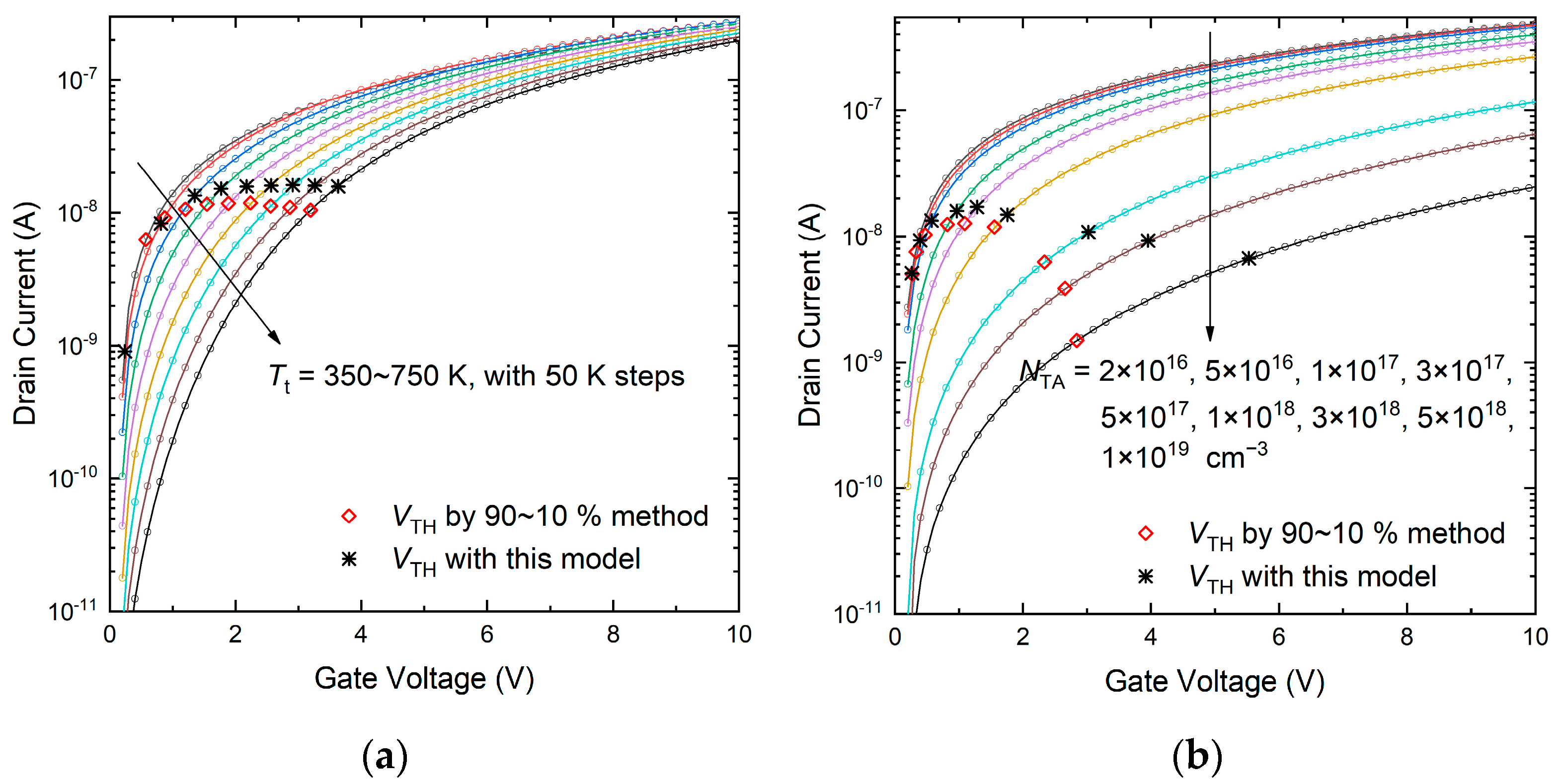
3. Results and Discussion
| Parameter (Unit) | Value (Figure 2, Figure 3 and Figure 4) | Value (Figure 5a) | Value (Figure 5b) | Value (Figure 5c) |
|---|---|---|---|---|
| W/L (μm/μm) | 150/50 | 20/20 | 20/20 | 20/20 |
| Cox (nF/cm2) | 17.27 | 43.1 | 43.1 | 43.1 |
| NC (cm−3) | 5.2 × 1018 | 5.2 × 1018 | 5.2 × 1018 | 5.2 × 1018 |
| T (K) | 300 | 300 | 300 | 300 |
| φF0 (V) | 0.11 | 0.11 | 0.11 | 0.11 |
| NTA (cm−3) | variable | 2.07 × 1017 | 1.88 × 1017 | 2.59 × 1017 |
| Tt (K) | variable | 1200 | 1450 | 1500 |
| μe (cm2/Vs) | 10 | 5 | 6.3 | 6.6 |
| Vfb (V) | 0 | −1.3 | −1.85 | −2.8 |
| β | - | 0.014 | 0.018 | 0.018 |
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Nomura, K.; Ohta, H.; Takagi, A.; Kamiya, T.; Hirano, M.; Hosono, H. Room-temperature fabrication of transparent flexible thin-film transistors using amorphous oxide semiconductors. Nature 2004, 432, 488–492. [Google Scholar] [CrossRef] [PubMed]
- Fortunato, E.; Barquinha, P.; Martins, R. Oxide semiconductor thin-film transistors: A review of recent advances. Adv. Mater. 2012, 24, 2945–2986. [Google Scholar] [CrossRef] [PubMed]
- Wager, J.F. TFT Technology: Advancements and opportunities for improvement. Inf. Disp. 2020, 36, 9–13. [Google Scholar] [CrossRef]
- Liu, P.T.; Ruan, D.B.; Yeh, X.Y.; Chiu, Y.C.; Zheng, G.T.; Sze, S.M. Highly responsive blue light sensor with amorphous Indium-Zinc-Oxide thin-film transistor based architecture. Sci. Rep. 2018, 8, 8153. [Google Scholar] [CrossRef]
- Cantarella, G.; Costa, J.; Meister, T.; Ishida, K.; Carta, C.; Ellinger, F.; Lugli, P.; Münzenrieder, N.; Petti, L. Review of recent trends in flexible metal oxide thin-film transistors for analog applications. Flex. Print. Electron. 2020, 5, 033001. [Google Scholar] [CrossRef]
- Wang, W.; Li, X.X.; Wang, T.; Huang, W.; Ji, Z.-G.; Zhang, D.W.; Lu, H.-L. Investigation of light-stimulated α-IGZO based photoelectric transistors for neuromorphic applications. IEEE Trans. Electron Devices 2020, 67, 3141–3145. [Google Scholar] [CrossRef]
- Chen, C.; Abe, K.; Fung, T.C.; Kumomi, H.; Kanicki, J. Amorphous In-Ga-Zn-O thin film transistor current-scaling pixel electrode circuit for active-matrix organic light-emitting displays. Jpn. J. Appl. Phys. 2009, 48, 03B025. [Google Scholar] [CrossRef]
- Kamiya, T.; Nomura, K.; Hosono, H. Electronic structures above mobility edges in crystalline and amorphous In-Ga-Zn-O: Percolation conduction examined by analytical model. J. Disp. Technol. 2009, 5, 462–467. [Google Scholar] [CrossRef]
- Lee, S.; Ghaffarzadeh, K.; Nathan, A.; Robertson, J.; Jeon, S.; Kim, C.; Song, I.-H.; Chung, U.-I. Trap-limited and percolation conduction mechanisms in amorphous oxide semiconductor thin film transistors. Appl. Phys. Lett. 2011, 98, 203508. [Google Scholar] [CrossRef]
- Tsormpatzoglou, A.; Hastas, N.A.; Choi, N.; Mahmoudabadi, F.; Hatalis, M.K.; Dimitriadis, C.A. Analytical surface-potential-based drain current model for amorphous InGaZnO thin film transistors. J. Appl. Phys. 2013, 114, 184502. [Google Scholar] [CrossRef]
- Ghittorelli, M.; Torricelli, F.; Kovács-Vajna, Z.M. Physical modeling of amorphous InGaZnO thin-film transistors: The role of degenerate conduction. IEEE Trans. Electron Devices 2016, 63, 2417–2423. [Google Scholar] [CrossRef]
- Fang, J.; Deng, W.; Ma, X.; Huang, J.; Wu, W. A surface-potential-based DC model of amorphous oxide semiconductor TFTs including degeneration. IEEE Electron Device Lett. 2017, 38, 183–186. [Google Scholar] [CrossRef]
- He, H.; Xiong, C.; Yin, J.; Wang, X.; Lin, X.; Zhang, S. Analytical drain current and capacitance model for amorphous InGaZnO TFTs considering temperature characteristics. IEEE Trans. Electron Devices 2020, 67, 3637–3644. [Google Scholar] [CrossRef]
- Kamiya, T.; Nomura, K.; Hosono, H. Origins of high mobility and low operation voltage of amorphous oxide TFTs: Electronic structure, electron transport, defects and doping. J. Disp. Technol. 2009, 5, 273–288. [Google Scholar] [CrossRef]
- Fung, T.C.; Chuang, C.S.; Chen, C.; Abe, K.; Cottle, R.; Townsend, M.; Kumomi, H.; Kanicki, J. Two-dimensional numerical simulation of radio frequency sputter amorphous In-Ga-Zn-O thin-film transistors. J. Appl. Phys. 2009, 106, 084511. [Google Scholar] [CrossRef]
- Kim, D.K.; Park, J.; Zhang, X.; Park, J.; Bae, J.-H. Numerical study of sub-gap density of states dependent electrical characteristics in amorphous In-Ga-Zn-O thin-film transistors. Electronics 2020, 9, 1652. [Google Scholar] [CrossRef]
- Qiang, L.; Yao, R. A new definition of the threshold voltage for amorphous InGaZnO thin-film transistors. IEEE Trans. Electron Devices 2014, 61, 2394–2397. [Google Scholar] [CrossRef]
- Chen, C.L.; Chen, W.F.; Zhou, L.; Wu, W.-J.; Xu, M.; Wang, L.; Peng, J.-B. A physics-based model of threshold voltage for amorphous oxide semiconductor thin-film transistors. AIP Adv. 2016, 6, 035025. [Google Scholar] [CrossRef]
- Cai, M.; Yao, R. A threshold voltage definition for modeling asymmetric dual-gate amorphous InGaZnO thin-film transistors with parameter extraction technique. J. Appl. Phys. 2019, 125, 084503. [Google Scholar] [CrossRef]
- Kim, Y.; Bae, M.; Kim, W.; Kong, D.; Jeong, H.K.; Kim, H.; Choi, S.; Kim, D.M.; Kim, D.H. Amorphous InGaZnO thin-film transistors-Part I: Complete extraction of density of states over the full subband-gap energy range. IEEE Trans. Electron Devices 2012, 59, 2689–2698. [Google Scholar] [CrossRef]
- Arora, N. MOSFET Models for VLSI Circuit Simulation: Theory and Practice; Springer: New York, NY, USA, 1993. [Google Scholar]
- Ghittorelli, M.; Torricelli, F.; Colalongo, L.; Kovács-Vajna, Z.M. Accurate analytical physical modeling of amorphous InGaZnO thin-film transistors accounting for trapped and free charges. IEEE Trans. Electron Devices 2014, 61, 4105–4112. [Google Scholar] [CrossRef]
- Fung, T.C.; Abe, K.; Kumomi, H.; Kanicki, J. Electrical instability of RF sputter amorphous In-Ga-Zn-O thin-film transistors. J. Disp. Technol. 2009, 5, 452–461. [Google Scholar] [CrossRef]
- Jeong, C.Y.; Park, I.J.; Cho, I.T.; Lee, J.H.; Cho, E.S.; Ryu, M.K.; Park, S.H.K.; Song, S.H.; Kwon, H.I. Investigation of the low-frequency noise behavior and its correlation with the subgap density of states and bias-induced instabilities in amorphous InGaZnO thin-film transistors with various oxygen flow rates. Jpn. J. Appl. Phys. 2012, 51, 100206. [Google Scholar] [CrossRef]
- Ghittorelli, M.; Kovács-Vajna, Z.M.; Torricelli, F. Physical-based analytical model of amorphous InGaZnO TFTs including deep, tail, and free states. IEEE Trans. Electron Devices 2017, 64, 4510–4517. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cai, M.; Xu, P.; Liu, B.; Peng, Z.; Cai, J.; Cao, J. A Threshold Voltage Model for AOS TFTs Considering a Wide Range of Tail-State Density and Degeneration. Electronics 2022, 11, 3137. https://doi.org/10.3390/electronics11193137
Cai M, Xu P, Liu B, Peng Z, Cai J, Cao J. A Threshold Voltage Model for AOS TFTs Considering a Wide Range of Tail-State Density and Degeneration. Electronics. 2022; 11(19):3137. https://doi.org/10.3390/electronics11193137
Chicago/Turabian StyleCai, Minxi, Piaorong Xu, Bei Liu, Ziqi Peng, Jianhua Cai, and Jing Cao. 2022. "A Threshold Voltage Model for AOS TFTs Considering a Wide Range of Tail-State Density and Degeneration" Electronics 11, no. 19: 3137. https://doi.org/10.3390/electronics11193137





