Novel Voltage-Based Weighted Hybrid Force/Position Control for Redundant Robot Manipulators
Abstract
:1. Introduction
- (1)
- Mapping between the voltage of the joint motor and the terminal position and orientation of a redundant robot manipulator is established. The voltage-based control algorithm is improved on the basis of the above relationship, then it is combined with the hybrid force/position control algorithm. Accordingly, voltage-based hybrid force/position control can be realized for the redundant robot manipulator. It can simplify the force and position controllers at the same time and improve their control efficiency and response speed.
- (2)
- To avoid the problems of space decomposition and switching in the traditional hybrid force/position control, the force and position control laws are summed directly through a weighted way, and the selection matrix is eliminated. Then, voltage-based weighted hybrid force/position control can be realized for the redundant robot manipulator. On the premise of ensuring stability, a method for selecting the weighting coefficient is provided.
- (3)
- The proposed novel control algorithm overcomes the defects of impedance control and hybrid force/position control. Moreover, the controller can be simplified by adopting the motor current as the feedback to replace the tedious calculation of the dynamic model of the redundant robot manipulator. Therefore, the proposed algorithm is a general control method. It is suitable for hybrid force/position control and impedance control. It can also greatly simplify the controller design.
2. Voltage-Based Dynamic Model for a Redundant Robot Manipulator
2.1. Dynamic Model of a Redundant Robot Manipulator
2.2. Mapping between Voltage and the Terminal Position and Orientation
3. Weighted Hybrid Force/Position Control of a Redundant Robot Manipulator
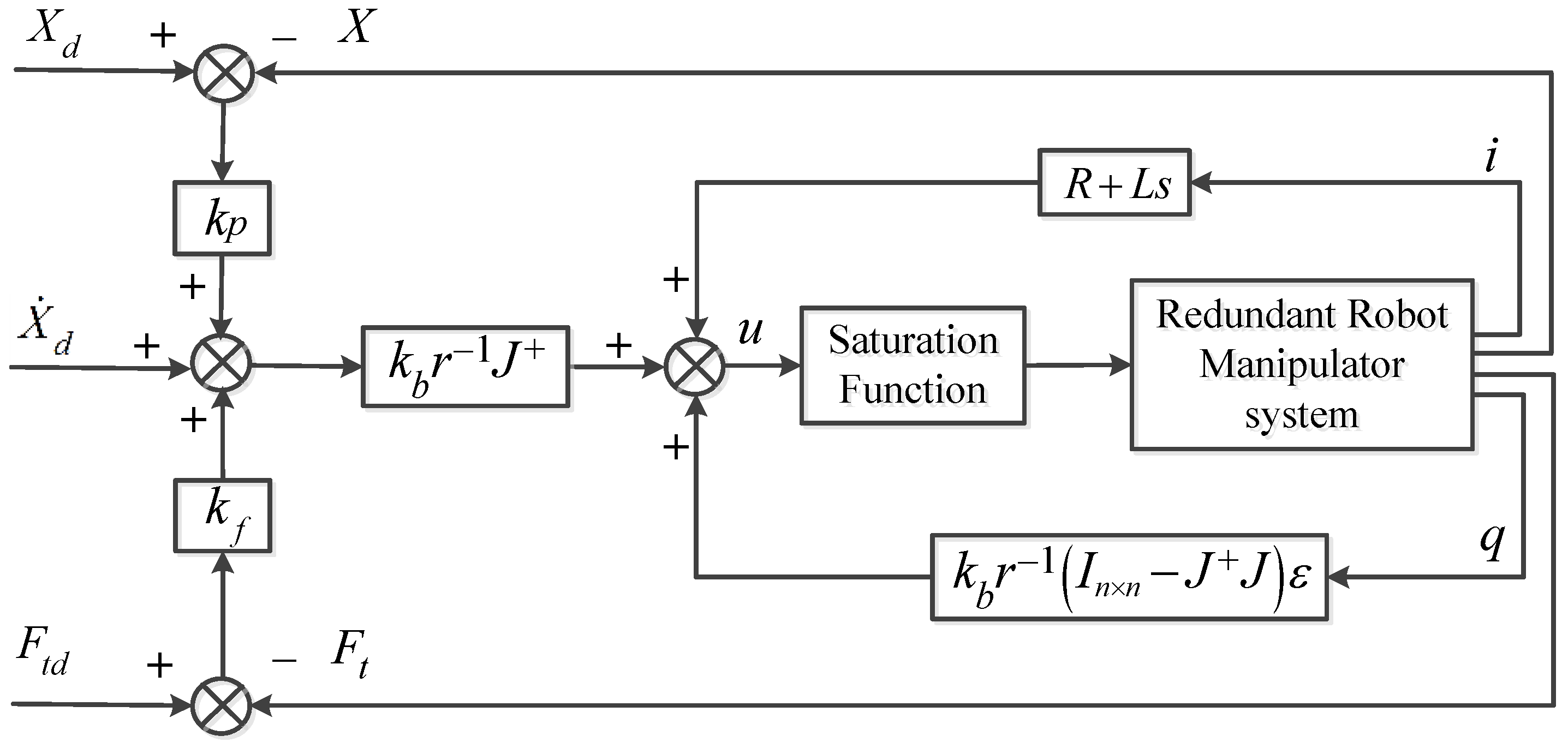
3.1. VBWHFPC
3.2. Selection of Weighting Coefficients and Stability Analysis
4. Simulation
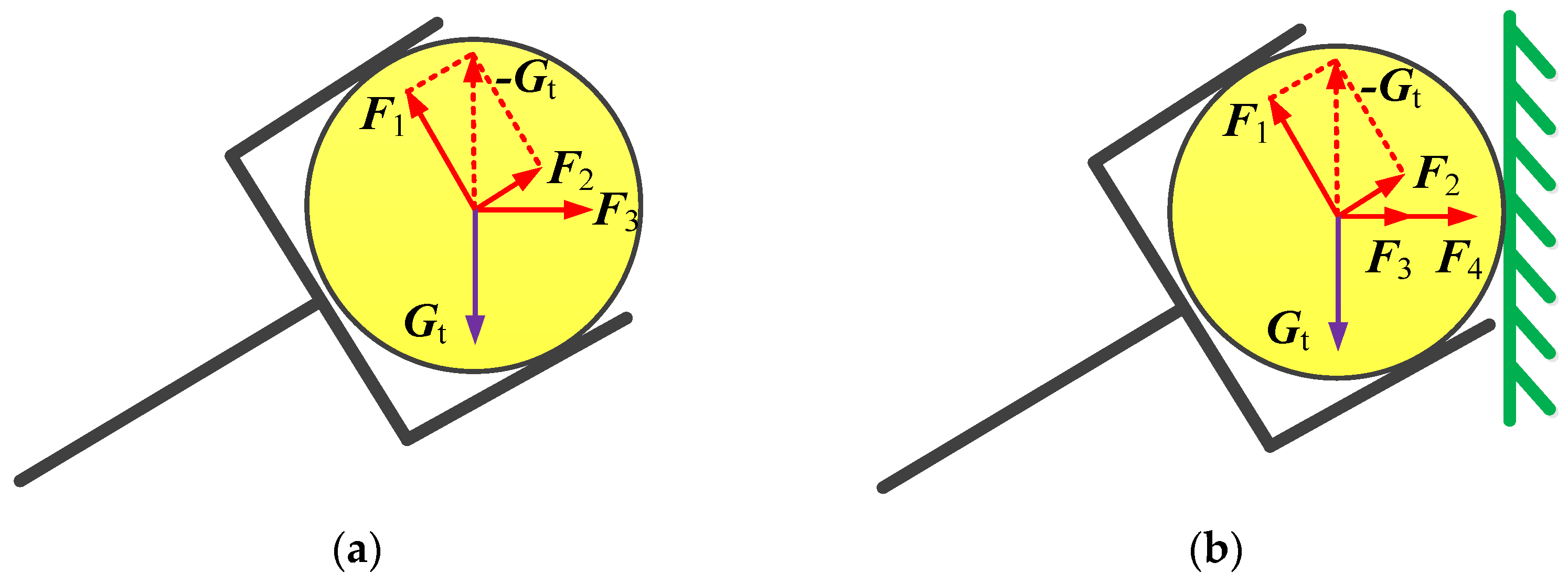
4.1. Wiping Operation of the Redundant Robot Manipulator
4.2. Transport Operations of the Redundant Robot Manipulator
4.2.1. The Workpiece Moves along a Straight Line under Constant Force
4.2.2. The Workpiece Moves along an Arc under Variable Force
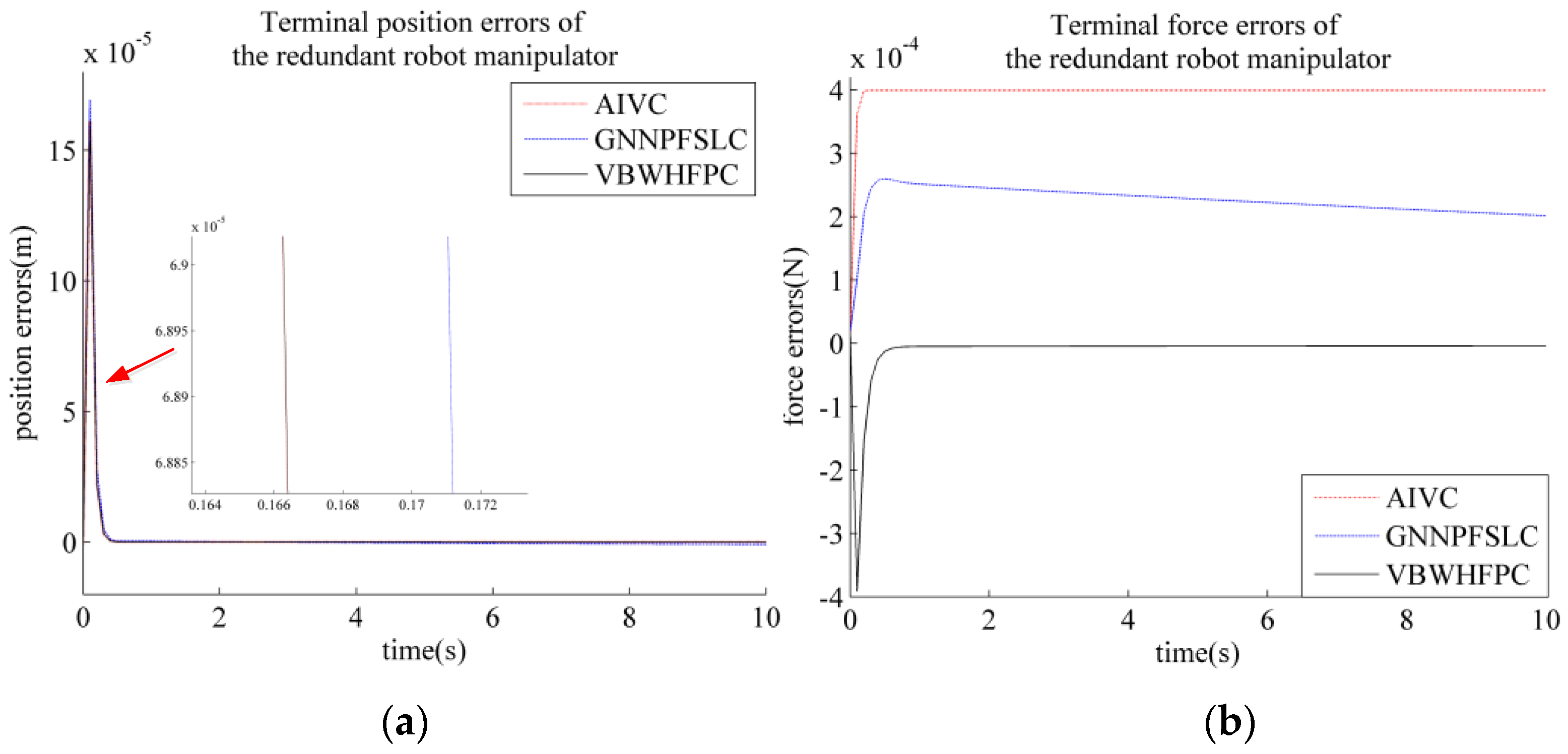
5. Experiment
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Al-Darraji, I.; Piromalis, D.; Kakei, A.A.; Khan, F.Q.; Stojmenovic, M.; Tsaramirsis, G.; Papageorgas, P.G. Adaptive Robust Controller Design-Based RBF Neural Network for Aerial Robot Arm Model. Electronics 2021, 10, 831. [Google Scholar] [CrossRef]
- Cheng, X.; Tu, X.; Zhou, Y.; Zhou, R. Active Disturbance Rejection Control of Multi-Joint Industrial Robots Based on Dynamic Feedforward. Electronics 2019, 8, 591. [Google Scholar] [CrossRef] [Green Version]
- Bouyarmane, K.; Chappellet, K.; Vaillant, J.; Kheddar, A. Quadratic Programming for Multirobot and Task-Space Force Control. IEEE Trans. Robot. 2019, 35, 64–77. [Google Scholar] [CrossRef]
- Su, Y.; Zheng, C.; Mercorelli, P. Robust approximate fixed-time tracking control for uncertain robot manipulators. Mech. Syst. Signal Process. 2020, 135, 106379. [Google Scholar] [CrossRef]
- Moe, S.; Gravdahl, J.T.; Pettersen, K.Y. Set-based Control for Autonomous Spray Painting. IEEE Trans. Autom. Sci. Eng. 2018, 15, 1785–1796. [Google Scholar] [CrossRef]
- Kovacs, A. Integrated task sequencing and path planning for robotic remote laser welding. Int. J. Prod. Res. 2016, 54, 1210–1224. [Google Scholar] [CrossRef]
- Alonso-Mora, J.; Baker, S.; Rus, D.L. Multi-robot formation control and object transport in dynamic environments via constrained optimization. Int. J. Robot. Res. 2017, 36, 1000–1021. [Google Scholar] [CrossRef]
- Liu, S.; Li, Y.F.; Xing, D. Sensing and Control for Simultaneous Precision Peg-in-Hole Assembly of Multiple Objects. IEEE Trans. Autom. Sci. Eng. 2020, 17, 310–324. [Google Scholar] [CrossRef]
- Zhang, Z.; Chen, S.; Zhu, X.; Yan, Z. Two Hybrid End-Effector Posture-Maintaining and Obstacle-Limits Avoidance Schemes for Redundant Robot Manipulators. IEEE Trans. Ind. Inform. 2020, 16, 754–763. [Google Scholar] [CrossRef]
- Zhang, H.; Jin, H.; Liu, Z.; Liu, Y.; Zhu, Y.; Zhao, J. Real-time Kinematic Control for Redundant Manipulators in a Time-varying Environment: Multiple-dynamic Obstacle Avoidance and Fast Tracking of a Moving Object. IEEE Trans. Ind. Inform. 2020, 16, 28–41. [Google Scholar] [CrossRef]
- Chang, Q.; Wang, H.; Wang, D.; Zhang, H.; Li, K.; Yu, B. Motion Planning for Vibration Reduction of a Railway Bridge Maintenance Robot with a Redundant Manipulator. Electronics 2021, 10, 2793. [Google Scholar] [CrossRef]
- Izadbakhsh, A.; Khorashadizadeh, S.; Ghandali, S. Robust adaptive impedance control of robot manipulators using Szász-Mirakyan operator as universal approximator. ISA Trans. 2020, 106, 1–11. [Google Scholar] [CrossRef]
- Cao, H.; Chen, X.; He, Y.; Zhao, X. Dynamic Adaptive Hybrid Impedance Control for Dynamic Contact Force Tracking in Uncertain Environments. IEEE Access 2019, 7, 83162–83174. [Google Scholar] [CrossRef]
- Li, Z.; Yang, D.; Zhou, H.; Cao, H. Research of a Self-adaptive Robot Impedance Control Method for Robot-Environment Interaction. Adv. Intell. Syst. Comput. 2015, 345, 221–238. [Google Scholar]
- Wei, C.; Shen, Z.; Xiao, D.; Wang, L.; Bai, X.; Chen, H. An optimal scheduling strategy for peer-to-peer trading in interconnected microgrids based on RO and Nash bargaining. Appl. Energy 2021, 295, 117024. [Google Scholar] [CrossRef]
- Xiao, D.; AlAshery, M.K.; Qiao, W. Optimal Price-Maker Trading Strategy of Wind Power Producer using Virtual Bidding. J. Mod. Power Syst. Clean Energy 2021, 1–13. [Google Scholar] [CrossRef]
- Erickson, D.; Weber, M.; Sharf, I. Contact Stiffness and Damping Estimation for Robotic Systems. Int. J. Robot. Res. 2003, 22, 41–57. [Google Scholar] [CrossRef]
- Yokokura, Y.; Ohishi, K.; Katsura, S. Fine Force Reproduction Based on Motion-Copying System Using Acceleration Observer. IEEE Trans. Ind. Electron. 2014, 61, 6213–6221. [Google Scholar] [CrossRef]
- Komada, S.; Machii, N.; Hori, T. Control of redundant manipulators considering order of disturbance observer. IEEE Trans. Ind. Electron. 2000, 47, 413–420. [Google Scholar] [CrossRef]
- Navvabi, H.; Markazi, A.H.D. Hybrid position/force control of Stewart Manipulator using Extended Adaptive Fuzzy Sliding Mode Controller (E-AFSMC). ISA Trans. 2019, 88, 280–295. [Google Scholar] [CrossRef]
- Li, L.; Xie, L.; Luo, X.; Wang, Z. Compliance Control Using Hydraulic Heavy-Duty Manipulator. IEEE Trans. Ind. Inform. 2019, 15, 1193–1201. [Google Scholar] [CrossRef]
- Kumar, N.; Rani, M. A new hybrid force/position control approach for time-varying constrained reconfigurable manipulators. ISA Trans. 2020, 110, 138–147. [Google Scholar] [CrossRef]
- Baek, J.; Jung, J. A Model-Free Control Scheme for Attitude Stabilization of Quadrotor Systems. Electronics 2020, 9, 1586. [Google Scholar] [CrossRef]
- Li, M.; Kang, R.; Branson. D.; Dai, J. Model-Free Control for Continuum Robots Based on an Adaptive Kalman Filter. IEEE/ASME Trans. Mech. 2018, 23, 286–297. [Google Scholar] [CrossRef]
- Zheng, C.; Su, Y.; Mercorelli, P. A simple nonlinear PD control for faster and high-precision positioning of servomechanisms with actuator saturation. Mech. Syst. Signal Process. 2019, 121, 215–226. [Google Scholar] [CrossRef]
- Gao, P.; Zhang, G.; Lv, X. Model-Free Hybrid Control with Intelligent Proportional Integral and Super-Twisting Sliding Mode Control of PMSM Drives. Electronics 2020, 9, 1427. [Google Scholar] [CrossRef]
- Keel, L.H.; Bhattacharyya, S.P. Controller Synthesis Free of Analytical Models: Three Term Controllers. IEEE Trans. Autom. Control 2008, 53, 1353–1369. [Google Scholar] [CrossRef]
- Martin, S.C.; Whitcomb, L.L. Nonlinear Model-Based Tracking Control of Underwater Vehicles with Three Degree-of-Freedom Fully Coupled Dynamical Plant Models: Theory and Experimental Evaluation. IEEE Trans. Control Syst. Trans. 2018, 26, 404–414. [Google Scholar] [CrossRef]
- Fateh, M.M. On the Voltage-Based Control of Robot Manipulators. Int. J. Control Autom. 2008, 6, 702–712. [Google Scholar]
- Fateh, M.M.; Khoshdel, V. Voltage-based adaptive impedance force control for a lower-limb rehabilitation robot. Adv. Robot. 2015, 29, 961–971. [Google Scholar] [CrossRef]
- Veysi, M.; Soltanpour, M.R. Voltage-Base Control of Robot Manipulator Using Adaptive Fuzzy Sliding Mode Control. Int. J. Fuzzy Syst. 2017, 19, 1430–1443. [Google Scholar] [CrossRef]
- Zaare, S.; Soltanpour, M.R.; Moattari, M. Voltage based sliding mode control of flexible joint robot manipulators in presence of uncertainties. Robot. Auton. Syst. 2019, 118, 204–219. [Google Scholar] [CrossRef]
- Xu, Q. Robust Impedance Control of a Compliant Microgripper for High-Speed Position/Force Regulation. IEEE Trans. Ind. Electron. 2015, 62, 1201–1209. [Google Scholar] [CrossRef]
- Jiang, J.; Liu, J.; Chen, W.; Wen, C.; Chen, W. An Impedance-Based Force Control Scheme to a Plate-to-Plate Nanoimprinter. IEEE Trans. Nanotechnol. 2016, 15, 328–336. [Google Scholar] [CrossRef]
- Xu, S.; He, B.; Zhou, Y.; Wang, Z.; Zhang, C. A Hybrid Position/Force Control Method for a Continuum Robot with Robotic and Environmental Compliance. IEEE Access 2019, 7, 100467–100479. [Google Scholar] [CrossRef]
- Pomares, J.; Torres, F. Movement-Flow-Based Visual Servoing and Force Control Fusion for Manipulation Tasks in Unstructured Environments. IEEE Trans. Syst. Man Cybern. C 2005, 35, 4–15. [Google Scholar] [CrossRef]
- Isermann, R. Estimation of physical parameters for dynamic processes with application to an industrial robot. Int. J. Control 2002, 55, 1287–1298. [Google Scholar] [CrossRef]
- Xin, G.; Deng, H.; Zhong, G. Closed-form dynamics of a 3-DOF spatial parallel manipulator by combining the Lagrangian formulation with the virtual work principle. Nonlinear Dyn. 2016, 86, 1329–1347. [Google Scholar] [CrossRef]
- Li, H.; Zhao, Y.; Li, B.; Li, G.; Cui, L. Torque Calculation of Permanent Magnet Spherical Motor Based on Virtual Work Method. IEEE Trans. Ind. Electron. 2020, 67, 7736–7745. [Google Scholar] [CrossRef]
- Mansard, N.; Chaumette, F. Directional Redundancy for Robot Control. IEEE Trans. Autom. Control 2009, 54, 1179–1192. [Google Scholar] [CrossRef] [Green Version]
- Colomé, A.; Torras, C. Closed-Loop Inverse Kinematics for Redundant Robots: Comparative Assessment and Two Enhancements. IEEE/ASME Trans. Mech. 2015, 20, 944–955. [Google Scholar] [CrossRef] [Green Version]
- Xu, W.; Zhang, J.; Liang, B.; Li, B. Singularity Analysis and Avoidance for Robot Manipulators with Nonspherical Wrists. IEEE Trans. Ind. Electron. 2016, 63, 277–290. [Google Scholar] [CrossRef]
- Fateh, M.M.; Babaghasabha, R. Impedance control of robots using voltage control strategy. Nonlinear Dyn. 2013, 74, 277–286. [Google Scholar] [CrossRef]
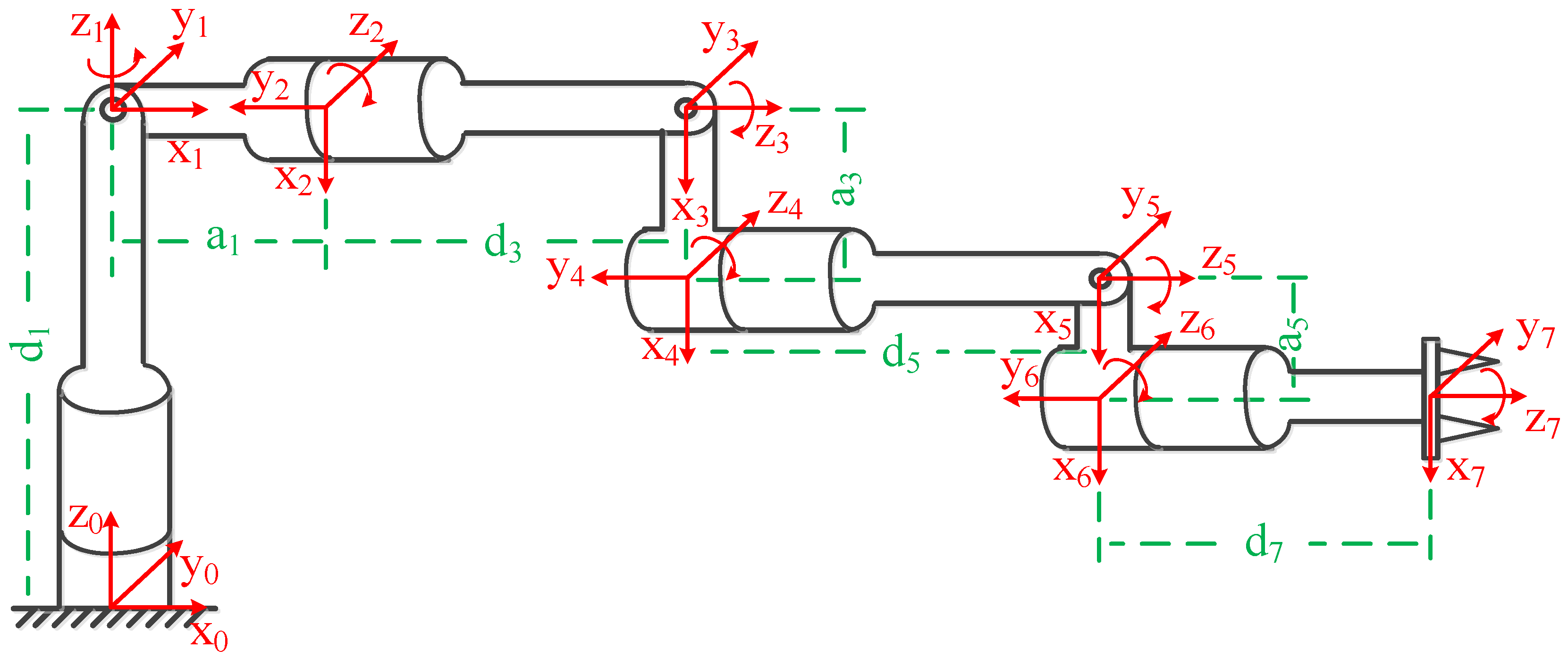

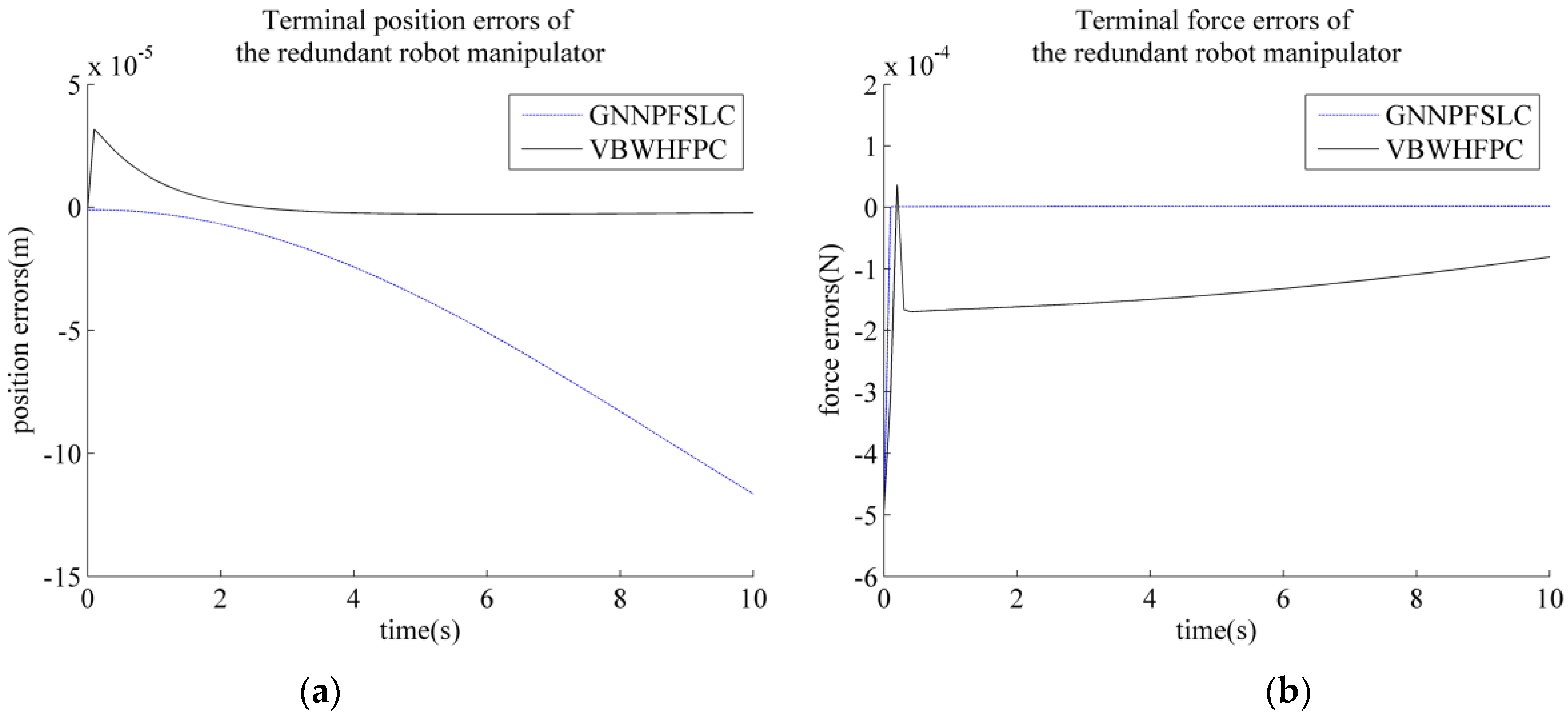
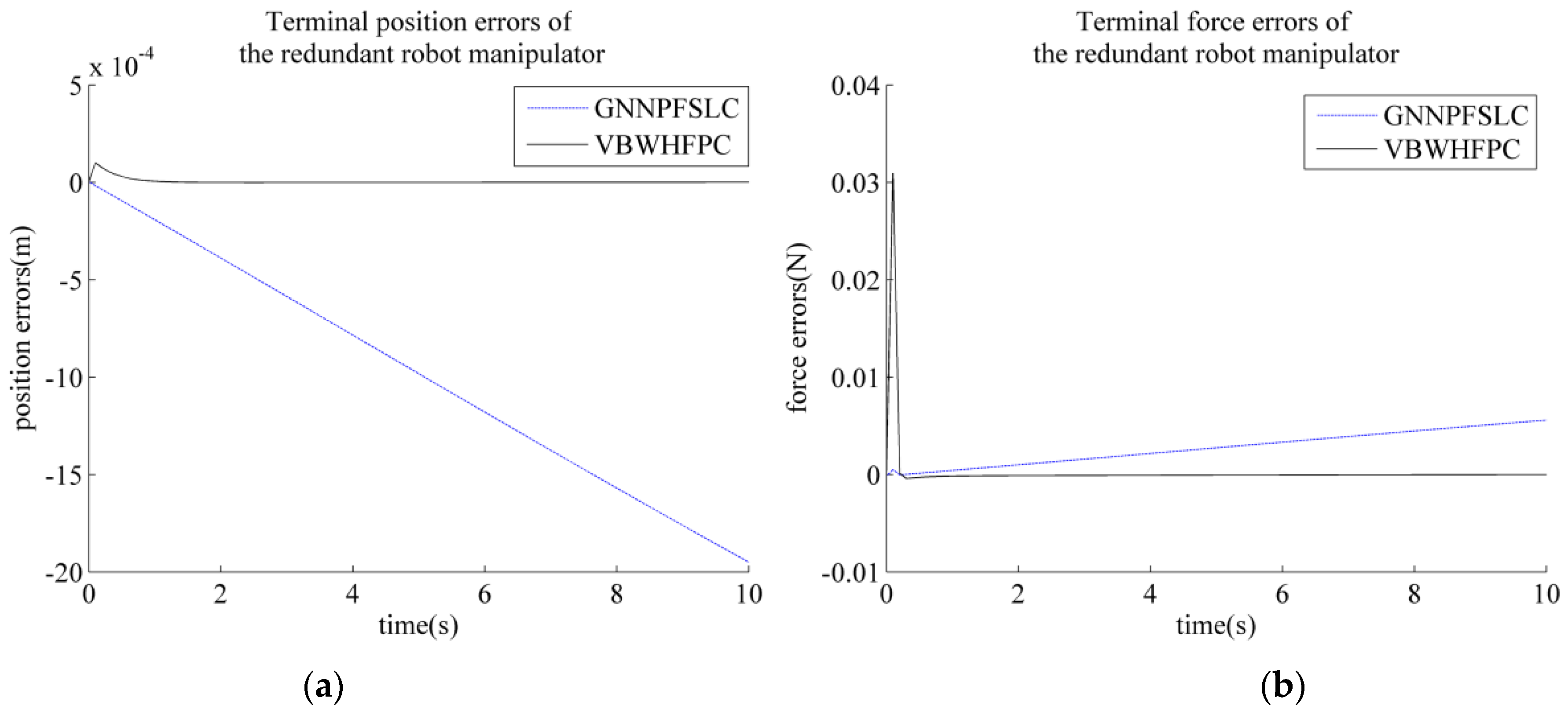

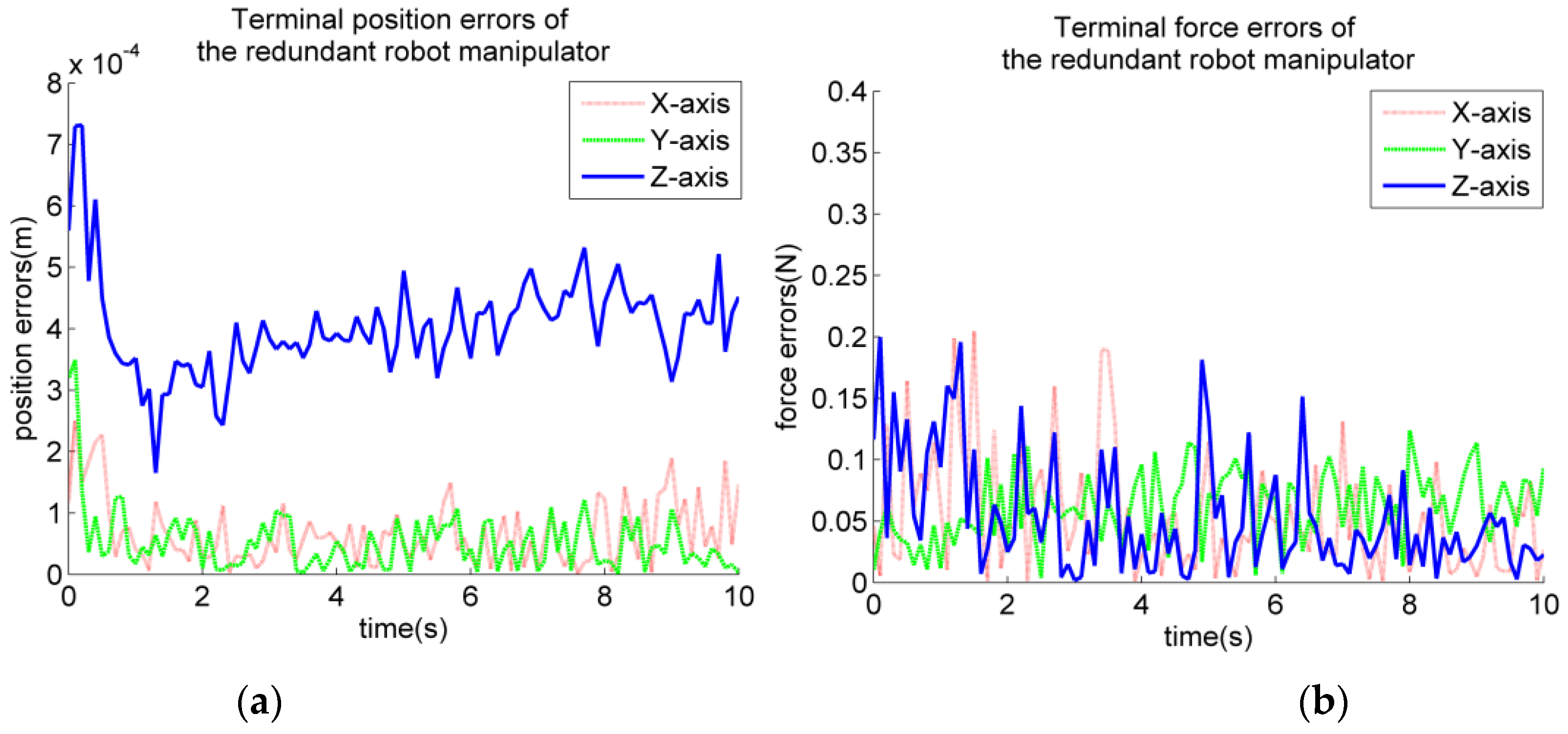
| Joint i | ai−1 (mm) | αi−1 (°) | di (mm) | θi (°) |
|---|---|---|---|---|
| 1 | 0 | 0 | 270.35 | 0 |
| 2 | 69 | −90 | 0 | 90 |
| 3 | 0 | 90 | 364.35 | 0 |
| 4 | 69 | −90 | 0 | 0 |
| 5 | 0 | 90 | 374.29 | 0 |
| 6 | 10 | −90 | 0 | 0 |
| 7 | 0 | 90 | 229.525 | 0 |
| AIVC | 4.000 × 10−5 | 1.611 × 10−4 | 3.029 × 10−6 | 3.991 × 10−4 | 9.398 × 10−16 | 9.398 × 10−16 |
| GNNPFSLC | 2.607 × 10−5 | 1.694 × 10−4 | 3.029 × 10−6 | 2.598 × 10−4 | 9.398 × 10−16 | 9.398 × 10−16 |
| VBWHFPC | 3.901 × 10−5 | 1.612 × 10−4 | 3.029 × 10−6 | 3.910 × 10−4 | 9.398 × 10−16 | 9.398 × 10−16 |
| GNNPFSLC | 1.629 × 10−6 | 1.082 × 10−5 | 1.871 × 10−3 | 1.150 × 10−31 | 9.389 × 10−16 | 5.507 × 10−3 |
| VBWHFPC | 1.629 × 10−6 | 6.865 × 10−5 | 4.265 × 10−5 | 1.150 × 10−31 | 9.389 × 10−16 | 3.004 × 10−3 |
| GNNPFSLC | 1.848 × 10−5 | 1.165 × 10−4 | 1.950 × 10−3 | 3.022 × 10−19 | 4.933 × 10−4 | 5.587 × 10−3 |
| VBWHFPC | 3.819 × 10−5 | 3.171 × 10−5 | 9.995 × 10−5 | 3.022 × 10−19 | 4.936 × 10−4 | 3.094 × 10−2 |
| VBWHFPC | 2.501 × 10−4 | 3.489 × 10−4 | 7.313 × 10−4 | 2.043 × 10−1 | 1.238 × 10−1 | 1.997 × 10−1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dai, J.; Zhang, Y.; Deng, H. Novel Voltage-Based Weighted Hybrid Force/Position Control for Redundant Robot Manipulators. Electronics 2022, 11, 179. https://doi.org/10.3390/electronics11020179
Dai J, Zhang Y, Deng H. Novel Voltage-Based Weighted Hybrid Force/Position Control for Redundant Robot Manipulators. Electronics. 2022; 11(2):179. https://doi.org/10.3390/electronics11020179
Chicago/Turabian StyleDai, Jun, Yi Zhang, and Hua Deng. 2022. "Novel Voltage-Based Weighted Hybrid Force/Position Control for Redundant Robot Manipulators" Electronics 11, no. 2: 179. https://doi.org/10.3390/electronics11020179
APA StyleDai, J., Zhang, Y., & Deng, H. (2022). Novel Voltage-Based Weighted Hybrid Force/Position Control for Redundant Robot Manipulators. Electronics, 11(2), 179. https://doi.org/10.3390/electronics11020179







