Approximate Computing Circuits for Embedded Tactile Data Processing
Abstract
:1. Introduction
- (1)
- What could be the impact of ACTs on the performance of the SVD?
- (2)
- What could be the impact of ACTs in tactile data processing tasks?
- We assess the performance of the Approx-BW multiplier with respect to the approximate multipliers presented in the state-of-the-art. The work presented in this paper is an extension of the work proposed in [20] where an extensive comparison among the BW multiplier with different state-of-the-art multipliers has been addressed. The results in [20] have shown that the Approx-BW multiplier achieves power consumption reduction up to 60% with respect to a Rounding based approximate multiplier (ROBA) [21] and multiplier based on inexact ETA adder (META) [22] multipliers with degradation of MRE of less than 4%.
- We propose the implementation of the approximate SVD circuit based on the Approx-BW multiplier [20]. The approximate SVD circuit shows a reduction of energy consumption by up to 16% at the cost of an MRE increase of less than 5%.
- We analyze the impact of the approximate SVD on the accuracy of the classification in a case study, i.e., classification of two touch modalities (sliding a finger vs. rolling a washer). We show that the Error increases from 1% to less than 8% when using approximate SVD circuits. We show that energy consumption could be reduced by more than 5% at the same accuracy loss when applying a hybrid approach, which consists of implementing three different approximate SVD having different numbers of approximated Least Significant Bits (LSBs).
2. Related Works
3. Machine Learning-Based Tensorial Kernel Approach
3.1. General Approach
3.2. Dataset Preparation
3.3. Data Preprocessing
4. Proposed Methodology
5. Experimental Results
5.1. First Step Analysis
5.1.1. Approximate Adders
5.1.2. Approximate Multiplier Circuits
- Mul-LOA and Mul-AXA, which are based on lower-part-OR and XNOR-based adders, respectively.
- MNAND, MAND, and MIPP multipliers are based, respectively, on NAND-carry out a bit, AND-carry out bit, and Input pre-processing approximate adders.
5.2. Second Step Analysis
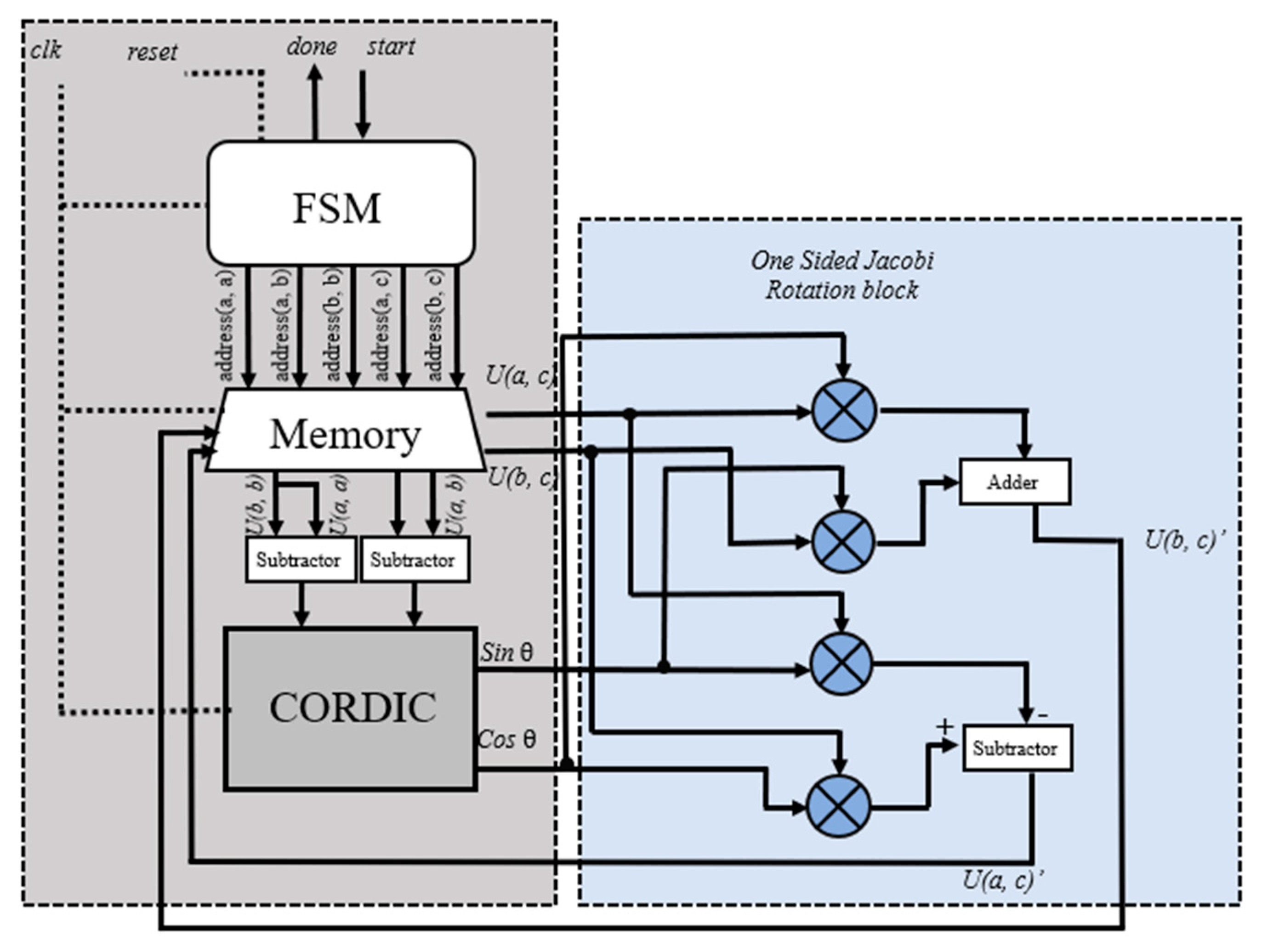
5.2.1. SVD Hardware Implementation Details
5.2.2. Error Resilience Analysis
- The approximation is enabled for the eight LSBs of the Approx-BW into the SVD (SVD-approx8), where 8 LSBs are approximated while the rest bits are exact.
- The number of the approximated LSBs is increased to 12 bits, where the rest MSBs are exact.
- The same procedure is applied until approximating 28 LSBs.
5.3. Third Step Analysis
6. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zhou, Z.; Yu, H.; Shi, H. Human Activity Recognition Based on Improved Bayesian Convolution Network to Analyze Health Care Data Using Wearable IoT Device. IEEE Access 2020, 8, 86411–86418. [Google Scholar] [CrossRef]
- Benatti, S.; Montagna, F.; Kartsch, V.; Rahimi, A.; Rossi, D.; Benini, L. Online Learning and Classification of EMG-Based Gestures on a Parallel Ultra-Low Power Platform Using Hyperdimensional Computing. IEEE Trans. Biomed. Circuits Syst. 2019, 13, 516–528. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Seminara, L.; Pinna, L.; Ibrahim, A.; Noli, L.; Caviglia, S.; Gastaldo, P.; Valle, M. Towards integrating intelligence in electronic skin. Mechatronics 2016, 34, 84–94. [Google Scholar] [CrossRef]
- Gastaldo, P.; Pinna, L.; Seminara, L.; Valle, M.; Zunino, R. A tensor-based approach to touch modality classification by using machine learning. Rob. Auton. Syst. 2015, 63, 268–278. [Google Scholar] [CrossRef]
- Vapnik, V. Statistical Learning Theory; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1999. [Google Scholar]
- Schölkopf, B. Learning with Kernels. Support Vector Machines, Regularization, Optimization, and Beyond; MIT Press: Cambridge, MA, USA, 2002. [Google Scholar]
- Ibrahim, A.; Valle, M. Real-Time embedded machine learning for tensorial tactile data processing. IEEE Trans. Circuits Syst. I Regul. Pap. 2018, 65, 3897–3906. [Google Scholar] [CrossRef]
- Fontenla-Romero, O.; Pérez-Sánchez, B.; Guijarro-Berdiñas, B. LANN-SVD: A Non-Iterative SVD-Based Learning Algorithm for One-Layer Neural Networks. IEEE Trans. Neural Networks Learn. Syst. 2018, 29, 3900–3905. [Google Scholar]
- Wang, Y.; Zhu, L. Research and implementation of SVD in machine learning. In Proceedings of the 2017 IEEE/ACIS 16th International Conference on Computer and Information Science (ICIS), Wuhan, China, 24–26 May 2017; pp. 471–475. [Google Scholar]
- Narwaria, M.; Lin, W. SVD-based quality metric for image and video using machine learning. IEEE Trans. Syst. Man. Cybern. Part B Cybern. 2012, 42, 347–364. [Google Scholar] [CrossRef]
- Mittal, S. A survey of techniques for approximate computing. ACM Comput. Surveys. 2016, 48, 1–33. [Google Scholar] [CrossRef] [Green Version]
- Han, J.; Orshansky, M. Approximate computing: An emerging paradigm for energy-efficient design. In Proceedings of the 2013 18th IEEE European Test Symposium, ETS 2013, Avignon, France, 27–30 May 2013. [Google Scholar]
- Seva, R.; Metku, P.; Kim, K.K.; Bin Kim, Y.; Choi, M. Approximate stochastic computing (ASC) for image processing applications. In Proceedings of the ISOCC 2016—International SoC Design Conference: Smart SoC for Intelligent Things, Jeju, Korea, 23–26 October 2016. [Google Scholar]
- Zhang, Q.; Wang, T.; Tian, Y.; Yuan, F.; Xu, Q. ApproxANN: An approximate computing framework for artificial neural network. In Proceedings of the Design, Automation and Test in Europe, DATE, Grenoble, France, 9–13 March 2015. [Google Scholar]
- Ibrahim, A.; Gastaldo, P.; Chible, H.; Valle, M. Real-time digital signal processing based on FPGAs for electronic skin implementation. Sensors 2017, 17, 558. [Google Scholar] [CrossRef] [Green Version]
- Mohapatra, D.; Karakonstantis, G.; Roy, K. Significance driven computation: A voltage-scalable, variation-aware, quality-tuning motion estimator. In Proceedings of the International Symposium on Low Power Electronics and Design, San Fancisco, CA, USA, 19–21 August 2009. [Google Scholar]
- Irofti, P.; Dumitrescu, B. Pairwise Approximate K-SVD. In Proceedings of the ICASSP, IEEE International Conference on Acoustics, Speech and Signal Processing, Brighton, UK, 12–17 May 2019. [Google Scholar]
- Foster, B.; Mahadevan, S.; Wang, R. A GPU-based approximate SVD algorithm. In Lecture Notes in Computer Science, Proceedings of the International Conference on Parallel Processing and Applied Mathematics, Torun, Poland, 11–14 September 2011; Springer: Berlin/Heidelberg, Germany, 2011; pp. 569–578. [Google Scholar]
- Shim, K.; Lee, M.; Choi, I.; Boo, Y.; Sung, W. SVD-softmax: Fast softmax approximation on large vocabulary neural networks. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Osta, M.; Ibrahim, A.; Chible, H.; Valle, M. Inexact Arithmetic Circuits for Energy-Efficient IoT Sensors Data Processing. In Proceedings of the IEEE International Symposium on Circuits and Systems, Florence, Italy, 27–30 May 2018. [Google Scholar]
- Zendegani, R.; Kamal, M.; Bahadori, M.; Afzali-Kusha, A.; Pedram, M. RoBA Multiplier: A Rounding-Based Approximate Multiplier for High-Speed yet Energy-Efficient Digital Signal Processing. IEEE Trans. Very Large Scale Integr. Syst. 2017, 25, 393–401. [Google Scholar] [CrossRef]
- Osta, M.; Ibrahim, A.; Seminara, L.; Chible, H.; Valle, M. Low power approximate multipliers for energy-efficient data processing. J. Low Power Electron. 2018, 14, 110–117. [Google Scholar] [CrossRef]
- Fukiage, T. Visibility-based blending for real-time applications. In Proceedings of the Visibility-Based Blending for Real-Time Applications, Munich, Germany, 10–12 September 2014; IEEE: Piscataway, NJ, USA; pp. 63–72. [Google Scholar]
- Himavathi, S.; Anitha, D.; Muthuramalingam, A. Feedforward neural network implementation in FPGA using layer multiplexing for effective resource utilization. IEEE Trans. Neural Netw. 2007, 18, 880–888. [Google Scholar] [CrossRef] [PubMed]
- Yeam, T.C.; Ismail, N.; Mashiko, K.; Matsuzaki, T. FPGA implementation of extreme learning machine system for classification. In Proceedings of the IEEE Region 10 Annual International Conference, TENCON, Penang, Malaysia, 5–8 November 2017. [Google Scholar]
- Ortega-Zamorano, F.; Jerez, J.M.; Munoz, D.U.; Luque-Baena, R.M.; Franco, L. Efficient Implementation of the Backpropagation Algorithm in FPGAs and Microcontrollers. IEEE Trans. Neural Netw. Learn. Syst. 2015, 27, 1840–1850. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Schapire, R.E.; Verma, N. Error Adaptive Classifier Boosting (EACB): Leveraging Data-Driven Training towards Hardware Resilience for Signal Inference. IEEE Trans. Circuits Syst. I Regul. Pap. 2015, 62, 1136–1145. [Google Scholar] [CrossRef]
- Anguita, D.; Boni, A.; Ridella, S. A Digital Architecture for Support Vector Machines: Theory, Algorithm, and FPGA Implementation. IEEE Trans. Neural Netw. 2003, 14, 993–1009. [Google Scholar] [CrossRef]
- Fafoutis, X.; Marchegiani, L.; Elsts, A.; Pope, J.; Piechocki, R.; Craddock, I. Extending the battery lifetime of wearable sensors with embedded machine learning. In Proceedings of the IEEE World Forum on Internet of Things, WF-IoT, Singapore, 5 February 2018; pp. 269–274. [Google Scholar]
- Zhou, Y.; Lin, J.; Wang, Z. Energy-efficient SVM classifier using approximate computing. In Proceedings of the 2017 IEEE 12th International Conference on ASIC (ASICON), Guiyang, China, 25–28 October 2017; pp. 1045–1048. [Google Scholar] [CrossRef]
- Van Leussen, M.; Huisken, J.; Wang, L.; Jiao, H.; de Gyvez, J.P. Reconfigurable Support Vector Machine Classifier with Approximate Computing. In Proceedings of the 2017 IEEE Computer Society Annual Symposium on VLSI (ISVLSI), Bochum, Germany, 3–5 July 2017; pp. 13–18. [Google Scholar] [CrossRef]
- Koliogeorgi, K.; Zervakis, G.; Anagnostos, D.; Zompakis, N.; Siozios, K. Optimizing SVM Classifier Through Approximate and High-Level Synthesis Techniques. In Proceedings of the 2019 8th International Conference on Modern Circuits and Systems Technologies (MOCAST), Piscataway, NJ, USA, 13–15 May 2019; pp. 1–4. [Google Scholar] [CrossRef]
- Alasad, Q.; Yuan, J.-S.; Bi, Y. Logic locking using hybrid CMOS and emerging SiNW FETs. Electronics 2017, 6, 69. [Google Scholar] [CrossRef] [Green Version]
- Alasad, Q.; Lin, J.; Yuan, J.-S.; Fan, D.; Awad, A. Resilient and Secure Hardware Devices Using ASL. ACM J. Emerg. Technol. Comput. Syst. 2021, 17, 1–26. [Google Scholar] [CrossRef]
- Ibrahim, A.; Osta, M.; Alameh, M.; Saleh, M.; Chible, H.; Valle, M. Approximate Computing Methods for Embedded Machine Learning. In Proceedings of the 2018 25th IEEE International Conference on Electronics Circuits and Systems, ICECS 2018, Bordeaux, France, 9–12 December 2018. [Google Scholar]
- Sarwar, S.S.; Srinivasan, G.; Han, B.; Wijesinghe, P.; Jaiswal, A.; Panda, P.; Raghunathan, A.; Roy, K. Energy-efficient neural computing: A study of cross-layer approximations. IEEE J. Emerg. Sel. Top. Circuits Syst. 2018, 8, 796–809. [Google Scholar] [CrossRef]
- Du, Z.; Lingamneni, A.; Chen, Y.; Palem, K.V.; Temam, O.; Wu, C. Leveraging the Error Resilience of Neural Networks for Designing Highly Energy Efficient Accelerators. IEEE Trans. Comput. Des. Integr. Circuits Syst. 2015, 34, 1223–1235. [Google Scholar] [CrossRef]
- Mahdiani, H.R.; Ahmadi, A.; Fakhraie, S.M.; Lucas, C. Bio-inspired imprecise computational blocks for efficient VLSI implementation of soft-computing applications. IEEE Trans. Circuits Syst. I Regul. Pap. 2010, 57, 850–862. [Google Scholar] [CrossRef]
- Hammad, A.; El-Sankary, K. Impact of approximate multipliers on VGG deep learning network. IEEE Access 2018, 6, 60438–60444. [Google Scholar] [CrossRef]
- Gastaldo, P.; Pinna, L.; Seminara, L.; Valle, M.; Zunino, R. Computational intelligence techniques for tactile sensing systems. Sensors 2014, 14, 10952–10976. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ibrahim, A.; Valle, M.; Noli, L.; Chible, H. FPGA implementation of fixed-point CORDIC-SVD for E-skin systems. In Proceedings of the 2015 11th Conference on Ph.D. Research in Microelectronics and Electronics, PRIME 2015, Glasgow, UK, 29 June–2 July 2015. [Google Scholar]
- Available online: https://github.com/osta1/Multipliers-adders.git (accessed on 26 September 2021).
- Osta, M.; Ibrahim, A.; Magno, M.; Eggimann, M.; Pullini, A.; Gastaldo, P.; Valle, M. An energy-efficient system for touch modality classification in electronic skin applications. In Proceedings of the 2019 IEEE International Symposium on Circuits and Systems, Hokkaido, Japan, 26–29 May 2019; Volume 2019, pp. 1–4. [Google Scholar]
- Prabakaran, B.S.; Rehman, S.; Shafique, M. XBioSiP: A methodology for approximate bio-signal processing at the edge. In Proceedings of the 56th Annual Design Automation Conference, Las Vegas, NV, USA, 2–6 June 2019. [Google Scholar]
- Liang, J.; Han, J.; Lombardi, F. New metrics for the reliability of approximate and probabilistic adders. IEEE Trans. Comput. 2013, 62, 1760–1771. [Google Scholar] [CrossRef]
- Kozak, A.; Kozak, R.A.; Staudhammer, C.L.; Watts, S.B. Sampling distributions: The foundation of inference. In Introductory Probability and Statistics: Applications for Forestry and Natural Sciences; CABI: Wallingford, UK, 2019; pp. 111–145. [Google Scholar]
- Yang, Z.; Jain, A.; Liang, J.; Han, J.; Lombardi, F. Approximate XOR/XNOR-based adders for inexact computing. In Proceedings of the 2013 13th IEEE International Conference on Nanotechnology, Beijing, China, 5–8 August 2013; pp. 690–693. [Google Scholar]
- Liu, C.; Han, J.; Lombardi, F. A low-power, high-performance approximate multiplier with configurable partial error recovery. In Proceedings of the Design, Automation and Test in Europe, DATE, Dresden, Germany, 24–28 March 2014. [Google Scholar]
- Allen, C.I.; Langley, D.; Lyke, J.C. Inexact computing with approximate adder application. In Proceedings of the NAECON 2014—IEEE National Aerospace and Electronics Conference, Dayton, OH, USA, 24--27 June 2014; Volume 2015, pp. 21–28. [Google Scholar]
- Zhu, N.; Goh, W.L.; Zhang, W.; Yeo, K.S.; Kong, Z.H. Design of Low-Power High-Speed Truncation-Error-Tolerant Adder and Its Application in Digital Signal Processing. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2010, 18, 1225–1229. [Google Scholar]
- Mrazek, V.; Hrbacek, R.; Vasicek, Z.; Sekanina, L. EvoApproxSb: Library of approximate adders and multipliers for circuit design and benchmarking of approximation methods. In Proceedings of the 2017 Design, Automation and Test in Europe, DATE 2017, Lausanne, Switzerland, 27–31 March 2017. [Google Scholar]
- Kumar, M.; Zhang, X.; Liu, L.; Wang, Y.; Shi, W. Energy-efficient machine learning on the edges. In Proceedings of the 2020 IEEE 34th International Parallel and Distributed Processing Symposium Workshops (IPDPSW), New Orleans, LA, USA, 18–22 May 2020; pp. 912–921. [Google Scholar]














| Approximate Adders | PDP (pJ) | PDP-MRED |
|---|---|---|
| AFA | 0.09 | 0.13% |
| LOA | 0.11 | 0.16% |
| AND-C | 0.17 | 0.47% |
| NAND-C | 0.16 | 0.71% |
| IPP | 0.14 | 0.43% |
| AXA | 0.17 | 0.83% |
| Cases | Partial Products | Sum Bit | Carry Bit |
|---|---|---|---|
| First | |||
| Second | |||
| Third | Or Or: |
| Approximate Multipliers | PDP (pJ) | PDP-MRED |
|---|---|---|
| Approx-BW | 0.13 | 1.29% |
| Mul-LOA | 0.13 | 1.38% |
| Mul-AXA | 0.57 | 8.85% |
| MAND | 0.5 | 4.53% |
| MNAND | 0.51 | 7.61% |
| MIPP | 0.43 | 5.67% |
| ROBA | 0.67 | 6.09% |
| META | 0.48 | 4.31% |
| Evo0 | 0.37 | 2.96% |
| Evo25 | 0.08 | 1.72% |
| Kulkarni | 0.41 | 3.13% |
| Shafique | 0.32 | 5.12% |
| Characteristics | Power Consumption(mW) |
|---|---|
| Dynamic power | 22 |
| I/O | 19 |
| Signal | 1 |
| Logic | 2 |
| SVD (A) | SVD (B) | SVD (C) | Error Rate (%) | Error Difference (%) |
|---|---|---|---|---|
| Exact | Exact | Exact | 16.25 | 0 |
| Approx12 | Approx16 | Approx20 | 18.12 | 1.88 |
| Approx16 | Approx20 | Approx12 | 18.12 | 1.88 |
| Approx20 | Approx24 | Approx16 | 25.62 | 9.38 |
| Approx16 | Approx20 | Approx24 | 29.38 | 13.12 |
| Approx20 | Approx24 | Approx28 | 35 | 18.75 |
| Approx24 | Approx28 | Approx20 | 36.25 | 20 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Osta, M.; Ibrahim, A.; Valle, M. Approximate Computing Circuits for Embedded Tactile Data Processing. Electronics 2022, 11, 190. https://doi.org/10.3390/electronics11020190
Osta M, Ibrahim A, Valle M. Approximate Computing Circuits for Embedded Tactile Data Processing. Electronics. 2022; 11(2):190. https://doi.org/10.3390/electronics11020190
Chicago/Turabian StyleOsta, Mario, Ali Ibrahim, and Maurizio Valle. 2022. "Approximate Computing Circuits for Embedded Tactile Data Processing" Electronics 11, no. 2: 190. https://doi.org/10.3390/electronics11020190
APA StyleOsta, M., Ibrahim, A., & Valle, M. (2022). Approximate Computing Circuits for Embedded Tactile Data Processing. Electronics, 11(2), 190. https://doi.org/10.3390/electronics11020190








