An Analysis of Some Properties and the Use of the Twist Map for the Finite Frenkel–Kontorova Model
Abstract
:1. Introduction
2. Equations for Stationary States
3. A Remark on the Length of the Chain
4. The Meaning of the Tensile Force
5. The Meaning of the Free Boundary Conditions
6. The Twist Map for a Finite FK Chain
7. The Disappearence of Incommensurabilities
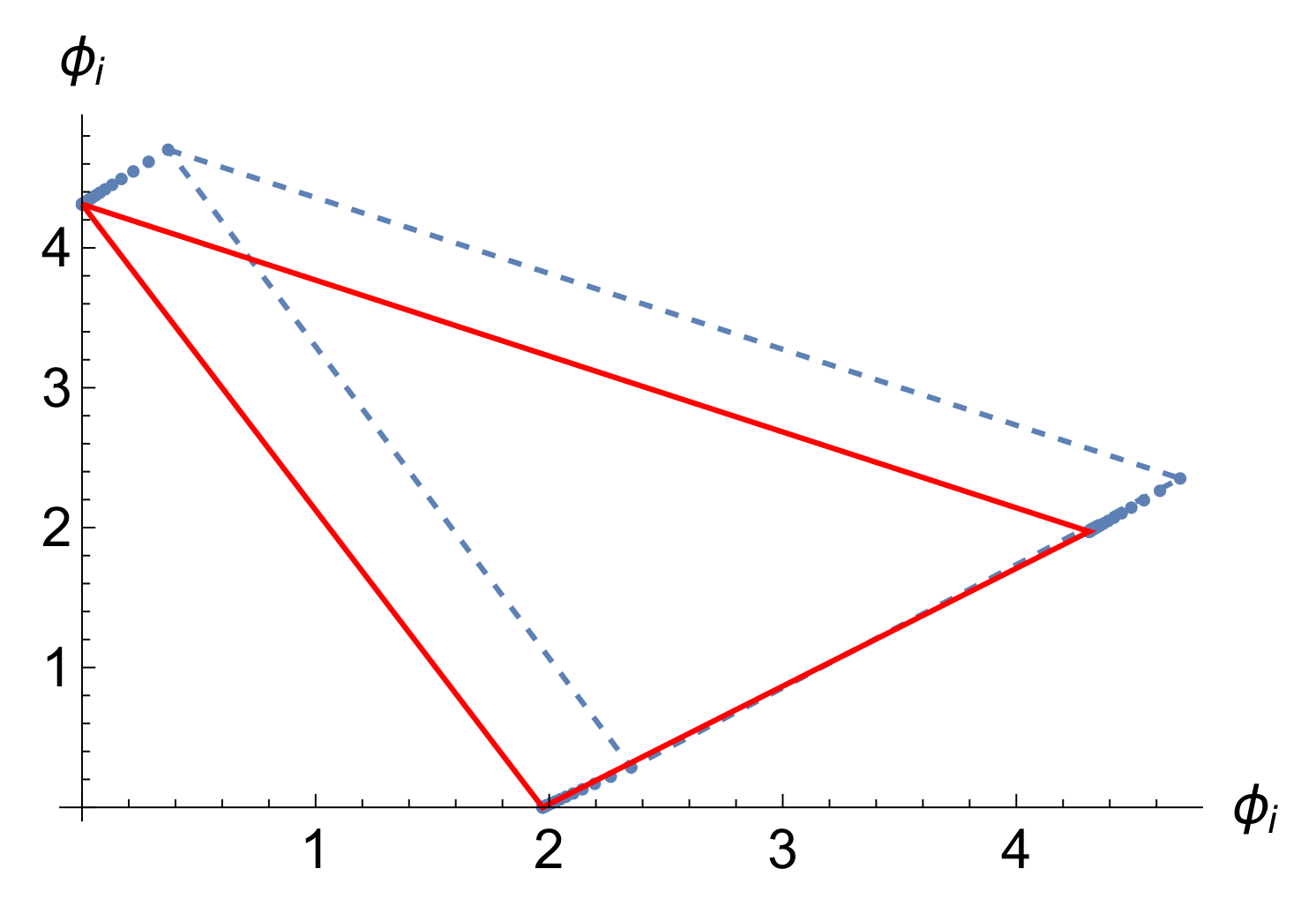
8. Remark on the Aubry Transformation of a Finite Chain
9. Discussion
10. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| BC | Boundary condition |
| FK | Frenkel–Kontorova |
Appendix A
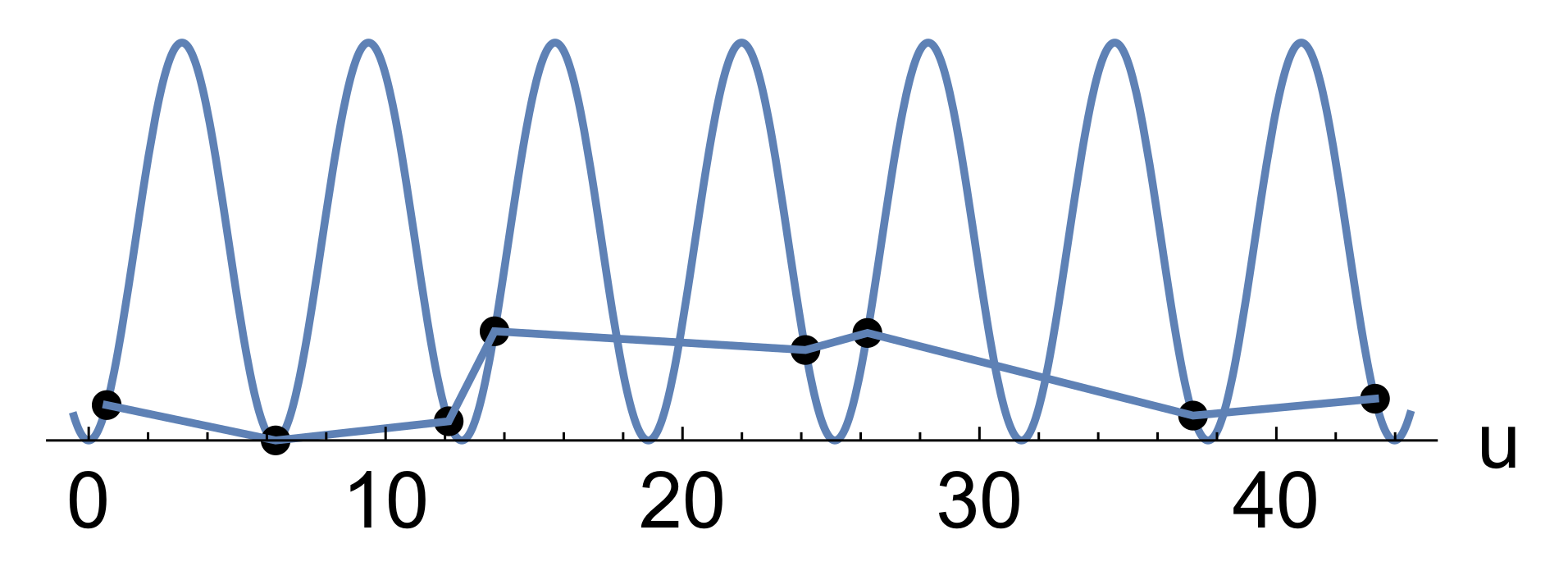
References
- Kontorova, T.A.; Frenkel, Y.I. To the theory of plastic deformations and twinnings I. Zh. Eksp. Teor. Fis. 1938, 8, 89–95. (In Russian) [Google Scholar]
- Lin, J.Y.; Smorodin, A.V.; Badrutdinov, A.O.; Konstantinov, D. Transport Properties of a Quasi-1D Wigner Solid on Liquid Helium Confined in a Microchannel with Periodic Potential. J. Low Temp. Phys. 2019, 195, 289–299. [Google Scholar] [CrossRef] [Green Version]
- Quapp, W.; Lin, J.Y.; Bofill, J.M. The movement of a one-dimensional Wigner solid explained by a modified Frenkel-Kontorova model. Eur. Phys. J. B 2020, 93, 227. [Google Scholar] [CrossRef]
- Duwel, A.E.; Watanabe, S.; Triás, E.; Orlando, T.P.; van der Zant, H.S.J.; Strogatz, S.H. Discreteness-induced resonances and ac voltage amplitudes in long one-dimensional Josephson junction arrays. J. Appl. Phys. 1997, 82, 4661–4668. [Google Scholar] [CrossRef] [Green Version]
- Ustinov, A.V. Solitons in Josephson-junction arrays. Phys. D 1998, 123, 315–329. [Google Scholar] [CrossRef]
- Quapp, W.; Bofill, J.M. Description of Shapiro steps on the potential energy surface of a Frenkel-Kontorova model Part II: Free boundaries. Eur. Phys. J. B 2021, 94, 64. [Google Scholar] [CrossRef]
- Quapp, W.; Bofill, J.M. Description of zero field steps on the potential energy surface of a Frenkel-Kontorova model for annular Josephson junction arrays. Eur. Phys. J. B 2021, 94, 105. [Google Scholar] [CrossRef]
- Grüner, G. The dynamics of charge-density waves. Rev. Mod. Phys. 1988, 60, 1129–1181. [Google Scholar] [CrossRef]
- Garcia-Mata, I.; Zhirov, O.V.; Shepelyansky, D.L. The Frenkel-Kontorova model with cold trapped ions. Eur. Phys. J. D 2007, 41, 325–330. [Google Scholar] [CrossRef] [Green Version]
- Pouget, J.P. The Peierls instability and charge density wave in one-dimensional electronic conductors. Comptes Rendus Phys. 2016, 17, 332–356. [Google Scholar] [CrossRef] [Green Version]
- Braun, O.; Dauxois, T.; Paliy, M.V.; Peyrard, M. Mobility and diffusivity in a generalized Frenkel-Kontorova model. Phys. Rev. B 1996, 54, 321. [Google Scholar] [CrossRef]
- Ekomasov, E.G.; Murtazin, R.R.; Bogomazova, O.B.; Gumerov, A.M. One-dimensional dynamics of domain walls in two-layer ferromagnet structure with different parameters of magnetic anisotropy and exchange. J. Magn. Magn. Mater. 2013, 339, 133–137. [Google Scholar] [CrossRef]
- Trallori, L. Magnetic superlattices, classical spin chains, and the Frenkel-Kontorova model. Phys. Rev. B 1998, 57, 5923. [Google Scholar] [CrossRef]
- Que, W.; Walker, M.B. Generalized Frenkel-Kontorova model for structural modulations in bismuth high-Tc superconductors and related compounds. Phys. Rev. B 1992, 46, 14772. [Google Scholar] [CrossRef] [PubMed]
- Dinsmore, R.C., III; Bae, M.H.; Bezryadin, A. Fractional order Shapiro steps in superconducting nanowires. Appl. Phys. Lett. 2008, 93, 192505. [Google Scholar] [CrossRef] [Green Version]
- Besseling, R.; Niggebrugge, R.; Kes, P.H. Transport properties of vortices in easy flow channels: A Frenkel-Kontorova study. Phys. Rev. Lett. 1999, 82, 3144–3147. [Google Scholar] [CrossRef] [Green Version]
- Kokubo, N.; Besseling, R.; Vinokur, V.M.; Kes, P.H. Mode Locking of Vortex Matter Driven through Mesoscopic Channels. Phys. Rev. Lett. 2002, 88, 247004. [Google Scholar] [CrossRef] [Green Version]
- Iaroshenko, O.; Rybalko, V.; Vinokur, V.M.; Berlyand, L. Vortex phase separation in mesoscopic superconductors. Sci. Rep. 2013, 3, 1758. [Google Scholar] [CrossRef] [Green Version]
- Quapp, W.; Bofill, J.M. Newton Trajectories for the Frenkel-Kontorova model. Mol. Phys. 2019, 117, 1541–1558. [Google Scholar] [CrossRef] [Green Version]
- Kochendörfer, A.; Seeger, A. Theorie der Versetzungen in eindimensionalen Atomreihen. I. Periodisch angeordnete Versetzungen. Zeitschr. Phys. 1950, 127, 533–550. [Google Scholar] [CrossRef]
- Aubry, S. The twist map, the extended Frenkel-Kontorova model and the devil’s staircase. Phys. D 1983, 7, 240–258. [Google Scholar] [CrossRef]
- Hobart, R.; Celli, V. A Solution to the Frenkel-Kontorova Dislocation Model. J. Appl. Phys. 1962, 33, 60–62. [Google Scholar] [CrossRef]
- Hu, B.; Shi, J. Nonanalytic twist maps and Frenkel-Kontorova models. Phys. D 1994, 71, 23–38. [Google Scholar] [CrossRef] [Green Version]
- Aubry, S. Defectibility and frustration in incommensurate structures: The devil’s stair case transformation. Ferroelectrics 1980, 24, 53–60. [Google Scholar] [CrossRef]
- Guo, Y.; Qu, Z.; Zhang, Z. Lyapunov stability and precise control of the frictional dynamics of a one-dimensional particle array. Phys. Rev. B 2006, 73, 094118. [Google Scholar] [CrossRef]
- Theodorakopoulos, N.; Peyrard, M.; MacKay, R.S. Nonlinear Structures and Thermodynamic Instabilities in a One-Dimensional Lattice System. Phys. Rev. Lett. 2004, 93, 258101. [Google Scholar] [CrossRef] [Green Version]
- Aubry, S. Devils staircase and order without periodicity in classical condensed matter. J. Phys. Fr. 1983, 44, 147–162. [Google Scholar] [CrossRef] [Green Version]
- Frank, F.C.; van der Merwe, J.H. One-Dimensional Dislocations. I. Static Theory. Proc. R. Soc. Lond. A 1949, 198, 205–216. [Google Scholar]
- Blass, T.; de la Llave, R. The Analyticity Breakdown for Frenkel-Kontorova Models in Quasi-periodic Media: Numerical Explorations. J. Stat. Phys. 2013, 150, 1183–1200. [Google Scholar] [CrossRef] [Green Version]
- Tong, P.; Li, B.; Hu, B. Wave transmission, phonon localization, and heat conduction of a one-dimensional Frenkel-Kontorova chain. Phys. Rev. B 1999, 59, 8639. [Google Scholar] [CrossRef] [Green Version]
- Aubry, S.; MacKay, R.S.; Baesens, C. Equivalence of uniform hyperbolicity for symplectic twist maps and phonon gap for Frenkel-Kontorova models. Phys. D 1992, 56, 123–134. [Google Scholar] [CrossRef]
- Salahshoor, H.; de la Llave, R. A Numerical Investigation of the Pinning Phenomenon in Quasi-Periodic Frenkel-Kontorova Model Under an External Force. J. Stat. Phys. 2018, 173, 398–410. [Google Scholar] [CrossRef]
- Hu, B.; Li, B.; Zhao, H. Mode-locking of incommensurate phase by quantum zero point energy in the Frenkel-Kontorova model. Europhys. Lett. 2001, 53, 342. [Google Scholar] [CrossRef]
- Griffiths, R.B.; Chou, W. Effective Potentials: A New Approach and New Results for One-Dimensional Systems with Competing Length Scales. Phys. Rev. Lett. 1986, 56, 1929. [Google Scholar] [CrossRef] [PubMed]
- Sharma, S.R.; Bergersen, B.; Joos, B. Aubry transition in a finite modulated chain. Phys. Rev. B 1984, 29, 6335–6340. [Google Scholar] [CrossRef]
- Baesens, C.; MacKay, R.S. Gradient dynamics of tilted Frenkel-Kontorova models. Nonlinearity 1998, 11, 949–964. [Google Scholar] [CrossRef]
- Aubry, S.; Abramovici, G. Chaotic trajectories in the standard map. The concept of anti-intergability. Phys. D 1990, 43, 199–219. [Google Scholar] [CrossRef]
- Aubry, S.; Le Daeron, P.Y. The diskrete Frenkel-Kontorova model and its extensions I. Exact results for the ground-states. Phys. D 1983, 8, 381. [Google Scholar] [CrossRef]
- Avdoshenko, S.M.; Makarov, D.E. Reaction Coordinates and Pathways of Mechanochemical Transformations. J. Phys. Chem. B 2015, 120, 1537–1545. [Google Scholar] [CrossRef]
- Bofill, J.M.; Ribas-Ariño, J.; García, S.P.; Quapp, W. An Algorithm to Locate Optimal Bond Breaking Points on a Potential Energy Surface. J. Chem. Phys. 2017, 147, 152710. [Google Scholar] [CrossRef] [Green Version]
- Quapp, W. Can We Understand the Branching of Reaction Valleys for more than two Degrees of Freedom? J. Math. Chem. 2015, 54, 137–148. [Google Scholar] [CrossRef]
- Quapp, W.; Bofill, J.M. A contribution to a theory of mechanochemical pathways by means of Newton trajectories. Theor. Chem. Acc. 2016, 135, 113. [Google Scholar] [CrossRef]
- Quapp, W.; Bofill, J.M. Mechanochemistry on the Müller-Brown Surface by Newton Trajectories. Int. J. Quant. Chem. 2018, 118, e25522. [Google Scholar] [CrossRef]
- Quapp, W.; Bofill, J.M.; Ribas-Ariño, J. Towards a Theory of Mechanochemistry, Simple Models from the Very Beginnings. Int. J. Quant. Chem. 2018, 118, e25775. [Google Scholar] [CrossRef] [Green Version]
- Hirsch, M.; Quapp, W. Reaction Channels of the Potential Energy Surface: Application of Newton Trajectories. J. Mol. Struct. Theochem 2004, 683, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Quapp, W.; Bofill, J.M. A Model for a Driven Frenkel-Kontorova Chain. Eur. Phys. J. B 2019, 92, 95–117. [Google Scholar] [CrossRef]
- Quapp, W.; Bofill, J.M. Sliding Paths for Series of Frenkel-Kontorova Models—A Contribution to the Concept of 1D-superlubricity. Eur. Phys. J. B 2019, 92, 193. [Google Scholar] [CrossRef]
- Quapp, W.; Bofill, J.M. Description of Shapiro steps on the potential energy surface of a Frenkel-Kontorova model Part I: Chain in a box. Eur. Phys. J. B 2021, 94, 66. [Google Scholar] [CrossRef]
- Bichoutskaia, E.; Heggie, M.I.; Lozovik, Y.E.; Popov, A.M. Multi-Walled Nanotubes: Commensurate-Incommensurate Phase Transition and NEMS Applications. Fuller. Nanotubes Carbon Nanostruct. 2006, 14, 131–140. [Google Scholar] [CrossRef]
- Black, R.C.; Satija, I.I. Universal phase diagram in the generalized Frenkel-Kontorova model. Phys. Rev. B 1991, 44, 4089–4096. [Google Scholar] [CrossRef]
- Vanossi, A.; Bechinger, C.; Urbakh, M. Structural lubricity in soft and hard matter systems. Nat. Commun. 2020, 11, 4657. [Google Scholar] [CrossRef] [PubMed]
- Stoyanov, S.; Müller-Krumbhaar, H. Resonance-induced Cluster-mobility: Dynemics of a finite Frenkel-Kontorova model. Surf. Sci. 1985, 159, 49–68. [Google Scholar] [CrossRef]
- Quapp, W.; Bofill, J.M. Comment on ’Out-of-equilibrium Frenkel-Kontorova model’ (A. Imparato, 2021, J. Stat. Mech. 013214). J. Stat. Mech. 2022, 2022, 013204. [Google Scholar] [CrossRef]
- Muñoz, J.M.; Sawant, R.; Maffei, A.; Wang, X.; Barontini, G. Realizing the Frenkel-Kontorova model with Rydberg-dressed atoms. Phys. Rev. A 2020, 102, 043308. [Google Scholar] [CrossRef]
- Axel, F.; Aubry, S. Polarisation and transition by breaking of analyticity in a one-dimensional model for incommensurate structures in an electric field. J. Phys. A 1987, 20, 487. [Google Scholar] [CrossRef]
- Peyrard, M.; Aubry, S. Critical behaviour at the transition by breaking of analyticity in the discrete Frenkel-Kontorova model. J. Phys. C Solid State Phys. 1983, 16, 1593–1608. [Google Scholar] [CrossRef]
- Bylinskii, A.; Gangloff, D.; Counts, I.; Vuletić, V. Observation of Aubry-type transition in finite atom chains via friction. Nat. Mater. 2016, 15, 717–721. [Google Scholar] [CrossRef]
- Babushkin, A.Y.; Abkaryan, A.K.; Dobronets, B.S.; Krasikov, V.S.; Filonov, A.N. The Ground State of the Frenkel-Kontorova Model. Phys. Solid State 2016, 58, 1834–1845. [Google Scholar] [CrossRef]
- Ma, Y.; Wang, J.; Xu, X.; Wei, Q.; Kais, S. A density-matrix renormalization group Study of one-dimensional incommensurate quantum Frenkel-Kontorova model. J. Phys. Soc. Jpn. 2014, 83, 094605. [Google Scholar] [CrossRef] [Green Version]
- Mikheikin, I.D.; Kuznetsov, M.Y.; Makhonina, E.V.; Pervov, V.S. Defects in Inorganic Suprastructures with Incommensurate Structural Elements: The Static Frenkel-Kontorova Model for Finite Systems. Dokl. Phys. Chem. 2001, 376, 52–55. [Google Scholar] [CrossRef]
- Nasilowski, R. An unorthodox analysis of the Frenkel-Kontorova model. Phys. A 1996, 230, 266–284. [Google Scholar] [CrossRef]
- Novak, I.; Truskinovsky, L. Segmentation in cohesive systems constrained by elastic environments. Phil. Trans. R. Soc. A 2017, 375, 20160160. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.L.; Tekić, J.; Duan, W.S.; Shao, Z.G.; Yang, L.P. Existence and stability of the resonant phenomena in the dc- and ac-driven overdamped Frenkel-Kontorova model with the incommensurate structure. Phys. Rev. E 2011, 84, 046603. [Google Scholar] [CrossRef] [PubMed]
- Zhirov, O.V.; Lages, J.; Shepelyansky, D.L. Thermoelectricity of cold ions in optical lattices. Eur. Phys. J. D 2019, 73, 149. [Google Scholar] [CrossRef] [Green Version]
- Zhirov, O.V.; Lages, J.; Shepelyansky, D.L. Thermoelectricity Modeling with Cold Dipole Atoms in Aubry Phase of Optical Lattice. Appl. Sci. 2020, 10, 2090. [Google Scholar] [CrossRef] [Green Version]
- Thomas, A.; Leoni, T.; Siri, O.; Becker, C.; Unzog, M.; Kern, C.; Puschnig, P.; Zeppenfeld, P. A one-dimensional high-order commensurate phase of tilted molecules. Phys. Chem. Chem. Phys. 2022, 24, 9118. [Google Scholar] [CrossRef] [PubMed]






| 3 | −0.769 | 0.6224 | 47 | 0.390 | 0.6700 |
| 4 | 0.117 | 0.6542 | 74 | 0.370 | 0.6688 |
| 8 | 0.751 | 0.6801 | 99 | 0.358 | 0.6621 |
| 9 | −0.341 | 0.6386 | 500 | 0.368 | 0.6670 |
| 10 | 0.239 | 0.6582 | 1000 | 0.369 | 0.6665 |
| 20 | 0.632 | 0.6736 | 5000 | 0.369 | 0.6667 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Quapp, W.; Bofill, J.M. An Analysis of Some Properties and the Use of the Twist Map for the Finite Frenkel–Kontorova Model. Electronics 2022, 11, 3295. https://doi.org/10.3390/electronics11203295
Quapp W, Bofill JM. An Analysis of Some Properties and the Use of the Twist Map for the Finite Frenkel–Kontorova Model. Electronics. 2022; 11(20):3295. https://doi.org/10.3390/electronics11203295
Chicago/Turabian StyleQuapp, Wolfgang, and Josep Maria Bofill. 2022. "An Analysis of Some Properties and the Use of the Twist Map for the Finite Frenkel–Kontorova Model" Electronics 11, no. 20: 3295. https://doi.org/10.3390/electronics11203295
APA StyleQuapp, W., & Bofill, J. M. (2022). An Analysis of Some Properties and the Use of the Twist Map for the Finite Frenkel–Kontorova Model. Electronics, 11(20), 3295. https://doi.org/10.3390/electronics11203295






