Mobile Anchor and Kalman Filter Boosted Bounding Box for Localization in Wireless Sensor Networks
Abstract
:1. Introduction
2. Related Works
3. Background: The Bounding Box Method (Min–Max Method)
4. Proposed Kalman Filter-Based Bounding Box Localization Algorithm (KF-BBLA)
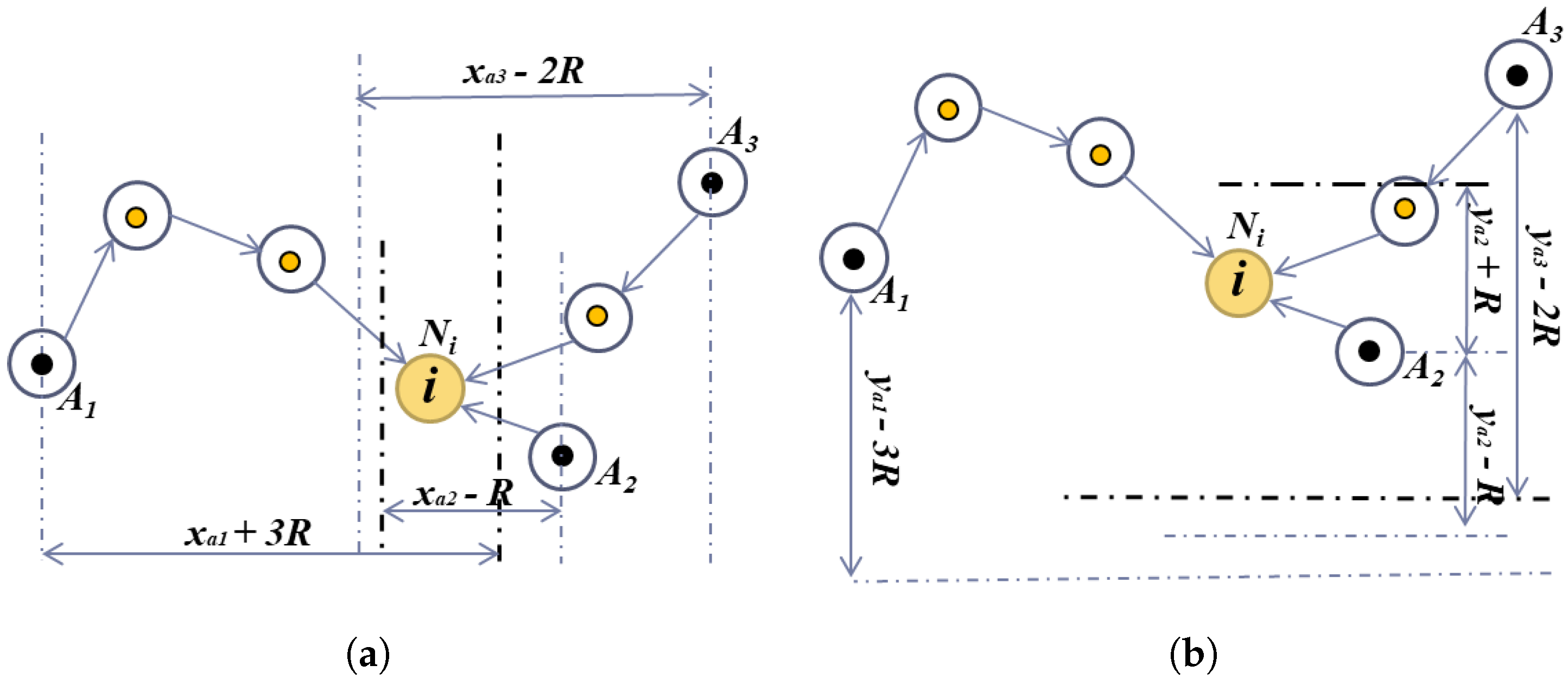
4.1. Proposed Bounding Box Localization Technique
4.2. Proposed Kalman Filter Localization Technique
5. Simulation Results
5.1. Variation of Localization Performance over Time
5.2. Localization Accuracy with Node Number Variation
5.3. Comparison of Localization Accuracy of Localization Techniques
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Muzammal, M.; Talat, R.; Sodhro, A.H.; Pirbhulal, S. A multi-sensor data fusion enabled ensemble approach for medical data from body sensor networks. Inf. Fusion 2020, 53, 155–164. [Google Scholar]
- Atiga, J.; Hamdi, M.; Ejbali, R.; Zaied, M. Recurrent neural network NARX for distributed fault detection in wireless sensor networks. Int. J. Sens. Netw. 2021, 37, 100–111. [Google Scholar] [CrossRef]
- Alomari, A.; Comeau, F.; Phillips, W.; Aslam, N. New path planning model for mobile anchor-assisted localization in wireless sensor networks. Wirel. Netw. 2018, 24, 2589–2607. [Google Scholar]
- Hajjej, F.; Hamdi, M.; Ejbali, R.; Zaied, M. A New Optimal Deployment Model of Internet of Things Based on Wireless Sensor Networks. In Proceedings of the 2019 15th International Wireless Communications & Mobile Computing Conference (IWCMC), Tangier, Morocco, 24–28 June 2019; pp. 2092–2097. [Google Scholar] [CrossRef]
- Sodhro, A.H.; Sangaiah, A.K.; Sodhro, G.H.; Sekhari, A.; Ouzrout, Y.; Pirbhulal, S. Energy-efficiency of tools and applications on Internet. In Computational Intelligence for Multimedia Big Data on the Cloud with Engineering Applications; Elsevier: Amsterdam, The Netherlands, 2018; pp. 297–318. [Google Scholar]
- Mershad, K.; Cheikhrouhou, O.; Ismail, L. Proof of Accumulated Trust: A new consensus protocol for the security of the IoV. Veh. Commun. 2021, 32, 100392. [Google Scholar]
- Jamil, F.; Cheikhrouhou, O.; Jamil, H.; Koubaa, A.; Derhab, A.; Ferrag, M.A. PetroBlock: A blockchain-based payment mechanism for fueling smart vehicles. Appl. Sci. 2021, 11, 3055. [Google Scholar] [CrossRef]
- Cheikhrouhou, O.; Koubâa, A. Blockloc: Secure localization in the internet of things using blockchain. In Proceedings of the 2019 15th International Wireless Communications & Mobile Computing Conference (IWCMC), Tangier, Morocco, 24–28 June 2019; pp. 629–634. [Google Scholar]
- Zaabar, B.; Cheikhrouhou, O.; Ammi, M.; Awad, A.I.; Abid, M. Secure and Privacy-aware Blockchain-based Remote Patient Monitoring System for Internet of Healthcare Things. In Proceedings of the 2021 17th International Conference on Wireless and Mobile Computing, Networking and Communications (WiMob), Bologna, Italy, 11–13 October 2021; pp. 200–205. [Google Scholar]
- Cheikhrouhou, O. Secure group communication in wireless sensor networks: A survey. J. Netw. Comput. Appl. 2016, 61, 115–132. [Google Scholar]
- Sodhro, A.H. A review on 802.11 MAC protocols industrial standards, architecture elements for providing QoS guarantee, supporting emergency traffic, and security: Future directions. J. Ind. Inf. Integr. 2021, 4, 100225. [Google Scholar]
- Cheikhrouhou, O.; Mahmud, R.; Zouari, R.; Ibrahim, M.; Zaguia, A.; Gia, T.N. One-dimensional CNN approach for ECG arrhythmia analysis in fog-cloud environments. IEEE Access 2021, 9, 103513–103523. [Google Scholar]
- Frikha, T.; Chaari, A.; Chaabane, F.; Cheikhrouhou, O.; Zaguia, A. Healthcare and fitness data management using the iot-based blockchain platform. J. Healthc. Eng. 2021, 2021, 9978863. [Google Scholar] [CrossRef]
- Zaabar, B.; Cheikhrouhou, O.; Jamil, F.; Ammi, M.; Abid, M. HealthBlock: A secure blockchain-based healthcare data management system. Comput. Netw. 2021, 200, 108500. [Google Scholar]
- Cheikhrouhou, O.; Koubâa, A.; Zarrad, A. A cloud based disaster management system. J. Sens. Actuator Netw. 2020, 9, 6. [Google Scholar]
- Sharma, K.; Anand, D.; Sabharwal, M.; Tiwari, P.K.; Cheikhrouhou, O.; Frikha, T. A Disaster Management Framework Using Internet of Things-Based Interconnected Devices. Math. Probl. Eng. 2021, 2021, 916440. [Google Scholar]
- Han, G.; Jiang, J.; Zhang, C.; Duong, T.Q.; Guizani, M.; Karagiannidis, G.K. A survey on mobile anchor node assisted localization in wireless sensor networks. IEEE Commun. Surv. Tutorials 2016, 18, 2220–2243. [Google Scholar]
- Ullah, I.; Qian, S.; Deng, Z.; Lee, J.H. Extended Kalman Filter-based localization algorithm by edge computing in Wireless Sensor Networks. Digit. Commun. Netw. 2021, 7, 187–195. [Google Scholar]
- Messous, S.; Liouane, H.; Liouane, N. Improvement of DV-Hop localization algorithm for randomly deployed wireless sensor networks. Telecommun. Syst. 2020, 73, 75–86. [Google Scholar]
- Messous, S.; Liouane, N.; Pegatoquet, A.; Auguin, M. Hop-based routing protocol based on energy efficient Minimum Spanning Tree for wireless sensor network. In Proceedings of the 2018 International Conference on Advanced Systems and Electric Technologies (IC_ASET), Hammamet, Tunisia, 22–25 March 2018; pp. 421–426. [Google Scholar]
- Koubâa, A.; Jamâa, M.B. Taxonomy of Fundamental Concepts of Localization in Cyber-Physical and Sensor Networks. Wirel. Pers. Commun. 2013, 72, 461–507. [Google Scholar] [CrossRef] [Green Version]
- Liouane, H.; Messous, S.; Cheikhrouhou, O.; Baz, M.; Hamam, H. Regularized Least Square Multi-Hops Localization Algorithm for Wireless Sensor Networks. IEEE Access 2021, 9, 136406–136418. [Google Scholar]
- Girod, L.; Estrin, D. Robust range estimation using acoustic and multimodal sensing. In Proceedings of the 2001 IEEE/RSJ International Conference on Intelligent Robots and Systems. Expanding the Societal Role of Robotics in the the Next Millennium (Cat. No. 01CH37180), Maui, HI, USA, 29 October–3 November 2001; Volume 3, pp. 1312–1320. [Google Scholar]
- Priyantha, N.B.; Chakraborty, A.; Balakrishnan, H. The cricket location-support system. In Proceedings of the 6th Annual International Conference on Mobile Computing and Networking, Boston, MA, USA, 6–11 August 2000; pp. 32–43. [Google Scholar]
- Niculescu, D.; Nath, B. Ad hoc positioning system (APS) using AOA. In Proceedings of the IEEE INFOCOM 2003, Twenty-second Annual Joint Conference of the IEEE Computer and Communications Societies (IEEE Cat. No. 03CH37428), San Francisco, CA, USA, 30 March–03 April 2003; Volume 3, pp. 1734–1743. [Google Scholar]
- Viani, F.; Lizzi, L.; Rocca, P.; Benedetti, M.; Donelli, M.; Massa, A. Object tracking through RSSI measurements in wireless sensor networks. Electron. Lett. 2008, 44, 653–654. [Google Scholar] [CrossRef] [Green Version]
- Jamâa, M.B.; Koubâa, A.; Kayani, Y. EasyLoc: RSS-Based Localization Made Easy. Procedia Comput. Sci. 2012, 10, 1127–1133. [Google Scholar] [CrossRef] [Green Version]
- Kalman, R.E. A new approach to linear filtering and prediction problems. J. Basic Eng. 1960, 82, 35–45. [Google Scholar] [CrossRef] [Green Version]
- Cappelletti, C.; Battistini, S.; Malphrus, B. CubeSat Handbook: From Mission Design to Operations; Academic Press: Cambridge, MA, USA, 2020. [Google Scholar]
- Messous, S.; Liouane, H.; Cheikhrouhou, O.; Hamam, H. Improved Recursive DV-Hop Localization Algorithm with RSSI Measurement for Wireless Sensor Networks. Sensors 2021, 21, 4152. [Google Scholar] [PubMed]
- Messous, S.; Liouane, H. Online sequential DV-hop localization algorithm for wireless sensor networks. Mob. Inf. Syst. 2020, 2020, 8195309. [Google Scholar]
- Liouane, H.; Messous, S.; Cheikhrouhou, O. Regularized least square multi-hops localization algorithm based on DV-Hop for wireless sensor networks. Telecommun. Syst. 2022, 80, 349–358. [Google Scholar] [CrossRef]
- Campos, A.N.; Souza, E.L.; Nakamura, F.G.; Nakamura, E.F.; Rodrigues, J.J. On the impact of localization and density control algorithms in target tracking applications for wireless sensor networks. Sensors 2012, 12, 6930–6952. [Google Scholar] [PubMed] [Green Version]
- Han, G.; Zhang, C.; Jiang, J.; Yang, X.; Guizani, M. Mobile anchor nodes path planning algorithms using network-density-based clustering in wireless sensor networks. J. Netw. Comput. Appl. 2017, 85, 64–75. [Google Scholar]
- Johnson, D.B.; Maltz, D.A. Dynamic source routing in ad hoc wireless networks. In Mobile computing; Springer: Berlin/Heidelberg, Germany, 1996; pp. 153–181. [Google Scholar]
- Hu, L.; Evans, D. Localization for mobile sensor networks. In Proceedings of the 10th annual international conference on Mobile computing and networking, Philadelphia, PA, USA, 26 September–1 October 2004; pp. 45–57. [Google Scholar]
- Baggio, A.; Langendoen, K. Monte Carlo localization for mobile wireless sensor networks. Ad Hoc Netw. 2008, 6, 718–733. [Google Scholar] [CrossRef]
- Correia, S.D.; Beko, M.; da Silva Cruz, L.A.; Tomic, S. Elephant herding optimization for energy-based localization. Sensors 2018, 18, 2849. [Google Scholar]
- Wang, W.; Zhu, Q. RSS-based Monte Carlo localisation for mobile sensor networks. IET Commun. 2008, 2, 673–681. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, B.; Wang, X.; Chai, S.; Bai, Y. Cooperative Localization With Bounding Constraints in Mobile Wireless Sensor Networks. IEEE Access 2018, 6, 47011–47025. [Google Scholar] [CrossRef]
- Hu, Z.; Gu, D.; Song, Z.; Li, H. Localization in wireless sensor networks using a mobile anchor node. In Proceedings of the 2008 IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Xi’an, China, 2–5 July 2008; pp. 602–607. [Google Scholar]
- Han, G.; Xu, H.; Jiang, J.; Shu, L.; Hara, T.; Nishio, S. Path planning using a mobile anchor node based on trilateration in wireless sensor networks. Wirel. Commun. Mob. Comput. 2013, 13, 1324–1336. [Google Scholar] [CrossRef]
- Han, G.; Zhang, C.; Lloret, J.; Shu, L.; Rodrigues, J.J. A mobile anchor assisted localization algorithm based on regular hexagon in wireless sensor networks. Sci. World J. 2014, 2014, 219371. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, L.; Yang, Z.; Zhang, S.; Yang, H. Three-dimensional localization algorithm of WSN nodes based on RSSI-TOA and single mobile anchor node. J. Electr. Comput. Eng. 2019, 2019, 4043106. [Google Scholar] [CrossRef] [Green Version]
- Hamdi, M.; Mhiri, S. Dynamic mesh router placement for connectivity maximization in wireless mesh networks. In Proceedings of the 2015 5th International Conference on Information & Communication Technology and Accessibility (ICTA), Marrakech, Morocco, 21–23 December 2015; pp. 1–6. [Google Scholar] [CrossRef]
- Ullah, I.; Shen, Y.; Su, X.; Esposito, C.; Choi, C. A localization based on unscented Kalman filter and particle filter localization algorithms. IEEE Access 2019, 8, 2233–2246. [Google Scholar] [CrossRef]
- Silmi, S.; Doukha, Z.; Moussaoui, S. A self-localization range free protocol for wireless sensor networks. Peer-Netw. Appl. 2021, 14, 2061–2071. [Google Scholar] [CrossRef]
- Meng, Y.; Zhi, Q.; Dong, M.; Zhang, W. A Node Localization Algorithm for Wireless Sensor Networks Based on Virtual Partition and Distance Correction. Information 2021, 12, 330. [Google Scholar] [CrossRef]
- Boukhari, N.; Bouamama, S.; Moussaoui, A. Path Parameters Effect on Localization Using a Mobile Anchor in WSN. Int. J. Inform. Appl. Math. 2020, 3, 12–22. [Google Scholar]
- Rezazadeh, J.; Moradi, M.; Ismail, A.S.; Dutkiewicz, E. Impact of static trajectories on localization in wireless sensor networks. Wirel. Netw. 2015, 21, 809–827. [Google Scholar] [CrossRef]
- Han, G.; Chao, J.; Zhang, C.; Shu, L.; Li, Q. The impacts of mobility models on DV-hop based localization in mobile wireless sensor networks. J. Netw. Comput. Appl. 2014, 42, 70–79. [Google Scholar] [CrossRef]
- Sabale, K.; Mini, S. Localization in wireless sensor networks with mobile anchor node path planning mechanism. Inf. Sci. 2021, 579, 648–666. [Google Scholar] [CrossRef]
- de Oliveira, L.L.; Eisenkraemer, G.H.; Carara, E.A.; Martins, J.B.; Monteiro, J. Mobile Localization Techniques for Wireless Sensor Networks: Survey and Recommendations. ACM Trans. Sens. Netw. (TOSN) 2022. [Google Scholar] [CrossRef]
- Singh, P.; Khosla, A.; Kumar, A.; Khosla, M. Optimized localization of target nodes using single mobile anchor node in wireless sensor network. AEU-Int. J. Electron. Commun. 2018, 91, 55–65. [Google Scholar] [CrossRef]
- Lalama, Z.; Boulfekhar, S.; Semechedine, F. Localization Optimization in WSNs Using Meta-Heuristics Optimization Algorithms: A Survey. Wirel. Pers. Commun. 2022, 122, 1197–1220. [Google Scholar] [CrossRef]
- Ghorpade, S.; Zennaro, M.; Chaudhari, B. Survey of localization for internet of things nodes: Approaches, challenges and open issues. Future Internet 2021, 13, 210. [Google Scholar] [CrossRef]
- Yi, J.; Yang, S.; Cha, H. Multi-hop-based monte carlo localization for mobile sensor networks. In Proceedings of the 2007 4th Annual IEEE Communications Society Conference on Sensor, Mesh and Ad Hoc Communications and Networks, San Diego, CA, USA, 18–21 June 2007; pp. 162–171. [Google Scholar]






| Parameter | Value |
|---|---|
| Sensing field | 100 m × 100 m |
| Amount of unknown nodes | 30, 100, 200, 400 |
| Communication range | 30 m |
| Time of iteration | 100 |
| Number of iterations | 50 |
| Covariance matrix for prediction Q | 0.1 |
| Covariance matrix for observation H | 1 |
| Parameter | Value |
|---|---|
| Sensing field | 100 m × 100 m |
| Amount of unknown nodes | 90 |
| Communication range | 30 m |
| Time of iteration | 100 |
| Number of iterations | 50 |
| Covariance matrix for prediction Q | 0.1 |
| Covariance matrix for observation H | 1 |
| Error (m) | 10 | 20 | 30 | 40 | 50 |
|---|---|---|---|---|---|
| KF-BBLA | 64% | 100% | 100% | 100% | 100% |
| MCL | 48% | 79% | 95% | 99% | 100% |
| MCB | 31% | 65% | 80% | 92% | 98% |
| VMP | 27% | 58% | 78% | 90% | 95% |
| BP-VMP | 11% | 25% | 52% | 72% | 85% |
| PM | 11% | 25% | 49% | 65% | 78% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liouane, H.; Messous, S.; Cheikhrouhou, O.; Koubaa, A.; Hamdi, M. Mobile Anchor and Kalman Filter Boosted Bounding Box for Localization in Wireless Sensor Networks. Electronics 2022, 11, 3296. https://doi.org/10.3390/electronics11203296
Liouane H, Messous S, Cheikhrouhou O, Koubaa A, Hamdi M. Mobile Anchor and Kalman Filter Boosted Bounding Box for Localization in Wireless Sensor Networks. Electronics. 2022; 11(20):3296. https://doi.org/10.3390/electronics11203296
Chicago/Turabian StyleLiouane, Hend, Sana Messous, Omar Cheikhrouhou, Anis Koubaa, and Monia Hamdi. 2022. "Mobile Anchor and Kalman Filter Boosted Bounding Box for Localization in Wireless Sensor Networks" Electronics 11, no. 20: 3296. https://doi.org/10.3390/electronics11203296
APA StyleLiouane, H., Messous, S., Cheikhrouhou, O., Koubaa, A., & Hamdi, M. (2022). Mobile Anchor and Kalman Filter Boosted Bounding Box for Localization in Wireless Sensor Networks. Electronics, 11(20), 3296. https://doi.org/10.3390/electronics11203296






