On Secrecy Performance of a Dual-Hop UAV-Assisted Relaying Network with Randomly Distributed Non-Colluding Eavesdroppers: A Stochastic Geometry Approach

Abstract

Unmanned aerial vehicle (UAV)-based relaying has been considered to offer an excellent performance due to its flexible mobility, on-demand deployment, and cost effectiveness compared to conventional ground-relaying methods. This paper studies the secrecy performance of a dual-hop UAV-assisted relay network, where the base station communicates with the ground user via a low altitude UAV in the presence of randomly distributed eavesdroppers. A stochastic geometric approach is employed to model the spatial locations of the ground user and the eavesdroppers which follows a Homogeneous Poisson Point Process (HPPP). Based on this theory, cumulative distribution functions (CDF) of the ground user and the eavesdroppers are obtained. Considering the decode-and-forward (DF) relay protocol, the CDF equivalent end-to-end instantaneous signal-to-noise ratio (SNR) of the network is derived. To characterize the network secrecy performance, the exact analytical expressions for the network security outage probability (SOP), the strictly positive secrecy capacity (SPSC), and the average secrecy capacity (ASC) are derived. Moreover, a Monte-Carlo simulation is provided to show the accuracy of the derived analytical expressions. The results depict that both the network and channel parameters that include the fading parameter, the density of the eavesdroppers, the average SNR of the B-to-U link, the average SNR of the U-to-E link, the UAV altitude, and the coverage radius have a significant influence on the network secrecy performance.

1. Introduction

1.1. Background Information

Wireless transmission in some special scenarios such as those encountered in urban areas, remote areas, and disaster environments is highly challenging as a result of long distance and obstacles that make it difficult to establish a line-of-sight (LoS) between the source and destination. Under this circumstance, satellite communication has been suggested as a promising solution to provide wireless services due to its ability to offer long distance transmission and a wide coverage [1]. However, the high cost of the deployment of a satellite hinders its wide employment in civil communications [2]. As a results of this, unmanned aerial vehicles (UAVs) have recently attracted significant research attention since they can improve the reliability of communication systems by acting as flying wireless access platforms or relays [3]. Compared to conventional fixed terrestrial relays, a UAV-based relay can significantly overcome the coverage problems and adjust its position to accommodate changes in communication environments [4,5]. Owing to their flexible mobility, easy deployment, fast networking, and cost effectiveness, UAVs have the potential to enable connectivity during temporary events and after disasters [6]. Moreover, they have also found applications in weather-monitoring systems, forest fire prevention technology, cargo delivery, aerial cameras, and so on.

Despite the great benefits of UAV-relay technology, a UAV relay network is highly susceptible to wiretapping from eavesdroppers due to the inherent open medium and broadcasting features of wireless channels [7]. To guarantee the security of the network, a physical layer security technique has been suggested as a promising solution to complement and/or replace the conventional upper layer cryptography. This is because the advancement in computation resources has enabled the eavesdroppers to generate secret keys to decode encrypted information [8]. Therefore, a physical layer security technique can enhance the security of wireless transmissions by exploiting the wireless channel’s characteristics such as fading, interference, and noise to prevent the eavesdroppers from intercepting the network’s confidential information [9].

1.2. Prior Work

Consequently, the utilization of a UAV as a relay node to enhance the performance of wireless communication networks has been widely studied in the literature. The outage performance of a UAV-based relaying system was studied in [10] with energy-harvesting functionality in an urban environment. In [2], the authors presented the outage performance of a dual-hop UAV-relaying network with multiple sources and the destination was assumed to experience co-channel interference. Moreover, the performance of a multiple UAV-relay-assisted network in an internet of things system with energy harvesting applied was evaluated in [11], where the destination was subjected to co-channel interference. Alkama et al. [12] presented the analytical framework to analyze the coverage and capacity of a UAV-assisted network with 3D beamforming through the stochastic cellular network. In addition, the performance analysis of a UAV-assisted cellular network over a Nakagami-m channel with imperfect beam alignment was evaluated in [13]. In addition, the performance of a reconfigurable intelligent surface UAV-assisted dual-hop system was studied in [14] under the DF relaying protocol. Furthermore, the authors of [15] presented a UAV-based relay network with multiple ground users where the opportunistic user scheduling was employed over a Rician fading channel. In [16], the authors investigated the performance of a hybrid satellite/UAV terrestrial non-orthogonal multiple access (NOMA) network, where a satellite aims to communicate with ground users with the aid of a DF UAV relay. Under the influence of hardware impairments, the performance of a UAV-aided-relaying system was studied in [17] based on an amplified and forward (AF) relaying protocol. In addition, the authors of [18] evaluated the performance of a UAV-relaying-assisted wireless network by considering different energy-harvesting techniques for UAVs. Ajam et al. [19] presented the ergodic sum rate analysis of a UAV-based communication system with mixed radio frequency(RF)/free space optics (FSO) channels. In addition, the authors in [20] studied the outage performance of a UAV-based relay in FSO downlink satellite systems under the effect of hovering fluctuation of the links. However, in all these works on the UAV-assisted-relaying network, the physical layer’s security performance was not considered. More recently, the research studies on the security performance of UAV-assisted-relaying networks are gaining more attention in the research community. The security performance of UAV-enabled-relaying NOMA systems under the presence of an eavesdropper was presented in [21]. Furthermore, the secrecy performance of a low altitude UAV-enabled AF relaying network was presented in [22], where a cooperative jammer was adopted to secure the network. The authors of [23] investigated the security of a ground-wiretapped channel for which a UAV was employed to transmit a jammer signal.

1.3. Motivations and Contribution

As stated above, physical layer security has been studied in various UAV-assisted relay communication networks; however, none of the works have considered the spatial locations of the users and eavesdroppers, which motivates the current contribution. In this case, a stochastic geometry theory is employed as a suitable statistical description for the positions of the users and eavesdroppers in the network. This is because the locations of nodes can be treated as completely random according to an HPPP model. In this paper, the secrecy performance of a dual-hop UAV-assisted-relaying network is studied under the presence of randomly distributed non-colluding eavesdroppers. The spatial positions of both the ground user and eavesdroppers follow the HPPP and are modelled by the stochastic geometry approach. It is assumed that the base station to the UAV link follows a Nakagami-m distribution. In addition, the UAV’s connection to the ground user and eavesdroppers follows Rician and Rayleigh fading distributions, respectively. Through this, the CDF of the ground user and the eavesdroppers are derived. Based on these distributions, the network CDF equivalent end-to-end SNR is derived for the proposed network. Thus, the network’s SOP, SPSC, and ASC are obtained to quantify the secrecy performance of the network. The main contributions of this work are summarized as follows:

• The CDF of the UAV with respect to the user and the eavesdroppers’ link are obtained through the stochastic geometric approach.
• The network CDF equivalent end-to-end SNR is derived via the DF relaying protocol.
• The analytical closed-form expressions of the security outage probability and strictly positive secrecy capacity (SPSC) at a lower bound are obtained for the proposed network.
• The exact closed-form expression of the average secrecy capacity is derived for the proposed network.
• With respect to [4], where the secrecy performance of a UAV-assisted-relaying network was studied under the presence of a single eavesdropper, the position of both the ground user and the eavesdropper were not considered. In this paper, the locations of nodes in the network are modeled through a stochastic geometric approach and multiple eavesdroppers are considered.

The rest of this paper is organized as follows. Section 2 illustrates the network description and channels’ model. In Section 3, the CDF equivalent end-to-end SNR for the network is presented based on a stochastic geometry approach. In Section 4, we conduct the secrecy performance analysis of the network. Numerical results and a discussion are detailed in Section 5; finally, conclusions are drawn in Section 6.

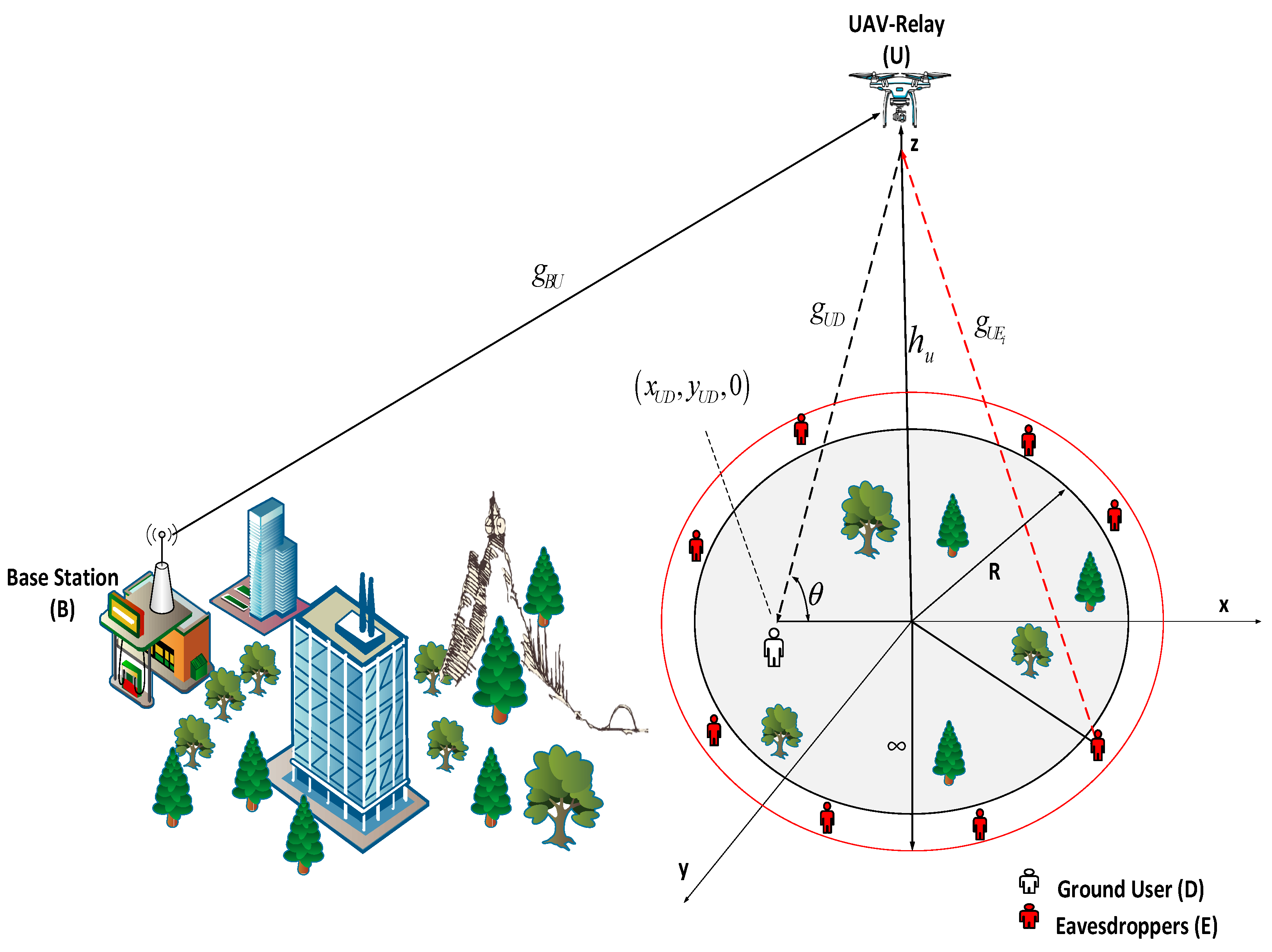
2. Network Description and Channels Model

The network scenario presented in this paper is based on a dual-hop cooperative network where a DF-UAV acts as a relay node between the base station (BS) and the ground user (D) under the presence of randomly distributed eavesdroppers (E), as demonstrated in Figure 1. The UAV is located at a constant height $h_u$ with a coverage radius $R$ wherein the ground user is positioned. In addition, a number of randomly distributed non-colluding eavesdroppers are positioned across the infinite two-dimensional plane with powerful capacities to detect and decode the network’s confidential information. Owning to natural or man-made obstacles such as mountains or high buildings, the wireless link between the BS and the ground user is assumed to be negligible. Thus, it is assumed that the BS-to-UAV link and eavesdroppers-to-UAV link follow the Nakagami-m and Rayleigh fading distributions, respectively, while the UAV-to-user link experiences Rician fading distributions. The spatial positions of the ground user and the eavesdroppers are modeled using the HPPP model. Thus, the overall communication takes place in two phases for the base station to transmit its information to the ground user.

2.1. Base Station-to-UAV Link

During the first phase, the base station transmits its information to the UAV and the received signal at the UAV can be defined as:

$$y_{BU}=\sqrt{P_B}{g}_{BU}{x}_B+n_{BU}$$

(1)

where $P_B$ denotes the base station’s transmission power, $g_{BU}$ is the B-to-UAV channel coefficient and is modeled by using the Nakagami-m fading distribution, $x_B$ signifies the BS information transmitted to the UAV, and $n_{BU}$ indicates the additive white Gaussian noise (AWGN) with zero mean and variance ${\sigma }^2$. Thus, the instantaneous SNR of the link can be obtained as:

$${\gamma }_{BU}=\frac{P_B{\left|g_{BU}\right|}^2}{{\sigma }^2}={\overline{\gamma }}_{BU}{\left|g_{BU}\right|}^2$$

(2)

where ${\overline{\gamma }}_{BU}=P_s/{\sigma }^2$ denotes the average SNR of the link. The channel coefficient $g_{BU}$ is assumed to follow the Nakagami-m fading distribution, and the probability distribution function (PDF) of $f_{{\gamma }_{BU}}$ can be expressed as [8]:

$$f_{{\gamma }_{BU}}\left(\gamma \right)=\frac{{\gamma }^{m_s-1}}{\mathsf{\Gamma }\left(m_s\right){\psi }^{m_s}}\exp \left(-\frac{\gamma }{\psi }\right)$$

(3)

where $\psi ={\overline{\gamma }}_{SR}/m_s$ in which $m_s$ denotes the fading parameter of the base station-to-UAV link. In addition, the CDF of $F_{{\gamma }_{BU}}$ for the link can be defined as:

$$F_{{\gamma }_{BU}}\left(\gamma \right)=1-\exp \left(-\frac{\gamma }{\psi }\right){\displaystyle \sum }_{n=0}^{m_s-1}\frac{{\gamma }^n}{{\psi }^{n}n!}$$

(4)

2.2. UAV-to-User and Eavesdroppers’ Links

In the course of the second hop, the UAV decodes and forwards the source information to the ground user. The signal received by the ground user can be expressed as:

$$y_{UD}=\sqrt{P_U}{g}_{UD}{x}_U+n_{UD}$$

(5)

where $P_U$ is the UAV’s transmission power; $g_{UD}$ is the channel coefficient of the UAV-to destination link, which is model by using the Rician fading distribution; $x_U$ denotes the information transmitted by the UAV to the ground user; and $n_{UD}$ represents the AWGN with zero mean and variance ${\sigma }^2$. During this time, the eavesdroppers thus attempt to intercept the UAV signal and the received signal at the $i\text{-}th$ eavesdropper can be expressed as:

$$y_{U{E}_i}=\sqrt{P_U}{g}_{U{E}_i}{x}_U+n_{U{E}_i}$$

(6)

where $g_{U{E}_i}$ is the channel-fading coefficient of the UAV-to-eavesdroppers links, and $n_{U{E}_i}$ denotes the AWGN at the eavesdroppers with zero mean and variance ${\sigma }^2$. The instantaneous SNR of the ground user can thus be expressed as:

$${\gamma }_{UD}=\frac{P_u{\left|g_{UD}\right|}^2}{{\sigma }^2{d}_{UD}^{{\alpha }_g}}={\overline{\gamma }}_{UD}{\left|g_{UD}\right|}^2$$

(7)

where ${\overline{\gamma }}_{UD}=P_u/{\sigma }^2{d}_{UD}^{{\alpha }_g}$ is the average SNR of the link, in which $d_{UD}$ represents the distance between the ground user and the UAV and ${\alpha }_g$ represents the path loss factor of the UAV-to-ground link. With the coordinates of the ground user and the UAV given as $\left(x_{UD},y_{UD},h_u\right)$ and $\left(0,0,h_u\right),$ respectively, the distance $d_{UD}$ can be expressed as:

$$d_{UD}=\sqrt{x_{UD}^2+y_{UD}^2+h_u^2}$$

(8)

Since non-colluding eavesdroppers are considered in this paper, the instantaneous SNR of the eavesdroppers can be expressed as:

$${\gamma }_{UE}={\overline{\gamma }}_{UE}\underset{Eϵ{\mathsf{\Phi }}_e}{\max }\left\{{\left|g_{U{E}_i}\right|}^2\right\}$$

(9)

where ${\overline{\gamma }}_{UE}=P_u/{\sigma }^2$ is the average SNR of the link.

To achieve a better network performance, it is assumed that there is a LoS between the UAV and the ground user. Thus, the Rican fading distribution is considered to model the channel coefficient $g_{UD}$ and the PDF of $f_{{\gamma }_{UD}}$ can be expressed as [10,14,24]:

$$f_{{\gamma }_{UD}}\left(\gamma \right)=\xi \exp \left(-K\right)\exp \left(-\xi \gamma \right)I_o\left(\sqrt{K\xi \gamma }\right)$$

(10)

where $\xi =d_{SU}^{{\alpha }_g}\left(K+1\right)/{\overline{\gamma }}_{RD}$, while $K$ denotes the Rician fading factor model as a function of the angle $\theta$ between the UAV and the ground user. Based on [25], it follows that $K\left(\theta \right)=a_2\exp \left(b_2\theta \right)$, where $a_2=K\left(0\right)$ and $b_2=\frac{2}{\pi }ln\left(K\left(2/\pi \right)/K\left(0\right)\right)$. In addition, the CDF of $F_{{\gamma }_{UD}}$ for the link can be expressed as:

$$F_{{\gamma }_{UD}}\left(\gamma \right)=1-\exp \left(-K\right){\displaystyle \sum }_{p=0}^{\infty }{\displaystyle \sum }_{q=0}^p\frac{K^p{\xi }^q}{p!q!}{\gamma }^q\exp \left(-\xi \gamma \right)$$

(11)

Furthermore, the channel-fading coefficient $g_{U{E}_i}$ for the UAV-to-eavesdroppers is assumed to follow Rayleigh fading distributions and the CDF of $F_{{\gamma }_{UE}}\left(\gamma \right)$ can be expressed as [26]:

$$F_{{\gamma }_{UE}}\left(\gamma \right)=1-\exp \left(-\frac{\gamma }{{\overline{\gamma }}_{U{E}_i}}\right)$$

(12)

3. Statistical Characteristics of Equivalent SNR

Owing to the spatial location of the ground user and the eavesdroppers, the stochastic geometry approach is applied to describe their locations in a particular environment. Therefore, based on this theory, new channel statistics are derived for the user and the eavesdroppers in order to obtain the network’s CDF equivalent end-to-end SNR. In this case, the distribution of the ground user is modeled by HPPP ${\beth }_D$, which provides information about the user position $w_D$, and the corresponding PDF can be defined as [27]:

$$f_{w_D}\left(w_D\right)=\frac{1}{\pi R^2}$$

(13)

Hence, the CDF of ${\left|g_{UD}\right|}^2$ can be expressed as:

$${\overline{F}}_{{\gamma }_{UD}}\left(\gamma \right)=\underset{{\beth }_U}{\overset{ }{{\displaystyle \int }}}\left(1-{\displaystyle \sum }_{p=0}^{\infty }{\displaystyle \sum }_{q=0}^p\frac{K^p{\xi }^q{\gamma }^q{\left(1+r^{{\alpha }_g}\right)}^q}{\exp \left(K\right)p!q!}\exp \left(-\xi \gamma \left(1+r^{{\alpha }_g}\right)\right)\right)f_{w_D}\left(w_D\right)d{w}_D$$

$$\triangleq 1-\frac{2}{R^2}{{\displaystyle \int }}_0^R\exp \left(-K\right){\displaystyle \sum }_{p=0}^{\infty }{\displaystyle \sum }_{q=0}^p\frac{K^p{\xi }^q}{p!q!}{\gamma }^{q}r{\left(1+r^{{\alpha }_g}\right)}^q\exp \left(-\xi \gamma \left(1+r^{{\alpha }_g}\right)\right)dr$$

(14)

Based on the binomial expansion given in ([28], Equation (1.111)), ${\left(1+r^{{\alpha }_g}\right)}^q={\displaystyle \sum }_{t=0}^q\left(\begin{array}{c}q\\ t\end{array}\right)r^{q{\alpha }_g}$; therefore, (14) can be further expressed as:

$${\overline{F}}_{{\gamma }_{UD}}\left(\gamma \right)=1-\frac{2}{R^2}\exp \left(-K\right){\displaystyle \sum }_{p=0}^{\infty }{\displaystyle \sum }_{q=0}^p{\displaystyle \sum }_{t=0}^q\left(\begin{array}{c}q\\ t\end{array}\right)\frac{K^p{\xi }^q}{p!q!}\exp \left(-\xi \gamma \right){\gamma }^q\underset{0}{\overset{R}{{\displaystyle \int }}}{r}^{q{\alpha }_g+1}\exp \left(-\xi \gamma r^{{\alpha }_g}\right)dr$$

(15)

By applying (3.381.8) of [28], the CDF in (15) can be solved as:

$${\overline{F}}_{{\gamma }_{UD}}\left(\gamma \right)=1-\frac{2}{R^2}\exp \left(-K\right){\displaystyle \sum }_{p=0}^{\infty }{\displaystyle \sum }_{q=0}^p{\displaystyle \sum }_{t=0}^q\left(\begin{array}{c}q\\ t\end{array}\right)\frac{K^p{\xi }^{q-\lambda }}{p!q!{\alpha }_g}\exp \left(-\xi \gamma \right){\gamma }^{q-\lambda }\mathsf{{\rm Y}}\left(\lambda ,\xi \gamma R^{{\alpha }_g}\right)$$

(16)

where $\lambda =\left({\alpha }_{g}q+2\right)/{\alpha }_g$ and $\mathsf{{\rm Y}}\left(.,.\right)$ denotes the lower incomplete Gamma function.

Similarly, the eavesdroppers are distributed according to the independent HPPP ${\mathsf{\Phi }}_e$ with a density ${\rho }_e$; the CDF of ${\left|g_{UE}\right|}^2$ can be expressed as:

$${\overline{F}}_{{\gamma }_{UE}}\left(\gamma \right)={\mathsf{{\rm E}}}_{{\mathsf{\Phi }}_e}\left\{{\displaystyle \prod }_{iϵ{\mathsf{\Phi }}_e}{F}_{U{E}_i}\left(\gamma \right)\right\}$$

(17)

By applying a probability-generating function for the HPPP ${\mathsf{\Phi }}_e$, the CDF can be expressed as:

$${\overline{F}}_{{\gamma }_{UE}}\left(\gamma \right)=\exp \left[-{{\displaystyle \int }}_{R^2}^{ }\left(1-F_{UE}\left(\gamma \right)\right)rdr\right]$$

(18)

By placing (12) into (18), (18) can be expressed as:

$${\overline{F}}_{{\gamma }_{UE}}\left(\gamma \right)=\exp \left[-2\pi {\rho }_e\underset{0}{\overset{\infty }{{\displaystyle \int }}}r\exp \left(-\frac{\gamma }{{\overline{\gamma }}_{UE}}{r}^{{\alpha }_g}\right)dr\right]$$

(19)

By utilizing the (3.325.2) of [28] given as ${\displaystyle {{\displaystyle \int }}_0^{\infty }}{x}^j\exp \left(-\tau x^t\right)=\mathsf{\Gamma }\left(\mathsf{{\rm E}}\right)/t{\tau }^{\mathsf{{\rm E}}}$ with $\mathsf{{\rm E}}=\left(j+1\right)/t$, Equation (19) can be solved as:

$${\overline{F}}_{{\gamma }_{UE}}\left(\gamma \right)=\exp \left[-{\eta }_e{\gamma }^{-\beta }\right]$$

(20)

where ${\eta }_e=\frac{2\pi {\rho }_e}{{\alpha }_g}{\overline{\gamma }}_{UE}^{\beta }\mathsf{\Gamma }\left(\beta \right)$, $\beta =2/{\alpha }_g$ and $\mathsf{\Gamma }\left(.\right)$ denotes the Gamma function.

In addition, the PDF of the link can be obtained by determining the derivative of the CDF given in (20) as:

$${\overline{f}}_{{\gamma }_{UE}}\left(\gamma \right)=\frac{d{\overline{F}}_{UE}\left(\gamma \right)}{d\gamma }$$

$$\triangleq \beta {\eta }_e\exp \left[-{\eta }_e{\gamma }^{-\beta }\right]{\gamma }^{-\beta -1}$$

(21)

Thus, the CDF equivalent end-to-end SNR of the ground user for the proposed network can be defined as [29,30]:

$$F_{{\gamma }_{eq}}\left(\gamma \right)=F_{{\gamma }_{BU}}\left(\gamma \right)+{\overline{F}}_{{\gamma }_{UD}}\left(\gamma \right)-F_{{\gamma }_{BU}}\left(\gamma \right){\overline{F}}_{{\gamma }_{UD}}\left(\gamma \right)$$

(22)

By putting (4) and (16) into (22), the equivalent end-to-end SNR can be obtained as:

$$F_{{\gamma }_{eq}}\left(\gamma \right)=1-\frac{2\exp \left(-K\right)}{R^2}{\displaystyle \sum }_{p=0}^{\infty }{\displaystyle \sum }_{q=0}^p{\displaystyle \sum }_{t=0}^q{\displaystyle \sum }_{n=0}^{m-1}\left(\begin{array}{c}q\\ t\end{array}\right)\frac{K^p{\xi }^{q-\lambda }}{p!q!n!{\alpha }_g{\psi }^n}\times \exp \left(-\left(\frac{1+\xi \psi }{\psi }\right)\gamma \right){\gamma }^{q+n-\lambda }\mathsf{{\rm Y}}\left(\lambda ,\xi \gamma R^{{\alpha }_g}\right)$$

(23)

4. Secrecy Performance Analysis

In this section, the secrecy performance of the proposed network is characterized in terms of the SOP, SPSC, and ASC. Thus, the closed expressions for each are obtained through the CDF equivalent end-to-end SNR.

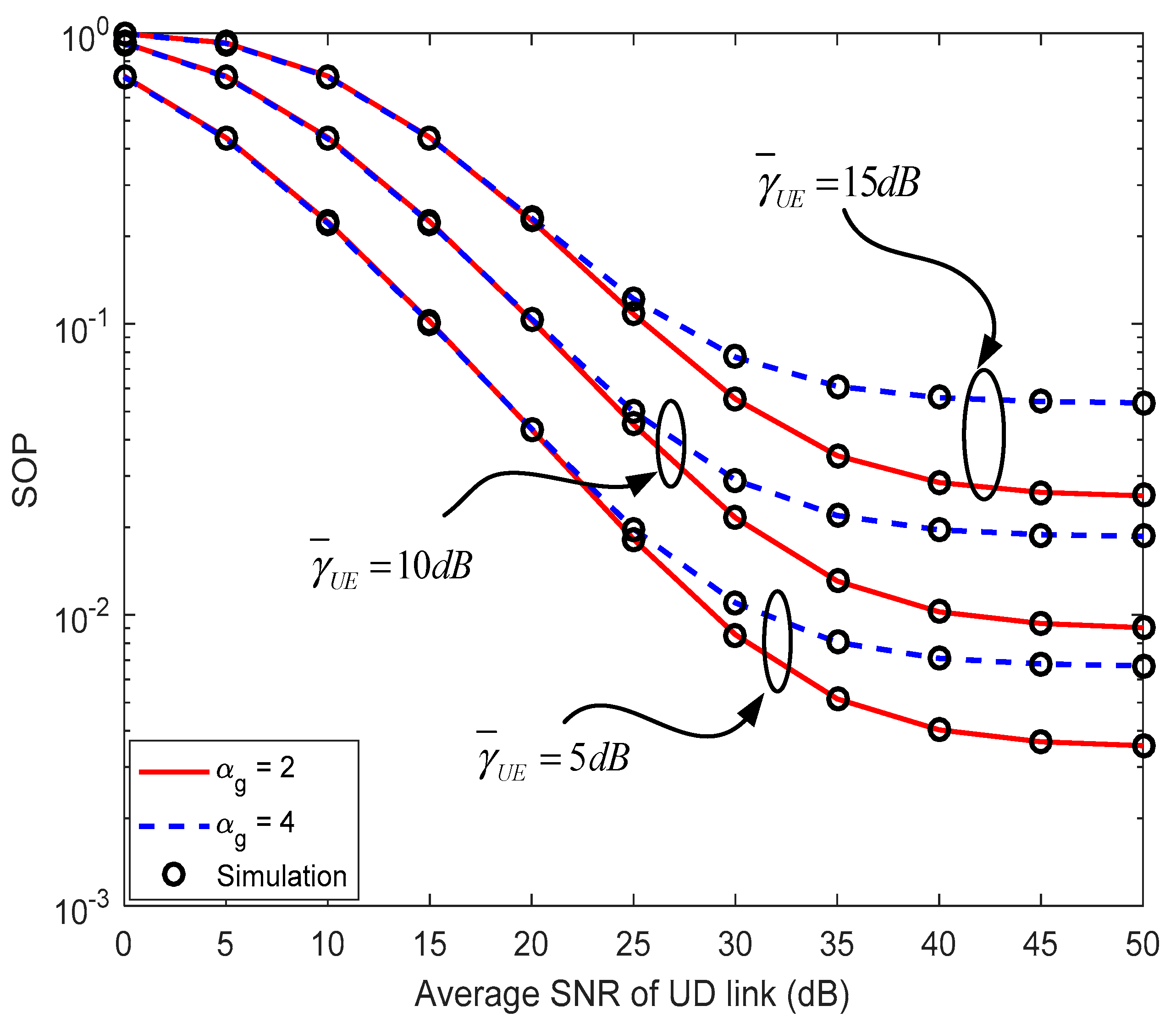
4.1. Secrecy Outage Probability (SOP)

In a wireless network, perfect secrecy is obtainable only if the value of the instantaneous secrecy capacity $C_s$ is higher than the predetermined threshold secrecy rate $R_s$; otherwise, an outage occurs. Thus, the lower bound SOP expression for the network can be defined as [31,32]:

$$SOP=\underset{0}{\overset{\infty }{{\displaystyle \int }}}{F}_{eq}\left(\gamma \phi \right){\overline{f}}_{EU}\left(\gamma \right)d\gamma$$

(24)

where $\phi =\exp \left(R_s\right)$.

By putting (23) and (21) into (24), the SOP of the system can be defined as:

$$SOP=1-\frac{2\beta {\eta }_e\exp \left(-K\right)}{R^2}{\displaystyle \sum }_{p=0}^{\infty }{\displaystyle \sum }_{q=0}^p{\displaystyle \sum }_t^q{\displaystyle \sum }_{n=0}^{m_s-1}\left(\begin{array}{c}q\\ t\end{array}\right)\frac{K^p{\xi }^{q-\lambda }{\phi }^{q+n+z}}{p!q!n!{\alpha }_g{\psi }^n}$$

$$\times \underset{0}{\overset{\infty }{{\displaystyle \int }}}{\gamma }^{q+n-\lambda -\beta -1}\exp \left(-{\eta }_e{\gamma }^{-\beta }\right)\exp \left(-\left(\frac{1+\xi \psi }{\psi }\right)\phi \gamma \right)\mathsf{{\rm Y}}\left(\lambda ,\xi \gamma R^{{\alpha }_g}\right)d\gamma$$

(25)

By converting the exponential functions to a Meijer-G function through (11) of [33] and using the infinite series of the lower incomplete gamma function detailed in ([28], Equation (8.354(1)), the SOP can be further expressed as:

$$SOP=1-\frac{2\beta {\eta }_e\exp \left(-K\right)}{R^2}{\displaystyle \sum }_{p=0}^{\infty }{\displaystyle \sum }_{z=0}^{\infty }{\displaystyle \sum }_{q=0}^p{\displaystyle \sum }_{t=0}^q{\displaystyle \sum }_{n=0}^{m_s-1}\left(\begin{array}{c}q\\ t\end{array}\right)\frac{{\left(-1\right)}^z{K}^p{\xi }^{q-\lambda }{\left(\xi R^{{\alpha }_g}\right)}^{\lambda +z}{\phi }^{q+n+z}}{p!q!n!z!{\alpha }_g{\psi }^n\left(\lambda +z\right)}$$

$$\times \underset{0}{\overset{\infty }{{\displaystyle \int }}}{\gamma }^{q+n+z-\beta -1}{G}_{0,1}^{1,0}\left(\left(\frac{1+\xi \psi }{\psi }\right)\phi \gamma |\begin{array}{c}-\\ 0\end{array}\right)G_{1,0}^{0,1}\left(\frac{{\gamma }^{\beta }}{{\eta }_e}|\begin{array}{c}1\\ -\end{array}\right)d\gamma$$

(26)

By employing (21) of [33], the integral in (26) can be solved as:

$$SOP=1-\frac{2{\eta }_e\exp \left(-K\right)}{R^2{\left(\sqrt{2\pi }\right)}^{\beta -1}}{\displaystyle \sum }_{p=0}^{\infty }{\displaystyle \sum }_{z=0}^{\infty }{\displaystyle \sum }_{q=0}^p{\displaystyle \sum }_{t=0}^q{\displaystyle \sum }_{n=0}^{m_s-1}\left(\begin{array}{c}q\\ t\end{array}\right)\frac{{\left(-1\right)}^z{K}^p{\xi }^{q-\lambda }{\left(\xi R^{{\alpha }_g}\right)}^{\lambda +z}{\phi }^{q+n+z}}{p!q!n!z!{\alpha }_g{\psi }^n\left(\lambda +z\right)}$$

$$\times {\beta }^{q+n+z-\beta -1}{\left(\left(\frac{1+\xi \psi }{\psi }\right)\phi \right)}^{-\left(q+n+z-\beta \right)}{G}_{1+\beta , 0}^{0, 1+\beta }\left(\frac{{\psi }^{\beta }}{{\eta }_e{\left(\phi \left(1+\xi \psi \right)\right)}^{\beta }}|\begin{array}{c}1, \mathsf{\Delta }\left(\beta ,1+\beta -q-n-z\right)\\ -\end{array}\right)$$

(27)

where $\mathsf{\Delta }\left(s,v\right)=\frac{v}{s},\frac{v+1}{s},\dots ,\frac{v+s-1}{s}$.

If we assume the path loss ${\alpha }_a=2$; thus, $\beta =1$ and Equation (27) can be expressed as:

$$SOP=1-\frac{2\beta {\eta }_e\exp \left(-K\right)}{R^2}{\displaystyle \sum }_{p=0}^{\infty }{\displaystyle \sum }_{z=0}^{\infty }{\displaystyle \sum }_{q=0}^p{\displaystyle \sum }_{t=0}^q{\displaystyle \sum }_{n=0}^{m_s-1}\left(\begin{array}{c}q\\ t\end{array}\right)\frac{{\left(-1\right)}^z{K}^p{\xi }^{q-\lambda }{\left(\xi R^{\alpha }\right)}^{\lambda +z}{\phi }^{q+n+z}}{p!q!n!z!\alpha {\psi }^n\left(\lambda +z\right)}$$

$$\times {\left(\left(\frac{1+\xi \psi }{\psi }\right)\phi \right)}^{-\left(q+n+z-\beta \right)}{G}_{2,0}^{0,2}\left(\frac{\psi }{{\eta }_e\phi \left(1+\xi \psi \right)}|\begin{array}{c}1, 1-q-n-z+\beta \\ -\end{array}\right)$$

(28)

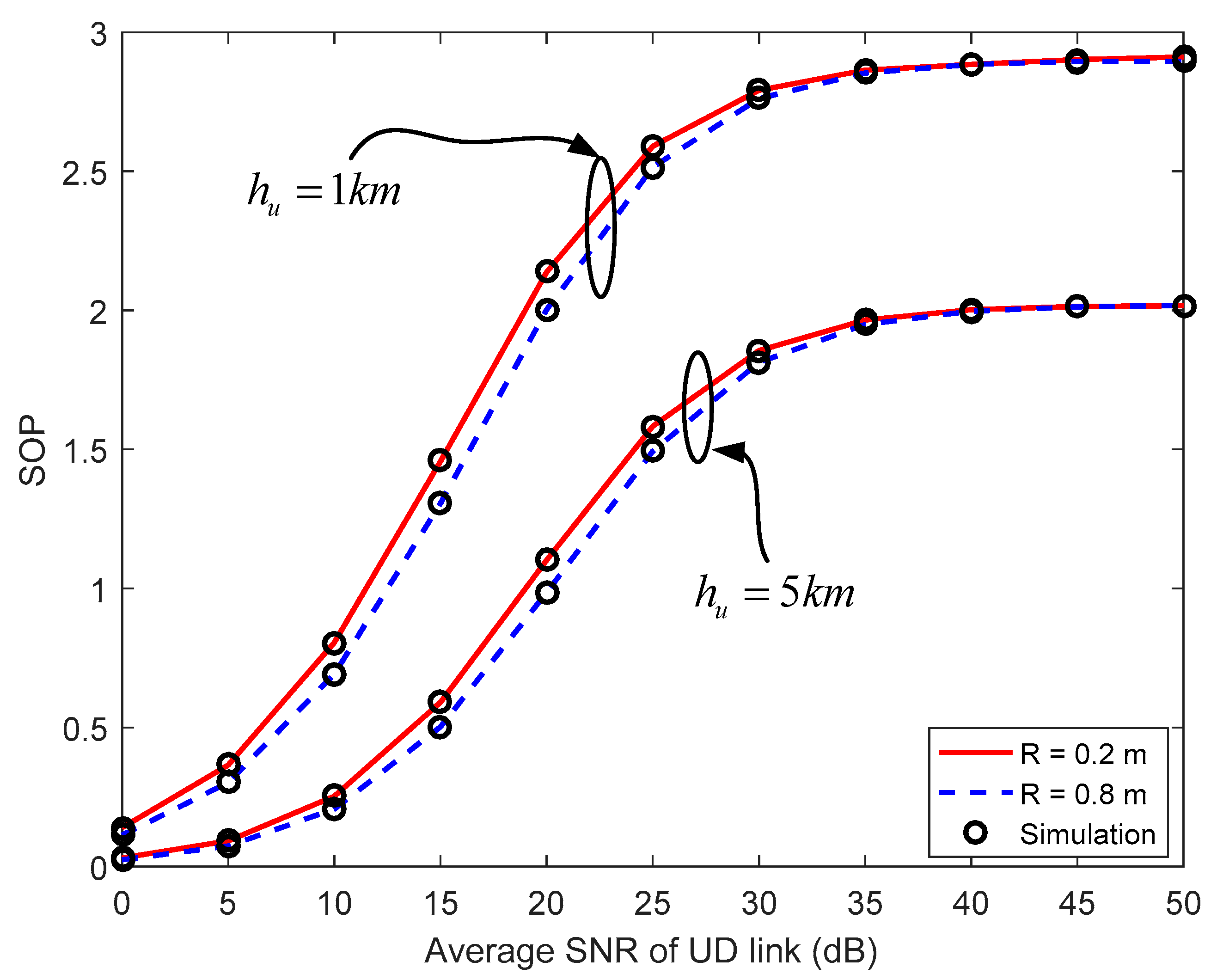
4.2. Strictly Positive Secrecy Capacity (SPSC)

In a secure network, the SPSC is another performance secrecy measure that is realizable only if the secrecy capacity holds a positive quantity, which is when the main link becomes superior to the eavesdropper’s link. Mathematically, it can be expressed as [34]:

$$SPSC=Pr\left({\gamma }_{eq}>\gamma \right)$$

$$\triangleq 1-\underset{0}{\overset{\infty }{{\displaystyle \int }}}{F}_{eq}\left(\gamma \right){\overline{f}}_{EU}\left(\gamma \right)d\gamma$$

(29)

Hence,

$$SPSC=1-SOP, \mathrm{for} \phi =1$$

(30)

Putting (27) into (30), the network SPSC can be derived as:

$$SPSC=\frac{2{\eta }_e\exp \left(-K\right)}{R^2{\left(\sqrt{2\pi }\right)}^{\beta -1}}{\displaystyle \sum }_{p=0}^{\infty }{\displaystyle \sum }_{z=0}^{\infty }{\displaystyle \sum }_{q=0}^p{\displaystyle \sum }_{t=0}^q{\displaystyle \sum }_{n=0}^{m_s-1}\left(\begin{array}{c}q\\ t\end{array}\right)\frac{{\left(-1\right)}^z{K}^p{\xi }^{q-\lambda }{\left(\xi R^{{\alpha }_g}\right)}^{\lambda +z}}{p!q!n!z!{\alpha }_g{\psi }^n\left(\lambda +z\right)}{\beta }^{q+n+z-\beta -1}$$

$$\times {\left(\frac{1+\xi \psi }{\psi }\right)}^{-\left(q+n+z-\beta \right)}{G}_{1+\beta , 0}^{0, 1+\beta }\left(\frac{{\psi }^{\beta }}{{\eta }_e{\left(1+\xi \psi \right)}^{\beta }}|\begin{array}{c}1, \mathsf{\Delta }\left(\beta ,1+\beta -q-n-z\right)\\ -\end{array}\right)$$

(31)

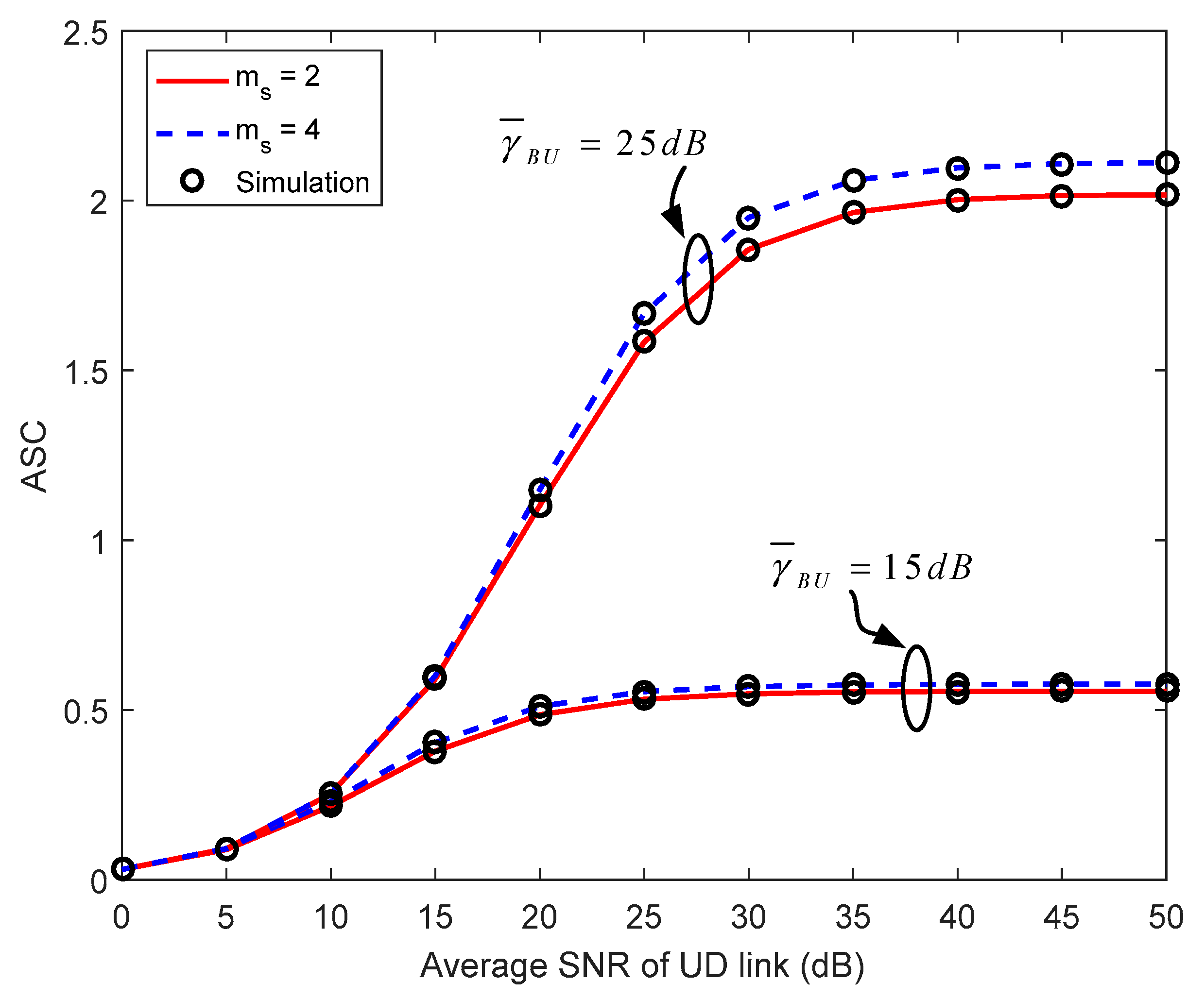
4.3. Average Secrecy Capacity

This is an important metric for evaluating the secrecy performance of active eavesdroppers and can be expressed as [32,35]:

$$C_s=\underset{0}{\overset{\infty }{{\displaystyle \int }}}\frac{{\overline{F}}_{UE}\left(\gamma \right)}{1+\gamma }\left(1-F_{eq}\left(\gamma \right)\right)d\gamma$$

(32)

By substituting (20) and (23) into (32), the system security capacity can be defined as:

$$C_s=\frac{2\exp \left(-K\right)}{R^2}{\displaystyle \sum }_{p=0}^{\infty }{\displaystyle \sum }_{q=0}^p{\displaystyle \sum }_t^q{\displaystyle \sum }_{n=0}^{m_s-1}\left(\begin{array}{c}q\\ t\end{array}\right)\frac{K^p{\xi }^{q-\lambda }}{p!q!n!{\alpha }_g{\psi }^n}$$

$$\times \underset{0}{\overset{\infty }{{\displaystyle \int }}}\frac{{\gamma }^{q+n-\lambda }}{1+\gamma }\exp \left(-{\eta }_e{\gamma }^{-\beta }\right)\exp \left(-\left(\frac{1+\xi \psi }{\psi }\right)\gamma \right)\mathsf{{\rm Y}}\left(\lambda ,\xi \gamma R^{{\alpha }_g}\right)d\gamma$$

(33)

By employing Taylor’s series expansion, $\exp \left(-{\eta }_e{\gamma }^{-\beta }\right)={\displaystyle \sum }_{k=0}^{\infty }\frac{{\left(-1\right)}^k}{k!}{\left(\frac{{\eta }_e}{{\gamma }^{\beta }}\right)}^k$, (33) can be expressed as:

$$C_s=\frac{2\exp \left(-K\right)}{R^2}{\displaystyle \sum }_{p=0}^{\infty }{\displaystyle \sum }_{k=0}^{\infty }{\displaystyle \sum }_{q=0}^p{\displaystyle \sum }_{t=0}^q{\displaystyle \sum }_{n=0}^{m_s-1}\left(\begin{array}{c}q\\ t\end{array}\right)\frac{{\left(-1\right)}^k{K}^p{\xi }^{q-\lambda }{\eta }_e{}^k}{p!q!n!k!{\alpha }_g{\psi }^n}$$

$$\times \underset{0}{\overset{\infty }{{\displaystyle \int }}}\frac{{\gamma }^{q+n-\lambda -\beta k}}{1+\gamma }\exp \left(-\left(\frac{1+\xi \psi }{\psi }\right)\gamma \right)\mathsf{{\rm Y}}\left(\lambda ,\xi \gamma R^{{\alpha }_g}\right)d\gamma$$

(34)

By using (10) and (11) of [33] and (8.4.16.1) of [36], Equation (34) can be expressed in terms of the Meijer-G function, as follows:

$$C_s=\frac{2\exp \left(-K\right)}{R^2}{\displaystyle \sum }_{p=0}^{\infty }{\displaystyle \sum }_{k=0}^{\infty }{\displaystyle \sum }_{q=0}^p{\displaystyle \sum }_{t=0}^q{\displaystyle \sum }_{n=0}^{m_s-1}\left(\begin{array}{c}q\\ t\end{array}\right)\frac{{\left(-1\right)}^k{K}^p{\xi }^{q-\lambda }{\eta }_e{}^k}{p!q!n!k!{\alpha }_g{\psi }^n}$$

$$\times \underset{0}{\overset{\infty }{{\displaystyle \int }}}{G}_{1,1}^{1,1}\left(\gamma |\begin{array}{c}q+n-\lambda -\beta k\\ q+n-\lambda -\beta k\end{array}\right)G_{0,1}^{1,0}\left(\mho \gamma |\begin{array}{c}-\\ 0\end{array}\right)G_{1,2}^{1,1}\left(\xi R^{{\alpha }_g}\gamma |\begin{array}{c}1\\ \lambda , 0\end{array}\right)d\gamma$$

(35)

where $\mho =\frac{\left(1+\xi \psi \right)}{\psi }$.

By applying (20) of [37], the network average secrecy capacity can be obtained as:

$$C_s=\frac{2\exp \left(-K\right)}{R^2}{\displaystyle \sum }_{p=0}^{\infty }{\displaystyle \sum }_{k=0}^{\infty }{\displaystyle \sum }_{q=0}^p{\displaystyle \sum }_{t=0}^q{\displaystyle \sum }_{n=0}^{m_s-1}\left(\begin{array}{c}q\\ t\end{array}\right)\frac{{\left(-1\right)}^k{K}^p{\xi }^{q-\lambda }{\eta }_e{}^k}{p!q!n!k!{\alpha }_g{\psi }^n\mho }$$

$$\times G_{1,0:1,1:1,2}^{1,0:1,1:1,1}\left(\begin{array}{c}1\\ -\end{array}|\left.\begin{array}{c}q+n-\lambda -\beta k\\ q+n-\lambda -\beta k\end{array}\right|\left.\begin{array}{c}1\\ \lambda , 0\end{array}\right| \frac{1}{\mho },\frac{\xi R^{{\alpha }_g}}{\mho }\right)$$

(36)

5. Numerical Results and Discussion

In this section, the numerical results are provided to quantify the security performance of the proposed UAV-assisted wireless network based on the derived exact analytical expressions of the SOP, SPSC, and ASC. In addition, Monte-Carlo simulations are conducted to validate the correctness of the derived analytical expressions. Except where otherwise stated, the target rate $R_s=0.1 b/s/Hz$, path loss factor ${\alpha }_g=2$, fading parameter of BS-to-U link $m_s=2$, $R=0.2 \mathrm{m}$, and the coordinate position of the ground user is set to $\left(2,1,0\right)$.

The SOP performance of the proposed network under the influence of the fading parameters of the BS-to-U link and the link average SNR is presented in Figure 2. The results show that the greater the increase in both the $m_s$ and ${\overline{\gamma }}_{BU}$ of the link, the better the network secrecy performance. This is because a high value of $m_s$ denotes a better channel condition and at a high value of ${\overline{\gamma }}_{BU}$ more power is used for information transmission. In addition, at a low average SNR of the $UD$ link, the results show that there is no significant change in the network secrecy performance at any value of $m_s$. This is because no information is leaked to the eavesdroppers as a of result the low transmission power to the ground user. In addition, it can be observed that the simulation results perfectly agreed with the analytical results, which proves the correctness of the derived analytical expression.

The impact of the UAV’s altitude and the density of the eavesdropper on the network SOP performance is depicted in Figure 3. It can be noticed that the network has a worse SOP performance at a high altitude compared to a lower altitude position. This shows that a better SOP can be achieved at a low UAV altitude. In addition, as the density of eavesdroppers increased within the network, the network SOP deteriorated to a greater extent. This is because a large value of ${\rho }_e$ indicates more eavesdroppers within a fixed range and a higher probability of information leakage.

In Figure 4, the effect of the UAV coverage under different UAV altitudes is illustrated. It can be deduced that the network SOP is improved with a decrease in the UAV’s altitude. In addition, the results depict that the SOP of the network degraded with an increase in the value of the UAV coverage radius $R$ due to the closeness of the user to the eavesdroppers. Moreover, there is perfect collaboration between the simulation results and the analytical results, which validates the accuracy of the derived expression.

The influence of the average SNR at the eavesdroppers and the path loss exponent on the network SOP is demonstrated in Figure 5. The results show that the network SOP deteriorates as the eavesdroppers’ average SNR increases. This is because of the power utilized by the eavesdroppers to decode the UAV’s information. In addition, it can be noticed that the network secrecy performance worsens as the value of ${\alpha }_g$ increases. This is because a high of value of ${\alpha }_g$ indicates an unfavorable condition of the UAV channel.

The SPSC performance of the proposed network is presented in Figure 6 under different densities of the eavesdroppers at under different UAV coverage radii. It can be deduced from the results that the larger the density of eavesdroppers, the larger the SPSC network and the more information is leaked to the eavesdroppers. The results also show that the network SPSC improves with the decrease in the UAV coverage radius $R$, as the user is far away from the eavesdroppers.

The impact of the eavesdroppers’ average SNR at different UAV altitudes is presented in Figure 7. It can be noticed from the results that the network SPSC performance deteriorates with the increase in the eavesdroppers’ average SNR since more power is used by the eavesdroppers to decode network information. In addition, at a lower UAV altitude, a better SPSC performance is achieved due to the lower path loss experienced by the UAV.

The performance of the system’s ASC at different values of $m_s$ and ${\overline{\gamma }}_{BU}$ of the BS-to-U link is demonstrated in Figure 8. The results show that the increase in the value of ${\overline{\gamma }}_{BU}$ enhances the ASC performance of the network. In addition, the results depict that a better ASC performance is achieved at a high value of $m_s$ since the link experiences a weak fading condition. In addition, it is observed that the simulation results agreed with the analytical results, which proves the accuracy of the derived expression. Moreover, at a low value of the average SNR of the UD link, there is no significant variation in the network secrecy performance, which indicates that no information is leaked to the eavesdropper due to the low transmission power of the UAV to the ground user.

In Figure 9, the influence of the UAV’s altitude and coverage on the network ASC performance is illustrated. The results show that the increase in the UAV altitude significantly degrades the network ASC performance owing to the increase in path loss at high altitude. In addition, superior ASC performance is observed as the UAV coverage radius decreases since the user is far from the interception point of the eavesdroppers.

The impact of the path loss exponent on the network ASC performance is depicted in Figure 10. The results show that the network performance degrades as the path loss exponent of the UAV link to the ground increases, leading to a high fading condition for the network.

6. Conclusions

This paper studied the secrecy performance of a dual-hop UAV-assisted-relaying network with randomly distributed non-colluding eavesdroppers. It is assumed that the position of both the ground user and eavesdroppers follow the HPPP model. Based on a DF relaying protocol, the equivalent end-to-end distribution at the ground user was derived. Thus, the closed-form expressions of the network SOP, SPSC, and ASC were derived. A Monte-Carlo simulation was provided to verify the correctness of the derived expressions. The results demonstrated that the network and channel parameters such as the fading parameter $m_s$, density of eavesdroppers ${\rho }_e$, average SNR of the B-to-U link ${\overline{\gamma }}_{BU}$, average SNR of U-to-E link ${\overline{\gamma }}_{UE}$, UAV altitude $h_u$, and UAV coverage $R$ exhibit significant effects on the secrecy performance of the UAV-assisted wireless network.