Mixed Electric Field of Multi-Shaft Ship Based on Oxygen Mass Transfer Process under Turbulent Conditions
Abstract
:1. Introduction
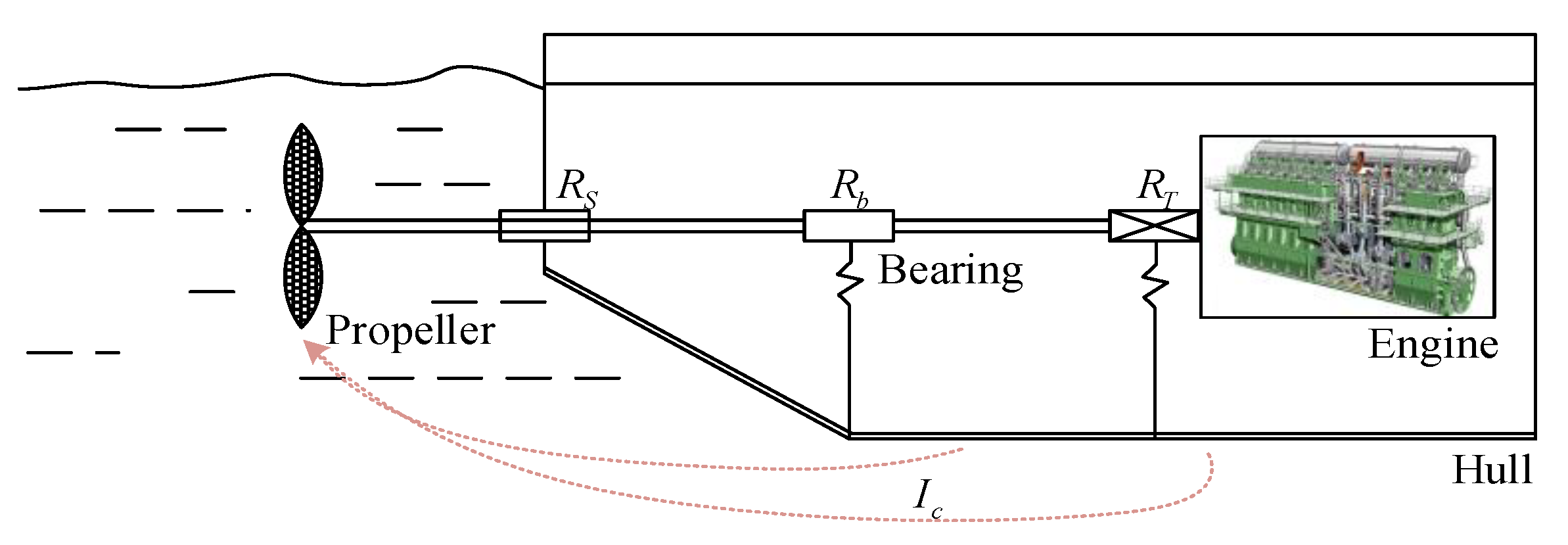
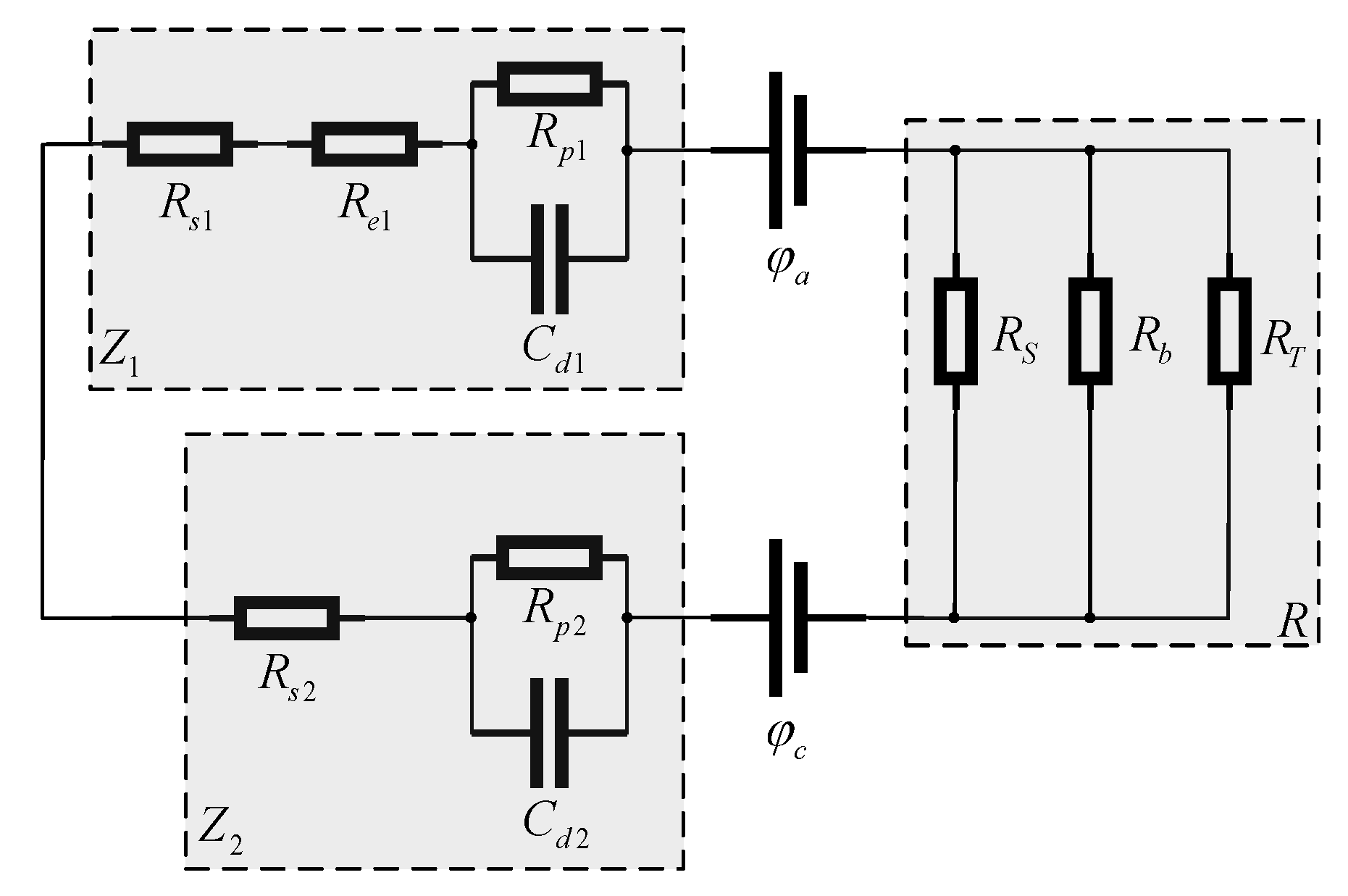
2. Equivalent Model of Shafting Mechanical Structure
3. Ship’s Electric Field Model
3.1. Turbulence Physics Modeling
3.2. Modeling for Mass Transfer of Oxygen
3.3. Modeling for a Ship’s Electric Field with the Boundary Element Method
4. Simulation Analysis
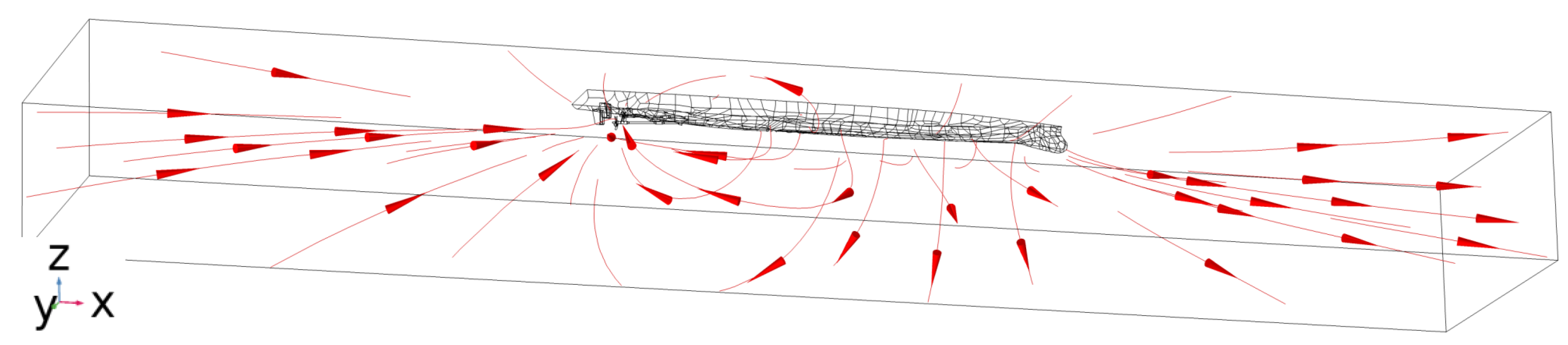
4.1. Ship Surface Flow Rate and Oxygen Concentration Distribution
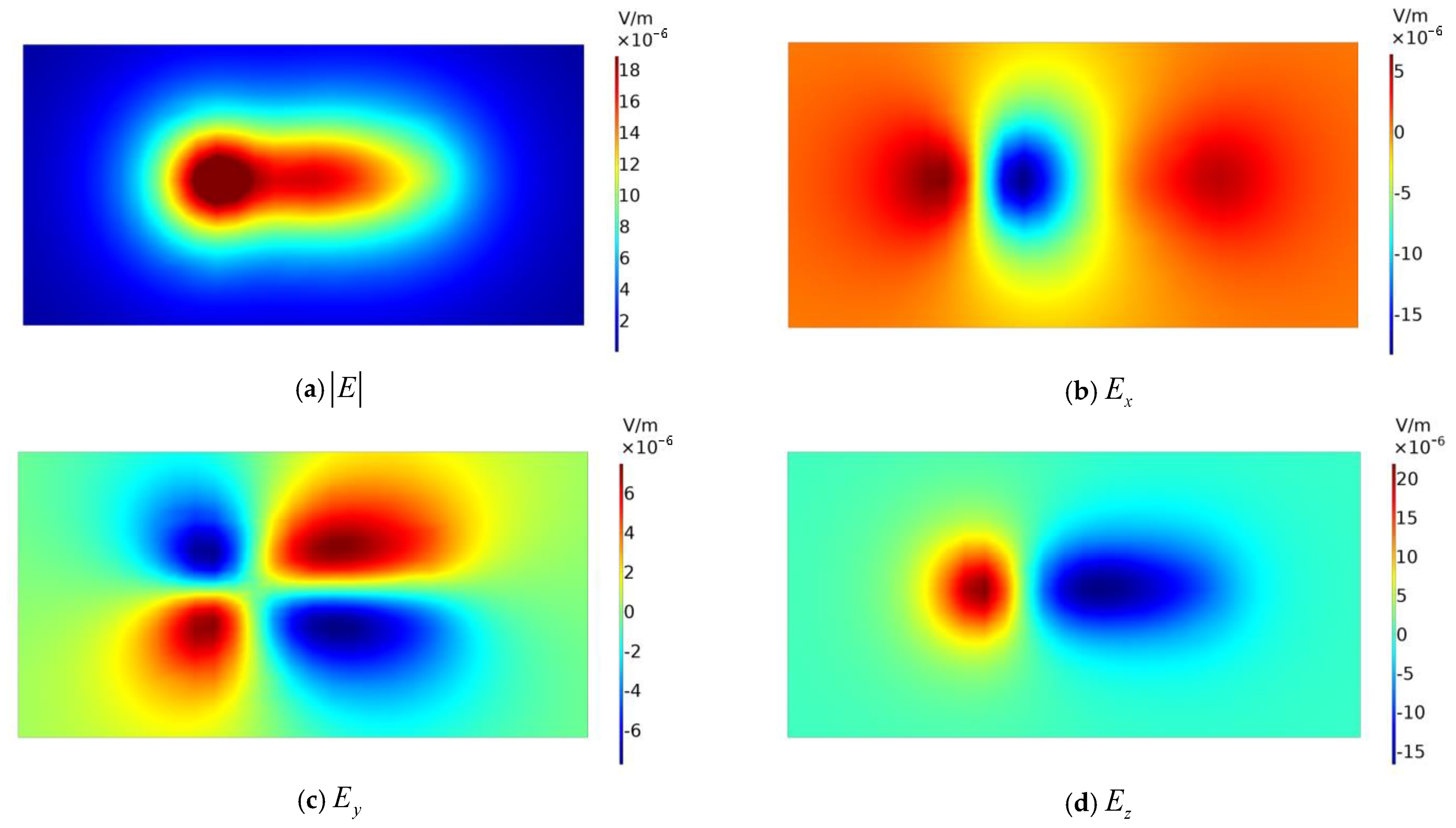
4.2. Ship’s Electric Field Distribution
5. Experiment
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yu, P.; Cheng, J.; Zhang, J. Ship target tracking using underwater electric field. Prog. Electromagn. Res. M 2019, 86, 49–57. [Google Scholar] [CrossRef] [Green Version]
- Xu, Q.; Wang, X.; Tong, Y.; Song, Y. The effect of hydrostatic pressure on corrosion electric field considering the mechanochemical coupling effect. Chem. Phys. Lett. 2020, 754, 137761. [Google Scholar] [CrossRef]
- Guibert, A.; Coulomb, J.-L.; Chadebec, O.; Rannou, C. Corrosion Diagnosis of a Ship Mock-Up from Near Electric-Field Measurements. IEEE Trans. Magn. 2010, 46, 3205–3208. [Google Scholar] [CrossRef] [Green Version]
- Kim, Y.S.; Lee, S.K.; Kim, J.G. Influence of anode location and quantity for the reduction of underwater electric fields under cathodic protection. Ocean Eng. 2018, 163, 476–482. [Google Scholar] [CrossRef]
- Zakowski, K.; Iglinski, P.; Orlikowski, J.; Darowicki, K.; Domanska, K. Modernized cathodic protection system for legs of the production rig—Evaluation during ten years of service. Ocean Eng. 2020, 218, 108074. [Google Scholar] [CrossRef]
- Choe, S.-B.; Lee, S.-J. Effect of flow rate on electrochemical characteristics of marine material under seawater environment. Ocean Eng. 2017, 141, 18–24. [Google Scholar] [CrossRef]
- Kim, J.-H.; Kim, Y.-S.; Kim, J.-G. Cathodic protection criteria of ship hull steel under flow condition in seawater. Ocean Eng. 2016, 115, 149–158. [Google Scholar] [CrossRef]
- Traverso, P.; Canepa, E. A review of studies on corrosion of metals and alloys in deep-sea environment. Ocean Eng. 2014, 87, 10–15. [Google Scholar] [CrossRef]
- Kim, Y.S.; Lee, S.K.; Chung, H.J.; Kim, J.G. Influence of a simulated deep sea condition on the cathodic protection and electric field of an underwater vehicle. Ocean Eng. 2018, 148, 223–233. [Google Scholar] [CrossRef]
- Zhang, J.; Yu, P.; Jiang, R.; Xie, T. Real-time localization for underwater equipment using an extremely low frequency electric field. Def. Technol. 2022. [Google Scholar] [CrossRef]
- Yu, P.; Cheng, J.; Jiang, R. Inversion of UEP signatures induced by ships based on PSO method. Def. Technol. 2020, 16, 172–177. [Google Scholar]
- Chung, H.; Yang, C.; Jeung, G.; Jeon, J.; Kim, D.H. Accurate Prediction of Unknown Corrosion Currents Distributed on the Hull of a Naval Ship Utilizing Material Sensitivity Analysis. IEEE Trans. Magn. 2011, 47, 1282–1285. [Google Scholar] [CrossRef]
- Jiang, R.; Chen, G.; Zhang, J. Ship Electric Fields and Their Applications; Defense Industry Press: Beijing, China, 2021. [Google Scholar]
- Zhang, J.; Wang, X. Electric field induced by omni-dirctional electric dipole rotating in three layers medium. J. Detect. Control 2019, 45, 30–33. [Google Scholar]
- Wang, X.; Xu, Q.; Zhang, J.; Liu, F. Simulating underwater electric field signal of ship using the boundary element method. Prog. Electromagn. Res. M 2018, 76, 43–54. [Google Scholar] [CrossRef] [Green Version]
- Kalovelonis, D.T.; Rodopoulos, D.C.; Gortsas, T.V.; Polyzos, D.; Tsinopoulos, S.V. Cathodic Protection of a Container Ship Using A Detailed BEM Model. J. Mar. Sci. Eng. 2020, 8, 359. [Google Scholar] [CrossRef]
- Jiang, R.; Zhang, J.; Chen, X. Ship’s shaft-related electric field mechanism of production and countermeasure technology. J. Natl. Univ. Def. Technol. 2019, 41, 111–117. [Google Scholar]
- Pena, B.; Huang, L. A review on the turbulence modelling strategy for ship hydrodynamic simulations. Ocean Eng. 2021, 241, 110082. [Google Scholar] [CrossRef]
- Xu, Q.; Wang, X.; Xu, C. Frumkin correction of corrosion electric field generated by 921A-B10 galvanic couple. J. Electroanal. Chem. 2019, 855, 113599. [Google Scholar] [CrossRef]
- Liu, D.; Zhang, J.; Wang, X. Influence of environmental factors on corrosive electrostatic field under laminar current. ACTA Armamentarii 2020, 41, 567–576. [Google Scholar]



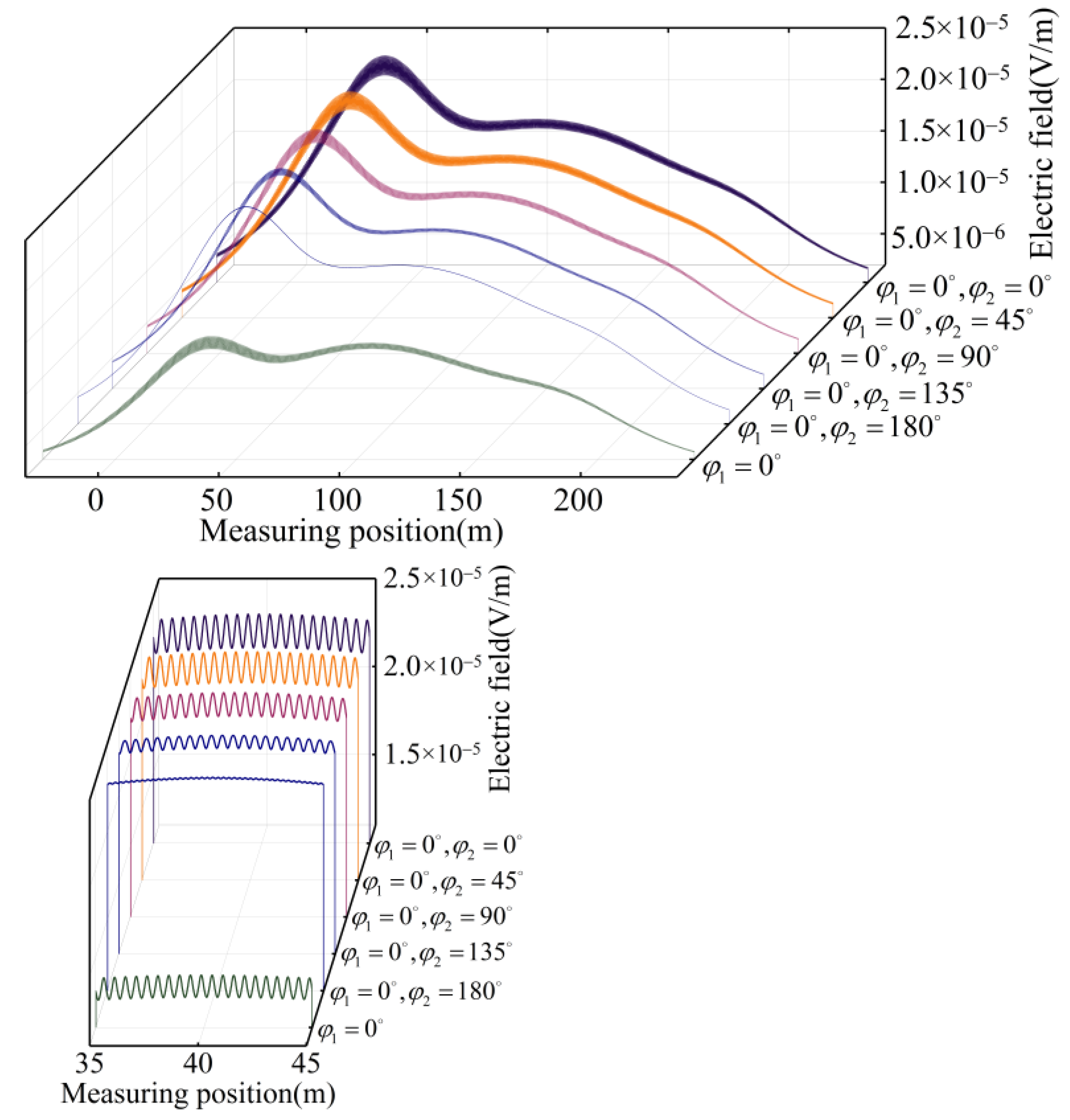
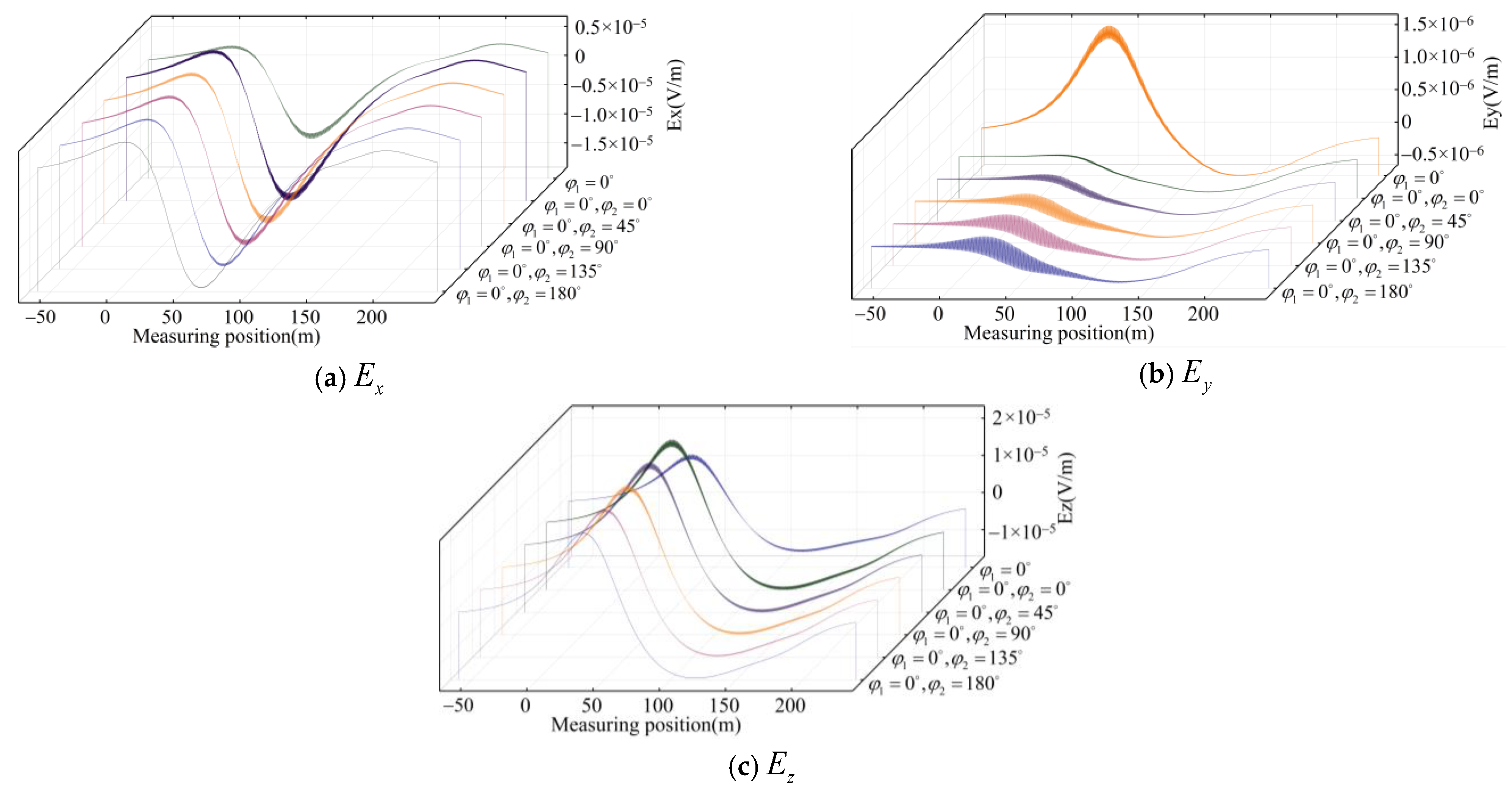


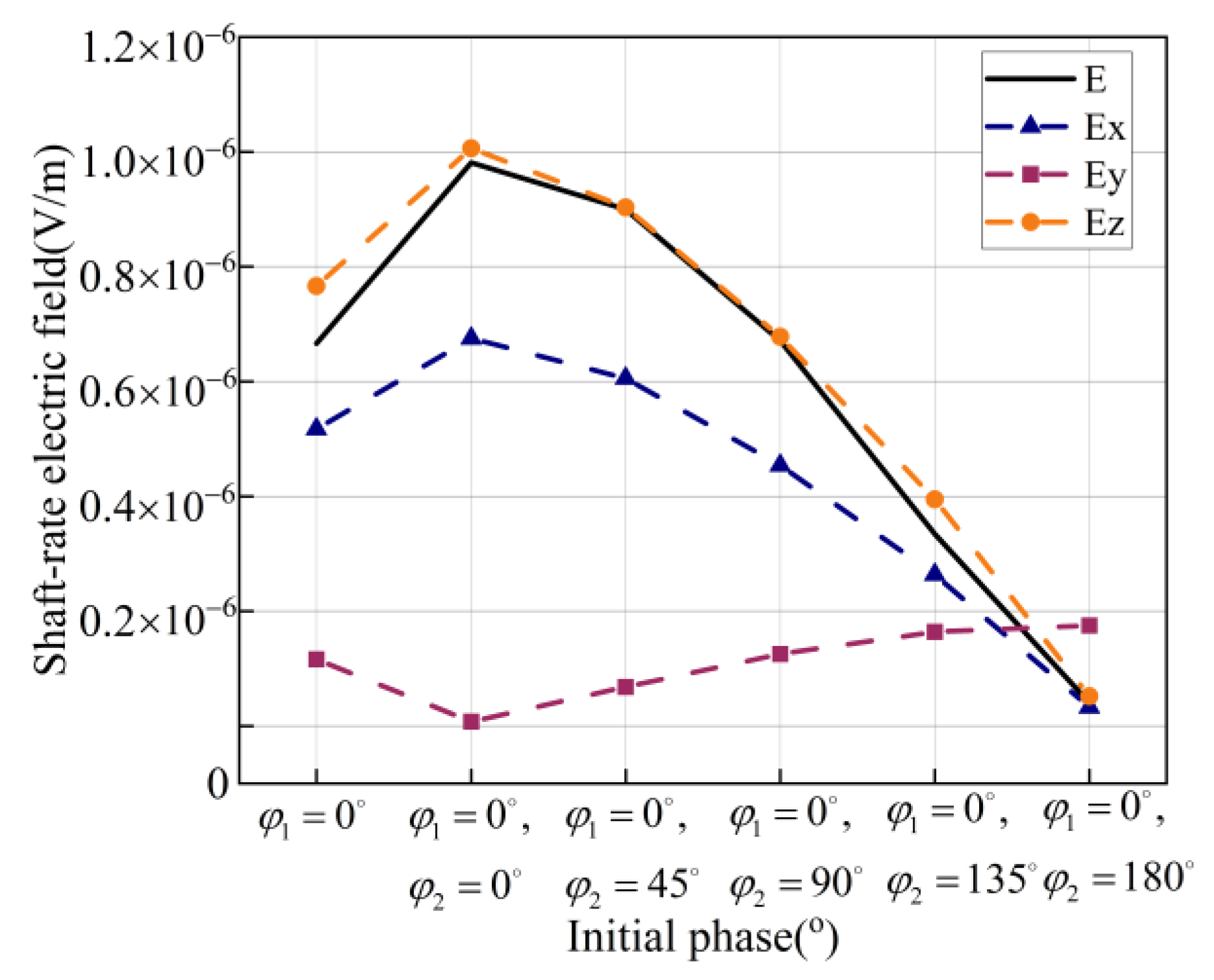

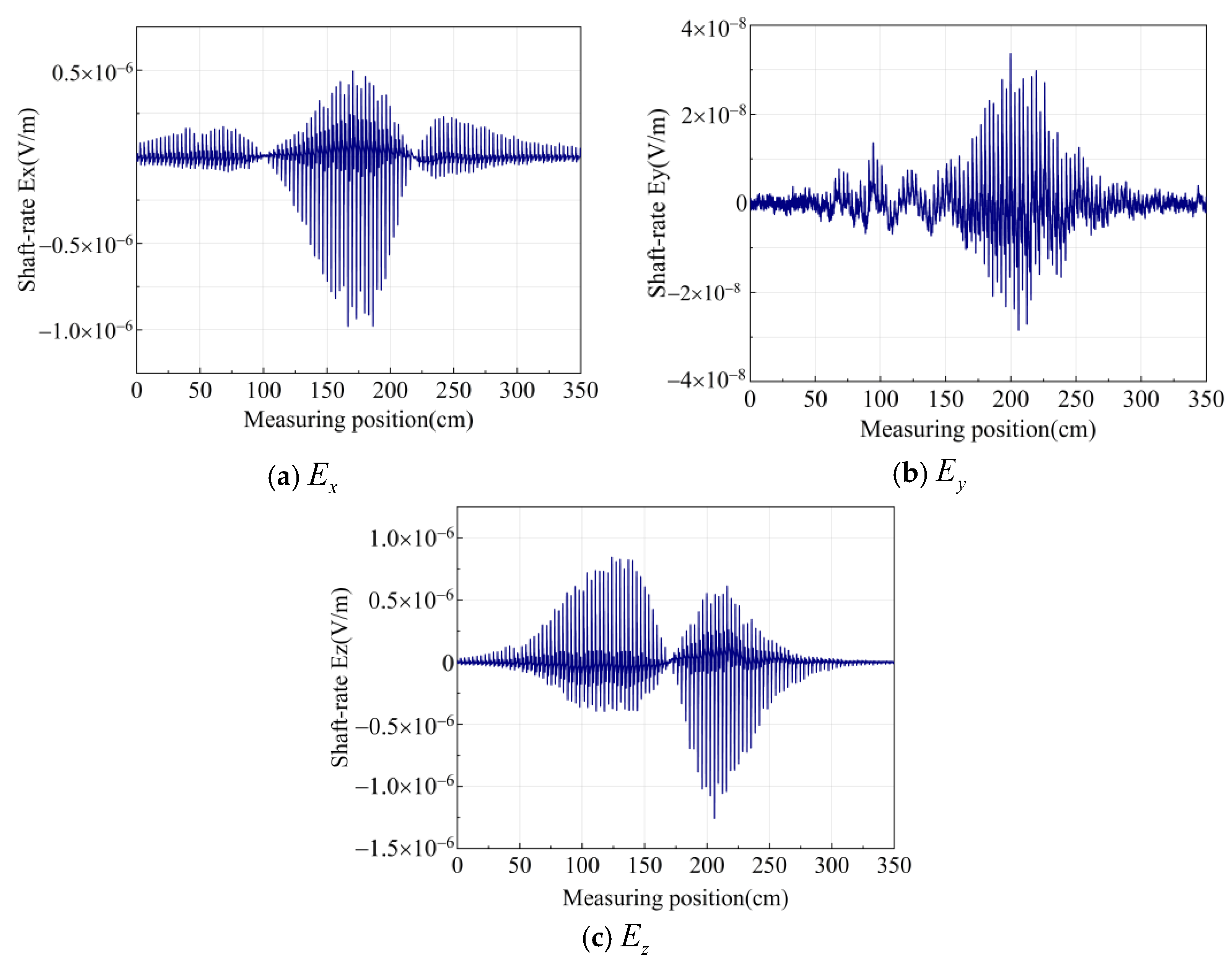

| Initial Phase φ | φ1 = 0° φ2 = 0° | φ1 = 0° φ2 = 45° | φ1 = 0° φ2 = 90° | φ1 = 0° φ2 = 135° | φ1 = 0° φ2 = 180° | φ1 = 0° |
|---|---|---|---|---|---|---|
| Initial Phase φ | φ1 = 0° φ2 = 0° | φ1 = 0° φ2 = 45° | φ1 = 0° φ2 = 90° | φ1 = 0° φ2 = 135° | φ1 = 0° φ2 = 180° | φ1 = 0° |
|---|---|---|---|---|---|---|
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Wang, S.; Hu, Y.; Tong, Y. Mixed Electric Field of Multi-Shaft Ship Based on Oxygen Mass Transfer Process under Turbulent Conditions. Electronics 2022, 11, 3684. https://doi.org/10.3390/electronics11223684
Wang X, Wang S, Hu Y, Tong Y. Mixed Electric Field of Multi-Shaft Ship Based on Oxygen Mass Transfer Process under Turbulent Conditions. Electronics. 2022; 11(22):3684. https://doi.org/10.3390/electronics11223684
Chicago/Turabian StyleWang, Xiangjun, Shichuan Wang, Yucheng Hu, and Yude Tong. 2022. "Mixed Electric Field of Multi-Shaft Ship Based on Oxygen Mass Transfer Process under Turbulent Conditions" Electronics 11, no. 22: 3684. https://doi.org/10.3390/electronics11223684




