GR(1)-Guided Deep Reinforcement Learning for Multi-Task Motion Planning under a Stochastic Environment
Abstract
1. Introduction
2. Related Work
3. Preliminaries
- iff ;
- iff ;
- iff and ;
- iff or ;
- iff or ;
- iff ;
- iff ;
- iff .
3.1. GR(1) Synthesis
- : a temporal formula characterizing the initial state;
- : the conjunction of LTL formulas that denote the system invariants, where is a temporal formula;
- : the conjunction of LTL formulas that denote the liveness goals, where is a temporal formula.
3.2. Deep Reinforcement Learning with Reward Shaping
3.2.1. Deep Q-Network
3.2.2. Double Deep Q-Network
3.2.3. Dueling Double Deep Q-Network
3.2.4. Reward Shaping
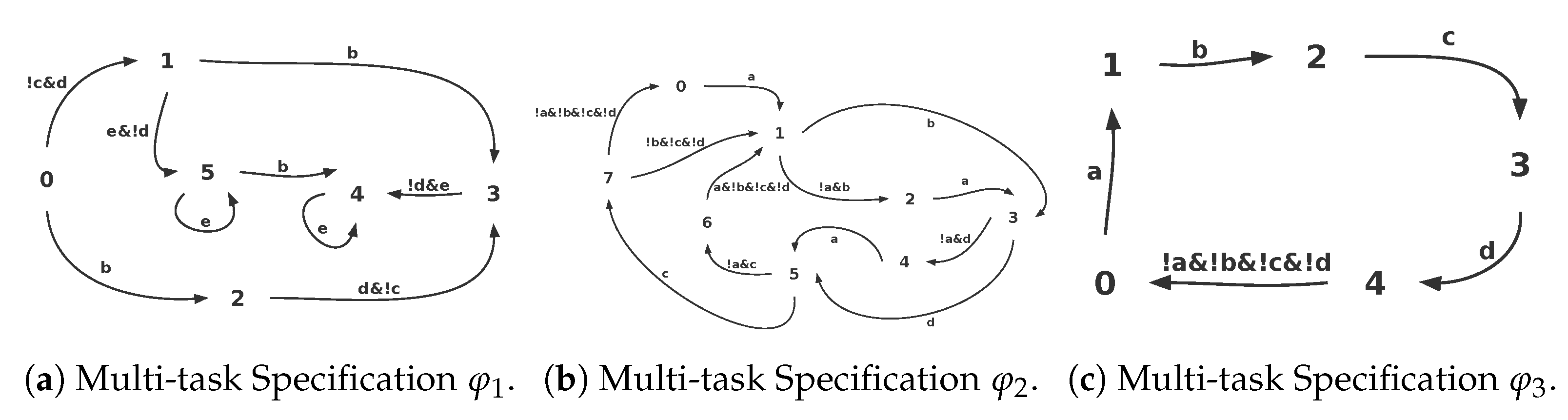
4. Multi-Task Deep Reinforcement Learning with Generalized Reactivity Specifications
- should reach a if it has not reached a;
- should reach b only when has reached a and perform the collecting task;
- should not reach c and d if has not reached a;
- should not reach simultaneously.
- should reach a infinitely often;
- should reach infinitely often if has reached location a infinitely often.

4.1. Framework
4.2. Integrating Deep Reinforcement Learning with the GR(1) Strategy
| Algorithm 1: Dueling Double Deep Q-Network on synthesized from GR(1) formula. |
 |
4.3. Topological-Sort-Based Reward Shaping
| Algorithm 2: Topological-sort-Based Reward-Shaping Algorithm. |
 |
5. Experimental Section
5.1. Experiment Setup
- Different GR(1) specifications under the same environment;
- Different environments under the same GR(1) specification.
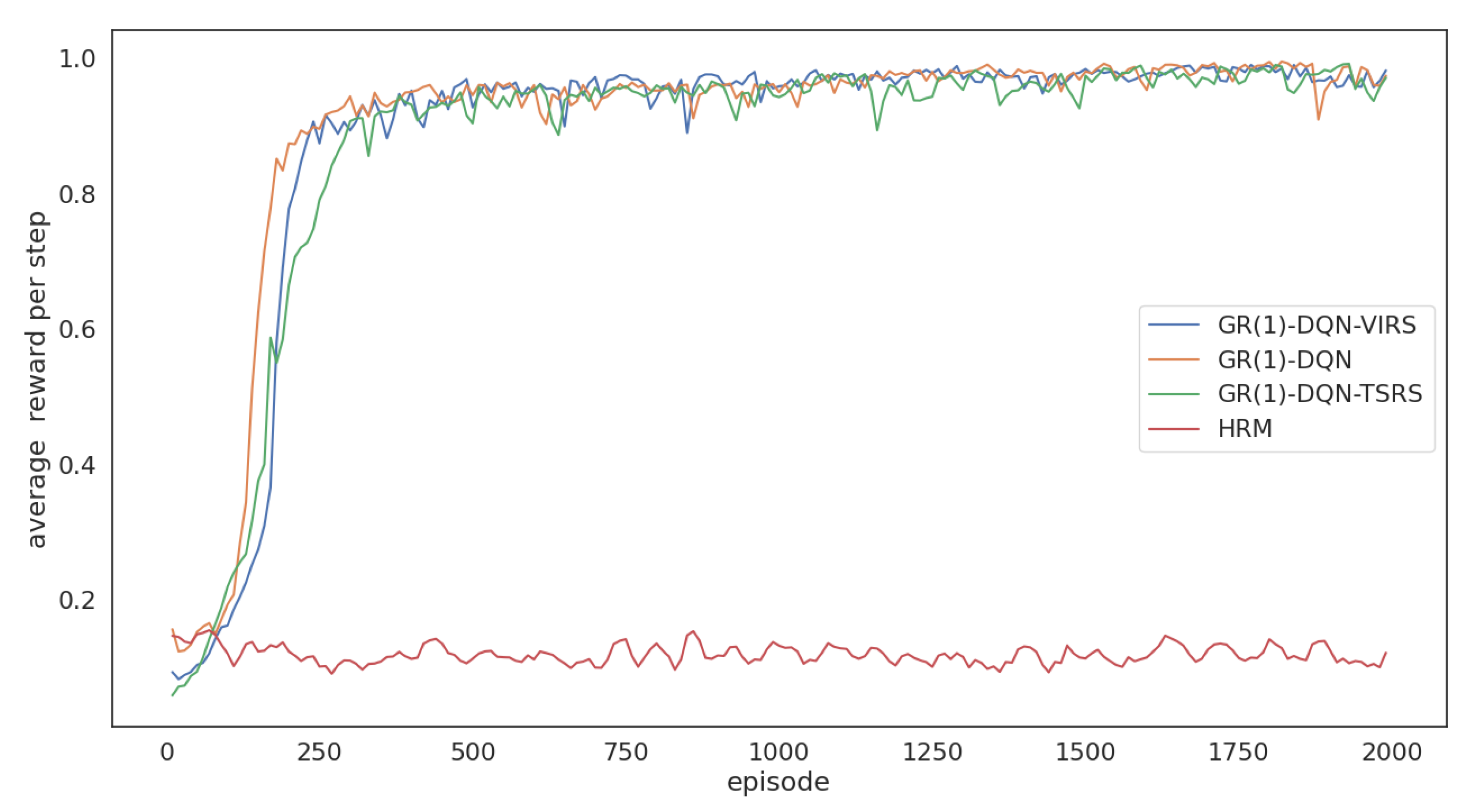
5.2. Performance Evaluation under Different GR(1) Specifications
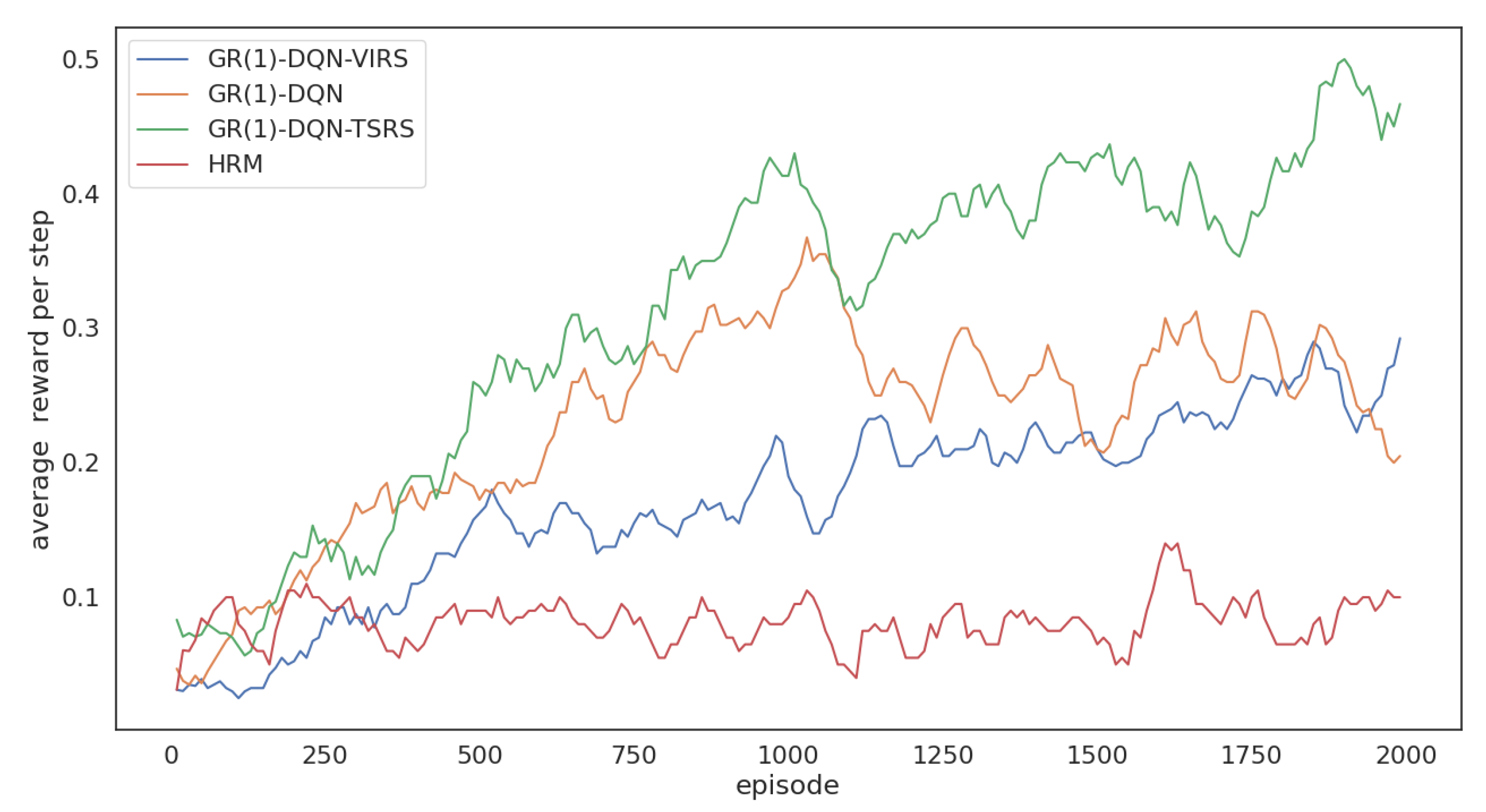
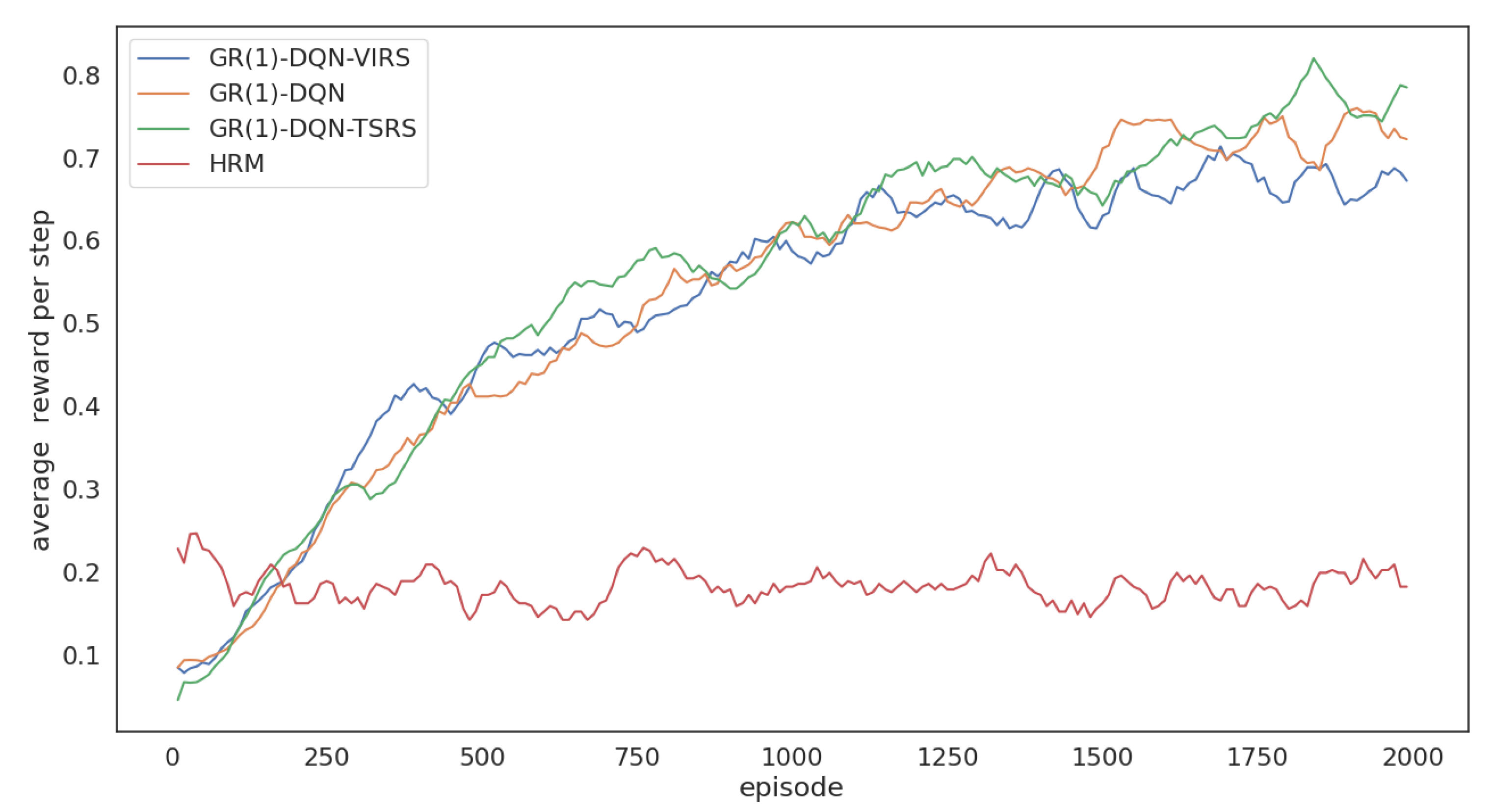
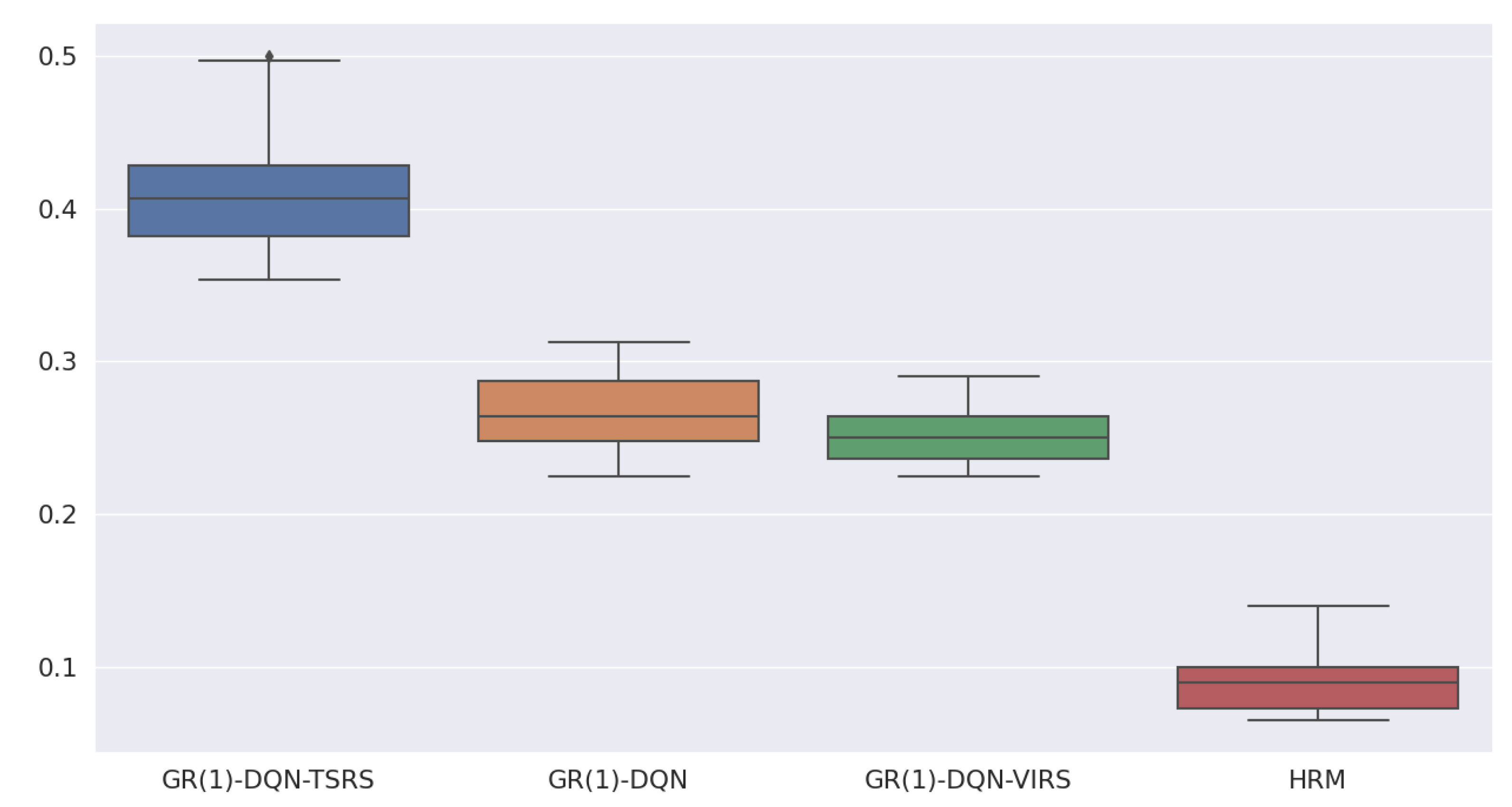
5.3. Ablation Study under Different Environment Settings
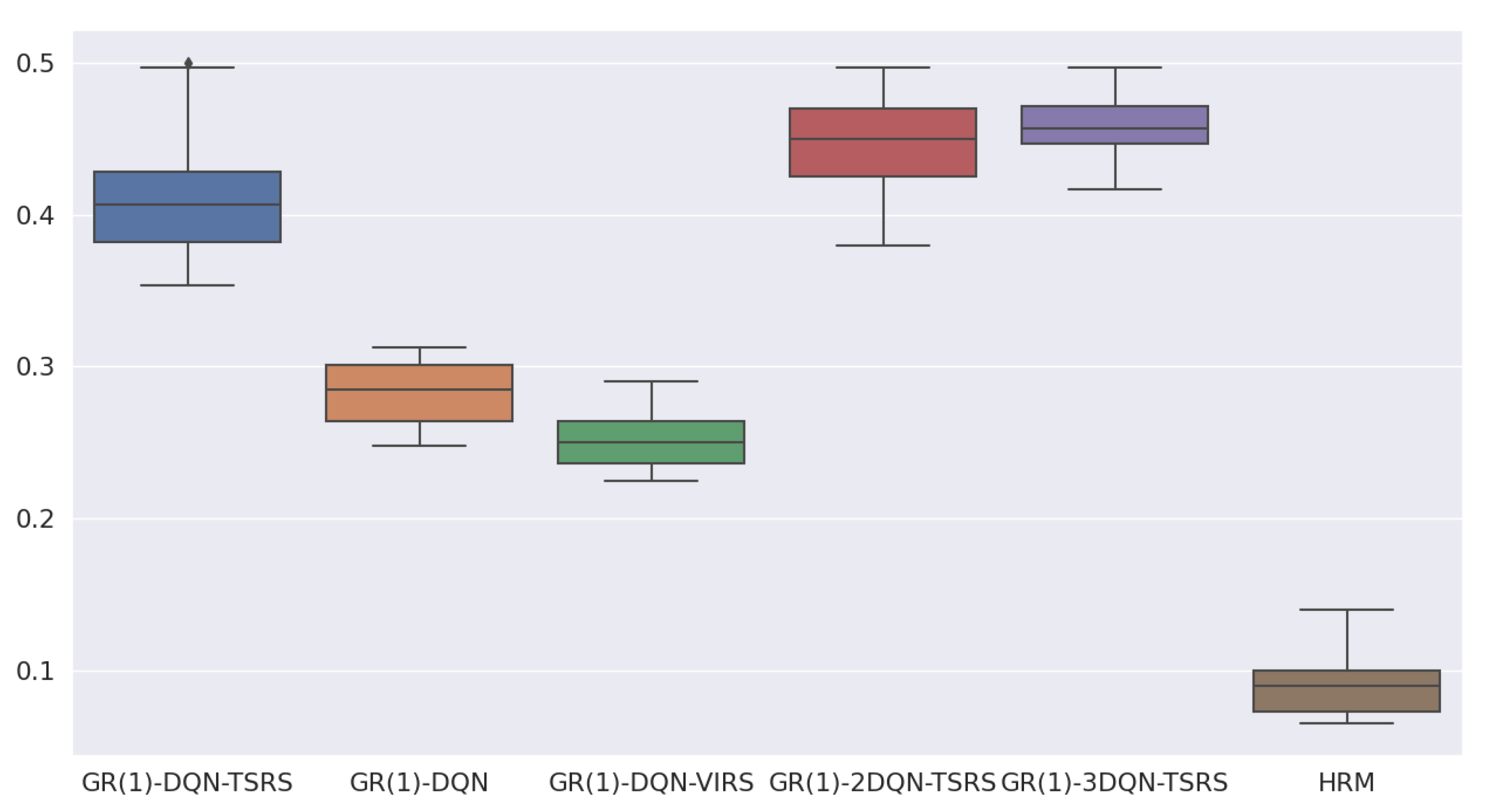
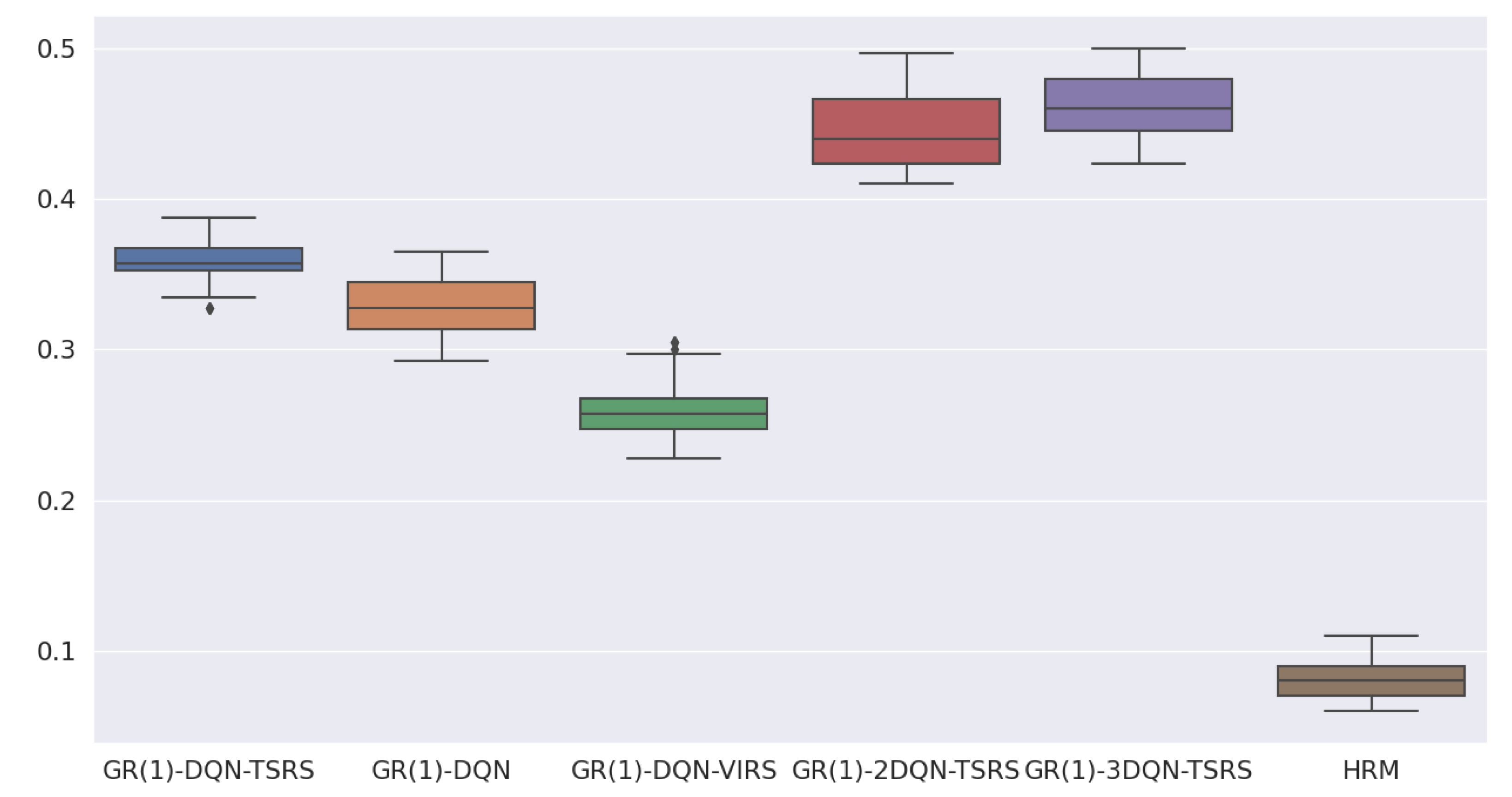
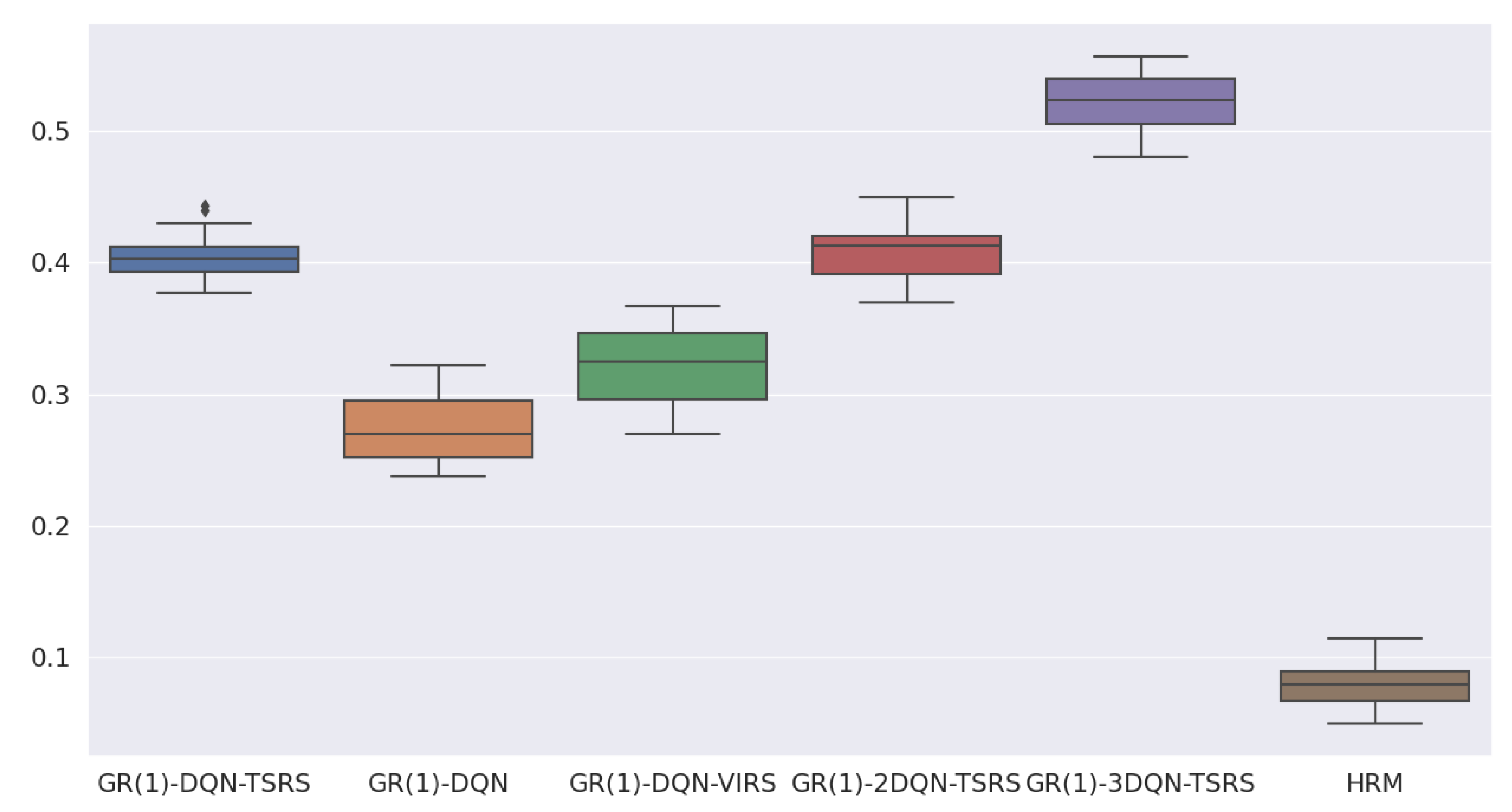
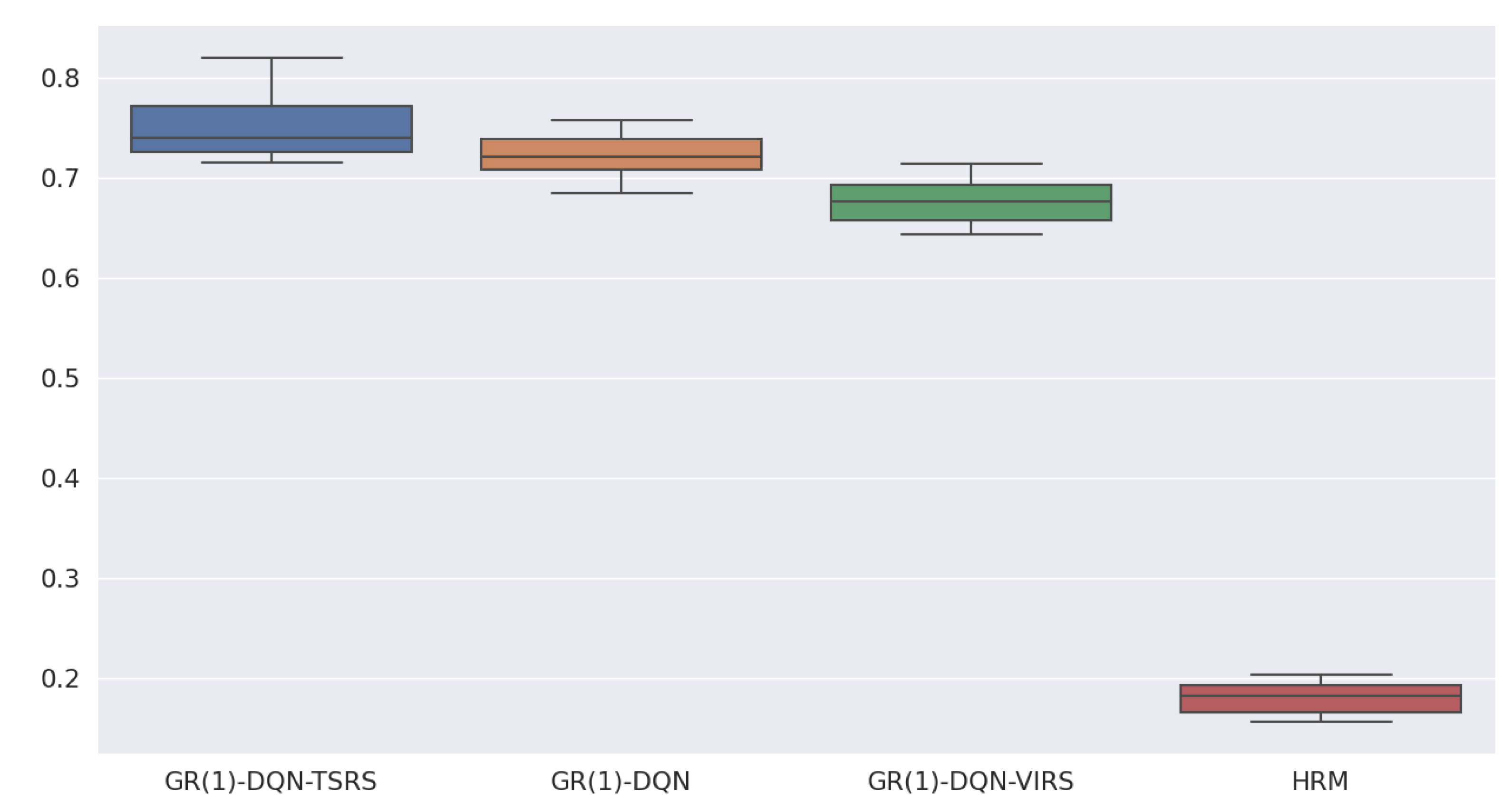
- HRM obtains the lowest reward compared with the other five algorithms;
- GR(1)-DQN and GR(1)-DQN-VIRS have similar performances, but their reward per step is smaller than the topological-sort-based reward-shaping approaches;
- It is evident that topological-sort-based reward shaping could help GR(1)-DQN obtain more rewards during training;
- Overall GR(1)-2DQN-TSRS is better than GR(1)-DQN-TSRS, and GR(1)-3DQN-TSRS is better than GR(1)-2DQN-TSRS.



6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| DRL | Deep Reinforcement Learning |
| LTL | Linear Temporal Logic |
| GR(1) | Generalized Reactivity of rank 1 |
| DCG | Directed Cyclic Graphs |
| DAG | Directed Acyclic Graphs |
| 3DQN | Dueling Double Deep Q-Network |
| 2DQN | Double Deep Q-Network |
| DQN | Deep Q-Network |
| RL | Reinforcement Learning |
| PBRM | Potential-Based Reward Machine |
| PBRS | Potential-based Reward Shaping |
| SCC | Strongly Connected Components |
| LDBA | Limit-Deterministic Büchi Automata |
| DFA | Deterministic Finite Automata |
References
- Kulkarni, T.D.; Narasimhan, K.; Saeedi, A.; Tenenbaum, J. Hierarchical deep reinforcement learning: Integrating temporal abstraction and intrinsic motivation. Adv. Neural Inf. Process. Syst. 2016, 29, 1–11. [Google Scholar]
- Toro Icarte, R.; Klassen, T.Q.; Valenzano, R.; McIlraith, S.A. Teaching multiple tasks to an RL agent using LTL. In Proceedings of the 17th International Conference on Autonomous Agents and MultiAgent Systems(AAMAS), Stockholm, Sweden, 10–15 July 2018; pp. 452–461. [Google Scholar]
- Icarte, R.T.; Klassen, T.Q.; Valenzano, R.; McIlraith, S.A. Reward machines: Exploiting reward function structure in reinforcement learning. J. Artif. Intell. Res. 2022, 73, 173–208. [Google Scholar] [CrossRef]
- Pnueli, A.; Rosner, R. On the synthesis of a reactive module. In Proceedings of the 16th ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages, Austin, TX, USA, 11–13 January 1989; pp. 179–190. [Google Scholar]
- Kress-Gazit, H.; Fainekos, G.E.; Pappas, G.J. Temporal-logic-based reactive mission and motion planning. IEEE Trans. Robot. 2009, 25, 1370–1381. [Google Scholar] [CrossRef]
- Li, R.; Shi, H.; Liu, W.; Dong, W. Synthesizing Cooperative Controllers from Global Tasks of Multi-robot Systems. In Proceedings of the 2020 IEEE 27th Asia-Pacific Software Engineering Conference (APSEC), Singapore, 1–4 December 2020; pp. 109–118. [Google Scholar]
- Wang, C.; Li, Y.; Smith, S.L.; Liu, J. Continuous motion planning with temporal logic specifications using deep neural networks. arXiv 2020, arXiv:2004.02610. [Google Scholar]
- Li, X.; Serlin, Z.; Yang, G.; Belta, C. A formal methods approach to interpretable reinforcement learning for robotic planning. Sci. Robot. 2019, 4, eaay6276. [Google Scholar] [CrossRef] [PubMed]
- Fu, J.; Topcu, U. Probably approximately correct MDP learning and control with temporal logic constraints. arXiv 2014, arXiv:1404.7073. [Google Scholar]
- Jothimurugan, K.; Bansal, S.; Bastani, O.; Alur, R. Compositional reinforcement learning from logical specifications. Adv. Neural Inf. Process. Syst. 2021, 34, 10026–10039. [Google Scholar]
- Li, X.; Vasile, C.I.; Belta, C. Reinforcement learning with temporal logic rewards. In Proceedings of the IEEE 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; pp. 3834–3839. [Google Scholar]
- Bozkurt, A.K.; Wang, Y.; Zavlanos, M.M.; Pajic, M. Model-free reinforcement learning for stochastic games with linear temporal logic objectives. In Proceedings of the IEEE 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; pp. 10649–10655. [Google Scholar]
- Kantaros, Y.; Zavlanos, M.M. Stylus*: A temporal logic optimal control synthesis algorithm for large-scale multi-robot systems. Int. J. Robot. Res. 2020, 39, 812–836. [Google Scholar] [CrossRef]
- De Giacomo, G.; Iocchi, L.; Favorito, M.; Patrizi, F. Foundations for restraining bolts: Reinforcement learning with LTLf/LDLf restraining specifications. In Proceedings of the International Conference on Automated Planning and Scheduling(ICAPS), Berkeley, CA, USA, 10–15 July 2019; Volume 29, pp. 128–136. [Google Scholar]
- Wen, M. Reinforcement Learning With High-Level Task Specifications. Ph.D. Thesis, University of Pennsylvania, Philadelphia, PA, USA, 2019. [Google Scholar]
- Bozkurt, A.K.; Wang, Y.; Zavlanos, M.M.; Pajic, M. Control synthesis from linear temporal logic specifications using model-free reinforcement learning. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; pp. 10349–10355. [Google Scholar]
- Hasanbeig, M.; Abate, A.; Kroening, D. Certified reinforcement learning with logic guidance. arXiv 2019, arXiv:1902.00778. [Google Scholar]
- Icarte, R.T.; Klassen, T.; Valenzano, R.; McIlraith, S. Using reward machines for high-level task specification and decomposition in reinforcement learning. In Proceedings of the International Conference on Machine Learning (ICML), PMLR, Stockholm, Sweden, 10–15 July 2018; pp. 2107–2116. [Google Scholar]
- Camacho, A.; Toro Icarte, R.; Klassen, T.Q.; Valenzano, R.; McIlraith, S.A. LTL and Beyond: Formal Languages for Reward Function Specification in Reinforcement Learning. In Proceedings of the Twenty-Eighth International Joint Conference on Artificial Intelligence (IJCAI), Macao, China, 10–16 August 2019; pp. 6065–6073. [Google Scholar]
- Pnueli, A. The temporal logic of programs. In Proceedings of the IEEE 18th Annual Symposium on Foundations of Computer Science (sfcs 1977), Providence, RI, USA, 31 October–2 November 1977; pp. 46–57. [Google Scholar] [CrossRef]
- Piterman, N.; Pnueli, A.; Sa’ar, Y. Synthesis of reactive (1) designs. In Proceedings of the International Workshop on Verification, Model Checking, and Abstract Interpretation; Springer: Berlin/Heidelberg, Germany, 2006; pp. 364–380. [Google Scholar]
- Kaelbling, L.P.; Littman, M.L.; Moore, A.W. Reinforcement learning: A survey. J. Artif. Intell. Res. 1996, 4, 237–285. [Google Scholar] [CrossRef]
- Watkins, C.J.; Dayan, P. Q-learning. Mach. Learn. 1992, 8, 279–292. [Google Scholar] [CrossRef]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Graves, A.; Antonoglou, I.; Wierstra, D.; Riedmiller, M. Playing atari with deep reinforcement learning. arXiv 2013, arXiv:1312.5602. [Google Scholar]
- Thrun, S.; Schwartz, A. Issues in using function approximation for reinforcement learning. In Proceedings of the 1993 Connectionist Models Summer School; Lawrence Erlbaum: Hillsdale, NJ, USA, 1993; Volume 6, pp. 1–9. [Google Scholar]
- Van Hasselt, H.; Guez, A.; Silver, D. Deep reinforcement learning with double q-learning. In Proceedings of the AAAI conference on Artificial Intelligence, Phoenix, AZ, USA, 12–17 February 2016; Volume 30. [Google Scholar]
- Wang, Z.; Schaul, T.; Hessel, M.; Hasselt, H.; Lanctot, M.; Freitas, N. Dueling network architectures for deep reinforcement learning. In Proceedings of the International Conference on Machine Learning, PMLR, New York, NY, USA, 20–22 June 2016; pp. 1995–2003. [Google Scholar]
- Hu, Y.; Wang, W.; Jia, H.; Wang, Y.; Chen, Y.; Hao, J.; Wu, F.; Fan, C. Learning to utilize shaping rewards: A new approach of reward shaping. Adv. Neural Inf. Process. Syst. 2020, 33, 15931–15941. [Google Scholar]
- Livingston, S. GR1C: A collection of Tools for GR(1) Synthesis and Related Activities. Github. Available online: https://scottman.net/2012/gr1c (accessed on 26 October 2022).
- Ng, A.Y.; Harada, D.; Russell, S. Policy invariance under reward transformations: Theory and application to reward shaping. In Proceedings of the Sixteenth International Conference on Machine Learning, Bled, Slovenia, 27–30 June 1999; Volume 99, pp. 278–287. [Google Scholar]
- Brockman, G.; Cheung, V.; Pettersson, L.; Schneider, J.; Schulman, J.; Tang, J.; Zaremba, W. Openai gym. arXiv 2016, arXiv:1606.01540. [Google Scholar]



| Hyper-Parameter | Definition | Value |
|---|---|---|
| replay buffer size | 50,000 | |
| number of layers | 4 | |
| activation function | Relu | |
| batch size | 32 | |
| target network update frequency | 100 | |
| number of steps per episode | 1000 | |
| total number of episodes | 2000 |
| HRM | GR(1)-DQN | GR(1)-DQN-VIRS | GR(1)-DQN-TSRS | ||
|---|---|---|---|---|---|
| mean | 0.126 | 0.982 | 0.981 | 0.974 | |
| std | 0.0001 | 0.0003 | 0.0001 | 0.0001 | |
| max | 0.148 | 0.996 | 0.991 | 0.991 | |
| mean | 0.092 | 0.284 | 0.251 | 0.411 | |
| std | 0.0005 | 0.0004 | 0.0003 | 0.0017 | |
| max | 0.140 | 0.313 | 0.290 | 0.500 | |
| mean | 0.181 | 0.722 | 0.676 | 0.752 | |
| std | 0.0002 | 0.0004 | 0.0004 | 0.0009 | |
| max | 0.203 | 0.756 | 0.714 | 0.820 |
| HRM | GR(1) -DQN | GR(1) -DQN -VIRS | GR(1) -DQN -TSRS | GR(1) -2DQN -TSRS | GR(1) -3DQN -TSRS | ||
|---|---|---|---|---|---|---|---|
| mean | 0.091 | 0.248 | 0.251 | 0.411 | 0.450 | 0.458 | |
| M1 | std | 0.0005 | 0.0004 | 0.0003 | 0.0017 | 0.0010 | 0.0004 |
| max | 0.140 | 0.313 | 0.290 | 0.500 | 0.497 | 0.497 | |
| mean | 0.082 | 0.328 | 0.261 | 0.358 | 0.445 | 0.461 | |
| M2 | std | 0.0002 | 0.0004 | 0.0004 | 0.0002 | 0.0006 | 0.0005 |
| max | 0.110 | 0.365 | 0.305 | 0.388 | 0.497 | 0.500 | |
| mean | 0.080 | 0.270 | 0.320 | 0.404 | 0.408 | 0.522 | |
| M3 | std | 0.0002 | 0.0006 | 0.0008 | 0.0003 | 0.0004 | 0.0004 |
| max | 0.115 | 0.323 | 0.368 | 0.443 | 0.450 | 0.557 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, C.; Cai, Y.; Zhu, J.; Hu, C.; Bi, J. GR(1)-Guided Deep Reinforcement Learning for Multi-Task Motion Planning under a Stochastic Environment. Electronics 2022, 11, 3716. https://doi.org/10.3390/electronics11223716
Zhu C, Cai Y, Zhu J, Hu C, Bi J. GR(1)-Guided Deep Reinforcement Learning for Multi-Task Motion Planning under a Stochastic Environment. Electronics. 2022; 11(22):3716. https://doi.org/10.3390/electronics11223716
Chicago/Turabian StyleZhu, Chenyang, Yujie Cai, Jinyu Zhu, Can Hu, and Jia Bi. 2022. "GR(1)-Guided Deep Reinforcement Learning for Multi-Task Motion Planning under a Stochastic Environment" Electronics 11, no. 22: 3716. https://doi.org/10.3390/electronics11223716
APA StyleZhu, C., Cai, Y., Zhu, J., Hu, C., & Bi, J. (2022). GR(1)-Guided Deep Reinforcement Learning for Multi-Task Motion Planning under a Stochastic Environment. Electronics, 11(22), 3716. https://doi.org/10.3390/electronics11223716






